FQ2
人教版高中物理必修三第9章库仑定律

3.实验结论 1
(1)力 F 与距离 r 的二次方成反___比_,F∝_r2_。 (42.)力库F仑与定电律荷表量达q式1 和:Fq2=的_k乘_qr1_q积2_2,成其_正_中_比_静,电F∝力_常_q_量1_q_2k_=___9。_.0__×__1_09
N·m2/C2。
栏目导航
三、静电力计算
(3)点电荷是一个带有电荷的点,它是实际带电体的抽象,是一
种理想化模型。
(√ )
(4)
(5)很大的带电体也有可能看作点电荷。
(√ )
栏目导航
2.(多选)如图所示,O 是一个带电的物体,若把系在丝线上的带 电小球先后挂在横杆上的 P1、P2、P3 位置,可以比较小球在不同位 置所受带电物体的作用力的大小,这个力的大小可以通过丝线偏离 竖直方向的角度 θ 显示出来(小球与物体 O 在同一水平线上)。若物体 O 的电荷量用 Q 表示,小球的电荷量用 q 表示,物体与小球间距离 用 d 表示,物体和小球之间的作用力大小用 F 表示。则下列对该实 验的判断正确的是( )
栏目导航
自主预习 探新知
栏目导航
一、电荷之间的作用力 1.实验探究 (1)带电小球由于受到带电体对其的作用力而使丝线偏离竖直方 向 θ 角。
栏目导航
(2)在电荷量不变的情况下,小球离带电体越近,角度 θ 越_大_, 离带电体越远,角度 θ 越_小_。
(3)在距离不变的情况下,带电体电荷量越大,角度 θ 越大__,电 荷量越小,角度 θ 越小__。
栏目导航
合作探究 攻重难
栏目导航
对点电荷的理解
1.点电荷是物理模型 只有电荷量,没有大小、形状的理想化模型,类似于力学中的 质点,实际中并不存在。
漏电保护(安全用电)

欠压功能
(2) 组合型漏电保护装置(漏电保护继电 器 )。它是一种由漏电继电器和主开关通
过电气连接组合而成的漏电保护装置。当发 生触电、漏电故障时,由漏电继电器进行信 号检测、处理和比较,通过其脱扣器或继电 器动作,发出报警信号;也可通过控制触点
(2) 电子式漏电保护装置。其中间环节使用 了由电子元件构成的电子电路,有的是分立 元件电路,也有的是集成电路。中间环节的
电子电路用来对漏电信号进行放大、处理和
比较。其特点是灵敏度高、动作电流和动作
时间调整方便、使用耐久。但电子式漏电保 护装置对使用条件要求严格,抗电磁干扰性 能差,当主电路缺相时,可能会失去辅助电 源而丧失保护功能。
按照主开关的极数和穿过零序电流互感器的 线数可将漏电保护装置分为:单极二线漏电 保护装置、二极漏电保护装置、二极三线漏 电保护装置、三极漏电保护装置、三极四线 漏电保护装置和四极漏电保护装置。其中单 极二线漏电保护装置、二极三线漏电保护装 置、三 极四线漏电保护装置均有一根直接
结论:不同分支回路工作零 线接错引起漏电保护器误动
案例2:某商场采用三相四线制供电,负荷主要为FI光灯及 风扇。因电源箱离商场较远, 电工图省事采用不同回路同 一塑料线槽布线。两回路各用I台漏电保护开关(DZ47L-16/ 2)进行短路及漏电保护安装完毕后, 当给其中一路送电后 正常,再给另一回路送电时,前一路漏电保护器跳闸 试验 几次结果都一样。把两路的负荷关闭,结果一样。
结论:两相不同回路同装于一塑料线槽引起漏电保 护器动作
案例3:某安装公司在安装一工棚(支架采用金 属角钢结构并铺上彩色钢板作为棚顶)时,顶 棚需用电钻打孔。由于手电钻电源线长度不 够而采用一段塑料胶质线加长。塑料胶质线 直接与插头连接, 连接处用电胶布包扎好。 作业完毕后,在电钻F放至地面过程中,由于 电钻自身重量而将接头处导线拽出并裸露, 1 名作业人员因手握导线裸露部分而触电身亡。
建筑人防工程的结构设计

浅谈建筑人防工程的结构设计【摘要】:简述了人防工程的概念,从平面布置、构件计算、构造要求三方面对人防工程的结构设计进行了系统的阐述,并总结了整个人防工程结构设计的方法和过程,以期对人防工程结构设计工作带来方便。
【关键词】:人防工程,结构设计,防护单元中图分类号:k826.16 文献标识码:a 文章编号:近些年,随着我国国民经济的迅猛发展,建筑行业也呈现出前所未有的繁荣景象,但是建筑的大量兴建同时也带来了各级城市土地贫乏的缺陷,所以高层建筑和地下建筑已成为必然的发展趋势。
按照建筑行业规范要求,高层建筑必须设计地下室,有地下室就不可避免的需要设计人防工程,同时地下建筑更是需要人防工程,所以人防工程越来越重要。
1.人防工程的简述人防工程是指人民防空地下室工程,其设计等级分两类:甲类和乙类。
甲类人防设计是要满足战时对核武器、常规武器、生化武器的防护要求,乙类人防设计是要满足战时对常规武器和生化武器的防护要求,为此我们通常设计中都是定义为“甲类核n常n级”和“乙类常n级”,这样同时注明了人防工程的设计等级和抗力等级。
人防的抗力等级有甲类核4,4b,5,6,6b级和乙类常5,6级。
人防工程的设计可以分为专业人防设计和普通人防设计,专业人防设计主要是指挥工程、中心医院、防空专业队掩蔽所,普通人防设计主要是指人员掩蔽所和人防物资库,专业人防设计由人防办专业设计,我们通常说的人防工程设计都是指普通人防设计。
根据人防面积的大小可将建筑地下室划分为人防区和非人防区,人防区又可按规范划分为多个防护单元,防护单元再分为多个抗爆单元。
人防区又分为染毒区和清洁区,清洁区是满足防毒要求的区域,染毒区是允许染毒的区域,如防毒通道、密闭通道、洗消间、简易洗消间、滤毒室、除尘室、扩散室,清洁区和染毒区间有防毒要求,染毒区和非人防区间有防毒和抗力要求。
2.人防工程的结构设计人防工程的建筑设计主要是总体方案的合理设计,包括人防分区的合理划分和人防口部的合理布置,灵活性比较大,而人防结构设计则灵活性较小,关键是计算准确、构造合理,是人防工程设计中的主要计算部分。
湖北汽车工业学院数字电子技术第二章习题答案

湖北汽车工业学院数字电子技术第二章习题答案1. JK触发器在CP作用下,若状态必须发生翻转,则J、 K的状态为()。
[单选题] *A J=K=0B J=K=1(正确答案)C J=0,K=1D A.J=1,K=02. 在 CP 脉冲作用下,只具有置 0 、置1功能的触发器是()触发器。
[单选题] *A JK 触发器B T 触发器C D触发器(正确答案)D RS 触发器3. 欲使D触发器按工作,应使输入D =()。
[单选题] *A 0B 1C QD /Q(正确答案)4.从74LS74的功能表中可以解读,该触发器的触发方式是()。
[单选题] *A 边沿触发(正确答案)B 电平触发5. 基本RS触发器的特性方程,它的约束条件为。
[单选题] *ABC(正确答案)D6. 触发器输出端有两个稳定状态,即0态和1态。
[单选题] *A) 正确(正确答案)B) 错误7.电路输入频率1KHZ,幅度为5V的方波信号。
Q2 输出波形的频率()。
[单选题] *A 1KHZB 500HZC 250HZ(正确答案)8. 在 CP脉冲作用下,只具有保持和翻转功能的触发器是()触发器。
[单选题] *A JK 触发器B T 触发器(正确答案)C T/触发器D RS 触发器9. T触发器,在T=1时,加上时钟脉冲,则触发器()。
[单选题] *A 保持原态B 置0C 置1D 翻转(正确答案)10. 为实现将JK触发器转换为D触发器,应使()。
[单选题] *A J=D,K=/D(正确答案)B J=/D,K=DC J=K=DD J=K=/D11. 满足特征方程的触发器称为()。
[单选题] *A D触发器B JK触发器C T/触发器(正确答案)D T触发器电路输入频率1KHZ,幅度为5V的方波信号。
Q1 、Q2输出什么波形()。
[单选题] *A 方波(正确答案)B 三角波C 正弦波13. 为实现将JK触发器转换为D触发器,应使()。
水平垂直弯头支墩计算书解析
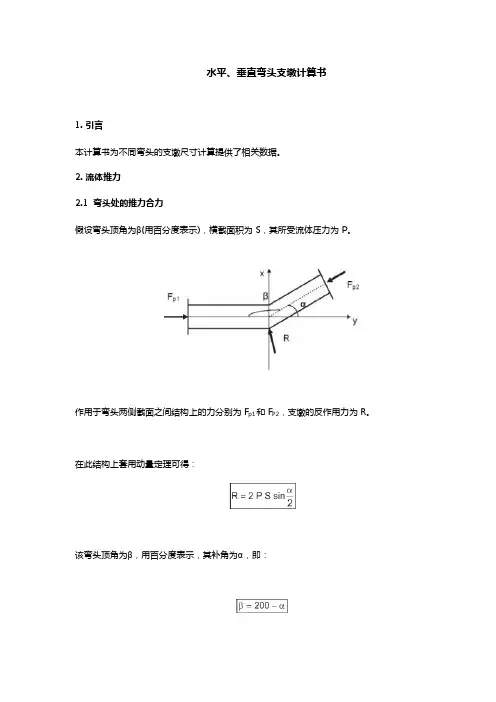
水平、垂直弯头支墩计算书1.引言本计算书为不同弯头的支墩尺寸计算提供了相关数据。
2.流体推力2.1 弯头处的推力合力假设弯头顶角为β(用百分度表示),横截面积为S,其所受流体压力为P。
作用于弯头两侧截面之间结构上的力分别为F p1和F P2,支墩的反作用力为R。
在此结构上套用动量定理可得:该弯头顶角为β,用百分度表示,其补角为α,即:合力R由次可得:2.2 管道的压力流体推力随管道压力而发生变化,此压力存在一个正常值,即为管道的运行压力,用PS表示,此外还有一个较大的值,为管道的试验压力,用PE表示。
管道的试验压力导致最大的流体推力。
3.支墩支墩的形状取决于其所受合力的方向。
当为水平弯头时,合力位于水平方向,我们称该支墩为水平支墩。
当为垂直弯头时,分为两种情况,合力朝上时,我们称该支墩为垂直向上支墩,反之,当合力朝下,我们称之为下部垂直支墩垂直向下支墩。
3.1 水平支墩3.1.1 水平支墩的一般形状水平支墩的一般形状如下图所示。
支墩之上需要铺设一定厚度的回填料(厚度用h表示)。
3.1.2稳定性的研究支墩稳定性研究类似于挡土墙稳定性的研究,需检查其防滑稳定性、倾覆稳定性和基础稳定性。
根据弯头的位置,关于施工现场土壤力学特性的相关假设可根据地质研究报告确定:比重,内摩擦角,黏附系数Co:●比重= 1,6 t/m3●内摩擦角=30°作用于支墩上的力下图呈现的便是支墩的受力情况:h回填↓超负荷对支墩受力总结如下:●P m为支墩的自重●P r为回填料的重量●F ph为流体推力●F Q1为超负荷支墩作用力●F Q2为与基座内壁相接触的土壤支墩作用力N代表竖直方向上的合力:B代表支墩作用合力:由于超负载而产生且作用在支墩壁中间位置的作用力可按照以下公式进行计算:由与支墩接触的土壤而产生的,且作用于支墩内壁三分之一高度处的作用力:根据两处作用在支墩上的力,可得出支墩系数:由于作用于支墩上的力只能得到近似值,应为此作用力设定一个安全系数,一般情况下该安全系数取1.5. 作用于支墩上的力应除以该安全系数。
(完整word)重点高中自招必备九年级专题24平面几何的定值问题

专题24平面几何的定值问题【阅读与思考】所谓定值问题,是指按照一定条件构成的几何图形,当某些几何元素按一定的规律在确定的范围内变化时,与它有关的元素的量保持不变(或几何元素间的某些几何性质或位置关系不变).几何定值问题的基本特点是:题设条件中都包含着变动元素和固定元素,变动元素是指可变化运动的元素,固定元素也就是“不变量”,有的是明显的,有的是隐含的,在运动变化中始终没有发生变化的元素,也就是我们要探求的定值.解答定值问题的一般步骤是:1.探求定值;2.给出证明.【例题与求解】—^ PA + PC .【例1】如图,已知P为正方形ABCD的外接圆的劣弧AD上任意一点.求证:一后一为定值.PB解题思路:线段的和差倍分考虑截长补短,利用圆的基本性质,证明三角形全等.【例2】如图,AB为。
O的一固定直径,它把。
O分成上、下两个半圆,自上半圆上一点C作弦CD±AB,Z OCD的平分线交。
O于点P,当点C在上半圆(不包括A,B两点)上移动时,点P()A.到CD的距离保持不变B.位置不变C.等分DBD.随C点的移动而移动(济南市中考试题)解题思路:添出圆中相关辅助线,运用圆的基本性质,用排除法得出结论.【例3】如图,定长的弦ST在一个以AB为直径的半圆上滑动,M是ST的中点,P是S对AB作垂线的垂足.求证:不管ST滑到什么位置,Z SPM是一定角.(加拿大数学奥林匹克试题)解题思路:不管ST滑到什么位置,Z SOT的度数是定值.从探寻Z SPM与Z SOT的关系入手.【例4】如图,扇形OAB的半径OA=3,圆心角/AOB=90°.点C是箫上异于A, B的动点,过点C作CD±OA于点D,作CE±OB于点E.连接DE,点G, H在线段DE上,且DG=GH=HE.(1)求证:四边形OGCH是平行四边形;(2)当点C在箫上运动时,在CD, CG, DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3 CH2是定值. (广州市中考试题)解题思路:延长OG交CD于N,利用题中的三等分点、平行四边形和三角形中位线的性质,实现把线段ON转化成线段CH的倍分关系,再以及△ OND为基础,通过勾股定理,使问题得以解决.【例5】如图1,在平面直角坐标系xOy中,点M在x轴的正半轴上,。
6第六章光子照射剂量学.
放射性核素的活度(强度)减少一半时所需 要的时间称为该放射性核素的半衰期(half life time).
二.几何学概念
1.放射源:产生辐射的靶面中心; 2.照射野: 几何学:表示射线束经准直器后垂直通过模体,距源特
定距离(SSD、SAD)处的平面上的投影; 剂量学:在上述特定平面上,在辐射范围内,相对中
4.深度量
在组织某一深度的放射量,实际上应为深度的吸收剂量,是 原射线的吸收量加上组织散射量,根据不同照射条件,用体 模测出。
5.肿瘤量(DT)
在肿瘤深度处的吸收剂量,即各照射方向的原射线 和散射线到达此点的剂量之和。
6.容积量
指某一体积的吸收剂量,此吸收剂量的多少与射线 的质及所照射的体积有关。容积量包含了照射靶区 和射线经过区域内正常组织的剂量,这在考虑放射 损伤和放射防护时有用。
TAR根据放射源能量、深度及照射野面积可以查表得到。 在固定野照射时,由于入射野面积和源皮距是固定不变的,照
射野范围内的任何深度的剂量均可通过某种能量射线的百分深 度量表查得。但当用放射源以肿瘤为中心旋转治疗时,由于人 体体表曲面的不规则和肿瘤不在体内中心部,其源皮距、入射 野面积(A)和皮肤量(或最大参考点剂量)均在不断改变, 只有放射源到肿瘤中心距离(F)和肿瘤水平的面积是固定不变 的,因此不能用计算固定野照射的肿瘤剂量方法来计算旋转治 疗时的肿瘤剂量。必须用组织-空气比(TAR)的方法计算。
11.反向散射因子(BSF)
定义为射野中心轴上最大剂量深度处的组织空气比。 实际上是TAR的一个特例。
BSF=Dm/ Dm空气
12.散射空气比(SAR)
定义为体模内某一点的散射剂量与该点空气中吸收 剂量之比。与组织空气比的性质类似,散射空气比 与源皮距无关,只受射线能量、组织深度和射野大 小影响。因为体模内某一点的散射剂量等于该点的 总吸收剂量与原射线剂量之差,因此某射野在深度 d处散射空气比在数值上等于该野在同一深度处的 组织空气比减去零射野的组织空气比。
消防设计专篇暖通部分
暖通专业消防设计说明1工程概况本工程为工项目,位于,规划建设用地面积m2。
本项目为 1#商办楼,地上24层,地下2层,建筑面积m2,建筑高度99. 75m,消防分类为一类高层公共建筑,主要功能为商务办公。
2设计依据(说明:根据工程项目情况进行增删,并确保为适用版本)《建筑设计防火规范》GB 50016-2014 (2018年版)《建筑防烟排烟系统技术标准》GB 51251-2017《通风与空调工程施工质量验收规范》GB 50243-2016《汽车库、修车库、停车场设计防火规范》GB 50067-2014《人民防空工程设计防火规范》GB 50098-2009《锅炉房设计标准》GB 50041-2020《建筑通风和排烟系统用防火阀门》GB 15930-2007《建筑内部装修设计防火规范》GB 50222-2017《气体灭火系统设计规范》GB 50370-2005《电动汽车分散充电设施工程技术标准》GB/T 51313-2018经批复的初步设计文件专家审查意见(编号)3防烟系统设计3.1防烟系统设置(建筑专业对楼梯间进行编号,暖通专业根据项目设计情况填写所有楼梯间、前室的防烟方式,系统高度指楼梯间实际服务的楼层高度,当需要分区时,分别给出不同分区的系统高度。
)本工程为超过50m的公共建筑,服务于1〜3层(系统高度不超过24m)的防烟楼梯间及其前室,满足自然通风条件,采用自然通风系统。
其他防烟楼梯间及其独立前室、合用前室均分别独立设置机械加压送风系统。
各部位防烟方式见表3-1 o表3-1防烟系统设置3.2自然通风(根据项目设计情况填写釆用自然通风防烟的所有楼梯间、前室的实际开窗面积,开窗面积计算由建筑专业提供。
)本工程自然通风防烟部位的可开启外窗面积统计见表3-2o3.3机械加压送风系统(根据项目设计情况填写釆用机械加压防烟的所有楼梯间、前室的计算风量;加压送风系统应进行编号,可与主要设备材料表中风机编号相对应;备注栏可填写一些特殊要求,如是否地上地下合用;超高层分区;楼梯间顶部固定窗、靠外墙每5层固定窗;首层扩大楼梯间、扩大前室防烟做法等。
求图示斜梁的支座反力6篇
求图示斜梁的支座反力6篇以下是网友分享的关于求图示斜梁的支座反力的资料6篇,希望对您有所帮助,就爱阅读感谢您的支持。
第一篇1 用截面法计算如图所示外伸梁1-1,2-2, 截面上的内力,其中:M=1Fpa2C解:1)求支座反力MB=0A(a)∑Fp⨯3a-M-FAy⨯2a=0FP⨯a-M+FBy⨯2a=0∑M=0解得:FAy校核:51=Fp(↑)FBy=Fp(↓)4451∑Fy=FAy+FBy-FP=4FP-4FP-FP=02) 用截面依次在1-1,2-2 截面处截开,取左段为研究对象; 图(b):M1∑Fy=0c-FP-FQ1=0Q1(b)FQ1=-FP1-1∑M=0Fpa+M1=0M1=-Fpa2Ay∑Fy=0FAy-FP-FQ2=0 FQ2(c)1FQ2=FP42-2pa22.悬臂梁AB,在自由端受集中力偶M作用,试绘出此梁的剪力图和弯矩图∑M=0F+M=0M2=-FpaAFQ解:1)列剪力方程和弯矩方程• 将坐标x的原点取在A端,由直接法可得3.作剪力图和弯矩图Q0≤x≤L,M(x)=mA(a)FFQ图FQ(x)= Fp左=FAY=bFp /L (0(a) FQ(x) = Fp右=- FBY =-aFp /L,(aMc(x)= Mc(Fp左)= FAY x=bFpx/L(0M(x)= MZ(Fp右) = FBY (L-x)=aFp (L-x) /L, (aFpab/L• AC段:• 在x= 0,处,M(0)=MA= 0• 在x= a处,M(a)=MC=abFp /l, • CB段:在x=a处, M(a)= MC =abFp /l, 在x=0处, M(l)=MB=0, 当aFQ图在x=a处, Mmax =M(a)= MC =abFp /LM4.简支梁受力如图所示,试作出该梁的剪力图和弯矩图。
(a)ANqFAY = FsAFscCAC:0≤x 2FQ(x)=∑FpL=5-2xM(x)=∑Mz(FpL)=5x-x2MCBMC-=6kNm,FSC-=1kNA5k NCD:2≤x≤3 FQ(x)=FpL=5-2⨯2 M(x)=Mz(FpL)=5x-4(x-1)-4=MC+=2kNm, FSC+=∑∑x5 1 24633DB:3≤x≤4FQ(x)=∑Fpr=-3M(x)=∑Mz(FpL)=-3(4-x)课程学习>> 第三章>>典型例题[例题3-2-1]作简支梁的剪力图与弯矩图。
初中数学重点模型14 动点在四边形中的分类讨论(基础)
专题14 动点在四边形中的分类讨论【专题说明】动点问题是中考中非常重要的一类问题,也是中考中的热点问题。
动点问题体现了数学中变化的思想,分类讨论的思想,对学生综合运用知识的能力要求非常高。
四边形中的动点问题是一类非常重要的问题,它将三角形和平行四边形、矩形、菱形、正方形结合在一起进行考察。
一、解题基本思路解决动点问题的思路,要注意以下几点:1、设出未知数动点问题一般都是求点的运动时间,通常设运动时间为t2、动点的运动路径就是线段长度题目通常会给动点的运动速度例如每秒两个单位,那么运动路程就是2t个单位。
而2t也就是这个点所运动的线段长。
进而能表示其他相关线段的长度。
所以我们在做动点问题的时候,第一步就是把图形中的线段都用含t的代数式来表示。
3、方程思想求出时间动点问题通常都是用方程来解决,根据题目找到线段之间的等量关系,然后用含有t的代数式表示出来,列出方程求解出t的值。
4、难点是找等量关系这种题的难点是找到等量关系。
这个等量关系往往不是题目中用语言叙述出来的,而是同学们根据题型自己挖掘出来的等量关系,所以对同学们图形分解的能力以及灵活运用知识的能力要求非常高。
5、注意分类讨论因为点的运动的位置不同,形成的图形就不同,符合结论的情况可能就不止一种,所以做动点问题要注意分类讨论。
【精典例题】1、如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,x ),则AP=2x cm,CM=3x cm,DN=x2cm.若BQ=x cm(0(1)当x为何值时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形;(2)当x 为何值时,以P ,Q ,M ,N 为顶点的四边形是平行四边形;(3)以P ,Q ,M ,N 为顶点的四边形能否为等腰梯形?如果能,求x 的值;如果不能,请说明理由.【解析】(1)当点P 与点N 重合或点Q 与点M 重合时,以PQ ,MN 为两边,以矩形的边(AD 或BC )的一部分为第三边可能构成一个三角形. ①当点P 与点N 重合时,(舍去).因为BQ +CM =,此时点Q 与点M 不重合.所以符合题意. ①当点Q 与点M 重合时,.此时,不符合题意.故点Q 与点M 不能重合.所以所求x 的值为.(2)由(1)知,点Q 只能在点M 的左侧,①当点P 在点N 的左侧时,由,解得. 当x =2时四边形PQMN 是平行四边形.①当点P 在点N 的右侧时,由, 解得.当x =4时四边形NQMP 是平行四边形.所以当时,以P ,Q ,M ,N 为顶点的四边形是平行四边形.(3)过点Q ,M 分别作AD 的垂线,垂足分别为点E ,F .由于2x >x ,所以点E 一定在点P 的左侧. 若以P ,Q ,M ,N 为顶点的四边形是等腰梯形, 则点F 一定在点N 的右侧,且PE =NF , 即.解得.由于当x =4时, 以P ,Q ,M ,N 为顶点的四边形是平行四边形,所以,以P ,Q ,M ,N 为顶点的四边形不能为等腰梯形2、如图1,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (1, 0)、C (3, 0)、D (3, 4).以A 为顶点的抛212220211211x x x x +==-=--由,得,34(211)20x x +=-<211x =-320,5x x x +==由得22520DN x ==>211-220(3)20(2)x x x x -+=-+120()2x x ==舍去,220(3)(2)20x x x x -+=+-1210()4x x =-=舍去,24x x ==或223x x x x -=-120()4x x ==舍去,ABDCPQ MN物线y =ax 2+bx +c 过点C .动点P 从点A 出发,沿线段AB 向点B 运动,同时动点Q 从点C 出发,沿线段CD 向点D 运动.点P 、Q 的运动速度均为每秒1个单位,运动时间为t 秒.过点P 作PE ①AB 交AC 于点E .(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)过点E 作EF ①AD 于F ,交抛物线于点G ,当t 为何值时,①ACG 的面积最大?最大值为多少? (3)在动点P 、Q 运动的过程中,当t 为何值时,在矩形ABCD 内(包括边界)存在点H ,使以C 、Q 、E 、H 为顶点的四边形为菱形?请直接写出t 的值.图1 思路点拨1.把①ACG 分割成以GE 为公共底边的两个三角形,高的和等于AD . 2.用含有t 的式子把图形中能够表示的线段和点的坐标都表示出来.3.构造以C 、Q 、E 、H 为顶点的平行四边形,再用邻边相等列方程验证菱形是否存在. 满分解答(1)A (1, 4).因为抛物线的顶点为A ,设抛物线的解析式为y =a (x -1)2+4,代入点C (3, 0),可得a =-1.所以抛物线的解析式为y =-(x -1)2+4=-x 2+2x +3. (2)因为PE //BC ,所以2AP AB PE BC ==.因此1122PE AP t ==.所以点E 的横坐标为112t +. 将112x t =+代入抛物线的解析式,y =-(x -1)2+4=2144t -.所以点G 的纵坐标为2144t -.于是得到2211(4)(4)44GE t t t t =---=-+.因此22111()(2)1244ACG AGE CGE S S S GE AF DF t t t ∆∆∆=+=+=-+=--+. 所以当t =1时,①ACG 面积的最大值为1.(3)2013t =或20t =-考点伸展第(3)题的解题思路是这样的:因为FE //QC ,FE =QC ,所以四边形FECQ 是平行四边形.再构造点F 关于PE 轴对称的点H ′,那么四边形EH ′CQ 也是平行四边形.再根据FQ =CQ 列关于t 的方程,检验四边形FECQ 是否为菱形,根据EQ =CQ 列关于t 的方程,检验四边形EH ′CQ 是否为菱形.1(1,4)2E t t +-,1(1,4)2F t +,(3,)Q t ,(3,0)C .如图2,当FQ =CQ 时,FQ 2=CQ 2,因此2221(2)(4)2t t t -+-=.整理,得240800t t -+=.解得120t =-220t =+. 如图3,当EQ =CQ 时,EQ 2=CQ 2,因此2221(2)(42)2t t t -+-=.整理,得213728000t t -+=.(1320)(40)0t t --=.所以12013t =,240t =(舍去).图2 图33、如图1,在Rt①ABC 中,①C =90°,AC =6,BC =8,动点P 从点A 开始沿边AC 向点C 以每秒1个单位长度的速度运动,动点Q 从点C 开始沿边CB 向点B 以每秒2个单位长度的速度运动,过点P 作PD //BC ,交AB 于点D ,联结PQ .点P 、Q 分别从点A 、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t 秒(t ≥0).(1)直接用含t 的代数式分别表示:QB =_______,PD =_______;(2)是否存在t 的值,使四边形PDBQ 为菱形?若存在,求出t 的值;若不存在,说明理由,并探究如何改变点Q 的速度(匀速运动),使四边形PDBQ 在某一时刻为菱形,求点Q 的速度; (3)如图2,在整个运动过程中,求出线段PQ 的中点M 所经过的路径长.图1 图2思路点拨1.菱形PDBQ 必须符合两个条件,点P 在①ABC 的平分线上,PQ //AB .先求出点P 运动的时间t ,再根据PQ //AB ,对应线段成比例求CQ 的长,从而求出点Q 的速度.2.探究点M 的路径,可以先取两个极端值画线段,再验证这条线段是不是点M 的路径. 满分解答(1)QB =8-2t ,PD =43t .(2)如图3,作①ABC 的平分线交CA 于P ,过点P 作PQ //AB 交BC 于Q ,那么四边形PDBQ 是菱形.过点P 作PE ①AB ,垂足为E ,那么BE =BC =8.在Rt①ABC 中,AC =6,BC =8,所以AB =10. 在Rt①APE 中,23cos 5AE A AP t ===,所以103t =.当PQ //AB 时,CQ CP CB CA =,即106386CQ-=.解得329CQ =.所以点Q 的运动速度为3210169315÷=.(3)以C 为原点建立直角坐标系.如图4,当t =0时,PQ 的中点就是AC 的中点E (3,0). 如图5,当t =4时,PQ 的中点就是PB 的中点F (1,4). 直线EF 的解析式是y =-2x +6.如图6,PQ 的中点M 的坐标可以表示为(62t -,t ).经验证,点M (62t -,t )在直线EF 上.所以PQ 的中点M 的运动路径长就是线段EF 的长,EF =25.图3图4 图5 图6考点伸展第(3)题求点M 的运动路径还有一种通用的方法是设二次函数: 当t =2时,PQ 的中点为(2,2).设点M 的运动路径的解析式为y =ax 2+bx +c ,代入E (3,0)、F (1,4)和(2,2),得930,4,42 2.a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩解得a =0,b =-2,c =6. 所以点M 的运动路径的解析式为y =-2x +6.4、如图1,在平面直角坐标系中,抛物线y =ax 2-2ax -3a (a <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),经过点A 的直线l :y =kx +b 与y 轴负半轴交于点C ,与抛物线的另一个交点为D ,且CD =4AC .(1)直接写出点A 的坐标,并求直线l 的函数表达式(其中k 、b 用含a 的式子表示); (2)点E 是直线l 上方的抛物线上的动点,若①ACE 的面积的最大值为54,求a 的值; (3)设P 是抛物线的对称轴上的一点,点Q 在抛物线上,以点A 、D 、P 、Q 为顶点的四边形能否成为矩形?若能,求出点P 的坐标;若不能,请说明理由.图1 备用图 思路点拨1.过点E 作x 轴的垂线交AD 于F ,那么①AEF 与①CEF 是共底的两个三角形.2.以AD 为分类标准讨论矩形,当AD 为边时,AD 与QP 平行且相等,对角线AP =QD ;当AD 为对角线时,AD 与PQ 互相平分且相等.满分解答(1)由y=ax2-2ax-3a=a(x+1)(x-3),得A(-1, 0).由CD=4AC,得x D=4.所以D(4, 5a).由A(-1, 0)、D(4, 5a),得直线l的函数表达式为y=ax+a.(2)如图1,过点E作x轴的垂线交AD于F.设E(x, ax2-2ax-3a),F(x, ax+a),那么EF=y E-y F=ax2-3ax-4a.由S①ACE=S①AEF-S①CEF=11()() 22E A E C EF x x EF x x---=1()2C AEF x x-=21(34)2ax ax a--=21325()228a x a--,得①ACE的面积的最大值为258a-.解方程25584a-=,得25a=-.(3)已知A(-1, 0)、D(4, 5a),x P=1,以AD为分类标准,分两种情况讨论:①如图2,如果AD为矩形的边,那么AD//QP,AD=QP,对角线AP=QD.由x D-x A=x P-x Q,得x Q=-4.当x=-4时,y=a(x+1)(x-3)=21a.所以Q(-4, 21a).由y D-y A=y P-y Q,得y P=26a.所以P(1, 26a).由AP2=QD2,得22+(26a)2=82+(16a)2.整理,得7a2=1.所以a=P(1,.①如图3,如果AD为矩形的对角线,那么AD与PQ互相平分且相等.由x D+x A=x P+x Q,得x Q=2.所以Q(2,-3a).由y D+y A=y P+y Q,得y P=8a.所以P(1, 8a).由AD2=PQ2,得52+(5a)2=12+(11a)2.整理,得4a2=1.所以12a=-.此时P(14)-,.图1 图2 图3考点伸展第(3)题也可以这样解.设P(1,n).①如图2,当AD时矩形的边时,①QPD=90°,所以AM DNMD NP=,即5553a na-=-.解得235ana+=.所以P235(1,)aa+.所以Q3(4,)a-.将Q3(4,)a-代入y=a(x+1)(x-3),得321aa=.所以a=.①如图3,当AD为矩形的对角线时,先求得Q(2,-3a).由①AQD=90°,得AG QKGQ KD=,即32335aa a-=--.解得12a=-.5、如图1,已知抛物线C:y=-x2+bx+c经过A(-3,0)和B(0, 3)两点.将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.(1)求抛物线C的表达式;(2)求点M的坐标;(3)将抛物线C平移到抛物线C′,抛物线C′的顶点记为M′,它的对称轴与x轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?图1思路点拨1.抛物线在平移的过程中,M′N′与MN保持平行,当M′N′=MN=4时,以点M、N、M′、N′为顶点的四边形就是平行四边形.2.平行四边形的面积为16,底边MN=4,那么高NN′=4.3.M′N′=4分两种情况:点M′在点N′的上方和下方.4.NN′=4分两种情况:点N′在点N的右侧和左侧.满分解答(1)将A (-3,0)、B (0, 3)分别代入y =-x 2+bx +c ,得 930,3.b c c --+=⎧⎨=⎩解得b =-2,c =3. 所以抛物线C 的表达式为y =-x 2-2x +3.(2)由y =-x 2-2x +3=-(x +1)2+4,得顶点M 的坐标为(-1,4).(3)抛物线在平移过程中,M′N′与MN 保持平行,当M′N′=MN =4时,以点M 、N 、M ′、N ′为顶点的四边形就是平行四边形.因为平行四边形的面积为16,所以MN 边对应的高NN′=4.那么以点M 、N 、M ′、N ′为顶点的平行四边形有4种情况:抛物线C 直接向右平移4个单位得到平行四边形MNN ′M ′(如图2); 抛物线C 直接向左平移4个单位得到平行四边形MNN ′M ′(如图2);抛物线C 先向右平移4个单位,再向下平移8个单位得到平行四边形MNM ′N ′(如图3); 抛物线C 先向左平移4个单位,再向下平移8个单位得到平行四边形MNM ′N ′(如图3).图2 图3考点伸展本题的抛物线C 向右平移m 个单位,两条抛物线的交点为D ,那么①MM ′D 的面积S 关于m 有怎样的函数关系?如图4,①MM ′D 是等腰三角形,由M (-1,4)、M ′(-1+m , 4),可得点D 的横坐标为22m -. 将22m x -=代入y =-(x +1)2+4,得244m y =-+.所以DH =244m -.所以S =2311(4)2248m m m m -=-.图4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
请参见如下图2
请参见如下图3
广视野型(近距离)
FQ-CR10100N-M FQ-CR15100N-M
请参见如下图4
中视野型
FQ-CR20050F-M FQ-CR25050F-M
广视野型(远距离) 35万像素
FQ-CR20100F-M
FQ-CR25100F-M
FQ2-S350100F-08
FQ2-S30050F-08M
FQ2-S30100F-08M
FQ2-S35050F-08M
FQ2-S35100F-08M
请参见下一页图6
请参见下一页图7
中视野型
FQ2-S40050F FQ2-S45050F FQ2-S40050F-M FQ2-S45050F-M
广视野型(远距离) 35万像素
FQ2-S1系列 [单功能型]
视野分类
像素数
彩色
NPN PNP
视野、安装距离 (mm)
窄视野型
FQ2-S10010F FQ2-S15010F
请参见下一页图1
FQ2-S2系列 [标准型]
视野分类
像素数
彩色
NPN PNP
视野、安装距离 (mm)
窄视野型
FQ2-S20010F FQ2-S25010F
请参见下一页图1
䇏ⷕ఼
● 检查ID型
FQ2-S4系列 [标准型]
视野分类
像素数
彩色
NPN PNP
黑白
NPN PNP
视野、安装距离 (mm)
窄视野型
FQ2-S40010F FQ2-S45010F FQ2-S40010F-M FQ2-S45010F-M
请参见下一页图1
[高分辨率型]
视野分类
像素数
彩色
NPN PNP
黑白
NPN PNP
C卡口类型 130万像素 FQ2-S30-13型 FQ2-S35-13型 FQ2-S30-13M型 FQ2-S35-13M型 请通过网站 进行确认。
C卡口类型 130万像素 FQ2-S40-13 FQ2-S45-13 FQ2-S40-13M FQ2-S45-13M 请通过网站 进行确认。
282
䆶⬉䆱 400-820-4535 ᳔ᮄֵᙃ
请参见如下图1
FQ-CR2系列 [二维读码器]
视野分类
像素数
黑白
NPN PNP
视野、安装距离 (mm)
窄视野型
FQ-CR20010F-M FQ-CR25010F-M
请参见如下图1
■ 视野、安装距离
视野分类
窄视野型
外观
图1
中视野型
广视野型(远距离)
35万像素
FQ2-CH10050F-M
FQ2-CH10100F-M
● ID型
FQ2-CH系列 [文字识别传感器]
视野分类
像素数
黑白
NPN PNP
视野、安装距离 (mm)
窄视野型
FQ2-CH10010F-M FQ2-CH15010F-M
请参见如下图1
FQ-CR1系列 [多功能读码器]
视野分类
像素数
黑白
NPN PNP
视野、安装距离 (mm)
窄视野型
FQ-CR10010F-M FQ-CR15010F-M
FQ2-S40100F-08M
FQ2-S45050F-08M
FQ2-S45100F-08M
请参见下一页图6
请参见下一页图7
广视野型(近距离) FQ2-S10100N FQ2-S15100N
请参见下一页图4
广视野型(近距离) FQ2-S20100N FQ2-S25100N
请参见下一页图4
广视野型(近距离) FQ2-S30100N-08 FQ2-S35100N-08 FQ2-S30100N-08M FQ2-S35100N-08M
请参见如下图2
请参见如下图3
广视野型(近距离)
FQ-CR20100N-M FQ-CR25100N-M
请参见如下图4
中视野型
广视野型(远距离)
ܝ㑸Ӵᛳ఼
请参见下一页图2
请参见下一页图3
中视野型
FQ2-S20050F FQ2-S25050F
广视野型(远距离) 35万像素
FQ2-S20100F FQ2-S25100F
请参见下一页图2
请参见下一页图3
中视30050F-08
FQ2-S30100F-08
FQ2-S35050F-08
视野、安装距离 (mm)
窄视野型
FQ2-S40010F-08 FQ2-S45010F-08 FQ2-S40010F-08M FQ2-S45010F-08M
请参见下一页图5
中视野型
FQ2-S10050F FQ2-S15050F
广视野型(远距离) 35万像素
FQ2-S10100F FQ2-S15100F
ѻક䗝ൟ 㾚㾝Ӵᛳ఼
FZ4㋏߫ FQ2㋏߫
FL㋏߫
FQ2-S3系列 [高分辨率型]
视野分类
像素数
彩色
NPN PNP
黑白
NPN PNP
视野、安装距离 (mm)
窄视野型
FQ2-S30010F-08 FQ2-S35010F-08 FQ2-S30010F-08M FQ2-S35010F-08M
请参见下一页图5
FQ2-CH15050F-M
FQ2-CH15100F-M
请参见如下图2
请参见如下图3
广视野型(近距离)
FQ2-CH10100N-M FQ2-CH15100N-M
请参见如下图4
㾚
FQ2系列
㾝 Ӵ
ᛳ
఼
/䇏 ⷕ ఼
中视野型
FQ-CR10050F-M FQ-CR15050F-M
广视野型(远距离) 35万像素
㾚 㾝 Ӵ ᛳ
智能摄像机
FQ2系列
఼
/䇏 ⷕ ఼
在小型机身中浓缩了高功能图像处理功能
备有丰富多彩的产品系列,用作图像检查的标 准机型十分方便
ܝ㑸Ӵᛳ఼
⬉ܝӴᛳ఼
ԡ鼠Ӵᛳ఼/ ⌟䭓Ӵᛳ఼ 㾚㾝Ӵᛳ఼/
䇏ⷕ఼ 䖥Ӵᛳ఼
ᖂൟ ⬉ܝӴᛳ఼
ᮟ䕀㓪ⷕ఼
䍙ໄ⊶Ӵᛳ఼
ⓣ⎆Ẕ⌟఼
■ 智能摄像机
● 检查型
FQ2-S40100F FQ2-S45100F FQ2-S40100F-M FQ2-S45100F-M
请参见下一页图2
请参见下一页图3
中视野型
广视野型(远距离)
76万像素
FQ2-S40050F-08
FQ2-S40100F-08
FQ2-S45050F-08
FQ2-S45100F-08
FQ2-S40050F-08M
请参见下一页图8
广视野型(近距离) FQ2-S40100N FQ2-S45100N FQ2-S40100N-M FQ2-S45100N-M
请参见下一页图4
广视野型(近距离) FQ2-S40100N-08 FQ2-S45100N-08 FQ2-S40100N-08M FQ2-S45100N-08M
请参见下一页图8
