统计学第四章习题答案解析贾俊平
统计学课后答案(贾俊平版)人大出版之欧阳引擎创编

第三章节:数据的图表展示 (1)欧阳引擎(2021.01.01)第四章节:数据的概括性度量 (15)第六章节:统计量及其抽样分布 (26)第七章节:参数估计 (28)第八章节:假设检验 (38)第九章节:列联分析 (41)第十章节:方差分析 (43)3.1 为评价家电行业售后服务的质量,随机抽取了由100个家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C一般;D.较差;E.差。
调查结果如下:B EC C AD C B A ED A C B C DE C E EA DBC C A ED C BB ACDE A B D D C C B C E D B C C B C D A C B C D E C E B B E C C A D C B A E B A C E E A B D D C A D B C C A E D C B CBCEDBCCBC要求:(1)指出上面的数据属于什么类型。
顺序数据(2)用Excel 制作一张频数分布表。
用数据分析——直方图制作:(3)绘制一张条形图,反映评价等级的分布。
用数据分析——直方图制作:(4)绘制评价等级的帕累托图。
逆序排序后,制作累计频数分布表:接收 频数 频率(%) 累计频率(%) C 32 32 32 B 21 21 53 D 17 17 70 E 16 16 86 A 14 14 1003.2 某行业管理局所属40个企业2002年的产品销售收入数据如下:152124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 9788123115119138112146113126要求:(1)根据上面的数据进行适当的分组,编制频数分布表,并计接收频率E 16 D 17 C 32 B 21 A14算出累积频数和累积频率。
统计学(第五版)贾俊平-课后思考题和练习题答案(完整版)

统计学(第五版)贾俊平课后思考题和练习题答案(最终完整版)第一部分思考题第一章思考题1。
1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论.1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1。
3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的.(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据.时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1。
6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1。
7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数"连续型变量,取之连续不断,不能一一列举,比如“温度”。
贾俊平《统计学》考研真题(含复试)与典型习题详解(数据的概括性度量)【圣才出品】

2.统计学期中考试非常简单,为了评估简单程度,教师记录了 9 名学生交上考试试卷
的时间如下(分钟)
33 29
45 60 42 19 52 38 36[东北财经大学
2012 研]
(1)这些数据的极差为( )。
A.3.00
B.-3.00
C.41.00
D.-41.00
【答案】C
【解析】数据按从小到大排序结果如下:
A.0.38
B.0.40
C.0.54
D.2.48
【答案】A
【解析】离散系数也称为变异系数,它是一组数据的标准差与其相应的平均数之比。其
计算公式为: vs
s x
。得到 vs
22.85 0.38 。 12.45
9.已知某工厂生产的某零件的平均厚度是 2 厘米,标准差是 0.25 厘米。如果已知该 厂生产的零件厚度为正态分布,可以判断厚度在 1.5 厘米到 2.5 厘米之间的零件大约占 ( )。[浙江工商大学 2011 研]
圣才电子书 十万种考研考证电子书、题库视频学习平台
5.随机变量 X 的方差为 2,随机变量 Y=2X,那么 y 的方差是( )。[中央财经大学 2011 研]
A.1 B.2 C.4 D.8 【答案】D
【解析】Var(cX ) c2Var(X ) 22 2 8
7.设 X1,X2,…,X n 为随机样本,则哪个统计量能较好地反映样本值的分散程度( )。
[中山大学 2012 研] A.样本平均 B.样本中位数 C.样子书
【答案】C
十万种考研考证电子书、题库视频学习平台
【解析】集中趋势是指 一 组 数 据 向 某 一 中 心 值 靠 拢 的 程 度 ,它 反 映 了 一 组 数 据 中 心
贾俊平第四版统计学-第四章-习题

第四章习题一、选择题1. 一组数据中出现频数最多的变量值称为()。
A.众数B.中位数C.四分位数D.均值2.一组数据排序后处于中间位置上的变量值称为()。
A.众数B.中位数C.四分位数D.均值3. n个变量值乘积的n次方根称为()。
A.众数B.中位数C.四分位数D.几何平均数4. 非众数组的频数占总频数的比率称为()。
A.异众比率B.离散系数C.平均差D.标准差5. 一组数据的最大值与最小值之差称为()。
A.平均差B.标准差C.极差D.四分位差6. 如果一个数据的标准分数是-2,表明该数据()。
A.比平均数高出2个标准差B.比平均数低2个标准差C.等于2倍的平均数D.等于2倍的标准差7. 一组数据的标准分数,其()。
A.均值为1,方差为0 B.均值为0,方差为1C.均值为0,方差为0 D.均值为1,方差为18. 经验法则表明,当一组数据对称分布式,在均值加减1个标准差的范围内大约有()。
A.68%的数据B.95%的数据C.99%的数据D.100%的数据9. 离散系数的主要用途是()。
A.反映一组数据的离散程度B.反映一组数据的平均水平C.比较多组数据的离散程度D.比较多组数据的平均水平10. 两组数据相比较()。
A.标准差大的离散程度也大B.标准差大的离散程度也小C.离散系数大的离散程度也大D.离散系数大的离散程度也小11. 某大学经济管理学院有1200名学生,法学院有800名学生,医学院有320名学生,理学院有200名学生。
在上面的描述中,众数是()。
A.1200 B.经济管理学院C.200 D.理学院12. 对于分类数据,测度其离散程度使用的统计量主要是()。
A.众数B.异众比率C.标准差D.均值13. 对于右偏分布,均值、中位数和众数之间的关系是()。
A.均值>中位数>众数B.中位数>均值>众数C.众数>中位数>均值D.众数>均值>中位数14. 在某行业中随即抽取10家企业,第一季度的利润额(单位:万元)分别为72,63.1,54.7,54.3,29,26.9,25,23.9,23,20。
统计学教材(贾俊平版)课后习题详细答案

统计学(第五版)贾俊平课后思考题和练习题答案(最终完整版)第一部分思考题第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
统计学贾俊平_第四版课后习题答案
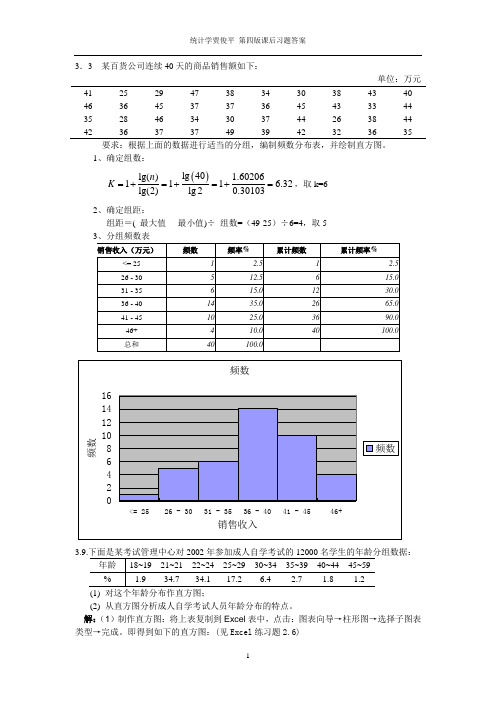
3.3 某百货公司连续40天的商品销售额如下:单位:万元41 25 29 47 38 34 30 38 43 40 46 36 45 37 37 36 45 43 33 44 35 28 46 34 30 37 44 26 38 44 42363737493942323635要求:根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图。
1、确定组数: ()l g 40l g () 1.60206111 6.32l g (2)l g 20.30103n K =+=+=+=,取k=62、确定组距:组距=( 最大值 - 最小值)÷ 组数=(49-25)÷6=4,取5(1) 对这个年龄分布作直方图;(2) 从直方图分析成人自学考试人员年龄分布的特点。
解:(1)制作直方图:将上表复制到Excel 表中,点击:图表向导→柱形图→选择子图表类型→完成。
即得到如下的直方图:(见Excel 练习题2.6)(2)年龄分布的特点:自学考试人员年龄的分布为右偏。
解:(1)根据上面的数据,画出两个班考试成绩的对比条形图和环形图。
3.14 已知1995—2004年我国的国内生产总值数据如下(按当年价格计算):要求:(2)绘制第一、二、三产业国内生产总值的线图。
4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics汽车销售数量N Valid 10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075 12.50种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
统计学贾俊平课后思考题和练习题

统计学(第五版)贾俊平课后思虑题和练习题答案(最后完好版)第一部分思虑题第一章思虑题什么是统计学统计学是对于数据的一门学科,它采集,办理,剖析,解说来自各个领域的数据并从中得出结论。
解说描绘统计和推测统计描绘统计;它研究的是数据采集,办理,汇总,图表描绘,归纳与剖析等统计方法。
推测统计;它是研究如何利用样本数据来推测整体特色的统计方法。
统计学的种类和不一样种类的特色统计数据;按所采纳的计量尺度不一样分;(定性数据)分类数据:只好归于某一类其余非数字型数据,它是对事物进行分类的结果,数据表现为类型,用文字来表述;(定性数据)次序数据:只好归于某一有序类其余非数字型数据。
它也是有类其余,但这些类型是有序的。
(定量数据)数值型数据:按数字尺度丈量的察看值,其结果表现为详细的数值。
统计数据;按统计数据都采集方法分;观察数据:是经过检查或观察而采集到的数据,这种数据是在没有对事物人为控制的条件下获取的。
实验数据:在实验中控制实验对象而采集到的数据。
统计数据;按被描绘的现象与实践的关系分;截面数据:在相同或相像的时间点采集到的数据,也叫静态数据。
时间序列数据:准时间次序采集到的,用于描绘现象随时间变化的状况,也叫动向数据。
解说分类数据,次序数据和数值型数据答案同举例说明整体,样本,参数,统计量,变量这几个看法对一千灯泡进行寿命测试,那么这千个灯泡就是整体,从中抽取一百个进行检测,这一百个灯泡的会合就是样本,这一千个灯泡的寿命的均匀值和标准差还有合格率等描绘特色的数值就是参数,这一百个灯泡的寿命的均匀值和标准差还有合格率等描绘特色的数值就是统计量,变量就是说明现象某种特色的看法,比方说灯泡的寿命。
变量的分类变量能够分为分类变量,次序变量,数值型变量。
变量也能够分为随机变量和非随机变量。
经验变量和理论变量。
举例说明失散型变量和连续性变量失散型变量,只好取有限个值,取值以整数位断开,比方“公司数”连续型变量,取之连续不停,不可以一一列举,比方“温度”。
统计学第五版课后答案(贾俊平)之欧阳术创编

第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.00754.2 随机抽取25个网络用户,得到他们的年龄数据如下:单位:周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄数Me=23。
(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652 (4)计算偏态系数和峰态系数: Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
为分组情况下的直方图:为分组情况下的概率密度曲线: 分组:1、确定组数:()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=62、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:4.3 某银行为缩短顾客到银行办理业务等待的时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075 12.50单位:周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数: ()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
为比较哪种排队方式使顾客等待的时间更短.两种排队方式各随机抽取9名顾客。
得到第一种排队方式的平均等待时间为7.2分钟,标准差为1.97分钟。
第二种排队方式的等待时间(单位:分钟)如下:5.5 6.6 6.7 6.8 7.1 7.3 7.4 7.8 7.8要求:(1)画出第二种排队方式等待时间的茎叶图。
第二种排队方式的等待时间(单位:分钟) Stem-and-Leaf PlotFrequency Stem & Leaf1.00 Extremes (=<5.5)3.00 6 . 6783.00 7 . 1342.00 7 . 88Stem width: 1.00Each leaf: 1 case(s)(2)计算第二种排队时间的平均数和标准差。
Mean7Std. Deviation0.714143Variance0.51(3)比较两种排队方式等待时间的离散程度。
第二种排队方式的离散程度小。
(4)如果让你选择一种排队方式,你会选择哪—种?试说明理由。
选择第二种,均值小,离散程度小。
4.4 某百货公司6月份各天的销售额数据如下:单位:万元257 276 297 252 238 310 240 236 265 278271 292 261 281 301 274 267 280 291 258272 284 268 303 273 263 322 249 269 295要求:(1)计算该百货公司日销售额的平均数和中位数。
(2)按定义公式计算四分位数。
(3)计算日销售额的标准差。
解:Statistics30Missing 0 Mean 274.1000Median 272.5000Std. Deviation 21.17472Percentiles 25 260.250050 272.500075 291.2500的产品多,乙的低成本的产品多。
(1)计算120家企业利润额的平均数和标准差。
(2)计算分布的偏态系数和峰态系数。
解:Statistics120Missing 0Mean 426.6667Std. Deviation 116.48445Skewness 0.208Std. Error of Skewness 0.221Kurtosis -0.625Std. Error of Kurtosis 0.4384.7 为研究少年儿童的成长发育状况,某研究所的一位调查人员在某城市抽取100名7~17岁的少年儿童作为样本,另一位调查人员则抽取了1 000名7~17岁的少年儿童作为样本。
请回答下面的问题,并解释其原因。
(1)两位调查人员所得到的样本的平均身高是否相同?如果不同,哪组样本的平均身高较大?(2)两位调查人员所得到的样本的标准差是否相同?如果不同,哪组样本的标准差较大?(3)两位调查人员得到这l 100名少年儿童身高的最高者或最低者的机会是否相同?如果不同,哪位调查研究人员的机会较大?解:(1)不一定相同,无法判断哪一个更高,但可以判断,样本量大的更接近于总体平均身高。
(2)不一定相同,样本量少的标准差大的可能性大。
(3)机会不相同,样本量大的得到最高者和最低者的身高的机会大。
4.8 一项关于大学生体重状况的研究发现.男生的平均体重为60kg,标准差为5kg;女生的平均体重为50kg,标准差为5kg。
请回答下面的问题:(1)是男生的体重差异大还是女生的体重差异大?为什么?女生,因为标准差一样,而均值男生大,所以,离散系数是男生的小,离散程度是男生的小。
(2)以磅为单位(1ks=2.2lb),求体重的平均数和标准差。
都是各乘以2.21,男生的平均体重为60kg×2.21=132.6磅,标准差为5kg×2.21=11.05磅;女生的平均体重为50kg×2.21=110.5磅,标准差为5kg×2.21=11.05磅。
(3)粗略地估计一下,男生中有百分之几的人体重在55kg一65kg之间?计算标准分数:Z1=x xs-=55605-=-1;Z2=x xs-=65605-=1,根据经验规则,男生大约有68%的人体重在55kg一65kg之间。
(4)粗略地估计一下,女生中有百分之几的人体重在40kg~60kg之间? 计算标准分数:Z1=x xs-=40505-=-2;Z2=x xs-=60505-=2,根据经验规则,女生大约有95%的人体重在40kg一60kg之间。
4.9 一家公司在招收职员时,首先要通过两项能力测试。
在A项测试中,其平均分数是100分,标准差是15分;在B项测试中,其平均分数是400分,标准差是50分。
一位应试者在A项测试中得了115分,在B项测试中得了425分。
与平均分数相比,该应试者哪一项测试更为理想?解:应用标准分数来考虑问题,该应试者标准分数高的测试理想。
Z A=x xs-=11510015-=1;Z B=x xs-=42540050-=0.5因此,A项测试结果理想。
4.10 一条产品生产线平均每天的产量为3 700件,标准差为50件。
如果某一天的产量低于或高于平均产量,并落人士2个标准差的范围之外,就认为该生产线“失去控制”。
下面(1)如果比较成年组和幼儿组的身高差异,你会采用什么样的统计量?为什么?均值不相等,用离散系数衡量身高差异。
(2)4.12 一种产品需要人工组装,现有三种可供选择的组装方法。
为检验哪种方法更好,随机抽取15个工人,让他们分别用三种方法组装。
下面是15个工人分别用三种方法在相同的时间内组装的产品数量:要求:(1)你准备采用什么方法来评价组装方法的优劣?均值不相等,用离散系数衡量身高差异。
(2)如果让你选择一种方法,你会作出怎样的选择?试说明理由。
解:对比均值和离散系数的方法,选择均值大,离散程度小的。
方法A方法B方法C平均165.6平均128.7333333平均125.5333333标准差2.131397932标准差1.751190072标准差2.774029217离散系数: V A=0.01287076,V B= 0.013603237,V C= 0.022097949均值A方法最大,同时A的离散系数也最小,因此选择A方法。
4.13 在金融证券领域,一项投资的预期收益率的变化通常用该项投资的风险来衡量。
预期收益率的变化越小,投资风险越低;预期收益率的变化越大,投资风险就越高。
下面的两个直方图,分别反映了200种商业类股票和200种高科技类股票的收益率分布。
在股票市场上,高收益率往往伴随着高风险。
但投资于哪类股票,往往与投资者的类型有一定关系。
(1)你认为该用什么样的统计量来反映投资的风险?标准差或者离散系数。
(2)如果选择风险小的股票进行投资,应该选择商业类股票还是高科技类股票?选择离散系数小的股票,则选择商业股票。
(3)如果进行股票投资,你会选择商业类股票还是高科技类股票?考虑高收益,则选择高科技股票;考虑风险,则选择商业股票。
