§3. 用树状图或表格求概率
3.1 用树状图或表格求概率_精选教学PPT课件(2)

本课小结
由“配紫色”游戏得到了什么
用树状图和列表的方法求概率时应 注意各种结果出现的可能性务必相 同. “配紫色”游戏体现了概率模型的思 想,它启示我们:概率是对随机现象 的一种数学描述,它可以帮助我们更 好地认识随机现象,并对生活中的一 些不确定情况作出自己的决策.
十五岁那年我第一次收到了男孩的情书,那时的我青涩懵懂,根本不知何为爱情。只知道打开情书的那一瞬间我的心跳加速,脸红的像滴血的玫瑰一般,生怕被其他同学知道班上的男同学暗恋我。于是又偷偷的把那封情书夹在我的作文本里带回家再次拿来阅读,一边读还一边红着脸偷偷的抿嘴微笑。自己心中思虑着原来被人喜欢的感觉是这样的。 时间让我的思想日渐成熟起来,慢慢的我也长成了一个亭亭玉立的大姑娘。我开始从书中寻找爱情,那时的我总是把那些书写美好爱情的诗词歌赋一遍一遍的读着,我爱读诗也爱写诗,看着柳永——衣带渐宽终不悔,为伊消得人憔悴时,他对爱情的执着让我真的敬佩;看着徐再思在《折桂令》中写到平生不会相思,才会相思,便害相思,我总是在思考者相思的滋味到底如何;在看着《红楼梦》中是一个阆苑奇葩,一个是美玉无瑕,有情却终究虚无一场空而感到忧伤,我感叹为何他俩不能长相见兮呢! 当然我也在很多戏曲中看到很多爱情故事,但是这些终究是艺术传达出,而不是我自己真心体会的爱情,我渴望爱情,但是没有面包的爱情真的能够执子之手天长地久吗?但是,大学二年级的我看着喜欢自己的男生千里迢迢下着雨赶来看我时,心里怎能不会有些感动。 当我见到他的一瞬间我真的好紧张,我好像拥抱他。可是我是一个传统而矜持的女孩子,即使见到再喜欢的男孩子我都会克制自己的情绪,当我俩走在大学的校园里,两人记在小小的雨伞下面,两只手随着步伐时不时碰在一起时,彼此的心跳声呼吸声都能听见,听着不远处时不时传来萨克斯吹奏的曲子《罗密欧与朱丽叶》时,真是别有一番风味。在这样的情境下我们这对互相暗恋的年轻人始终两只手没有牵在一起,他的眼神时如此的温柔,回到寝室后我一夜未眠写下了这首简单的小诗: 今忆梦 雨夜魂牵梦几回。 烟雨袅袅, 心语徘徊, 七个雨夜,七种相思。 倒是花无人红, 情无依倚。 今雨期欲子青, 七日相许期期相依。 原来思念一个人是这样的滋味。可是一个对自己未来都如此懵懂的我怎么能真正对爱情负责人呢,当我拒绝他时,我眼睛有了泪花了;原来离开一个自己喜欢的人时这样的痛苦。当我看见不久后他牵着一个女孩的手自然都走在街上时,我的心流血了;原来看着自己爱恋的对象爱上别人的那种滋味,简直比咖啡更苦! 我将这份苦涩的校园之恋深藏心底,当成是一种回忆。我无法左右我的爱情,但我可以左右的我的人生。当我成功的走近了我所规划的职业生涯时,我已经到了谈婚论嫁的年纪,这几年间不乏追求者,可我一再拒绝。 因为我再也找不到当初一见倾心的感觉了,我听不到紧凑的呼吸声、看不到温柔的眼神、也没有一句句关切的问候,有的只是百无聊赖的比较,学历、单位、家境,这样的相亲让我机器厌倦,我真的很 怀念大学的生活,怀念大学时间那一段段纯纯的山楂树之恋,而社会如此现实,看着街上的小情侣如此开放时,我始终坚持我医生一次的恋爱准则。 缘分真的是一件很奇怪的东西,在你不经意间偷偷的溜走了,又悄悄的像你走来。我仍然那般强淡定的面对我的爱情,似乎对一切异性都是那么不屑一顾,而我那一天的那一个眼神如此灼热的看着我,而这双囧囧有神的眼睛看着我一看就是一生。 当我被一个异性第一次十指相扣握住我的手时,我好有安全感,心里一股暖流划过我的心房,几年未曾有过的急促的心跳再一次频率如此之快,我对这个男人有一种直觉,总觉得我们之间会发生什么,结果一年之后我和这个男人就走进了婚姻的殿堂。我曾经许诺的唯一的爱情我终于做到了,我把我女人最美好的东西留给了这个男人,当在新婚之夜落在床单上的那一抹殷红时,他向我曾诺“我将一生对你不离不弃”。 当时的我处在24岁这样的年纪里对于不离不弃这个概念尚且模糊不清,我只知道这个男人让我有心动的感觉,他很执着的追求我,他很浪漫,他曾经单膝跪下求我做她的恋人,曾经捧着一大束玫瑰带给我惊喜,曾经脱下他的外套披在我的身上、曾经无数次容忍我的坏脾气、曾经给我冬日里送来一碗碗鲜美的汤汁、曾经生病时一口一口喂我吃药——太多的小事情发生在我的身上。当时的我没有所谓的两情若是久长时的概念,有的只是只争朝夕。 一年之后我们可爱的宝贝也出生了,可是我们的婚姻并不是一帆风顺的,我是一个爱美的女孩,我喜欢漂亮的包包,喜欢好看的裙子、喜欢香水化妆品。但是孩子的出生打乱了我们的生活节奏,也让我们的经济压力越发的大,我们的争吵声越来越多,我开始排斥他,我甚至后悔当初为什么没有选择那些经济能力强的男人结婚生孩子,我开始胡思乱想。我讨厌他给我带来的枯燥的奶妈生活、我讨厌他让我过早的走近的婚姻生活、我讨厌他给我买不起我想要的物质用品,我甚至有了放弃这段婚姻的念头,我不想把一生都献给这样一个平凡的男人身上、我讨厌他每天只知道洗床单洗被套、讨厌他整天唠唠叨叨。我要的丈夫是一个思想前进、事业心强的男人,而不是一个过 小日子的男人,我终于开始放弃我们的家庭、我们的爱情、甚至我们可爱的孩子。我们分居了——。 分居之后我开始思考自己,难道我不配拥有这样的爱情:下班后两人一起谈诗论词、切磋文学艺术、一起看电影、一起听音乐,偶尔再有一份小礼物送上。我憧憬的爱情时如此的罗曼蒂克,而现实呢,我们每天都在换着尿布、冲着奶粉、拿着奶瓶精打细算着每天的开支,跟我想象的婚姻生活简直风马牛不相及。 一个人的独居生活难眠有时落寞,我觉得自己是一个女汉子,我什么都可以做,我站在凳子上换灯泡,可是弄了许久还是搞不定,刚好周末大家都回家了,今晚没有灯怎么过,我躺在床上始终不好意思开口找他给我帮忙。突然电话那头打来了问我几时回我妈妈那边,他买了奶粉让我提回去,我很生气的大声囔囔“不回家,寝室灯都坏了心情不好不回家”当时就挂了电话,我还在床上生气着一刻钟之后门铃响了。 我打开门,原来是他,他提这个一大堆东西,拿出来的都是孩子的奶粉、纸尿裤。他拿来一个凳子站着看了看灯,说是灯烧掉了,于是给我从他的一大堆东西里找出一个新的灯泡给我换上拧好。做好这件事情后他又在袋子里找来找去说“你上次看中的这条粉色短裙我问了问80元,我给他讲价了,他收了我60块钱,你穿上肯定好看,还有你爱吃的话梅、苏打饼干、酸奶我给你买了你待会就着奶粉纸尿裤一起带回去,顺便路上肚子饿了可以吃。这时的我不知道说什么好,心里酸酸的,原来他知道我喜欢这条裙子,我突然哭出声来来,他回过头来看着我摸着我的头说“跟我回家吧,我开车送你回你妈妈家,宝贝看见我们一起回家肯定高兴!”。 也许是许久未见的原因,也许是他很爱他的孩子的原因、也许是我太害怕孤单的原因,也许是我从来舍不得离开他的原因,我就这样很轻易的回家了。我一直以为他不会像以前那样宠着我,没想到他仍然如此每天清早陪我上班,下班接我回家,跟我讲宝贝的小故事,我俩都笑得很开心。 傍晚时分他带着我出去散步,我问他我都这样的伤害你,你为什么还是对我这般迁就,他说“从跟你结婚那一天起,我就没想过离婚,你是我的老婆,一辈子都是我的老婆”我听着这话我很惊愕,我们恋爱时他长在我耳边小声说“我爱你”而现在他的回答不再是我爱你而是——。 夕阳下我们着对小夫妻牵着手,我看着他浅浅一笑,他一句话也没有说只是看着我很从容的笑了笑。我突然间读懂了什么是爱情—— 夕阳下许多的恋人都牵着手幸福的走着,不知道他们能不能像我们一样结婚、生孩子、一起到老呢! 岁月里,总有美丽暗香浮动,生命有热烈也有平淡,有欢喜也有忧伤,记忆的花瓣总要找一个灵魂的支点。时光的角落里,总会隐藏着惊喜,也许就在下一个巷口,美好的懂得便会如约而至。 喜欢如约而至这个词,藏着暗香,和一份对未来的期待,等得很苦,却从不辜负,花儿和暖阳如约而至,为你演绎了一个春天,你踏着春风如约而至,便是我生命中的盛大欢喜。 一杯茶,在等一个懂它的人,有的时候,人也是在等一杯倾心的茶,你若愿等,茶不负你;一朵花,是在等懂得欣赏她知己,你若懂得,她必欢颜。其实我们终其一生,不过是寻找一份懂得,寻一份温暖的陪伴,找一个,能够牵手的人。 懂是轻柔岁月里的那一缕暗香,是平淡生活中的相依相随的陪伴;是繁花落尽后的那份珍藏,是百转千回回后的那一份执着,长路漫漫,一份懂得,是风风雨雨中为你的坚强,岁月无声,一种温暖,是不言不语的那一份相随。 懂你的人,从你的举止言行中,便能看穿你的心思,想你所想,解你烦忧,懂你的人,不需要太多的表达,只是一个眼神便能会意,你的所有。懂你的人,会在人山人海中一眼便能看到你,懂真的无需要多言,无言亦是深情。 每个人心中都有一段过往,每个人的故事里都有一段刻骨铭心。你清澈的眼眸曾穿过岁月的迷茫,给我欢喜,你的微笑曾暖过我光阴的薄凉。懂得,是在人山人海中,只一眼凝眸的欢喜;是中的叶子,便希望能以最美的姿态落下,因为不想让你看到我的忧伤,如果我是一抹暖阳,希望在风雨来之前,多为你储藏些温暖,好让明媚照亮你的心房,也许是这世上的美,都有些苍凉,缘是云水深处无言的守候,是一纸素笺的暖,是光阴写意最美的诗行。最美的懂得,是你来,正好我在,共度一段指尖葱茏的时光。 美好的遇见如途中的一抹光,照亮一个人的生活,那份懂得,甚至能点燃了一个人的生命。灯火阑珊处,总有一些执念,诉说着一往情深,你的深情,他的一往,或许成了多年以后的那一抹相思,那也是生命中,最惊艳的一笔。时光是最好的记录者,他收藏着那些花瓣和暗香,芬芳着如烟的过往。你的笑容,如春风十里,妥贴在那些唇红齿白的光阴里,那些用柔情似水中的诗句,婉约了经年的一首歌。 多少懂得,能在心灵的国度里成就一场花开?多少懂得,能在岁月的云烟里,清晰如昨?懂得,让两颗孤独的心不再迷茫;懂得,让漫漫长路人不再枯燥,懂得,让脚步在前行中不再孤单。如若你懂,一个人的路途,也有温暖和诗意;如若懂得,寒凉风雨中也能寻到暖意;如若懂得,峰回路转处,便是柳岸花明;如若懂得,月缺月圆,亦都是风景。 懂得,如一阕诗行,写的人,走字如简,读的人,见字如面。若是一个名字,在另一个人的心里,有了生命的体温,含泪带笑,知寒懂暖,那简单的文字就不再只是一个符号,而一种真实而灵动的存在,因为懂得,所以相信,你若安好,便是晴天。 人生,有多少别离,就会有多少相逢,喧嚣的尘世,总有一些孤独的灵魂,走在寂寞的路上,而懂得,便是一缕暗香,穿过茫茫人海,幽幽而来,如花间清露,润人心田。它静静地流淌在光阴中,让相见或不见,天涯或咫尺,都变成一场欣喜和期待。因为懂得,岁月,将不再写意迷茫;因为懂得,人生将不再枯燥;因为懂得,所有的千回百转都是值得。 一份爱,若珍惜过,已足够感念,一个喜欢的人,若能遇见,已足够幸福。这一生,没有什么比结缘更美好的事情,与一朵花结缘,与一丛绿结缘,与你结缘,然后相依相偎,笑看世间万千。也许终有些缘份无从把握,昨日枝头的光阴,也曾红了樱桃,绿了芭蕉,一些人或事,念起或忘记,也都是风景。青山绿水音幽在,不知谁曾抚弦,但总会有一些记忆,暖了这一路的山高水长,纵使隔着岁月,因了懂得,喜悦安生也会常驻心底。 因为懂得,所以慈悲。人世间,有多少牵挂和相知,与风月无关,多少铭心刻骨,终敌不过岁月深远,春花绚烂,曾绽放在谁的指尖?千里明月,曾为谁相思一片?又有多少初见,今生还能再来一遍?回眸间,那些凡尘呓语,也只是参不透的清禅,唱不了的挽歌,曾经十里红妆,芳心暗许,终是一场烟火盛宴,如今写下一程山水,一页诗篇,却早已与相思无染,与懂得有关。 想与你午后听风,沐温暖的阳光,想与你并肩,看同样的风景,有一种懂得,是经过百转千回后的那一抹眷恋,是与你走过长长岁月后写下的那一首诗,是千帆过后你为我写就最安稳的落笔。 光阴,将日子描摹成一朵花的模样,留一抹春色于心底,便会有一隅温暖,收留我的漂泊。许一段寻常的时光,与你在一枚旧词里,用寂寂的字符,写风花雪月,亦写柴米油盐,将最深的情,私藏在心中,安放于最远的天涯。当你在我身旁时,我感到百花齐放,鸟鸣蝉唱。世间浮华,都不及你的陪伴,无论是春暖花开,还是落英缤纷,灵魂的相悦,在爱的原乡,懂你,是最深的情,你在,便是此生圆满。
九年级数学上册 3.1.3 用树状图或表格求概率教案 北师大版(1)(2021年整理)

九年级数学上册3.1.3 用树状图或表格求概率教案(新版)北师大版(1) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(九年级数学上册3.1.3 用树状图或表格求概率教案(新版)北师大版(1))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为九年级数学上册3.1.3 用树状图或表格求概率教案(新版)北师大版(1)的全部内容。
课题:3.1.3用树状图或表格求概率教学目标:1.能运用画树状图或列表的方法计算一些简单事件的概率,并能利用概率解决一些简单的实际问题,提高运用所学的概率知识解决问题的能力.2.鼓励学生思维的多样性,发展学生的合作交流的意识和发现问题、提出问题的能力.教学重、难点:重点:借助树状图、列表法计算随机事件的概率.难点:在利用树状图或者列表法求概率时,各种情况出现可能性不同时的情况处理.课前准备:多媒体课件.教学过程:一、创设情境,导入新课活动内容1:“配紫色”游戏游戏1:小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形。
游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了, 因为红色和蓝色在一起配成了紫色。
(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.(2)游戏者获胜的概率是多少?处理方式:教师利用课件展示游戏规则及演示转动每个转盘,让学生了解到每个转盘转出的结果都是等可能的.然后让两名学生板书借助树状图、借助表格的方法求出游戏者所有可能出现的结果,并计算出游戏者获胜的概率,其他同学在练习本上完成,完成后让其他学生进行点评,体会每个转盘转出的结果都是等可能的.解法一:借助树状图解:所有可能出现的结果如下:总共有6种结果,每种结果出现的可能性相同.其中,能够配成紫色的结果有1种:(红色,蓝色),所以游戏者的概率P (游戏者获胜)=61.解法二: 借助表格解:所有可能出现的结果如下:总共有6种结果,每种结果出现的可能性相同.其中,能够配成紫色的结果有1种:(红色,蓝色),所以游戏者的概率P (游戏者获胜)=61.活动内容2:导入新课导语:同学们,前面我们已经学习了利用树状图或列表的方法求出每种事件发生的可能性相同的概率,当每种事件发生的可能性不同时,你能想法解决吗?本节课我们来继续学习用树状图或表格求每种事件发生的可能性不同时的概率.【教师板书课题:3。
3.1.3用树状图或表格求概率(3)教案
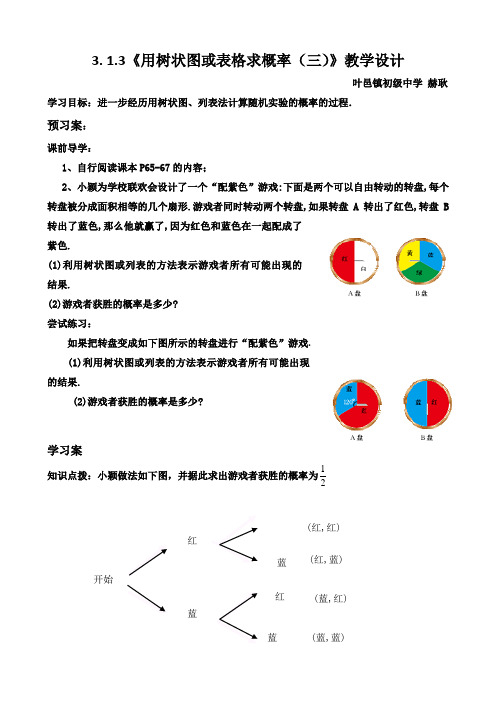
3. 1.3《用树状图或表格求概率(三)》教学设计叶邑镇初级中学赫耿学习目标:进一步经历用树状图、列表法计算随机实验的概率的过程.预习案:课前导学:1、自行阅读课本P65-67的内容;2、小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B 转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.(2)游戏者获胜的概率是多少?尝试练习:如果把转盘变成如下图所示的转盘进行“配紫色”游戏.(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.(2)游戏者获胜的概率是多少?学习案知识点拨:小颖做法如下图,并据此求出游戏者获胜的概率为21开始红蓝蓝红蓝(红,红)(红,蓝)(蓝,红)(蓝,蓝)小亮则先把左边转盘的红色区域等分成2份,分别记作“红色1”“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是21.你认为谁做得对?说说你的理由.(小组合作交流)指出“小颖的做法不正确,小亮的做法正确.而用列表法或者树状图求随机事件发生的概率时,应注意各种情况出现的可能性务必相同.课内训练:一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其它都相同,从中随机摸出一球,记下颜色后放回,再从中随机摸出一球。
求两次摸到的球的颜色能配成紫色的概率.反馈案:基础训练:1、 从1、2、3、4、5、6这六个数字中,先随意抽取一个,然后从剩下的五个数中再抽取一个,则两次抽到的数字之和为偶数的概率是__________;2、甲口袋中装有2个相同的小球,它们分别写有字母A 和B ;乙口袋中装有3个相同的小球,它们分别写有字母C 、D 和E ;从两个口袋中各随机地取出1个小球。
用列表法写出所有可能的结果3、用如图所示的两个转盘进行配“紫色”游戏,其概率是多少?拓展提高:1、一个盒子中装有一个红球、一个白球。
3.1.3 用树状图或表格求概率

例题解析,应用新知
解:先将两个红球分别记作“红1”“红2”, 两个白球分 别记作 “白1”“白2”,然后列表如下:
第一次 第二次 红1 红2 白1 红1 (红1,红1) 红2 (红1,红2) 白1 (红1,白1) 白2 (红1,白2) 蓝
(红1,蓝)
(红2,红1)
(白1,红1)
(红2,红2)
(白1,红2)
zxxk
2
B盘 A盘 红色1 红色2 蓝色
红色 (红1,红) (红2,红) (蓝,红)
蓝色 (红1,蓝) (红2,蓝) (蓝,蓝)
探究学习,获取新么?
利用树状图或列表的方法求概率时, 各种结果出现的可能性必须相同,若可 能性不同,就必须想法进行处理,务必 使各种结果出现的可能性相同.
B盘 A盘 红色 白色
黄色
蓝色
绿色
(红,黄) (红,蓝) (红,绿)
.
(白,黄) (白,蓝) (白,绿)
总共有6种结果,而能够配成紫色的结果有1种,
1 所以,P(游戏者获胜)= . 6
探究学习,获取新知
活动内容1: 想一想
游戏2:如果把转盘变成如下图所示的转盘进 行“配紫色”游戏.
(1)利用树状图或列表的方法表示游戏者所有 可能出现的结果. (2)游戏者获胜的概率是多少?
创设情境,导入新课
解法一:借助树状图 解:所有可能出现的结果如下:
zxxk
黄 (红,黄)
红
开始
绿 (红,绿) 蓝 (红,蓝)
黄 (白,黄) 白
绿 (白,绿) 蓝 (白,蓝) 总共有6种结果,而能够配成紫色的结果有1种,
1 所以,P(游戏者获胜)= . 6
解法二: 借助表格 解:所有可能出现的结果如下:
3.1用树状图和表格求概率(第3课时)

某电脑公司现有A,B,C三种型号的甲品牌电脑 和D,E两种型号的乙品牌电脑.希望中学要从甲、 乙两种品牌电脑中各选购一种型号的电脑. (1) 写出所有选购方案; (2) 如果(1)中各种选购方案被选中的可能性相 同,那么A型号电脑被选中的概率是多少? (3) 现知希望中学购买甲、乙两种品 牌电脑共36台(价格如图所示),恰好 用了10万元人民币,其中甲品牌电 脑为A型号电脑,求购买的A型号电 脑有几台.
拓广探索
• 在围棋盒中有x颗黑色棋子 和y颗白色棋子,从盒中随 机地取出一个棋子,如果它 是黑色棋子的概率是3/8, 写出表示x和y关系的表达 式.如果往盒中再放进10颗 黑色棋子,则取得颗黑色棋 子的概率为1/2,求x和y的 值.
唉……….
3.1用树状图和表格求概率3
回 味 无 穷 用树状图或表格表示概率
1、利用树状图或表格可以清晰地表示出某 个事件发生的所有可能出现的结果;从而较 方便地求出某些事件发生的概率.
2.当试验包含两步时,列表法比较方便,当然, 此时也可以用树形图法,当试验在三步或三 步以上时,用树形图法方便.
1、经过某十字路口的汽车,它可能继续直 行,也可能左转或右转,如果这三种可能性 大小相同,同向而行的三辆汽车都经过这个 十字路口时,求下列事件的概率:
(1)三辆车全部继续直行
(2)两辆车右转,一辆车左转
(3)至少有两辆车左转
2.“手心手背”是同学们中间广为流传的游戏, 游戏时甲、乙、丙三方每次做“手心”“手背” 两种手势中的一种,规定:⑴出现三个相同手 势不分胜负须继续比赛;⑵出现一个“手心” 和或一个“手背”和两个“手心”时,则一种 手势者为胜,两种相同手势者为负。 假定甲、乙、丙三人每次都是等可能地做这 两种手势,那么,甲、乙、丙三位同学胜的 概率是否一样?这个游戏对三方是否公平? 若公平,请说明理由,若不公平,如何修改 游戏规则才能使游戏对三方都公平?
用树状图或表格求概率获奖公开课教案
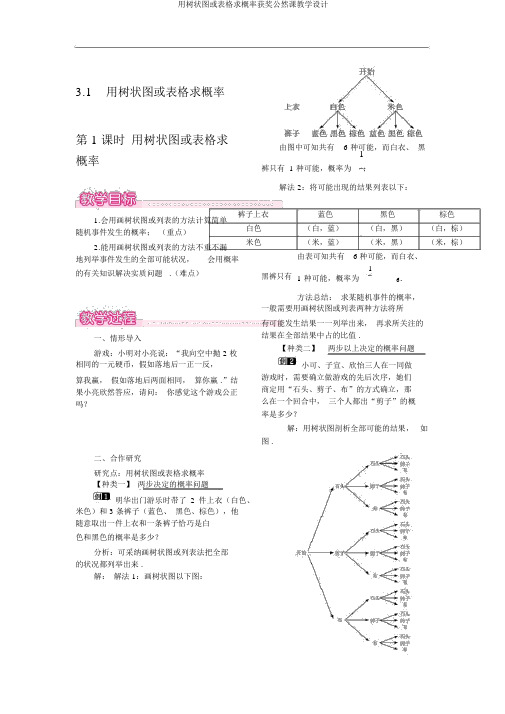
3.1用树状图或表格求概率第 1 课时用树状图或表格求概率由图中可知共有 6 种可能,而白衣、黑1裤只有 1 种可能,概率为;解法 2:将可能出现的结果列表以下:1.会用画树状图或列表的方法计算简单裤子上衣白色随机事件发生的概率;(重点)2.能用画树状图或列表的方法不重不漏米色地列举事件发生的全部可能状况,会用概率的有关知识解决实质问题 .(难点)黑裤只有蓝色黑色棕色(白,蓝)(白,黑)(白,棕)(米,蓝)(米,黑)(米,棕)由表可知共有 6 种可能,而白衣、11 种可能,概率为6.一、情形导入游戏:小明对小亮说:“我向空中抛 2 枚相同的一元硬币,假如落地后一正一反,算我赢,假如落地后两面相同,算你赢 .”结果小亮欣然答应,请问:你感觉这个游戏公正吗?二、合作研究研究点:用树状图或表格求概率【种类一】两步决定的概率问题明华出门游乐时带了2 件上衣(白色、米色)和 3 条裤子(蓝色、黑色、棕色),他随意取出一件上衣和一条裤子恰巧是白色和黑色的概率是多少?分析:可采纳画树状图或列表法把全部的状况都列举出来 .解:解法 1:画树状图以下图:方法总结:求某随机事件的概率,一般需要用画树状图或列表两种方法将所有可能发生结果一一列举出来,再求所关注的结果在全部结果中占的比值 .【种类二】两步以上决定的概率问题小可、子宣、欣怡三人在一同做游戏时,需要确立做游戏的先后次序,她们商定用“石头、剪子、布”的方式确立,那么在一个回合中,三个人都出“剪子”的概率是多少?解:用树状图剖析全部可能的结果,如图 .由树状图可知全部可能的结果有27 种,三人都出“剪子”的结果只有 1 种, 因此在一个回合中三个人都出“剪子”的概率为 271.方法总结: 当一次试验波及三个或更多的因素时, 为了不重不漏地列出全部可能的结果,往常采纳树状图 .【种类三】 有无放回试验一只箱子里共有3 个球,此中有 2个白球, 1 个红球,它们除了颜色外均相同 .( 1)从箱子中随意摸出一个球,不将它放回箱子,搅匀后再摸出一个球, 求两次摸出的球都是白球的概率;( 2)从箱子中随意摸出一个球,将它放回箱子, 搅匀后再摸出一个球,求两次摸出的球都是白球的概率 .分析: 题中( 1)( 2 )的差别在于第一次摸出的球能否放回了箱子.由题可知,第二次摸球时( 1 )的箱子中应减少第一次摸出 的那个球,那么还剩两个球能够摸,而( 2)的箱子中仍是有三个球能够摸 .因此,两个白球应当差别开来, 我们用 “ 白 1”“ 白 2”表示 .解:(1)列表以下:第一次序二次白 1 白 2白 1 ——(白 2,白 1)白 2 (白 1,白 2) ——红(白 1,红)(白 2,红)由上表可知,共有 6 种结果,且每种结果是等可能的, 此中两次摸出白球的结果有 2 种,因此 P (两次摸出的球都是白球) =2=1;63( 2)列表以下:第一次序二次白 1白 2白 1 (白 1,白 1) (白 2,白 1) 白 2 (白 1,白 2) (白 2,白 2) 红(白 1,红) (白 2,红)由上表可知,共有9 种结果,且每种结果是等可能的, 此中两次摸出白球的结 果有 4 种,因此 P (两次摸出的球都是白球) = 4 .9方法总结: 在试验中,常出现 “ 放回 ” 和 “ 不放回 ” 两种状况, 即能否重复进行的事件, 在求概率时要正确划分, 如利用列表法求概率时,不重复在列表中有空格, 重复在列表中则不会出现空格.三、板书设计画树状图法用树状图或表格求概率列表法经过与学生现实生活相联系的游戏为载体,培育学生成立概率模型的思想意识 . 在活动中进一步发展学生的合作沟通意识,提高学生对所研究问题的反省和拓展的能力,逐渐形成优秀的反省意识 . 鼓舞学生思想的多样性,发展学生的创新意识 . 别想一下造出海洋,一定先由小河川开始。
用树状图或表格求概率(2)

课题 §3.1 用树状图或表格求概率(二) 主 备 人 执 教 教学目标
知识与能力:通过两种求概率方法的选择使用,理解两种方法各自的特点,并能根据不同情境选择适当的方法;
过程与方法:通过具体情境,感受一件事情公平与否在现实生活中广泛存在,体现数学的价值; 情感态度与价值观:让学生掌握一定判断事件公平性的方法,提高其决策能力。 重点 理解树状图和表格法各自的特点,并能根据不同情境选择适当的方法求比较复杂的事件发生的概率。 难点 掌握一定判断事件公平性的方法,提高其决策能力。 教法
教 学 过 程
集 体 备 课 个 案 修 改 一、复习旧知 上节课,你学会了用什么方法求某个事件发生的概率? 二、创设情景,探究新知 小明、小颖和小凡做“石头、剪刀、布”的游戏,游戏规则如下:由小明和小颖玩“石头、剪刀、布”游戏,如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者. 假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗? 三、激发兴趣,探求新知 小明和小军两人一起做游戏.游戏规则如下:每人从1,2,…,12中任意选择一个数,然后两人各掷一次均匀的骰子,谁事先选择的数等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负.如果你是游戏者,你会选择哪个数? 四、、巩固基础,检测自我 有三张大小一样而画面不同的画片,先将每一张从中间剪开,分成上下两部分;然后把三张画片的上半部分都放在第一个盒子中,把下半部分都放在第二个盒子中.分别摇匀后,从每个盒子中各随机地摸出一张,求这两张恰好能拼成原来的一幅画的概率。
五、课堂小结 本节课我们进一步学习、感受了用数学解决问题的幸福,在今后更要自我探究,寻求方法,进行推理,得到判断游戏公平与否的依据。六、布置作业 课后作业:习题3.2 1.2.3
用树状图或表格求概率 (3)

一种常用方法.
用树状图和列表的方法求概率时应注意些什么?
用树状图和列表的方法求概率时应注意各种结 果出现的可能性务必相同.
典型例题
一个盒子中有两个红球,两个白球和一个蓝球, 这些球除颜色外其它都相同,从中随机摸出一球, 记下颜色后放回,再从中随机摸出一球。求两次 摸到的球的颜色能配成紫色的概率.
把两个红球记为红1、红2;两个白球记为白1、 白2.则列表格如下:
黄 (红,黄)
蓝 (红,蓝)
白
(白,黄) (白,蓝)
绿
(红,绿) (白,绿)
总共有6种可能的结果,每种结果出现的可能性相同, 所以,游戏者获胜的概率是 1
6
想一想 5
“配紫色”游戏的变异
用如图所示的转盘进行“配紫色”游戏. 蓝
小颖制作了下图,并据此求出游戏者
获胜的概率是1
1200
红
2
红
红
(红,红)
红白 A盘
蓝 黄
绿 B盘
议一议 3
“配紫色”游戏
树状图可以是:
黄
红
蓝
绿 开始
黄
白
蓝
绿
(红,黄) (红,蓝) (红,绿) (白,黄) (白,蓝) (白,绿)
总共有6种可能的结果,每种结果出现的可能性相同, 所以,游戏者获胜的概率是 1
6
想一想 4
“配紫色”游戏
表格可以是:
第二个 转盘
第一个 转盘
红
种结果出现的可能性务必相同. “配紫色”游戏体现了概率模型的思想,它 启示我们:概率是对随机现象的一种数学描 述,它可以帮助我们更好地认识随机现象, 并对生活中的一些不确定情况作出自己的 决策.
下课了!
时间是一个常数,但对勤奋者来说,是一个 “变数”.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3.1 用树状图或表格求概率
教学目标
1、经历试验、统计等活动过程,在活动中进一步发展学生合作交流的意识和水平。
通过试验,
理解当试验次数较大时试验频率稳定于理论概率,并可据此估计某一事物发生的概率
2、经历试验、统计等活动过程,在活动中进一步发展学生合作交流的意识和水平
3、能使用树状图和列表法计算简单事件发生的概率
教学重点和难点
重点:使用树状图和列表法计算简单事件发生的概率
难点:使用树状图和列表法计算简单事件发生的概率
教法:
学法:
教学过程设计
一、从学生原有的认知结构提出问题
现实生活当中,我们常常遇到一些概率的问题,如买彩票等游戏,都需要一些概率的知识。
通过求某事件发生的概率,指导我们做出抉择。
这节课,我们来学习求概率。
二、师生共同研究形成概念
1、频数、频率与概率
频数是指每个对象出现的次数。
频率是指每个对象出现的次数与总次数的比值。
概率表示一个事件在实验中发生的可能性的大小的数,概率的值大于等于0,小于等于1。
频数与频率都能反映每个对象出现的频繁水准,频数是某个对象出现的次数,是个数,而频率是每个对象出现的次数与总次数的比,是比值。
频率是在实验的基础上一个事件发生的次数与总实验次数的比,而概率是从理论上推算事件发生的可能性,两者的意义不同,一个事件的发生有随机性,所以通常情况下不等于概率,仅仅实验次数越多,频率越趋向于概率。
一个事件发生的频率在概率的附近上下波动,多次实验的频率接近概率。
☆做一做书本扑克游戏
通过这个试验活动,探索出“试验次数很大时试验的频率渐趋稳定”这个规律,然后通过与旧知识类比,得出频率稳定值与理论概率之间的关系。
此游戏让学生小组内完成。
☆议一议书本P 158 议一议
通过上面图表的交流与研讨,能够发现它的规律。
☆做一做书本P 做一做
进一步汇总试验数据,检验上面的估计,让学生进一步体会频率的稳定性。
2、试验数据与理论概率
为了考查频率与概率之间的关系,我们要做一系列的实验,随着实验次数的增加,我们可使用折线统计图,随时记录下频率随实验次数的变化而变化的情况。
所以,能够通过多次实验,用一个事件发生的频率来估计这个事件发生的概率,这就是我们通过多次实验总结出的结果。
☆想一想书本摸牌游戏
通过对上面所做试验的进一步分析,体会两步试验中“两步”之间的相互独立性,进而理解两步试验所有可能出现的结果及每种结果出现的等可能性。
在此基础上,引出计算涉及两步试验的随机事件发生的概率的方法——树状图和列表法。
3、树状图和列表法
☆做一做书本做一做
此游戏让学生同位一起做,然后统计数据。
☆议一议书本议一议
鼓励学生实行不同观点的交流。
☆想一想书本想一想
让学生理解到这种情况与另外两种情况发生的可能性是不同的。
从表面上看,我们不能一下子算出概率是多少,但我们可用列表法列出有可能出现的搭配,从中得出事件发生的概率。
利用树状图或表格,能够比较方便地求出某些事件发生的概率。
☆做一做书转盘游戏“配紫色”
此游戏让学生同位一起做,然后统计数据。
☆议一议书本议一议
用树状图和列表的方法求概率时,应注意各种结果出现的可能性务必相同。
4、用树状图和列表法求概率时的注意点
1)列表法只适于求两步实验的随机实验的随机事件概率的求解;
2)各种情况出现的可能性务必相同。
5、讲解例题
例1随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少?
例2在我们班中抽出六位同学,其中“潘、陈、关”作为A组,“李、陈、关”作为B组。
现在要从A、B两组各选一人出席会议,则:
a)选出的两位同学是同姓“潘”、“曾”的概率是多少?
b)选出的两位同学是同姓的概率是多少?
c)选出的两位同学中,至少有一位姓“关”的概率是多少?
d)选出的两位同学中,没有姓“陈”的概率是多少?
三、随堂练习
1、书本随堂练习
2、《练习册》P
四、小结
运用树状图和列表法计算简单事件发生的概率的方法。
五、作业
随机掷一枚均匀的硬币两次,两次都是正面朝上的概率是多少?
六、教学后记
七、。
