北京交通大学信号与系统第四章典型例题

第四章 典型例题
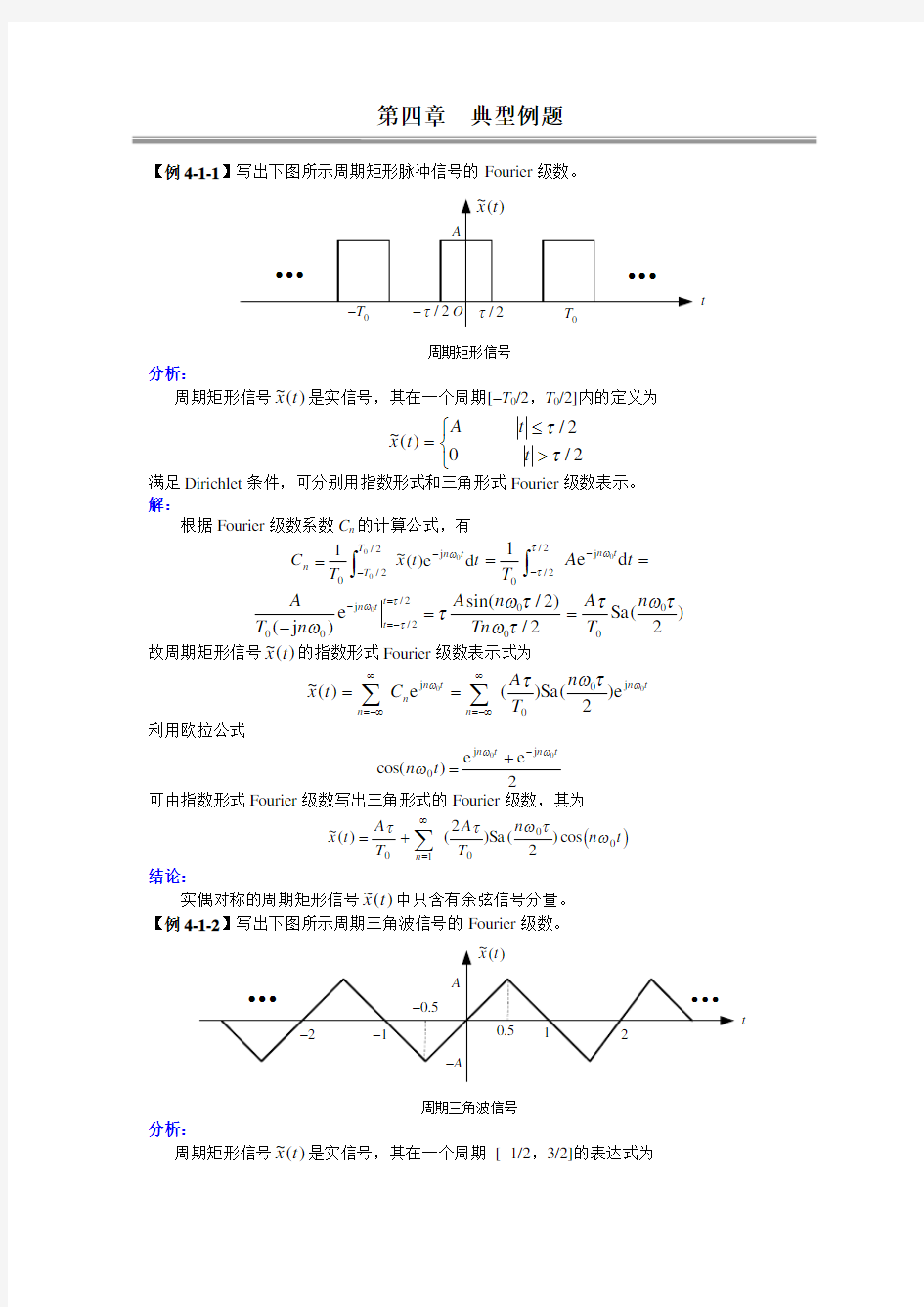
【例4-1-1】写出下图所示周期矩形脉冲信号的Fourier 级数。
t
周期矩形信号
分析:
周期矩形信号)(~t x 是实信号,其在一个周期[-T 0/2,T 0/2]内的定义为
???>≤=2/
02/ )(~ττt t A t x
满足Dirichlet 条件,可分别用指数形式和三角形式Fourier 级数表示。
解:
根据Fourier 级数系数C n 的计算公式,有
t t x T C t n T T n d e )(~
1000j 2/2/0ω--?===
--?
t A T t n d e 10j 2/2
/0ωττ 2/2/j 000e )j (ττωω=-=--t t t n n T A 2/)2/sin(00τωτωτTn n A =)2
(Sa 00τωτn T A =
故周期矩形信号)(~
t x 的指数形式Fourier 级数表示式为
t n n t n n n n T A C t x 00j 00j e )2(Sa )(e )(~ωωτωτ∑∑∞
-∞
=∞-∞===
利用欧拉公式
2
e e )cos(00j j 0t
n t n t n ωωω-+=
可由指数形式Fourier 级数写出三角形式的Fourier 级数,其为
()t n n T A T A t x n 0001
0cos )2(Sa )2()(~ωτωττ∑
∞
=+=
结论:
实偶对称的周期矩形信号)(~
t x 中只含有余弦信号分量。 【例4-1-2】写出下图所示周期三角波信号的Fourier 级数。
t
周期三角波信号
分析:
周期矩形信号)(~
t x 是实信号,其在一个周期 [-1/2,3/2]的表达式为
????
?
≤<-≤=2
3
21 )1(221 2)(~t t A t At t x
满足Dirichlet 条件,可分别用指数形式和三角形式Fourier 级数表示。 解:
由于该三角波信号)(~t x 的周期T 0=2,所以ππ
200==T ω。
根据Fourier 级数系数的计算公式,有
t t x T C t n T T n d e )(~1000j 2/2/0ω--?=t t A t At t n t
n d e )1(221d e 221πj 2/32
/1πj 2/12/1----+=?
?
计算上式积分可得三角波信号的频谱C n 为
?????=≠-=0,
00
),2
πsin(πj
422n n n n A C n 所以周期三角波信号的Fourier 级数表示式为
t
n n n n n A t x πj 2
20,e )2πsin(π
j 4)(~-=
∑
∞
≠-∞= 利用欧拉公式
j
2e e )sin(00j j 0t
n t n t n ωωω--=
可由指数形式Fourier 级数写出三角形式的Fourier 级数,其为
==
∑
∞
=t n n n A t x n πsin )2πsin(
π8)(~2
21
??
?
???+-+- t t t t A π7sin 491π5sin 251π3sin 91πsin π82 结论:
(1) 实奇对称的周期三角波信号)(~
t x 中只含有正弦信号分量。 (2) 例4-1-1的周期矩形信号和例4-1-2的周期三角波信号均可用Fourier 级数
t
n n
n C t x 0j e
)(~ω∑∞
-∞
==
表示,所不同的是两者的Fourier 系数不同。因此,研究Fourier 系数也
可获得信号的某些特性。
【例4-1-3】判断下图所示周期矩形信号和周期三角波信号的Fourier 系数的特性。
t
(a)周期矩形信号
t
(b)周期三角波信号
分析:
首先判断信号时域的对称关系,再利用周期信号的对称特性和Fourier 系数的关系,即可得出相应信号Fourier 系数的特性。 解:
(a)信号为实偶对称,满足)(~)(~t x t x -=,故Fourier 系数C n 实偶对称,其三角形式Fourier 级数表示式中只含有直流项和余弦项。 (b) 信号既满足)(~)(~t x t x --=,又满足)2/(~)(~0T t x t x ±=,为实奇对称半波镜像信号,其三角形式Fourier 级数表示式中只含有奇次谐波的正弦信号分量。 结论:
利用周期信号的对称特性和Fourier 系数的关系可以建立信号时频的对应关系,定性地判断信号的频谱成份。
【例4-1-4】判断下图所示周期信号)(~t x 的Fourier 系数的特性。
t
分析:
从信号)(~t x 的波形来看,其不具有任何对称关系。在这种情况下可以去掉信号的直流分量,再观察波形的对称性。 解:
信号的直流分量为
A t t x T C T 4.0d )(~100
00==?
)(~t x 去掉直流分量后的波形如下图所示,是半波镜像信号,故只含有奇次谐波分量。
t
综合上面的分析,)(~t x 的三角形式Fourier 级数表示式中含有直流项、奇次谐波(正弦和余
弦)分量。
结论:
某些信号波形经上下或左右平移后,才呈现出某种对称特性。
【例4-1-5】利用连续时间Fourier 级数的性质,写出下图所示周期矩形信号)(~t x 的Fourier 级数表示式。
t
分析:
周期信号)(~t x 可以看成直流分量与例4-1-1周期矩形信号之差,利用Fourier 级数的线性特性和例4-1-1周期矩形信号Fourier 级数表示即可求解本题。 解:
周期信号)(~t x 可以看成下图所示直流分量)(~
1t x 和周期矩形信号)(~2t x 之差,即 )(~2)(~)(~)(~2
21t x t x t x t x -=-= 令例4-1-1中周期矩形信号的A =1,2=τ,40=T ,可得)(~2t x 的Fourier 级数表示式为
()t n n T A T A t x n 0001
02cos )2(Sa )2()(~ωτωττ∑
∞
=+=)2
πcos(
)2π
(Sa 5.01
t
n n n ∑∞
=+
= 因此)(~t x 的Fourier 级数表示式为
)(~2)(~2t x t x -=)2
πcos()2π(
Sa 5.11
t
n n n ∑
∞
=-
=
t
t
结论:
利用常用周期信号的Fourier 系数和Fourier 级数的性质,可计算其它周期信号的Fourier 系数。
【例4-1-6】利用连续时间Fourier 级数的性质,写出下图所示周期矩形信号)(~t g
的Fourier 级数表示式。
周期信号g (t )
分析:
周期信号)(~t g
可以看成例4-1-1周期矩形信号右移0.5,利用Fourier 级数的时移特性和例4-1-1周期矩形信号Fourier 级数表示即可求解本题。 解:
周期信号)(~t g 可以表示为)5.0(~)(~-=t x t g 。
令例4-1-1中周期矩形信号的1=τ,20=T , ω0=2π/ T 0=π,可得)(~t x 的Fourier 系数为
)2(Sa 00τωτn T A C n =)2
π
(Sa 2n A =
令)(~t g
的Fourier 系数为D n ,利用Fourier 级数的时移特性可得 n n n C D 05.0j e ω-=2/πj e )2
π
(Sa 2n n A -=
因此,周期信号)(~t g
的Fourier 级数表示式为 =
=∑∞
-∞
=n t
n n
C t g
0j e
)(~ωt n n n n A πj π/2j e e )2/π(/2)Sa (-∞
-∞
=∑
??
?
???++++
= t t t A A π5sin 51π3sin 31πsin π22/
t
结论:
)(~t g 与)(~t x 具有)5.0(~)(~-=t x t g 的关系,两者Fourier 级数的模相等,即n n D C =,
但相位不同。这充分体现了周期信号Fourier 级数时移特性的物理含义,即信号在时域的时
移对应其在频域的相移。
【例4-1-7】画出例4-1-1以原点为中心对称的周期矩形信号)(~t x 的频谱。
t
周期矩形信号
分析:
周期信号的Fourier 系数就是该信号的频谱。
解:
由例4-1-1的计算结果,以原点为中心对称的周期矩形信号)(~t x 的频谱为
)2
(Sa 00τωτ
n T A C n =, 2,1,0±±=n
由于C n 为实数,因而各谐波分量的相位或为零(C n 为正)或为±π(C n 为负),因此不需分别画
出幅度频谱| C n |与相位频谱φ n 。可以直接画出Fourier 系数C n 的分布图。根据抽样函数Sa( t )
的曲线便可得信号)(~t x 的频谱图。
ω
00
周期矩形信号的频谱
结论:
周期矩形脉冲的频谱具有以下特性:
(1)离散频谱特性:频谱是以基频ω0为间隔分布的离散频谱。由于谱线的间隔ω0=2π/T 0,故信号的周期T 0越大,其基频ω0就越小,谱线越密。
频谱都是由间隔为ω0的谱线组成的离散谱。不同的周期信号其频谱分布的形状不同,但都 (2)幅度衰减特性:随着谐波n ω0增大,幅度频谱|C n |不断衰减,并最终趋于零。 不同的周期信号对应的频谱不同,但上述特性是周期信号频谱的普遍性质。
【例4-1-8】画出周期信号)(~t x =1+cos(ω0t -π/2)+0.5 cos(2ω0t +π/3)的频谱。 分析:
根据周期信号的频谱基本概念,将)(~
t x 表示为虚指数信号t n 0j e ω的线性组合(指数形式Fourier 级数),虚指数信号t n 0j e ω的系数就是该信号的频谱。 解:
由Euler 公式,周期信号)(~t x 可表示为
)e e e e (4
1)e e e e (211)(~00002j 3j π2j 3/j πj 2/j πj 2/j πt /t t t t x ωωωω----++++=
与∑∞
-∞
==n t
n n
C t x 0j e
)(~
ω比较,可得
3j π23/j π22/j π12/j π10e 4
1
,e 41,e 21,e 21,1/C C C C C ----=====
所以周期信号)(~t x 的频谱C n 如下图所示。
ω
周期信号)(~t x 的幅度频谱和相位频谱
结论:
根据周期信号)(~t x 的幅度频谱和相位频谱,
可以清楚看到周期信号中各谐波分量分布情况。如果已知周期信号的频谱C n ,则可由式∑∞
-∞
==n t
n n
C t x 0j e
)(~
ω重建信号)(~t x 。信号的时域
描述和频域描述是深入分析和研究信号的理论基础。
【例4-2-1】试求图(a )所示非周期矩形脉冲信号x (t )的频谱函数X (j ω)。
t
ω
(a ) 非周期矩形脉冲信号 (b ) 信号频谱函数
分析:
非周期矩形脉冲信号x (t )满足Dirichlet 条件,其Fourier 变换X (j ω)存在。 解:
非周期矩形脉冲信号x (t )的时域表示式为
??
??
?
>
≤=2|| 02|| )(τ
τt t A t x ,, 由连续信号Fourier 变换定义可得
t A t t x X ττt t
d e d e
)()j (22
j j ?
?
--∞
∞
--?==
ωωω
)2
Sa(
)2
sin(
2e j 2
/2
/ j ωτ
τωτ
ω
ω
ττωA A A t
==
--
结论:
(1) 连续非周期信号的频谱是连续谱,其形状与周期矩形信号离散频谱的包络线相似。 (2) 信号在时域中持续时间有限,则在频域中其频谱将延续到无限。
(3) 信号的频谱分量主要集中在零频到第一个过零点之间,工程中往往将此宽度作为信号的有效带宽。非周期矩形信号的有效带宽为2π/τ (rad/s)或1/τ (Hz),在时域的宽度为τ 。即
【例4-2-2】试求单位冲激信号x (t )=δ(t )的频谱。 分析:
非周期矩形脉冲信号x (t )满足Dirichlet 条件,由Fourier 变换的定义直接求得其频谱。 解:
利用冲激信号的抽样特性,可由Fourier 变换的定义直接求得其频谱
1d e )(d e )()]([)j (j j ==
=
=?
?
∞
∞
--∞
∞
--t t t t x t X t t ωωδδωF
下图画出了冲激信号δ(t )及其频谱。
单位冲激信号及其频谱
结论:
(1) 冲激信号的频谱为一常数。
(2) 信号在时域中持续时间有限,则在频域中其频谱将延续到无限。 【例4-2-3】试求直流信号x (t )=1 ( -∞ < t < ∞ )的频谱。
分析:
直流信号不满足绝对可积,但其Fourier 变换X (j ω)存在,可借助δ(t )的Fourier 反变换计算。 解:
利用δ(t )的频谱及Fourier 反变换公式可得
ωδωd e 1π
21)( j t
t ?=
?∞∞- (1)
由于δ(t )是t 的偶函数,所以(1)式可等价写为
ωδωd e π
21)(j t
t ±∞∞-?=
(2)
由连续信号Fourier 变换定义及(2)式可得
t X t d e 1]1[)j (j ωω-∞
∞
-?=
=?
F )(π2ωδ=
下图为直流信号x (t )=1(-∞ < t
<∞)及其频谱。
直流信号及其频谱
结论:
(1) 直流信号的频谱只在ω=0处有一冲激。
(2) 信号在时域中持续时间无限,则在频域中其频谱有限。
【例4-2-4】试求符号函数sgn(t )的频谱。 分析: sgn(t )的定义为
??
?
??>=<-=0 10 00 1)sgn(t t t t
虽然符号函数不满足绝对可积,但其Fourier 变换存在。借助双边指数衰减信号然后取极限
的方法可以求解符号函数的频谱。 解: 因为
t
t t σσ-→=e
)sgn(lim )sgn(0
而
=+
-=
--∞
-∞
--?
?
t t t t t t t t
d e e d e e )1(]e )[sgn(j 0
j 0
ωσωσσF
∞
=+--∞
=-+-
--
)j (0
)j (j e j e t t t t ω
σω
σωσωσω
σωσj 1
j 1++
--=
所以 {
}
]e
)[sgn( lim )][sgn(0
t
t t σσ-→=F F ω
j 2=
幅度频谱 ω
ωωω)
sgn(22)j (=
=
X
相位频谱
)sgn(2π
,2/π0 ,2/π)(ωωωω?-=???>-<=
符号函数的幅度谱和相位谱如下图所示。
符号函数的幅度频谱和相位频谱
【例4-2-5】试求单位阶跃信号x (t )=u (t )的频谱。 分析:
单位阶跃信号不满足绝对可积,但其Fourier 变换存在。可以利用符号函数和直流信号的频谱来求单位阶跃信号的频谱。 解:
将单位阶跃信号表示为符号函数和直流信号的线性组合,即
)sgn(2
1
21)(t t u +=
所以单位阶跃信号u (t )的频谱为
ω
ωδωj 1)(π)]([)j (+
==t u X F
单位阶跃信号u (t )的幅度谱和相位谱如下图所示。
阶跃信号的幅度频谱和相位频谱
【例4-2-6】试求单边指数信号x (t ) = e -αt u (t ), (α > 0)的频谱。 分析:
单边指数信号满足Dirichlet 条件,由Fourier 变换的定义直接求得其频谱。 解:
由连续信号Fourier 变换定义,可得
t t x X t d e )()j (j ?∞∞
--=ωωt t t d e e 0
j ?∞
--=ωαω
j 1
+=
a
幅度频谱为
2
2
1
)j (ω
ω+=
a X
相位频谱为
)/arctan()(αωω?-=
单边指数信号的幅度频谱和相位频谱如下图所示。
ω
单边指数信号的幅度频谱和相位频谱
【例4-2-7】试求虚指数信号x (t ) =e j ω0t (-∞ 虚指数信号在整个信号区间(-∞,+∞)上不满足绝对可积,但其Fourier 变换存在,可借助δ(t )的Fourier 反变换计算。 解: 利用δ(t )的频谱及Fourier 反变换公式可得 ωδωd e 1π21)( j t t ?=?∞ ∞- (1) 由于δ(t )是t 的偶函数,所以(1)式可等价写为 ωδωd e π21)(j t t ±∞∞ -?= (2) 由连续信号Fourier 变换定义及(2)式可得虚指数信号的频谱函数为 )(π2d e ]e [)j (0)j(j 00ωωδωωωω-== =? ∞ ∞ ---t X t t F 虚指数信号的频谱如下图所示。 虚指数信号的频谱 结论: 虚指数信号的频谱只在ω=ω0处有一冲激,因此也称虚指数信号为单频信号。 【例4-2-8】试求正弦型信号)cos(0t ω和)sin(0t ω的频谱X (j ω)。 分析: 正弦型信号在整个信号区间(-∞,+∞)上不满足绝对可积,但其Fourier 变换存在,可利用虚指数信号的频谱计算。 解: 利用Euler 欧拉公式,将正弦型信号用虚指数信号表示为 )e e (2 1 )cos(00j j 0t t t ωωω-+=,)e e (j 21)sin(00j j 0t t t ωωω--= 利用虚指数信号的频谱,可得正、余弦信号的频谱函数为 )]()([π)e e (21)cos(00j j 000ωωδωωδωωω++-?→←+=-F t t t )]()([j π)e e (j 21)sin(00j j 000ωωδωωδωωω+---?→←-=-F t t t 其时域波形和频谱分别如下图所示。 (a)余弦信号 (b)余弦信号的频谱 (c)正弦信号 (d)正弦信号的频谱 结论: 正弦型信号的频谱在0ωω±=处各有一冲激。 【例4-2-9】试求任意周期信号)(~t x 的频谱X (j ω)。 分析: 周期信号在整个信号区间(-∞,+∞)上不满足绝对可积,但其Fourier 变换存在。在求其Fourier 变换时,应先写出其Fourier 级数表示式,再利用虚指数信号的Fourier 变换计算。 解: 周期信号的Fourier 级数表示式为 t n n n C t x 0j e )(~ω∑ ∞ -∞ == , 0 0π 2T = ω 利用虚指数信号的Fourier 变换,对上式两边进行Fourier 变换,可得 ]e [)](~[)j (0j t n n n C t x X ωω∑+∞ -∞ ===F F ]e [0j t n n n C ω∑+∞ -∞ == F ) (π 20ω ωδn C n n -=∑+∞ -∞ = 结论: 连续周期信号的频谱密度函数X (j ω)是冲激串函数,冲激串前的系数为2πC n 。因此,连续周期信号的Fourier 系数C n 与其频谱密度函数X (j ω)是一致的。 【例4-2-10】试求周期冲激串∑+∞ -∞ =-= n T nT t t )()(0 0δδ的频谱X (j ω)。 分析: 利用任意周期信号)(~t x 的Fourier 变换即可求出。 解: 周期信号)(0t T δ的Fourier 系数C n 为 2 /2 /j 0 2 /2 /j 0 1d e )(1d e )(1 000 000 T t t T t t T C T T t n T T t n T n = = = ? ? --ωωδδ 利用任意周期信号)(~t x 的Fourier 变换,可得 )]([)j (0t X T δωF =)(π20ωωδn C n n -=∑ +∞ -∞ =) (π21 00ω ωδn T n -= ∑+∞ -∞ = )(00 ωωδωn n -=∑ +∞ -∞ =, 0 0π 2T = ω 周期冲激串信号)(0t T δ及其频谱如下图所示。 t (a) 周期冲激串信号 (b) 周期冲激串的频谱 结论: (1)周期冲激串信号)(0t T δ的频谱也是一个周期冲激串,并且它的周期ω0和)(0t T δ的周期T 0成反比。 (2) 周期信号的频谱C n 是计算周期信号频谱密度X (j ω)的关键。 (3) 周期冲激串信号在信号分析中具有重要作用。 【例4-2-11】已知信号x (t )的波形如下图所示,试求信号x (t )的频谱。 分析: 用基本信号的线性组合表示x (t )。 解: x (t )可以表示为直流信号与宽度为1矩形信号的相减,即 x (t ) = 2 – p 1(t ) 由连续时间Fourier 变换的线性特性可得 X (j ω)=4πδ(ω)-Sa(ω/2) 结论: (1)复杂信号可以表示为基本信号,根据基本信号的Fourier 变换以及信号Fourier 变换的性质就可以得到复杂的信号的Fourier 变换。 (2)当信号x (t )中存在直流分量时,其频谱X (j ω)中一般含有冲激函数。 【例4-2-12】试求双边指数信号t t x α-=e )()(∞<<-∞t 的频谱。 分析: t t x α-=e )(可以看成是单边指数信号)(e t u t α-的偶分量,利用)(e t u t α-的频谱和Fourier 变换的对称特性即可求出。 解: 单边指数信号)(e t u t α-的频谱为 2 222j j 1)(e ωαωωαα ωαα+-+=+?→ ←-F t u t 因为)(e t u t α-的偶分量为 )(e 2 1)](e )(e [21)(e t u t u t u t x t t t ααα--=-+= 利用实信号偶分量x e (t )的频谱为 X (j ω)的实部,可得 22j 1Re e 21ωααωαα+=??? ? ??+?→←-F t 故 2 22e ω αα α+?→ ←-F t 结论: 当x (t )为实偶对称信号时,其频谱函数X (j ω)也为实偶对称函数。 【例4-2-13】试求信号t t x π1 )(=的频谱函数X (j ω)。 分析: 利用符号函数的频谱和Foruier 变换的互易对称特性计算。 解: 符号函数的频谱为 ωj 2)sgn(?→ ←F t 根据Foruier 变换的互易对称特性可得 )sgn(π2)sgn(π2j 2ωω-=-?→←F t 再根据Fourier 变换的线性特性得 )sgn(j π1ω-?→←F t 结论: 在信号Hilbert 变换和信号单边带幅度调制中,信号t t x π1)(= 及其Fourier 变换)sgn(j )j (ωω-=X 得到广泛应用。 【例4-2-14】求连续时间信号)(Sa t 的频谱函数X (j ω)。 分析: 利用非周期矩形脉冲信号的频谱和Foruier 变换的互易对称特性计算。 解: 由常见信号的频谱可知,幅度为1宽度为2的矩形脉冲p 2 (t )的频谱为 )(Sa 2)(2ω?→←F t p 分别如下图(a)(b)所示。由Fourier 变换的互易对称特性可得 )(π2)(π2)(2Sa 22ωωp p t =-?→←F 其时、频谱波形分别如下图(c)(d)所示。由Fourier 变换的线性特性可得 )(π)(Sa 2ωp t ?→←F 式中)(2ωp 表示幅度为1宽度为2的矩形脉冲。 t (a) 矩形脉冲信号 (b) 矩形脉冲信号的频谱 t ω (c) 抽样信号)(Sa t (d) 抽样信号)(Sa t 的频谱 结论: (1)时域的矩形信号对应的频谱为抽样函数,而时域的抽样信号对应的频谱为矩形函数。 (2)从系统来看,若)(2ωp 是理想低通滤波器的频率响应,则其单位冲激响应h (t )是抽样函数)(Sa π 1 t 。 【例4-2-15】试求抽样信号)(Sa )(0t t x ω=的频谱函数X (j ω)。 分析: 利用抽样信号)(Sa t 的频谱和Fourier 变换的展缩特性计算。 解: 抽样信号)(Sa t 的频谱为 )(π)(Sa 2ωp t ?→←F 根据连续信号Fourier 变换的展缩特性可得 )(π)(π)(Sa 020 0200ωωωωωωωp p t =?→←F )(02ωωp 表示幅度为1宽度为2ω0的矩形脉冲。 结论: (1))(Sa t 的频谱是宽度为2的矩形脉冲,而)(Sa 0t ω的频谱是宽度为2ω0的矩形脉冲。这充分表明信号时域压缩,其对应的频谱函数扩展;信号时域扩展,其对应的频谱函数压缩。 (2)从系统来看,若)(02ωωp 是理想低通滤波器的频率响应,则其单位冲激响应h (t )是抽样函数 )(Sa π 00 t ωω。 【例4-2-16】试求信号x (t )=u (t +1)-u (t -3)的频谱函数X (j ω)。 分析: u (t +1)-u (t -3)是矩形脉冲信号,利用矩形脉冲信号的频谱和Foruier 变换的时移特性计算。 解: 因为 x (t )=u (t +1)-u (t -3)=p 4(t -1) p 4(t )表示宽度为4,幅度为1的矩形信号。 由于 )2(Sa 4)}({4ω=t p F 利用Fourier 变换的时移特性可得 )2(Sa e 4)}1({)j (j 4ωωω-=-=t p X F 结论: 信号在时域的时移将导致其频域的相移。若信号在时域的时移为常数,则在频域产生线性相移。 【例4-2-17】已知)j ()}({ωX t x =F ,g (t )=x (2t +4), 求信号g (t )的频谱。 分析: 信号x (2t +4)是x (t )经过压缩、平移两种基本运算而产生的信号,需要分别利用Fourier 变换的展缩特性和时移特性求其频谱。可以将x (t ) 先进行压缩再平移,也可以将x (t ) 先进行平移再压缩,两种方法的计算过程稍有不同,但结果一致。 解: 方法一:先对x (t )进行压缩 t t 2?→?,利用Fourier 变换的展缩特性得 )2 j (21)2(ωX t x ?→←F 再对x (2t )进行左移 2+?→?t t ,并利用Fourier 变换的时移特性得 ωω2j e )2j (21)42()]2(2[X t x t x ?→←+=+F 方法二:先对x (t )进行左移 4+?→?t t ,利用Fourier 变换的时移特性得 ωω4j e )j ()4(X t x ??→←+F 再对x (t +4)进行压缩 t t 2?→?,并利用Fourier 变换的展缩特性得 ωω 2j e )2 j (21)42(X t x ? ?→←+F 结论: 若信号g (t )=x (at +b ),(a ≠0),则存在ω ωωa b a X a G j e )j (||1)j (=。因为信号g (t )相对于信号 x (t ),存在a 倍的展缩和b /a 的时移。 【例4-2-18】已知信号x (t )的频谱函数X (j ω)如图(a)所示,试求信号x (t )与余弦信号cos(ω0t )相乘后信号a (t )的频谱函数。(ω0>ωm ) 分析: 将)cos(0t ω用虚指数信号表示为)e (e 2 1)cos(00j j 0t t t ωωω-+= , 再利用频移特性即可计算。 解: 由于 = ==)]cos()([)]([)j (0t t x t a A ωωF F ] e )([2 1 ]e )([2100j j t t t x t x ωω-+F F 故根据Fourier 变换的频移特性可得 x (t ) cos(ω0t ))](j [2 1 )](j [2100ωωωω++-? ?→←X X F 上式表明,信号x (t )与余弦信号cos(ω0t )相乘后,信号x (t ) cos(ω0t )的频谱是原来信号x (t )的频谱经左、右搬移ω0后相加,然后幅度减半。 ω (a) 信号x (t )的频谱 (b) 信号x (t ) cos(ω0t )的频谱 结论: 信号x (t )与余弦信号cos(ω0t )相乘后的频谱函数为 ()()[])(j )(j 2 1 )cos()(000ωωωωω++-?→ ←X X t t x F 信号x (t )与正弦信号sin(ω0t )相乘后的频谱函数为 ()()[])(j )(j 2 j )sin()(000ωωωωω+---??→←X X t t x F 这是连续时间信号幅度调制与解调的理论基础。 【例4-2-19】求下图(a)所示宽度为τ、幅度为A 的三角波信号的频谱。 分析: 等腰三角形可以看成是两个等宽矩形脉冲信号的卷积,利用卷积特性即可计算。 解: 设x 1(t )是一宽度为2、幅度为1的三角波信号。由于x 1(t )可由两个幅度为1、宽度为1的矩形信号p 1(t )卷积构成,即 p 1(t ) * p 1(t ) = x 1(t ) 因为 )2/(Sa )}({1ω=t p F 所以,利用Fourier 变换的卷积特性可得 )2/(Sa )}({21ω=t x F 利用Fourier 变换的线性特性和展缩特性,即可求出宽度为τ 、幅度为A 的三角波x (t )的频谱 函数为 )]2 /([)]([1τt Ax t x F F =)4(Sa 22ωτ τA = t (a) 宽度为τ 的三角波信号 (b) 宽度为2的三角波信号 结论: 由于任意等腰三角波信号都可以表示为两个等宽的矩形信号的卷积,而矩形信号的的频谱为抽样函数,因此,任意等腰三角波信号的的频谱必然为抽样函数的平方。 【例4-2-20】 已知信号x (t )的频谱函数X (j ω)如图(a)所示,试求)cos()()(0t t x t a ω=的频谱函数。(ω0>ωm ) 分析: 利用)cos(0t ω的Fourier 变换,和乘积特性即可计算。 解: )cos(0t ω的Fourier 变换为 )(π)(π)cos(000ωωδωωδω++-?→←F t 根据Fourier 变换的乘积特性,可得 )(π)(π*)(j π21 )]cos()([000ωωδωωδωω++-= X t t x F )](j [2 1 )](j [2100ωωωω++-=X X 上式表明,信号x (t )与余弦信号cos(ω0t )相乘后,信号x (t ) cos(ω0t )的频谱是原来信号x (t )的频谱经左、右搬移ω0后相加,然后幅度减半。 ω (a) 信号x (t )的频谱 (b) 信号x (t ) cos(ω0t )的频谱 结论: 信号x (t )乘以正弦型信号后的频谱,即可利用Fourier 变换的频移特性计算,也可利用Fourier 变换的乘积特性计算。 【例4-2-21】试求下图(a)所示三角波信号x (t )的频谱函数X (j ω)。 分析: 三角波信号x (t )的导数x 1(t )如下图(b)所示,从图中可以看出x 1(t )的面积为零,即 t t x X d )()0(11? ∞ ∞ -= =0。因此利用时域微分特性或时域积分特性均可计算其频谱。 解: 三角波信号x (t )的导数x 1(t )可以用矩形脉冲表示为 )2 1()21()()('111--+==t p t p t x t x 利用矩形脉冲p 1(t )的频谱,以及Fourier 变换的线性特性和时移特性,得 =)j (1ωX 2/j 2/j e )2/(Sa e )2/(Sa )]('[ωωωω--=t x F )2/sin()2/(jSa 2ωω= 方法一:利用Fourier 变换的时域微分特性,有 )j (j )j (1ωωωX X = 由此可得x (t )的频谱为 ω ωωj )j ()j (1X X = ωωω) 2/sin()2/(jSa 2= )2/(Sa 2ω= 方法二:利用Fourier 变换的时域积分特性,有 )()0(πj ) j ()j (111ωδω ωωX X X +=ωωj )j (1 X =)2/(Sa 2ω= t t (a)三角波信号 (b)三角波信号的导数 结论: 等腰三角波信号的Fourier 变换可以通过两个等宽的矩形信号的卷积来求解,也可以通过Fourier 变换的微分特性或积分特性来求解,该方法特别适合不等腰三角波信号的频谱分析。因此也可以推出,不等腰三角波信号的Fourier 变换不可能表示为抽样函数的平方。 【例4-2-22】试求下图(a)所示信号x (t )的频谱函数X (j ω)。 分析: 信号x (t )的导数x 1(t )如下图(b)所示,从图中可以看出x 1(t )的面积为1,即 t t x X d )()0(11? ∞ ∞ -= =1。因此不能利用时域微分特性,只能利用时域积分特性或修正的微分 特性计算其频谱。 解: 信号x (t )的导数x 1(t )可以用矩形脉冲表示为 )2 1()()('11-==t p t x t x 利用矩形脉冲p 1(t )的频谱,以及Fourier 变换的时移特性,得 )2 (Sa e )j (2/j 1ω ωω-=X 方法一:利用连续信号Fourier 变换的积分特性,可得 )()0(π)j (j 1)j (11ωδωωωX X X +=)(πe )2 (Sa j 12/j ωδω ωω+=- 方法二:利用修正的微分特性,由图(a)可知0)(,1)(=-∞=∞x x ,故可得 ωωωδωj )j ()()]()([π)j (1X x x X +-∞+∞=)(πe )2 (Sa j 12/j ωδω ωω+=- t t (a)信号x (t )波形 (b) x (t )导数的波形 结论: 设X 1(j ω)是信号x (t )的导数x 1(t )的频谱,若0)0(1≠X ,则不能利用微分特性计算,只能利用时域积分特性或修正的微分特性计算其频谱。 【例4-2-23】试求下图(a)所示信号x (t )的频谱函数X (j ω)。 分析: 信号x (t )的导数x 1(t )如下图(b)所示,从图中可以看出x 1(t )的面积为1,即 t t x X d )()0(11? ∞ ∞ -= =1,因此不能利用时域微分特性。若利用时域积分特性,则计算出的频 谱与例5-3-12相同,即得出的是例5-3-12信号的频谱,忽略了本题信号中的直流分量1, 因此本题只能利用修正的微分特性计算频谱。 解: 信号x (t )的导数x 1(t )可以用矩形脉冲表示为 )2 1()()('11-==t p t x t x 利用矩形脉冲p 1(t )的频谱,以及Fourier 变换的时移特性,得 )2 (Sa e )j (2/j 1ω ωω-=X 由图(a)可知1)(,2)(=-∞=∞x x ,利用修正的微分特性可得 ωωωδωj )j ()()]()(π[)j (1X x x X + -∞++∞=2/j e )2 (Sa j 1)(π3ωω ωωδ-+= t t (a) 信号x (t )波形 (b) x (t )导数的波形 结论: (1)若信号含有直流分量,则只能利用修正的微分特性计算其频谱。 (2)综合例5-3-11、例5-3-12和例5-3-13可以看出,若信号x (t )的频谱需要借助其导数x 1(t )的频谱计算,则直接利用修正的微分特性计算其频谱较为简便。因为这样可以不必进行信号中是否含有直流,以及)0(1X 是否为零的判断。 【例4-2-24】分别求信号)(e )(),()(,)(,)(t u t t x t tu t x t t x t t x t α-====的频谱。 分析: 分别利用直流信号、符号函数、阶跃信号及单边指数信号的频谱和频域微分特性计算。 解: 利用常见信号的频谱函数,以及Fourier 变换的频域微分特性,可得其频谱。 由于 )(π21ωδ??→ ←F 因此有 )('πj 2ωδ?→←F t 由于 ω j 2 )sgn(?→ ←F t 因此有 22 )j 2(d d j )sgn(ω ωω-=??→←=F t t t 由于ωωδj 1)(π)(+ ??→←F t u 因此有 }j 1)(π{d d j )(ωωδω+??→←F t tu 21)('j πω ωδ-= 由于ωααj 1 )(e +? →←-F t u t 因此有 )j 1(d d j )(e ωαωα+??→ ←-F t u t t 2) j (1ωα+= 结论: 这些信号是常用信号,其与基本信号之间存在密切关系,应理解和掌握这些常用信号的Fourier 变换及其求解方法。 【例4-2-25】已知能量信号x (t )=e -3 t u (t ),若以 %95d )j (B B ≥?- E G ωω ωω 信号与系统期末考试试题 一、选择题(共10题,每题3分 ,共30分,每题给出四个答案,其中只有一个正确的) 1、 卷积f 1(k+5)*f 2(k-3) 等于 。 (A )f 1(k)*f 2(k) (B )f 1(k)*f 2(k-8)(C )f 1(k)*f 2(k+8)(D )f 1(k+3)*f 2(k-3) 2、 积分 dt t t ? ∞ ∞ --+)21()2(δ等于 。 (A )1.25(B )2.5(C )3(D )5 3、 序列f(k)=-u(-k)的z 变换等于 。 (A ) 1-z z (B )-1-z z (C )11-z (D )1 1--z 4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。 (A ) )2(41t y (B ))2(21t y (C ))4(41t y (D ))4(2 1 t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时,系 统的零状态响应y f (t)等于 (A )(-9e -t +12e -2t )u(t) (B )(3-9e -t +12e -2t )u(t) (C ))(t δ+(-6e -t +8e -2t )u(t) (D )3)(t δ +(-9e -t +12e -2t )u(t) 6、 连续周期信号的频谱具有 (A ) 连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性 7、 周期序列2)455.1(0 +k COS π的 周期N 等于 (A ) 1(B )2(C )3(D )4 8、序列和 ()∑∞ -∞ =-k k 1δ等于 (A )1 (B) ∞ (C) ()1-k u (D) ()1-k ku 9、单边拉普拉斯变换()s e s s s F 22 12-+= 的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u te t f t 的单边拉氏变换()s F 等于 ()A ()()()232372+++-s e s s ()() 2 23+-s e B s 第四章 典型例题 【例4-1-1】写出下图所示周期矩形脉冲信号的Fourier 级数。 t 周期矩形信号 分析: 周期矩形信号)(~t x 是实信号,其在一个周期[-T 0/2,T 0/2]内的定义为 ???>≤=2/ 02/ )(~ττt t A t x 满足Dirichlet 条件,可分别用指数形式和三角形式Fourier 级数表示。 解: 根据Fourier 级数系数C n 的计算公式,有 t t x T C t n T T n d e )(~ 1000j 2/2/0ω--?=== --? t A T t n d e 10j 2/2 /0ωττ 2/2/j 000e )j (ττωω=-=--t t t n n T A 2/)2/sin(00τωτωτTn n A =)2 (Sa 00τωτn T A = 故周期矩形信号)(~ t x 的指数形式Fourier 级数表示式为 t n n t n n n n T A C t x 00j 00j e )2(Sa )(e )(~ωωτωτ∑∑∞ -∞ =∞-∞=== 利用欧拉公式 2 e e )cos(00j j 0t n t n t n ωωω-+= 可由指数形式Fourier 级数写出三角形式的Fourier 级数,其为 ()t n n T A T A t x n 0001 0cos )2(Sa )2()(~ωτωττ∑ ∞ =+= 结论: 实偶对称的周期矩形信号)(~ t x 中只含有余弦信号分量。 【例4-1-2】写出下图所示周期三角波信号的Fourier 级数。 t 周期三角波信号 分析: 周期矩形信号)(~ t x 是实信号,其在一个周期 [-1/2,3/2]的表达式为 《信号与系统》复习题 1. 已知f(t)如图所示,求f(-3t-2)。 2. 已知f(t),为求f(t0-at),应按下列哪种运算求得正确结果?(t0和a 都为正值) 3.已知f(5-2t)的波形如图,试画出f(t)的波形。 解题思路:f(5-2t)?????→?=倍 展宽乘22/1a f(5-2×2t)= f(5-t) ??→?反转f(5+t)??→?5 右移 f(5+t-5)= f(t) 4.计算下列函数值。 (1) dt t t u t t )2(0 0--?+∞ ∞-) (δ (2) dt t t u t t )2(0 --?+∞ ∞-) (δ (3) dt t t e t ?+∞ ∞ --++)(2)(δ 5.已知离散系统框图,写出差分方程。 解:2个延迟单元为二阶系统,设左边延迟单元输入为x(k) 左○ ∑:x(k)=f(k)-a 0*x(k-2)- a 1*x(k-1)→ x(k)+ a 1*x(k-1)+ a 0*x(k-2)=f(k) (1) 右○ ∑: y(k)= b 2*x(k)- b 0*x(k-2) (2) 为消去x(k),将y(k)按(1)式移位。 a 1*y(k-1)= b 2* a 1*x(k-1)+ b 0* a 1*x(k-3) (3) a 0*y(k-2)= b 2* a 0*x(k-2)-b 0* a 0*x(k-4) (4) (2)、(3)、(4)三式相加:y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b 2*[x(k)+ a 1*x(k-1)+a 0*x(k-2)]- b 0*[x(k-2)+a 1*x(k-3)+a 0*x(k-4)] ∴ y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b 2*f(k)- b 0*f(k-2)═>差分方程 6.绘出下列系统的仿真框图。 )()()()()(10012 2t e dt d b t e b t r a t r dt d a t r dt d +=++ 7.判断下列系统是否为线性系统。 (2) 8.求下列微分方程描述的系统冲激响应和阶跃响应。 )(2)(3)(t e dt d t r t r dt d =+ 1.一线性时不变系统在相同的初始条件下,当激励为f(t)[t<0时,f(t)=0]时,其全响应为y 1(t)=2e -t +cos2t,t>0时;当激励为2f(t)时,其全响应为y 2(t)=e -t +2cos2t,t>0;试求在同样的初始条件下,当激励为4f(t)时系统全响应。 解:设系统的零输入响应为x y )(t ,激励为f(t)时的零状态响应为)(t y f ,则有 y 1(t) = x y )(t +)(t y f =2e -t +cos2t y 2(t)= x y )(t +)(t y f = e -t +2cos2t 联解得 )(t y f = -e -t +cos2t x y )(t = 3e -t 故得当输入激励为4f(t)时的全响应为 y(t)= x y )(t +4)(t y f =3e -t +4[-e -t +cos2t]= -e -t +4cos2t t>0 2.如图2.1(a )所示电路,激励f(t)的波形如图2.1(b)所示。试求零状态响应)(t u c ,并画出波形。 解 该电路的微分方程为 )(22 t f u dt u d c c =+ 即 ()1(2t f u p c =+ 转移算子为 1 1)(2 +=p p H 故得单位冲激响应为 )(sin )(t tU t h = 故得 ?∞ -'==t c d U t f t h t f t u τττ)(sin *)()(*)()( =?--t d t t 0 sin *)]6()([ττπδδ =t t t 0]cos [*)]6()([τπδδ--- =)(]cos 1[*)]6()([t U t t t ---πδδ 试题一 一. 选择题(共10题,20分) 1、n j n j e e n x )3 4( )3 2(][ππ+=,该序列是 。 A.非周期序列 B.周期3=N C.周期8/3=N D. 周期24=N 2、一连续时间系统y(t)= x(sint),该系统是 。 A.因果时不变 B.因果时变 C.非因果时不变 D.非因果时变 3、一连续时间LTI 系统的单位冲激响应)2() (4-=-t u e t h t ,该 系统是 。 A.因果稳定 B.因果不稳定 C.非因果稳定 D. 非因果不稳定 4、若周期信号x[n]是实信号和奇信号,则其傅立叶级数系数a k 是 。 A.实且偶 B.实且为奇 C.纯虚且偶 D. 纯虚且奇 5、一信号x(t)的傅立叶变换?? ?><=2||02||1)(ωωω, , j X ,则x(t)为 。 A. t t 22sin B. t t π2sin C. t t 44sin D. t t π4sin 6、一周期信号∑∞ -∞ =-= n n t t x )5()(δ,其傅立叶变换 ) (ωj X 为 。 A. ∑∞-∞ =- k k ) 5 2(5 2πωδπ B. ∑∞ -∞ =- k k )5 2(25 πωδπ C. ∑∞ -∞ =-k k )10(10πωδπ D. ∑∞ -∞ =-k k )10(101 πωδπ 7、一实信号x[n]的傅立叶变换为)(ω j e X ,则x[n]奇部的傅立叶变 换为 。 A. )}(Re{ωj e X j B. )}(Re{ωj e X C. )}(Im{ωj e X j D. )}(Im{ωj e X 8、一信号x(t)的最高频率为500Hz ,则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 。 A. 500 B. 1000 C. 0.05 D. 0.001 9、一信号x(t)的有理拉普拉斯共有两个极点s=-3和s=-5,若 ) ()(4t x e t g t =,其傅立叶变换 ) (ωj G 收敛,则x(t) 是 。 A. 左边 B. 右边 C. 双边 D. 不确定 10、一系统函数1}Re{1 )(->+=s s e s H s ,,该系统是 。 A. 因果稳定 B. 因果不稳定 C. 非因果稳定 D. 非因果不稳定 二. 简答题(共6题,40分) 1、 (10分)下列系统是否是(1)无记忆;(2)时不变;(3)线性; (4)因果;(5)稳定,并说明理由。 (1) y(t)=x(t)sin(2t); (2)y(n)= ) (n x e 2、 (8分)求以下两个信号的卷积。 ?? ?<<=值 其余t T t t x 0 01)(, ?? ?<<=值 其余t T t t t h 0 20)( 3、 (共12分,每小题4分)已知)()(ωj X t x ?,求下列信号的傅里叶变换。 (1)tx(2t) (2) (1-t)x(1-t) (3)dt t dx t ) ( 4. 求 2 2)(22++=-s s e s s F s 的拉氏逆变换(5分) 5、已知信号sin 4(),t f t t t ππ=-∞<<∞,当对该信号取样时,试求 能恢复原信号的最大抽样周期T max 。(5分) ,求系统的响应。 )若(应;)求系统的单位冲激响(下列微分方程表征: 系统的输入和输出,由分)一因果三、(共)()(21) (2)(15) (8)(LTI 1042 2t u e t x t x t y dt t dy dt t dy t -==++ 四、(10分)求周期矩形脉冲信号的傅立叶级数(指数形式),并大概画出其频谱图。 不是因果的。 )系统既不是稳定的又()系统是因果的; (系统是稳定的;系统的单位冲激响应)求下列每一种情况下(的零极点图;,并画出)求该系统的系统函数(下列微分方程表征:系统的输入和输出,由分)一连续时间五、(共c b a t h s H s H t x t y dt t dy dt t dy )() (2)()(1)()(2) ()(LTI 202 2=-- 试题二 一、选择题(共10题,每题3分 ,共30分,每题给出四个答案, 其中只有一个正确的) 1、 卷积f 1(k+5)*f 2(k-3) 等于 。 A )f 1(k)*f 2(k) Bf 1(k)*f 2(k-8) C )f 1(k)*f 2(k+8) D)f 1(k+3)*f 2(k-3) 2、 积分dt t t ?∞ ∞--+)21()2(δ等于 。 (A )1.25 (B )2.5 (C )3 (D )5 3、 序列f(k)=-u(-k)的z 变换等于 。 αω ωδα+=+==-s e L s s t L t L t 1 ][)][cos(1)]([2 2;;t t t Sa j F t u e t f t sin )(1 )()()(= +=?=-; 注:ωαωα 信科0801《信号与系统》复习参考练习题一、单项选择题: 14、已知连续时间信号,) 2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为() A .400rad /s B 。200 rad /s C 。100 rad /s D 。50 rad /s f如下图(a)所示,其反转右移的信号f1(t) 是() 15、已知信号)(t f如下图所示,其表达式是() 16、已知信号)(1t A、ε(t)+2ε(t-2)-ε(t-3) B、ε(t-1)+ε(t-2)-2ε(t-3) C、ε(t)+ε(t-2)-ε(t-3) D、ε(t-1)+ε(t-2)-ε(t-3) 17、如图所示:f(t)为原始信号,f1(t)为变换信号,则f1(t)的表达式是() A、f(-t+1) B、f(t+1) C、f(-2t+1) D、f(-t/2+1) 18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是( ) 19。信号)2(4sin 3)2(4cos 2)(++-=t t t f π π 与冲激函数)2(-t δ之积为( ) A 、2 B 、2)2(-t δ C 、3)2(-t δ D 、5)2(-t δ ,则该系统是()>-系统的系统函数.已知2]Re[,6 51)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统 C 、因果稳定系统 D 、非因果不稳定系统 21、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是( ) A 、常数 B 、 实数 C 、复数 D 、实数+复数 22、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是( ) A 、阶跃信号 B 、正弦信号 C 、冲激信号 D 、斜升信号 《信号与系统》练习题 1、线性性质包含两个内容: 和 。(可加性、齐次性) 2、线性时不变(LTI )连续系统的数学模型是线性常系数 方程。(微分) 线性时不变(LTI )离散系统的数学模型是线性常系数 方程。(差分) 3、线性时不变系统具有 、 和 。(微分特性、积分特性、频率保持性。) 4、连续系统的基本分析方法有: 分析法, 分析法和 分析法。(时域、频域、复频域或s 域) 系统依处理的信号形式,可以分为三大类:连续系统、离散系统和混合系统。 5、周期信号频谱的特点是 、 、 。(离散性、谐波性、收敛性) 6、(1)LTI 连续系统稳定的充要条件是 。( ∞ 《信号与系统》复习题 1.已知 f(t) 如图所示,求f(-3t-2) 。 2.已知 f(t) ,为求 f(t0-at) ,应按下列哪种运算求得正确结果?(t0 和 a 都为正值) 3.已知 f(5-2t) 的波形如图,试画出f(t) 的波形。 解题思路:f(5-2t)乘a 1 / 2展宽 2倍f(5-2 × 2t)= f(5-t) 反转 右移 5 f(5+t) f(5+t-5)= f(t) 4.计算下列函数值。 ( 1) ( 2) ( t ) t 0 )dt t 0 u(t 2 (t t 0)u(t 2t 0 )dt ( 3) (e t t ) (t 2)dt 5.已知离散系统框图,写出差分方程。 解: 2 个延迟单元为二阶系统,设左边延迟单元输入为 x(k) ∑ 0 1 1) → 左○ :x(k)=f(k)-a *x(k-2)- a*x(k- x(k)+ a 1*x(k-1)+ a 0*x(k-2)=f(k) (1) ∑ y(k)= b 2*x(k)- b 0*x(k-2) (2) 右○ : 为消去 x(k) ,将 y(k) 按( 1)式移位。 a 1*y(k-1)= b 2 * a 1*x(k-1)+ b * a 1*x(k-3) (3) a 0*y(k-2)= b 2 * a 0*x(k-2)-b 0* a 0*x(k-4) (4) (2) 、( 3)、( 4)三式相加: y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b *[x(k)+ a 1 *x(k-1)+a *x(k-2)]- b *[x(k-2)+a 1*x(k-3)+a *x(k-4)] 2 0 0 0 ∴ y(k)+ a 1 *y(k-1)+ a *y(k-2)= b 2 *f(k)- b *f(k-2) ═ >差分方程 第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。 (2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。 (1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6 sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5) )2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6 sin()(--=k k k k f εεπ (12) )]()3([2)(k k k f k ---=εε 1-3 写出图1-3所示各波形的表达式。 1-4 写出图1-4所示各序列的闭合形式表达式。 1-5 判别下列各序列是否为周期性的。如果是,确定其周期。 (2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+= 信号与系统 习题 1 一、填空题 1.离散信号()2()k f k k ε=,则该信号的单边Z 变换为 ① 。 2.信号()f t 的傅里叶变换为()F j ω,则(23)f t -的傅里叶变换为 ① 。 3.已知周期信号()cos(230)sin(4+60)f t t t =++,则其周期为 ① s ,基波频率为 ② rad/s 。 4、已知)(1t f 和)(2t f 的波形如下图所示,设)()()(21t f t f t f *=,则=-)1(f ① , =)0(f ② 。 5、单边拉氏变换()) 4(2 2 += s s s F ,其反变换()=t f ① 。 6、一离散系统的传输算子为2 3)(22+++=E E E E E H ,则系统对应的差分方程为 ① , 单位脉冲响应为 ② 。 二、单项选择题 1. 下列说法不正确的是______。 A. 每个物理系统的数学模型都不相同。 B. 同一物理系统在不同的条件下,可以得到不同形式的数学模型。 C. 不同的物理系统经过抽象和近似,有可能得到形式上完全相同的数学模型。 D. 对于较复杂的系统,同一系统模型可有多种不同的数学表现形式。 2. 周期信号f (t )的傅立叶级数中所含有的频率分量是______。 A. 余弦项的奇次谐波,无直流 B. 正弦项的奇次谐波,无直流 C. 余弦项的偶次谐波,直流 D. 正弦项的偶次谐波,直流 3. 当周期矩形信号的脉冲宽度缩小一半时,以下说确的是_____。 A. 谱线间隔增加一倍 B. 第一个过零点增加一倍 C. 幅值不变 D. 谱线变成连续的 4. 图3所示的变化过程,依据的是傅立叶变换的_____。 图3A. 时移性 B. 频移性 C. 尺度变换 D. 对称性 5. 对抽样信号进行恢复,需将信号通过_____。 A. 理想带通滤波器 B. 理想电源滤波器 C. 理想高通滤波器 D. 理想低通滤波器 6. 连续周期信号的频谱有_____。 A. 连续性、周期性 B. 连续性、收敛性 C. 离散性、周期性 D. 离散性、收敛性 7. 若对)(t f 进行理想取样,其奈奎斯特取样频率为s f ,对)231 (-t f 进行取样,其奈奎斯 特取样频率为_____。 A. 3s f B. s f 31 C. 3(s f -2) D. )2(3 1 -s f 8. 信号f (t )变成)12 1 (+t f 的过程为_____。 A. 先将f (t )的图形向左移一个单位,再时间上展宽1/2倍 B. 先将f (t )的图形向左移一个单位,再时间上展宽1/2倍 C. 先将f (t )的图形向左移一个单位,再时间上展宽1/2倍 D. 先将f (t )的图形向左移一个单位,再时间上展宽1/2倍 9. 下列傅里叶变换性质中错误的是_____。 A. 时间与频率标度)(1 )(ω? F a at f F B. 时移特性)()(00ω-ω-?F e t t f t j F C. 频移特性)()(00ω-ω?ωF t f e F t j (b ) ω (ω)ω π 2πτ4πτ (d )2π τ - 4πτ - o -π ?(b ) (a ) -1 第四章习题 4.6求下列周期信号的基波角频率 Ω和周期T 解 ⑴角频率为Ω = IOO rad∕s,周期丁=盲=p÷ξ ⑵角频率为I fi=号■ rad∕s,周期= 4 s (3) 角频率为Ω = 2 rad 倉,周期T = ~ = Tr S (4) 角频率为Q =兀rad∕ s,周期T=^ = 2 s Ω (5) 角频率为 Ω — rad∕s*周期 T=-^ = 8 s 4 12 ⑹角频率为C =話rad∕s,周期T = -jy = 60 s 4.7用直接计算傅里叶系数的方法, 求图4-15所示周期函数 的傅里叶系数(三角形式或指数形式) (1) e j100t (2) cos[,t - 3)] (3) cos(2t) sin(4t) ⑷ cos(2 兀 t) +cos(3πt) +cos(5 兀 t) (5) π π cos( t) sin( t) 2 4 (6) JEJITE cos( t) cos( t) cos( t) 2 3 5 -2 -1 O 1 2 3 r (IJ) 图4-15 f >~ 十 解 ⑴周期T = 4,1Ω = Y =亍r 则有 H , 4? - 1 ≤ r ≤ 4?+ 1 /⑺=I I ∣07 4? + 1 < r < 4? + 3 由此可得 -T u rt = ~? ' τ fit) cost nΩt)dt = -∣^∣ /(f)cos(^ψ^)df J- J —? 乙-.:—2 I (2}周期丁=2?0 =年=兀,则有 由此可得 1 + e -jrhr 2π( I - √ ) 所含有的频率分量 )dr = 2 J -[ 2『亍 =Wl f(t)sm(ττΩt)dt = 1 J -T 2 ——SIn nπ (才),= om 小山 (竽)出 I Sin(Jrt) 9 fm =! 0, 2? ≤ r ≤ 2? + 1 2? + 1 < r < 2? + 2 F ri ]ft 1 Γl = TJV Cf)^dr = ?J r ∣ /(r)e -7iβ, dr — -7- Sin(^f)e - dr -I ZJV 4.10利用奇偶性判断图 4-18示各周期信号的傅里叶系数中 扣 =O* ± 1 * + 2?? 信号与系统 考试方式:闭卷 考试题型:1、简答题(5个小题),占30分;计算题(7个大题),占70分。 一、简答题: 1.dt t df t f x e t y t ) ()()0()(+=-其中x(0)是初始状态, 为全响应,为激励,)()(t y t f 试回答该系统是否是线性的?[答案:非线性] 2.)()(sin )('t f t ty t y =+试判断该微分方程表示的系统是线性的还是非线性的,是时 变的还是非时变的?[答案:线性时变的] 3.已知有限频带信号)(t f 的最高频率为100Hz ,若对)3(*)2(t f t f 进行时域取样, 求最小取样频率s f =?[答案:400s f Hz =] 4.简述无失真传输的理想条件。[答案:系统的幅频特性为一常数,而相频特性为通过原点的直线] 5.求[]?∞ ∞ --+dt t t e t )()('2δδ的值。[答案:3] 6.已知)()(ωj F t f ?,求信号)52(-t f 的傅立叶变换。 [答案:521(25)()22 j f t e F j ωω --?] 7.已知)(t f 的波形图如图所示,画出)2()2(t t f --ε的波形。 [答案: ] 8.已知线性时不变系统,当输入)()()(3t e e t x t t ε--+=时,其零状态响应为 )()22()(4t e e t y t t ε--+=,求系统的频率响应。[答案:()) 4)(2(52)3(++++ωωωωj j j j ] 9.求象函数2 ) 1(3 2)(++=s s s F ,的初值)0(+f 和终值)(∞f 。 [答案:)0(+f =2,0)(=∞f ] 10.若LTI 离散系统的阶跃响应为)(k g ,求其单位序列响应。 其中:)()2 1 ()(k k g k ε=。 [答案:1111 ()()(1)()()()(1)()()(1)222 k k k h k g k g k k k k k εεδε-=--=--=--] 11.已知()1 1 , 0,1,20 , k f k else ==??? ,()2 1 , 0,1,2,3 0 , k k f k else -==??? 设()()()12f k f k f k =*,求()3?f =。[答案:3] 12.描述某离散系统的差分方程为()()()122()y k y k y k f k +---= 求该系统的单位序列响应()h k 。[答案:21()[(2)]()33 k h k k ε=-+] 13.已知函数()f t 的单边拉普拉斯变换为()1 s F s s =+,求函数()()233t y t e f t -=的单边拉普 拉斯变换。[答案:()2 5 Y s s s = ++] 14.已知()()12f t f t 、的波形如下图,求()()()12f t f t f t =*(可直接画出图形) 信号与系统复习参考练习题一、单项选择题: 14、已知连续时间信号,)2(100) 2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为() A .400rad /s B 。200 rad /s C 。100 rad /s D 。50 rad /s f如下图(a)所示,其反转右移的信号f1(t) 是() 15、已知信号)(t f如下图所示,其表达式是() 16、已知信号)(1t A、ε(t)+2ε(t-2)-ε(t-3) B、ε(t-1)+ε(t-2)-2ε(t-3) C、ε(t)+ε(t-2)-ε(t-3) D、ε(t-1)+ε(t-2)-ε(t-3) 17、如图所示:f(t)为原始信号,f1(t)为变换信号,则f1(t)的表达式是() A、f(-t+1) B、f(t+1) C、f(-2t+1) D、f(-t/2+1) 18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是() 19。信号)2(4sin 3)2(4cos 2)(++-=t t t f π π 与冲激函数)2(-t δ之积为( ) A 、2 B 、2)2(-t δ C 、3)2(-t δ D 、5)2(-t δ ,则该系统是()>-系统的系统函数.已知2]Re[,6 51)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统 C 、因果稳定系统 D 、非因果不稳定系统 21、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是( ) A 、常数 B 、 实数 C 、复数 D 、实数+复数 22、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是( ) A 、阶跃信号 B 、正弦信号 C 、冲激信号 D 、斜升信号 23. 积分 ?∞ ∞-dt t t f )()(δ的结果为( ) A )0(f B )(t f C.)()(t t f δ D.)()0(t f δ 24. 卷积)()()(t t f t δδ**的结果为( ) A.)(t δ B.)2(t δ C. )(t f D.)2(t f 专业课习题解析课程 第2讲 第一章信号与系统(二) 1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。 (2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4)) t fε= (sin )(t (5)) t f= r )(t (sin (7))( t f kε )(k 2 = (10))(])1( 1[ k f kε )(k = - + 1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。 (1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11) )]7()()[6 sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε (2) )2()1(2)()(-+--=t r t r t r t f (5) )2()2()(t t r t f -=ε 1、 若系统的输入f (t)、输出y (t) 满足()3()4t y t e f t -=,则系统为 线性的 (线性的、非线性 的)、 时变的 (时变的、时不变)、 稳定的 (稳定的、非稳定的)。 2、 非周期、连续时间信号具有 连续 、非周期频谱;周期、连续时间信号具有离散、非周期 频谱; 非周期、离散时间信号具有 连续 、周期频谱;周期、离散时间信号具有离散、 周期 频谱。 3、 信号f(t)的占有频带为0-10KHz,被均匀采样后,能恢复原信号的最大采样周期为 5×10-5 s . 4、 )100()(2 t Sa t f =是 能量信号 (功率信号、能量信号、既非功率亦非能量信号)。 5、 ()2cos()f t t =+是 功率信号 (功率信号、能量信号、既非功率亦非能量信号)。 6、 连续信号f(t)=sint 的周期T 0= 2π ,若对f(t)以fs=1Hz 进行取样,所得离散序列f(k)= sin(k) ,该离散序列是周期序列? 否 。 7、 周期信号2sin(/2)()j n t n n f t e n ππ+∞ =-∞ = ∑,此信号的周期为 1s 、直流分量为 2/π 、频率为5Hz 的谐波分量的幅值为 2/5 。 8、 f (t) 的周期为0.1s 、傅立叶级数系数**033555 32F F F F F j --=====、其余为0。试写 出此信号的时域表达式f (t) = 5 + 6 cos ( 60 π t ) - 4 sin (100 π t ) 。 9、 f (k) 为周期N=5的实数序列,若其傅立叶级数系数()205=F ()5 2511, πj e F -+= ()5 4512πj e F -+=、 则F 5 (3 )= ()5 4512πj e F +=- 、F 5 (4 )= ()5 2511π j e F +=- 、F 5 (5 )= 2 ; f(k) =())1.725 4 cos(62.052)9.3552cos(62.152525140525?-?+?-?+=∑=k k e n F n k jn πππ 。 10、 离散序列f(k) = e j 0.3k 的周期N 不存在 。 11、 离散序列f (k) = cos (0.3πk)的周期N= 20 。 12、 若有系统()dx x f e t y t x t ? ∞ ----= 2)()(,则其冲激响应=)(t h ()2)2(---t e t ε 。 13、 若有系统()dt t f t y t ? ∞ -=)(,则其=)(t h ()t ε 、=)(ωj H ()ωπδω +j 1 。 14、 若有系统dt t df t y ) ()(= ,则其=)(t h ()t 'δ 、ωωj j H =)( 。 第三章 典型例题 共计 13 题 【例3-1-1】已知)1()()(--=t u t u t x 通过一个连续时间LTI 系统的响应为)1()1()(-++=t t t y δδ 试求图3-1-1所示信号)(t g 通过该系统的响应)(t y g ,并画出其波形。 t 题3-1-1图 分析: 连续时间LTI 系统的特点是“对输入信号进行线性变换、延时,相应的输出信号也为原输出信号的相应线性变换和延时”。利用系统特点,找到)(t g 与)(t x 的线性和时间关系,从而得到相应的系统响应。 解: 根据信号x (t )、g (t )的波形可以确定出g (t )与x (t )的关系为 [k ] x [k ] 利用线性非时变系统的特性,可得系统响应y g (t )与y (t )的关系为 )2()1()()1()1(---=--t y t y t y g 由此可得 ττδτδττδτδd )]1()1([d )]1()1([)(2 1 -++--++=? ? -∞ --∞ -t t g t y )3()2()1()(---+--=t u t u t u t u 结论: 通过分析比较,发现原输入信号与新输入信号之间的关系是关键。 【例3-2-1】已知某二阶连续时间LTI 系统的微分方程 0),()(8)('6)(">=++t t x t y t y t y 初始状态y (0-)=1, y '(0-)=2。 分析: 根据微分方程的理论和零输入响应的定义,零输入响应对应齐次微分方程的齐次解,所以可以利用初始状态条件及特征方程求得系统的齐次解,即得)(zi t y 。 解:系统的特征方程为 s 2+6s +8 = 0 解特征方程,得特征根为 s 1 = -2, s 2 = -4(两不等实根) 故设系统的零输入响应)(zi t y 为 t t K K t y 4221zi e e )(--+= ,-≥0t 代入初始状态y (0-)和y '(0-)的值,有 y (0-)=K 1+K 2=1 )0('-y =2142K K --=2 解得K 1=3,K 2= -2 。因此零输入响应为 t t t y 42zi e 2e 3)(---= ,-≥0t 结论:系统零输入响应与输入无关,系统微分方程对应的特征根决定系统零输入响应的形式, 1,某系统(7,4)码 )()(01201230123456c c c m m m m c c c c c c c ==c 其三位校验位与信息位的关 系为: (1)求对应的生成矩阵和校验矩阵; (2)计算该码的最小距离; (3)列出可纠差错图案和对应的伴随式; (4)若接收码字R =1110011,求发码。 解:(1)10001100 10001100101110 001101G ?? ??? ?=?? ???? 101110011100100111001H ?? ??=?????? (2)d min =3 (3) S E 000 0000000 001 0000001 010 ******* 100 0000100 101 0001000 111 0010000 011 0100000 110 1000000 (4).RH T =[001]接收出错 E =0000001R+E=C =1110010(发码) 2. 已知(),X Y 的联合概率(),p x y 为: 求()H X ,()H Y ,(),H X Y ,();I X Y 解: (0)2/3p x ==(1)1/3p x == ()()(1/3,2/3)H X H Y H ===0.918bit/symbol (),(1/3,1/3,1/3)H X Y H ==1.585bit/symbol ();()()(,)I X Y H X H Y H X Y =+-=0.251bit/symbol 3.一阶齐次马尔可夫信源消息集},,{321a a a X ∈, 状态集},,{321S S S S ∈,且令3,2,1,==i a S i i ,条件转移概率为 [ ] ?? ?? ? ?????=03132313131214141)/(i j S a P ,(1)画出该马氏链的状态转移图; (2)计算信源的极限熵。 01 X Y 011/31/30 1/3 信号与系统 习题 1 号 f(k) 2k (k),则该信号的单边 Z 变换为 ① 。 2.信号 f (t)的傅里叶变换为 F(j ),则 f (2t 3)的傅里叶变换为 ① 。 3.已知周期信号 f (t) cos(2t 30o ) sin(4t+60o ),则其周期为 ① s ,基波频率为 ② rad/s 。 4、已知 f 1(t)和 f 2 (t )的波形如下图所示,设 f(t) f 1(t) f 2(t),则 f( 1) ① , 单位脉冲响应为 ② 。 、单项选择题 1. 下列说法不正确的是 _______ 。 A. 每个物理系统的数学模型都不相同。 B. 同一物理系统在不同的条件下,可以得到不同形式的数学模型。 C. 不同的物理系统经过抽象和近似,有可能得到形式上完全相同的数学模型 D. 对于较复杂的系统,同一系统模型可有多种不同的数学表现形式。 2. 周期信号 f (t)的傅立叶级数中所含有的频率分量是 _______ 。 A. 余弦项的奇次谐波,无直流 B. 正弦项的奇次谐波,无直流 C. 余弦项的偶次谐波,直流 D. 正弦项的偶次谐波,直流 3. 当周期矩形信号的脉冲宽度缩小一半时,以下说法正确的是 ______ 。 A. 谱线间隔增加一倍 B. 第一个过零点增加一倍 C. 幅值不变 D. 谱线变成连续的 4. 图 3 所示的变化过程,依据的是傅立叶变换的 _____ 。 F(j ) 5、单边拉氏变换 Fs 2 2 其反变换 f t ① 。 6、 离散系统的传输算子为 H (E) ,则系统对应的差分方程为 ① , s(s 4) E 2 E E 2 3E 2 f (0) ② 。 第2章 线性时不变连续系统的时域分析 2.6本章习题全解 2.1如题图2-1所示机械位移系统,质量为m 的刚体一端由弹簧牵引,弹簧的另一端固定在壁上,弹簧的刚度系数为k 。刚体与地面间的摩擦系数为f ,外加牵引力为)(t F S ,求外加牵引力)(t F S 与刚体运动速度)(t v 间的关系。 题图2-1 解:由机械系统元件特性,拉力k F 与位移x 成正比,即k F kx = 又()()t x t v d ττ-∞ = ? 所以,()()()t k F t kx t k v d ττ-∞ ==? 刚体在光滑表面滑动,摩擦力与速度成正比,即()()f F t fv t = 根据牛顿第二定律以及整个系统力平衡的达朗贝尔原理,可得 ()()()()t s d F t fv t k v d m v t dt ττ-∞ --=? 整理得22()()()()s d d d m v t f v t kv t F t dt dt dt --= 2.2题图2-2所示电路,输入激励是电流源)(t i s ,试列出电流)(t i L 及1R 上电压)(1t u 为输出响应变量的方程式。 题图2-2 解:由电路的基尔霍夫电流定律可得:()()()C L S i t i t i t += (1) 根据电容特性,()()C C d i t C u t dt = (2) 由电路的基尔霍夫电压定律可得:12()()()()C C L L d u t R i t L i t R i t dt +=+ (3) 将21()()()()C L L C d u t L i t R i t R i t dt =+-代入(2)得 2212()()()()C L L C d d d i t LC i t R C i t R C i t dt dt dt =+-(4) ()()()C S L i t i t i t =-代入(4)得, 22112()()()()()()S L L L S L d d d d i t i t LC i t R C i t R C i t R C i t dt dt dt dt -=+-+ 整理得,21 212()11 ()()()()()L L L S S R R R d d d i t i t i t i t i t dt L dt LC L dt LC +++=+ (5) 将111()()(()())C S L u t i t R i t i t R ==-,即11 () ()()L S u t i t i t R =- 代入(5)得 21121112111()()()()11(())(())(())()()S S S S S u t R R u t u t R d d d i t i t i t i t i t dt R L dt R LC R L dt LC +-+-+-=+ 整理得,22 1211211122()()()()()()S S R R u t R R d d d u t u t R i t i t dt L LC dt L dt ++ +=-- 2.3某连续系统的输入输出方程为 )(')(4)('3)("2t x t y t y t y =++已知)()(t u t x =,1)0(=-y ,1)0('=-y ,试计算)0(+y 和)0('+y 值。 解:将输入代入系统方程可得()t t y t y t y δ=++)(4)('3)("2 采用冲激函数匹配法求)0(+y 和)0(' +y 方程右端的冲激函数项最高阶数为()t δ,设信号与系统期末考试试题(有答案的)
北京交通大学信号与系统第四章典型例题
信号与系统习题答案
信号与系统例题
信号与系统复习题(含答案)
信号与系统试题附答案
信号与系统练习题附答案
(完整版)信号与系统习题答案.docx
信号与线性系统分析习题答案
信号与系统习题集
信号和线性系统分析(吴大正第四版)第四章习题答案解析
信号与系统试题库史上最全(内含答案)
信号与系统试题附答案
信号与线性系统分析吴大正知识题目解析
信号与系统复习题(答案全)
北京交通大学信号与系统第三章典型例题
信号与系统习题
信号与系统习题集
信号与系统王明泉科学出版社第二章知识题解答
