总体方差

总体方差(标准差)的估计
教学要求:理解方差和标准差的意义,会求样本方差和标准差。 教学过程:
看一个问题:甲乙两个射击运动员在选拔赛中各射击20次,成绩如下:
一、方差和标准差计算公式: 样本方差:s 2=n
1〔(x 1—x )2
+(x 2—x )2+…+(x n —x )2〕
样本标准差:s=
])()()[(n
122
221----++-+-x x x x x x n Λ 方差和标准差的意义:描述一个样本和总体的波动大小的特征数。标准差大说明波动大。一般的计算器都有这个键。
例一、要从甲乙两名跳远运动员中选拔一名去参加运动会,选拔的标准是:先看他们的平均成绩,如果两人的平均成绩相差无几,就要再看他们成绩的稳定程度。为此对两人进行了15次比赛,得到如下数据:(单位:cm ):
如何通过对上述数据的处理,来作出选人的决定呢?
x 甲≈ x 乙≈
s 甲≈ s 乙≈
说明:总体平均数描述一总体的平均水平,方差和标准差描述数据的波动情况或者叫稳定程度。
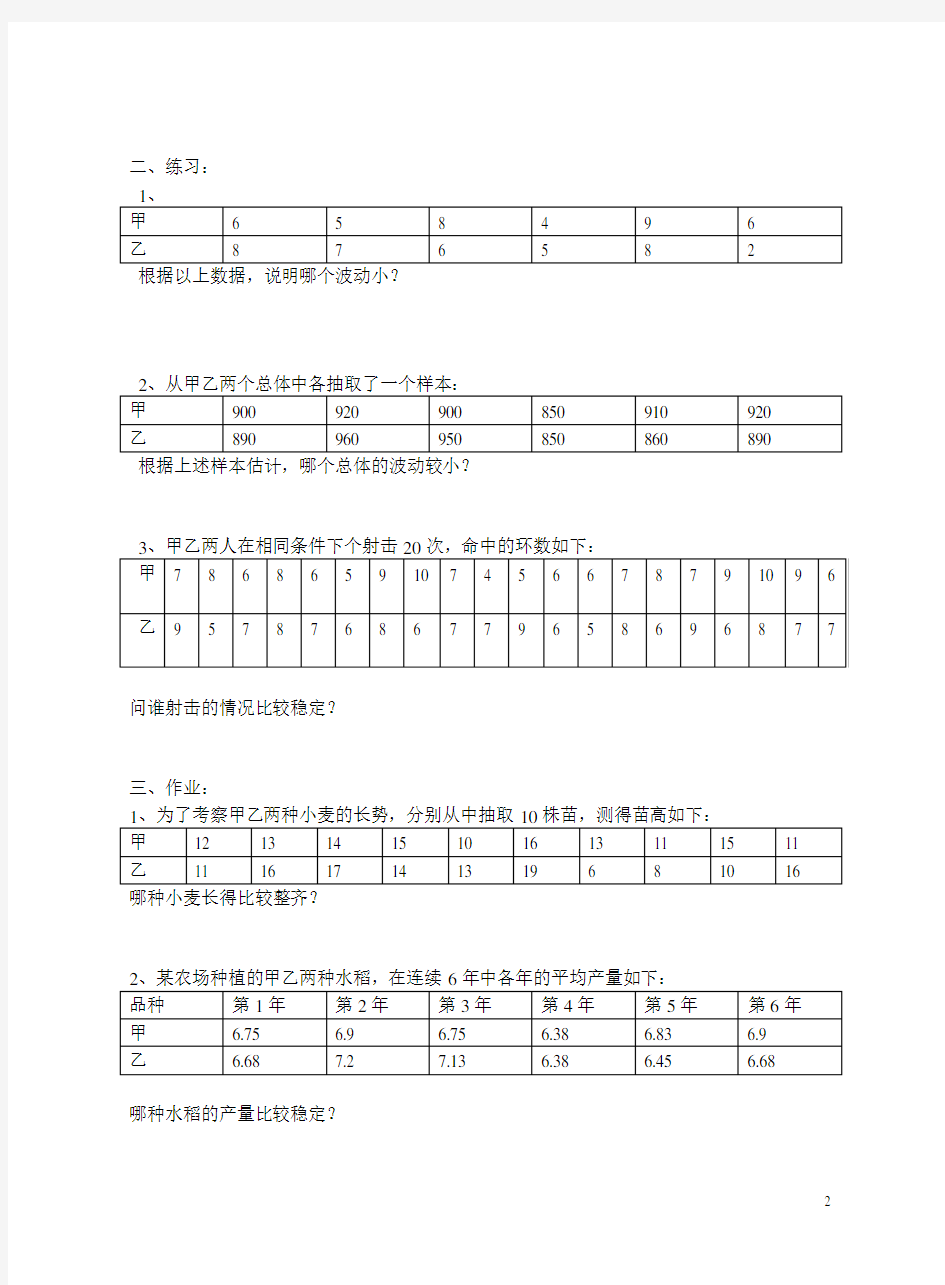
二、练习:
根据以上数据,说明哪个波动小?
根据上述样本估计,哪个总体的波动较小?
问谁射击的情况比较稳定?
三、作业:
哪种小麦长得比较整齐?
哪种水稻的产量比较稳定?
第十九讲正态总体均值及方差的区间估计
第十九讲 正态总体均值及方差的 区间估计 1. 单个正态总体方差的区间估计 设总体),(~2σμN X , ),,(21n X X X 为来自X 的一个样本,已给定置信度(水平)为α-1,求2σ的置信区间。 ①当μ已知时,由于),(~2σμN X i ,因此, )1,0(~N X i σ μ -(,2,1=i n , )。 由2χ分布的定义知: ∑ =-n i i n X 1 22 2 )(~)(χσ μ, 据)(2n χ分布上α分位点的定义,有: αχσμχαα-=<-<∑ =-1)}()()({2 1 2 2 212 2 n X n P n i i 从而 αχμσχμαα-=????? ??-<
总体分布的估计、总体期望和方差的
§12.2总体分布的估计、总体期望和方差的估计 (时间:45分钟满分:100分) 一、选择题(每小题7分,共35分) 1.为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110 cm的株数大约是() A.3 000 B.6 000 C.7 000 D.8 000 2.(2010·山东)在某项体育比赛中,七位裁判为一选手打出的分数如下: 90899095939493 去掉一个最高分和一个最低分后,所剩数据的期望值和方差分别为() A.92,2 B.92,2.8 C.93,2 D.93,2.8 3.为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图(如图),已知从左到右各长方形高的比为2∶3∶5∶6∶3∶1,则该班学生数学成绩在(80,100)之间的学生人数是() A.32 B.27 C.24 D.33
4.(2010·陕西)如图,样本A和B分别取自两个不同的总体,它们的样本期望值分别为x A 和x B,样本标准差分别为s A和s B,则() A.x A>x B,s A>s B B.x A 第5章用样本推断总体 5.1总体平均数与方差的估计 【知识与技能】 1.掌握用样本平均数估计总体平均数 2.掌握用样本方差估计总体方差. 【过程与方法】 通过对具体事例的分析、探讨,掌握简单随机样本在大多数情况下,当样本容量足够大时,样本的平均数和方差能反应总体相应的情况. 【情感态度】 感受数学在生活中的应用. 【教学重点】 样本平均数、方差估计总体平均数、方差的综合应用. 【教学难点】 体会统计思想,并会用样本平均数和方差估计总体平均数和方差. 一、情景导入,初步认知 一所学校要从两名短跑速度较快的同学中选拔一名去参加市里的比赛,为了使选拔公平,每名同学都进行10次测试,结果两名同学测试的结果的平均数是相同的,那么,派谁去参加比赛更好呢? 【教学说明】通过具体事例的引入,提高学生学习的兴趣. 二、思考探究,获取新知 1.我们在研究某个总体时,一般用数据表示总体中每个个体的某种数量特性,所有这些数据组成一个总体,而样本则是从总体中抽取的部分数据,因此,样本蕴含着总体的许多信息,这使我们有可能通过样本的某些特性去推断总体的相应特性. 2.从总体中抽取样本,然后通过对样本的分析,去推断总体的情况,这是统计的基本思想,用样本平均数,样本方差分别去估计总体平均数,总体方差就是 这一思想的体现,实践和理论都表明:对于简单的随机样本,在大多数情况下,当样本容量足够大时,这种估计是合理的. 3.思考:(1)如何估计某城市所有家庭一年内平均丢弃的塑料袋个数? (2)在检查甲、乙两种棉花的纤维长度时,如何估计哪种棉花的纤维长度比较整齐? 【归纳结论】由于简单随机样本客观地反映了实际情况,能够代表总体,因此我们可以用简单随机样本的平均数与方差分别去估计总体的平均数与方差. 4.探究:某农科院在某地区选择了自然条件相同的两个试验区,用相同的管理技术试种甲、乙两个品种的水稻各100亩.如何确定哪个品种的水稻在该地区更有推广价值呢? 为了选择合适的稻种,我们需要关心这两种水稻的平均产量及产量的稳定性(即方差),于是,待水稻成熟后,各自从这100亩水稻随机抽取10亩水稻,记录它们的亩产量(样本),数据如下表所示: 我们可以求出这10亩甲、乙品种的水稻的平均产量.因此,我们可以用这个产量来估计这两种水稻大面积种植后的平均产量. 我们还可以计算出这10亩甲、乙品种的水稻的方差,从而利用这两个方差来估计. 这两种水稻大面积种植后的稳定性(即方差),从而得出哪种水稻值得推广. 5.通过上面的探究,怎样用样本去估计总体,才能使估计更加合理? 【归纳结论】①抽取的样本要具有随机性;②样本容量要足够大. 6.如何用样本方差估计总体方差? 【归纳结论】方差能够反映一组数据与其平均值的离散程度的大小.方差越大,离散程度越大,稳定性越差.用样本方差估计总体方差的具体方法为:①计算样本平均数;②计算样本方差;③用样本方差估计总体方差. 【教学说明】引导学生思考,让学生讨论,合作完成.培养学生互助、协作的精神. §3 检验母体方差 3.1 检验正态母体的方差 ——2 χ检验 母体),(~2σμN X ,2 ,σμ均未知,试对 2 σ与2 0σ有无显著差异作假设检验. ①在母体上作 假设 ?=2 020:σσH 2021:σσ≠H ②检验统计量 )1( ~ )1(22 02 2 --=*n S n H χσχ ③给定显著水平α,如图存在 )1(22 1-- n α χ 和)1(2 2 -n αχ,使 2 )}1({)}1({2 2 222 12α χχχ χαα = ->=-<- n P n P 故取拒绝域 } )1()1(),,,{(2 2 222 12 21->-<=- n n x x x W n αα χχχ χ或 ④决策:当抽样结果是 W x x x n ∈),,,(21 时,拒绝0 H ,认为2 σ与2 0σ有 显著差异;否则接受0 H ,认为2 σ与20 σ无 显著差异. 例3.3.1 某细纱车间纺出的一种细纱支数的标准差2.10=σ,现从某日纺出的一批细纱中随机抽出16缕进行支数测 量,算得子样标准差1.2* =s ,问:纱的均 匀度有无显著变化(取05.0=α)?假定 母体分布是正态的。 解: 设该日纺出的纱的支数 ),(~2 σμN X ,2 ,σμ均未知, 作假设?=2.1:20σH 2.1:21 ≠σH 检验统计量)1(~ )1(22 22 --= *n S n H χσ χ 给定显著水平α,拒绝域为 } )1()1(),,,{(2 2 222 1221->-<=-n n x x x W n ααχχχχ或 这时16=n ,2.10=σ,1.2* =s ,从而94.452 =χ,又05.0=α,查表得 262.6)15()1(975.02 1==-- χχ α n , 488.27)15()1(025.02 ==-χχαn , 可见)1(2 2 ->n αχχ,故应拒绝0H ,认为 这天细纱的均匀度有显著变化。 例3.3.2 ),(~2 σμN X , 2 ,σμ均未知, 当45>n ,作如下假设检验 ?=2 2 0:σσH 2021:σσ≠H 检验统计量取为2 02 2 )1(σχ *-= S n ,证明:给 定显著水平α,则拒绝域为 } )1(2)1({})1(2)1({2 22 2ααχχu n n u n n W ---≤-+-≥= . 证明:作假设?=2020:σσH 2 021:σσ≠H , 0H 成立时检验统计量 几何分布的期望与方差 康永清 高中数学教科书新版第三册(选修II )比原来的修订本新增加随机变量的几何分布,但书中只给出了结论:(1)E p ξ=1,(2)D p p ξ=-12 ,而未加以证明。本文给出证明,并用于解题。 (1)由P k q p k ()ξ==-1,知 E p pq q p kq p q q kq p k k ξ=++++=+++++--231232121 () 下面用倍差法(也称为错位相减法)求上式括号内的值。记 S q q kq k k =++++-12321 qS q q k q kq k k k =+++-+-2121 () 两式相减,得 ()1121-=++++--q S q q q kq k k k S q q kq q k k k =----1112() 由01< 记S q q kq k =+++++-12321 qS q q k q k =+++-+-2121 () 相减, ()111121-=+++++=--q S q q q q k 则S q p =-=11122() 还可用导数公式()'x nx n n =-1,推导如下: 12321+++++-x x kx k =+++++=+++++x x x x x x x x k k '()'()'()'()' 2323 =-=----=-( )'()()()()x x x x x x 111112 2 上式中令x q =,则得 1231112122 +++++=-=-q q kq q p k () (2)为简化运算,利用性质D E E ξξξ=-22()来推导(该性质的证明,可见本刊6页)。 可见关键是求E ξ2 。 E p qp q p k q p k ξ22222123=+++++- =+++++-p q q k q k ()12322221 对于上式括号中的式子,利用导数,关于q 求导:k q kq k k 21-=()',并用倍差法求和,有 考点174 用样本数字特征估计总体数字特征(平均数,方差,标准差等) 1.(13辽宁T16) 为了考察某校各班参加课外书法小组的人数,在全校随机抽取5个班级,把每个班级参加 该小组 的人数作为样本数据.已知样本平均数为7,样本方差为4,且样本数据互相不相同,则样本 数据中的 最大值为 . 【测量目标】用样本数字特征估计总体数字特征. 【难易程度】较难 【参考答案】10 【试题解析】设5个班级中参加的人数分别为12345,,,,,x x x x x 则由题意知 2222212345 123457,(7)(7)(7)(7)(7)20,5 x x x x x x x x x x ++++=-+-+-+-+-=五个 整数的平 方和为20,则必为0119920++++=,由73x -=可得10x =或4x =,由71x -=可 得8x =或6x =,由上可知参加的人数分别为4,6,7,8,10,故样本数据中的最大值为10. 2.(13上海T10)设非零常d 是等差数列12319,,,,x x x x L 的公差,随机变量ξ等可能地取值12319,,,,x x x x L ,则方差_______D ξ=. 【测量目标】方差. 【难易程度】中等 |d 【试题解析】 1 1219 110 1918 19 +2 9 1919 x d x x x E x d x ξ ? + ++ ===+= … (步骤1) 2 2222222 (981019)30 19 d D d ξ=+++++++= L L.(步骤2) 3.(13北京T16) 下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天. JC113 (Ⅰ)求此人到达当日空气重度污染的概率; (Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望; (Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)【测量目标】离散型随机变量的分布列,期望和方差;用样本数字特征估计总体数字特征. 【难易程度】中等 【试题解析】(Ⅰ)设 i A表示事件“此人于3月i日到达该市”(i=1,2,…,13). 根据题意,P( i A)= 1 13 ,且 i j A A I=?(i≠j). 设B为事件“此人到达当日空气重度污染”,则B= 58 A A U. 所以P(B)=P( 58 A A U)=P( 5 A)+P( 8 A)= 2 13 .(步骤1) (Ⅱ)由题意可知,X的所有可能取值为0,1,2,且 P(X=1)=()()()()() 3671136711 4 13 P A A A A P A P A P A P A =+++= U U U, 项目八假设检验、回归分析与方差分析 实验3 方差分析 实验目的学习利用Mathematica求单因素方差分析的方法. 基本命令 1.调用线性回归软件包的命令< 中,向量Y是因变量,也称作响应变量.矩阵X称作设计矩阵, ?是参数向量??是误差向量? ????????DesignedRegress也是作一元和多元线性回归的命令, 它的应用范围更广些. 其格式与命令Regress的格式略有不同: DesignedRegress[设计矩阵X,因变量Y的值集合, RegressionReport ->{选项1, 选项2, 选项3,…}] RegressionReport(回归报告)可以包含:ParameterCITable(参数?的置信区间表???? ?PredictedResponse (因变量的预测值), MeanPredictionCITable(均值的预测区间), FitResiduals(拟合的残差), SummaryReport(总结性报告)等, 但不含BestFit. 实验准备—将方差分析问题纳入线性回归问题 在线性回归中, 把总的平方和分解为回归平方和与误差平方和之和, 并在输出中给出了方差分析表. 而在方差分析问题 中, 也把总的平方和分解为模型平方和与误差平方和之和, 其方法与线性回归中的方法相同. 因此只要把方差分析问题转化为线性模型的问题, 就可以利用线性回归中的设计回归命令DesignedRegress 做方差分析. 单因素试验方差分析的模型是 ?? ? ??==+=. ,,2,1;,,2,1,),,0(~,2s j n i N Y j ij ij ij j ij ΛΛ独立各εσεεμ (3.1) 上式也可改写成 ?? ? ??===+-+==+=.,,2,1;,,2,1,),,0(~; ,,3,2,)(, ,,2,1,2111111s j n i N s j Y n i Y j ij ij ij j ij i i ΛΛΛΛ独立各εσεεμμμεμ (3.2) 给定具体数据后, 还可(2.2)式写成线性模型的形式: 正态总体样本标准差S 不是总体标准差σ的无偏估计量 设12,,,n X X X ???是来自正态总体2 (,)N μσ的一个样本,1 1n i i X X n == ∑ 为样本均值, 2 2 1 1 ()1 n i i S X X n == --∑为样本方差。众所周知,对任何总体来说样本方差2 S 是总体方差 2 σ的无偏估计两,正态总体更不是例外。但样本标准差S 却不是总体标准差σ的无偏估计 量。 证明: 由于 2 2 2 (1)~(1)n S n χσ --,若令2 2 (1)n S Y σ -= ,则2 ~(1)Y n χ-的概率密度为 11 () 22110 22()200 n n n y y e y P y y --Γ-? ->?=?? ≤? 从而 11 22 2 2 1 22()11 2()11 ()2() 2() 22 2 n y n y n n n E y dy y e dy y e dy n n n +∞ +∞ +∞ ---- --∞ = = =--ΓΓΓ? ? ? ① () 21() 2 n n = -Γ 另一方面, )()E E E S σσ == , 所以有1()2 n E S E C σσ= = =≠, 所以,样本标准差S 却不是总体标准差σ的无偏估计量。 如果进行修正,则可以得到σ的无偏估计量 n C S σ= ,其中2 n C = 评注: 1. 理论依据: 正态总体样本的抽样分布,2 χ分布与Γ分布的有关性质。 2. 应用与推广: 无论总体X 服从什么分布,修正的样本方差 2 2 1 1()1 n i i S X X n == --∑ 是总体方差()D X 的无偏估计量,但是样本方差S 不是总体标准差 ()X σ= 的无偏估计量。只有在正态总体的情况下才有确定性的修正方法,使得 n C S σ= 是总体标准差的无偏估计量,对于非正态总体,情况极为复杂,一般不对其进行讨论。 参考文献: 茆诗松等,概率论与数理统计。本经:中国统计出版社,2000 参数估计方法在捕鱼问题中的应用 设湖中有鱼N 条,做上记号后放回湖中(记号不消失),一段时间后让湖中的鱼(做上记号的和没做记号的)混合均匀,再从湖中捕出鱼数s 条()s r ≥ ,其中有t 条(0)t r ≤≤标有记号。试根据这些信息,估计湖中鱼数的N 值。 (1)根据概率的统计定义:湖中有记号的鱼的比例应是r N (概率),而在捕出的s 条中有记号的鱼为t 条,有记号的鱼的比例是 t s (频率)。设想捕鱼是完全随机的,每条 鱼被捕的机会都相等,于是根据用频率来近似概率的道理,便有 r t N s = 即 rs N t = 故 rs N t ≈(取最接近的整数)。 (2)用矩估计法:设捕出的s 条鱼中,标有记号的鱼为ξ,因为ξ是超几何分布, 正态总体均值及方差的假设检验表: 单正态总体均值及方差的假设检验表(显著性水平α) 1 a n ~N (0,1)2 01 a S n ~t 2 2 02 1 0n i n i a ~ 2或 2 21 2 n 2 2n 2 21 n 20 ~ 22 21 1 2 n 2 21n 21 1 n 2 212 12 n n ~N (0,1) 2 1 2 11W S n n ~ 2 , 22 1122 122 n S n S n n 22 22 21112 2 1 2 1i i n i i a a n ~12,F n n 2 或 2 2 221 n S n ~21,1n 1 2或 2 Z =ξ-η~N (a 1-a 2,21σ+2 2σ),Z i =ξi -ηi . 2 21 2 Z n ) 2 1 S n ~ 2 单正态总体均值及方差的区间估计(置信度1-α) 已知 1 a n ~N (0,1)0 1 1 , n n u u n n 1 a S n ~t , 1 1 t t n n 2 02 1 n i n i a ~ 001 122, 12 2 i i i i n n a a 20 ~ 21 ,12 2 n 2个正态总体均值差及方差比的区间估计(置信度1-α) 12 212 12 a n n ~N (0,1) 2212 12 u n n 112 11W a S n n 22 n t 1 22 12 11W n n t S n n )2 a ξ-12 ,1 ,2 2 n n A F A 2 112 222 2 11n S n S ~ 2 2 21112W n S n S n n 212 1212 2 2 1 n i i n i i n a A n a ,2 122 2 21111n n S B n n S . (注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。可复制、编制,期待你的好评与关注) 期望与方差的相关公式 -、数学期望的来由 早在17世纪,有一个赌徒向法国著名数学家帕斯卡挑战,给他出了一道题目,题目是这样的:甲乙两个人赌博,他们两人获胜的机率相等,比赛规则是先胜三局者为赢家,赢家可以获得100法郎的奖励。当比赛进行到第三局的时候,甲胜了两局,乙胜了一局,这时由于某些原因中止了比赛,那么如何分配这100法郎才比较公平? 用概率论的知识,不难得知,甲获胜的概率为1/2+(1/2)*(1/2)=3/4,或者分析乙获胜的概率为(1/2)*(1/2)=1/4。因此由此引出了甲的期望所得值为100*3/4=75法郎,乙的期望所得值为25法郎。 这个故事里出现了“期望”这个词,数学期望由此而来。 定义1 若离散型随机变量ξ可能取值为i a (i =1,2,3 ,…),其分布列为i p (i =1,2,3, …),则当i i i p a ∑∞ =1 <∞时,则称ξ存在数学期望,并且数学期望为E ξ=∑∞ =1 i i i p a , 如果i i i p a ∑∞ =1 =∞,则数学期望不存在。[]1 定义2 期望:若离散型随机变量ξ,当ξ=x i 的概率为P (ξ=x i )=P i (i =1, 2,…,n ,…),则称E ξ=∑x i p i 为ξ的数学期望,反映了ξ的平均值. 期望是算术平均值概念的推广,是概率意义下的平均.E ξ由ξ的分布列唯一确定. 二、数学期望的性质 (1)设C 是常数,则E(C )=C 。 (2)若k 是常数,则E (kX )=kE (X )。 (3))E(X )E(X )X E(X 2121+=+。 三、 方差的定义 前面我们介绍了随机变量的数学期望,它体现了随机变量取值的平均水平, 常见分布的期望和方差 概率与数理统计重点摘要 1、正态分布的计算:()()()X F x P X x μ σ-=≤=Φ。 2、随机变量函数的概率密度:X 是服从某种分布的随机变量,求()Y f X =的概率密度:()()[()]'()Y X f y f x h y h y =。(参见P66~72) 3、分布函数(,)(,)x y F x y f u v dudv -∞-∞=??具有以下基本性质: ⑴、是变量x ,y 的非降函数; ⑵、0(,)1F x y ≤≤,对于任意固定的x ,y 有:(,)(,)0F y F x -∞=-∞=; ⑶、(,)F x y 关于x 右连续,关于y 右连续; ⑷、对于任意的11221212(,),(,),,x y x y x x y y << ,有下述不等式成立: 22122111(,)(,)(,)(,)0F x y F x y F x y F x y --+≥ 4、一个重要的分布函数:1(,)(arctan )(arctan )23 x y F x y πππ2=++22的概率密度为:22226(,)(,)(4)(9)f x y F x y x y x y π?==??++ 5、二维随机变量的边缘分布: 边缘概率密度:()(,)()(,)X Y f x f x y dy f y f x y dx +∞-∞ +∞-∞==? ? 边缘分布函数:()(,)[(,)]()(,)[(,)]x X y Y F x F x f u y dy du F y F y f x v dx dv +∞ -∞ -∞+∞-∞-∞=+∞==+∞=???? 二维正态分布的边缘分布为一维正态分布。 6、随机变量的独立性:若(,)()()X Y F x y F x F y =则称随机变量X ,Y 相互独立。简称X 与Y 独立。 .总体平均数与方差的估计 ————————————————————————————————作者:————————————————————————————————日期: 第5章用样本推断总体 5.1总体平均数与方差的估计 【知识与技能】 1.掌握用样本平均数估计总体平均数 2.掌握用样本方差估计总体方差. 【过程与方法】 通过对具体事例的分析、探讨,掌握简单随机样本在大多数情况下,当样本容量足够大时,样本的平均数和方差能反应总体相应的情况. 【情感态度】 感受数学在生活中的应用. 【教学重点】 样本平均数、方差估计总体平均数、方差的综合应用. 【教学难点】 体会统计思想,并会用样本平均数和方差估计总体平均数和方差. 一、情景导入,初步认知 一所学校要从两名短跑速度较快的同学中选拔一名去参加市里的比赛,为了使选拔公平,每名同学都进行10次测试,结果两名同学测试的结果的平均数是相同的,那么,派谁去参加比赛更好呢? 【教学说明】通过具体事例的引入,提高学生学习的兴趣. 二、思考探究,获取新知 1.我们在研究某个总体时,一般用数据表示总体中每个个体的某种数量特性,所有这些数据组成一个总体,而样本则是从总体中抽取的部分数据,因此,样本蕴含着总体的许多信息,这使我们有可能通过样本的某些特性去推断总体的相应特性. 2.从总体中抽取样本,然后通过对样本的分析,去推断总体的情况,这是统计的基本思想,用样本平均数,样本方差分别去估计总体平均数,总体方差就是 这一思想的体现,实践和理论都表明:对于简单的随机样本,在大多数情况下,当样本容量足够大时,这种估计是合理的. 3.思考:(1)如何估计某城市所有家庭一年内平均丢弃的塑料袋个数? (2)在检查甲、乙两种棉花的纤维长度时,如何估计哪种棉花的纤维长度比较整齐? 【归纳结论】由于简单随机样本客观地反映了实际情况,能够代表总体,因此我们可以用简单随机样本的平均数与方差分别去估计总体的平均数与方差. 4.探究:某农科院在某地区选择了自然条件相同的两个试验区,用相同的管理技术试种甲、乙两个品种的水稻各100亩.如何确定哪个品种的水稻在该地区更有推广价值呢? 为了选择合适的稻种,我们需要关心这两种水稻的平均产量及产量的稳定性(即方差),于是,待水稻成熟后,各自从这100亩水稻随机抽取10亩水稻,记录它们的亩产量(样本),数据如下表所示: 我们可以求出这10亩甲、乙品种的水稻的平均产量.因此,我们可以用这个产量来估计这两种水稻大面积种植后的平均产量. 我们还可以计算出这10亩甲、乙品种的水稻的方差,从而利用这两个方差来估计. 这两种水稻大面积种植后的稳定性(即方差),从而得出哪种水稻值得推广. 5.通过上面的探究,怎样用样本去估计总体,才能使估计更加合理? 【归纳结论】①抽取的样本要具有随机性;②样本容量要足够大. 6.如何用样本方差估计总体方差? 【归纳结论】方差能够反映一组数据与其平均值的离散程度的大小.方差越大,离散程度越大,稳定性越差.用样本方差估计总体方差的具体方法为:①计算样本平均数;②计算样本方差;③用样本方差估计总体方差. 【教学说明】引导学生思考,让学生讨论,合作完成.培养学生互助、协作的精神. 样本方差与总体方差的区别 之前一直对于样本方差与总体方差的概念区分不清,对于前者不仅多了样本”两个字,而且公式中除数是N-1 ,而不是N。现在写下这么写东西,以能彻底把他们的区别搞清楚。 总体方差: 也叫做有偏估计,其实就是我们从初高中就学到的那个标准定义的方差,除数是N。女0果实现已知期望值,比如测水的沸点,那么测量 立的(期望值不依测量值而改变,随你怎么折腾,温度计坏了也好,看反了也好,总之,期望值应该是100度),那么E『(X-期望)人2』,就有10个自由度。事实上,它等于(X- 期望)的方差,减去(X-期望)的平方。”所以叫做有偏估计,测量结果偏于那个”已知的期望值“。样本方差: 无偏估计、无偏方差(unbiased varianee )。对于一组随机变量,从中随机抽取N个样本, 这组样本的方差就是Xi^2平方和除以N-1。这可以推导出来的。如果现在往水里撒把盐, 水的沸点未知了,那我该怎么办?我只能以样本的平均值,来代替原先那个期望100度。同 样的过程,但原先的(X-期望),被(X-均值)所代替。设想一下(Xi-均值)的方差,它 不在等于Xi的方差,而是有一个协方差,因为均值中,有一项Xi/n是和Xi相关的,这就 是那个”偏"的由来 刊屮)二 Ei a.—-£(A;-W) f=l 9 =rr 一 证明: 10次,测量值和期望值之间是独 DGH 兀) 担工加D (X ;)) g ? u 曰右力m-工P) 占E (m :-寸) __________ ■!■ A^(E :=iCV —2A ;T + X-)) 闵肯) ) + £:D) n(<7- + //-) E(X 力二丫) nE(X~) MD(X) + E2(X)) M 吟+ “?) 尙e + //-) - 角F + "') t7- 证毕?? D(X)二 --- ◎ E(f)= D(X) + Eh 工) E{S-)= £(E ; =1 A ;y )= 考点2 用样本估计总体(频率分布直方图、平均数、方差等) 1. (15泰州一模)若数据2,x ,2,2的方差为0,则x= . 【考点】极差、方差与标准差. 【答案】2 【分析】因为数据2,x ,2,2的方差为0,由其平均数为 64 x +,得到22166320444x x x ?? ++????-+-=?? ? ??????? ??,解得x =2. 2.(15江苏高考压轴)样本容量为10的一组数据,它们的平均数是5,频率如图所示,则 这组数据的方差等于 . 第2题图 cqn17 【答案】7.2 【分析】2出现100.44?=次,5出现100.22?=次,8出现100.44?=次,所以 2222 14(25)2(55)4(85)7.210s ??= ?-+?-+?-=? ? 3.(2015江苏苏州市高三上调考)如图是小王所做的六套数学附加题得分(满分40)的 茎叶图,则其平均得分为 . JSY33 第3题图 【考点】茎叶图. 【答案】31. 【分析】根据茎叶图的数据,得; 数据的平均分为 x = 182830323840 6 +++++=31. 故答案为:31. 4.(淮安都梁中学2015届高三10月调研)某校为了解2015届高三同学寒假期间学习情况, 抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这100名同学中学习时间在6~8小时内的同学为 人. zl085 第4题图 【考点】频率分布直方图;用样本的频率分布估计总体分布. 【答案】30 【分析】∵这100名同学中学习时间在6~8小时外的频率为 (0.04+0.12+0.14+0.05)×2=0.7 ∴这100名同学中学习时间在6~8小时内为1-0.7=0.3 ∴这100名同学中学习时间在6~8小时内的同学为100×0.3=30. 5.(徐州市2014届高考信息卷)甲、乙两个学习小组各有10名学生,他们在一次数学测 验中成绩的茎叶图如图所示,则在这次测验中成绩较好的是 组. 【考点】茎叶图. 第5题图 zl060 【答案】甲 【分析】甲的平均分为63747981838486868890 81.410 x +++++++++= =甲, 5864677475767679808273.110 x +++++++++==乙; x x >乙甲,且甲的成绩多集中在80分上,乙的成绩多集中在70分上, ∴甲组的成绩较好些; 故答案为:甲. 6. (南通市2015届高三第三次调研) 为了解学生课外阅读的情况,随机统计了n 名学生 的课外阅读时间,所得数据都在[]50,150中,其频率分布直方图如图所示.已知在 概率与统计 知识点一:常见的概率类型与概率计算公式; 类型一:古典概型; 1、 古典概型的基本特点: (1) 基本事件数有限多个; (2) 每个基本事件之间互斥且等可能; 2、 概率计算公式: A 事件发生的概率()A P A = 事件所包含的基本事件数 总的基本事件数 ; 类型二:几何概型; 1、 几何概型的基本特点: (1) 基本事件数有无限多个; (2) 每个基本事件之间互斥且等可能; 2、 概率计算公式: A 事件发生的概率()A P A = 构成事件的区域长度(或面积或体积或角度) 总的区域长度(或面积或体积或角度) ; 注意: (1) 究竟是长度比还是面积比还是体积比,关键是看表达该概率问题需要几个变量,如 果需要一个变量,则应该是长度比或者角度比;若需要两个变量则应该是面积比;当然如果是必须要三个变量则必为体积比; (2) 如果是用一个变量,到底是角度问题还是长度问题,关键是看谁是变化的主体,哪 一个是等可能的; 例如:等腰ABC ?中,角C= 23 π ,则: (1) 若点M 是线段AB 上一点,求使得AM AC ≤的概率; (2) 若射线CA 绕着点C 向射线CB 旋转,且射线CA 与线段AB 始终相交且交点是M ,求 使得AM AC ≤的概率; 解析:第一问中明确M 为AB 上动点,即点M 是在AB 上均匀分布,所以这一问应该是长度 之比,所求概率: 13P =; 而第二问中真正变化的主体是射线的转动,所以角度的变化是均匀的,所以这一问应该是角度之比的问题,所以所求的概率:2755 = =1208 P ?; 知识点二:常见的概率计算性质; 类型一:事件间的关系与运算; A+B (和事件):表示A 、B 两个事件至少有一个发生; A B ?(积事件) :表示A 、B 两个事件同时发生; A (对立事件) :表示事件A 的对立事件; 第七章 假设检验与方差分析 习题答案 一、名词解释 用规范性的语言解释统计学中的名词。 1. 假设检验:对总体分布或参数做出某种假设,然后再依据抽取的样本信息,对假设是否正确做出统计判断,即是否拒绝这种假设。 2. 原假设:又叫零假设或无效假设,是待检验的假设,表示为 H 0,总是含有等号。 3. 备择假设:是零假设的对立,表示为 H 1,总是含有不等号。 4. 单侧检验:备择假设符号为大于或小于时的假设检验。 5. 显著性水平:原假设为真时,拒绝原假设的概率。 6. 方差分析:是检验多个总体均值是否相等的一种统计分析方法。 二、填空题 根据下面提示的内容,将适宜的名词、词组或短语填入相应的空格之中。 1. u ,n x σμ0 -,标准正态; ),(),(2/2/+∞--∞n z n z σ σ αα 2. 参数检验,非参数检验 3. 弃真,存伪 4. 方差 5. 卡方, F 6. 方差分析 7. t ,u 8. n s x 0 μ-,不拒绝 9. 单侧,双侧 10.新产品的废品率为5% ,0.01 11.相关,总变异,组间变异,组内变异 12.总变差平方和=组间变差平方和+组内变差平方和 13.连续,离散 14.总体均值 15.因子,水平 16.组间,组内 17.r-1,n-r 18. 正态,独立,方差齐 三、单项选择 从各题给出的四个备选答案中,选择一个最佳答案,填入相应的括号中。 1.B 2.B 3. B 4.A 5. C 6. B 7. C 8. A 9. D 10. A 11. D 12. C 四、多项选择 从各题给出的四个备选答案中,选择一个或多个正确的答案,填入相应的括号中。 1.AC 2.A 3.B 4.BD 5. AD 五、判断改错 对下列命题进行判断,在正确命题的括号内打“√”;在错误命题的括号内打“×”,并在错误的地方下划一横线,将改正后的内容写入题下空白处。 1. 在任何情况下,假设检验中的两类错误都不可能同时降低。 ( × ) 样本量一定时 2. 对于两样本的均值检验问题,若方差均未知,则方差分析和t 检验均可使用,且两者检验结果一致。 ( √ ) 3. 方差分析中,组间离差平方和总是大于组内离差平方和。( × ) 不一定 4. 在假设检验中,如果在显著性水平0.05下拒绝了 00:μμ≤H ,则在同一水平一定可以拒绝假设00:μμ=H 。( × ) 不一定 5. 为检验k 个总体均值是否显著不同,也可以用t 检验,且与方差分析相比,犯第一类错误的概率不变。( × ) 会增加 6. 方差分析中,若拒绝了零假设,则认为各个总体均值均有显著性差异。( × ) 不完全相等 六、简答题 根据题意,用简明扼要的语言回答问题。 1. 假设检验与统计估计有何区别与联系? 【答题要点】 假设检验是在给定显著性水平下,计算出拒绝域,并根据样本统计量信息来做出是否拒 期望与方差的相关公式 -、数学期望的来由 早在17世纪,有一个赌徒向法国著名数学家帕斯卡挑战,给他出了一道题目,题目是这样的:甲乙两个人赌博,他们两人获胜的机率相等,比赛规则是先胜三局者为赢家,赢家可以获得100法郎的奖励。当比赛进行到第三局的时候,甲胜了两局,乙胜了一局,这时由于某些原因中止了比赛,那么如何分配这100法郎才比较公平? 用概率论的知识,不难得知,甲获胜的概率为1/2+(1/2)*(1/2)=3/4,或者分析乙获胜的概率为(1/2)*(1/2)=1/4。因此由此引出了甲的期望所得值为100*3/4=75法郎,乙的期望所得值为25法郎。 这个故事里出现了“期望”这个词,数学期望由此而来。 定义1 若离散型随机变量ξ可能取值为i a (i =1,2,3 ,…),其分布列为i p (i =1,2,3, …),则当i i i p a ∑∞=1<∞时,则称ξ存在数学期望,并且数学期望为E ξ=∑∞ =1i i i p a ,如果i i i p a ∑∞ =1=∞,则数学期望不存在。[]1 定义2 期望:若离散型随机变量ξ,当ξ=x i 的概率为P (ξ=x i )=P i (i =1, 2,…,n ,…),则称E ξ=∑x i p i 为ξ的数学期望,反映了ξ的平均值. 期望是算术平均值概念的推广,是概率意义下的平均.E ξ由ξ的分布列唯一确定. 二、数学期望的性质 (1)设C 是常数,则E(C )=C 。 (2)若k 是常数,则E (kX )=kE (X )。 (3))E(X )E(X )X E(X 2121+=+。 三、 方差的定义 前面我们介绍了随机变量的数学期望,它体现了随机变量取值的平均水平, 第2课时 用样本方差估计总体方差 1.会用样本方差估计总体方差;(重点、难点) 2.体会样本代表性的重要意义. 一、情境导入 某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在五天中进球的个数统计结果如下: 他们的平均进球数都是8,现在从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么? 二、合作探究 探究点一:用样本方差估计总体方差 【类型一】 质量问题 两台机床同时生产直径(单位:mm)为10的零件,为了检验产品的质量,质量检 验员从两台机床的产品中各抽出5件进行测量,结果如下: 如果你是质量检验员,在收集到上述数据后,你将利用哪些统计知识来判断这两台机床生产的零件的质量优劣? 解析:求出每组数据的平均数,根据方差公式求出每组的方差,然后根据方差的大小进行比较. 解:x 甲=15(8+9+10+11+12)=10(mm),x 乙=1 5(7+10+10+10+13)=10(mm).由于 x 甲=x 乙,因此平均直径不能反映两台机床生产出的零件的质量优劣; 再计算方差,可得s 2甲=2,s 2乙=3.6,∵s 2甲 §3 检验母体方差 3.1检验正态母体的方差——2 χ检验 母体),(~2σμN X ,2 ,σμ均未知,试对 2 σ与2 0σ有无显著差异作假设检验. ① 在 母体上作 假设 ?=2 2 0:σσH 2 021:σσ≠H ②检验统计量)1( ~ )1(2 20 2 20 --=*n S n H χσχ ③给定显著水平α,如图存在 )1(22 1-- n α χ 和)1(2 2 -n αχ,使 2 )}1({)}1({2 2 22 2 12α χχχ χαα = ->=-<- n P n P 故取拒绝域 } )1()1(),,,{(2 2 222 1221->-<=-n n x x x W n ααχχχχ或 ④决策:当抽样结果是 W x x x n ∈),,,(21 时,拒绝0H ,认为2 σ与20σ有 显著差异;否则接受0H ,认为2 σ与20 σ无 显著差异. 例3.3.1 某细纱车间纺出的一种细纱支数X 的标准差2.10=σ,现从某日纺出的一批细纱中随机抽出16缕进行支数 测量,算得子样标准差1.2*=s ,问:纱的 均匀度有无显著变化(取05.0=α)?假 定母体X 的分布是正态的。 解: 设该日纺出的纱的支数 ),(~2 σμN X ,2 ,σ μ均未知, 作假设?=2202.1:σH 2 21 2.1:≠σH 检验统计量)1(~ )1(22 022 --=*n S n H χσχ 给定显著水平α,拒绝域为 } )1()1(),,,{(2 2 222 1221->-<=-n n x x x W n ααχχχχ或 这时16=n ,2.10=σ,1.2* =s ,从而 94.452 =χ,又05.0=α,查表得 262.6)15()1(22975 .02 1==-- χχαn , 488.27)15()1(22 025 .02 ==-χχαn , 可见)1(2 2->n αχχ,故应拒绝0H ,认为 这天细纱的均匀度有显著变化。 例3.3.2 ),(~2 σμN X , 2 ,σμ均未知, 当45>n ,作如下假设检验 ?=2020:σσH 2021:σσ≠H 检验统计量取为2 02 2 )1(σχ*-= S n ,证明:给 定显著水平α,则拒绝域为 } )1(2)1({})1(2)1({2 22 2ααχχu n n u n n W ---≤-+-≥= . 证明:作假设?=2020:σσH 2 021:σσ≠H , 0H 成立时检验统计量总体平均数与方差的估计
3[1]3总体方差的假设检验
几何分布的期望与方差的证明
用样本数字特征估计总体数字特征(平均数,方差,实用标准差等)
案例库 项目八假设检验 回归分析与方差分析
正态总体样本标准差
正态总体均值及方差的假设检验表
期望-方差公式-方差和期望公式
常见分布的期望和方差
总体平均数与方差的估计
样本方差与总体方差的区别
用样本估计总体(频率分布直方图、平均数、方差等)课案
概率、期望与方差的计算和性质
07第七章 假设检验与方差分析 习题答案
期望-方差公式-方差和期望公式
用样本方差估计总体方差
3.3总体方差的假设检验
