初二数学-特殊四边形中的动点问题(教师版)

特殊四边形中的动点问题及解题方法

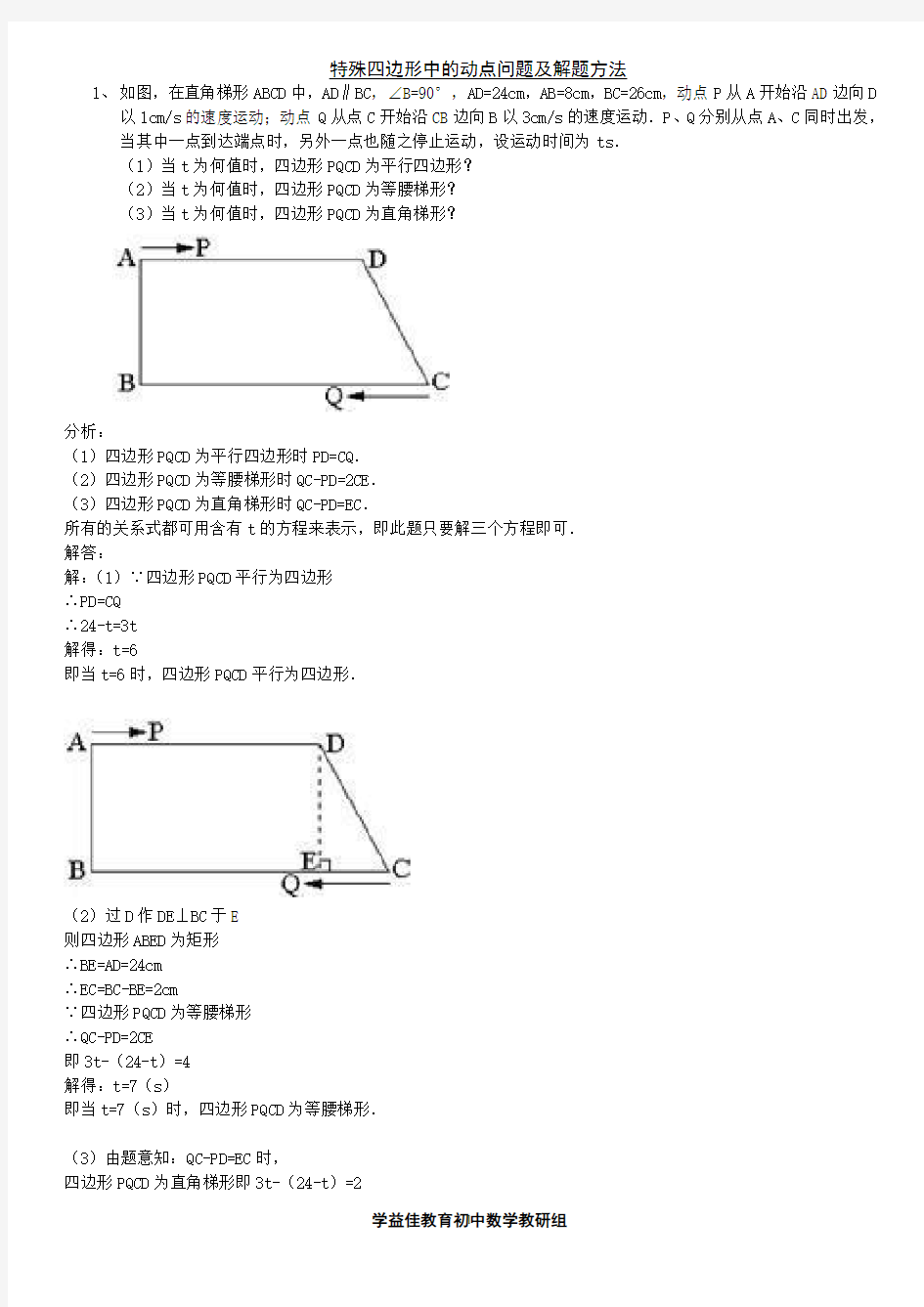
1、如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从A开始沿AD边向D

以1cm/s的速度运动；动点Q从点C开始沿CB边向B以3cm/s的速度运动．P、Q分别从点A、C同时出发，当其中一点到达端点时，另外一点也随之停止运动，设运动时间为ts．

（1）当t为何值时，四边形PQCD为平行四边形？

（2）当t为何值时，四边形PQCD为等腰梯形？

（3）当t为何值时，四边形PQCD为直角梯形？

分析：

（1）四边形PQCD为平行四边形时PD=CQ．

（2）四边形PQCD为等腰梯形时QC-PD=2CE．

（3）四边形PQCD为直角梯形时QC-PD=EC．

所有的关系式都可用含有t的方程来表示，即此题只要解三个方程即可．

解答：

解：（1）∵四边形PQCD平行为四边形

∴PD=CQ

∴24-t=3t

解得：t=6

即当t=6时，四边形PQCD平行为四边形．

（2）过D作DE⊥BC于E

则四边形ABED为矩形

∴BE=AD=24cm

∴EC=BC-BE=2cm

∵四边形PQCD为等腰梯形

∴QC-PD=2CE

即3t-（24-t）=4

解得：t=7（s）

即当t=7（s）时，四边形PQCD为等腰梯形．

（3）由题意知：QC-PD=EC时，

四边形PQCD为直角梯形即3t-（24-t）=2

解得：t=6.5（s）

即当t=6.5（s）时，四边形PQCD为直角梯形．

点评：

此题主要考查了平行四边形、等腰梯形，直角梯形的判定，难易程度适中．

2、如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点

F，交∠ACB内角平分线CE于E．

（1）试说明EO=FO；

（2）当点O运动到何处时，四边形AECF是矩形并证明你的结论；

（3）若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论．

分析：

（1）根据CE平分∠ACB，MN∥BC，找到相等的角，即∠OEC=∠ECB，再根据等边对等角得OE=OC，同理OC=OF，可得EO=FO．

（2）利用矩形的判定解答，即有一个内角是直角的平行四边形是矩形．

（3）利用已知条件及正方形的性质解答．

解答：

解：（1）∵CE平分∠ACB，

∴∠ACE=∠BCE，

∵MN∥BC，

∴∠OEC=∠ECB，

∴∠OEC=∠OCE，

∴OE=OC，

同理，OC=OF，

∴OE=OF．

（2）当点O运动到AC中点处时，四边形AECF是矩形．

如图AO=CO，EO=FO，

∴四边形AECF为平行四边形，

∵CE平分∠ACB，

∴∠ACE= ∠ACB，

同理，∠ACF= ∠ACG，

∴∠ECF=∠ACE+∠ACF= （∠ACB+∠ACG）= ×180°=90°，

∴四边形AECF是矩形．

（3）△ABC是直角三角形

∵四边形AECF是正方形，

∴AC⊥EN，故∠AOM=90°，

∵MN∥BC，

∴∠BCA=∠AOM，

∴∠BCA=90°，

∴△ABC是直角三角形．

点评：

本题主要考查利用平行线的性质“等角对等边”证明出结论（1），再利用结论（1）和矩形的判定证明结论（2），再对（3）进行判断．解答时不仅要注意用到前一问题的结论，更要注意前一问题为下一问题提供思路，有相似的思考方法．是矩形的判定和正方形的性质等的综合运用．

3、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，已知AD=AB=3，BC=4，动点P从B点出发，沿线段BC向点

C作匀速运动；动点Q从点D出发，沿线段DA向点A作匀速运动．过Q点垂直于AD的射线交AC于点M，交BC于点N．P、Q两点同时出发，速度都为每秒1个单位长度．当Q点运动到A点，P、Q两点同时停止运动．设点Q运动的时间为t秒．

（1）求NC，MC的长（用t的代数式表示）；

（2）当t为何值时，四边形PCDQ构成平行四边形；

（3）是否存在某一时刻，使射线QN恰好将△ABC的面积和周长同时平分？若存在，求出此时t的值；若不存在，请说明理由；

（4）探究：t为何值时，△PMC为等腰三角形．

分析：

（1）依据题意易知四边形ABNQ是矩形∴NC=BC-BN=BC-AQ=BC-AD+DQ，BC、AD已知，DQ就是t，即解；∵AB∥QN，∴△CMN∽△CAB，∴CM：CA=CN：CB，（2）CB、CN已知，根据勾股定理可求CA=5，即可表示CM；

四边形PCDQ构成平行四边形就是PC=DQ，列方程4-t=t即解；

（3）可先根据QN平分△ABC的周长，得出MN+NC=AM+BN+AB，据此来求出t的值．然后根据得出的t的值，求出△MNC的面积，即可判断出△MNC的面积是否为△ABC面积的一半，由此可得出是否存在符合条件的t值．

（4）由于等腰三角形的两腰不确定，因此分三种情况进行讨论：

①当MP=MC时，那么PC=2NC，据此可求出t的值．

②当CM=CP时，可根据CM和CP的表达式以及题设的等量关系来求出t的值．

③当MP=PC时，在直角三角形MNP中，先用t表示出三边的长，然后根据勾股定理即可得出t的值．

综上所述可得出符合条件的t的值．

解答:

解：（1）∵AQ=3-t

∴CN=4-（3-t）=1+t

在Rt△ABC中，AC2=AB2+BC2=32+42

∴AC=5

在Rt△MNC中，cos∠NCM= = ，CM= ．

（2）由于四边形PCDQ构成平行四边形

∴PC=QD，即4-t=t

解得t=2．

（3）如果射线QN将△ABC的周长平分，则有：

MN+NC=AM+BN+AB

即：（1+t）+1+t= （3+4+5）

解得：t= （5分）

而MN= NC= （1+t）

∴S△MNC= （1+t）2= （1+t）2

当t= 时，S△MNC=（1+t）2= ≠ ×4×3

∴不存在某一时刻t，使射线QN恰好将△ABC的面积和周长同时平分．

（4）①当MP=MC时（如图1）

则有：NP=NC

即PC=2NC∴4-t=2（1+t）

解得：t=

②当CM=CP时（如图2）

则有：

（1+t）=4-t

解得：t=

③当PM=PC时（如图3）

则有：

在Rt△MNP中，PM2=MN2+PN2

而MN= NC= （1+t）

PN=NC-PC=（1+t）-（4-t）=2t-3

∴[ （1+t）]2+（2t-3）2=（4-t）2

解得：t1= ，t2=-1（舍去）

∴当t= ，t= ，t= 时，△PMC为等腰三角形

点评：

此题繁杂，难度中等，考查平行四边形性质及等腰三角形性质．考查学生分类讨论和数形结合的数学思想方法．4、直线y=- 34x+6与坐标轴分别交于A、B两点，动点P、Q同时从O点出发，同时到达A点，运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O?B?A运动．

（1）直接写出A、B两点的坐标；

（2）设点Q的运动时间为t（秒），△OPQ的面积为S，求出S与t之间的函数关系式；

（3）当S= 485时，求出点P的坐标，并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标．

分析：

（1）分别令y=0，x=0，即可求出A、B的坐标；

（2））因为OA=8，OB=6，利用勾股定理可得AB=10，进而可求出点Q由O到A的时间是8秒，点P的速度是2，从而可求出，

当P在线段OB上运动（或0≤t≤3）时，OQ=t，OP=2t，S=t2，当P在线段BA上运动（或3＜t≤8）时，OQ=t，AP=6+10-2t=16-2t，作PD⊥OA于点D，由相似三角形的性质，得 PD=48-6t5，利用S= 12OQ×PD，即可求出答案；（3）令S= 485，求出t的值，进而求出OD、PD，即可求出P的坐标，利用平行四边形的对边平行且相等，结合简单的计算即可写出M的坐标．

解答：

解：（1）y=0，x=0，求得A（8，0）B（0，6），

（2）∵OA=8，OB=6，∴AB=10．

∵点Q由O到A的时间是 81=8（秒），

∴点P的速度是 6+108=2（单位长度/秒）．

当P在线段OB上运动（或O≤t≤3）时，

OQ=t，OP=2t，S=t2．

当P在线段BA上运动（或3＜t≤8）时，

OQ=t，AP=6+10-2t=16-2t，

如图，做PD⊥OA于点D，

由 PDBO=APAB，得PD= 48-6t5．

∴S= 12OQ?PD=- 35t2+245t．

（3）当S= 485时，∵ 485＞12×3×6∴点P在AB上

当S= 485时，- 35t2+245t= 485

∴t=4

∴PD= 48-6×45= 245，AD=16-2×4=8

AD= 82-(245)2= 325 ∴OD=8- 325= 85 ∴P （ 85， 245） M1（ 285， 245），M2（- 125， 245），M3（ 125，- 245） 点评：

本题主要考查梯形的性质及勾股定理．在解题（2）时，应注意分情况进行讨论，防止在解题过程中出现漏解现象． 5.已知：如图，在直角梯形COAB 中，OC AB ∥，以O 为原点建立平面直角坐标系，A B C ，，三点的坐标分别为(80)(810)(04)A B C ，，，，，，点D 为线段BC 的中点，动点P 从点O 出发，以每秒1个单位的速度，沿折线OABD 的路线移动，移动的时间为t 秒． （1）求直线BC 的解析式；

（2）若动点P 在线段OA 上移动，当t 为何值时，四边形OPDC 的面积是梯形COAB 面积的

27

？ （3）动点P 从点O 出发，沿折线OABD 的路线移动过程中，设OPD △的面积为S ，请直接写出S 与t 的函数关系式，并指出自变量t 的取值范围；

6.如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点．

（1）如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动． ①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由； ②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？ （2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？

四边形中的动点问题课后作业

1. 如图，已知AD 与BC 相交于E ，∠1＝∠2＝∠3，BD ＝CD ，∠ADB ＝90°，CH ⊥AB 于H ，CH 交AD 于F.

（1）求证：CD ∥AB ；

（2）求证：△BDE ≌△ACE ；

（3）若O 为AB 中点，求证：OF ＝

1

2

BE.

2、如图1―4―2l ，在边长为a 的菱形ABCD 中，∠DAB ＝60°，E 是异于A 、D 两点的动点，F 是CD 上的动点，满足A E ＋CF=a ，说明：不论E 、F 怎样移动，三角形BEF 总是正三角形．

3、在平行四边形ABCD 中，E 为BC 的中点，连接AE 并延长交DC 的延长线于点F ． (1)求证：CF AB ；

(2)当BC 与AF 满足什么数量关系时， 四边形ABFC 是矩形，并说明理由．

4、如图l －4－80，已知正方形ABCD 的对角线AC 、BD 相交于点O ，E 是AC 上一点，过点A 作AG ⊥EB ，垂足为G ，AG 交BD 于F ，则OE=OF ． （1）请证明0E=OF

（2）解答（1）题后，某同学产生了如下猜测：对上述命题，若点E 在AC 的延长线上，AG ⊥EB ，AG 交 EB 的延长线于 G ，AG 的延长线交DB 的延长线于点F ，其他条件不变，则仍有OE=OF ．问：猜测所得结论是否成立？若成立，请给出证明；若不成立，请说明理由．

F

E

D

C

B

A

E

5、如图，在梯形ABCD 中，3545AD BC AD DC AB B ====?∥，，，．动点M 从B 点出发沿线段

BC 以每秒2个单位长度的速度向终点C 运动；动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动．设运动的时间为t 秒． （1）求BC 的长．

（2）当MN AB ∥时，求t 的值．

（3）试探究：t 为何值时，MNC △为等腰三角形．

6. 如图所示，有四个动点P 、Q 、E 、F 分别从正方形ABCD 的四个顶点出发，沿着AB 、BC 、CD 、DA 以同样的速度向B 、C 、D 、A 各点移动。

（1）试判断四边形PQEF 是正方形并证明。

（2）PE 是否总过某一定点，并说明理由。

（3）四边形PQEF 的顶点位于何处时，

其面积最小，最大？各是多少？

7、已知：如图，△ABC 是边长3cm 的等边三角形，动点P 、Q 同时从A 、B 两点出发，分别沿AB 、BC 方向匀速移

动，它们的速度都是1cm/s ，当点P 到达点B 时，P 、Q 两点停止运动．设点P 的运动时间为t （s ），解答下列问题：

（1）当t 为何值时，△PBQ 是直角三角形?

（2）设四边形APQC 的面积为y （cm 2

），求y 与t 的

关系式；是否存在某一时刻t ，使四边形APQC 的面积是△ABC 面积的三分之二？如果存在，求出相应的t 值；不存在，说明理由；

C