考研数学三模拟题

考研数学三模拟题

一、选择题：1~8小题，每小题4分，共32分。在每小题给出的四个选项中，只有一项符合

题目要求，把所选项前的字母填在题后的括号中。 （1）()f x 是在(0,)+∞内单调增加的连续函数，对任何0b a >>，记()b

a M xf x dx =?，

01[()()]2b

a N

b f x dx a f x dx =+??(中间的加号改成减号)，则必有（ ）

（A ）M N ≥；（B ）M N ≤；（C ）M N =；（D ）2M N =；

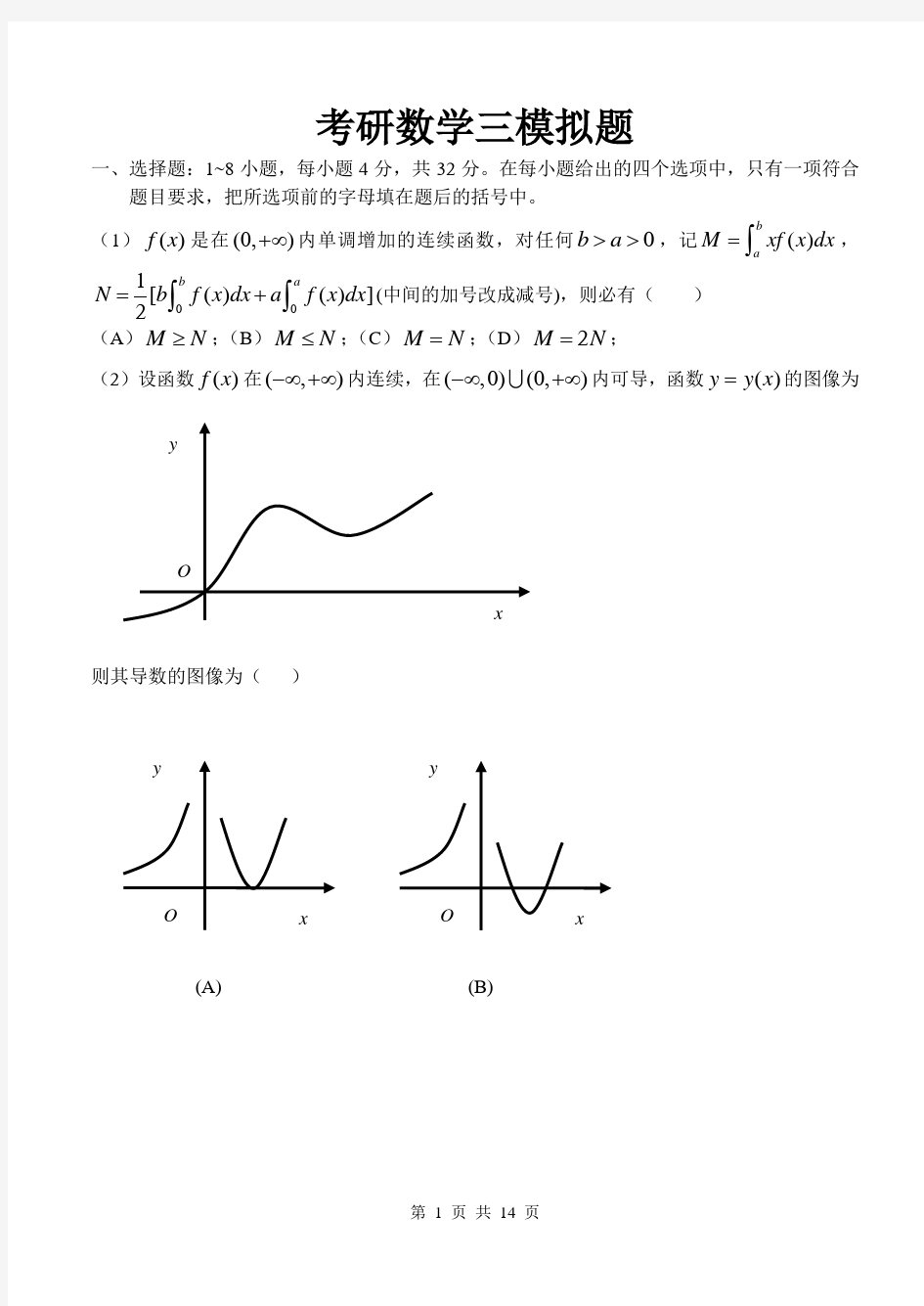
（2）设函数()f x 在(,)-∞+∞内连续，在(,0)(0,)-∞+∞U 内可导，函数()y y x =的图像为

则其导数的图像为（ ）

(A) (B)

(C) (D)

(3)设有下列命题： ①若

21

21

()n n n u

u ∞

-=+∑收敛，则1

n n u ∞=∑收敛； ②若1

n n u ∞=∑收敛，则10001

n n u ∞

+=∑收敛；

③若1

lim

1n n n

u u +→∞>，则1n n u ∞=∑发散； ④若1()n n n u v ∞=+∑收敛，则1n n u ∞=∑，1n n v ∞

=∑收敛 正确的是（ ）

（A ）①②（B ）②③（C ）③④（D ）①④

(4)设220ln(1)()

lim 2x x ax bx x

→+-+=，则（ ） （A ）51,2a b ==-

；（B ）0,2a b ==-；（C ）5

0,2

a b ==-；（D ）1,2a b ==- (5)设A 是n 阶矩阵，齐次线性方程组（I ）0Ax =有非零解，则非齐次线性方程组（II ）T

A x b =，

对任何12(,,)T

n b b b b =L

（A ）不可能有唯一解； （B ）必有无穷多解；

（C ）无解； （D ）可能有唯一解，也可能有无穷多解

(6)设,A B 均是n 阶可逆矩阵，则行列式1020

T

A B -??

-?

???

的值为 （A ）1

(2)n

A B

--； （B ）2T

A

B -； （

C ）12A B --； （

D ）1

2(2)n A B --

(7)总体~(2,4)X N ，12,,,n X X X L 为来自X 的样本，X 为样本均值，则（ ）

（A ）22

11()~(1)1n i i X X n n χ=---∑； （B ）221

1(2)~(1)1n i i X n n χ=---∑； （C ）22

12()~()2n

i i X n χ=-∑； （D ）221

()~()2n i i X X n χ=-∑； (8)设随机变量,X Y 相互独立且均服从正态分布2

(,)N μσ，若概率1

()2

P aX bY μ-<=则（ ） （A ）11,22a b =

=；

（B ）11,22a b ==-；（C ）11,22a b =-=；（D ）11

,22a b =-=-； 二、填空题：9~14小题，每小题4分，共24分。把答案填在题中的横线上。 (9)已知3232x y f x -??= ?

+??

，2

()arcsin f x x '=，则0

x dy dx == 。

(10) 方程

3

01()()3

x

x f x t dt x f t dt -=+?

?（把f(x-t)改为tf(x-t)）满足(0)0f =的特解

为 。

(11) 2222()D

x y d a b σ+=?? 。其中D 为22

1x y +≤。

(12)246

1

0(1)1!2!3!

x x x x dx -

+-+=?L 。 (13)设A 是三阶矩阵，已知0,20,30A E A E A E +=+=+=，B 与A 相似，则B 的相似对角形为 。

(14) 设10件产品中有4件不合格品，从中任取两件，已知所取的两件产品中有一件是不合格品，则另一件也是不合格品的概率为 。

三、解答题15~23小题，共94分。解答应写文字说明、证明过程或验算步骤。

(15)（本题满分10分）设函数(,)u f x y =具有二阶连续偏导数，且满足等式

22222430u u u

x x y y ???++=????。确定,a b 的值，使等式在变换,x ay x by ξη=+=+下简化为20u

ξη

?=??。

(16) （本题满分10分）求幂级数

1

(1)

n

n n x ∞

=-∑的收敛域及其在收敛域内的和函数；

至少0,ξ?∈(+∞)，使得()f ξξ+=0。

(18) （本题满分10分）过椭圆22

3231x xy y ++=上任一点作椭圆的切线，试求诸切线与两坐标轴所围成的三角形面积的最小值。

(19) （本题满分10分）设()0()0

x f x e x

x g x x

ax b x ?--

=??+≥?

，其中()f x 在0x =处二阶可导，

且(0)(0)1f f '==。

（I ）a 、b 为何值时()g x 在0x =处连续？ （II ）a 、b 为何值时()g x 在0x =处可导？

(20) （本题满分11分）设A 是实矩阵。证明：（I ）0T

A Ax =与0Ax =是同解方程组；（II ）秩()T

A A =秩()A

(21)（本题满分11分）设A 为三阶方阵，123,,ααα为三维线性无关列向量组，且有

123A ααα=+，213A ααα=+，312A ααα=+。求

（I ）求A 的全部特征值。 （II ）A 是否可以对角化？

（22）（本题满分11分）设两随机变量(,)X Y 在区域D 上均匀分布，其中

{(,):1}D x y x y =+≤，又设U X Y =+，V X Y =-，试求：

（I ）U 与V 的概率密度()U f u 与()V f v ； （II ）U 与V 的协方差cov(,)U V 和相关系数UV ρ

（23）（本题满分11分）设总体X 的概率密度函数为/1(,),()2x f x e x λ

λλ

-=

-∞<<+∞，其

中λ>0。12,,,n X X X L 是总体X 的一个容量为n 的样本。 （I ）求参数λ的矩估计量；

（II ）求参数λ的最大似然估计量；

（III ）说明由最大似然估计法所得λ的估计量是否为无偏估计量。

考研数学三模拟题参考答案

二、选择题：1~8小题，每小题4分，共32分。在每小题给出的四个选项中，只有一项符合

题目要求，把所选项前的字母填在题后的括号中。 （1） A 解：设0

()(),0x

F x x

f t dt x =>?

，则

()()()()()b

a

b a

b f x dx a f x dx F b F a F x dx '+=-=???

[()()][()()()]b x b x

a

a

f t dt xf x dx xf x tf t dt xf x dx '=+=-+????

[()()]2()b b

a

a

xf x xf x dx xf x dx ≤-=??

所以，0

01()[()()]2b

b

a a

M xf x dx b f x dx a f x dx N =

≥+=?

??

(2)B

解：由于函数可导（除0x =）且取得两个极值，故函数有两个驻点，即导函数图像与x 轴有且仅有两个交点，故A ，C 不正确。又由函数图像，极大值应小于极小值点，故D 不正确。 (3)B 解：因级数

1000

1

n n u

∞

+=∑是

1

n

n u

∞

=∑删除前1000项而得，故当

1

n

n u

∞

=∑收敛时，去掉有限项依然收敛，

因此

1000

1

n n u

∞

+=∑收敛，

若1

lim

1n n n

u u +→∞>，则存在正整数N ，使得n N ≥是，n u 不变号。若0n u >，有正项级数的比

值判别法知

n

n N

u

∞

=∑发散。同理可知，如果0n u <，则正项级数

()n

n N

u ∞=-∑发散，因此n

n N

u

∞

=∑发

散。故②③正确，选B （4）A

解：2200ln(1)()1/(1)(2)

lim lim 22x x x ax bx x a bx x x

→→+-++-+==，因0lim 0x x →=，则 0

lim1/(1)(2)0x x a bx →+-+=，故1a =。而

22200ln(1)()ln(1)lim lim 2x x x x bx x x b x x →→+-++-=+=，故122b +=-，所以52

b =- 【也可以用泰勒公式计算】 （5）A

解：0Ax =有非零解，充要条件是()r A n <，由此即可找到答案。 （6）D

解：1020

T

A B -??-?

???=1120

2202T

T A A B B --??-=--??-??=12(2)n

A B -- （7）C

解：由于2

~(2,2)i X N ，所以

2

~(0,1)2

i X N - 故2

22~(1)2i X χ-?? ???，2

212~()2n

i i X n χ=-?? ??

?∑

（8）B

因为aX bY -服从正态分布，股根据题设1

()2

P aX bY μ-<=

知， ()()()()E aX bY aE X bE Y a b μμ-=-=-=，从而有1a b -=，显然只有（B ）满足要求。 二、填空题：9~14小题，每小题4分，共24分。把答案填在题中的横线上。 （9）应填

32

π

。 解：由3232x y f x -??=

?+??

，2

()arcsin f x x '=得

22232323212arcsin()()arcsin()323232(32)dy x x x dx x x x x ---'==++++g g 0

123arcsin142

x dy dx

π==

= (10)应填()2(1)2x

f x x e =+- 解：令x t u -=，原方程变为3

001()()()3

x

x

x x

f u du uf u du x f t dt -=+?

??

方程两边对x 求导得

20

()()x

f u du x f x =+?

再两边对x 求导得()2()f x x f x '=+，即

2dy

y x dx

-=- [(2)]2(1)dx dx

y e x e dx C x C -??=-+=++?

由(0)0y =得2C =-，故()2(1)2x

y f x x e ==+- (11)应填

22

1

1(

)4a b π+

22222222221()()2D

D x y x y x y d d a b a b σσ+++=+=???? 2222111

()()2D

x y d a b σ=

++?? 213220

0111()2d r dr a b π

θ=+??

2211()4a b

π=+ (12)应填1

1(1)2

e --

解：因224622223

()()(1)[1]1!2!3!1!2!3!

x x x x x x x x x xe -----

+-+=++++=L L 故 原式2

221

1

1210

00

111

(1)222x x x xe

dx e dx e e ----=

==-=-?

?

(13)应填123-??

?

- ? ?-??

【形式不唯一，只要是对角线上为-1，-2，-3就对】 解：由0,20,30A E A E A E +=+=+=，知A 的特征值为11231,2,3λλλ=-=-=-，相似矩阵具有相同的特征值，所以B 的特征值也为11231,2,3λλλ=-=-=-，故B 相似的标准

形为123-?? ?

- ? ?-??

(14)应填0.2 解：设A ：“所取的两件产品中至少有一件事不合格品”，B ：“所取的两件都是不合格品” 因为2

2

6102()1()1(/)3P A P A C C =-=-=，22

4102()/)15

P B C C == 所以()()1

()()()5

P AB P B P B A P A P A =

==

三、解答题15~23小题，共94分。解答应写文字说明、证明过程或验算步骤。

(15) （本题满分10分）解：2222222

,2u u u u u u u

x x ξηξξηη???????=+=++????????， 2222

22222

,2u u u u u u u a b a ab b y y ξηξξηη???????=+=++????????， 222222()u u u u

a a

b b x y ξξηη

????=+++?????? 将以上各式代入原等式，得

2222

222(341)[64()2](341)0u u u a a ab a b b b ξξηη

???+++++++++=????，

由题意，令

2

2

3410,

3410,

a a

b b ?++=??++=??且64()20ab a b +++≠ 故1,1,31,1,

3a a b b =-??

=-??

??

=-??=-??或 (16) （本题满分10分）解：（I ）由于lim

11

n n

n →∞

=+，所以11x -<，即02x <<， 当0x =和2x =时幂级数变为

1

(1)

n

n n ∞

=-∑及1

n n ∞

=∑，均发散，故原级数的收敛域为(0,2)

设111

1

()(1)

(1)(1)(1)()n

n n n s x n x x n x x s x ∞

∞

-===

-=--=-∑∑

则

11

1

11

()(1)1(1)2x

n n x x s x dx x x x

∞

=--=-=

=---∑?

，

所以12

11()2(2)x s x x x '

-??== ?--??

，则21()(2)x s x x -=- (17) （本题满分10分）证明：作函数()()F x f x x =+，有

1

11

1

()[()]()02

F x dx f x x dx f x dx =+=+

??。 所以由积分中值定理，存在[0,1]a ∈， 使

1

()(10)()0,F x dx F a =-

即()0F a <。

又()()

lim

lim 11x x F x f x x x →+∞→+∞=+=，所以，由极限的保号性，存在b a >，

使()0F b b

>，即()0F b >。

因此，由介值定理，至少存在一个,(0,)a b ξ∈()?+∞，使()0F ξ=，即()f ξξ+=0。 (18) （本题满分10分）解：设(,)x y 为所给椭圆上任一点，则可求得在(,)x y 处的切线方程为

(3)()(3)()0x y X x x y Y y +-++-=

它与两坐标轴的交点为(3),03x y y x x y ??++

?+??和(3)0,3x y x y x y ??

++ ?+??

。

所以切线与坐标轴围成的三角形面积为

1(3)(3)11

2332(3)(3)x y y x y x S x y x y x y x y x y ????++=

++=????++++????

则只须求(3)(3)x y x y ++在条件2

2

3231x xy y ++=下的极值即可。 设2

2

(,,)(3)(3)3231F x y x y x y x xy y λλ=+++(++-)

由22

61062010626032310

x y F x y x y F x y x y x xy y λλλλ?'=+++=?

'=+++=??++-=?

解得44x y =±

=±或11,22

x ==±m 。 由此分别求的14S =

或1

2

S = 所以诸切线与坐标轴所围成的三角形面积的最小值为

1

4

(19) （本题满分10分） 解：（I ）000()()1

lim ()lim lim 11

x x x x x f x e x f x e g x x ---→→→'----===- 00

lim ()lim()x x g x ax b b +

+

→→=+= 若要()g x 在0x =处连续，必须0

lim ()lim ()(0)x x g x g x g -+→→==，即1b b =-= 故1b =-，a 为任意实数时，()g x 在0x =处连续。

（II ）若要()g x 在0x =处可导，则必须()g x 在0x =处连续（1b =-），且(0)(0)g g -

+''= 所以2

00()(0)()(1)(0)lim lim x x x g x g f x e x x

g x x ---→→-----'==

2

00000()()1()(0)1lim lim lim 221()(0)11lim lim [(0)1]22

x x x x x x x x x f x e f x e f x f e x x x

f x f e f x x ---

--

→→→→→'''----+===''??--''=-=-????

1(1)

(0)lim x ax g a x

+

+

→---'==

所以1

[(0)1]2

a f ''=

-，1b =-时，()g x 在0x =处可导 (20) （本题满分11分）证明：若0x 是0Ax =的解，显然0x 是0T

A Ax =的解；反之，设0x 是

0T A Ax =的解，则000T T x A Ax =。即00()0T Ax Ax =，从而

2

00000(,)()0T Ax Ax Ax Ax Ax ===，于是00Ax =，即0x 是0Ax =的解。0T A Ax =与

0Ax =是同解方程组

（II ）既然0T

A Ax =与0Ax =是同解方程组，两者的解空间维数相同，从而推知秩()T

A A =

秩()A

(21) （本题满分11分）

解：（I ）由已知得，123123()2()A αααααα++=++，2121()()A αααα-=--，

3131()()A αααα-=--，

又因为123,,ααα线性无关，所以1230ααα++≠，210αα-≠，310αα-≠ 所以1-,2是A 的特征值，123ααα++，21αα-，31αα-是相对应的特征向量。

又由123,,ααα线性无关，得123ααα++，21αα-，31αα-也线性无关，所以1-是矩阵A 的二重特征值，即A 得全部特征值为1-,2

（II ）由123,,ααα线性无关，可以证明123ααα++，21αα-，31αα-也线性无关，即A 有三个线性无关的特征向量，所以，矩阵A 可相似对角化。 （22）（本题满分11分）

解：区域D 实际是以(1,0),(1,0),(0,1),(0,1)--为顶点的正方形区域，D 的面积为2，(,)

X Y 的联合概率密度为1

(,)(,)2

x y D f x y ?∈?

=???其他

；有了(,)f x y 就可以求概率密度()U f u 与

()V f v ，特别可利用(,)f x y 的对称性。

（I ）U X Y =+，(){}{}(,)U x y u

F u P U u P X Y u f x y dxdy +≤=≤=+≤=??

当1u <-时，()0U F u =； 当11u -≤≤时，11

()22U x y u

u F u dxdy +≤+=

=??；

当1u >时，()1U F u =。

111()()2

U U u f u F u ?-≤≤?

'==???其他

，~[1,1]U U -。

U X Y =-，(){}{}(,)V x y v

F v P V v P X Y v f x y dxdy -≤=≤=-≤=

??

当1v <-时，()0V F v =； 当11v -≤≤时，11

()22V x y v

v F v dxdy -≤+==??； 当1v >时，()1V F v =。

1

11()()2

V V v f v F v ?-≤≤?

'==???其他

，~[1,1]V U -。

（II ）cov(,)()()()U V E UV E U E V =-。显然()()0E U E V ==。

2222()(()())()()()0E UV E X Y X Y E X Y E X E Y =+-=-=-=

所以cov(,)0,0UV U V ρ===

（23）（本题满分11分） 解：（I ）11()02x

E X x e dx λμλ

-

+∞

-∞

==

=?

g ； 2

2

222011()2222x

x E X x e dx x e dx λλ

μλλλ--+∞

+∞-∞

====?

?g g

所以22211??2n i i X n μλ===∑

，得2?λ=

（II ）1

12ln (,,,,)ln 2n

i

i n X

L X X X n λλλ

==--

∑L

2

1

ln 1

0n

i i d L n X d λλλ

==-+=∑

，得1

1?n

i i X n λ==∑ （III ）011()222x

x E X x e dx x e dx λλ

λλλ

--+∞

+∞-∞

==

==?

?g g

所以11111

()()n n

i i i i E X E X n n n n

λλ=====∑∑g

因此1

1?n i i X n λ==∑是λ的无偏估计量