数值分析计算实习题(二)

数值分析计算实习题(二)
SY1004114 全昌彪一:算法设计方案概述:
本题采用fortran90语言编写程序,依据题目要求,采用带双步位移QR分解法求出所给矩阵的所有特征值,并求出相应于其实特征值的特征向量,以及相关需要给出的中间结果。
1、矩阵的A的初始化(赋值):利用子函数initial(a,n)来实现,返回n×n 维二维数组a。
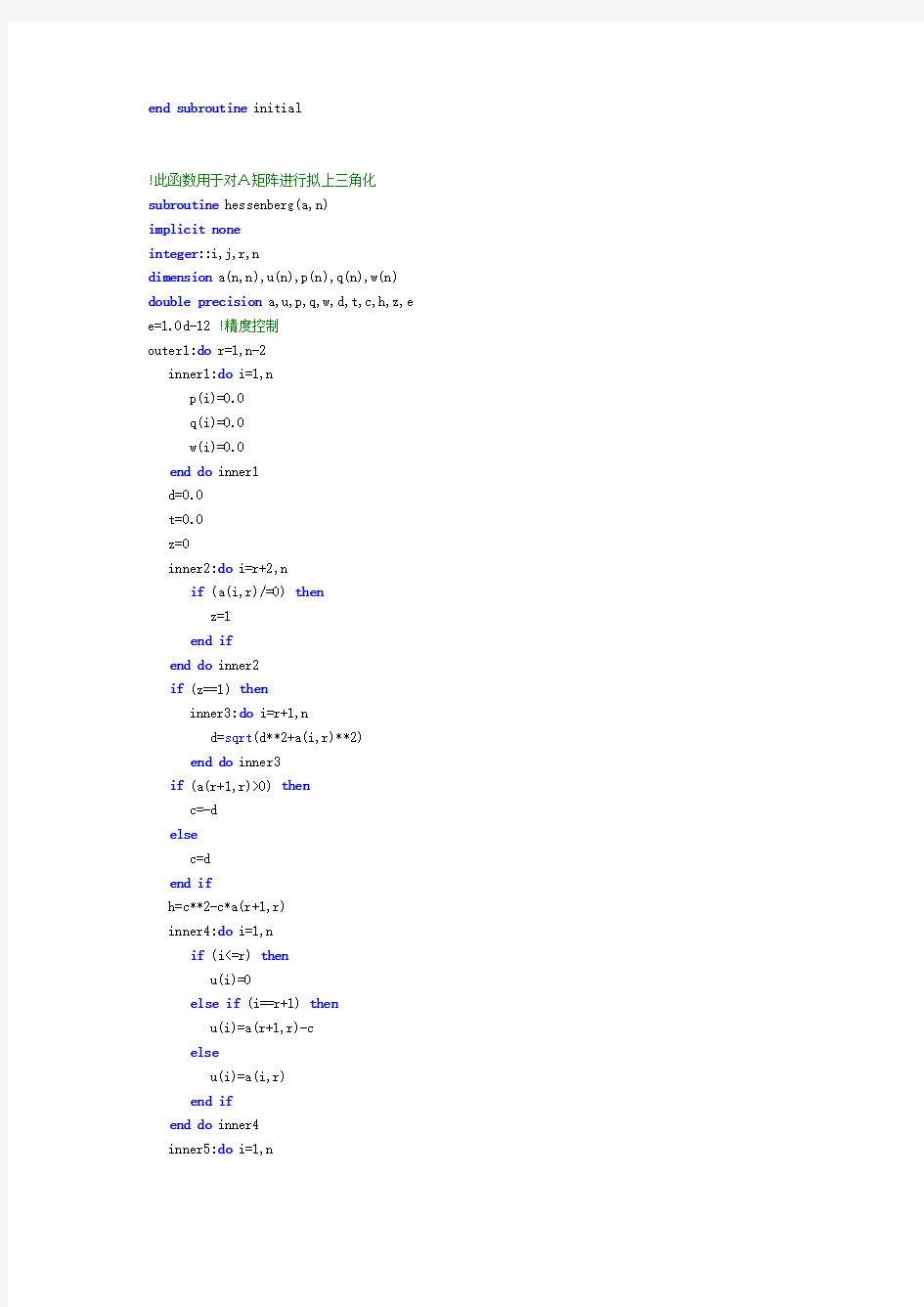
2、A矩阵的拟上三角化:利用子函数hessenberg(a,n),在对矩阵进行QR分解前进行拟上三角化,这样可以提高计算效率,减少计算量,返回A矩阵的相似矩阵Hessenberg阵A(n-1)。
3、对A(n-1)进行带双步位移QR分解得出Cm及A矩阵的所有特征值,这一步利用了两个子函数eigenvalue(a,n,lamda,lamdai)和qrresolve(b,c,m)
带双步位移QR分解可以加速收敛。每次QR分解前先进行判断,若可以直接得到矩阵的特征值,则对矩阵直接降阶处理;若不可以,则进行QR分解,这样就进一步减少了计算量,提高了计算效率。考虑到矩阵A可能有复特征值,采用两个一维数组lamda(n)及lamdai(n)分别存储其实部和虚部。在双步位移处理及降阶过程中,被分解的矩阵Ak(m ×m)及中间矩阵M k(m×m)的维数随m不断减少而降阶,于是引入了动态矩阵C(m×m)和B(m×m)分别存储,在使用前,先声明分配内存,使用结束后立即释放内存。返回A(n-1)经双步位移QR分解后的矩阵及A矩阵的所有特征值。
4、特征向量的求解:采用子函数eigenvector(a,lamda)实现求解A矩阵的属于实特征值的特征向量。核心算法为高斯列主元消去法,(A-λI)x=b,b=0,回代过程令x(10)=1,即可求出对应于每一实特征值的特征向量的各个元素。
5、相关输出结果:所有数据均采用e型输出,数据保留到小数点后12位。对于A矩阵的拟上三角化结果集双步位移QR分解结果比较庞大,为了更好的显示,还采用了f型输出,保留5位小数。所有计算精度水平E=10-12。
二:算法fortran源程序
!此函数用于给A赋值,即初始化A矩阵
subroutine initial(a,n)
integer :: i,j
dimension a(n,n)
double precision a
do i=1,n
do j=1,n
if (i==j) then
a(i,j)=1.5*cos(i+1.2*j)
else
a(i,j)=sin(0.5*i+0.2*j)
end if
end do
end do
end subroutine initial
!此函数用于对A矩阵进行拟上三角化subroutine hessenberg(a,n)
implicit none
integer::i,j,r,n
dimension a(n,n),u(n),p(n),q(n),w(n) double precision a,u,p,q,w,d,t,c,h,z,e e=1.0d-12 !精度控制
outer1:do r=1,n-2
inner1:do i=1,n
p(i)=0.0
q(i)=0.0
w(i)=0.0
end do inner1
d=0.0
t=0.0
z=0
inner2:do i=r+2,n
if (a(i,r)/=0) then
z=1
end if
end do inner2
if (z==1) then
inner3:do i=r+1,n
d=sqrt(d**2+a(i,r)**2)
end do inner3
if (a(r+1,r)>0) then
c=-d
else
c=d
end if
h=c**2-c*a(r+1,r)
inner4:do i=1,n
if (i<=r) then
u(i)=0
else if (i==r+1) then
u(i)=a(r+1,r)-c
else
u(i)=a(i,r)
end if
end do inner4
inner5:do i=1,n
do j=1,n
p(i)=p(i)+u(j)*a(j,i)/h
q(i)=q(i)+a(i,j)*u(j)/h
end do
end do inner5
inner6:do i=1,n
t=t+p(i)*u(i)
end do inner6
t=t/h
inner7:do i=1,n
w(i)=q(i)-t*u(i)
end do inner7
inner8:do i=1,n
do j=1,n
a(i,j)=a(i,j)-w(i)*u(j)-u(i)*p(j)
end do
end do inner8
end if
end do outer1
do i=1,n
do j=1,n
if (abs(a(i,j))<=e) then!a(i,j)输出精度控制
a(i,j)=0
end if
end do
end do
write(*,*) ('矩阵A拟上三角化得到的Hessenberg矩阵A(n-1)(位有效数字e型输出):') write(*,100) ((a(i,j),j=1,n),i=1,n)
write(*,*) ('矩阵A拟上三角化得到的Hessenberg矩阵A(n-1)(保留五位小数f型输出):') write(*,200) ((a(i,j),j=1,n),i=1,n)
!输出格式控制
100format (10e20.12)
200format (10f9.5)
end subroutine hessenberg
!QR分解子函数,求出A(n-1)矩阵QR分解的结果
!主要是用于eigenvalue(a,n,lamda,lamdai)的调用
subroutine qrresolve(b,c,m)
implicit none
integer::i,j,r,m
dimension b(m,m),c(m,m),u(m),p(m),q(m),w(m),v(m)
double precision b,c,u,p,q,w,v,d,c1,h,t,z
outer1:do r=1,m-1
inner1:do i=1,m
!中间量初始化
p(i)=0.0
q(i)=0.0
w(i)=0.0
v(i)=0.0
end do inner1
d=0.0
t=0.0
z=0
inner2:do i=r+1,m
if (b(i,r)/=0) then
z=1
end if
end do inner2
if (z==1) then
inner3:do i=r,m
d=sqrt(d**2+b(i,r)**2) end do inner3
if (b(r,r)>0) then
c1=-d
else
c1=d
end if
h=c1**2-c1*b(r,r)
inner4:do i=1,m
if (i u(i)=0 else if (i==r) then u(i)=b(r,r)-c1 else u(i)=b(i,r) end if end do inner4 inner5:do i=1,m do j=1,m v(i)=v(i)+u(j)*b(j,i)/h end do end do inner5 inner6:do i=1,m do j=1,m b(i,j)=b(i,j)-u(i)*v(j) end do end do inner6 inner7:do i=1,m do j=1,m p(i)=p(i)+u(j)*c(j,i)/h q(i)=q(i)+c(i,j)*u(j)/h end do end do inner7 inner8:do i=1,m t=t+p(i)*u(i) end do inner8 t=t/h inner9:do i=1,m w(i)=q(i)-t*u(i) end do inner9 inner10:do i=1,m do j=1,m c(i,j)=c(i,j)-w(i)*u(j)-u(i)*p(j) end do end do inner10 end if end do outer1 end subroutine qrresolve !此函数用于求A矩阵的特征值(包含实特征值即复特征值) !核心算法为双步位移QR方法(中间调用了QR分解法子函数) !此程序最大的特点是只用了一个goto语句 !(按课本上给出个goto语句将更易编写,笔者也编写了运行结果一样) !为了清晰显示,每一个循环语句,if语句基本上都有命名 subroutine eigenvalue(a,n,lamda,lamdai) implicit none dimension a(n,n),lamda(n),lamdai(n) double precision,allocatable,dimension(:,:) :: b,c !动态数组,用于保存Mk及C矩阵元素,维数是变化的 integer :: i,j,k,m,n,L double precision a,s,t,temp1,temp2,temp3,deta,lamda,lamdai,E E=1.0D-12 !精度 m=n L=150 !循环迭代最大次数限定 lamda=0 lamdai=0 do k=1,L outer1:if (abs(a(m,m-1))<=E) then lamda(m)=a(m,m) lamdai(m)=0 m=m-1 !m自减,降一维 10 inner1:if (m==1) then lamda(m)=a(1,1) lamdai(m)=0 exit else if (m==0) then exit else cycle end if inner1 else !Dk子块求根 temp1=(a(m-1,m-1)+a(m,m))/2.0 temp2=a(m-1,m-1)*a(m,m)-a(m,m-1)*a(m-1,m) deta=temp1**2-temp2 inner2:if (deta>0) then lamda(m)=temp1+sqrt(deta) lamdai(m)=0 lamda(m-1)=temp1-sqrt(deta) lamdai(m-1)=0 else if (deta<0) then lamda(m)=temp1 lamda(m-1)=temp1 lamdai(m)=sqrt(-deta) lamdai(m-1)=-sqrt(-deta) else lamda(m)=temp1 lamda(m-1)=temp1 lamdai(m)=0 lamdai(m-1)=0 end if inner2 inner3: if (m==2) then exit else inner4: if (abs(a(m-1,m-2))<=E) then m=m-2 !m自减,降两维 goto 10 else inner5: if (k==L) then exit else allocate(b(m,m)) !动态数组分配内存声明 allocate(c(m,m)) inner6: do i=1,m do j=1,m c(i,j)=a(i,j) end do end do inner6 s=a(m-1,m-1)+a(m,m) t=a(m-1,m-1)*a(m,m)-a(m,m-1)*a(m-1,m) b=matmul(c,c) !fotran90可直接用矩阵乘法 inner7: do i=1,m do j=1,m b(i,j)=b(i,j)-s*c(i,j) if (i==j) then b(i,j)=b(i,j)+t end if end do end do inner7 call qrresolve(b,c,m) !调用qr分解子函数 inner8: do i=1,m do j=1,m a(i,j)=c(i,j) end do end do inner8 !结束,释放可分配内存 deallocate(b) deallocate(c) end if inner5 end if inner4 end if inner3 end if outer1 end do do i=1,n do j=1,n if (abs(a(i,j))<=e) then!a(i,j)输出精度控制 a(i,j)=0 end if end do end do write(*,*) ('矩阵A(n-1)双步位移QR分解的结果(位有效数字e型输出):') write(*,100) ((a(i,j),j=1,n),i=1,n) write(*,*) ('矩阵A(n-1)双步位移QR分解的结果(保留五位小数f型输出):') write(*,200) ((a(i,j),j=1,n),i=1,n) write(*,*) ('矩阵A的全部特征值:') do i=1,n write(*,300) lamda(i),'+',lamdai(i),'i' end do !输出格式控制语句 100format (10e20.12) 200format (10f9.5) 300format (1x,1e20.12,a2,1x,1e20.12,a1) end subroutine eigenvalue !此函数用于求矩阵A属于实特征值的特征向量 !核心算法为高斯列主元消去法,(A-λI)x=b,b=0,x(10)=1回代subroutine eigenvector(a,lamda) parameter n=10 dimension a(n,n),m(n),b(n),x(n),e(n,n),a_max(n),i_k(n) double precision a,lamda,b,x,t,a_max,sum,e,i_k integer m,i,j,k,l call initial(a,n) !调用子函数,对A进行初始化 !单位矩阵 do i=1,n e(i,i)=1 end do !各参数初始化 b=0 m=0 a_max=0 t=0 a=a-lamda*e !A-λI !消元过程 do k=1,n-1 do i=k,n if (abs(a(i,k))>=a_max(k)) then a_max(k)=a(i,k) !选列主元 m(k)=i end if end do do j=k,n t=a(k,j) a(k,j)=a(m(k),j) a(m(k),j)=t t=b(k) b(k)=b(m(k)) b(m(k))=t end do do i=k+1,n i_k(i)=a(i,k)/a(k,k) do j=k+1,n a(i,j)=a(i,j)-i_k(i)*a(k,j) end do b(i)=b(i)-i_k(i)*b(k) end do end do !回代过程 x(n)=1 do k=n-1,1,-1 sum=0 do j=k+1,n sum=sum+a(k,j)*x(j) end do x(k)=(b(k)-sum)/a(k,k) end do write (*,100) 'A的属于lamda=',lamda,'的特征向量:' write (*,200) x(:) 100format (3x,a14,1e19.12,a11) 200format (1x,1e20.12) end subroutine eigenvector !主函数,用于调用各个子函数 program main_function implicit none dimension a(10,10),lamda(10),lamdai(10),x(10) integer :: i,j,n double precision a,lamda,lamdai,x n=10 call initial(a,n) !A矩阵初始化 call hessenberg(a,n) !A(n-1)矩阵拟上三角化 call eigenvalue(a,n,lamda,lamdai) !求A矩阵的所有特征值!求A矩阵属于实特征值的特征向量 call eigenvector(a,lamda(1)) call eigenvector(a,lamda(4)) call eigenvector(a,lamda(5)) call eigenvector(a,lamda(8)) call eigenvector(a,lamda(9)) call eigenvector(a,lamda(10)) end program main_function 三:程序输出结果汇总: 矩阵A拟上三角化得到的Hessenberg矩阵A(n-1)(12位有效数字e型输出): -0.882751733065E+00 -0.993313316411E-01 -0.110334955595E+01 -0.760044676830E+00 0.154909623840E+00 -0.194659168629E+01 -0.878226438751E-01 -0.925593370941E+00 0.603254375819E+00 0.151882370093E+00 -0.234787833029E+01 0.237236973917E+01 0.181929100012E+01 0.323780721082E+00 0.220580321938E+00 0.210269272044E+01 0.181611739616E+00 0.127884456394E+01 -0.638050158135E+00 -0.415402766732E+00 0.000000000000E+00 0.172827457015E+01 -0.117146801290E+01 -0.124383914708E+01 -0.639976054127E+00 -0.200283235265E+01 0.292496128495E+00 -0.641286862951E+00 0.978337580632E-01 0.255770647387E+00 0.000000000000E+00 0.000000000000E+00 -0.129166965220E+01 -0.111160388379E+01 0.117134648592E+01 -0.130735637674E+01 0.180370952121E+00 -0.424641232157E+00 0.798856288534E-01 0.160878411848E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.156012616609E+01 0.812504527179E+00 0.442174836453E+00 -0.358869742717E-01 0.469176590186E+00 -0.273656195621E+00 -0.735907113693E-01 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 -0.770777431331E+00 -0.158305209469E+01 -0.304282234567E+00 0.252871461915E+00 -0.670993649410E+00 0.254459252711E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 -0.746342926455E+00 -0.270872578791E-01 -0.948652518297E+00 0.119586353771E+00 0.192915386004E-01 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 -0.770179463681E+00 -0.469763787838E+00 0.498822338663E+00 0.113768224333E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.701315606266E+00 0.158220658011E+00 0.386262135075E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.484380788945E+00 0.399280281752E+00 矩阵A拟上三角化得到的Hessenberg矩阵A(n-1)(保留五位小数f型输出): -0.88275 -0.09933 -1.10335 -0.76004 0.15491 -1.94659 -0.08782 -0.92559 0.60325 0.15188 -2.34788 2.37237 1.81929 0.32378 0.22058 2.10269 0.18161 1.27884 -0.63805 -0.41540 0.00000 1.72827 -1.17147 -1.24384 -0.63998 -2.00283 0.29250 -0.64129 0.09783 0.25577 0.00000 0.00000 -1.29167 -1.11160 1.17135 -1.30736 0.18037 -0.42464 0.07989 0.16088 0.00000 0.00000 0.00000 1.56013 0.81250 0.44217 -0.03589 0.46918 -0.27366 -0.07359 0.00000 0.00000 0.00000 0.00000 -0.77078 -1.58305 -0.30428 0.25287 -0.67099 0.25446 0.00000 0.00000 0.00000 0.00000 0.00000 -0.74634 -0.02709 -0.94865 0.11959 0.01929 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 -0.77018 -0.46976 0.49882 0.11377 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.70132 0.15822 0.38626 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.48438 0.39928 矩阵A(n-1)双步位移QR分解的结果(12位有效数字e型输出): 0.338303924721E+01 0.894875525475E+00 -0.895678244508E+00 0.846512632866E-01 0.261267793959E+00 0.161043313340E+01 -0.102255900702E+01 0.937223229328E-01 -0.100257738993E+01 -0.408625114186E+00 0.000000000000E+00 -0.211848218734E+01 -0.236152888518E+01 -0.345573222905E-01 -0.473663572352E-01 0.181640642861E+01 -0.231836979306E+00 -0.143548828808E+00 -0.653703238456E+00 0.322737505939E-01 0.000000000000E+00 0.355512159597E+00 -0.252851058727E+01 -0.637526428692E+00 0.202388052178E-01 0.183862769119E+01 0.186937662765E+00 -0.293254867876E+00 0.198706730246E+01 0.100463175221E+01 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.157754818551E+01 -0.139621667385E-01 -0.697199695782E+00 0.155545542881E+00 0.840521541031E-02 -0.815438441765E-01 -0.108612039515E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 -0.148403977622E+01 -0.100530588729E+00 0.424954671617E-01 0.262346756601E-01 0.104004221001E+00 -0.118074774235E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 -0.694860436802E+00 -0.528901458582E+00 0.267916098808E+00 -0.596236908619E+00 -0.491158600319E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.178846387945E+00 -0.126620169756E+01 0.471455617468E-01 0.290478168004E+00 -0.357041410381E-01 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.935588710088E+00 0.187740659272E+00 0.136024981245E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.636050766399E+00 0.273703606786E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 0.245568085231E-04 0.565162119254E-01 矩阵A(n-1)双步位移QR分解的结果(保留五位小数f型输出): 3.38304 0.89488 -0.89568 0.08465 0.26127 1.61043 -1.02256 0.09372 -1.00258 -0.40863 0.00000 -2.11848 -2.36153 -0.03456 -0.04737 1.81641 -0.23184 -0.14355 -0.65370 0.03227 0.00000 0.35551 -2.52851 -0.63753 0.02024 1.83863 0.18694 -0.29325 1.98707 1.00463 0.00000 0.00000 0.00000 1.57755 -0.01396 -0.69720 0.15555 0.00841 -0.08154 -0.10861 0.00000 0.00000 0.00000 0.00000 -1.48404 -0.10053 0.04250 0.02623 0.10400 -0.11807 0.00000 0.00000 0.00000 0.00000 0.00000 -0.69486 -0.52890 0.26792 -0.59624 -0.49116 0.00000 0.00000 0.00000 0.00000 0.00000 0.17885 -1.26620 0.04715 0.29048 -0.03570 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.93559 0.18774 0.13602 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.63605 0.27370 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00002 0.05652 矩阵A的全部特征值: 0.338303924721E+01 + 0.000000000000E+00i -0.232349638731E+01 + -0.893040543164E+00i -0.232349638731E+01 + 0.893040543164E+00i 0.157754818551E+01 + 0.000000000000E+00i -0.148403977622E+01 + 0.000000000000E+00i -0.980531067180E+00 + -0.113949139468E+00i -0.980531067180E+00 + 0.113949139468E+00i 0.935588710088E+00 + 0.000000000000E+00i 0.565046144245E-01 + 0.000000000000E+00i 0.636062363900E+00 + 0.000000000000E+00i A的属于lamda= 0.338303924721E+01的特征向量: -0.436739834602E+00 -0.906357312937E+00 -0.196334018248E+01 -0.108285729157E+01 -0.126929785310E+01 -0.107244858764E+01 0.362510824633E+00 0.168290589916E+01 0.211274357722E+01 0.100000000000E+01 A的属于lamda= 0.157754818551E+01的特征向量: 0.621734685009E+00 -0.111511734070E+00 -0.248377525794E+01 -0.130686124886E+01 -0.381560716897E+01 0.811730907979E+01 -0.123917001440E+01 -0.680029414194E+00 0.269189633346E+01 0.100000000000E+01 A的属于lamda=-0.148403977622E+01的特征向量: -0.173077810726E+02 0.240818399765E+02 0.413384989796E+00 -0.857202156181E+01 0.928742697832E-01 -0.783266447227E-01 -0.637425984951E+00 -0.340318975687E+00 -0.378486114544E+00 0.100000000000E+01 A的属于lamda= 0.935588710088E+00的特征向量: 0.279242914534E+01 0.159824395408E+01 -0.520736954810E+00 -0.166788993965E+01 -0.122571220310E+02 0.724123969831E+01 -0.539823439712E+01 0.284100862311E+02 -0.121651397115E+02 0.100000000000E+01 A的属于lamda= 0.565046144245E-01的特征向量: -0.510500561103E+01 -0.488632284214E+01 0.950516391275E+01 -0.678833013260E+00 -0.960433257896E+01 -0.304574395607E+01 0.157487434454E+02 -0.739503192243E+01 -0.710966608732E+01 0.100000000000E+01 A的属于lamda= 0.636062363900E+00的特征向量: 0.474503250282E+01 0.315786893686E+01 0.172995116830E+02 -0.198004944728E+01 -0.318752699418E+02 0.779400967078E+01 -0.100425554520E+02 0.167075308672E+02 0.131053073601E+02 0.100000000000E+01 请按任意键继续. . . 四:编写程序过程中发现的一个问题 本程序运行正确,但是在编写过程中曾经产生一个很小的错误,将矩阵M k=A k2-s A k+t I 表达式中错写成了M k=A k2-s A k-t I,依旧可以得到A矩阵的所有特征值及属于实特征值的特征向量,而且和本程序的答案完全吻合,只是A(n-1)进行带双步位移QR分解结束后得到的矩阵C m相同(因为和同学对比了计算结果,发现不对),于是我调试了很久(也重新写过带双步位移QR分解子程序)方才发现这个小变动,而这个小变动只影响带双步位移QR分解,并不影响特征值的求解。 数值计算方法试题一 一、填空题(每空1分,共17分) 1、如果用二分法求方程在区间内的根精确到三位小数,需对分()次。 2、迭代格式局部收敛的充分条件是取值在()。 3、已知是三次样条函数,则 =( ),=(),=()。 4、是以整数点为节点的Lagrange插值基函数,则 ( ),( ),当时( )。 5、设和节点则 和。 6、5个节点的牛顿-柯特斯求积公式的代数精度为,5个节点的求积公式最高代数精度为。 7、是区间上权函数的最高项系数为1的正交多项式族,其中,则。 8、给定方程组,为实数,当满足,且时,SOR迭代法收敛。 9、解初值问题的改进欧拉法是 阶方法。 10、设,当()时,必有分解式,其中为下三角阵,当其对角线元素满足()条件时,这种分解是唯一的。 二、二、选择题(每题2分) 1、解方程组的简单迭代格式收敛的充要条件是()。(1), (2) , (3) , (4) 2、在牛顿-柯特斯求积公式:中,当系数是负值时,公式的稳定性不能保证,所以实际应用中,当()时的牛顿-柯特斯求积公式不使用。 (1),(2),(3),(4), (1)二次;(2)三次;(3)四次;(4)五次 4、若用二阶中点公式求解初值问题,试问为保证该公式绝对稳定,步长的取值范围为()。 (1), (2), (3), (4) 三、1、 2、(15 (1)(1) 试用余项估计其误差。 (2)用的复化梯形公式(或复化 Simpson公式)计算出该积分的近似值。 四、1、(15分)方程在附近有根,把方程写成三种不同的等价形式(1)对应迭代格式;(2)对应迭代格式;(3)对应迭代格式。判断迭代格式在的收敛性,选一种收敛格式计算附近的根,精确到小数点后第三位。选一种迭代格式建立Steffensen迭代法,并进行计算与前一种结果比较,说明是否有加速效果。 2、(8分)已知方程组,其中 , (1)(1)列出Jacobi迭代法和Gauss-Seidel迭代法的分量形式。 (2)(2)求出Jacobi迭代矩阵的谱半径,写出SOR 迭代法。 五、1、(15分)取步长,求解初值问题用改进的欧拉法求的值;用经典的四阶龙格—库塔法求的值。 2、(8分)求一次数不高于4次的多项式使它满足 ,,,, 六、(下列2题任选一题,4分) 1、1、数值积分公式形如 (1)(1)试确定参数使公式代数精度尽量高;(2)设,推导余项公式,并估计误差。 2、2、用二步法 求解常微分方程的初值问题时,如何选择参数使方法阶数尽可能高,并求局部截断误差主项,此时该方法是几阶的。 数值计算方法试题二 一、判断题:(共16分,每小题2分) 1、若是阶非奇异阵,则必存在单位下三角阵和上三角阵,使唯一成立。() 有限差分方法(FDM:Finite Difference Method)是计算机数值模拟最早采用的方法,至今仍被广泛运用。该方法将求解域划分为差分网格,用有限个网格节点代替连续的求解域。有限差分法以Taylor级数展开等方法,把控制方程中的导数用网格节点上的函数值的差商代替进行离散,从而建立以网格节点上的值为未知数的代数方程组。有限差分法主要集中在依赖于时间的问题(双曲型和抛物型方程)。有限差分法方面的经典文献有Richtmeyer & Morton的《Difference Methods for Initial-Value Problems》;R. LeVeque《Finite Difference Method for Differential Equations》;《Numerical Methods for C onservation Laws》。 注:差分格式: (1)从格式的精度来划分,有一阶格式、二阶格式和高阶格式。 (2)从差分的空间形式来考虑,可分为中心格式和逆风格式。 (3)考虑时间因子的影响,差分格式还可以分为显格式、隐格式、显隐交替格式等。 目前常见的差分格式,主要是上述几种形式的组合,不同的组合构成不同的差分格式。差分方法主要适用于有结构网格,网格的步长一般根据实际地形的情况和柯朗稳定条件来决定。 构造差分的方法: 构造差分的方法有多种形式,目前主要采用的是泰勒级数展开方法。其基本的差分表达式主要有三种形式:一阶向前差分、一阶向后差分、一阶中心差分和二阶中心差分等,其中前两种格式为一阶计算精度,后两种格式为二阶计算精度。通过对时间和空间这几种不同差分格式的组合,可以组合成不同的差分计算格式。 有限差分法的不足:由于采用的是直交网格,因此较难适应区域形状的任意性,而且区分不出场函数在区域中的轻重缓急之差异,缺乏统一有效的处理自然边值条件和内边值条件的方法,难以构造高精度(指收敛阶)差分格式,除非允许差分方程联系更多的节点(这又进一步增加处理边值条件韵困难)。另外它还有编制不出通用程序的困难。 有限差分法的优点:该方法是一种直接将微分问题变为代数问题的近似数值解法,数学概念 直观,表达简单,精度可选而且在一个时间步内,对于一个给定点来说其相关的空间点只是 与该相邻的几点,而不是全部的空间点。是发展较早且比较成熟的数值方法 广义差分法(有限体积法)(GDM:Generalized Difference Method):1953年,Mac—Neal 利用积分插值法(也称积分均衡法)建立了三角网格上的差分格 式,这就是以后通称的不规划网格上的差分法.这种方法的几何误差小,特别是给出了处理自然边值条件(及内边值条件)的有效方法,堪称差分法的一大进步。1978年,李荣华利用有限元空间和对偶单元上特征函数的推广——局部Taylor展式的公项,将积分插值法改写成广义Galerkin法形式,从而将不规则网格差分法推广为广义差分法.其基本思路是,将计算区域划分为一系列不重复的控制体积,并使每个网格点周围有 数值分析计算实习题 第二章 2-1 程序: clear;clc; x1=[0.2 0.4 0.6 0.8 1.0]; y1=[0.98 0.92 0.81 0.64 0.38]; n=length(y1); c=y1(:); for j=2:n %求差商 for i=n:-1:j c(i)=(c(i)-c(i-1))/(x1(i)-x1(i-j+1)); end end syms x df d; df(1)=1;d(1)=y1(1); for i=2:n %求牛顿差值多项式 df(i)=df(i-1)*(x-x1(i-1)); d(i)=c(i)*df(i); end disp('4次牛顿插值多项式'); P4=vpa(collect((sum(d))),5) %P4即为4次牛顿插值多项式,并保留小数点后5位数pp=csape(x1,y1, 'variational');%调用三次样条函数 q=pp.coefs; disp('三次样条函数'); for i=1:4 S=q(i,:)*[(x-x1(i))^3;(x-x1(i))^2;(x-x1(i));1]; S=vpa(collect(S),5) end x2=0.2:0.08:1.08; dot=[1 2 11 12]; figure ezplot(P4,[0.2,1.08]); hold on y2=fnval(pp,x2); x=x2(dot); y3=eval(P4); y4=fnval(pp,x2(dot)); plot(x2,y2,'r',x2(dot),y3,'b*',x2(dot),y4,'co'); title('4次牛顿插值及三次样条'); 结果如下: 4次牛顿插值多项式 P4 = - 0.52083*x^4 + 0.83333*x^3 - 1.1042*x^2 + 0.19167*x + 0.98 三次样条函数 第一章绪论 误差来源:模型误差、观测误差、截断误差(方法误差)、舍入误差 是的绝对误差,是的误差,为的绝对误差限(或误差限) 为的相对误差,当较小时,令 相对误差绝对值得上限称为相对误差限记为:即: 绝对误差有量纲,而相对误差无量纲 若近似值的绝对误差限为某一位上的半个单位,且该位直到的第一位非零数字共 有n位,则称近似值有n位有效数字,或说精确到该位。 例:设x==3.1415926…那么,则有效数字为1位,即个位上的3,或说精确到个位。 科学计数法:记有n位有效数字,精确到。 由有效数字求相对误差限:设近似值有n位有效数字,则其相对误差限为 由相对误差限求有效数字:设近似值的相对误差限为为则它有n位有效数字 令 1.x+y近似值为和的误差(限)等于误差(限) 的和 2.x-y近似值为 3.xy近似值为 4. 1.避免两相近数相减 2.避免用绝对值很小的数作除数 3.避免大数吃小数 4.尽量减少计算工作量 第二章非线性方程求根 1.逐步搜索法 设f (a) <0, f (b)> 0,有根区间为 (a, b),从x0=a出发,按某个预定步长(例如h=(b-a)/N)一步一步向右跨,每跨一步进行一次根的搜索,即判别f(x k)=f(a+kh)的符号,若f(x k)>0(而f(x k-1)<0),则有根区间缩小为[x k-1,x k] (若f(x k)=0,x k即为所求根), 然后从 x k-1出发,把搜索步长再缩小,重复上面步骤,直到满足精度:|x k-x k-1|< 为止,此时取 x*≈(x k+x k-1)/2作为近似根。 2.二分法 设f(x)的有根区间为[a,b]= [a0,b0], f(a)<0, f(b)>0.将[a0,b0]对分,中点x0= ((a0+b0)/2),计算f(x0)。 3.比例法 一般地,设 [a k,b k]为有根区间,过(a k, f(a k))、 (b k, f(b k))作直线,与x轴交于一 点x k,则: 1.试位法每次迭代比二分法多算一次乘法,而且不保证收敛。 2.比例法不是通过使求根区间缩小到0来求根,而是在一定条件下直接构造出一个点列(递推公式),使该点列收敛到方程的根。——这正是迭代法的基本思想。 事先估计: 事后估计 局部收敛性判定定理: 局部收敛性定理对迭代函数的要求较弱,但对初始点要求较高,即初始点必须选在精确解的附近 Steffensen迭代格式: Newton法: Newton下山法:是下山因子 弦割法: 目录 第一章非线性方程求根 (3) 1.1迭代法 (3) 1.2牛顿法 (4) 1.3弦截法 (5) 1.4二分法 (6) 第二章插值 (7) 2.1线性插值 (7) 2.2二次插值 (8) 2.3拉格朗日插值 (9) 2.4分段线性插值 (10) 2.5分段二次插值 (11) 第三章数值积分 (13) 3.1复化矩形积分法 (13) 3.2复化梯形积分法 (14) 3.3辛普森积分法 (15) 3.4变步长梯形积分法 (16) 第四章线性方程组数值法 (17) 4.1约当消去法 (17) 4.2高斯消去法 (18) 4.3三角分解法 (20) 4.4雅可比迭代法 (21) 4.5高斯—赛德尔迭代法 (23) 第五章常积分方程数值法 (25) 5.1显示欧拉公式法 (25) 5.2欧拉公式预测校正法 (26) 5.3改进欧拉公式法 (27) 5.4四阶龙格—库塔法 (28) 数值计算方法 第一章非线性方程求根 1.1迭代法 程序代码: Private Sub Command1_Click() x0 = Val(InputBox("请输入初始值x0")) ep = Val(InputBox(请输入误差限ep)) f = 0 While f = 0 X1 = (Exp(2 * x0) - x0) / 5 If Abs(X1 - x0) < ep Then Print X1 f = 1 Else x0 = X1 End If Wend End Sub 例:求f(x)=e2x-6x=0在x=0.5附近的根(ep=10-10) 1.2牛顿法 程序代码: Private Sub Command1_Click() b = Val(InputBox("请输入被开方数x0")) ep = Val(InputBox(请输入误差限ep)) f = 0 While f = 0 X1 = x0 - (x0 ^ 2 - b) / (2 * b) If Abs(X1 - x0) < ep Then Print X1 f = 1 Else x0 = X1 End If Wend End Sub 例:求56的值。(ep=10-10) 插值法 1.下列数据点的插值 x 0 1 4 9 16 25 36 49 64 y 0 1 2 3 4 5 6 7 8 可以得到平方根函数的近似,在区间[0,64]上作图. (1)用这9个点作8次多项式插值Ls(x). (2)用三次样条(第一边界条件)程序求S(x). 从得到结果看在[0,64]上,哪个插值更精确;在区间[0,1]上,两种插值哪个更精确? 解:(1)拉格朗日插值多项式,求解程序如下 syms x l; x1=[0 1 4 9 16 25 36 49 64]; y1=[0 1 2 3 4 5 6 7 8]; n=length(x1); Ls=sym(0); for i=1:n l=sym(y1(i)); for k=1:i-1 l=l*(x-x1(k))/(x1(i)-x1(k)); end for k=i+1:n l=l*(x-x1(k))/(x1(i)-x1(k)); end Ls=Ls+l; end Ls=simplify(Ls) %为所求插值多项式Ls(x). 输出结果为 Ls = -24221063/63504000*x^2+95549/72072*x-1/3048192000*x^8-2168879/435456000 *x^4+19/283046400*x^7+657859/10886400*x^3+33983/152409600*x^5-13003/2395008 000*x^6 (2)三次样条插值,程序如下 x1=[0 1 4 9 16 25 36 49 64]; y1=[0 1 2 3 4 5 6 7 8]; x2=[0:1:64]; y3=spline(x1,y1,x2); p=polyfit(x2,y3,3); %得到三次样条拟合函数 S=p(1)+p(2)*x+p(3)*x^2+p(4)*x^3 %得到S(x) 输出结果为: S = 23491/304472833/8*x+76713/*x^2+6867/42624*x^3 (3)在区间[0,64]上,分别对这两种插值和标准函数作图, plot(x2,sqrt(x2),'b',x2,y2,'r',x2,y3,'y') 蓝色曲线为y=函数曲线,红色曲线为拉格朗日插值函数曲线,黄色曲线为三次样条插值曲线 010203040506070 -200 20 40 60 80100 可以看到蓝色曲线与黄色曲线几乎重合,因此在区间[0,64]上三次样条插值更精确。 在[0,1]区间上由上图看不出差别,不妨代入几组数据进行比较 ,取x4=[0:0.2:1] 数值分析复习试题 第一章 绪论 一. 填空题 1.* x 为精确值 x 的近似值;() **x f y =为一元函数 ()x f y =1的近似值; ()**,*y x f y =为二元函数()y x f y ,2=的近似值,请写出下面的公式:**e x x =-: *** r x x e x -= ()()()*'1**y f x x εε≈? ()() () ()'***1**r r x f x y x f x εε≈ ? ()()()() ()* *,**,*2**f x y f x y y x y x y εεε??≈?+??? ()()()()() ** * *,***,**222r f x y e x f x y e y y x y y y ε??≈ ?+??? 2、 计算方法实际计算时,对数据只能取有限位表示,这时所产生的误差叫 舍入误 差 。 3、 分别用2.718281,2.718282作数e 的近似值,则其有效数字分别有 6 位和 7 位;又取 1.73≈-21 1.73 10 2 ≤?。 4、 设121.216, 3.654x x ==均具有3位有效数字,则12x x 的相对误差限为 0.0055 。 5、 设121.216, 3.654x x ==均具有3位有效数字,则12x x +的误差限为 0.01 。 6、 已知近似值 2.4560A x =是由真值T x 经四舍五入得 到,则相对误差限为 0.0000204 . 7、 递推公式,??? ? ?0n n-1y =y =10y -1,n =1,2, 如果取0 1.41y ≈作计算,则计算到10y 时,误 差为 81 10 2 ?;这个计算公式数值稳定不稳定 不稳定 . 8、 精确值 14159265.3* =π,则近似值141.3*1=π和1415.3*2=π分别有 3 《计算方法》期中复习试题 一、填空题: 1、已知3.1)3(,2.1)2(,0.1)1(===f f f ,则用辛普生(辛卜生)公式计算求得 ?≈3 1 _________ )(dx x f ,用三点式求得≈')1(f 。 答案:2.367,0.25 2、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2 x 的系数为 ,拉 格朗日插值多项式为 。 答案:-1, )2)(1(21 )3)(1(2)3)(2(21)(2--------= x x x x x x x L 3、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字; 4、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( ); 答案 )(1)(1n n n n n x f x f x x x '--- =+ 5、对1)(3 ++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 ); 6、计算方法主要研究( 截断 )误差和( 舍入 )误差; 7、用二分法求非线性方程 f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为 ( 1 2+-n a b ); 8、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( 0.15 ); 11、 两点式高斯型求积公式?1 d )(x x f ≈( ?++-≈1 )] 321 3()3213([21d )(f f x x f ),代数精度 为( 5 ); 12、 为了使计算 32)1(6 )1(41310-- -+-+ =x x x y 的乘除法次数尽量地少,应将该表达 式改写为 11 ,))64(3(10-= -++=x t t t t y ,为了减少舍入误差,应将表达式1999 2001- ¥ 数值分析思考题1 1、讨论绝对误差(限)、相对误差(限)与有效数字之间的关系。 2、相对误差在什么情况下可以用下式代替 3、查阅何谓问题的“病态性”,并区分与“数值稳定性”的不同点。 4、取 ,计算 ,下列方法中哪种最好为什么(1)(3 3-,(2)(2 7-,(3) ()3 1 3+ ,(4) ()6 1 1 ,(5)99- , 数值实验 数值实验综述:线性代数方程组的解法是一切科学计算的基础与核心问题。求解方法大致可分为直接法和迭代法两大类。直接法——指在没有舍入误差的情况下经过有限次运算可求得方程组的精确解的方法,因此也称为精确法。当系数矩阵是方的、稠密的、无任何特殊结构的中小规模线性方程组时,Gauss消去法是目前最基本和常用的方法。如若系数矩阵具有某种特殊形式,则为了尽可能地减少计算量与存储量,需采用其他专门的方法来求解。 Gauss消去等同于矩阵的三角分解,但它存在潜在的不稳定性,故需要选主元素。对正定对称矩阵,采用平方根方法无需选主元。方程组的性态与方程组的条件数有关,对于病态的方程组必须采用特殊的方法进行求解。 数值计算方法上机题目1 1、实验1. 病态问题 实验目的: 算法有“优”与“劣”之分,问题也有“好”和“坏”之别。所谓坏问题就是问题本身的解对数据变化的比较敏感,反之属于好问题。希望读者通过本实验对此有一个初步的体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 $ r e x x e x x ** * ** - == 141 . ≈)61 数值计算方法考试试题 一、选择题(每小题4分,共20分) 1. 误差根据来源可以分为四类,分别是( A ) A. 模型误差、观测误差、方法误差、舍入误差; B. 模型误差、测量误差、方法误差、截断误差; C. 模型误差、实验误差、方法误差、截断误差; D. 模型误差、建模误差、截断误差、舍入误差。 2. 若132)(3 56++-=x x x x f ,则其六阶差商 =]3,,3,3,3[6210 f ( C ) A. 0; B. 1; C. 2; D. 3 。 3. 数值求积公式中的Simpson 公式的代数精度为 ( D ) A. 0; B. 1; C. 2; D. 3 。 4. 若线性方程组Ax = b 的系数矩阵A 为严格对角占优矩阵,则解方程组的Jacobi 迭代法和Gauss-Seidel 迭代法 ( B ) A. 都发散; B. 都收敛 C. Jacobi 迭代法收敛,Gauss-Seidel 迭代法发散; D. Jacobi 迭代法发散,Gauss-Seidel 迭代法收敛。 5. 对于试验方程y y λ=',Euler 方法的绝对稳定区间为( C ) A. 02≤≤-h ; B. 0785.2≤≤-h ; C. 02≤≤-h λ; D. 0785.2≤≤-h λ ; 二、填空题(每空3分,共18分) 1. 已知 ? ??? ??--='-=4321,)2,1(A x ,则 =2 x 5,= 1Ax 16 ,=2A 22115+ 2. 已知 3)9(,2)4(==f f ,则 f (x )的线性插值多项式为)6(2.0)(1+=x x L ,且用线性插值可得f (7)= 2.6 。 3. 要使 20的近似值的相对误差界小于0.1%,应至少取 4 位有效数字。 三、利用下面数据表, 1. 用复化梯形公式计算积分 dx x f I )(6 .28 .1? =的近似值; 解:1.用复化梯形公式计算 取 2.048 .16.2,4=-= =h n 1分 分 分分7058337 .55))6.2()2.08.1(2)8.1((22.04)) ()(2)((231 1 1 4=+++=++=∑∑=-=f k f f b f x f a f h T k n k k 10.46675 8.03014 6.04241 4.42569 3.12014 f (x ) 2.6 2.4 2.2 2.0 1.8 x 第四章: 1、(1):复合梯形 建立m文件: function t=natrapz(fname,a,b,n) h=(b-a)/n; fa=feval(fname,a);fb=feval(fname,b); f=feval(fname,a+h:h:b-h+0.001*h); t=h*(0.5*(fa+fb)+sum(f)); 输入: >> syms x >> f=inline('sqrt(x).*log(x);'); >> natrapz(f,eps,1,10) 输出: ans = -0.417062831779470 输入: >> syms x >> f=inline('sqrt(x).*log(x);'); >> natrapz(f,eps,1,100) 输出: ans = -0.443117908008157 输入: >> syms x >> f=inline('sqrt(x).*log(x);'); >> natrapz(f,eps,1,1000) 输出: ans = -0.444387538997162 复合辛普森 建立m文件: function t=comsimpson(fname,a,b,n) h=(b-a)/n; fa=feval(fname,a);fb=feval(fname,b); f1=feval(fname,a+h:h:b-h+0.001*h); f2=feval(fname,a+h/2:h:b-h+0.001*h); t=h/6*(fa+fb+2*sum(f1)+4*sum(f2)); 输入: >> syms x >> f=inline('sqrt(x).*log(x);'); >> format long; >>comsimpson(f,eps,1,10) 输出: ans = -0.435297890074689 输入: >>syms x >>f=inline('sqrt(x).*log(x);'); >>comsimpson(f,eps,1,100) 输出: ans = -0.444161178415673 输入: >>syms x >>f=inline('sqrt(x).*log(x);'); >>comsimpson(f,eps,1,1000) 输出: ans = -0.444434117614180 (2)龙贝格 建立m文件: function [RT,R,wugu,h]=Romberg(fun,a,b,wucha,m) %RT是龙贝格积分表 %R是数值积分值 %wugu是误差估计 %h是最小步长 %fun是被积函数 %a b是积分下、上限 数值计算方法试题一 一、 填空题(每空1分,共17分) 1、如果用二分法求方程043=-+x x 在区间]2,1[内的根精确到三位小数,需对分( )次。 2、迭代格式 ) 2(2 1-+=+k k k x x x α局部收敛的充分条件是α取值在 ( )。 3、已知?????≤≤+-+-+-≤≤=31)1()1()1(2110)(2 33x c x b x a x x x x S 是三次样条函数, 则 a =( ), b =( ), c =( )。 4、)(,),(),(10x l x l x l n Λ是以整数点n x x x ,,,10Λ为节点的Lagrange 插值基函数,则 ∑== n k k x l 0)(( ), ∑== n k k j k x l x 0 )(( ),当2≥n 时 = ++∑=)()3(20 4 x l x x k k n k k ( )。 5、设 1326)(247+++=x x x x f 和节点,,2,1,0,2/Λ==k k x k 则=],,,[10n x x x f Λ 和=?07f 。 6、5个节点的牛顿-柯特斯求积公式的代数精度为 ,5个节点的求积公式最高代数精度为 。 7、{}∞=0)(k k x ?是区间]1,0[上权函数x x =)(ρ的最高项系数为1的正交多项式族,其中1)(0=x ?,则?= 1 4)(dx x x ? 。 8、给定方程组?? ?=+-=-221121b x ax b ax x ,a 为实数,当a 满足 ,且 20<<ω时,SOR 迭代法收敛。 9、解初值问题00 (,)()y f x y y x y '=?? =?的改进欧拉法 ??? ??++=+=++++)],(),([2),(] 0[111] 0[1n n n n n n n n n n y x f y x f h y y y x hf y y 是 阶方法。 10、设 ?? ??? ?????=11001a a a a A ,当∈a ( )时,必有分解式T LL A =,其中L 为下三角阵,当其对角线元素)3,2,1(=i l ii 满足( )条件时,这种分解是唯一的。 二、 二、选择题(每题2分) 1、解方程组b Ax =的简单迭代格式g Bx x k k +=+)() 1(收敛的充要条件是 ( )。 (1)1)(A ρ, (4) 1)(>B ρ 2、在牛顿-柯特斯求积公式: ?∑=-≈b a n i i n i x f C a b dx x f 0 )() ()()(中,当系数 ) (n i C 是负值时,公式的稳定性不能保证,所以实际应用中,当( )时的牛顿-柯特斯求积公式不使用。 (1)8≥n , (2)7≥n , (3)10≥n , (4)6≥n , 3、有下列数表 《数值分析》计算实习题 姓名: 学号: 班级: 第二章 1、程序代码 Clear;clc; x1=[0.2 0.4 0.6 0.8 1.0]; y1=[0.98 0.92 0.81 0.64 0.38]; n=length(y1); c=y1(:); for j=2:n %求差商 for i=n:-1:j c(i)=(c(i)-c(i-1))/(x1(i)-x1(i-j+1)); end end syms x df d; df(1)=1;d(1)=y1(1); for i=2:n %求牛顿差值多项式 df(i)=df(i-1)*(x-x1(i-1)); d(i)=c(i-1)*df(i); end P4=vpa(sum(d),5) %P4即为4次牛顿插值多项式,并保留小数点后5位数 pp=csape(x1,y1, 'variational');%调用三次样条函数 q=pp.coefs; q1=q(1,:)*[(x-.2)^3;(x-.2)^2;(x-.2);1]; q1=vpa(collect(q1),5) q2=q(1,:)*[(x-.4)^3;(x-.4)^2;(x-.4);1]; q2=vpa(collect(q2),5) q3=q(1,:)*[(x-.6)^3;(x-.6)^2;(x-.6);1]; q3=vpa(collect(q3),5) q4=q(1,:)*[(x-.8)^3;(x-.8)^2;(x-.8);1]; q4=vpa(collect(q4),5)%求解并化简多项式 2、运行结果 P4 = 0.98*x - 0.3*(x - 0.2)*(x - 0.4) - 0.625*(x - 0.2)*(x - 0.4)*(x - 0.6) - 0.20833*(x - 0.2)*(x - 0.4)*(x - 0.8)*(x - 0.6) + 0.784 q1 = - 1.3393*x^3 + 0.80357*x^2 - 0.40714*x + 1.04 《计算方法》实验内容 一.实验一:用两种不同的顺序计算 644834.110000 1 2 ≈∑=-n n ,分析其误差的变化。 1.实验目的:通过正序反序两种不同的顺序求和,比较不同算法的误差;了解在 计算机中大数吃小数的现象,以后尽量避免;体会单精度和双精度数据的差别。 2.算法描述:累加和s=0; 正序求和: 对于n=1,2,3,......,10000 s+=1.0/(n*n); 反序求和: 对于n=10000,9999,9998,.....,1 s+=1.0/(n*n); 3.源程序: #双精度型# #include 4.运行结果: 双精度型运行结果: 单精度型运行结果: 5.对算法的理解与分析:舍入误差在计算机中会引起熟知的不稳定,算法不同,肯结果也会不同,因此选取稳定的算法很重要。选取双精度型数据正反序求和时结果一致,但选用单精度型数据时,求和结果不一致,明显正序求和结果有误差,所以第一个算法较为稳定可靠。 二.实验二: 1、拉格朗日插值 按下列数据 x i -3.0 -1.0 1.0 2.0 3.0 y i 1.0 1.5 2.0 2.0 1.0 作二次插值,并求x 1=-2,x 2 =0,x 3 =2.75时的函数近似值 2牛顿插值 按下列数据 x i 0.30 0.42 0.50 0.58 0.66 0.72 y i 1.04403 1.08462 1.11803 1.15603 1.19817 1.23223 作五次插值,并求x 1=0.46,x 2 =0.55,x 3 =0.60时的函数近似值. 1.实验目的:通过拉格朗日插值和牛顿插值的实例,了解两种求解方法,并分析各自的优缺点。 2.算法描述: 3.源程序: 拉格朗日插值: #include 数值分析计算实习题(二) SY1004114 全昌彪一:算法设计方案概述: 本题采用fortran90语言编写程序,依据题目要求,采用带双步位移QR分解法求出所给矩阵的所有特征值,并求出相应于其实特征值的特征向量,以及相关需要给出的中间结果。 1、矩阵的A的初始化(赋值):利用子函数initial(a,n)来实现,返回n×n 维二维数组a。 2、A矩阵的拟上三角化:利用子函数hessenberg(a,n),在对矩阵进行QR分解前进行拟上三角化,这样可以提高计算效率,减少计算量,返回A矩阵的相似矩阵Hessenberg阵A(n-1)。 3、对A(n-1)进行带双步位移QR分解得出Cm及A矩阵的所有特征值,这一步利用了两个子函数eigenvalue(a,n,lamda,lamdai)和qrresolve(b,c,m) 带双步位移QR分解可以加速收敛。每次QR分解前先进行判断,若可以直接得到矩阵的特征值,则对矩阵直接降阶处理;若不可以,则进行QR分解,这样就进一步减少了计算量,提高了计算效率。考虑到矩阵A可能有复特征值,采用两个一维数组lamda(n)及lamdai(n)分别存储其实部和虚部。在双步位移处理及降阶过程中,被分解的矩阵Ak(m ×m)及中间矩阵M k(m×m)的维数随m不断减少而降阶,于是引入了动态矩阵C(m×m)和B(m×m)分别存储,在使用前,先声明分配内存,使用结束后立即释放内存。返回A(n-1)经双步位移QR分解后的矩阵及A矩阵的所有特征值。 4、特征向量的求解:采用子函数eigenvector(a,lamda)实现求解A矩阵的属于实特征值的特征向量。核心算法为高斯列主元消去法,(A-λI)x=b,b=0,回代过程令x(10)=1,即可求出对应于每一实特征值的特征向量的各个元素。 5、相关输出结果:所有数据均采用e型输出,数据保留到小数点后12位。对于A矩阵的拟上三角化结果集双步位移QR分解结果比较庞大,为了更好的显示,还采用了f型输出,保留5位小数。所有计算精度水平E=10-12。 二:算法fortran源程序 !此函数用于给A赋值,即初始化A矩阵 subroutine initial(a,n) integer :: i,j dimension a(n,n) double precision a do i=1,n do j=1,n if (i==j) then a(i,j)=1.5*cos(i+1.2*j) else a(i,j)=sin(0.5*i+0.2*j) end if end do end do 数值分析计算实习题一 学号: : 院系: 2015年11月5日 一、分析 1.1算法分析 题目要求求出: 1)特征值从小到大排列的最小特征值1λ和最大特征值501λ。 2)特征值中模最小的特征值s λ。 3)靠近一组数k μ的一组特征值k i λ。 4)矩阵A 的条件数cond(A)2。 5)行列式detA 。 解决方法: 1)若将所有行列式按模的大小排列则模最大的特征值一定是1λ和501λ中的一个,因此利用幂法求出模最大的特征值1m λ。然后利用带原点平移的幂法,将系数矩阵变为1m A I λ-即将所有特征值都减去1m λ,则特征值按大小顺序排列的次序不变,模最大的特征值依然在整个排列的两端,再用一次幂法得到模最大的特征值 21=m m λλλ-,其中λ为带原点平移的幂法求出的特征值,最后两个特征值1m λ、2m λ比较大小,大的为501λ,小的为1λ。 2)因为s λ为按模最小的特征值,因此用反幂法可求的其特征值。 3)因为k i λ靠近数k μ,因此k i k λμ-一定是所有的k λμ-中模最小的,因此可利用带原点平移的反幂法求出特征值k i λ,此时的系数矩阵变为k A I μ-。 4)条件数cond(A)2为模最小的特征值与模最大的特征值的比的绝对值,因此利用1和2中求出的1m λ和s λ可解出条件数。 5)可对矩阵A 进行LU 分解,即A LU =则det()det()det()A L U =?,又因为矩阵L 对角线元素为1,则det()L =1,所以det()det()A U =,U 为上三角阵,行列式为对角线元素的乘积,因此可得A 的行列式。 1.2程序分析 工程硕士《数值分析》总复习题(2011年用) [由教材中的习题、例题和历届考试题选编而成,供教师讲解和学生复习用] 一. 解答下列问题: 1)下列所取近似值有多少位有效数字( 注意根据什么? ): a) 对 e = 2.718281828459045…,取* x = 2.71828 b) 数学家祖冲之取 113355 作为π的近似值. c) 经过四舍五入得出的近似值12345,-0.001, 90.55000, 它们的有效 数字位数分别为 位, 位, 位。 2) 简述下名词: a) 截断误差 (不超过60字) b) 舍入误差 (不超过60字) c) 算法数值稳定性 (不超过60字) 3) 试推导( 按定义或利用近似公式 ): 计算3 x 时的相对误差约等于x 的相对 误差的3倍。 4) 计算球体积3 34r V π= 时,为使其相对误差不超过 0.3% ,求半径r 的相对 误差的允许范围。 5) 计算下式 341 8 )1(3)1(7)1(5)1(22345+-+---+---=x x x x x x P )( 时,为了减少乘除法次数, 通常采用什么算法? 将算式加工成什么形式? 6) 递推公式 ?????=-==- ,2,1,1102 10n y y y n n 如果取 * 041.12y y =≈= ( 三位有效数字 ) 作近似计算, 问计算到 10y 时误差为初始误差的多少倍? 这个计算过程数值稳定吗 ? 二. 插值问题: 1) 设函数 )(x f 在五个互异节点 54321,,,,x x x x x 上对应的函数值为 54321,,,,f f f f f ,根据定理,必存在唯一的次数 (A ) 的插值多项式 )(x P ,满足插值条件 ( B ) . 对此,为了构造Lagrange 插值多项式 )(x L ,由5个节点作 ( C ) 个、次数均为 ( D ) 次的插值基函数 航空航天大学 《数值分析》计算实习报告 第一大题 学院:自动化科学与电气工程学院 专业:控制科学与工程 学生姓名: 学号: 教师: 电话: 完成日期: 2015年11月6日 航空航天大学 Beijing University of Aeronautics and Astronautics 实习题目: 第一题 设有501501?的实对称矩阵A , ??? ???? ?????????=5011A a b c b c c b c b a 其中,064.0,16.0),501,,2,1(64.0)2.0sin()024.064.1(1 .0-==???=--=c b i e i i a i i 。矩阵A 的特征值为)501,,2,1(???=i i λ,并且有 ||min ||,501 150121i i s λλλλλ≤≤=≤???≤≤ 1.求1λ,501λ和s λ的值。 2.求A 的与数40 1 5011λλλμ-+=k k 最接近的特征值)39,,2,1(???=k k i λ。 3.求A 的(谱数)条件数2)A (cond 和行列式detA 。 说明: 1.在所用的算法中,凡是要给出精度水平ε的,都取12-10=ε。 2.选择算法时,应使矩阵A 的所有零元素都不储存。 3.打印以下容: (1)全部源程序; (2)特征值),,39,...,2,1(,s 5011=k k i λλλλ以及A det ,)A (cond 2的值。 4.采用e 型输出实型数,并且至少显示12位有效数字。 一、算法设计方案 1、求1λ,501λ和s λ的值。 由于||min ||,501 150121i i s λλλλλ≤≤=≤???≤≤,可知绝对值最大特征值必为1λ和501 λ其中之一,故可用幂法求出绝对值最大的特征值λ,如果λ=0,则1λ=λ,否则 501λ=λ。将矩阵A 进行一下平移: I -A A'λ= (1) 对'A 用幂法求出其绝对值最大的特征值'λ,则A 的另一端点特征值1λ或501λ为'λ+λ。 s λ为按模最小特征值,||min ||501 1i i s λλ≤≤=,可对A 使用反幂法求得。 2、求A 的与数40 1 5011λλλμ-+=k k 最接近的特征值)39,...,2,1(=k k i λ。 计算1)1,2,...,50=(i i λ-k μ,其模值最小的值对应的特征值k λ与k μ最接近。因此对A 进行平移变换: )39,,2,1k -A A k k ==(I μ (2) 对k A 用反幂法求得其模最小的特征值'k λ,则k λ='k λ+k μ。 3、求A 的(谱数)条件数2)(A cond 和行列式detA 。 由矩阵A 为非奇异对称矩阵可得: | | )(min max 2λλ=A cond (3) 其中max λ为按模最大特征值,min λ为按模最小特征值,通过第一问我们求得的λ和s λ可以很容易求得A 的条件数。 在进行反幂法求解时,要对A 进行LU 分解得到。因L 为单位下三角阵,行 列式为1,U 为上三角阵,行列式为主对角线乘积,所以A 的行列式等于U 的行列式,为U 的主对角线的乘积。 数值分析计算实习题第三章 第二次作业: 题一: x=-1:0.2:1;y=1./(1+25.*x.^2); f1=polyfit(x,y,3) f=poly2sym(f1) y1=polyval(f1,x) x2=linspace(-1,1,10) y2=interp1(x,y,x2) plot(x,y,'r*-',x,y1,'b-') hold on plot(x2,y2,'k') legend('数据点','3次拟合曲线','3次多项式插值') xlabel('X'),ylabel('Y') 输出:f1 = 0.0000 -0.5752 0.0000 0.4841 f = (4591875547102675*x^3)/81129638414606681695789005144064 - (3305*x^2)/5746 + (1469057404776431*x)/20282409603651670423947251286016 + 4360609662300613/9007199254740992 y1 = -0.0911 0.1160 0.2771 0.3921 0.4611 0.4841 0.4611 0.3921 0.2771 0.1160 -0.0911 x2 = -1.0000 -0.7778 -0.5556 -0.3333 -0.1111 0.1111 0.3333 0.5556 0.7778 1.0000 y2 = 0.0385 0.0634 0.1222 0.3000 0.7222 0.7222 0.3000 0.1222 0.0634 0.0385 题二: X=[0.0 0.1 0.2 0.3 0.5 0.8 1.0]; Y=[1.0 0.41 0.50 0.61 0.91 2.02 2.46]; p1=polyfit(X,Y,3) p2=polyfit(X,Y,4) Y1=polyval(p1,X) Y2=polyval(p2,X)数值计算方法试题及答案
数值计算方法比较
数值分析第五版计算实习题
数值分析(计算方法)总结
数值计算方法大作业
数值分析计算实习题
数值分析计算方法试题集及答案
数值计算方法》试题集及答案
数值分析作业思考题汇总
《数值计算方法》试题及答案
数值分析(第五版)计算实习题第四章作业
数值计算方法试题及答案
数值分析计算实习题
数值分析计算方法
数值分析计算实习题(二)
数值分析计算实习作业一
(整理)数值分析计算方法超级总结
北航数值分析计算实习报告一
数值分析(第五版)计算实习题第三章
