离散数学结构 第01部分 数理逻辑

第一部分数理逻辑
先看著名物理学家爱因斯坦出过的一道题:
一个土耳其商人想找一个十分聪明的助手协助他经商,有两人前来应聘,这个商人为了试试哪个更聪明些,就把两个人带进一间漆黑的屋子里,他打开灯后说:“这张桌子上有五顶帽子,两顶是红色的,三顶是黑色的,现在,我把灯关掉,而且把帽子摆的位置弄乱,然后我们三个人每人摸一顶帽子戴在自己头上,在我开灯后,请你们尽快说出自己头上戴的帽子是什么颜色的。”说完后,商人将电灯关掉,然后三人都摸了一顶帽子戴在头上,同时商人将余下的两顶帽子藏了起来,接着把灯打开。这时,那两个应试者看到商人头上戴的是一顶红帽子,其中一个人便喊道:“我戴的是黑帽子。”
请问这个人说得对吗?他是怎么推导出来的呢?
要回答这样的问题,实际上就是看由一些诸如“商人戴的是红帽子”这样的前提能否推出“猜出答案的应试者戴的是黑帽子”这样的结论来。这又需要经历如下过程:
(1) 什么是前提?有哪些前提?
(2) 结论是什么?
(3) 根据什么进行推理?
(4) 怎么进行推理?
下面的第一章,第二章回答第一个问题。第三章回答第二、三个问题。
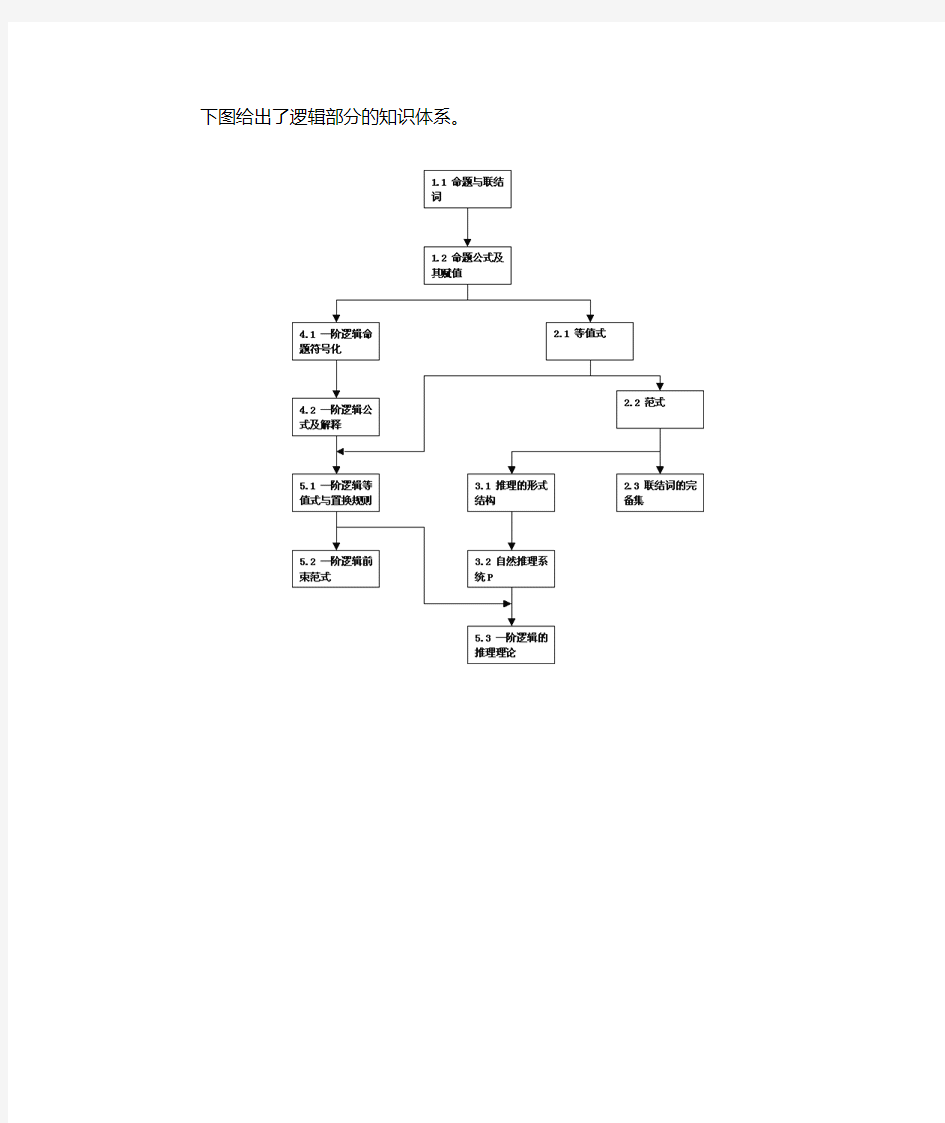
下图给出了逻辑部分的知识体系。
离散数学代数结构作业部分答案
第四章代数结构(作业) 作业:P86:4、7、9 4、 (1)若a和b是整数,则a+b+ab也是整数,故a*b也是整数,所以运算*是封闭的。(2)任选整数集合中的三个元素x,y和z。则有: (x*y)*z = (x+y+xy)*z = (x+y+xy)+z+(x+y+xy)×z = x+y+z+xy+xz+yz+xyz x*(y*z) = x*(y+z+yz) = x+(y+z+yz)+x×(y+z+yz) = x+y+z+yz+xy+xz+xyz = (x*y)*z 因此,*运算满足结合律。 (3)假设e为(Z,*)的幺元,则有: 任选整数集中的一个元素x,都有 0*x = 0+x+0×x=x且 x*0 = x+0+x×0=x 故0是(Z,*)的幺元。 7、N+上的所有元素都是(N+ ,*)等幂元; (N+ ,*)无幺元; (N+ ,*)的零元为1。 9、(A,*)中的等幂元:a、b、c、d; (A,*)中的幺元:b; (A,*)中的零元:c; a-1 = d,b-1 = b,c-1 不存在,d-1 = a, 作业:P87:12、13、18 12、(A,*)到(N4,⊕4)的同构映射f为: f(a)=0, f(b)=1, f(c)=2, f(d)=3; 或者: f(a)=0, f(b)=3, f(c)=2, f(d)=1; 13、同构映射f为: f(0)=?, f(1)={a}, f(2)={b}, f(3)={a,b};
或者: f(0)=?, f(1)={b}, f(2)={a}, f(3)={a,b}; 18、任选a ∈N +,b ∈N +, 只需证明f(a+b)=f(a)+f(b) 由f 的定义可知:f(a+b)=2a+2b=f(a)+f(b),故f 是(N +,+)到(E +,+)的同态映射。 作业:P96:3,P97:7 3、(1)显然,*运算对Z 是封闭的。 (2) (a*b)*c = (3(a+b+2)+ab)*c = 3((3(a+b+2)+ab)+c+2)+(3(a+b+2)+ab)×c = 3(3a+3b+c+ab+8+ac+bc+2c)+abc = 3(3a+3b+3c+ab+ac+bc+8)+abc a*(b*c) = a*(3(b+c+2)+bc) = 3(a+(3(b+c+2)+bc)+2)+a(3(b+c+2)+bc) = 3(a+3b+3c+bc+8+ab+ac+2a)+abc = 3(3a+3b+3c+ab+ac+bc+8)+abc = (a*b)*c 故*运算满足结合律。 (3)任选a ∈Z ,(-2)*a=a 且a*(-2)=a ,所以-2是(Z,*)的幺元。 所以(Z,*)是独异点。 7、因为1为(A,*)运算的幺元,而且对任意A 的子集A ’,*在A ’上都是封闭和可结合的运算,因此,(A,*)的所有子独异点为(A ’,*),其中A ’必须包含1。即:(A,*)的所有子独异点为: ({1},*),({1,2},*),({1,3},*),({1,4},*),({1,2,3},*),({1,2,4},*),({1,3,4},*),({1,2,3,4},*) P105:3、4、13 3、??????1100b a ×??????220 0b a =??? ?? ?212100b b a a ,a 1,a 2∈{1,-1}, 所以a 1×a 2∈{1,-1},b 1×b 2∈{1,-1}。 故(G,×)是封闭的。 而 (??????1100b a ×??????2200b a )×??????3300b a =??????212 100b b a a ×????? ?3300b a =??????3213 2100b b b a a a ??????1100b a ×(????? ?22 00b a ×??????3300b a )=??????1100b a ×??????323 200b b a a =??????3213210 0b b b a a a 故(G,×)是可结合的。(也可以说因为矩阵乘法是可结合的。)
组合数学
组合数学论文 现代数学可以分为两大类:一类是研究连续对象的,如分析、方程等,另一类就是研究离散对象的组合数学。组合数学不仅在基础数学研究中具有极其重要的地位,在其它的学科中也有重要的应用,如计算机科学、编码和密码学、物理、化学、生物等学科中均有重要应用。微积分和近代数学的发展为近代的工业革命奠定了基础。而组合数学的发展则是奠定了本世纪的计算机革命的基础。计算机之所以可以被称为电脑,就是因为计算机被人编写了程序,而程序就是算法,在绝大多数情况下,计算机的算法是针对离散的对象,而不是在作数值计算。正是因为有了组合算法才使人感到,计算机好像是有思维的。组合数学不仅在软件技术中有重要的应用价值,在企业管理,交通规划,战争指挥,金融分析等领域都有重要的应用。在美国有一家用组合数学命名的公司,他们用组合数学的方法来提高企业管理的效益,这家公司办得非常成功。此外,试验设计也是具有很大应用价值的学科,它的数学原理就是组合设计。用组合设计的方法解决工业界中的试验设计问题,在美国已有专门的公司开发这方面的软件。 广义的组合数学就是离散数学,离散数学是狭义的组合数学和图论、代数结构、数理逻辑等的总称。但这只是不同学者在叫法上的区别。总之,组合数学是一门研究离散对象的科学。随着计算机科学的日益发展,组合数学的重要性也日渐凸显,因为计算机科学的核心内容是使用算法处理离散数据。 狭义的组合数学主要研究满足一定条件的组态(也称组合模型)的存在、计数以及构造等方面的问题。组合数学的主要内容有组合计数、组合设计、组合矩阵、组合优化等。 组合数学中有几个著名的问题: 地图着色问题:对世界地图着色,每一个国家使用一种颜色。如果要求相邻国家的颜色相异,是否总共只需四种颜色?这是图论的问题。 船夫过河问题:船夫要把一匹狼、一只羊和一棵白菜运过河。只要船夫不在场,羊就会吃白菜、狼就会吃羊。船夫的船每次只能运送一种东西。怎样把所有东西都运过河? 这是线性规划的问题。 中国邮差问题:由中国组合数学家管梅谷教授提出。邮递员要穿过城市的每一条路至少一次,怎样行走走过的路程最短?这不是一个NP完全问题,存在多项式复杂度算法:先求出度为奇数的点,用匹配算法算出这些点间的连接方式,然后再用欧拉路径算法求解。这也是图论的问题。 货郎问题:一个货郎要去若干城镇卖货,然后会到出发地,给定各个城镇之间的旅行时间,应怎么样计划他的路线,使他可以去每个城镇而且所用的时间最短。这个问题至今都没有有效的算法。 这几个问题将组合数学研究的问题具体表现出来,同时也可以看出他在我们生活中有着很重要的地位。 组合数学中主要可以分成以下几个部分:排列组合与容斥原理、二项式定理、递推关系与生成函数、polya定理。下面我将以这四个部分分别介绍组合数学的各方面问题。 1、排列组合与容斥原理: 排列组合里面的4个重要的基本原理:加法原理、乘法原理、减法原理、除法原理 前面两个最为基本,后面两个是根据前两个派生出来的。乘法原理有的时候的应用很巧妙,可以作为一种打开思路的办法。
离散数学及其应用数理逻辑部分课后习题答案
作业答案:数理逻辑部分 P14:习题一 1、下列句子中,哪些是命题?在是命题的句子中,哪些是简单命题?哪些是真命题?哪些命题的真值现在还不知道? (3 答:简单命题,真命题。 (9)吸烟请到吸烟室去! 答:不是命题。 (12)8是偶数的充分必要条件是8能被3整除。 答:复合命题,假命题。 14、讲下列命题符号化。 (6)王强与刘威都学过法语。 答::p 王强学过法语;:q 刘威学过法语。 符号化为: p q ∧ (10)除非天下大雨,他就乘班车上班。 答::p 天下大雨;:q 他乘班车上班。 符号化为: p q → (13)“2或4是素数,这是不对的”是不对的。 答::p 2是素数;:q 4是素数。 符号化为:(())p q ??∨ 15、设:p 2+3=5. :q 大熊猫产在中国。 :r 太阳从西方升起。 求下列复合命题的真值。 (2)(())r p q p →∧?? (4)()(())p q r p q r ∧∧???∨?→ 解答: p 真值为1;q 真值为1;r 真值为0. (2)p q ∧真值为1;()r p q →∧真值为1;p ?真值为0; 所以(())r p q p →∧??真值为0. (4) p q r ∧∧?真值为1,p q ?∨?真值为0,()p q r ?∨?→真值为1; 所以()(())p q r p q r ∧∧???∨?→真值为1. 19、用真值表判断下列公式的类型。 (4)()()p q q p →→?→?
所以为重言式。 )s 所以为可满足式。 P36:习题二 3、用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出其成真赋值。 (1)()p q q ?∧→ 解答: 所以为永假式。 (2)(())()p p q p r →∨∨→ 解答: 所以因为永真式。 (3)()()p q p r ∨→∧
组合数学前沿介绍
组
合
数
学
Combinatorics
马昱春 MA Yuchun myc@https://www.360docs.net/doc/4d3800981.html,
1
组
合
数
学
Combinatorics
组合数学:有人认为广义的组合数学就是离散数学,也有人认 为离散数学是狭义的组合数学和图论、代数结构、数理逻辑 等的总称。但这只是不同学者在叫法上的区别。总之,组合 数学是一门研究离散对象的科学。
https://www.360docs.net/doc/4d3800981.html,/zh-cn/%E7%BB%84%E5%90%88%E6%95%B0%E5%AD%A6
Combinatorics: Combinatorics is a branch of pure mathematics concerning the study of discrete (and usually finite) objects. It is related to many other areas of mathematics, such as algebra, probability theory, ergodic theory and geometry, as well as to applied subjects in computer science and statistical physics.
https://www.360docs.net/doc/4d3800981.html,/wiki/Combinatorics 2
组合数学与离散数学
? 狭义的组合数学主要研究满足一定条件的组态( 也称组合模型)的存在、计数以及构造等方面的 问题。
– 组合数学的主要内容有组合计数、组合设计、组合矩 阵、组合优化等。
? 离散数学(Discrete mathematics)是数学的几个分 支的总称,以研究离散量的结构和相互间的关系 为主要目标,其研究对象一般地是有限个或可数 无穷个元素;因此它充分描述了计算机科学离散 性的特点。
– 离散数学通常研究的领域包括:数理逻辑、集合论、 关系论、函数论、组合学、代数系统与图论。 。
3
离散数学答案第二章习题解答
习题与解答 1. 将下列命题符号化: (1) 所有的火车都比某些汽车快。 (2) 任何金属都可以溶解在某种液体中。 (3) 至少有一种金属可以溶解在所有液体中。 (4) 每个人都有自己喜欢的职业。 (5) 有些职业是所有的人都喜欢的。 解 (1) 取论域为所有交通工具的集合。令 x x T :)(是火车, x x C :)(是汽车, x y x F :),(比y 跑得快。 “所有的火车都比某些汽车快”可以符号化为))),()(()((y x F y C y x T x ∧?→?。 (2) 取论域为所有物质的集合。令 x x M :)(是金属, x x L :)(是液体, x y x D :),(可以溶解在y 中。 “任何金属都可以溶解在某种液体中” 可以符号化为))),()(()((y x D y L y x M x ∧?→?。 (3) 论域和谓词与(2)同。“至少有一种金属可以溶解在所有液体中” 可以符号化为))),()(()((y x D y L y x M x →?∧?。 (4) 取论域为所有事物的集合。令 x x M :)(是人, x x J :)(是职业, x y x L :),(喜欢y 。 “每个人都有自己喜欢的职业” 可以符号化为))),()(()((y x L y J y x M x ∧?→? (5)论域和谓词与(4)同。“有些职业是所有的人都喜欢的”可以符号化为))),()(()((x y L y M y x J x →?∧?。 2. 取论域为正整数集,用函数+(加法),?(乘法)和谓词<,=将下列命题符号化: (1) 没有既是奇数,又是偶数的正整数。 (2) 任何两个正整数都有最小公倍数。 (3) 没有最大的素数。 (4) 并非所有的素数都不是偶数。 解 先引进一些谓词如下: x y x D :),(能被y 整除,),(y x D 可表示为)(x y v v =??。 x x J :)(是奇数,)(x J 可表示为)2(x v v =???。 x x E :)(是偶数,)(x E 可表示为)2(x v v =??。 x x P :)(是素数,)(x P 可表示为)1)(()1(x u u x u v v u x =∨=?=???∧=?。
离散数学 代数系统
第三部分:代数系统 1.在代数系统,S *中,若一个元素的逆元是唯一的,其运算*必定可结合。( ) 2.每一个有限整环一定是域,反之也对。( ) 3.任何循环群必定是阿贝尔群,反之亦真。( ) 4.设(),A ∧∨是布尔代数,则(),A ∧∨一定为有补分配格。( ) 5.设Q 为有理数集,Q 上运算*定义为max(,)a b a b *=,则 ,Q * 是半群。( ) 6.阶数为偶数的有限群中,周期为2的元素的个数一定为偶数。( ) 7.群中可以有零元(对阶数大于一的群)。( ) 8.循环群一定是阿贝尔群。( ) 9.每一个链都是分配格。( ) 1. 对自然数集合N ,哪种运算不是可结合的,运算定义为任,a b N ∈ ( ) A. min(,)a b a b *= B. 2a b a b *=+ C. 3a b a b *=+- D. a b a b *=+ (mod 3) 2. 任意具有多个等幂元的半群,它 ( ) A. 不能构成群 B. 不一定能构成群 C. 不能构成交换群 D. 能构成交换群 3. 循环群33,Z +的生成元为[][]1,2,它们的周期为 ( ) A. 5 B. 6 C. 3 D. 9 4. 设
组合数学作业答案1-2章2016
组合数学作业 第一章引言 Page 13, ex3,4,7,30 ex3. 想象一座有64个囚室组成的监狱,这些囚室被排列成8 8棋盘。所有相邻的囚室间都有门。某角落处意见囚室例的囚犯被告知,如果他能够经过其它每一个囚室正好一次之后,达到对角线上相对的另一间囚室,那么他就可以获释。他能获得自由吗? 解:不能获得自由。 方法一:对64个囚室用黑白两种颜色染色,使得横和竖方向相邻的囚室颜色不同。则对角线上两个囚室颜色为同黑或同白。总共偶数个囚室,若能遍历且不重复,则必然是黑出发白结束,矛盾。 方法二:64个囚室,若要经过每个囚室正好一次,需要走63步,即奇数步。 不妨假设该囚犯在第1行第1列,那么到第8行第8列,横着的方向需要走奇数步,竖着的方向需要走奇数步,即总共需要偶数步。 所以不能恰好经过每个囚室一次到达对角线上的囚室。 ex4. (a) 设f(n)是用多米诺牌(2-牌)对2×n棋盘作完美覆盖的个数。估计一下f(1),f(2),f(3),f(4)和f(5). 试寻找(或证明)这个计数函数f满足的简单关系。利用这个关系计算f(12)。 (b) 设g(n)是用多米诺牌(2-牌)对3×n棋盘作完美覆盖的个数。估计g(1),g(2),…,g(6). 解:(a) f(1)=1, f(2)=2, f(3)=3, f(n+2)=f(n+1)+f(n) f(4)=f(3)+f(2)=5, f(5)=f(4)+f(3)=8 f(6)=f(5)+f(4)=13 f(7)=f(6)+f(5)=21 f(8)=f(7)+f(6)=34 f(9)=f(8)+f(7)=55 f(10)=f(9)+f(8)=89 f(11)=f(10)+f(9)=144 f(12)=f(11)+f(10)=233 (b) g(1)=0, g(2)=3, g(3)=0, g(4)=9+2=11, g(n+4)=4g(n+2)-g(n), g(5)=0, g(6)=41. ex7. 设a和b是正整数,且a是b的因子。证明m×n棋盘有a×b的完美覆盖当且仅当a 既是m又是n的因子,而b是m或n的因子。(提示: 把a×b牌分割成a个1×b牌。) 解:充分性。当a既是m又是n的因子,而b是m或n的因子,则m×n棋盘有a×b的平凡完美覆盖。 必要性。假设m×n棋盘有a×b牌的完美覆盖。则m×n棋盘必有b牌的完美覆盖。根据书中的定理,b是m的因子或n的因子。 下面证明a既是m的因子又是n的因子。 方法一: 因为a是b的因子,所以a×b牌可以分割成b/a个a×a牌。m×n棋盘有a×a的完美覆盖,则必然有a×a牌的完美覆盖。而a×a牌是正方形的,所以只有唯一的一种平凡覆盖方式。从而m是a的倍数,n也是a的倍数。 方法二: 因为a是b的因子,不妨设b=ka。由m×n棋盘有a×b牌的完美覆盖,可任取一个完美覆盖。设第一行的n个方格由p个a×b牌和q个b×a牌盖住,则有n=pb+qa=(pk+q)a,所以n是a的倍数。同理,m也是a的倍数。
离散数学课后习题答案第二章
第四章部分课后习题参考答案 3. 在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为(a),(b)条件时命题的真值: (1) 对于任意x,均有2=(x+)(x). (2) 存在x,使得x+5=9. 其中(a)个体域为自然数集合. (b)个体域为实数集合. 解: F(x): 2=(x+)(x). G(x): x+5=9. (1)在两个个体域中都解释为) ?,在(a)中为假命题,在(b)中为真命题。 (x xF (2)在两个个体域中都解释为) (x ?,在(a)(b)中均为真命题。 xG 4. 在一阶逻辑中将下列命题符号化: (1) 没有不能表示成分数的有理数. (2) 在北京卖菜的人不全是外地人. 解: (1)F(x): x能表示成分数 H(x): x是有理数 命题符号化为: )) x x∧ ? ?? F ( ) ( (x H (2)F(x): x是北京卖菜的人 H(x): x是外地人 命题符号化为: )) x F H x→ ?? (x ) ( ( 5. 在一阶逻辑将下列命题符号化: (1) 火车都比轮船快. (3) 不存在比所有火车都快的汽车. 解: (1)F(x): x是火车; G(x): x是轮船; H(x,y): x比y快 命题符号化为: )) F x G y x→ ? ? y ∧ )) ( , ( ) x ((y ( H (2) (1)F(x): x是火车; G(x): x是汽车; H(x,y): x比y快 命题符号化为: ))) y x F G y→ ?? ∧ ? x ( ) ( , H ( x ) (y ( 9.给定解释I如下: (a) 个体域D为实数集合R.
离散数学代数系统练习
一、填空 1.下列集合中, 对普通加法和普通乘法都封闭。 ( ) (A ){}1,0 (B ){}2,1 (C ){}N n n ∈2 (D ){} N n n ∈2 2、在自然数集N 上,下面哪种运算是可结合的? ( ) (A )b a - (B )),max(b a (C )b a 2+ (D )b a - 3、有理数集Q 关于下列哪个运算能构成代数系统? ( ) (A )b a b a =* (B )()1ln 22++=*b a b a (C )()b a b a +=*sin (D )ab b a b a -+=* 4、下列运算中,哪种运算关于整数集I 不能构成半群? ( ) (A )()b a b a ,max =* (B )b b a =* (C )ab b a 2=* (D )b a b a -=* 5.设代数系统?A ,·?,则( )成立. A .如果?A ,·?是群,则?A ,·?是阿贝尔群 B .如果?A ,·?是阿贝尔群,则?A ,·?是循环群 C .如果?A ,·?是循环群,则?A ,·?是阿贝尔群 D .如果?A ,·?是阿贝尔群,则?A ,·?必不是循环群 6.设?L ,∧∨,?是格,?L ,≤?是由这个格诱导的偏序集,则( )不成立. A .对任意a L b a ,,∈≤b b a b =∨? B .∧∨对是可分配 C .∧∨,都满足幂等律 D .?L,≤?的每对元素都有最小上界与最大下界 7.在下列四个哈斯图表示的偏序集中( )是格.
8. 已知偏序集的哈斯图,如图所示,是格的为( ) 9. 6阶有限群的任何子群一定不是()。 (A) 2阶(B) 3 阶(C) 4 阶(D) 6 阶 10. 下列哪个偏序集构成有界格() (1) (N,≤)(2) (Z,≥) (3) ({2,3,4,6,12},|(整除关系))(4) (P(A),?) 11. 下面代数系统中(G、*)中()不是群 A、G为整数集合*为加法 B、G为偶数集合*为加法 C、G为有理数集合*为加法 D、G为有理数集合*为乘法 12. 设
离散数学数理逻辑部分考试试题
离散数学形成性考核作业(四) 数理逻辑部分 本课程形成性考核作业共4次,内容由中央电大确定、统一布置。本次形考作业是第四次作业,大家要认真及时地完成数理逻辑部分的形考作业,字迹工整,抄写题目,解答题有解答过程。 第6章命题逻辑 1.判断下列语句是否为命题,若是命题请指出是简单命题还是复合命题. (1)8能被4整除. (2)今天温度高吗? (3)今天天气真好呀! (4)6是整数当且仅当四边形有4条边. (5)地球是行星. (6)小王是学生,但小李是工人. (7)除非下雨,否则他不会去. (8)如果他不来,那么会议就不能准时开始. 解:此题即是教材P.184习题6(A)1 (1)、(4)、(5)、(6)、(7)、(8)是命题,(2)、(3)不是命题。 其中(1)、(5)是简单命题,(4)、(6)、(7)、(8)是复合命题。 2.翻译成命题公式 (1)他不会做此事. (2)他去旅游,仅当他有时间. (3)小王或小李都会解这个题. (4)如果你来,他就不回去. (5)没有人去看展览. (6)他们都是学生. (7)他没有去看电影,而是去观看了体育比赛. (8)如果下雨,那么他就会带伞. 解:此题即是教材P.184习题6(A)2
会带伞。:如果下雨,那么他就:他会带伞。:天下雨。)(。 是去观看了体育比赛。:他没有去看电影,而。 :他去观看了体育比赛:他去看电影。)(:他们都是学生。 )(:没有人去看展览。:有人去看展览。)(去。:如果你来,他就不回:他回去。 :你来。)(道题。 :小王或小李都会解这:小李会解这道题。 :小王会解这道题。)(时间。 :他去旅游,仅当他有:他有时间。:他去游泳。)(:他不会做此事。 :他会做此事。)(Q P Q P Q P Q P P P P Q P Q P Q P Q P Q P Q P P P →∧???→∧→?87654321 3.设P ,Q 的真值为1;R ,S 的真值为0,求命题公式(P ∨Q )∧R∨S ∧Q 的真值. 解:此题即是教材P.184习题6(A )4(2) (P ∨Q )真值为1,(P ∨Q)∧R真值为0,S ∧Q 真值为0, 从而(P ∨Q )∧R ∨S ∧Q 真值为0。 4.试证明如下逻辑公式 (1) ┐(A ∧┐B )∧(┐B ∨C )∧┐C ? ┐(A ∨C ) (2) (P →Q)∧(Q →R)∧┐R ??P (此题即是教材P .185习题6(A )5(1)、(4)) ) 7()()8()6)(5() 7()4)(2() 6()4)(3() 5() 4() 3()1() 2()() 1()(),(),(由由由由由证明:结论: 前提: T B A T B A T A T B P C P C B T B A P B A B A C C B B A ∨??∧????∨?∨??∧?∨??∨??∧? ) 4)(3()5() 4()2)(1() 3() 2() 1(),(),(由由证明:结论: 前提: T P P R T R P P R Q P Q P P R R Q Q P ??→→→??→→
北大代数结构与组合数学期中试题_计算机基础数学
信息科学技术学院2003-2004学年第二学期 本科生期末考试试卷 一、(每小题3分,共18分)判断以下命题的真假.如果为真在后面括弧内打 √,否则打?. 1.A ={x |x ∈N 且(x ,5)=1},则构成代数系统,+为普通加法 ( ) 2.?x , y ∈R ,x o y =|x -y |,则0为
离散数学(第一讲)
一、离散数学介绍 离散数学是研究离散量的结构及其相互关系的数学学科,是现代数学的一个重要分支。它在各学科领域,特别在计算机科学与技术领域有着广泛的应用,同时离散数学也是计算机专业的许多专业课程,如程序设计语言、数据结构、操作系统、编译技术、人工智能、数据库、算法设计与分析、理论计算机科学基础等必不可少的先行课程。通过离散数学的学习,不但可以掌握处理离散结构的描述工具和方法,为后续课程的学习创造条件,而且可以提高抽象思维和严格的逻辑推理能力,为将来参与创新性的研究和开发工作打下坚实的基础。 离散数学常常被分成三门课程进行教学,即集合论与图论、代数结构与组合数学、数理逻辑。 其中各部分内容在本书中又有如下涉及: 1.集合论部分:集合及其运算(3.1)、二元关系(3.2)与函数(3.5)、自然数及自然数集、集合的基数注:集合这个概念比较了解,在数学上,基数(cardinal number)也叫势(cardinality),指集合论中刻画任意集合所含元素数量多少的一个概念。这是康托尔在1874年~1884年引入最原始的集合论(现称朴素集合论)时, 给出的基数概念。他最先考虑的是集合{1,2,3} 和 {2,3,4},它们并非相同,但有相同的基数。 那何谓两个集合有相同数目的元素? 康托尔的答案,是所谓一一对应,即把两个集合的元素一对一的排起来,若能做到,两个集合的基数自然相同。 这个答案虽然简单,却起到了革命性的作用,因为用相同的方法即可比较任意集合,包括无穷集合的大小。 2.图论部分(第5章):图的基本概念、欧拉图与哈密顿图、树、图的矩阵表示、平面图、图着色、支配
集、覆盖集、独立集与匹配、带权图及其应用3.代数结构部分(第6、7章):代数系统的基本概念、半群与独异点、群、环与域、格与布尔代数4.组合数学部分:组合存在性定理、基本的计数公式、组合计数方法、组合计数定理 组合数学在本书中没有介绍,而关于组合数学的问题却是十分有趣的,可以供大家思考一下。 组合数学中的著名问题 ?计算一些物品在特定条件下分组的方法数目。这些是关于排列、组合和整数分拆的。 ?地图着色问题:对世界地图着色,每一个国家使用一种颜色。如果要求相邻国家的颜色相异,是 否总共只需四种颜色?这是图论的问题。 ?船夫过河问题:船夫要把一匹狼、一只羊和一棵白菜运过河。只要船夫不在场,羊就会吃白菜、 狼就会吃羊。船夫的船每次只能运送一种东西。 怎样把所有东西都运过河?这是线性规划的问 题。 ?中国邮差问题:由中国组合数学家 ?管梅谷教授① ?提出。邮递员要穿过城市的每一条路至少一次,怎样行走走过的路程最短?这不是一个NP完全 问题,存在多项式复杂度算法:先求出度为奇数 的点,用匹配算法算出这些点间的连接方式,然 后再用欧拉路径算法求解。这也是图论的问题。 ?任务分配问题(也称婚配问题):有一些员工要完成一些任务。各个员工完成不同任务所花费的时 间都不同。每个员工只分配一项任务。每项任务 只被分配给一个员工。怎样分配员工与任务以使 所花费的时间最少?这是线性规划的问题。 ?如何构作幻方。
离散数学 杨圣洪等著 第二章习题二解答
第二章习题二 1、求证?x?y(P(x)→Q(y))??xP(x)→?yQ(y) ?x?y(P(x)→Q(y)) ??x?y(?P(x)∨Q(y)) 条件式的等值式 ??x(?P(x)∨?yQ(y)) 辖域的扩充与收缩规律 ??x?P(x)∨?yQ(y) 辖域的扩充与收缩规律 ???xP(x)∨?yQ(y) 量词的德摩律 ??xP(x)→?yQ(y) 条件式的等值式 2、把下列各式转换为前束范式 (1) ?x(?(?yP(x,y)→(?zQ(z)→R(x)))) ??x(?(?yP(x,y)→(??zQ(z)∨R(x)))) 条件式的等值式 ??x(?(??yP(x,y)∨(??zQ(z)∨R(x)))) 条件式的等值式 ??x((???yP(x,y)∧(???zQ(z)∧?R(x)))) 德摩律 ??x((?yP(x,y)∧(?zQ(z)∧?R(x)))) 否定的否定 ??x?y?z ((P(x,y)∧(Q(z)∧?R(x)))) 量词辖域的扩张与收缩 ??x?y?z (P(x,y)∧Q(z)∧?R(x)) 量词辖域的扩张与收缩 (2) ?x?y((?zP(x,y,z)∧?uQ(x,u))→?vQ(y,v)) ??x?y(? (?zP(x,y,z)∧?uQ(x,u)) ∨?vQ(y,v)) 条件式的等值式 ??x?y( (??zP(x,y,z) ∨??uQ(x,u)) ∨?vQ(y,v)) 德摩律 ??x?y( (?z?P(x,y,z) ∨?u?Q(x,u)) ∨?vQ(y,v)) 德摩律 ??x?y?z?u?v ( (?P(x,y,z) ∨?Q(x,u)) ∨Q(y,v)) 德摩律 ??x?y?z?u?v ( ?P(x,y,z) ∨?Q(x,u)∨Q(y,v)) 德摩律 (3) ?xF(x) →?yP(x,y) ??zF(z) →?yP(x,y) 约束变元与自由变元同名,故约束变元改名 ???zF(z)∨?yP(x,y) 条件式的等值式 ??z?F(z)∨?yP(x,y) 德摩律 ??z?y(?F(z)∨P(x,y)) 德摩律 (4) ?x(P(x,y)→?yQ(x,y,z)) ??x(P(x,y)→?sQ(x,s,z)) 约束变元y与自由变元y同名,故约束变元改名 ??x(?P(x,y) ∨?sQ(x,s,z)) 条件式的等值式 ??x?s(?P(x,y)∨Q(x,s,z)) 辖域的扩充与收缩 (5) ?x(P(x,y)??yQ(x,y,z)) ??x(P(x,y)??sQ(x,s,z)) 约束变元y与自由变元y同名,故约束变元改名 ??x((P(x,y)→?sQ(x,s,z)) ∧(?sQ(x,s,z)→P(x,y))) 双条件的等值式 ??x((P(x,y)→?sQ(x,s,z)) ∧(?tQ(x,t,z)→P(x,y))) 后面约束变元与前面同则后面换名??x((?P(x,y)∨?sQ(x,s,z))∧(??tQ(x,t,z)∨P(x,y))) 条件式的等值式 ??x((?P(x,y)∨?sQ(x,s,z))∧(?t?Q(x,t,z)∨P(x,y))) 德摩律
离散数学第二章
离散数学第二章 1. 有序二元组也称序偶,设 A , B 为任意集合,A 和 B 的笛卡尔积用 A × B 表示,定义为 A × B = {(a , b ) | a ∈ A , b ∈ B }。 2. 推广 n 个集合的笛卡儿积为A 1 × A 2 × … × A n = {(x 1, x 2, …, x n ) | x i ∈ A i , i = 1, 2, …, n }。 3. 笛卡尔乘与交并集符号之间满足分配率: A × (B ? C ) = (A × B ) ? (A × C ) 4. 笛卡尔积 A × B 的任意一个子集 ρ 称为由 A 到 B 的一个二元关系,当 A = B 时,称 ρ 是 A 上 的二元关系。 5. 几种特殊的关系:空关系,全关系(普遍关系)记为U A ,恒等关系I A = {(a , a ) | a ∈ A }。 6. 关系的表示方法:集合表示法,矩阵表示法,关系图表示法(结点,单边)自环 7. A,B 上的关系的交,并,补,运算结果都是A 到B 的关系。 8. ,称为关系p 的逆运算也记为p-1 9. 关系的复合运算:当且仅当存在元素 b ∈ B ,使得 a ρ1 b ,b ρ2 c 时,有 a (ρ1 ? ρ2) c 。 10. I A ? ρ = ρ ? I B =p ,关系的复合满足结合律:(ρ1 ? ρ2) ? ρ3 = ρ1 ? (ρ2 ? ρ3)。 11. 规定:ρ 0 = {(a , a ) | a ∈ A },即 ρ 0 = I A 12. 复合关系的求法:定义,关系图,矩阵 13. 设 A 、B 均是有限集,ρ1、ρ2 都是由 A 到 B 的关系,它们的关系矩阵分别为和 ,则下列关系的关 系矩阵如何? ρ1 ? ρ2,ρ1 ? ρ2,ρ1',ρ1 - ρ2 ,ρ1-1。 14. 设 ρ1, ρ2 是集合 A 上的任意的关系,则 (ρ1 ? ρ2)-1 = ρ2-1 ? ρ1-1 15. 关系的性质:自反,非自反,反自反;对称,非对称,反对称;可传递,不可传递; 16. 反自反的关系一定是非自反的关系;若ρ是 A 上的反对称关系,则由定义知,在ρ中,(a , b ) 与 (b , a ) 至多有一个出现,其中 a ≠ b 。 17. {(1, 2), (3, 0), (3, 2)}这个关系可传递 18. 设 ρ 为 A 上的关系,(1) ρ 在 A 上自反当且仅当 I A ? ρ (2) ρ 在 A 上反自反当且仅当 ρ ∩I A = Φ (3) ρ 在 A 上对称当且仅当 ρ = ρ -1 (4) ρ 在 A 上反对称当且仅当 ρ ∩ ρ -1 ? I A (5) ρ 在 A 上传递当且仅当 ρ ? ρ ? ρ 。(自证,ppt 中有过程) 19.利用关系矩阵判断: }),(|),{(~ρρ ∈=b a a b
离散数学答案 第八章 代数系统
第八章 代数系统 习题8.1 1.解 ⑴是,⑵不是,⑶是,⑷不是。 2.解 若﹡对 是可分配的,则有任意a,b,c ∈* I ,均有 a ﹡( b c)=(a ﹡b) (a ﹡c)= a b a c =( a b ? a c )= a b+c 而a ﹡(b c)=a ﹡(b ?c)= a b ?c ≠a b+c 故﹡对 是不可分配的。 3.解 ⑴对于任意A ∈P(S), 因为A ?S ,所以,A ?S =S ,因此,S 是关于?运算的零元; ⑵对于任意A ∈P(S), 因为A ?S ,所以,A ?S = A ,因此,S 是关于?运算的零元单。 4.解 ⑴①因为x*y=xy-2x-2y+6,则y*x=yx-2y-2x+6= x*y ,满足交换律; ②任意x,y,z ∈R 有 x*(y*z)=x*(yz-2y-2 z +6)=x(yz-2y-2 z +6)-2x-2(yz-2y-2z+6)+6 =xyz-2xy-2xz+6x-2x -2yz+4y+4z-12+6= xyz-2xy-2xz-2yz+4x+4y+4z-6. (x*y)*z=(xy-2x-2y+6) *z =(xy-2x-2y+6)z-2(xy-2x-2y+6)-2z+6 =xyz-2xz-2yz+6z-2xy+4x+4y-2z-6=x*(y*z). 故满足结合律。 (2) ①设任意a ∈R,存在e ∈R,要e*a= ea-2e-2a+6=a ,由于a 的任意性则e=3。 因此e=3是其单位元; ②设任意b ∈R, z ∈R ,要有z*b= zb-2 z-2b+6= z ,由于b 的任意性则z=2,因此 z=2是其零元。 (3)因为*是满足交换律,对于x ∈R ,要存在1 -x ∈R ,须有x*1 -x = x 1 -x -2x-21 -x +6= e=3, 当x ≠2 时,2 321 --= -x x x 。即对于任意的x ,当x ≠2时x 都是可逆的,且2 321 --= -x x x 。 5.解 f 1,f 2,f 3都满足交换律,f 4满足等幂率,f 2有单位元a ,f 1有零元a ,f 3有零元b 。 习题8.2 1.解 构成代数系统的运算有(2),(3),(4)。 2.解 >⊕<>⊕<>⊕<444},3,2,1,0{,},2,0{,},0{ 1f b a a a a a b a 2f b a b a a b b a 3f b a a b a a b a 4f b a b a b a b a 表8-2
离散数学数理逻辑部分定义与概念
命题逻辑 1.(论域)定义:论域是一个数学系统,记为D。它由三部分组成: (1)一个非空对象集合S,每个对象也称为个体; (2)一个关于D的函数集合F; (3)一个关于D的关系集合R。 2.(逻辑联结词)定义: ?设n > 0,称{0, 1}n到{0, 1}的函数为n元函数,真值函数也称为联结词; ?若n = 0,则称为0元函数。 3.(命题合式公式)定义: (1)常元0和1是合式公式; (2)命题变元是合式公式; (3)若Q是合式公式,则(?Q)是合式公式; (4)若Q, R是合式公式,则(Q∧R)、(Q∨R)、(Q→R)、(Q?R)、(Q⊕R)是合式公式; (5)只有有限次应用(1)-(4)构成的公式是合式公式。 4.(生成公式)定义:设S是联结词的集合。由S生成的公式定义如下: (1)若c是S中的0元联结词,则c是由S生成的公式; (2)原子公式是由S生成的公式; (3)若n≥1,F是S中的n元联结词,A1, …, A n是由S生成的公式,则F A1…A n是由S 生成的公式。 5.(复杂度)公式A的复杂度表示为FC(A)。 ?常元复杂度为0; ?命题变元复杂度为0,如果P是命题变元,则FC(P) = 0; ?如果公式A = ?B,则FC(A) = FC(B) + 1; ?如果公式A = B1∧B2, 或A = B1∨B2, 或A = B1→B2, 或A = B1?B2, 或A = B1⊕B2, 则FC(A) = max{FC(B1), FC(B2)} + 1。 6.命题合式公式语义: ?论域:研究对象的集合。 ?解释:用论域的对象对应变元。 ?结构:论域和解释称为结构。 ?语义:符号指称的对象。公式所指称对象。合式公式的语义是其对应的逻辑真值。
集合论与代数结构
集合论与代数结构 课程名称:集合论与代数结构 课号:00830690 任课老师:于江生(副教授) 开课时间:每学年的下学期 学时:4学时/周 学分:4 授课对象:北大本科生(公共辅修课) 课程概要: 1.介绍Cantor的朴素集合论(包括基数理论和序数理论)和集合论ZF公理体系、GB公 理体系。回顾20世纪初数学基础之争和为解决Russell悖论所作的努力,科普G?del 不完全性定理、连续统假设及其意义。 2.介绍格论(Lattice Theory)及其应用,介绍抽象代数(Abstract Algebra)的基本概念(群、 环、域)。着重讲授群论及其应用(详细内容见《群论的应用_学生作业》)。课程的最后部分介绍域的扩张和Galois理论,并证明三等分角和倍立方体的尺规作图问题不可能。 课程目标:培养学生的数学美感,锻炼其逻辑思维能力和想象力,并使之了解近代集合论和代数学的发展。鼓励学生运用数学知识解决各自学科的实际问题,培养他们的独立科研的能力和理论联系实践的能力。 参考书及课外读物: [1]H. B. Enderton (1977), Elements of Set Theory, Academic Press, Inc. [2]L. C. Grove (1983), Algebra, Academic Press, Inc. [3]T. W. Hungerford (1980), Algebra, GTM series, Springer-Verlag [4]Jacobson, Lectures in Abstract Algebra (Vol 1, 2, 3), GTM series (No. 30, 31, 32), Springer-Verlag [5]Takeuti and Zaring, Introduction to Axiomatic Set Theory, GTM series (No. 1), Springer-Verlag [6]Takeuti and Zaring, Axiomatic Set Theory, GTM series (No. 8), Springer-Verlag [7] B. L. van der Waerden (1955), Algebra, Springer-Verlag [8]耿素云、屈婉玲、王捍贫(2002),《离散数学教程》,北京大学出版社 [9]耿素云(1998),《集合论与图论》,北京大学出版社 [10]屈婉玲(1998),《代数结构与组合数学》,北京大学出版社
