离散数学及其应用数理逻辑部分课后习题集规范标准答案

作业答案:数理逻辑部分
P14:习题一
1、下列句子中,哪些是命题?在是命题的句子中,哪些是简单命题?哪些是真命题?哪些命题的真值现在还不知道?
(3 答:简单命题,真命题。 (9)吸烟请到吸烟室去! 答:不是命题。
(12)8是偶数的充分必要条件是8能被3整除。 答:复合命题,假命题。
14、讲下列命题符号化。 (6)王强与刘威都学过法语。
答::p 王强学过法语;:q 刘威学过法语。
符号化为:p q ∧
(10)除非天下大雨,他就乘班车上班。 答::p 天下大雨;:q 他乘班车上班。
符号化为:p q →
(13)“2或4是素数,这是不对的”是不对的。 答::p 2是素数;:q 4是素数。 符号化为:(())p q ??∨
15、设:p 2+3=5. :q 大熊猫产在中国。
:r 太阳从西方升起。 求下列复合命题的真值。 (2)(())r p q p →∧??
(4)()(())p q r p q r ∧∧???∨?→ 解答: p 真值为1;q 真值为1;r 真值为0.
(2)p q ∧真值为1;()r p q →∧真值为1;p ?真值为0;
所以(())r p q p →∧??真值为0.
(4)p q r ∧∧?真值为1,p q ?∨?真值为0,()p q r ?∨?→真值为1;
所以()(())p q r p q r ∧∧???∨?→真值为1.
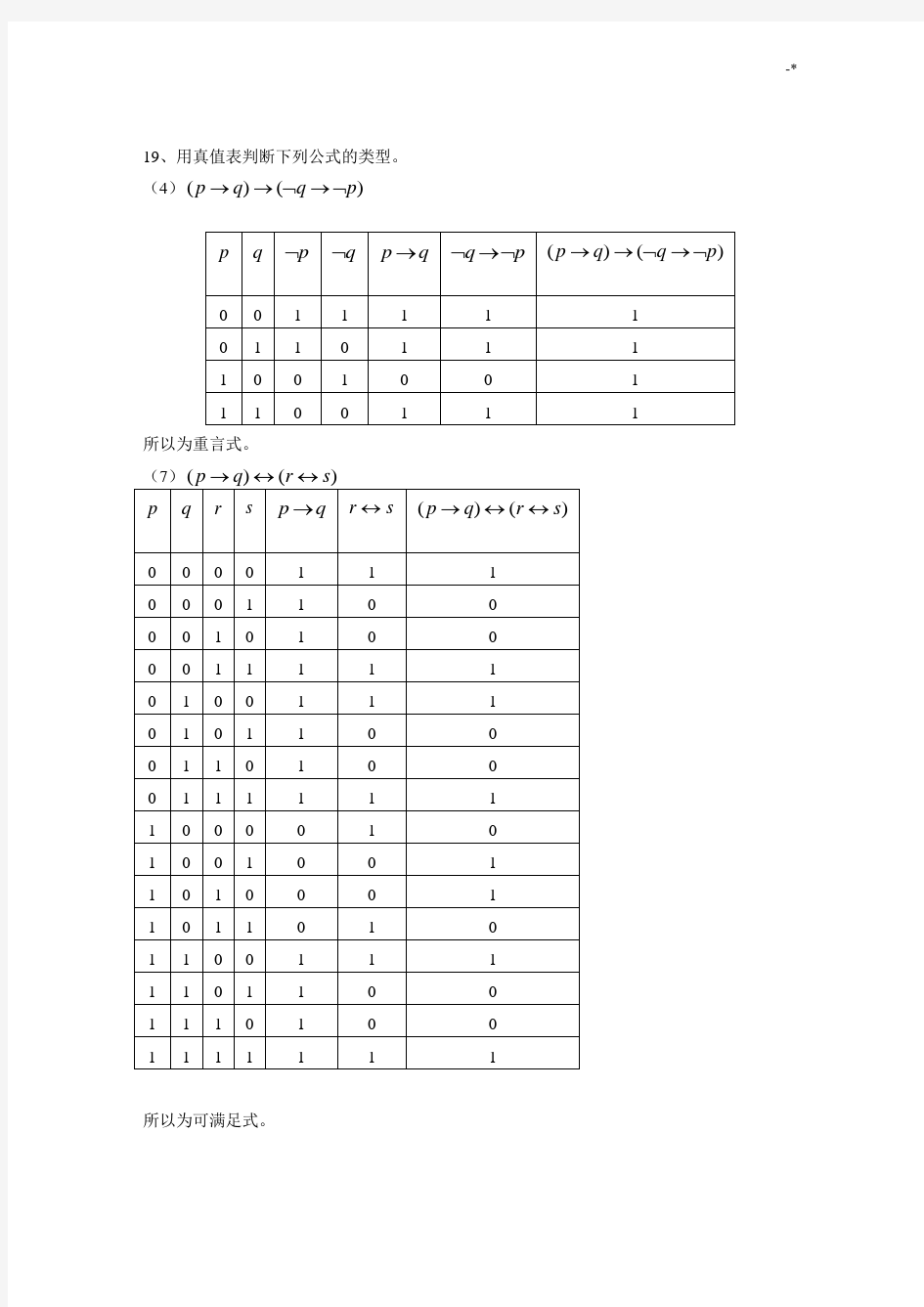
19、用真值表判断下列公式的类型。 (4)()()p q q p →→?→?
所以为重言式。
(7)
所以为可满足式。
P36:习题二
3、用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出其成真赋值。
(1)()p q q ?∧→ 解答:
()(())(())
()10
p q q p q q p q q p q q ?∧→???∧∨???∨?∨???∨?∨???
所以为永假式。
(2)(())()p p q p r →∨∨→ 解答:
(())()(())()()()1()1
p p q p r p p q p r p p q p r p r →∨∨→??∨∨∨?∨??∨∨∨?∨?∨?∨? 所以因为永真式。
(3)()()p q p r ∨→∧ 解答:
()()
()()()()
p q p r p q p r p q p r ∨→∧??∨∨∧??∧?∨∧
为可满足式。 真值表为
4、用等值演算法证明下面的等值式。 (2)(()())(())p q p r p q r →∧→?→∧ 解答:
(()())()()
()()
p q p r p q p r p q r p q r →∧→??∨∧?∨??∨∧?→∧
(4)()()()()p q p q p q p q ∧?∨?∧?∨∧?∨ 解答:
()()
()()()()
()()()()
p q p q p p p q q p q q p q q p p q q p ∧?∨?∧?∨?∧∨∧?∨?∧?∨?∨∧?∨??∨∧?∧
5、求下列公式的主析取范式,并求它们的成真赋值。 (1)()()p q q p ?→→?∨ 解答:
023
()()()()()()()()()(()(())(())
()(()())(()())()())()p q q p p q q p p q q p p q q p p q q p
p q p p q p q q p q p q p q p q p q p q p q p q m m m ?→→?∨?∨→?∨??∨∨?∨??∧?∨?∨??∧?∨?∨??∧?∨?∨∧?∨∧?∨??∧?∨?∧?∨∧?∨∧?∨∧??∧?∨∧?∨∧?∨∨析取范式)
所以成真赋值为00,10,11 (3)(())()p q r p q r ∨∧→∨∨ 解答:
(())()(())()(())()(())()()()()
p q r p q r p q r p q r p q r p q r p q r p q r p q p r p q r
∨∧→∨∨??∨∧∨∨∨??∧?∧∨∨∨??∧?∨?∨∨∨??∧?∨?∧?∨∨∨析取范式
(())(())(()())(()())(()())()()()()()()()()()()()()(p q r r p q q r p q q r r p p q r r p p q q r p q r p q r p q r p q r p q r p q r p q r p q r p q r p q r p q r p q r ??∧?∧?∨∨?∧?∨∧?∨∧?∨∧?∨∨
?∨∧∧?∨∨?∨∧?∨∧??∧?∧?∨?∧?∧∨?∧?∧?∨?∧∧?∨∧?∧?∨∧?∧∨∧∧?∨∧∧∨?∧∧?∨?∧∧∨∧∧?∨∧∧∨01234567
)()()()()()()()()()()()p q r p q r p q r p q r p q r p q r p q r p q r p q r p q r p q r p q r m m m m m m m m ?∧?∧∨?∧∧∨∧?∧∨∧∧??∧?∧?∨?∧?∧∨?∧∧?∨?∧∧∧?∧?∨∧?∧∨∧∧?∨∧∧?∨∨∨∨∨∨∨
所以为永真式,成真赋值为000,001,010,011,100,101,110,111
6、求下列公式的主合取范式,并求它们的成假赋值。 (1)()q p p ?→?∧? 解答:
0123
()()()()
(())(())(())
()()()()()()()()()()q p p q p p q p p p p q
p q q p q q p p q p q p q p q p q p q p q p q p q p q p q M M M M ?→?∧????∨?∧??∧∧??∧?∧?∨∨?∧?∨∨?∧∨?∨?∨∧∨?∧?∨∧?∨?∧∨∧?∨?∨∧∨?∧?∨∧?∨??∧∧∧合取范式
为永假式,成假赋值为00,01,10,11
(3)(())p p q r →∨∨ 解答:
(())(())()1
p p q r p p q r p p q r →∨∨??∨∨∨??∨∨∨?
永真式,无成假赋值
7、求下列公式的主析取范式,再用主析取范式求主合取范式。 (1)()p q r ∧∨ 解
答
:
13567024
()()
(())(()())
()()()()()()()()()()()p q r p q r r p p q q r p q r p q r p q r p q r p q r p q r p q r p q r p q r p q r p q r m m m m m M M M ∧∨?∧∧?∨∨?∨∧?∨∧?∧∧?∨∧∧∨?∧?∧∨?∧∧∨∧?∧∨∧∧??∧?∧∨?∧∧∨∧?∧∨∧∧?∨∧∧?∨∨∨∨?∧∧已经是析取范式
8、求下列公式的主合取范式,再用主合取范式求主析取范式。 (2)()p q r ?→ 解答:
06
123457
()(()())(()())(()())(()())()()()()()()()()p q r
p q q p r p q q p r p q q p r p q q p r
p q r p p r q q r q p r p q r q p r p q r p q r M M m m m m m m ?→?→∧→→??∨∧?∨→???∨∧?∨∨?∧?∨∧?∨?∨∨∧∨?∨∧?∨∨∧?∨?∨?∨∨∧?∨?∨?∨∨∧?∨?∨?∧?∨∨∨∨∨
13、已知公式A 含3个命题变项,,p q r ,并且它的成假赋值为010,011,110,111,求A 的主析取范式和主合取范式。 解答:成真赋值为000,001,100,101 所以主析取范式为0145m m m m ∨∨∨ 而主合取范式为2367M M M M ∧∧∧ 15、用主析取范式判断下列公式是否等值。 (2)()p q ?∧和()p q ?∨ 解答:
012
()(())(())
()()()()()()()p q p q
p q q p p q p q p q p q p q p q p q p q m m m ?∧??∨???∧?∨∨?∨∧???∧?∨?∧∨?∧?∨∧???∧?∨?∧∨∧??∨∨
()p q p q m ?∨??∧?? 所以两式并不等值。
18、将下列公式化成与之等值且仅含有{,}?∧中联结词的公式 (3)(())p q r p →∧∨ 解答:
(())(())()1
p q r p p q r p p p q r →∧∨??∨∧∨??∨∨∧?
29、在某班班委成员的选举中,已知王小红、李强、丁金生3位同学被选进了班委会。该班的的甲、乙、丙3位同学预言: 甲说:王小红为班长,李强为生活委员; 乙说:丁金生为班长,王小红为生活委员。
丙说:李强为班长,王小红为学习委员。
班委会分工名单公布后发现,甲乙丙三人都恰好猜对了一半。问王小红、李强、丁金生各任何职?(用等值演算求解) 解答:命题符号化:
:p 王小红为班长;:q 李强为生活委员;:r 丁金生为班长;:s 王小红为生活委员;
:u 李强为班长;:v 王小红为学习委员。
设1:A p q ∧?;2:A p q ?∧;1:B r s ∧?;2:B r s ?∧;1:C u v ∧?;2:C u v ?∧; 由题意可知:
0;0;0;0;0;0;0;0
p r p s p u p v q s q u r u s v ∧?∧?∧?∧?∧?∧?∧?∧?所以1112111222210;0;0;0;0;0;A B A B A C A C A B A C ∧?∧?∧?∧?∧?∧?
11220,0B C B C ∧?∧?
所以
121212111112121122211212221222212212
()()()
()()()()()()()()00000()00A A B B C C A B C A B C A B C A B C A B C A B C A B C A B C A B C A B C ∨∧∨∧∨?∧∧∨∧∧∨∧∧∨∧∧∨
∧∧∨∧∧∨∧∧∨∧∧?∨∨∨∨∨∧∧∨∨?∧∧ 所以选举结果为:李强为生活委员;丁金生为班长;王小红为学习委员。
30、某公司要从赵、钱、孙、李、周5名新毕业的大学生中选派一些人出国学习。选派必须满足条件:
(1)若赵去,钱也去; (2)李、周两人中必有一人去; (3)钱、孙两人中去且仅去一人; (4)孙、李两人同去或同不去; (5)若周去,则赵、钱也同去。
用等值演算法分析该公司该如何选派他们出国。 解答:命题符号化:
:p 赵去;:q 钱去;:r 孙去;:s 李去;:t 周去。
所满足的条件即为
(1)若赵去,钱也去:p q →; (2)李、周两人中必有一人去:s t ∨;
(3)钱、孙两人中去且仅去一人:()()q r q r ∧?∨?∧; (4)孙、李两人同去或同不去:()()r s r s ∧∨?∧?; (5)若周去,则赵、钱也同去:()t p q →∧。 将所有条件进行合取,然后求其主析取范式
()()(()())(()())(())()()
p q s t q r q r r s r s t p q p q r s t p q r s t →∧∨∧∧?∨?∧∧∧∨?∧?∧→∧??∧?∧∧∧?∨∧∧?∧?∧
(过程省略)
所以最终方案有两套:
(1)赵钱周不去,孙李去;(2)赵钱周去,孙李不去。
P50:习题三
9、用3种方法(真值表、等值演算、主析取范式)证明下面推理是正确的。
若a 是奇数,则a 不能被2整除。若a 是偶数,则a 能被2整除。因此,如果a 是偶数,则a 不是奇数。
解答:命题符号化::p a 为奇数;:q a 为偶数;:r a 能被2整除 推理的形式结构:
前提:p r →?;q r →;q 结论:q ?
推理的形式结构的另外一种描述:
()()p r q r q p →?∧→∧??
所以()()p r q r q p →?∧→∧→?为永真式;推理()()p r q r q p →?∧→∧??是正确的。
(2)等值演算:
()()()()(()())(()())()()(())(())
(()())(()())(1())(1())()()(p r q r q p p r q r q p p r q r q p p r q r q p p r q r q p p r p q r q p p r p q q r q r p r q r p r q r p →?∧→∧→???∨?∧?∨∧→????∨?∧?∨∧∨??∧∨∧?∨?∨??∧∨∧?∨?∨??∧∨?∨∧?∨??∨?∧∨?∨∨?∧?∨??∧∨?∨∧?∨??∨?∨?∨??∨?)()1
r q r r p q ∨?∨??∨?∨?∨??
(3)主析取范式
01234567
()()()()(()())(()())()()(())(())(()())(()())........
m p r q r q p p r q r q p p r q r q p p r q r q p p r q r q p
p q q r p p q r p p q r r p q q r r m m m m m m m →?∧→∧→???∨?∧?∨∧→????∨?∧?∨∧∨??∧∨∧?∨?∨??∧∨∧?∨?∨??∧?∨∧∨?∨∧∧?∨?∨∧?∧?∨∨?∧?∨∧?∨?∨∨∨∨∨∨∨
12、填充下面推理证明中没有写出的推理规则。 前提:()p q r →→,()q r s →→ 结论:()p q s ∨→ 证明: ①p q ∨ 附加前提引入 ②p ①化简 ③q
①化简 ④()p q r →→ 前提引入 ⑤q r → ②④假言推理 ⑥r
③⑤假言推理 ⑦()q r s →→ 前提引入 ⑧r s → ③⑦假言推理 ⑨s
⑥⑧假言推理
14、在自然推理系统P 中构造下面推理的证明: (2)前提:,(),p q q r r →?∧
结论:p ? 证明: ①()q r ?∧ 前提引入 ②q r ?∨? ①置换 ③r
前提引入 ④q ? ②③析取三段论 ⑤p q → 前提引入 ⑥p ?
④⑤拒取式
(4)前提:,,,q p q s s t t r →??∧
结论:p q ∧
证明: ①t r ∧ 前提引入 ②t ①化简 ③r
①化简 ④s t ?
前提引入
⑤()()s t t s →∧→ ④置换 ⑥t s → ⑤化简 ⑦q s ?
前提引入
⑧()()q s s q →∧→ ⑦置换 ⑨s q → ⑧化简 ⑩t q →
⑥⑨假言三段论
○
11q ②⑩假言推理 ○12q p → 前提引入
○
13p
○11○12假言推理 ⑨p q ∧
○
12○13合取
15、在自然推理系统P 中用附加前提法证明下面推理: (1)前提:(),,p q r s p q →→→ 结论:s r → 证明: ①s
附加前提引入 ②s p → 前提引入 ③p
①②假言推理 ④()p q r →→ 前提引入 ⑤q r → ③④假言推理 ⑥q 前提引入
⑦r
⑤⑥假言推理
16、在自然推理系统P 中用归谬法证明下面推理: (1)前提:,,p q p r q s ∨→→ 结论:r s ∨ 证明: ①()r s ?∨ 结论否定引入 ②r s ?∧? ①置换
③s ?
②化简
④r ?
②化简 ⑤p r → 前提引入 ⑥q s → 前提引入 ⑦p ? ④⑤拒取式 ⑧q ?
③⑥拒取式 ⑨p q ?∧? ⑦⑧合取 ⑩()p q ?∨
⑨置换
○
11p q ∨
前提引入
⑩○
11矛盾。 17:在自然推理系统P 中构造下面推理的证明:
只要A 曾到过受害者房间并且11点以前没有离开,A 就是谋杀嫌疑犯。A 曾到过受害者房间。如果A 在11点以前离开,看门人会看见过他。看门人没有看见他。所以,A 是谋杀嫌疑犯。 解答:
(1) 命题符号化::p A 曾到过受害者房间;:q A 在11点以前离开;
:r A 就是谋杀嫌疑犯;:s 看门人会看见过A ;
(2) 推理的形式结构:
前提:();;;p q r p q s s ∧?→→? 结论:r (3) 证明
①s ?
前提引入 ②q s → 前提引入 ③q ? ①②拒取式 ④p
前提引入 ⑤p q ∧?
③④合取 ⑥()p q r ∧?→ 前提引入 ⑦r
⑤⑥假言推理。
P63:习题四
5、在一阶逻辑中讲下列命题符号化。 (3)不存在比所有火车都快的汽车。 (4)凡是汽车就比火车慢是不对的。
解答:():()(,)F x x G y y H x y y x 为火车;:为汽车;:比快。
(3)((()()(,)))y x G y F x H x y ???∧→
(4)(()()(,))y x G y F x H y x ???∧→
6、将下列命题符号化,个体域为实数集合R ,并指出各命题的真值。 (1)对所有的x ,都存在y 使得0x y ?=。 (3)对所有的x ,都存在y 使得1y x =+。 解答:(,):0;(,):1F x y x y G x y y x ?==+ (1)(,)x yF x y ??,真值为1; (3)(,)x yG x y ??,真值为1; 9、给定解释I 如下。 (a )个体域为实数集合R 。 (b )特定元素0a =。
(c )函数(,),,f x y x y x y R =-∈
(d )谓词(,):,(,):,,F x y x y G x y x y x y R =<∈。 给出下列公式在I 下的解释,并指出它们的真值。 (1)((,)(,))x y G x y F x y ??→? (3)((,)((,),))x y G x y F f x y a ??→?
解答:(1)对任意的x 和y ,如果x y <,那么x y ≠。真值为1; (3)对任意的x 和y ,如果x y <,那么0x y -≠。真值为1;
11、判断下列各式的类型。
(2)(()())(()())x F x F x y G y G y ?→→?∧? (4)(,)(,)x yF x y y xF x y ??→??
解答:(2)(()())x F x F x ?→真值为1;(()())y G y G y ?∧?真值为0;
所以(()())(()())x F x F x y G y G y ?→→?∧?真值为0,所以为永假式。 (4)(,)x yF x y ??与(,)y xF x y ??真值相同,所以为永真式。
13、给出下列各公式的一个成真解释和一个成假解释。 (1)(()())x F x G x ?∨ (2)(()()())x F x G x H x ?∧∧ (3)(()(()(,))x F x y G y H x y ?∧?∧ 解答:
(1)成真解释:():():F x x G x x 为偶数;为奇数
成假解释:():():F x x G x x 为偶数;为素数
(2)成真解释:():2():3():5F x x G x x H x x 能被整除;能被整除;能被整除。
成假解释:():():():F x x G x x H x x 为偶数;为奇数,为素数
(3)成真解释:():():():F x x G x x H x y x y >为正数;负数;,。
成假解释:():():():F x x G x x H x y x y <为正数;负数;,。
离散数学数理逻辑部分考试试
离散数学形成性考核作业(四) 数理逻辑部分 本课程形成性考核作业共4次,内容由中央电大确定、统一布置。本次形考作业是第四次作业,大家要认真及时地完成数理逻辑部分的形考作业,字迹工整,抄写题目,解答题有解答过程。 第6章命题逻辑 1.判断下列语句是否为命题,若是命题请指出是简单命题还是复合命题. (1)8能被4整除. (2)今天温度高吗? (3)今天天气真好呀! (4)6是整数当且仅当四边形有4条边. (5)地球是行星. (6)小王是学生,但小李是工人. (7)除非下雨,否则他不会去. (8)如果他不来,那么会议就不能准时开始. 解:此题即是教材P.184习题6(A)1 (1)、(4)、(5)、(6)、(7)、(8)是命题,(2)、(3)不是命题。 其中(1)、(5)是简单命题,(4)、(6)、(7)、(8)是复合命题。 2.翻译成命题公式 (1)他不会做此事. (2)他去旅游,仅当他有时间. (3)小王或小李都会解这个题. (4)如果你来,他就不回去. (5)没有人去看展览. (6)他们都是学生. (7)他没有去看电影,而是去观看了体育比赛. (8)如果下雨,那么他就会带伞. 解:此题即是教材P.184习题6(A)2
会带伞。 :如果下雨,那么他就:他会带伞。 :天下雨。)(。是去观看了体育比赛。:他没有去看电影,而。 :他去观看了体育比赛:他去看电影。)(:他们都是学生。 )(:没有人去看展览。 :有人去看展览。)(去。 :如果你来,他就不回:他回去。:你来。)(道题。:小王或小李都会解这:小李会解这道题。 :小王会解这道题。)(时间。 :他去旅游,仅当他有:他有时间。 :他去游泳。)(:他不会做此事。:他会做此事。)(Q P Q P Q P Q P P P P Q P Q P Q P Q P Q P Q P P P →∧???→∧→?87654321 3.设P ,Q 的真值为1;R ,S 的真值为0,求命题公式(P ∨Q )∧R ∨S ∧Q 的真值. 解:此题即是教材P.184习题6(A )4(2) (P ∨Q )真值为1,(P ∨Q )∧R 真值为0,S ∧Q 真值为0, 从而(P ∨Q )∧R ∨S ∧Q 真值为0。 4.试证明如下逻辑公式 (1) ┐(A ∧┐B )∧(┐B ∨C )∧┐C ? ┐(A ∨C ) (2) (P →Q )∧(Q →R )∧┐R ??P (此题即是教材P.185习题6(A )5(1)、(4)) ) 7() () 8()6)(5()7()4)(2()6()4)(3()5()4()3()1() 2()() 1()(), (),(由由由由由证明:结论:前提:T B A T B A T A T B P C P C B T B A P B A B A C C B B A ∨??∧????∨?∨??∧?∨??∨??∧? ) 4)(3() 5()4()2)(1()3() 2() 1(), (),(由由证明:结论:前提:T P P R T R P P R Q P Q P P R R Q Q P ??→→→??→→
离散数学期末测试卷I及答案
离散数学期末测试卷I及答案 第一部分、考试形式和时间 答题时限:120 分钟考试形式:闭卷笔试 第二部分、考试题型和得分构成 一、选择题:对每一道小题,从其4个备选答案中选择最适合的一项,每小题2分,共10 道小题,20分。 二、填空题:每空1分,共5道小题,10个空白处待填,10分。 三、判断题:每一道小题均以陈述语句描述,对的打√,错的打х。每小题1分,共10 道小题,10分。 四、综合题:每小题10分,共6道小题,60分。 第三部分、考试复习范围 一、选择题 1.含n个元素的集合A的幂集的元素个数为多少? 答案:2n个。 2.数理逻辑的创始人是谁?
答案:莱布里茨。 3.设(R,+,?)是环,它有哪些特性? 答案:1.(R,+)是阿贝尔群。2.(R,?)是半群。3.?对+可分配。 4.排中律满足哪些性质? 答案:A ∧ 不成立。(不应同时否认一个命题(A )及其否定(非A )) x (F (x )∨F (x ))对任何个体x 而言,x 有性质F 或没有性质F 。 5.什么是真命题?命题“如果雪是黑的,则1+1=0”是真命题吗? 答案:真值为真的命题为真命题。命题“如果雪是黑的,则1+1=0”是真命题! 解析:p:雪是黑的;q:1+1=0;如果雪是黑的,则1+1=0:p →q 。由于p 为假,所以无论的真值如何,“p →q ”的真值都为真。 6. 下列哪个等价公式有错? A .P Q Q P →?→; B .P Q P Q →??∨; C .P Q Q P →??∨; 答案:A 7. 设G 为4阶有向图,度数列为(3,4,2,3),若它的入度列为(1,2,2,1), 则出度列为哪项? A .(1,2,1,2); B .(2,2,0,2); C .(2,1,1,2). 答案:B 解析:有向图中:度数=出度数+入度数。 8. 设{}{},3,4,S a φ=,则表示空元素属于S 怎样写? 答案:?∈S 9. 什么是前束范式?下面哪个是前束范式? A
数理逻辑考试题及答案
“离散数学”数理逻辑部分考核试题答案 ━━━━━━━━━━━━━━━━━━★━━━━━━━━━━━━━━━━━━ 一、命题逻辑基本知识(5分) 1、将下列命题符号化(总共4题,完成的题号为学号尾数取4的余,完成1题。共2分) (0)小刘既不怕吃苦,又爱钻研。 解:p∧q,其中,P:小刘怕吃苦;q:小刘爱钻研。 (1)只有不怕敌人,才能战胜敌人。 解:q→p,其中,P:怕敌人;q:战胜敌人。 (2)只要别人有困难,老张就帮助别人,除非困难已经解决了。 解:r→(p→p),其中,P:别人有困难;q:老张帮助别人;r:困难解决了。 (3)小王与小张是亲戚。 解:p,其中,P:小王与小张是亲戚。 2、判断下列公式的类型(总共5题,完成的题号为学号尾数取5的余,完成1题。共1分) (0)A:((p q)((p q) (p q))) r (1)B:(p(q p)) (r q) (2)C:(p r) (q r) (3)E:p(p q r) (4)F:(q r) r 解:用真值表判断,A为重言式,B为矛盾式,C为可满足式,E为重言式,F为矛盾式。 3、判断推理是否正确(总共2题,完成的题号为学号尾数取2的余,完成1题。共2分) (0)设y=2|x|,x为实数。推理如下:如y在x=0处可导,则y在x=0处连续。发现y在x=0处连续,所以,y在x=0处可导。 解:设y=2|x|,x为实数。令P:y在x=0处可导,q:y在x=0处连续。由此,p为假,q为真。本题推理符号化为:(p q) q p。由p、q的真值,计算推理公式真值为假,由此,本题推理不正确。 (1)若2和3都是素数,则6是奇数。2是素数,3也是素数。所以,5或6是奇数。 解:令p:2是素数,q:3是素数,r:5是奇数,s:6是奇数。由此,p=1,q=1,r=1,s=0。本题推理符号化为: ((p q) →s) p q) →(r s)。计算推理公式真值为真,由此,本题推理正确。 二、命题逻辑等值演算(5分) 1、用等值演算法求下列公式的主析取范式或主合取范式(总共3题,完成的题号为学号尾数取3的余,完成1题。共2分) (0)求公式p→((q∧r) ∧(p∨(q∧r)))的主析取范式。 解:p→((q∧r) ∧(p∨(q∧r)))p∨(q∧r∧p) ∨(q∧r∧q∧r) p∨(q∧r∧p) ∨0 (p∧q∧r) ∨ (p∧1∧1) ∨(q∧r∧p) (p∧(q∨q)∧(r∨r)) ∨(q∧r∧p) (p∧(q∨q)∧(r∨r)) ∨m7 (p∧q∧r)∨(p∧q∧r)∨(p∧q∧r)∨(p∧q∧r)∨m7 m0∨m1∨m2∨m3∨m7. (1)求公式((p→q)) ∨(q→p)的主合取范式。 解:((p→q)) (q→p) (p→q) (p→q) (p→q) p q M2.
离散数学及其应用 重要名词中英对应以及重要概念解释与举例
离散数学及其应用重要名词中英对应以及重要概念解释与举例 1 The Foundations: Logic and Proofs(逻辑与证明) 1.1 Propositional Logic(命题逻辑) Propositions(命题)——declarative sentence that is either true or false, but not both.判断性语句,正确性唯一。 Truth Table(真值表) Conjunction(合取,“与”,and),Disjunction(析取,or,“相容或”),Exclusive(异或),Negation(非,not),Biconditional(双条件,双向,if and only if) Translating English Sentences 1.2 Propositional Equivalences(命题等价) Tautology(永真式、重言式),Contradiction(永假式、矛盾式),Contingency(偶然式) Logical Equivalences(逻辑等价)——Compound propositions that have the same truth values in all possible cases are called logical equivalent.(真值表相同的式子,p<->q是重言式) Logical Equivalences——Page24 Disjunctive normal form(DNF,析取范式) Conjunctive normal form(CNF,合取范式) 见Page27~29 1.3 Predicates and Quantifiers(谓词和量词) Predicates——谓词,说明关系、特征的修饰词 Quantifiers——量词 ? Universal Quantifier(全称量词) "
离散数学之集合论
第二篇集合与关系 集合论是现代各科数学的基础,它是德国数学家康托(Geog Cantor, 1845~1918)于1874年创立的,1876~1883年康托一系列有关集合论的文章,对任意元的集合进行了深入的探讨,提出了关于基数、序数和良序集等理论,奠定了集合论深厚的基础,19世纪90年代后逐渐为数学家们采用,成为分析数学、代数和几何的有力工具。 随着集合论的发展,以及它与数学哲学密切联系所作的讨论,在1900年前后出现了各种悖论,使集合的发展一度陷入僵滞的局面。1904~1908年,策墨罗(Zermelo)列出了第一个集合论的公理系统,它的公理,使数学哲学中产生的一些矛盾基本上得到了统一,在此基础上以后就逐渐形成了公理化集合论和抽象集合论,使该学科成为在数学中发展最为迅速的一个分支。 现在,集合论已经成为内容充实、实用广泛的一门学科,在近代数学中占据重要地位,它的观点已渗透到古典分析、泛函、概率、函数论、信息论、排队论等现代数学各个分支,正在影响着整个数学科学。集合论在计算机科学中也具有十分广泛的应用,计算机科学领域中的大多数基本概念和理论几乎均采用集合论的有关术语来描述和论证,成为计算机科学工作者必不可少的基础知识。集合论可作为数学学科的通用语言,一切必要的数据结构都可以利用集合这个原始数据结构而构造出来,计算机科学家或许也可以利用这种方法。 本篇介绍集合论的基础知识,主要内容包括集合及其运算、性质、序偶、关系、映射、函数、基数等。 第2-1章集合及其运算 §2-1-1 集合的概念及其表示 一、集合的概念 “集合”是集合论中的一个原始的概念,因此它不能被精确地定义出来。一般地说,把具有某种共同性质的许多事物,汇集成一个整体,就形成一个集合。构成这个集合的每一个事物称为这个集合的一个成员(或一个元素),构成集合的这些成员可以是具体东西,也可以是抽象东西。例如:教室内的桌椅;图书馆的藏书;全国的高等学校;自然数的全体;程序设计语言C的基本字符的全体等均分别构成一个集合。通常用大写的英文字母表示集合的名称;用小写的英文字母表示元素。若元素a属于集合A记作
暨南大学离散数学周密试卷数理逻辑与集合论—参考试卷
暨 南 大 学 考 试 试 卷 一、填空题(共10小题,每小题2分,共20分) 1. 设命题 p :罗素悖论的真值为假,q :暨南大学的校训是信敏廉毅,r :离散数学是计算机科学不可分割的一门基础课程,则复合命题: ()()()()() p q r q p r p ?∧?∨∧???→∨的真值 为 ; 2. 下列各式中为永真式的有: (1) Q Q P P →→∧))(( (2) Q Q P →→)( (3) )(Q P P ∨→ (3) Q Q P P →∨∧?))(( (5) )(Q P Q ∧→
3. A 是个10元集合,B 是个2元集合,则集合A B 中元素的个数为 4. 设M(x):x 是人,C(x):x 很聪明,则命题:“尽管有人很聪明,但未必一切人都聪明。”可符号化为: 5. 设R(x):x 是实数;L(x, y):x 小于y ,则谓词公式: (()(()(,)))x R x y R y L x y ?→?∧用自然语言表述就是: 6. 设个体域为A={a, b, c},消去公式()()xP x xQ x ?→?中的量词得到的与之等值的谓词公式为: 7. P(A)表示集合A 的幂集,则((()))P P P ? = 8. ())(B A B B A ?-??= 9. 设D 为同一平面上直线的集合,并且 // 表示两直线的平行关系,⊥表示两直线间的垂直关系,则 20// = ,21⊥= 10.设 {}c ,b ,a A =,{} ,,,A R a b b a I =<><>?是A 上的等价关系, 设自然映射,R /A A :g →,那么()=a g 二、简答题(共4小题,每小题6分,共24分) 1.(1)求公式()()?∨?→??P Q P Q 的主析取式(要有过程);(4分) (2)根据主析取式直接写出该公式的主合取式;(2分)
数理逻辑测试题
玛 氏 食 品 ( 中国 ) 有 限 公 司 姓名:武英杰 性别:男 1-25 题均为选择题,只有一个正确答案。答案写在( ) 内 1-6 题根据下列数字规律,选择( )内应填数字: ( B ) 1、 2,9,16,23,30,( ) A.35 B.37 C.39 D.41 ( C ) 2、 5,11,20,32,( ) A .43 B .45 C .47 D .49 ( C )3、 1,2,3,5,( ),13 A 9 B 11 C 8 D7 ( A )4、 5,7,( ),19,31,50 A 12 B 13 C 10 D11 ( C )5、 8,4,2,2,( ) A 、2 B 、3 C 、4 D 、5 ( C)6、 14,20,29,41,( ) A.45 B.49 C.56 D.72 ( A ) 7、. 15.025.053÷?的值是: A .1 B .1.5 C .1.6 D .2.0 ( C ) 8、 1994年第二季度全国共卖出汽车297600辆,与上年同期相比增长了 24%。上年同期卖出多少辆汽车?
A.714224 B.226176 C.240000 D.369024 ( D ) 9、甲、乙两地相距42公里,A、B两人分别同时从甲乙两地步行出发, A的步行速度为3公里/小时,B的步行速度为4公里/小时,问A、B步行几小时后相遇? A. 3 B. 4 C. 5 D. 6 ( A)10、一根绳子长40米,将它对折剪断;再对剪断;第三次对折剪断,此时每根绳子长多少米? A、5 B、10 C、15 D、20 ( B ) 11、如果一米远栽一棵树,则285米远可栽多少棵树? A、285 B、286 C、287 D、284 (B ) 12、在一本300页的书中,数字“1”在书中出现了多少次? A、140 B、160 C、180 D、120 ( D ) 13、自然数A、B、 C、 D的和为90,已知A加上2,B减去2,C乘以 2,D除以2之后所得结果相同,则B等于() A、26 B、24 C、28 D、22 ( B ) 14、某人工作一年的报酬是18000元和一台全自动洗衣机,他干了7个月, 得到9500和一台全自动洗衣机,问这台洗衣机值多少元? A.8500元 B.2400元 C.2000元 D.1700元 ( B ) 15、橱窗:商品;相当于 A 电影:明星 B 书架:书籍 C 宇宙:星球 D 餐馆:厨师
浅谈数理逻辑在计算机科学中的应用
浅谈数理逻辑在计算机科学中的应用 文章整理编辑---论文文库工作室(QQ1548927986) 摘要:数理逻辑是离散数学课程中研究推理的逻辑学科,它为确定一个给出的论证是否有效提供各种法则和技巧,在计算机科学里用来检验程序的正确性,也可以验证定理和推论,同时在计算机模型、计算机程序设计语言、计算机硬件系统等方面有着重要作用。研究数理逻辑在计算机科学领域中的应用,必须从研究数理逻辑的符号化开始讨论、加以分析、验证结论。 关键词:数理逻辑;命题逻辑;一阶逻辑;推理理论 离散数学是现代数学的重要分支,是研究离散量的结构及相互关系的学科,它在计算机理论研究及软、硬件开发的各个领域都有着广泛的应用。其内容大致包含数理逻辑、集合论、代数结构、组合数学、图论和初等数论6部分,这6部分从不同的角度出发,研究各种离散量之间数与形的关系。本文主要研究数理逻辑部分在计算机科学领域中的应用。 1.为计算机的可计算性研究提供依据 数理逻辑分为命题逻辑和一阶逻辑两部分,命题逻辑是一阶逻辑的特例。在研究某些推理问题时,一阶逻辑比命题逻辑更准确。数理逻辑中的可计算谓词和计算模型中的可计算函数是等价的,互相可以转化,计算可以用函数演算来表达,也可以用逻辑系统来表达。 某些自然语言的论证看上去很简单,直接就可以得出结论,但是通过数理逻辑中的两种符号化表达的结果却截然不同,让人们很难理解,这就为计算机的可计算性研究埋下伏笔。下面举一个简单例子加以说明。 例1 凡是偶数都能被2整除。6是偶数,所以6能被2整除。 可见,一个复杂的命题或者公式可以利用符号的形式来说明含义,来判断正确性,这使得计算机科学中的通过复杂文字验证的推理过程变得简单、明了了。 2.为计算机硬件系统的设计提供依据 数理逻辑部分在计算机硬件设计中的应用尤为突出,数字逻辑作为计算机科学的一个重要理论,在很大程度上起源于数理逻辑中的布尔运算。计算机的各种运算是通过数字逻辑技术实现的,而代数和布尔代数是数字逻辑的理论基础,布尔代数在形式演算方面虽然使用了代数的方法,但其内容的实质仍然是逻辑。范式正是基于布尔运算和真值表给出的一个典型公式。 下面以计算机科学中比较典型的开关电路的设计为实例说明数理逻辑中布尔代数和范式的应用。整个开关电路从功能上可以看做是一个开关,把电路接通的状态记为1(即结果为真),把电路断开的状态记为0(即结果为假),开关电路中的开关也要么处于接通状态,要么处于断开状态,这两种状态也可以用二值布尔代数来描述,对应的函数为布尔函数,也叫线路的布尔表达式。接通条件相同的线路称为等效线路,找等效线路的目的是化简线路,使线路中包含的节点尽可能地少。利用布尔代数可设计一些具有指定的节点线路,数学上既是按给定的真值表构造相应的布尔表达式,理论上涉及到的是范式理论,但形式上并不难构造。 例2 关于选派参赛选手,赵,钱,孙三人的意见分别是:赵:如果不选派甲,那么不选派乙。钱:如果不选派乙,那么选派甲;孙:要么选甲,要么选乙。以下诸项中,同时满足赵,钱,孙三人意见的方案是什么? 解答:把赵,钱,孙三个人的意见看做三条不同的线路,对三条线路化简得到接通状态
离散数学集合论部分测试题
离散数学集合论部分测试题
离散数学集合论部分综合练习 本课程综合练习共分3次,分别是集合论部分、图论部分、数理逻辑部分的综合练习,这3次综合练习基本上是按照考试的题型安排练习题目,目的是通过综合练习,使同学自己检验学习成果,找出掌握的薄弱知识点,重点复习,争取尽快掌握。本次是集合论部分的综合练习。 一、单项选择题 1.若集合A={a,b},B={ a,b,{ a,b }},则(). A.A?B,且A∈B B.A∈B,但A?B C.A?B,但A?B D.A?B,且A?B 2.若集合A={2,a,{ a },4},则下列表述正确的是( ). A.{a,{ a }}∈A B.{ a }?A C.{2}∈A D.?∈A 3.若集合A={ a,{a},{1,2}},则下列表述正确的是( ). A.{a,{a}}∈A B.{2}?A C.{a}?A D.?∈A 4.若集合A={a,b,{1,2 }},B={1,2},则(). A.B? A,且B∈A B.B∈ A,但B?A C.B ? A,但B?A D.B? A,且B?A 5.设集合A = {1, a },则P(A) = ( ). A.{{1}, {a}} B.{?,{1}, {a}} C.{?,{1}, {a}, {1, a }} D.{{1}, {a}, {1, a }} 6.若集合A的元素个数为10,则其幂集的元素个数为(). A.1024 B.10 C.100 D.1 7.集合A={1, 2, 3, 4, 5, 6, 7, 8}上的关系R={
离散数学模拟试卷和答案
北京语言大学网络教育学院 《离散数学》模拟试卷一 注意: 1.试卷保密,考生不得将试卷带出考场或撕页,否则成绩作废。请监考老师负责监督。 2.请各位考生注意考试纪律,考试作弊全部成绩以零分计算。 3.本试卷满分100分,答题时间为90分钟。 4.本试卷分为试题卷和答题卷,所有答案必须答在答题卷上,答在试题卷上不给分。 一、【单项选择题】(本大题共15小题,每小题3分,共45分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在答题卷相应题号处。 1、在由3个元素组成的集合上,可以有 ( ) 种不同的关系。 [A] 3 [B] 8 [C]9 [D]27 2、设{}{}1,2,3,5,8,1,2,5,7A B A B ==-=,则( )。 [A] 3,8 [B]{}3 [C]{}8 [D]{}3,8 3、若X 是Y 的子集,则一定有( )。 [A]X 不属于Y [B]X ∈Y [C]X 真包含于 Y [D]X∩Y=X 4、下列关系中是等价关系的是( )。 [A]不等关系 [B]空关系 [C]全关系 [D]偏序关系 5、对于一个从集合A 到集合B 的映射,下列表述中错误的是( )。 [A]对A 的每个元素都要有象 [B] 对A 的每个元素都只有一个象 [C]对B 的每个元素都有原象 [D] 对B 的元素可以有不止一个原象 6、设p:小李努力学习,q:小李取得好成绩,命题“除非小李努力学习,否则他不能取得好成绩”的符号化形式为( )。 [A]p→q [B]q→p [C]┐q→┐p [D]┐p→q 7、设A={a,b,c},则A 到A 的双射共有( )。 [A]3个 [B]6个 [C]8个 [D]9个
(完整版)离散数学及其应用(课后习题)
习题1.1 2. 指出下列命题是原子命题还是复合命题。 (3)大雁北回,春天来了。 (4)不是东风压倒西风,就是西风压倒东风。 (5)张三和李四在吵架。 解:(3)和(4)是复合命题,(5)是原子命题。 习题1.2 1. 指出下列命题的真值: (1)若224+>,则太阳从西方升起。 解:该命题真值为T (因为命题的前件为假)。 (3)胎生动物当且仅当是哺乳动物。 解:该命题真值为F (如鸭嘴兽虽是哺乳动物,但不是胎生动物)。 2. 令P :天气好。Q :我去公园。请将下列命题符号化。 (2)只要天气好,我就去公园。 (3)只有天气好,我才去公园。 (6)天气好,我去公园。 解:(2)P Q →。 (3)Q P →。 (6)P Q ?。 习题1.3 2. 将下列命题符号化(句中括号内提示的是相应的原子命题的符号表示): (1)我去新华书店(P ),仅当我有时间(Q )。 (3)只要努力学习(P ),成绩就会好的(Q )。 (6)我今天进城(P ),除非下雨(Q )。 (10)人不犯我(P ),我不犯人(Q );人若犯我,我必犯人。 解:(1)P Q →。 (3)P Q →。 (6)Q P ?→。 (10)()()P Q P Q ?→?∧→。 习题1.4 1. 写出下列公式的真值表: (2)()P Q R ∨→。
解:该公式的真值表如下表: 2. 证明下列等价公式: (2)()()()P Q P Q P Q ∨∧?∧???。 证明: ()(()()) ()()) ()() ()() P Q P Q P Q P Q P Q P Q P Q P Q P Q ????∧∨?∧???∧∧??∧???∧∧∨?∨∧?∧ (4)()()()P Q P R P Q R →∧→?→∧。 证明: ()()()() () () P Q P R P Q P R P Q R P Q R →∧→??∨∧?∨??∨∧?→∧ 3. 甲、乙、丙、丁4人参加考试后,有人问他们谁的成绩最好,甲说,不是我。乙说:是丁。丙说:是乙。丁说:不是我。已知4个人的回答只有一个人符合实际,问成绩最好的是谁? 解:设A :甲成绩最好。B :乙成绩最好。C :丙成绩最好。D :丁成绩最好。 四个人所说的命题分别用P Q R S 、、、表示,则 P A ??;Q A B C D ??∧?∧?∧;R A B C D ??∧∧?∧?;S D ??。 则只有一人符合实际的命题K 符号化为 ()()()() K P Q R S P Q R S P Q R S P Q R S ?∧?∧?∧?∨?∧∧?∧?∨?∧?∧∧?∨?∧?∧?∧
数理逻辑心得
数理逻辑的心得 数理逻辑:是计算机科学的基础,应熟练掌握将现实生活中的条件化成逻辑公式,并能做适当的推理,这对程序设计等课程是极有用处的。是大四接触到的,现简单介绍一下数理逻辑的发展史,算是一点感悟吧 1数理逻辑的发展前期 ·前史时期——古典形式逻辑时期:亚里斯多德的直言三段论理论 ·初创时期——逻辑代数时期(17世纪末) ·资本主义生产力大发展,自然科学取得了长足的进步,数学在认识自然、发展技术方面起到了相当重要的作用。 ·人们希望使用数学的方法来研究思维,把思维过程转换为数学的计算。 ·莱布尼兹(Leibniz, 1646~1716)完善三段论,提出了建立数理逻辑或者说理性演算的思想: ·提出将推理的正确性化归于计算,这种演算能使人们的推理不依赖于对推理过程中的命题的含义内容的思考,将推理的规则变为演算的规则。 ·使用一种符号语言来代替自然语言对演算进行描述,将符号的形式和其含义分开。使得演算从很大程度上取决与符号的组合规律,而与其含义无关。 ·布尔(G. Boole, 1815~1864)代数:将有关数学运算的研究的代数系统推广到逻辑领域,布尔代数既是一种代数系统,也是一种逻辑演算。 数理逻辑的奠基时期 ·弗雷格(G. Frege, 1848~1925):《概念语言——一种按算术的公式语言构成的纯思维公式语言》(1879)的出版标志着数理逻辑的基础部分——命题演算和谓词演算的正式建立。 ·皮亚诺(Giuseppe Peano, 1858~1932):《用一种新的方法陈述的算术原理》(1889)提出了自然数算术的一个公理系统。 ·罗素(Bertrand Russell, 1872~1970):《数学原理》(与怀特黑合著,1910, 1912, 1913)从命题演算和谓词演算开始,然后通过一元和二元命题函项定义了类和关系的概念,建立了抽象的类演算和关系演算。由此出发,在类型论的基础上用连续定义和证明的方式引出了数学(主要是算术)中的主要概念和定理。 ·逻辑演算的发展:甘岑(G. Gentzen)的自然推理系统(Natural Deduction System),逻辑演算的元理论:公理的独立性、一致性、完全性等。 ·各种各样的非经典逻辑的发展:路易斯(Lewis, 1883~1964)的模态逻辑,实质蕴涵怪论和严格蕴涵、相干逻辑等,卢卡西维茨的多值逻辑等。 集合论的悖论使得人们觉得数学产生了第三次危机,提出了数学的基础到底是什么这样的问题。 ·罗素等的逻辑主义:数学的基础是逻辑,倡导一切数学可从逻辑符号推出,《数学原理》一书是他们这一思想的体现。为解决悖论产生了逻辑类型论。 ·布劳维尔(Brouwer, 1881~1966)的直觉主义:数学是心灵的构造,只承认可构造的数学,强调构造的能行性,与计算机科学有重要的联系。坚持潜无穷,强调排中律不能用于无穷集合。海丁(Heyting)的直觉主义逻辑。 ·希尔伯特(D. Hilbert)的形式主义:公理化方法与形式化方法,元数学和证明论,提倡将逻辑演算和数学证明本身形式化,把用普通的语言传达的内容上的数学科学变为用数学符号和逻辑符号按一定法则排列的一堆公式。为了消除悖论,要数学建立在公理化基础上,将
离散数学集合论部分测试题
离散数学集合论部分综合练习 本课程综合练习共分3次,分别是集合论部分、图论部分、数理逻辑部分的综合练习,这3次综合练习基本上是按照考试的题型安排练习题目,目的是通过综合练习,使同学自己检验学习成果,找出掌握的薄弱知识点,重点复习,争取尽快掌握。本次是集合论部分的综合练习。 一、单项选择题 1.若集合A={a,b},B={ a,b,{ a,b }},则(). A.A?B,且A∈B B.A∈B,但A?B C.A?B,但A?B D.A?B,且A?B 2.若集合A={2,a,{ a },4},则下列表述正确的是( ). A.{a,{ a }}∈A B.{ a }?A C.{2}∈A D.?∈A 3.若集合A={ a,{a},{1,2}},则下列表述正确的是( ). A.{a,{a}}∈A B.{2}?A C.{a}?A D.?∈A 4.若集合A={a,b,{1,2 }},B={1,2},则(). A.B? A,且B∈A B.B∈ A,但B?A C.B ? A,但B?A D.B? A,且B?A 5.设集合A = {1, a },则P(A) = ( ). A.{{1}, {a}} B.{?,{1}, {a}} C.{?,{1}, {a}, {1, a }} D.{{1}, {a}, {1, a }} 6.若集合A的元素个数为10,则其幂集的元素个数为(). A.1024 B.10 C.100 D.1 7.集合A={1, 2, 3, 4, 5, 6, 7, 8}上的关系R={
离散数学模拟试卷和答案
北京语言大学网络教育学院 《离散数学》模拟试卷一 注意: 1.试卷保密,考生不得将试卷带出考场或撕页,否则成绩作废。请监考老师负责监督。 2.请各位考生注意考试纪律,考试作弊全部成绩以零分计算。 3.本试卷满分100分,答题时间为90分钟。 4.本试卷分为试题卷和答题卷,所有答案必须答在答题卷上,答在试题卷上不给分。 一、【单项选择题】(本大题共15小题,每小题3分,共45分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在答题卷相应题号处。 1、在由3个元素组成的集合上,可以有 ( ) 种不同的关系。 [A] 3 [B] 8 [C]9 [D]27 2、设{}{}1,2,3,5,8,1,2,5,7A B A B ==-=,则( )。 [A] 3,8 [B]{}3 [C]{}8 [D]{}3,8 3、若X 是Y 的子集,则一定有( )。 [A]X 不属于Y [B]X ∈Y [C]X 真包含于 Y [D]X∩Y=X 4、下列关系中是等价关系的是( )。 [A]不等关系 [B]空关系 [C]全关系 [D]偏序关系 5、对于一个从集合A 到集合B 的映射,下列表述中错误的是( )。 [A]对A 的每个元素都要有象 [B] 对A 的每个元素都只有一个象 [C]对B 的每个元素都有原象 [D] 对B 的元素可以有不止一个原象 6、设p:小李努力学习,q:小李取得好成绩,命题“除非小李努力学习,否则他不能取得好成绩”的符号化形式为( )。 [A]p→q [B]q→p [C]┐q→┐p [D]┐p→q 7、设A={a,b,c},则A 到A 的双射共有( )。 [A]3个 [B]6个 [C]8个 [D]9个
数理逻辑与集合论作业二 - 参考解答
數理邏輯與集合論作業二 1. 解:該題應該理解為此列表中每一句都是形如“i: 在這個列表中,恰有i條語句為假”的形式。 a)思路:考慮這100句裡可能有幾句為真。是否可能沒有一句為真?是否可能 祗有一句為真,是哪一句?是否可能多餘等於兩句為真? b)思路:“至少i+1句為假”蘊含“至少i句為假”,若第i句為真,則1…… i-1句都為真,所以第 100, 99, 98, ……句都為假,一直到第50句為真 c) 思路同上,但是…… 2. 解答:如果我說右邊的路通往遺跡你將回答“是”,對嗎? 3.
解答: ))))a q p b p q c q p d q p →∧→?→? 4. 也就是上述描述是否自相矛盾? 5. 解答: 条件符号化 ::::(1)(2)(C G)(3)(G W)G W (4)G W G W S C G W S C G W S C C G W C C S C S →?∧=?∨???∧?=∨→?????男管家廚師園丁雜役假設為真,則由(2)得:再由(1)得:但無法判定的真假 假設為假,則由(3)得:再由(4)得:由(1)得:綜上所述:和說了假話,,的話真假未知 6. 四个朋友被认定为非法进入某计算机系统的嫌疑人。他们已对调查员作了陈述。
艾丽斯说“卡罗斯干的” 约翰说“我没幹。” 卡罗斯说“戴安娜干的。” 戴安娜说“卡罗斯说是我幹的,他说谎。” a)如果调查员知道四个嫌疑人中恰有一人说真话,那么准幹的?解释你的推理。 b)如果调查员知道恰有一人说谎,谁干的?解释你的推理。 解:前提符號化為 (1)A: C (2)J: ? J (3)C: D (4)D: ? (C: D) a) 祗有一句話為真,而(3)(4)有且僅有一句為真,分別討論(3)(4)為真的情況。 b)分析步驟同上。 7. 用真值表證明德摩根律和吸收律。 解答略 8. 使用等值演算證明下列命題公式為永真式(不得用真值表) 解答: a
《离散数学》复习题及答案
《离散数学》试题及答案 一、选择或填空 (数理逻辑部分) 1、下列哪些公式为永真蕴含式?( ) (1)?Q=>Q→P (2)?Q=>P→Q (3)P=>P→Q (4)?P∧(P∨Q)=>?P 答:(1),(4) 2、下列公式中哪些是永真式?( ) (1)(┐P∧Q)→(Q→?R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q) 答:(2),(3),(4) 3、设有下列公式,请问哪几个是永真蕴涵式?( ) (1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q (4)P∧(P→Q)=>Q (5) ?(P→Q)=>P (6) ?P∧(P∨Q)=>?P 答:(2),(3),(4),(5),(6) 4、公式?x((A(x)?B(y,x))??z C(y,z))?D(x)中,自由变元是( ),约束变元是( )。 答:x,y, x,z 5、判断下列语句是不是命题。若是,给出命题的真值。( ) (1)北京是中华人民共和国的首都。 (2) 陕西师大是一座工厂。 (3) 你喜欢唱歌吗? (4) 若7+8>18,则三角形有4条边。 (5) 前进! (6) 给我一杯水吧! 答:(1)是,T (2)是,F (3)不是 (4)是,T (5)不是(6)不是 6、命题“存在一些人是大学生”的否定是( ),而命题“所有的人都是要死的”的否定是( )。 答:所有人都不是大学生,有些人不会死
7、设P:我生病,Q:我去学校,则下列命题可符号化为( )。 (1) 只有在生病时,我才不去学校 (2) 若我生病,则我不去学校 (3) 当且仅当我生病时,我才不去学校(4) 若我不生病,则我一定去学校答:(1)P ?(4)Q P→ ? P? Q→ ?(2)Q P? →(3)Q 8、设个体域为整数集,则下列公式的意义是( )。 (1) ?x?y(x+y=0) (2) ?y?x(x+y=0) 答:(1)对任一整数x存在整数 y满足x+y=0(2)存在整数y对任一整数x满足x+y=0 9、设全体域D是正整数集合,确定下列命题的真值: (1) ?x?y (xy=y) ( ) (2) ?x?y(x+y=y) ( ) (3) ?x?y(x+y=x) ( ) (4) ?x?y(y=2x) ( ) 答:(1) F (2) F (3)F (4)T 10、设谓词P(x):x是奇数,Q(x):x是偶数,谓词公式?x(P(x)?Q(x))在哪个个体域中为真?( ) (1) 自然数(2) 实数 (3) 复数(4) (1)--(3)均成立 答:(1) 11、命题“2是偶数或-3是负数”的否定是()。 答:2不是偶数且-3不是负数。 12、永真式的否定是() (1) 永真式(2) 永假式(3) 可满足式(4) (1)--(3)均有可能 答:(2) 13、公式(?P∧Q)∨(?P∧?Q)化简为(),公式 Q→(P∨(P∧Q))可化简为()。 答:?P ,Q→P 14、谓词公式?x(P(x)??yR(y))→Q(x)中量词?x的辖域是()。 答:P(x)??yR(y) 15、令R(x):x是实数,Q(x):x是有理数。则命题“并非每个实数都是有理数”的符号化表示为()。
数理逻辑考试题及答案
“离散数学”数理逻辑部分考核试题答案 --------------------------- ★----------------------------- 一、命题逻辑基本知识(5分) 1、将下列命题符号化(总共4题,完成的题号为学号尾数取4的余,完成1题。共2分) (0)小刘既不怕吃苦,又爱钻研。 解:—p ∧q ,其中,P :小刘怕吃苦;q :小刘爱钻研。 (1)只有不怕敌人,才能战胜敌人。 解:q→-p ,其中,P :怕敌人;q :战胜敌人。 (2)只要别人有困难,老张就帮助别人,除非困难已经解决了。 解:—r→(P→P),其中,P:别人有困难;q :老张帮助别人;r:困难解决了。 (3)小王与小张是亲戚。 解:p,其中,P:小王与小张是亲戚。 2、判断下列公式的类型(总共5题,完成的题号为学号尾数取5的余,完成1题。共1分) (0)A :(-(p^q)_;((P -q)(.p^q))) r (1)B : (P 一9一;P))(r q) (2)C: (P -r)>(q r) (3)E : p-;(P q r) (4)F :—(q-;r) r------------------------------------------------------------------------ 解:用真值表判断,A为重言式,B为矛盾式,C为可满足式,E为重言式,F为矛盾式。 3、判断推理是否正确(总共2题,完成的题号为学号尾数取.2的余,完成1题。共2分) (0)设y=2∣x∣,X为实数。推理如下:如y在x=0处可导,则y在x=0处连续。发现y在x=0处连续,所以,y在x=0处可导。 解:设y=2|x|,X为实数。令P: y在x=0处可导,q:y在x=0处连续。由此,P为假,q为真。本题推理符号化为:(p—;q) q—;P。由P、q的真值,计算推理公式真值为假,由此,本题推理不正确。 (1)若2和3都是素数,则6是奇数。2是素数,3也是素数。所以,5或6是奇数。 解:令P:2是素数,q:3是素数,r:5是奇数,S:6是奇数。由此,p=1,q=1,r=1,S=O。本题推理符号化为:((P q)→ S) P q)→ (r S)。计算推理公式真值为真,由此,本题推理正确。 二、命题逻辑等值演算(5分) 1、用等值演算法求下列公式的主析取范式或主合取范式(总共3题,完成的题号为学号尾数取3的余,完 成1题。共2分) (0)求公式p→ ((q ∧r) ∧(P ∨(―q ∧-r)))的主析取范式。 解:p→((q ∧r) ∧(P ∨(—q ∧-「))):= 一p∨(q ∧r∧P) ∨(q ∧r ∧一q ∧—r)二一P ∨(q ∧r∧P) ∨0 二(P ∧q∧r) ∨= (一p∧1 ∧1) ∨(q ∧r∧P) 二(—p ∧(q ∨-q) ∧(r ∨-r)) ∨(q ∧r∧P) U (~p ∧(q ∨-q) ∧(r ∨一r)) ∨m7 二(一P ∧—q ∧ F ∨ (一P ∧—q ∧r) ∨ (一P ∧q ∧_r) ∨ (一P ∧q ∧r) ∨m7 m0 ∨m1 ∨m2 ∨m3 ∨m7. (1)求公式一(一(P → q)) ∨(—q → 一P)的主合取范式。 解:一(一(P → q)) (—q →-p)二(P → q) (P →q) U (P → q)
数理逻辑与集合论试卷
2006年的考题 一、A={a,b,c},B={X|a∈X且X?A},求B-A, B-{A}, ∪B, ∩B。 二、A={1,2,3,5,9},R是A上的关系且R={
