回归分析的应用及回归分析的类型

回归分析的应用及回归分析的类型
什么是回归分析?
正确问题的近似答案要比近似问题的精确答案更有价值
这正是回归分析所追求的目标,它是最常用的预测建模技术之一,有助于在重要情况下做出更明智的决策。
回归分析是作为数据科学家需要掌握的第一个算法。它是数据分析中最常用的预测建模技术之一。即使在今天,大多数公司都使用回归技术来实现大规模决策。
要回答“什么是回归分析”这个问题,我们需要深入了解基本面。简单的回归分析定义是一种用于基于一个或多个独立变量(X)预测因变量(Y)的技术。
经典的回归方程看起来像这样:
等式中,hθ(x)是因变量Y,X是自变量,θ0是常数,并且θ1是回归系数。
回归分析的应用
回归分析有三个主要应用:
?解释他们理解困难的事情。例如,为什么客户服务电子邮件在上一季度有所下降。
?预测重要的商业趋势。例如,明年会要求他们的产品看起来像什么?
?选择不同的替代方案。例如,我们应该进行PPC(按点击付费)还是内容营销活动?
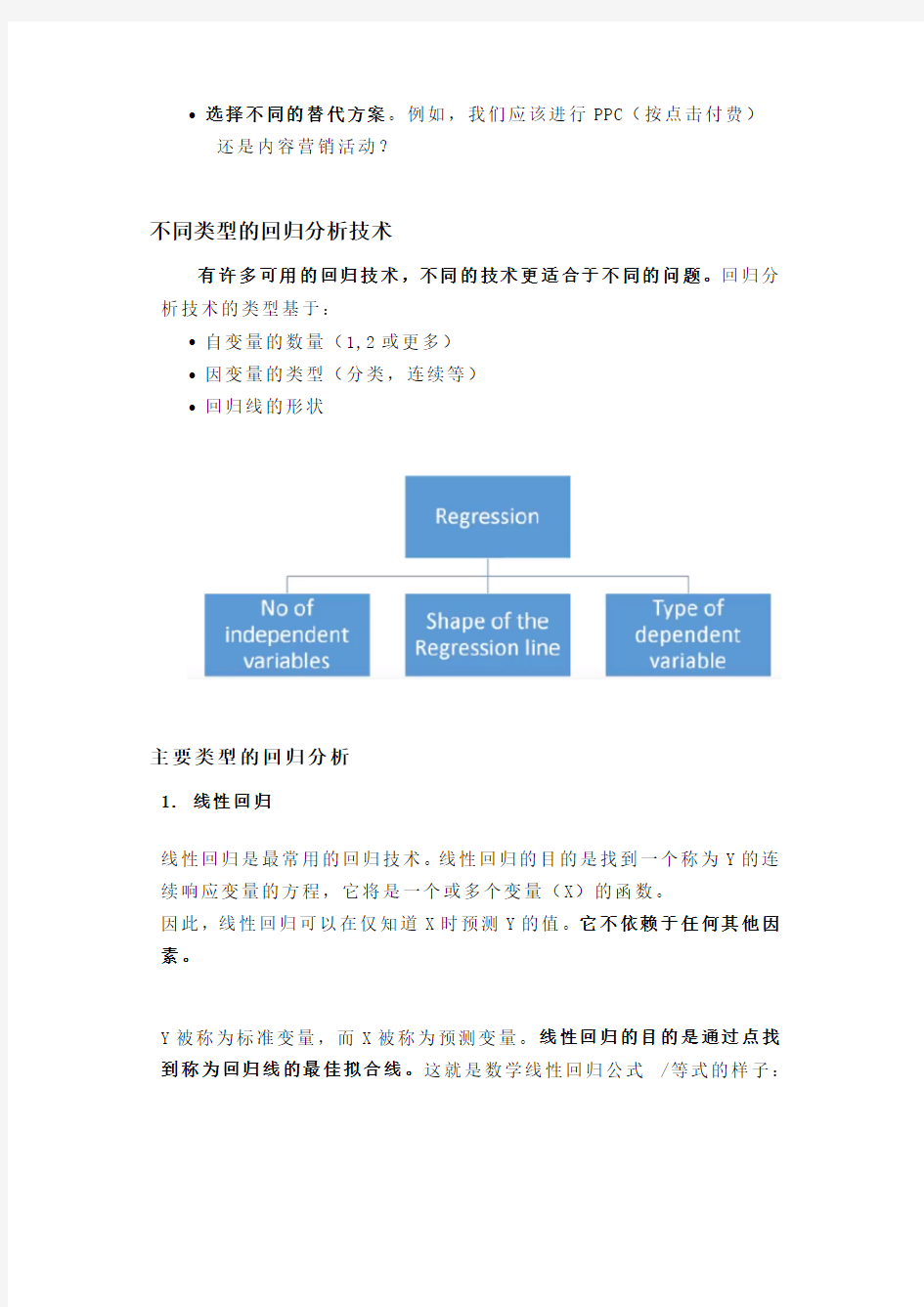
不同类型的回归分析技术
有许多可用的回归技术,不同的技术更适合于不同的问题。回归分析技术的类型基于:
?自变量的数量(1,2或更多)
?因变量的类型(分类,连续等)
?回归线的形状
主要类型的回归分析
1. 线性回归
线性回归是最常用的回归技术。线性回归的目的是找到一个称为Y的连续响应变量的方程,它将是一个或多个变量(X)的函数。
因此,线性回归可以在仅知道X时预测Y的值。它不依赖于任何其他因素。
Y被称为标准变量,而X被称为预测变量。线性回归的目的是通过点找到称为回归线的最佳拟合线。这就是数学线性回归公式/等式的样子:
在上面的等式中,hθ(x)是标准变量Y,X是预测变量,θ0是常数,并且θ1是回归系数
线性回归可以进一步分为多元回归分析和简单回归分析。在简单线性回归中,仅使用一个独立变量X来预测因变量Y的值。
另一方面,在多元回归分析中,使用多个自变量来预测Y,当然,在这两种情况下,只有一个变量Y,唯一的区别在于自变量的数量。
例如,如果我们仅根据平方英尺来预测公寓的租金,那么这是一个简单的线性回归。
另一方面,如果我们根据许多因素预测租金;平方英尺,房产的位置和建筑物的年龄,然后它成为多元回归分析的一个例子。
2. Logistic回归
要理解什么是逻辑回归,我们必须首先理解它与线性回归的不同之处。为了理解线性回归和逻辑回归之间的差异,我们需要首先理解连续变量和分类变量之间的区别。
连续变量是数值。它们在任何两个给定值之间具有无限数量的值。示例包括视频的长度或收到付款的时间或城市的人口。
另一方面,分类变量具有不同的组或类别。它们可能有也可能没有逻辑顺序。示例包括性别,付款方式,年龄段等。
在线性回归中,因变量Y始终是连续变量。如果变量Y是分类变量,则不能应用线性回归。
如果Y是只有2个类的分类变量,则可以使用逻辑回归来克服此问题。这些问题也称为二元分类问题。
理解标准逻辑回归只能用于二元分类问题也很重要。如果Y具有多于2个类,则它变为多类分类,并且不能应用标准逻辑回归。
逻辑回归分析的最大优点之一是它可以计算事件的预测概率分数。这使其成为数据分析的宝贵预测建模技术。
3. 多项式回归
如果自变量(X)的幂大于1,那么它被称为多项式回归。这是多项式回归方程的样子:y=a+b* x ^3
与线性回归不同,最佳拟合线是直线,在多项式回归中,它是适合不同数据点的曲线。这是多项式回归方程的图形:
对于多项式方程,人们倾向于拟合更高次多项式,因为它导致更低的错
误率。但是,这可能会导致过度拟合。确保曲线真正符合问题的本质非
常重要。
检查曲线朝向两端并确保形状和趋势落实到位尤为重要。多项式越高,它在解释过程中产生奇怪结果的可能性就越大。
4. 逐步回归
当存在多个独立变量时,使用逐步回归。逐步回归的一个特点是自动选
择自变量,而不涉及人的主观性。
像R-square和t-stats这样的统计值用于识别正确的自变量。当数据
集具有高维度时,通常使用逐步回归。这是因为其目标是使用最少数量
的变量最大化模型的预测能力。
逐步回归基于预定义的条件一次增加或减少一个共变量。它一直这样做,直到适合回归模型。
5. 岭回归
当自变量高度相关(多重共线性)时,使用岭回归。当自变量高度相关时,最小二乘估计的方差非常大。
结果,观察值与实际值有很大差异。岭回归通过在回归估计中增加一定程度的偏差来解决这个问题。这是岭回归方程式的样子:
在上面的等式中,收缩参数λ(λ)用于解决多重共线性的问题。
6. 套索回归
就像岭回归一样,Lasso回归也使用收缩参数来解决多重共线性问题。它还通过提高准确性来帮助线性回归模型。
它与岭回归的不同之处在于惩罚函数使用绝对值而不是正方形。这是Lasso回归方程:
7. 弹性网络回归
ElasticNet回归方法线性地组合了Ridge和Lasso方法的L1和L2惩罚。以下是ElasticNet回归方程的样子:
应用回归分析
第五章 自变量选择对回归参数的估计有何影响 答:全模型正确而误用选模型时,我们舍去了m-p 个自变量,用剩下的p 个自变量去建立选模型,参数估计值是全模型相应参数的有偏估计。选模型正确而误用全模型时,参数估计值是选模型相应参数的有偏估计。 自变量选择对回归预测有何影响 (一)全模型正确而误用选模型的情况 估计系数有偏,选模型的预测是有偏的,选模型的参数估计有较小的方差,选模型的预测残差有较小的方差,选模型预测的均方误差比全模型预测的方差更小。 (二)选模型正确而误用全模型的情况 全模型的预测值是有偏的,全模型的预测方差的选模型的大,全模型的预测误差将更大。 如果所建模型主要用于预测,应该用哪个准则来衡量回归方程的优劣 答:应该用自由度调整复决定系数达到最大的准则。当给模型增加自变量时,复决定系数也随之增大,然而复决定系数的增大代价是残差自由度的减小,自由度小意味着估计和预测的可靠性低。应用自由度调整复决定系数达到最大的准则可以克服样本决定系数的这一缺点,把2 R 给予适当的修正,使得只有加入“有意义”的变量时,经过修正的样本决定系数才会增加,从而提高预测的精度。 试述前进法的思想方法。 解:主要是变量由少到多,每次增加一个,直至没有可引入的变量为止。 具体做法是:首先将全部m 个自变量,分别对因变量y 建立m 个一元线性回归方程,并分别计算这m 个一元回归方程的m 个回归系数的F 检验值,记为 111 12{,,,} m F F F ,选其最大者 1111 12max{,, ,} j m F F F F =,给定显著性水平α,若 1(1,2) j F F n α≥-,则首先将 j x 引入回 归方程,假设 1 j x x =。其次,将 12131(,),(,),,(,)m y x x x x x x 分别与建立m-1个二元线性 回归方程,对这m-1个回归方程中 23,, ,m x x x 的回归系数进行F 检验,计算F 值,记为 222 23{,, ,} m F F F ,选其最大的记为 2222 23max{,, ,} j m F F F F =,若 2(1,3) j F F n α≥-,则 接着将j x 引入回归方程。以上述方法做下去。直至所有未被引入方程的自变量的F 值均小
第7章 相关与回归分析。
第七章相关与回归分析 学习内容 一、变量间的相关关系 二、一元线性回归 三、线性回归方程拟合优度的测定 学习目标 1. 掌握相关系数的含义、计算方法和应用 2. 掌握一元线性回归的基本原理和参数的最小二 3. 掌握回归方程的显著性检验 4. 利用回归方程进行预测 5. 了解可化为线性回归的曲线回归 6. 用Excel 进行回归分析 一、变量间的相关关系 1. 变量间的关系(函数关系) 1)是一一对应的确定关系。 2)设有两个变量x和y,变量y 随变量x一起变化, 并完全依赖于x,当变量x 取某个数值时,y依确定的关系取相应的值, 则称y 是x的函数,记为y = f (x),其中x 称为自变量,y 称为因变量。 3)各观测点落在一条线上。 4)函数关系的例子 –某种商品的销售额(y)与销售量(x)之间的关系可表示为 y = p x (p 为单价)。 –圆的面积(S)与半径之间的关系可表示为S = π R2。 –企业的原材料消耗额(y)与产量x1、单位产量消耗x2、原材料价格x3间的关系可表 示为y =x1 x2 x3。 单选题 下面的函数关系是() A、销售人员测验成绩与销售额大小的关系 B、圆周的长度决定于它的半径 C、家庭的收入和消费的关系 D、数学成绩与统计学成绩的关系
2. 变量间的关系(相关关系) 1)变量间关系不能用函数关系精确表达。 2)一个变量的取值不能由另一个变量唯一确定。 3)当变量 x 取某个值时,变量 y 的取值可能有几个。 4)各观测点分布在直线周围。 5)相关关系的例子 –商品的消费量(y)与居民收入(x)之间的关系。 –商品销售额(y)与广告费支出(x)之间的关系。 –粮食亩产量(y)与施肥量(x1)、降雨量(x2)、温度 (x3)之间的关系。 –收入水平(y)与受教育程度(x)之间的关系。 –父亲身高(y)与子女身高(x)之间的关系。 3. 相关图表 1)相关表:将具有相关关系的原始数据,按某一顺序平行排列在一张表上,以观察它 们之间的相互关系。 2)相关图:也称为分布图或散点图,它是在平面直角坐标中把相关关系的原始数据用 点描绘出来,通常以直角坐标轴的横轴代表自变量x,纵轴代表因变量y。 4. 相关关系的类型
第三章回归分析基础
第三章 回归分析基础 3.1 回归模型简介 一、数据、变量与模型 数据是进行模型分析的基础。一般地,数据可分为三类:一类为截面数据(Cross-Section Data ),一类为时间序列数据(Time-Series Data), 另一类为平行数据(Panel Data )或混合数据(Mixed Data)。 截面数据研究个体在某个时点上的变化情况。例如,2001年1月末,全国各省、自治区、直辖市的国内生产总值(GDP )、财政收入、财政支出、货币发行量、固定资产投资额、进出口总额等,均为截面数据。再如,在某一时点上,某地区家庭费用开支数据,也是典型的截面数据。 时间序列数据是研究个体在一定时期内的变化情况。时间序列数据在日常生活中随处可见。例如,建国以来我国历年的国内生产总值(GDP )数据、居民消费额数据、零售物价指数数据等,均为时间序列数据。 平行数据是截面数据与时间序列数据的复合体,它既研究某段时间内个体的变化情况,又研究个体在每个时点上的变化情况。 变量是构成模型的框架,是对个体不确定性的一种因素度量。一般可将它分为两类:内生变量(Endogenous Variable )和外生变量(Exogenous Variable )。 内生变量是指由经济系统本身决定的变量。外生变量则指经济系统本身无法决定、并由外部因素决定的变量。内生产变量也称联合决定变量(Jointly-Determined Variables)。外生变量也称前定变量(Predetermined Variables)。例如,在简单的原油供求模型: 1111q a b p c y ε=+++(需求方程) 2222 q a b p c R ε=+++(供给方程) 中,原油总量q 和原油价格p 均为内生变量,而国民收入y 和降雨量R 均为外生变量。 值得注意的是,内生变量与外生变量的认定并不是一成不变的,在一定条件下二者可以相互转换,应视研究对象和研究目的的不同而不同。此外,内生变量与外生变量的划分直接关系到模型参数的估计与推断,这是后话。
应用回归分析课后答案
应用回归分析课后答案 第二章一元线性回归 解答:EXCEL结果: SUMMARY OUTPUT 回归统计 Multiple R R Square Adjusted R Square 标准误差 观测值5 方差分析 df SS MS F Significance F 回归分析125 残差3 总计410 Coefficients标准误差t Stat P-value Lower 95%Upper 95%下限%上限% Intercept X Variable 15 RESIDUAL OUTPUT 观测值预测Y残差 1 2 3 4 5 SPSS结果:(1)散点图为:
(2)x 与y 之间大致呈线性关系。 (3)设回归方程为01y x ββ∧ ∧ ∧ =+ 1β∧ = 12 2 1 7()n i i i n i i x y n x y x n x -- =- =-=-∑∑ 0120731y x ββ-∧- =-=-?=- 17y x ∧ ∴=-+可得回归方程为 (4)22 n i=1 1()n-2i i y y σ∧∧=-∑ 2 n 01i=1 1(())n-2i y x ββ∧∧=-+∑ =222 22 13???+?+???+?+??? (10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1 169049363 110/3= ++++= 1 330 6.13 σ∧=≈ (5)由于2 11(, )xx N L σββ∧ :
t σ ∧ == 服从自由度为n-2的t分布。因而 /2 |(2)1 P t n α α σ ?? ?? <-=- ?? ?? 也即: 1/211/2 (p t t αα βββ ∧∧ ∧∧ -<<+=1α - 可得 1 95% β∧的置信度为的置信区间为(7-2.3537+2.353即为:(,) 2 2 00 1() (,()) xx x N n L ββσ - ∧ + : t ∧∧ == 服从自由度为n-2的t分布。因而 /2 (2)1 P t n α α ∧ ?? ?? ?? <-=- ?? ?? ?? ?? ?? 即 0/200/2 ()1 pβσββσα ∧∧∧∧ -<<+=- 可得 1 95%7.77,5.77 β∧- 的置信度为的置信区间为() (6)x与y的决定系数 2 21 2 1 () 490/6000.817 () n i i n i i y y r y y ∧- = - = - ==≈ - ∑ ∑ (7)
应用回归分析第章课后习题答案
第6章 6.1 试举一个产生多重共线性的经济实例。 答:例如有人建立某地区粮食产量回归模型,以粮食产量为因变量Y,化肥用量为X1,水浇地面积为X2,农业投入资金为X3。由于农业投入资金X3与化肥用量X1,水浇地面积X2有很强的相关性,所以回归方程效果会很差。再例如根据某行业企业数据资料拟合此行业的生产函数时,资本投入、劳动力投入、资金投入与能源供应都与企业的生产规模有关,往往出现高度相关情况,大企业二者都大,小企业都小。 6.2多重共线性对回归参数的估计有何影响? 答:1、完全共线性下参数估计量不存在; 2、参数估计量经济含义不合理; 3、变量的显著性检验失去意义; 4、模型的预测功能失效。 6.3 具有严重多重共线性的回归方程能不能用来做经济预测? 答:虽然参数估计值方差的变大容易使区间预测的“区间”变大,使预测失去意义。但如果利用模型去做经济预测,只要保证自变量的相关类型在未来期中一直保持不变,即使回归模型中包含严重多重共线性的变量,也可以得到较好预测结果;否则会对经济预测产生严重的影响。 6.4多重共线性的产生于样本容量的个数n、自变量的个数p有无关系? 答:有关系,增加样本容量不能消除模型中的多重共线性,但能适当消除多重共线性造成的后果。当自变量的个数p较大时,一般多重共线性容易发生,所以自变量应选择少而精。 6.6对第5章习题9财政收入的数据分析多重共线性,并根据多重共线性剔除变量。将所得结果与逐步回归法所得的选元结果相比较。 5.9 在研究国家财政收入时,我们把财政收入按收入形式分为:各项税收收入、企业收入、债务收入、国家能源交通重点建设收入、基本建设贷款归还收入、国家预算调节基金收入、其他收入等。为了建立国家财政收入回归模型,我们以财政收入y(亿元)为因变量,自变量如下:x1为农业增加值(亿元),x2为工业增加值(亿元),x3为建筑业增加值(亿元),x4为人口数(万人),x5为社
应用回归分析课后习题第7章第6题
7.6一家大型商业银行有多家分行,近年来,该银行的贷款额平稳增长,但不良贷款额也有较大比例的提高。为弄清楚不良贷款形成的原因,希望利用银行业务的有关数据做定量分析,以便找出控制不良贷款的方法。表7-5是该银行所属25家分行2002年的有关业务数据。 (1)计算y 与其余4个变量的简单相关系数。 由系数表可知,y 与其余4个变量的简单相关系数分别为0.844,0.732,0.700,0.519. (2)建立不良贷款对4个自变量的线性回归方程,所得的回归系数是否合理? 由上表可知,回归方程为为: 022.1029.0015.0148.04.0?4321--++=x x x x y 从上表可看出,方程的自变量2x 、3x 、4x 未通过t 检验,说明回归方程不显著,而且由实际意义出发,4x 的系数不能是负的,所以所得的回归系数不合理。 (3)分析回归模型的共线性。
由上表可知,所有自变量对应的VIF 全部小于10,所以自变量之间不存在共线性。但进行特征根检验见下表: 由这个表可以看出来,第5行中1x 、3x 的系数分别为0.87和0.63,可以说明这两个变量之间有共线性。 (4)采用后退法和逐步回归法选择变量,所得的回归系数是否合理?是否还存在共线性? 采用后退法(见上表),所得回归方程为972.0029.0149.0041.0y ?421--+=x x x 采用逐步回归法(见上表),所得回归方程为443.0032.005.0?41--=x x y 所得4x 的系数不合理(为负),说明存在共线性. (5)建立不良贷款y 对4个变量的岭回归。
应用回归分析第三章课后习题整理
y1 1 x11 x12 x1p 0 1 3.1 y2 1 x21 x22 x2p 1 + 2 即y=x + yn 1 xn1 xn2 xnp p n 基本假定 (1) 解释变量x1,x2…,xp 是确定性变量,不是随机变量,且要求 rank(X)=p+1 n 注 tr(H) h 1 3.4不能断定这个方程一定很理想,因为样本决定系数与回归方程中 自变量的数目以及样本量n 有关,当样本量个数n 太小,而自变量又较 多,使样本量与自变量的个数接近时, R 2易接近1,其中隐藏一些虚 假成分。 3.5当接受H o 时,认定在给定的显著性水平 下,自变量x1,x2, xp 对因变量y 无显著影响,于是通过x1,x2, xp 去推断y 也就无多大意 义,在这种情况下,一方面可能这个问题本来应该用非线性模型去描 述,而误用了线性模型,使得自变量对因变量无显著影响;另一方面 可能是在考虑自变量时,把影响因变量y 的自变量漏掉了,可以重新 考虑建模问题。 当拒绝H o 时,我们也不能过于相信这个检验,认为这个回归模型 已经完美了,当拒绝H o 时,我们只能认为这个模型在一定程度上说明 了自变量x1,x2, xp 与自变量y 的线性关系,这时仍不能排除排除我 们漏掉了一些重要的自变量。 3.6中心化经验回归方程的常数项为0,回归方程只包含p 个参数估计 值1, 2, p 比一般的经验回归方程减少了一个未知参数,在变量较 SSE (y y)2 e12 e22 1 2 1 E( ) E( - SSE* - n p 1 n p n 2 [D(e) (E(e ))2 ] 1 n (1 1 n 2 en n E( e 1 1 n p 1 1 n p 1 1 "1 1 n p 1 J (n D(e) 1 (p 1)) 1_ p 1 1 1 n p 1 2 2 n E(e 2 ) (1 h ) 2 1 第7章岭回归 思考与练习参考答案 7.1 岭回归估计是在什么情况下提出的? 答:当自变量间存在复共线性时,|X’X|≈0,回归系数估计的方差就很大,估计值就很不稳定,为解决多重共线性,并使回归得到合理的结果,70年代提出了岭回归(Ridge Regression,简记为RR)。 7.2岭回归的定义及统计思想是什么? 答:岭回归法就是以引入偏误为代价减小参数估计量的方差的一种回归方法,其统计思想是对于(X’X)-1为奇异时,给X’X加上一个正常数矩阵 D, 那么X’X+D接近奇异的程度就会比X′X接近奇异的程度小得多,从而完成回归。但是这样的回归必定丢失了信息,不满足blue。但这样的代价有时是值得的,因为这样可以获得与专业知识相一致的结果。 7.3 选择岭参数k有哪几种方法? 答:最优 是依赖于未知参数 和 的,几种常见的选择方法是: 岭迹法:选择 的点能使各岭估计基本稳定,岭估计符号合理,回归系数没有不合乎经济意义的绝对值,且残差平方和增大不太多; 方差扩大因子法: ,其对角线元 是岭估计的方差扩大因子。要让 ; 残差平方和:满足 成立的最大的 值。 7.4 用岭回归方法选择自变量应遵循哪些基本原则? 答:岭回归选择变量通常的原则是: 1. 在岭回归的计算中,我们通常假定涉及矩阵已经中心化和标准化了,这样可以直接比较标准化岭回归系数的大小。我们可以剔除掉标准化岭回归系数比较稳定且绝对值很小的自变量; 2. 当k值较小时,标准化岭回归系数的绝对值并不很小,但是不稳定,随着k的增加迅速趋近于零。像这样岭回归系数不稳定、震动趋于零的自变量,我们也可以予以剔除; 3. 去掉标准化岭回归系数很不稳定的自变量。如果有若干个岭回归系数不稳定,究竟去掉几个,去掉那几个,要根据去掉某个变量后重新进行岭回归分析的效果来确定。 3.11研究货运总量y (万吨)与工业总产值1x (亿元)、农业总产值2x (亿元)、居民非商品支出3x (亿元)的关系。数据如表3-9所示。 (1)计算出y ,1x ,2x ,3x 的相关系数矩阵。 所以y ,1x ,2x ,3x 的相关系数矩阵为: ????? ? ? ??1547.0398.0724.0547.01113.0731.0398.0113.01556 .0724.0731.0556.01 (2)求y 关于1x ,2x ,3x 的三元线性回归方程。 编号 1 2 3 4 5 6 7 8 9 10 货运总量y (万吨) 160 260 210 265 240 220 275 160 275 250 工业总产值x1(亿 元) 70 75 65 74 72 68 78 66 70 65 农业总产值x2(亿 元) 35 40 40 42 38 45 42 36 44 42 居民非商品支出x3 (亿元) 1.0 2.4 2.0 3.0 1.2 1.5 4.0 2.0 3.2 3.0 由系数表可以知道,y 关于1x ,2x ,3x 的三元线性回归方程为: 280.348447.12101.7574.3321-++=x x x y (3)对所求得的方程作拟合优度检验。 由模型汇总可知,样本的决定系数为0.806,所以可以认为回归方程为样本观测值的拟合程度较好,即回归方程的显著性较高。 (4)对回归方程作显著性检验。 对方差分析表可以知道p 值为0.015<0.05 说明自变量1x ,2x ,3x 对因变量y 产生的线性影响较显著。而F=8.283>74.405.0=F 时,就拒绝原假设,认为在显著性水平0.05下,y 与1x , 2x ,3x 有显著的线性关系,即回归方程是显著的。 第3章 多元线性回归 思考与练习参考答案 3.1 见教材P64-65 3.2 讨论样本容量n 与自变量个数p 的关系,它们对模型的参数估计有何影响? 答:在多元线性回归模型中,样本容量n 与自变量个数p 的关系是:n>>p 。如果n<=p 对模型的参数估计会带来很严重的影响。因为: 1. 在多元线性回归模型中,有p+1个待估参数β,所以样本容量的个数应该大于解释变量的个数,否则参数无法估计。 2. 解释变量X 是确定性变量,要求()1rank p n =+ 第七章岭回归 1.岭回归估计是在什么情况下提出的? 答:当解释变量间出现严重的多重共线性时,用普通最小二乘法估计模型参数,往往参数估计方差太大,使普通最小二乘法的效果变得很不理想,为了解决这一问题,统计学家从模型和数据的角度考虑,采用回归诊断和自变量选择来克服多重共线性的影响,这时,岭回归作为一种新的回归方法被提出来了。 2.岭回归估计的定义及其统计思想是什么? 答:一种改进最小二乘估计的方法叫做岭估计。当自变量间存在多重共线性,∣X'X∣≈0时,我们设想给X'X加上一个正常数矩阵kI(k>0),那么X'X+kI 接近奇异的程度小得多,考虑到变量的量纲问题,先对数据作标准化,为了计算方便,标准化后的设计 阵仍然用X表示,定义为 ()()1 ?'' X X I X y βκκ- =+ ,称为 β的岭回归估计,其中k 称为岭参数。 3.选择岭参数k有哪几种主要方法? 答:选择岭参数的几种常用方法有1.岭迹法,2.方差扩大因子法,3.由残差平方和来确定k值。 4.用岭回归方法选择自变量应遵从哪些基本原则? 答:用岭回归方法来选择变量应遵从的原则有: (1)在岭回归的计算中,我们假定设计矩阵X已经中心化和标准化了,这样可以直接比较标准化岭回归系数的大小,我们可以剔除掉标准化岭回归系数比较稳定且绝对值很小的自变量。 (2)当k值较小时标准化岭回归系数的绝对值并不是很小,但是不稳定,随着k的增加迅速趋于零。像这样的岭回归系数不稳定,震动趋于零的自变量,我们也可以予以删除。 (3)去掉标准化岭回归系数很不稳定的自变量,如果有若干个岭回归系数不稳定,究竟去掉几个,去掉哪几个,这并无一般原则可循,这需根据去掉某个变量后重新进行岭回归分析的效果来确定。 5.对第5章习题9的数据,逐步回归的结果只保留了3个自变量x1,x2,x5,用y对这3个自变量做岭回归分析。 答:依题意,对逐步回归法所保留的三个自变量做岭回归分析。 程序为: include'C:\Program Files\SPSSEVAL\Ridge regression.sps'. ridgereg dep=y/enter x1 x2 x5 /start=0.0/stop=1/inc=0.01. 应用回归分析第三章习题 3.1 y x =β 基本假定: (1) 诸1234n x ,x x ,x x ……非随机变量,rank (x )=p+1,X 为满秩矩阵 (2) 误差项()()200i i j E ,i j cov ,,i j ?ε=? ?δ=?εε=??≠?? (3)()2 0i i j ~N ,,?εδ??εε??诸相互独立 3.2 ()10111 ?X X X X |rank(X X )p rank(X )p n p -'β'≠'=+≥+≥+存在,必须使存在。即|则必有故 3.3 ()()()() ()22 11 122 12 22211111111 n n n i i ii i i i n ii i n i i E e D e h n h n p ?E E e n p n p n p =====??==-δ ????? =-δ=--δ ??? ??∴δ ==--δ=δ ? ----??∑∑∑∑∑ 3.4 并不能这样武断地下结论。2 R 与回归方程中的自变量数目以及样本量n 有关,当样本量n 与自变量个数接近时,2 R 易接近1,其中隐含着一些虚假成分。因此,并不能仅凭很大的2 R 就模型的优劣程度。 3.5 首先,对回归方程的显著性进行整体上的检验——F 检验 001230p H :β=β=β=β==β=…… 接受原假设:在显著水平α下,表示随机变量y 与诸x 之间的关系由线性模型表示不合适 拒绝原假设:认为在显著性水平α下,y 与诸x 之间有显著的线性关系 第二,对单个自变量的回归系数进行显著性检验。 00i H :β= 接受原假设:认为i β=0,自变量i x 对y 的线性效果并不显著 3.6 原始数据由于自变量的单位往往不同,会给分析带来一定的困难;又由于设计的数据量较大,可能会以为舍入误差而使得计算结果并不理想。中心化和标准化回归系数有利于消除由于量纲不同、数量级不同带来的影响,避免不必要的误差。 3.7 11 22 011122201122p p p p p p p ?????y x x x ??????y y (x x )(x x )(x x )????y x x )x x )x x )y =β +β+β++β-=β+β-+β-++β--ββ=-+-++-=对最小二乘法求得一般回归方程: ……对方程进行如下运算: …… ……*j j ?+β=……即 3.8 121321233132212312212331 312311232332 13 231313********* 111 r r r r r r r r r r r r r r r r r r r r r ?? ?= ? ????==-?= =-?= =-即证 第4章违背基本假设的情况 思考与练习参考答案 试举例说明产生异方差的原因。 答:例:截面资料下研究居民家庭的储蓄行为 Y i=β0+β1X i+εi 其中:Y i表示第i个家庭的储蓄额,X i表示第i个家庭的可支配收入。 由于高收入家庭储蓄额的差异较大,低收入家庭的储蓄额则更有规律性,差异较小,所以εi的方差呈现单调递增型变化。 例:以某一行业的企业为样本建立企业生产函数模型 Y i=A iβ1K iβ2L iβ3eεi 被解释变量:产出量Y,解释变量:资本K、劳动L、技术A,那么每个企业所处的外部环境对产出量的影响被包含在随机误差项中。由于每个企业所处的外部环境对产出量的影响程度不同,造成了随机误差项的异方差性。这时,随机误差项ε的方差并不随某一个解释变量观测值的变化而呈规律性变化,呈现复杂型。异方差带来的后果有哪些 答:回归模型一旦出现异方差性,如果仍采用OLS估计模型参数,会产生下列不良后果: 1、参数估计量非有效 2、变量的显著性检验失去意义 3、回归方程的应用效果极不理想 总的来说,当模型出现异方差性时,参数OLS估计值的变异程度增大,从而造成对Y的预测误差变大,降低预测精度,预测功能失效。 简述用加权最小二乘法消除一元线性回归中异方差性的思想与方法。 答:普通最小二乘估计就是寻找参数的估计值使离差平方和达极小。其中每个平方项的权数相同,是普通最小二乘回归参数估计方法。在误差项等方差不相关的条件下,普通最小二乘估计是回归参数的最小方差线性无偏估计。然而在异方差 的条件下,平方和中的每一项的地位是不相同的,误差项的方差大的项,在残差平方和中的取值就偏大,作用就大,因而普通最小二乘估计的回归线就被拉向方差大的项,方差大的项的拟合程度就好,而方差小的项的拟合程度就差。由OLS 求出的仍然是的无偏估计,但不再是最小方差线性无偏估计。所以就是:对较大的残差平方赋予较小的权数,对较小的残差平方赋予较大的权数。这样对残差所提供信息的重要程度作一番校正,以提高参数估计的精度。 加权最小二乘法的方法: 简述用加权最小二乘法消除多元线性回归中异方差性的思想与方法。 答:运用加权最小二乘法消除多元线性回归中异方差性的思想与一元线性回归的类似。多元线性回归加权最小二乘法是在平方和中加入一个适当的权数i w ,以调整各项在平方和中的作用,加权最小二乘的离差平方和为: ∑=----=n i ip p i i i p w x x y w Q 1211010)( ),,,(ββββββ (2) 加权最小二乘估计就是寻找参数p βββ,,,10 的估计值pw w w βββ?,,?,?10 使式(2)的离差平方和w Q 达极小。所得加权最小二乘经验回归方程记做 p pw w w w x x y βββ????110+++= (3) 22011 1 ???()()N N w i i i i i i i i Q w y y w y x ββ===-=--∑∑22 __ 1 _ 2 _ _ 02 222 ()() ?()?1 11 1 ,i i N w i i i w i w i w w w w w kx i i i i m i i i m i w x x y y x x y x w kx x kx w x σβββσσ==---=-= = ===∑∑1N i =1 1表示=或 第三章 回归分析原理 3·1、一元线性回归数学模型 按理说,在研究某一经济现象时,应该尽量考虑到与其有关各种有影响的因素或变量。但作为理论的科学研究来说,创造性地简化是其的基本要求,从西方经济学的基本理论中,我们可以看到在一般的理论分析中,至多只包含二、三个 变量的数量关系的分析或模型。 这里所讨论的一元线性回归数学模型,是数学模型的最简单形式。当然要注意的是,这里模型讨论是在真正回归意义上来进行的,也可称之为概率意义上的线性模型。 在非确定性意义上,或概率意义上讨论问题,首先要注意一个最基本的概念或思路问题,这就是总体和样本的概念。 我们的信念是任何事物在总体上总是存在客观规律的,虽然我们无论如何也不可能观察或得到总体,严格说来,总体是无限的。而另一方面,我们只可能观察或得到的是样本,显然样本肯定是总体的一部分,但又是有限的。 实际上概率论和数理统计的基本思想和目的,就是希望通过样本所反映出来的信息来揭示总体的规律性,这种想法或思路显然存在重大的问题。但另一方面,我们也必须承认,为了寻找总体的规律或客观规律,只能通过样本来进行,因为我们只可能得到样本。 在前面我们已经知道,用回归的方法和思路处理非确定性问题或散点图,实际上存在一些问题,亦即只有在某些情况下,回归的方法才是有效的。因此,在建立真正回归意义上建立其有效方法时,必须作出相应的假设条件。 基本假设条件: (1)假设概率函数)|(i i X Y P 或随机变量i Y 的分布对于所有i X 值,具有相同的方差2σ ,且2σ 是一个常数,亦即)(i Y Var =)(i Var μ=2σ。 (2)假设i Y 的期望值)(i Y E 位于同一条直线上,即其回归直线为 )(i Y E =i X βα+ 等价于 0)(=i E μ 这个假设是最核心的假设,它实际上表明)(i Y E 与i X 之间是确定性的关系。 (3)假设随机变量i Y 是完全独立的,亦即。j i u u Cov Y Y Cov j i j i ≠==,0),(),( 2.1 一元线性回归有哪些基本假定? 答: 假设1、解释变量X 是确定性变量,Y 是随机变量; 假设2、随机误差项ε具有零均值、同方差和不序列相关性: E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关: Cov(X i , εi )=0 i=1,2, …,n 假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n 误差εi (i=1,2, …,n )仍满足基本假定。求β1的最小二乘估计 解: 得: 2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。 证明: 其中: 即: ∑e i =0 ,∑e i X i =0 2.4回归方程E (Y )=β0+β1X 的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。 ∑∑+-=-=n i i i n i X Y Y Y Q 1 21021 ))??(()?(ββ211 1 2 )?()?(i n i i n i i i e X Y Y Y Q β∑∑==-=-= 01????i i i i i Y X e Y Y ββ=+=-0 1 00??Q Q β β ??==?? 答:由于εi ~N(0, σ2 ) i=1,2, …,n 所以Y i =β0 + β1X i + εi ~N (β0+β1X i , σ2 ) 最大似然函数: 使得Ln (L )最大的0 ?β,1?β就是β0,β1的最大似然估计值。 同时发现使得Ln (L )最大就是使得下式最小, 上式恰好就是最小二乘估计的目标函数相同。值得注意的是:最大似然估计是在εi ~N(0, σ2 )的假设下求得,最小二乘估计则不要求分布假设。 所以在εi ~N(0, σ2 ) 的条件下, 参数β0,β1的最小二乘估计与最大似然估计等价。 2.5 证明0 ?β是β0的无偏估计。 证明:)1[)?()?(111 0∑∑==--=-=n i i xx i n i i Y L X X X Y n E X Y E E ββ )] )(1 ([])1([1011i i xx i n i i xx i n i X L X X X n E Y L X X X n E εββ++--=--=∑∑== 1010)()1 (])1([βεβεβ=--+=--+=∑∑==i xx i n i i xx i n i E L X X X n L X X X n E 2.6 证明 证明: )] ()1([])1([)?(102110i i xx i n i i xx i n i X Var L X X X n Y L X X X n Var Var εβββ++--=--=∑∑== 2 2221 2]1[])(2)1[(σσxx xx i xx i n i L X n L X X X nL X X X n +=-+--=∑= 2.7 证明平方和分解公式:SST=SSE+SSR ∑∑+-=-=n i i i n i X Y Y Y Q 1 2102 1 ))??(()?(ββ() ) 1()1()?(2 2 2 1 2 2 xx n i i L X n X X X n Var +=-+=∑=σσβ 第7章 岭回归 思考与练习参考答案 7.1 岭回归估计是在什么情况下提出的? 答:当自变量间存在复共线性时,|X’X |≈0,回归系数估计的方差就很大, 估计值就很不稳定,为解决多重共线性,并使回归得到合理的结果,70年代提出了岭回归(Ridge Regression,简记为RR)。 7.2岭回归的定义及统计思想是什么? 答:岭回归法就是以引入偏误为代价减小参数估计量的方差的一种回归方法,其 统计思想是对于(X ’X )-1为奇异时,给X’X 加上一个正常数矩阵D, 那么X’X+D 接近奇异的程度就会比X ′X 接近奇异的程度小得多,从而完成回归。但是这样的回归必定丢失了信息,不满足blue 。但这样的代价有时是值得的,因为这样可以获得与专业知识相一致的结果。 7.3 选择岭参数k 有哪几种方法? 答:最优k 是依赖于未知参数β和2σ的,几种常见的选择方法是: ○ 1岭迹法:选择0k 的点能使各岭估计基本稳定,岭估计符号合理,回归系数没有不合乎经济意义的绝对值,且残差平方和增大不太多; ○ 2方差扩大因子法:11()()()c k X X kI X X X X kI --'''=++,其对角线元()jj c k 是岭估计的方差扩大因子。要让()10jj c k ≤; ○ 3残差平方和:满足()SSE k cSSE <成立的最大的k 值。 7.4 用岭回归方法选择自变量应遵循哪些基本原则? 答:岭回归选择变量通常的原则是: 1. 在岭回归的计算中,我们通常假定涉及矩阵已经中心化和标准化了,这 样可以直接比较标准化岭回归系数的大小。我们可以剔除掉标准化岭回归系数比较稳定且绝对值很小的自变量; 2. 当k 值较小时,标准化岭回归系数的绝对值并不很小,但是不稳定,随 第二章 一元线性回归分析 思考与练习参考答案 一元线性回归有哪些基本假定? 答: 假设1、解释变量X 是确定性变量,Y 是随机变量; 假设2、随机误差项ε具有零均值、同方差和不序列相关性: E(εi )=0 i=1,2, …,n Var (εi )=?2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关: Cov(X i , εi )=0 i=1,2, …,n 假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, ?2 ) i=1,2, …,n 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n 误差εi (i=1,2, …,n )仍满足基本假定。求 β1的最小二乘估计 解: 得: 证明(式),?e i =0 ,?e i X i =0 。 证明:∑∑+-=-=n i i i n i X Y Y Y Q 1 2102 1 ))??(()?(ββ 其中: 即: ?e i =0 ,?e i X i =0 211 1 2)?()?(i n i i n i i i e X Y Y Y Q β∑∑==-=-=0)?(2?11 1 =--=??∑=i i n i i e X X Y Q ββ) () (?1 2 1 1 ∑∑===n i i n i i i X Y X β01????i i i i i Y X e Y Y ββ=+=-0 1 00??Q Q β β ??==?? 回归方程E (Y )=β0+β1X 的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。 答:由于εi ~N(0, ?2 ) i=1,2, …,n 所以Y i =β0 + β1X i + εi ~N (β0+β1X i , ?2 ) 最大似然函数: 使得Ln (L )最大的0 ?β,1?β就是β0,β1的最大似然估计值。 同时发现使得Ln (L )最大就是使得下式最小, ∑∑+-=-=n i i i n i X Y Y Y Q 1 21021 ))??(()?(ββ 上式恰好就是最小二乘估计的目标函数相同。值得注意的是:最大似然估计是在εi ~N (0, ?2 )的假设下求得,最小二乘估计则不要求分布假设。 所以在εi ~N(0, ?2 ) 的条件下, 参数β0,β1的最小二乘估计与最大似然估计等价。 证明0 ?β是β0的无偏估计。 证明:)1[)?()?(1 110∑∑==--=-=n i i xx i n i i Y L X X X Y n E X Y E E ββ )] )(1 ([])1([1011i i xx i n i i xx i n i X L X X X n E Y L X X X n E εββ++--=--=∑∑== 1010)()1 (])1([βεβεβ=--+=--+=∑∑==i xx i n i i xx i n i E L X X X n L X X X n E 证明 证明: )] ()1([])1([)?(102110i i xx i n i i xx i n i X Var L X X X n Y L X X X n Var Var εβββ++--=--=∑∑== () ) 1()1()?(2 2 2 1 2 2 xx n i i L X n X X X n Var +=-+=∑=σσβ 应用回归分析-第7章课后习题参考答案 第7章 岭回归 思考与练习参考答案 7.1 岭回归估计是在什么情况下提出的? 答:当自变量间存在复共线性时,|X’X |≈0,回归系数估计的方差就很大, 估计值就很不稳定,为解决多重共线性,并使回归得到合理的结果,70年代提出了岭回归(Ridge Regression,简记为RR)。 7.2岭回归的定义及统计思想是什么? 答:岭回归法就是以引入偏误为代价减小参数估计量的方差的一种回归方法,其统计思想是对于(X ’X )-1为奇异时,给X’X 加上一个正常数矩阵D, 那么X ’X+D 接近奇异的程度就会比X ′X 接近奇异的程度小得多,从而完成回归。但是这样的回归必定丢失了信息,不满足blue 。但这样的代价有时是值得的,因为这样可以获得与专业知识相一致的结果。 7.3 选择岭参数k 有哪几种方法? 答:最优k 是依赖于未知参数β和2σ的,几种常见的选择方法是: ○ 1岭迹法:选择0k 的点能使各岭估计基本稳定,岭估计符号合理,回归系数没有不合乎经济意义的绝对值,且残差平方和增大不太 多; ○ 2方差扩大因子法:11()()()c k X X kI X X X X kI --'''=++,其对角线元()jj c k 是岭估计的方差扩大因子。要让()10jj c k ≤; ○ 3残差平方和:满足()SSE k cSSE <成立的最大的k 值。 7.4 用岭回归方法选择自变量应遵循哪些基本原则? 答:岭回归选择变量通常的原则是: 1. 在岭回归的计算中,我们通常假定涉及矩阵已经中心化和标准化了,这 样可以直接比较标准化岭回归系数的大小。我们可以剔除掉标准化岭回归系数比较稳定且绝对值很小的自变量; 第三章 回归预测法 基本内容 一、一元线性回归预测法 是指成对的两个变量数据分布大体上呈直线趋势时,运用合适的参数估计方法,求出一元线性回归模型,然后根据自变量与因变量之间的关系,预测因变量的趋势。由于很多社会经济现象之间都存在相关关系,因此,一元线性回归预测具有很广泛的应用。进行一元线性回归预测时,必须选用合适的统计方法估计模型参数,并对模型及其参数进行统计检验。 1、建立模型 一元线性回归模型: i i i x b b y μ++=10 其中,0b ,1b 是未知参数,i μ为剩余残差项或称随机扰动项。 2、用最小二乘法进行参数的估计时,要求i μ满足一定的假设条件: ①i μ是一个随机变量; ②i μ的均值为零,即()0=i E μ; ③在每一个时期中,i μ的方差为常量,即()2 σμ=i D ; ④各个i μ相互独立; ⑤i μ与自变量无关; 3、参数估计 用最小二乘法进行参数估计,得到的0b ,1b 的公式为: ()()() ∑∑---= 2 1x x y y x x b x b y b 10-= 4、进行检验 ①标准误差:估计值与因变量值间的平均平方误差。其计算公式为:()2 ?2 --= ∑n y y SE 。 ②可决系数:衡量自变量与因变量关系密切程度的指标,在0与1之间取值。其计算公式 为:()()()() ()()∑∑∑∑∑---=??? ??? ? ? ----=222 2 2 2 ?1y y y y y y x x y y x x R 。 ③相关系数;计算公式为:()()()() ∑∑∑----=2 2 y y x x y y x x r 。 ④回归系数显著性检验 i 检验假设:0:10=b H ,0:11≠b H 。 ii 检验统计量:b S b t 1 = ~()2-n t ,其中() ∑-=2 x x SE S b 。 iii 检验规则:给定显著性水平α,若αt t >,则回归系数显著。 ⑤回归模型的显著性检验 i 检验假设::0H 回归方程不显著 ,:1H 回归方程显著。 ii 检验统计量:()()() 2??2 2 ---= ∑∑n y y y y F ~()2,1-n F 。 iii 检验规则:给定显著性水平α,若()2,1->n F F α,则回归方程显著。 ⑥得宾—沃森统计量(D —W ):检验i μ之间是否存在自相关关系。 ()∑∑==--= -n i i n i i i W D 1 222 1μ μμ,其中i i i y y ?-=μ。 5、进行预测 小样本情况下,近似的置信区间的常用公式为:置信区间=tSE y ±?。 二、多元线性回归预测法 社会经济现象的变化往往受到多个因素的影响,因此,一般要进行多元回归分析,我们把包括两个或两个以上自变量的回归成为多元回归。多元回归与医院回归类似,可以用最小二乘法估计模型参数。也需对模型及模型参数进行统计检验。选择合适的自变量是正确进行多元回归预测的前提之一,多元回归模型自变量的选择可以利用变量之间的相关矩阵来解决。 1、 建立模型—以二元线性回归模型为例 二元线性回归模型:222110i i x b x b b y μ+++=。类似使用最小二乘法进行参数估计。 2、 拟合优度指标 ①标准误差:对y 值与模型估计值之间的离差的一种度量。其计算公式为: ()3 ?2 --= ∑n y y SE应用回归分析,第7章课后习题参考答案
应用回归分析课后习题第3章11题
应用回归分析-第3章课后习题参考答案
应用回归分析第七章答案
应用回归分析第三版·何晓群-第三章所有习题答案
应用回归分析,第4章课后习题参考答案
第三章回归分析原理
应用回归分析 课后答案 浙江万里学院
应用回归分析,第7章课后习题参考答案
应用回归分析 课后习题参考答案
应用回归分析-第7章课后习题参考答案
第三章回归测法
