2010年保定市数学一模人教版
河北省保定市2011届高三第一学期期末调研考试(数学)

河北省保定市2010—2011学年度高三第一学期期末调研考试数 学 试 题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分,考试时间120分钟。
第I 卷(选择题,共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、学号、学校、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
3.考试结束后,监考人员将本试卷和答题卡一并收回。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.(理)i 是虚数单位,则(1)(2)i i i +-的虚部为 ( ) A .—1 B .1 C .—3 D .3(文)设全集U=R ,1{|0,},2R x P x x R C P x -=≥∈=-则( ) A .[1,2] B .(1,2] C .[1,2) D .(1,2)2.函数()sin()4f x x π=-的一个单调递增区间为 ( ) A .(,)22ππ- B .3(,)44ππ- C .3(,)44ππ- D .37(,)44ππ 3.若实数x ,y 满足1|1|lg 0,x y--=则y 关于x 的函数的图象形状大致是 ( )4.设a 、b 、c 表示三条直线,α、β表示两个平面,则下列命题中不正确的是 ( )A .//c c αβαβ⊥⎫⇒⊥⎬⎭B .//a b b a αα⎫⇒⊥⎬⊥⎭C .////b c b c c ααα⎫⎪⊂⇒⎬⎪⊄⎭D .a b b b c c a ββ⊥⎫⎪⊂⇒⊥⎬⎪⎭是在内的射影 5.圆221x y +=与直线2y kx =+没有..公共的充要条件是 ( )A.(k ∈ B.(,(2,)k ∈-∞+∞C.(k ∈D .(,(3,)k ∈-∞+∞6.某公司有普通职员150人,中级管理人员40人,高级管理人员10人,现采用分层抽样的方法从这200人中抽取40人进行问卷调查,若在己抽取的40人的问卷中随机抽取一张,则所抽取的恰好是一名高级管理人员的答卷的概率为 ( )A .14B .15C .120D .11007.设数列*12{}23,,{(,)}n n n a a a n N P n a +=∈满足且对任意的点列恒满足1(1,2)n n P P +=,则数列{}n n a n S 的前项和为( ) A .4()3n n -B .3()4n n -C .2()3n n -D .1()2n n - 8.已知二项式(32)n x +的展开式中所有项的系数和为3125,则此展开式中含4x 项的系数是( )A .240B .720C .810D .1080 9.设实数x ,y 满足2420x x y x y c ≥⎧⎪+≤⎨⎪-++≥⎩,且3z x y =+的最小值为5,则z 的最大值为( ) A .10 B .12 C .14 D .1510.(理)用5,6,7,8,9,组成没有重复数字的五位数,其中有且仅有一个偶数夹在两个奇数之间的五位数的个数为 ( )A .36B .48C .72D .120(文)用5,6,7,8,9,组成没有重复数字的五位数,其中有且仅有一个奇数夹在两个偶数之间的五位数的个数为 ( )A .36B .48C .72D .12011.(理)已知球的半径为5,相互垂直的两个平面分别截球面得两个圆,若两圆的公共弦长为6,则两圆的圆心距为 ( )A .4 BC .D .1(文)位于北纬x 的A 、B 两地经度相差90°,且A 、B 两地间的球面距离为3πR (R 为地球半径),则x 等于( )A .30B .45C .60D .7512.有一矩形纸片ABCD ,按图所示方法进行任意折叠,使每次折叠后点B 都落在边AD 上,将B 的落点记为B ',其中EF为折痕,点F 也可落在边CD 上,过B '作B H '//CD 交EF于点H ,则点H 的轨迹为 ( )A .圆的一部分B .椭圆的一部分C .双曲线的一部分D .抛物线的一部分第Ⅱ卷(共90分)二、填空题(本大题共4小题,每小题5分,共20分,把最简答案填在答题卡的横线上)13.曲线24y x x =-在点(—1,—3)处的切线方程是 。
2010年河北省中考数学仿真模拟(一) 人教新课标版
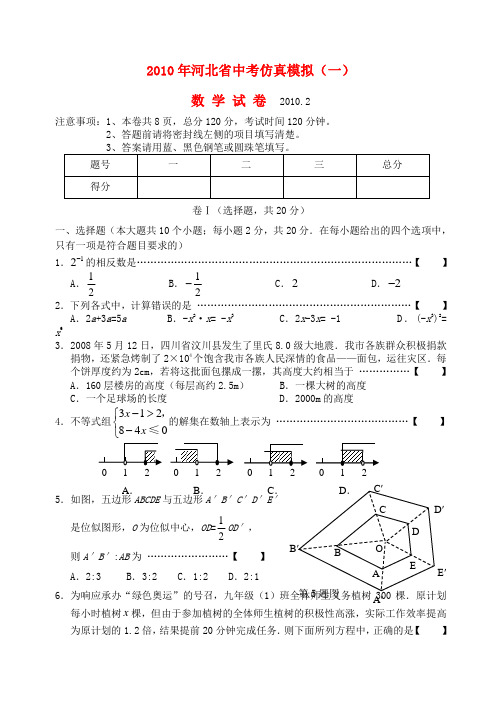
A′′E′A.B.C.2010年河北省中考仿真模拟(一)数学试卷2010.2注意事项:1、本卷共8页,总分120分,考试时间120分钟。
2、答题前请将密封线左侧的项目填写清楚。
卷Ⅰ(选择题,共20分)一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.12-的相反数是………………………………………………………………………【】A.12B.12- C.2 D.2-2.下列各式中,计算错误的是………………………………………………………【】A.2a+3a=5a B.-x2·x= -x3C.2x-3x= -1 D.(-x3)2= x63.2008年5月12日,四川省汶川县发生了里氏8.0级大地震.我市各族群众积极捐款捐物,还紧急烤制了2×104个饱含我市各族人民深情的食品——面包,运往灾区.每个饼厚度约为2cm,若将这批面包摞成一摞,其高度大约相当于……………【】A.160层楼房的高度(每层高约2.5m) B.一棵大树的高度C.一个足球场的长度D.2000m的高度4.不等式组312840xx->⎧⎨-⎩,≤的解集在数轴上表示为…………………………………【】5.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,OD=12O D′,则A′B′:AB为……………………【】A.2:3 B.3:2 C.1:2 D.2:16.为响应承办“绿色奥运”的号召,九年级(1每小时植树x棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,结果提前20分钟完成任务.则下面所列方程中,正确的是【】DCBACBA''C'第10题图图2图1第11题图A.3002030060 1.2x x-= B.300300201.2x x-=C.300300201.260x x x-=+D.300300201.260x x=-7.已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A、C、D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是…………【】A.r>15 B.15<r<20 C.15<r<25 D.20<r<258.在一个暗箱里放有a个除颜色外其他完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是……………………【】A.12 B.9 C.4 D.39.在平面直角坐标系中,函数1+-=xy与2)1(23--=xy的图象大致是………【】10.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动..对称变换.....在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称....变换..过程中,两个对应三角形(如图2)的对应点所具有的性质是…………【】A.对应点连线与对称轴垂直B.对应点连线被对称轴平分C.对应点连线被对称轴垂直平分D.对应点连线互相平行卷Ⅱ(非选择题,共100分)二、填空题(本大题共8个小题;每小题3分,共24分.把答案写在题中横线上)11.如图是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(下底挖去一小半圆),刀片上、下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=度.12.小华在解一元二次方程x2-4x=0时.只得出一个根是x=4,则被他漏掉的一个根第15题图做对题数是x =____. 13.如果11m m-=-,则2m m += ;2221m m +-= . 14.制作一个圆锥模型,已知圆锥底面圆的半径为3.5cm ,侧面母线长为6cm ,则此圆锥侧面展开图的扇形圆心角为 度.15.数学老师布置10道选择题作为课堂练习,科代表将全班同学的答题情况绘制成条形统计图,根据图 中信息,全班每位同学答对题数的中位数和众数分 别为______________.16.当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小 .(填“相同”、“不一定相同”、“不相同”之一). 17.已知反比例函数的图象经过点(m ,2)和(-2,3),则m 的值为 . 18.如图中的圆均为等圆,且相邻两圆外切,圆心连线构成正三角形,记各阴影部分面积从左到右依次为1S ,2S ,3S ,…,n S ,则124:S S 的值等于 .三、解答题(本大题共8个小题;共76分.解答应写出文字说明、证明过程或演算步骤)19.(本小题满分7分)已知30x y -=,求()y x yxy x yx -⋅+-+2222的值.第18题图 (n +1)个图……某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)(1)求出D级学生的人数占全班总人数的百分比;(2)求出扇形统计图中C级所在的扇形圆心角的度数;(3)该班学生体育测试成绩的中位数落在哪个等级内;(4)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?1 D C F a b A B 为缓解油价不稳给出租车业带来的成本压力,某巿自2009年1月1日起,调整出租车运营价,调整方案见下列表格及图像(其中a ,b ,c设行驶路程xkm 时,调价前的运价y 1(元),调价后的运价为y 2(元)如图,折线ABCD 表示y 2与x 之间的函数关系式,线段EF 表示当0≤x ≤3时,y 1与x 的函数关系式,根据图表信息,完成下列各题:①填空:a =______,b =______,c =_______.②写出当x >3时,y 1与x 的关系,并在上图中画出该函数的图象.③函数y 1与y 2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由. 22.(本小题满分9分)如图,河流两岸a b ,互相平行,C D ,是河岸a 上间隔50m 的两个电线杆.某人在河岸b 上的A 处测得30DAB ∠=,然后沿河岸走了100m 到达B 处,测得60CBF ∠=,求河流的宽度CF 的值(结果精确到个位).A B C E F DD A B CEF A DF C E B 图1 图2 图3如图所示,CD 为经过BCA ∠顶点C 的一条直线,CA CB =.E F ,分别是直线CD 上两点,且BEC CFA α∠=∠=∠.(1)若直线CD 经过BCA ∠的内部,且E F ,在射线CD 上,请解决下面两个问题:①如图1,若90BCA ∠=,90α∠=,则BE CF ;EFAF -(填“>”,“<”或“=”);②如图2,若0180B C A <∠<,请添加一个关于α∠与BCA ∠关系的条件 ,使①中的两个结论仍然成立,并简单说明两个结论仍然成立的理由.(2)如图3,若直线CD 经过BCA ∠的外部,BCA α∠=∠,请提出EF BE AF ,,三条线段数量关系的合理猜想(不要求证明). 24.(本小题满分10分)(1)如图1,图2,图3,在ABC △中,分别以AB AC ,为边,向ABC △外作正三角形,正四边形,正五边形,BE CD ,相交于点O .①如图1,求证:ABE ADC △≌△;②探究:如图1,BOC ∠= ;如图2,BOC ∠= ; 如图3,BOC ∠= .(2)如图4,已知:AB AD ,是以AB 为边向ABC △外所作正n 边形的一组邻边;AC AE ,是以AC 为边向ABC △外所作正n 边形的一组邻边.BE ,CD 的延长相交于点O .①猜想:如图4,BOC ∠= (用含n 的式子表示);②根据图4证明你的猜想. 25.(本小题满分12分)某宾馆有客房90间,当每间客房的定价为每天140元时,客房会全部住满.当每间客房每天的定价每涨10元时,就会有5间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出60元的各种费用.(1)请写出该宾馆每天的利润y (元)与每间客房涨价x (元)之间的函数关系式; (2)设某天的利润为8000元,8000元的利润是否为该天的最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时客房定价应为多少元? (3)请回答客房定价在什么范围内宾馆就可获得利润?26.(本小题满分12分)如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中一个动点到达端点时,另一个动点也随之停止运动.(1)求AD的长;(2)设CP=x,问当x为何值时△PDQ的面积达到最大,并求出最大值;(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.第26题图(备用图)。
河北省保定市2010届高三第一次模拟考试(语文B卷)扫描版

2010 年4 月高三4 月模拟考试语文答案A 卷一、(12分每小题3分)1、B (A 离经叛道肺腑之言C步履维艰寻章摘句物极必反D叶xié集腋成裘)2、B (心心相印:彼此的心意不用说出,就可以互相了解。
形容彼此思想感情完全一致。
A老气横秋:形容老练而自负的神态。
现形容自高自大,摆老资格。
也形容缺乏朝气。
C光怪陆离:形容奇形怪状,五颜六色,现象奇特,中性词(不能用来形容人)。
可用:斑驳陆离。
D举重若轻:举很重的东西也和举轻东西一样轻松。
比喻做很难的事都很容易。
举轻若重:举轻的东西也象举重东西一样稳重,比喻做简单的事也很认真,或做简单的事也能体现出重要的意义。
两个词都用错了。
)3、D(A。
逻辑错误。
应为“防范、猜疑与裁抑”。
B语序不当。
“一个非常严重的问题”C偷换主语。
应为王川所作的《狂石鲁》)4、D二、(9分,每小题3分)5、B6、C(A 应为“哺乳动物”B“各个神经元”应为“彼此临近的”D“FGF22 在失活的小鼠脑内”应为“在FGF22失活的小鼠脑内”)7、C(A“那些违禁药品也就可以放心使用了”错。
B“在其它地方神经元之间突触的形成中也起着重要作用”没有依据。
D原文是“是可能非常有用的”。
)B 卷一、(12分每小题3分)1、B (A 离经叛道肺腑之言C步履维艰寻章摘句物极必反D叶xié集腋成裘)2、D(A。
逻辑错误。
应为“防范、猜疑与裁抑”。
B 语序不当。
“一个非常严重的问题”C偷换主语。
应为王川所作的《狂石鲁》)3、B (心心相印:彼此的心意不用说出,就可以互相了解。
形容彼此思想感情完全一致。
A老气横秋:形容老练而自负的神态。
现形容自高自大,摆老资格。
也形容缺乏朝气。
C光怪陆离:形容奇形怪状,五颜六色,现象奇特,中性词(不能用来形容人)。
可用:斑驳陆离。
D举重若轻:举很重的东西也和举轻东西一样轻松。
比喻做很难的事都很容易。
举轻若重:举轻的东西也象举重东西一样稳重,比喻做简单的事也很认真,或做简单的事也能体现出重要的意义。
河北省保定市2010届高三第一次模拟考试(文综B卷)扫描版

2010年高三文科综合历史试题参考答案及评分标准A卷选择题答案12.B13.B14.A15.C16.D17.D18.C19.C20.A21.C22.D23.DB卷选择题答案12.B13.A 14.B 15.D 16.D17.C 18.C19.C20.D 21.D 22.A 23.C37.(32分)(1)不会取得外交成果。
(2分)它没有看清资本主义国家侵略中国的本质。
(2 分)也没有看到当时是以实力为基础的弱肉强食、强权外交下的国际秩序。
(2分)(2)材料一中表现出保守懦弱,(2分)五四运动中中国人民在积极勇敢的斗争中维护国家利益。
(2分)开辟了中国人民冲破帝国主义列强控制,独立决定自己命运的先例。
(2 分)(注:答外交史上的首次胜利不得分)(3)凡尔赛华盛顿体系建立过程中(或答一次大战前后),中国开始参与国际事务,国际地位开始回升(2分)例:中国参与巴黎和会和华盛顿会议,中国收回日本夺取的山东的权利等等。
(2分,举一例即可。
)雅尔塔体系形成过程中(或答二次世界大战及结束后),中国获得了大国地位,国际地位有了很大提高。
(2 分)例:中国废除了列强治外法权等特权,中国与美英苏一起领衔签署了《联合国家宣言》,《开罗宣言》签订后中国的领土完整得到了庄严的国际保证,1945 年中国成为联合国安全理事会常任理事国之一等等。
(2 分,举一例即可。
)两极格局结束以后,中国国际地位进一步提高和影响进一步扩大。
(2 分)例:在许多全球热点问题上,中国发挥着重要的作用;中国已经成为国际体系的重要成员;中国同许多第三世界国家建立了正式外交关系;中国同周边国家实现了关系正常化。
(2 分,举一例即可。
)相同原因:中国承担国际责任和义务,为国际事务做出了贡献;中国实力的增长;中国人民与政府的争取努力;国际格局变动与国际势力重新组合提供的机遇。
(8 分)39.(历史部分20分)(1)相同点:国家储备可以帮助国家度过灾荒之年。
(2 分)不同点:唐太宗认为过多设仓库会助长统治者奢侈之风,有害国家。
保定市小学六年级数学上学期全真模拟考试试题 附解析

乡镇(街道) 学校 班级 姓名 学号 ………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…保定市小学六年级数学上学期全真模拟考试试题 附解析题 号 填空题 选择题 判断题 计算题 综合题 应用题 总分得 分考试须知:1、考试时间:100分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
3、请在试卷指定位置作答,在试卷密封线外作答无效,不予评分。
一、填空题(共10小题,每题2分,共计20分)1、小明和爸爸从家走到学校,小明用了10分钟,爸爸用了8分钟,小明和爸爸的速度比是( )。
2、0.5和( )互为倒数,( )的倒数是它本身。
3、等腰三角形的其中两个角的比2:5,则其顶角可能是( )或( )。
4、下图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子中,能倒满________杯。
5、一副张数齐全的扑克牌是54张,从一副扑克牌(没有大小王)中任意抽取一张,抽红桃的可能性是( ),抽到10的可能性是( ),抽到黑桃2的可能性是( )。
6、一个圆柱与一个圆锥体积相等,底面积也相等。
已知圆柱的高是12厘米,圆锥的高是( )。
7、在一个长是7分米,宽是4分米的长方形纸板上剪下一个最大的圆,这个圆的面积是( )平方分米。
8、张师傅生产了200个零件,其中有两个零件不合格,张师傅生产的零件合格率为( )。
9、 0.4:0.25化简比是( ),比值是( )。
10、甲数是乙数的1.2倍,乙数和甲数的比是( )。
二、选择题(共10小题,每题1.5分,共计15分)1、一个三角形最小的锐角是50度,这个三角形一定是( )三角形。
A 、钝角B 、直角C 、锐角 2、把35%的“%”去掉,原数就( )。
A .扩大100倍B .缩小100倍C .大小不变3、一个两位数的十位数字是8,个位数字是α,表示这个两位数的式子是( )。
河北省邯郸市2010年高三数学第一次模拟考试(理)(2010邯郸一模)人教版

2010年邯郸市高三第一次模拟考试(邯郸一模)理科数学 2010.3说明:1. 本试卷共4页,包括三道大题,22道小题,共150分。
其中第一道大题为选择题。
2. 所有答案请在答题卡上作答,在本试卷和草稿纸上作答无效。
答题前请仔细阅读答题卡上的“注意事项”,按照“注意事项”的规定答题。
3. 做选择题时,如需改动,请用橡皮将原选涂答案擦干净,再选涂其他答案。
4. 考试结束后,请将本试卷和答题卡一并交回。
参考公式: 如果事件A B ,互斥,那么球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B ⋅=⋅球的体积公式如果事件A 在一次试验中发生的概率是P ,那么34π3V R =n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径()(1)(01,2)k kn k n n P k C P P k n -=-=,,,一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选 项中,只有一项是符合题目要求的.1.已知集合{|lg },{|lg },M x y x N y y x ====集合 则有A .M=NB .Φ=)(NC M R C .Φ=)(M C N RD .M N ⊆ 2.已知,a b 是两个单位向量,命题:“(2)+⊥a b b ”是命题:“,a b 的夹角等于23π”成立的 A .充分不必要条件 B.必要不充分条件 C.充要条件 D.非充分且非必要条件3.x →=A .0B .2C .3D .44.设随机变量ξ服从标准正态分布(01)N ,,已知( 1.96)0.025Φ-=,则(|| 1.96)P ξ<= A .0.025B .0.050C .0.950D .0.9755.点P 是直线:10l x y -+=上的动点,过P 作圆C:22430x y x +-+=的切线,则切线长的最小值是A .142 B.423C.22D.2 6.某家电制造集团为尽快完成家电下乡运输任务,提出四种运输方案.据预测,这四种方案均能在规定时间T 内完成预期的运输任务0Q ,各种方案的运输总量Q 与时间t 的函数关系如下图所示,在这四种方案中,运输效率(单位时间的运输量)逐步提高的是A B C D 7.设ΔABC 的内角A 、B 、C 所对的边长分别是a 、b 、c ,且111,,a b c成等差数列,则B 是 A .锐角 B .直角 C.钝角 D .锐角,直角,钝角都有可能8.函数()f x 对于任意实数x 均满足条件1(2)()f x f x +=,若(1)5f =-,则()5f f ⎡⎤⎣⎦等于 A .2B. 5C. -5D. 15-9.测体温是预防甲流感的有效措施.某学校医务室欲将23支相同的温度计分发到高三年级10个班中,要求分发到每个班的温度计不少于2支,则不同的分发方法共有 A . 120种 B. 175种 C. 220种 D .820种10.如图,设A 、B 、C 、D 为球O 上四点,若AB 、AC 、AD 两两互相垂直,且6AB AC ==2AD =,则直线DO 和平面ABC 所成的角等于 A .6π B .3π C .4π D .2π11.已知函数()sin()(0,0)f x x ωϕωϕπ=+>≤≤是R 上的偶函数,其图像关于点3(,0)4M π对称,且在区间[]0,π上是单调函数,则ωϕ+=A .223π+B .22π+C . 322π+D .1023π+12.已知双曲线C:22221(0,0)x y a b a b-=>>的左、右焦点分别是1F 、2F ,一条渐近线方程为x y =,抛物线28y x =的焦点与双曲线C 的右焦点重合,点),3(0y P 在双曲线上.则1PF ·2PF =A. 4B. 0C. -1D.-2二.填空题:本大题共4小题,每小题5分,共20分.13.函数()5432510105()f x x x x x x x R =++++∈的反函数()1f x -=__________ .14.若x 、y 满足条件11y x x y y ≤⎧⎪+≤⎨⎪≥-⎩, 则22(2)(1)z x y =-+-的最小值为__________.15.若01,01,01,a b c <≤<≤<≤则a b c abc ++-的最大值为__________.16.依次写出数11=a ,2a ,3a ,…,n a ,…,法则如下:如果2-n a 为自然数且未写出过,则写21-=+n n a a ,否则就写31+=+n n a a ,那么=6a .三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分) 已知33sin cos y θθ=+, sin cos x θθ=+, (Ⅰ)把y 表示为x 的函数()y f x =并写出定义域; (Ⅱ)求()y f x =的最值. 18.(本小题满分12分)某公司客服中心有四部咨询电话,某一时刻每部电话能否被接通是相互独立的.已知每部电话响第一声时被接通的概率是0.1,响第二声时被接通的概率是0.3,响第三声时被接通的概率是0.4,响第四声时被接通的概率是0.1.假设有ξ部电话在响四声内能被接通. (Ⅰ)求四部电话至少有一部在响四声内能被接通的概率; (Ⅱ) 求随机变量ξ的分布列及期望.19.(本小题满分12分)如图,在三棱锥P ABC -中,已知,PA AB PC BC ⊥⊥,AC PC ==PA =,PB =,D F 分别是,PB AC 的中点.(Ⅰ)求证:直线DF ⊥平面ABC ; (Ⅱ)求二面角C PA B --的大小.20.(本小题满分12分) 函数(1)()ln (0,)a x f x x x a R x-=->∈. (Ⅰ)求()f x 的单调区间; (Ⅱ) 求证:当12x <<时,不等式111ln 12x x -<-恒成立. 21.(本小题满分12分)已知椭圆E :22221(0)x y a b a b+=>>的右焦点为F , 过原点和x 轴不重合的直线与椭圆E 相交于,A B 两点. 4AF BF +=,sin sin sin AFB ABF BAF ∠∠+∠的最小值为12.(Ⅰ)求椭圆E 的方程;(Ⅱ) 若直线:l y kx m =+与椭圆E 交于,M N ,以线段MN 为直径的圆过E 的右顶点,求证直线l 过定点.22.(本小题满分12分)数列{a n }的前n 项和为n n S npa np n =-+(n ∈N * ,p 为常数),且12a a ≠. (Ⅰ)求p 的值;(Ⅱ) 求证:数列{a n }是等差数列;(III )将数列{a n }的前n 项随机打乱顺序得到数列{b n }的前n 项, 试比较21nii T a==∑和1ni i i S a b ==∑的大小.2010年邯郸市高三第一次模拟考试 理科数学参考答案 审核:王思亮 校对:韩卓艳1-5 BCBCA 6-10 BADCA 11-12 A B13.()11()f x x R -∈ 14.2 15. 2 16 .617. 解:(Ⅰ)22(sin cos )(sin cos sin cos )y θθθθθθ=++-2(sin cos )1(sin cos )[1]2θθθθ+-=+-23131222x x x x ⎛⎫-=-=-+ ⎪⎝⎭所以33()22x f x x =-+ …………………………………………………………………………3分由sin cos )4x πθθθ=+=+ x ∴≤≤所以函数的定义域为⎡⎣………………………………………………………………5分 (Ⅱ)/2333()(1)(1)222f x x x x =-+=--+ (7)()f x ∴在)(1-上单调递减,在)(1,1-上单调递增,在(上单调递减,((1)1f f =<=, (1)1f f -=-<=, ∴()y f x =的最大值为1,()y f x =的最小值-1………………………………10分18. 解:记事件“每部电话响铃第i 声后能被接通”为i A ,事件“一部电话能被接通”为A ,则P(A)=1234()()()()()0.10.30.40.10.9p A p A p A p A p A =+++=+++=………4分 (Ⅰ)四部电话在响四声内都未被接通的概率为44(10.9)0.10.0001-==,…………6分故四部电话至少有一部在响四声内能被接通的概率为410.10.9999-=…………8分(Ⅱ)电话在响前四声内能被接通的数ξ服从于二项分布即(4,0.9)B ξξ的所有可能取值为0,1,2,3,4.即:4(0)(10.9)p ξ==-,134(1)0.9(10.9)p C ξ==⋅-, 2224(2)0.9(10.9)p C ξ==⋅-;334(3)0.9(10.9)p C ξ==⋅-, 4404(4)0.9(10.9)p C ξ==⋅-,故ξ的分布列为…………………………………………………………………10分∴40.9 3.6E ξ=⨯=……………………………………………………12分19.解:(Ⅰ)取,AB BC 的中点,E G ,连接,,,DE EF DG FG . 则//,//,//FG AB EF BC DE PAPA AB DE AB⊥∴⊥由勾股定理可得2AB =,1BC =.又AC =222AC AB BC ∴=+AB BC ∴⊥ …………………………2分EF AB ∴⊥∴AB ⊥平面DEFDF AB ∴⊥ ………………………4分同理DF BC ⊥,又,AB BC 相交于B 点,∴ 直线DF ⊥平面ABC ……………6分EABC(Ⅱ)法一:取PA 的中点Q ,连接,QD DC ,QC ∵,PC CA PQ QA == ∴CQ PA ⊥ ∵//AB QD ,AB PA ⊥ ∴DQ PA ⊥∴DQC ∠为二面角C PA B --的平面角. …………8分在Rt PCB ∆中,CD =,在PAB ∆中,112QD AB ==,QAC ∆在中,CQ == 所以,在DQC ∆中,由余弦定理,可得cos DQC ∠=∴二面角C—PA—B的大小为arccos3…………………………12分法二:以F 为坐标原点,直线FE 、FG 、FD 分别为x 、y 、z 轴,建立空间直角坐标系,如图示.则F(0,0,0),E(12,0,0),G(0,1,0), 易知D(0,0,12). B(12,1,0),P(-12,-1,1)A(12,-1,0) C(-12,1,0),取AP 的中点Q, 则易求得Q(0,-1,12)(0,2,0)AB =,11(,2,)22QC =--,(1,0,1)PA =-0AB PA ⋅=,0QC PA ⋅=,∴二面角C—PA—B的平面角的余弦值为2cos , 3AB QCQC AB AB QC⋅==故二面角C—PA—B的大小为arccos 3…………………………12分 20.(Ⅰ)/221()(0)a x af x x x x x-=-=>,………………………………………………………2分YABC当0a ≤时,/()0f x >,()f x 在(0,)+∞上单调递增; (3)分当0a >时,(0,)x a ∈时,/()0f x <,()f x 在(0,)a 上单调递减; (4)分(,)x a ∈+∞时,/()0f x >,()f x 在(,)a +∞上单调递增. (5)分综上所述,当0a ≤时,()f x 的单调递增区间为(0,)+∞; 当0a >时,()f x 的单调递减区间为(0,)a()f x 的单调递增区间为(,)a +∞,. ……………………………………………………6分 (Ⅱ)证明:∵12x <<,∴111(1)ln 2(1)0ln 12x x x x x -<⇔+-->-. 令()(1)ln 2(1)F x x x x =+--,∴/1()ln 2x F x x x +=+-1ln 1x x=+-, (9)分由(Ⅰ)可知,当1a =时,1()ln 1f x x x=+-在(1,)x ∈+∞上单调递增. ∴当[1,2]x ∈时,min ()(1)0f x f ==,∴()(1)0f x f ≥=,即1ln 10x x+-≥.∴/()0F x ≥,∴()F x 在(1,2)上单调递增,又()F x 在1x =处连续, ∴()(1)0F x F >=,∴(1)ln 2(1)0x x x +-->. ∴111(12)ln 12x x x -<<<-恒成立. ……………12分 21解:(Ⅰ)由椭圆的对称性设1111(,),(,),A x y B x y --易知(,0),F c 因为2AF BF a +===所以24,2a a ==,……………………………………………………………………2分 在三角形AFB 中,由正弦定理得sin sin sin AFBABF BAF ∠∠+∠AB AF BF =+4AB===∵0≤221x a ≤∴sin 1sin sin 22AFB b ABF BAF ∠≥=∠+∠,所以1b =……………………4分∴所求的椭圆的方程为2214x y +=……………………………………………………6分 (Ⅱ) 由22,1,4y kx m x y =+⎧⎪⎨+=⎪⎩得222(14)8440k x kmx m +++-=,因为有两个交点,所以222(8)4(14)(44)0km k m ∆=-+->,即22140m k --<①设交点1122(,),(,)M x y N x y则2121222844,1414km m x x x x k k -+=-=++,因为以线段MN 为直径的圆过E 的右顶点()2,0,所以1212(2)(2)0x x y y --+=…………………………………………………………8分 即1212(2)(2)()()0x x kx m kx m --+++=,整理得:22516120m km k ++=,解得2,m k =-或65m k =-, ……………………10分当2,m k =-代入①中,可知满足条件,此时直线方程为(2)y k x =-,所以,直线恒过定点(2,0);……………………………………………………………11分 当65m k =-,代入①中,可知满足条件,此时 直线6:()5l y k x =-恒过定点6,05⎛⎫ ⎪⎝⎭.综上所述,直线l 恒过定点(2,0)或6,05⎛⎫ ⎪⎝⎭……………………………………………………12分22.解:(Ⅰ)当n =1时,111a pa p =-+即1(1)(1)0p a --=,所以1p =或11a =当n =2时,122222a a pa p +=-+若p =1,则12222222a a pa a +=-+=,得a 1=a 2与已知a 1≠a 2矛盾,故p ≠1.所以a 1=1又a 1≠a 221a ∴≠由122222a a pa p +=-+知221222a pa p +=-+,故12p =. ……………………4分(Ⅱ)证法1:由n n S npa np n =-+知2(1)n n S n a =+ 当2n ≥时111222(1)(1)(1)(1)1n n n n n n n a S S n a n a na n a ---=-=+--+=--+ 1(2)(1)1n n n a n a --=--…………………………① 1(1)1n n n a na +-=- …………………………②②-①整理得11(1)(2)0n n n n a a a +---+= 所以1120n n n a a a +--+=11n n n n a a a a +--=-(2n ≥,n N *∈)所以数列{a n }是等差数列。
河北省保定市2011届九年级上学期期末调研考试数学试题

保定市2010—2011学年第一学期期末调研考试九年级数学试题(人教版) (命题人:李秀峰 审题人:徐建乐) 本试卷满分为120分,考试时间为120分钟一、选择题(本大题共12个小题;每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)1、下列二次根式中,属于最简二次根式的是( )A. 8B. y x 2C. 50.D.22y x + 2、方程02=+x x 的根为( )A. 1-=xB. 0=xC. 01=x ,12-=xD. 01=x ,12=x3、已知抛物线122+-=x x y 与x 轴的一个交点为(m ,0)则代数式201022+-m m 的值为( )A. 2008B. 2009C. 2010D. 2011 4、不解方程,判别方程0233222=+-x x 的根的情况( ) A. 有两个相等的实数根 B. 有两个不相等的实数根 C. 没有实数根 D. 不能确定5、若二次函数322-++=a bx ax y (a 、b 为常数)的图象如图所示,则a 的值为( )A. 3-B. 3-C. 3D. 3±6、已知⊙O 1和⊙O 2的半径分别为1和4,如果两圆的位置关系为相交,那么圆心距O 1O 2的取值范围在数轴上表示正确的是( )7、如图,A 、B 、C 、D 四点都在⊙O 上,若OC ⊥AB ,∠AOC =60°,则圆周角∠D 的度数为()A. 15°B. 30°C. 45°D. 60°8、如图,晚饭后,小明到广场去散步,他站在广场中路灯杆的左侧距灯杆2米处,若小明的身高为1.6米,影长为1米,则路灯距离地面的高度为( ) A. 2.4米 B. 3.2米 C. 4米 D. 4.8米9、已知二次函数c bx ax y++=2的图象如图所示,则下列结论正确的是( )A. 0>aB. 0<cC. 042<-ac bD. 0>++c b a10、一扇形的半径为24cm ,若此扇形围成的圆锥的底面半径为10cm ,那么这个扇形的面积是( )A. 2120cm πB. 2240cm πC. 2260cm πD. 2480cm π11、如图,有四张背面相同的纸牌A 、B 、C 、D ,其正面分别画有四个不同的图形,小明将概率是( ) A.41 B. 21 C. 43D. 1 12、如图,直线AB 、CD 相交于点O ,∠AOC =30°,半径为1的⊙P 的圆心P 在射线OA 上,且与点O 的距离AB C D11题图)A. B. C. D.(第7题图)(第8题图)为4cm ,如果⊙P 以1cm/s 的速度沿由A 向B 的方向移动,那么⊙P 与直线CD 相切时的时刻为( )A. 2秒B. 6秒C. 2秒或6秒D. 4秒或6秒二、填空题(每小题3分,共18分.把答案写在 题中横线上) 13、函数42-+=x x y 中,自变量x 的取值范围是________________.14、已知二次函数m x x y ++-=22的部分图象如图所示,则关于x 的一元二次方程022=++-m x x 的解为_____________________. 15、从n 个苹果和3个雪梨中,任选1个,若选中苹果的概率是21,则n 的值是__________. 16、某市计划在今后两年将使全市的环保车(液化石油燃料汽车)由目前的325辆增加到637辆,若设这种环保车平均每年的增长率为x ,则列出的方程为__________________. 17、如图,一宽为2cm 的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm )则该圆的半径为__________cm. 18、如图,点D 是线段AB 的中点,AF ∥BC ,CG :GA =3:1,BC =6,则AF =_________.三、解答题(本大题共8个小题;共78分. 解答应写出文字说明、证明过程或演算步骤.)19、计算(本小题满分8分)()21223273-+÷17题图)(第18题图)AFDG20、(本小题满分8分)图中的小方格都是边长为1的正方形,△ABC 的的顶点和O 点都在正方形的顶点上. (1)以点O 为位似中心,在方格图中作出△ABC 的位似图形△A 1B 1C 1,使△ABC 与△A 1B 1C 1的位似比为1:2;(2)△A 1B 1C 1绕点B 1顺时针旋转90°,画出旋转后得到的△A 2B 1C 2,并求点A 1在旋转过程中经过路线的长度.(结果保留π)A C∙O(第20题图)21、(本小题满分9分)2010年上海世界博览会以“城市,让生活更美好”为主题,吸引了世界各地众多游客前来参观.某星期天小霞随爸爸、妈妈一起前去参观,但由于仅有一天的时间,小霞一家决定上午在中国馆(A )、日本馆(B )、法国馆(C )中选择一个参观;下午在埃及馆(D )、韩国馆(E )中选择一个参观.请你用画树形图或列表的方法,求出小霞一家这一天上午和下午恰好都参观亚洲国家展馆的概率.(用字母代替馆名)22、(本小题满分9分)某零售商在2010年广州亚运会期间购进一批“亚运纪念T 恤”,在销售中发现:该批T 恤平均每天可售出20件,每件盈利40元.该零售商为了扩大销售量,加快资金周转增加盈利,决定采取适当的降价措施.已知每件T 恤每降价1元,那么平均每天就可多售出2件.要想通过销售这种T 恤平均每天盈利1200元,同时还要照顾到消费者的利益,每件T 恤应降价多少元?23、(本小题满分10分)如图,用一段长为36m 的篱笆围成一个一边靠墙的矩形菜园,墙长为18m ,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?24、(本小题满分10分)如图,已知抛物线32-+=bx ax y 的对称轴为直线1=x ,抛物线交x 轴于A 、B 两点,交y 轴于C 点,其中B 点的坐标为(3,0).(1)直接写出A 点的坐标;(2)求二次函数32-+=bx ax y 的解析式,并用配方法确定抛物线的顶点坐标; (3)求△BOC 的面积.(第24题图)25、(本小题满分12分)O 是边长为a 的正多边形的中心,将一块半径足够长,圆心角为α的扇形纸板的圆心放在O 点处,并将纸板绕O 点旋转.(1)若正多边形为正三角形,扇形的圆心角α=120°,请你通过观察或测量,填空:①如图1,正三角形ABC 的边被扇形纸板覆盖部分的总长度为_______________; ②如图2,正三角形ABC 的边被扇形纸板覆盖部分的总长度为_______________;(2)若正多边形为正方形,扇形的圆心角α=90°时,①如图3,正方形ABCD 的边被扇形纸板覆盖部分的总长度为_______________; ②如图4,正方形ABCD 的边被扇形纸板覆盖部分的总长度为多少?并给予证明;图1图3图4(3)若正多边形为正五边形,如图5,当扇形纸板的圆心角α为____________时,正五边形的边被扇形纸板覆盖部分的总长度仍为定值a .(4)将一块半径足够长的扇形纸板的圆心放在边长为a 的正n 边形的中心O 点处,并将纸板绕O 点旋转. 当扇形纸板的圆心角为____________时,正n 边形的边被扇形纸板覆盖部分的总长度为定值a .26、(本小题满分12分)如图,直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,已知AD =AB =3,BC =4,动点P 从B 点出发,沿线段BC 向点C 作匀速运动;动点Q 从点D 出发,沿线段DA 向点A 做匀速运动.过Q 点垂直于AD 的射线交AC 于点M ,交BC 于点N .P 、Q 两点同时出发,速度都为每秒1个单位长度.当Q 点运动到A 点,P 、Q 两点同时停止运动.设运动时间为t 秒. (1)当t 为何值时,四边形PCDQ 构成平行四边形? (2)试用含t 的代数式分别表示NC 与MN ;(3)若设△PMC 的面积为S ,试求出S 关于t 的函数关系式.D图5(第26题图)。
保定10-11第一学期期末九年级数学试题答案

保定市2010—2011学年度第一学期期末考试九年级数学参考答案和评分标准说明:一、如果考生的解法与下面提供的参考解法不同,凡正确的,一律记满分;若某一步出现错误,则可参照评分标准给分;其它解法参考此标准给分。
二、评阅试卷,不要因解答中出现错误而中断对该题的评阅.当解答中某一步出现错误,影响了后继部分,但该步以后的解答未改变此题的内容和难度,在未发生新错误前,可视影响的程度决定后面部分的记分,这时原则上不应超过后面应给分数之半;明显的笔误,可酌情少扣;如果严重概念性错误,就不记分.在一道题解答过程中,对发生第二次错误起的部分,不能得分.三、涉及计算问题,允许合理省略非关键性步骤.四、以下解答中右端所注分数,表示考生正确做到这一步应得的累加分数.一、本大题共12个小题,每小题2分,共24分.13、x ≥-2且x ≠4 14、x 1=3,x 2= -1 15、3 16、637)x 13252=+( 17、41318、3 三、解答题(本大题共8个小题;共78分) 19.计算(本小题满分8分) 解:原式=122232273+-+⨯----------------------------------------(3分) =122229+-+----------------------------------------------(6分) = 327+ -----------------------------------------------------(8分)20.(本小题满分8分)(1)作图如右图----------------------------(3分)(2)作图如右图 ---------------------------(6分) ∵5242A B 2211=+=---------------(7分)∴1A 在旋转过程中经过路线的长度为:ππ55218090=⨯ ----------------(8分) 21.(本小题满分9分)(1)-----(6分)(2)由上表可知小霞一家人共有6种参观方式,其中上午和下午恰好都参观亚洲国家展馆的可能性有2种,所以小霞一家人上午和下午恰好都参观亚洲国家展馆的概率为:P=3162=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年保定市中考数学模拟试题一、选择题(共8道小题,每小题4分,共32分) 1.-3的立方是( )A .-27B .-9C .9D .272.据统计,2008中国某小商品城市场全年成交额约为348.4亿元.近似数348.4亿元的有效数字的个数是( )A .6个B . 5个C .4个D .11个 3.正方形网格中,AOB ∠如图放置,则cos AOB ∠的值为( ) A .255B .2C .12D .554.已知甲、乙两组数据的平均数分别是80x =甲,90x =乙,方差分别是210S =甲,25S =乙,比较这两组数据,下列说法正确的是( )A .乙组数据的波动较小B .乙组数据较好C .甲组数据的极差较大D .甲组数据较好5.某等腰三角形的两条边长分别为3cm 和6cm ,则它的周长为( ) A .9cm B .12cm C .15cm D .12cm 或15cm 6.下列四个三角形,与左图中的三角形相似的是( )7. 函数6y x =-与函数()40y x x=>的图象交于A 、B 两点,设点A 的坐标为()11,x y ,则边长分别为1x 、1y 的矩形面积和周长分别为( )A. 4,12B. 4,6C. 8,12D. 8,6 8.如图,在Rt △ABC 中,AB AC =,D 、E 是斜边BC 上两点,且∠DAE =45°,将△ADC 绕点A 顺时针旋转90︒后,得到△AFB ,连接EF ,下列结论: ①△AED ≌△AEF ; ②△ABE ∽△A C D ;③BE DC DE +=; ④222BE DC DE +=其中一定正确的是 A .②④ B .①③C .②③D .①④(第8题图)AB CD EF(第6题)A .B .C .D .ABO (第3题 )二、填空题(共4道小题,每小题4分,共16分) 9. 分解因式3244y y y -+= . 10. 函数13y x =-中,自变量x 的取值范围是 . 11. 一个口袋里有4个白球,5个红球,6个黄球,每个球除颜色外都相同,搅匀后随机从袋中摸出一个球,这个球是白球的概率是 12. 如图,OA=OB ,A 点坐标是(2,0)-,OB 与x 轴正方向夹角为45︒,则B 点坐标是 . AB 与y 轴交于点C ,若以OC 为轴,将OBC ∆沿OC 翻折,B 点落在第二象限内B '处,则BB '的长度为 .三、解答题(共13道小题,共 72 分)13.(本小题满分5分) 计算: ︒+-+--3tan60)4(27)21(02π.14.(本小题满分5分)解方程22011x x x -=+-.(第12题图)小明站在A 处放风筝,风筝飞到C 处时的线长为20米,这时测得∠CBD=60°,若牵引底端B 离地面1.5米,求此时风筝离地面高度。
(计算结果精确到0.1米,3 1.732≈).16(本小题满分5分)对于任何实数,我们规定符号c a db 的意义是:c a db =bc ad -.按照这个规定请你计算:当0132=+-x x 时,21-+x x 13-x x的值.第15题图如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.ABO △的三个顶点A 、B 、O 都在格点上.(1)画出ABO △绕点O 逆时针旋转90 后得到的三角形; (2)求ABO △在上述旋转过程中所扫过的面积.18.(本小题满分5分)如图,AB 为半圆O 的直径,点C 在半圆O 上,过点O 作BC 的平行线交AC 于点E ,交过点A 的直线于点D ,且BAC D ∠=∠. (1)求证:AD 是半圆O 的切线; (2)若2=BC ,2=CE ,求AD 的长.(第17题)A BOOBACED如图,在△ABC中,∠CAB、∠ABC的平分线交于点D,DE∥AC交BC于点E,DF∥BC交AC于点F.求证:四边形DECF为菱形.20.(本题满分5分)某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成下两幅统计图(如图),请你结合图中所给信息解答下列问题:(说明:A级:90分—100分;B级:75分—89分;C级:60分—74分;D级:60分以下)(1)D级学生的人数占全班人数的百分比为;(2)扇形统计图中C级所在扇形圆心角度数为;(3)该班学生体育测试成绩的中位数落在等级内;(4)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人。
25201510 5 0 1325102人数A B C D 等级DCA26%B50%第20题图1 第20题图2一辆经营长途运输的货车在高速公路的A 处加满油后匀速行驶,下表记录的是货车一次加满油后油箱内余油量y (升)与行驶时间x (时)之间的关系:行驶时间x (时) 0 1 2 2.5余油量y (升)100 80 60 50(1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y 与x 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)(2)按照(1)中的变化规律,货车从A 处出发行驶4.2小时到达B 处,求此时油箱内余油多少升?22.(本小题满分5分)定义[]p q ,为一次函数y px q =+的特征数.(1)若特征数是[]22k -,的一次函数为正比例函数,求k 的值;(2)设点A B ,分别为抛物线()(2)y x m x =+-与x 轴、y 轴的交点,其中0m >,且OAB △的面积为4,O 为坐标原点,求图象过A 、B 两点的一次函数的特征数.已知二次函数2441y ax ax a =++-的图象是C 1.(1)求C 1关于点R (1,0)中心对称的图象C 2的函数解析式;(2)在(1)的条件下,设抛物线C 1、C 2与y 轴的交点分别为A 、B ,当AB=18时,求a 的值.24.(本题满分7分)(1)已知:如图1,ABC ∆是⊙O 的内接正三角形,点P 为弧BC 上一动点,求证:PA PB PC =+ (2) 如图2,四边形ABCD 是⊙O 的内接正方形,点P 为弧BC 上一动点,求证: 2PA PC PB =+ (3) 如图3,六边形ABCDEF 是⊙O 的内接正六边形,点P 为弧BC 上一动点,请探究PA PB PC 、、三者之间有何数量关系,并给予证明.OCABPPODAB COPFEDCBA图1 图2图3如图,菱形OABC 的顶点O 在坐标原点,顶点B 在x 轴的正半轴上,OA 边在直线x y 33=上,AB 边在直线233+-=x y 上。
(1)直接写出O 、A 、B 、C 的坐标;(2)在OB 上有一动点P ,以O 为圆心,OP 为半径画弧MN ,分别交边OA 、OC 于 M 、N (M 、N 可以与A 、C 重合),作⊙Q 与边AB 、BC ,弧MN 都相切,⊙Q 分别与边AB 、BC 相切于点D 、E ,设⊙Q 的半径为r ,OP 的长为y ,求y 与r 之间的函数关系式,并写出自变量r 的取值范围;(3)以O 为圆心、OA 为半径做扇形OAC ,请问在菱形OABC 中,除去扇形OAC 后剩余部分内,是否可以截下一个圆,使得它与扇形OAC 刚好围成一个圆锥. 若可以,求出这个圆的面积,若不可以,说明理由。
(第25题图)DE参考答案及评分标准一、选择题(共8道小题,每小题4分,共32分)题号 12345 6 7 8 答案A C D AC BA D二、填空题(共4道小题,每小题4分,共16分)题号 910 11 12答案2(2)y y -3x ≠4151(,)1;2三、解答题(共13道小题,共72分)13.解:原式=331334++- ……………………………………………………………4分=5………………………………………………………………………………… 5分14.解:方程两边同乘(1)(1)x x -+,得2(1)0x x --=. ······································································································· 3分 解这个方程,得2x =. ························································································································ 4分 检验:当2x =时,(1)(1)0x x -+≠.所以2x =是原方程的解. ························································································· 5分 15. 解:在Rt △BCD 中,CD=BC×sin60°=20×3=1032…………………………………3分 又∵DE=AB=1.5∴CE=CD +DE=103 1.517.32 1.518.8+≈+≈(米)答:此时风筝离地面的高度约是18.8米.…………………………………………5分16.解: ………3分…………………5分17. 解:(1)画图正确(如图).…………2分 (2)AOB △所扫过的面积是:AOB OBD S S S =+△扇形290π444π4360=⨯+=+.…………5分 DE (第17题)AB O)2(3)1)(1(1321---+=--+x x x x x x x x .162631222-+-=+--=x x xx x .1121)32.13,013222=-=---=∴-=-∴=+-x x x x x x (原式18.(1)证明:∵AB 为半圆O 的直径,∴ 90=∠BCA又∵BC ∥OD , ∴AC OE ⊥, ∴090=∠+∠DAE D .∵BAC D ∠=∠, ∴90BAC DAE ∠+∠=︒. ∴半径OA ⊥AD 于点A ,∴AD 是半圆O 的切线. …………………2分(2)解:∵在⊙O 中,AC OE ⊥于E , ∴222==CE AC . 在ABC Rt ∆中,322)22(2222=+=+=BC AC AB ,3OA =. …3分∵D BAC ∠=∠,OAD C ∠=∠ ∴DOA ∆∽ABC ∆:∴BC OA AC AD =, ∴2322=AD ∴6=AD ………………………………………………………………………5分19.证法一:连结CD∵ DE ∥AC ,DF ∥BC , ∴ 四边形DECF 为平行四边形,∵∠CAB 、∠ABC 的平分线交于点D ∴点D 是△ABC 的内心, ∴ CD 平分∠ACB ,即∠FCD =∠ECD , ∵DF ∥BC ∴∠FDC =∠ECD ,∴ ∠FCD =∠FDC ∴ FC =FD , ∴ 平行四边形DECF 为菱形. ············································································· 5分 证法二:过D 分别作DG ⊥AB 于G ,DH ⊥BC 于H ,DI ⊥AC 于I .∵AD 、BD 分别平分∠CAB 、∠ABC , ∴DI =DG ,DG =DH .∴DH =DI . ∵DE ∥AC ,DF ∥BC ,∴四边形DECF 为平行四边形,∴S □DECF =CE ·DH =CF ·DI , ∴CE =CF . ∴平行四边形DECF 为菱形.…………………5分20. (1)4%. …………………………………………………………………………… 1分(2)72︒. ………………………………………………………………………… 2分(3)B 级.……………………………………………………………………………… 3分 (4)由题意可知,A 级和B 级学生的人数和占全班总人数的76%,∴76500⨯%380=. ∴估计这次考试中A 级和B 级的学生共有380人.………………………5分 21.解:(1)设y 与x 之间的关系为一次函数,其函数表达式为y kx b =+…………1分将(0100),,(180),代入上式得,10080b k b =⎧⎨+=⎩ 解得20100k b =-⎧⎨=⎩ F ED C B A HG I FED C B A20100y x ∴=-+ ····························································································· 3分 验证:当2x =时,20210060y =-⨯+=,符合一次函数20100y x ∴=-+; 当 2.5x =时,20 2.510050y =-⨯+=,也符合一次函数20100y x ∴=-+.∴可用一次函数20100y x =-+表示其变化规律,而不用反比例函数、二次函数表示其变化规律y ∴与x 之间的关系是一次函数,其函数表达式为20100y x =-+ ················ 4分(2)当 4.2x =时,由20100y x =-+可得16y =即货车行驶到B 处时油箱内余油16升.……………………………………… 5分22.解:(1) 特征数为[22]k -,的一次函数为22y x k =+-,20k ∴-=,2k ∴=.………………………………………………………………………1分(2) 抛物线与x 轴的交点为12(0)(20)A mA -,,,,与y 轴的交点为(02)B m -,. 若14OBA S =△,则4221=⨯⨯m m ,∴122,2m m ==-(舍); 若24OBA S =△,则42221=⨯⨯m ,∴2m =.综上,2m =.∴抛物线为(2)(2)y x x =+-,它与x 轴的交点为(20)(20)-,,,,与y 轴的交点为(04)-,,∴所求一次函数为24y x =--或24y x =-,∴特征数为[24]--,或[24]-,………………………………………………5分 23. 解:(1)由2(2)1y a x =+-,可知抛物线C 1的顶点为M (-2,-1).由图知点M (-2,-1)关于点R (1,0)中心对称的点为N (4,1),以N (4,1)为顶点,与抛物线C 1关于点R (1,0)中心对称的图像C 2也是抛物线,且C 1与C 2的开口方向相反,故抛物线C 2的函数解析式为()241y a x =--+,即28161y ax ax a =-+-+. …………………………………………………3分(2)令x =0,得抛物线C 1、C 2与y 轴的交点A 、B 的纵坐标分别为41a -和161a -+.∴220)116()14(-=+---=a a a AB . ∴20218a -=.CO 4321EPBA321ECBADOPOQ ABC DEFP当101≥a 时,有18220=-a ,得1=a ; 当a <101时,有18202=-a ,得45a =-. ……………………………………7分24. (1)证明:延长BP 至E ,使PE PC =,连结CE.1260,3460∠=∠=︒∠=∠=︒ 60,CPE PCE ∴∠=︒∴∆是等边三角形.,360,CE PC E ∴=∠=∠=︒又 EBC PAC ∠=∠,,APC BEC ∆≅∆∴ PC PB BE PA +==∴.…………2分(2) 证明:过点B 作BE PB ⊥交PA 于E ,122390,13∠+∠=∠+∠=︒∴∠=∠ ,又 ︒=∠45APB ,,2,BP BE PE PB ∴=∴=又,,AB BC ABE CBP PC AE =∴∆∆∴= ≌.2PA AE PE PC PB ∴=+=+ …………………………………………………4分(3)答:3PA PC PB =+证明:在AP 上截取AQ PC =,连结BQ ,,BAP BCP AB BC ∠=∠= , ,CBP ABQ ∆≅∆∴BP BQ =∴.又,30︒=∠APB PB PQ 3=∴,3PA PQ AQ PB PC ∴=+=+ …………………………………………………7分25.解:(1))0,0(O ,)1,3(A ,)0,32(B ,)1,3(-C ;………………………… 2分 (2)连结QD 、QE ,则QD ⊥AB ,QE ⊥BC.∵QD=QE ,∴点Q 在ABC ∠的平分线上.又∵OABC 是菱形,∴点Q 在OB 上. ∴⊙Q 与弧MN 相切于点P.在Rt ⊿QDB 中,︒=∠30QBD ,∴QB=2QD=2r . ∴323=+r y , r y 332-=∴.其中3323232<≤-r .………………………………………………… 5分 (3)可以. 理由:弧AC 的长为π32. 设截下的⊙G 符合条件,其半径为R ,则ππ322=R .31=∴R . 由(2)知,此时2==y OA ,则⊙Q 的半径232133r -=>, ∴能截下一个圆,使得它与扇形OAC 刚好围成一个圆锥,此圆的面积为ππ912==R S .………………………………………………8分。
