第五章 平均指标和变异指标
统计学基础平均指标和变异指标

统计学基础平均指标和变异指标平均指标和变异指标是统计学中常用的两种指标,用于描述数据分布的中心趋势和离散程度。
在统计分析中,这两个指标的应用非常广泛。
1.平均指标:平均指标是用来表示数据分布的中心位置的指标,常见的平均指标有平均数、中位数和众数。
-平均数:平均数是指一组数据之和除以数据个数,表示了数据的平均水平。
平均数的计算方法是将所有数据相加,然后除以数据个数。
例如,对于一组数据:2,3,5,7,10,平均数的计算方式为(2+3+5+7+10)/5=5.4-中位数:中位数是将数据按照大小顺序排列后位于中间位置的数值,它划分了数据的中间位置。
如果数据个数为奇数,则中位数为排序后的中间值;如果数据个数为偶数,则中位数为排序后中间两个值的平均值。
中位数对于数据的极端值不敏感,适用于数据有异常值的情况,能够更好地表示数据的中心位置。
例如,对于一组奇数个数据:1,3,5,7,9,中位数为5;对于一组偶数个数据:2,4,6,8,中位数为(4+6)/2=5-众数:众数是一组数据中出现次数最多的数值,表示了数据中的高频值。
一个数据集可以有一个或多个众数。
如果一个数据集没有重复值,那么它没有众数。
例如,对于一组数据:1,2,3,4,4,4,5,众数为42.变异指标:变异指标是用来度量数据分布的离散程度,可以用来描述数据的稳定性和可变性。
常见的变异指标有极差、方差和标准差。
-极差:极差是一组数据的最大值和最小值之间的差异,表示了数据的全距。
极差越大,数据的离散程度越大;极差越小,数据的离散程度越小。
例如,对于一组数据:2,3,5,7,10,极差为(10-2)=8-方差:方差是一组数据与其平均数之间偏离程度的平均值的统计量,表示了数据分布的离散程度。
方差的计算公式是每个数值与平均数之差的平方之和除以数据个数。
例如,对于一组数据:2,3,5,7,10,平均数为5.4,方差的计算方式为[(2-5.4)^2+(3-5.4)^2+(5-5.4)^2+(7-5.4)^2+(10-5.4)^2]/5≈7.04-标准差:标准差是方差的平方根,是一个衡量数据分布离散程度的指标。
统计学第五章(变异指标)

峰态及其度量
峰态定义
峰态是指数据分布的尖峭程度或扁平程度。在统计学中,峰态通常通过峰态系数 来度量。
峰态系数
峰态系数是描述数据分布峰态程度的一个统计量,通常表示为K。当K=3时,分 布呈正态分布,峰度适中;当K>3时,分布呈尖峰分布,即比正态分布更尖峭; 当K<3时,分布呈平峰分布,即比正态分布更扁平。
方差
要点一
定义
方差是在概率论和统计方差衡量随机 变量或一组数据时离散程度的度量, 用来度量随机变量和其数学期望(即 均值)之间的偏离程度。
要点二
计算公式
方差s^2=[(x1-x)^2+(x2x)^2+......(xn-x)^2]/n(x为平均数)。
要点三
性质
方差越大,说明随机变量取值越离散; 方差刻画了随机变量的取值对于其数学 期望的离散程度;若X的取值比较集 中,则方差D(X)较小,若X的取值比较 分散,则方差D(X)较大;因此,D (X)是刻画X取值分散程度的一个 量,它是衡量取值分散程度的一个尺 度。
变异系数的计算
01
注意事项
02
当数据集包含极端值时,变异系数可能会受到影响。
03
对于非正态分布的数据,变异系数的解释需谨慎。
变异系数的应用
比较不同数据集的离散程度
通过比较不同数据集的变异系数,可以评估它们 的相对波动程度。
在质量控制中的应用
通过计算产品质量的变异系数,计学第五章变异指
目
CONTENCT
录
• 变异指标概述 • 变异系数 • 极差、四分位差与平均差 • 标准差与方差 • 偏态与峰态的度量 • 变异指标在统计分析中的应用
01
变异指标概述
统计学基础课件 第五章 平均指标和变异指标
第一节 平均指标 第二节 变异指标
第五章 平均指标和变异指标
第一节 平均指标 ❖ 一、平均指标的意义和作用 ❖ 二、平均指标的种类和计算方法 ❖ 三、计算和运用平均指标应注意的问题
第五章 平均指标和变异指标
一、平均指标的意义和作用
❖概念:
又称统计平均数,是用以反映现象一般水平的指标,有静 态平均数和动态平均数之分。本节主要介绍静态平均数。
现资料之间存在一定数学关系,应首先考虑算术平均数 的变形公式 —— 调和平均法。
注: 调和平均法计算平均数时,依据的是加权算术平均法, 但又不能直接使用,须借助于某两个数值相除得到需要的 数值再计算平均数,故调和平均数是算术平均数的变型公 式。
第五章 平均指标和变异指标
数值平均数
❖ (二)调和平均数的计算公式
计算公式
简单式 未分组 加权式 已分组
x
n 1
x
单项式 组距式
m
x
m x
第五章 平均指标和变异指标
数值平均数
【例】某市场上有四种价格的苹果,每公斤分别为4、
5、8、10元,试计算:各买1元钱,平均每公斤多少 钱解?:平均单价:
xH
n
1 x
1 4
1 5
4 1 1
8 10
5.9(元/公斤)
第五章 平均指标和变异指标
数值平均数
【例】某小组5位成员某次考试的成绩分别为60分、88分、
75分、52分、96分,则该小组成员的平均成绩是多少?
解:平均成绩 x x 60 88 75 52 96 74.2(分)
n
5
第五章 平均指标和变异指标
数值平均数
【例】某商品有两种型号,单价分别为2元和3元,已
平均指标与变异指标

第五章平均指标与变异指标教学目的与要求:本章主要介绍了经济统计中广泛应用的一种综合指标,即平均指标。
并在此基础上,详细论述了反映总体特征的另一指标,即标志变异指标。
通过本章的学习和应用能力的训练,重点要求是:1、深刻理解平均指标和变异指标的基本理论和分析方法2、掌握计算平均指标的各种方法及运用原则3、对平均指标进行分析,阐述影响平均指标大小的原因4、明确平均指标与变异指标的区别与联系5、掌握变异指标的计算方法,并能运用标志变异指标说明平均数的代表性基本理论和分析方法。
重点掌握:1、平均制表的分析方法。
2、变异指标的计算意义。
教学方式:用多媒体课件讲练结合。
课时安排:理论4学时,实训2学时第一节平均指标的概念和作用一、平均指标的概念1、定义平均指标又称平均数,它是统计分析中最常用的统计指标之一。
它反映了社会经济现象中某一总体各单位某一数量在一定时间、地点条件下所达到的一般水平,或者反映某一总体、某一指标在不同时间上发展的一般水平。
2、特点第一,同质性,即总体内各单位的性质是相同的。
第二,抽象性,即总体内各同质单位虽然存在数量差异,但在计算平均数时并不考虑这种差异,即把这种差异平均掉了。
第三,代表性,即尽管各总体单位的标志值大小不一,但我们可以用平均数这一指标值来代表所有标志值。
二、平均指标的作用1、可以用来比较同类现象在不同地区、部门、单位(即不同总体)发展的一般水平,用以说明经济发展的高低和工作质量的好坏。
2、可以用来对统一总体某一现象在不同时期上进行比较,以反映该现象的发展趋势或规律。
如对同一地区人均年收入逐年进行比较来反映该地区居民生活水平的发展趋势或规律。
1、可以作为论断事物的一种数量标准。
2、可以用来分析现象之间的依存关系。
3、可以估算和推算其他有关数字三、平均指标的种类平均指标按其性质可分为静态平均数和动态平均数。
静态平均数反映的是同质总体内各单位某一数量标志在一定时间地点条件的一般水平,动态平均数反映的是某一总体某一指标值在不同时间上的一般水平。
平均指标与标志变异指标

G n x1 x2 x3 xn
若资料已分组,加权几何平均数计算公式:
G
f
x x x x f1 f2 f3
权算术平均数。其计算公式为:
n
X i fi
X
i 1 n
fi
i 1
式中: X(i 或X) fi (或f )
——标志值 ——标志值 Xi(或X )出现的次数或权数
n
——组数
n
Xi fi (或 Xf ) ——标志总量
i1
【例】下表资料是经过分组整理的,已知日产量 及工人人数,则加权算术平均数计算如下:
日产量x(件)
15 16 17 18 合计
工人人数f(人) 12 38 40 20 110
总产量xf(件) 180 608 680 360 1828
该企业加工车间生产工人的平均日产量为:
X 1512 1638 17 40 18 20 1828 16.6件
12 38 40 20
110
【例】设某厂职工按日产量分组后所得组距数 列如下,据此求平均日产量。
按日产量分组 (千克) 60 以下 60 – 70 70 – 80 80 – 90 90 – 100
100 – 110 110 以上 合计
组中值X (千克) 55 65 75 85 95 105 115 -
工人数f (人) 10 19 50 36 27 14 8 164
Xf
550 1235 3750 3060 2565 1470
调和平均数 X h
几何平均数
众数
XG
位置平均数
Mo
中位数
Me
二、算术平均数
算术平均数是指将总体标志总量除以同一总体单 位总数得到的平均指标。算术平均数的基本计算 公式如下:
统计 第五章 变异指标
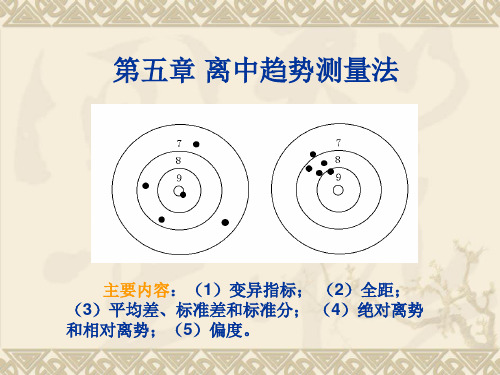
全距(R):最大值和最小值之差。也叫极差。 全距越大,表示变动越大。
对于未分组资料或者单项式分组资料 R =Xmax– Xmin
[例] 求74,84,69,91,87,74,69这些数 字的全距。 [解] 把数字按顺序重新排列:69,69,74, 74,84,87,91,显然有
绝对离势/平均指标=相对离势;
1. 变异系数
绝对离势统计量与其算术平均数的比率,用
V 表示。变异系数是最具有代表性的相对离势。 全距系数 平均差系数 标准差系数
全距系数 全距系数是众数据的全 距与其算术平均数之比,其计 算公式是 平均差系数 平均差系数是众数据的平 均差与其算术平均数之比,其 计算公式是
(4)受抽样变动的影响小,受极端值影响,处理开放组距 时要经过特殊处理
方差
值得注意的是,在推论统计中我们将发现,方差 是比标准差更有理论价值的概念。 。
所谓方差,即标准差的平方,它直接写成 也常被称为变准差的比值来测定变量 与 的 相对位置。使原来不能直接比较的离差标准化,可 以相互比较,加、减、平均。
第五节 偏态系数
变异指标——离中趋势 平均指标——集中趋势 偏度——偏斜情况 (1) 偏度的概念 反映总体次数分布偏斜程度的指标 (2)偏度的种类: 右偏分布(正偏) 左偏分布(负偏) (3)偏度的测算:算术平均数与众数比较法、动差法
A. 偏度=算术平均数-众数
若偏度>0,则右偏;若偏度<0,则左偏
2
f
f
45200 12.27(件) 300
1 (120 70) M0 L i 70 10 74.17 (件) 1 2 (120 70) (120 50) x M 0 75 74.17 0.07 S 12.27
第五章 平均指标和变异指标

第5章平均指标和变异指标【教学内容】本章包括平均指标和变异指标两部分内容,阐述了平均指标的概念和作用;各种平均数(算术平均数、调和平均数、几何平均数、众数和中位数)的计算原则、方法与应用条件;变异指标的作用、主要的变异指标(全距、平均差、标准差及其系数)的计算方法和运用条件。
【教学目标】1.理解平均指标和变异指标的概念、意义、作用;2.明确其种类及其区别;3.掌握平均指标和变异指标的计算方法、应用的原则和条件、平均指标与变异指标的关系。
【教学重点、难点】1.平均指标的特点和计算、应用原则;2.加权算术平均数;3.平均指标与变异指标的关系;4.标准差及其系数第一节平均指标的概念和作用一、平均指标的概念在社会经济现象的同质总体中,同一标志在各单位的数量表现不尽相同,标志值大小各异,这就需要利用平均指标来代表总体的一般水平。
总体各单位的同质性和某种标志值在各单位的差异性,是计算平均数的前提条件。
平均指标,是将同类社会经济现象总体内各单位某一数量标志值的差异抽象化的代表性水平指标,其数值表现为平均数。
平均指标一般是一种具有单位名称的数,它的计算单位是一个复合单位。
平均指标是社会经济统计中最常用的综合指标之一。
平均指标的显著特点是,把同质总体内各单位在某一数量标志值上的差异抽象化了,是对各单位具体数值的平均;它不是某一单位的具体数值,而是代表总体某种数量标志值的一般水平,是总体各单位的代表值。
需要注意的是,掩盖总体内部各单位某种数量标志值的差异,是平均数的局限性,必须充分认识,以防误用。
二、平均指标的作用平均指标由于能综合反映所研究现象的总体在具体条件下的一般水平,因此,在统计研究中,以及各项经济管理和分析中被广泛应用。
其作用概括起来主要有:1、利用平均指标,可以了解总体次数分布的集中趋势。
2、利用平均指标,可以对若干同类现象在不同单位、地区间进行比较研究。
3、利用平均指标,可以研究某一总体某种数值的平均水平在时间上的变化,说明总体的发展过程和趋势。
eST-5

累计人数(∑f)=500 465 ∑f/2=250 345 240 40 500 130 415
500
月收入:元 800 1100 1400 1700 2000
1128.57
常用的几种平均数总结
概 念 1. 算术平均数 标志总量 与总体单 ( x) 位总数的 比值 计算 公 式 简单: 简单: Σxi x= n 加权: 加权: 特 点
调和平均数(Harmonic mean)
次购买桔子, 例:某人分3次购买桔子,有关资料如下: 某人分 次购买桔子 有关资料如下: 序号 1 2 3 金额( 金额(元) 5 6 9 价格( 斤 价格(元/斤) 2.5 2.0 1.8
要求:计算平均价格。 要求:计算平均价格。
调和平均数
1、概念 、 2、种类 、 简单调和平均数 调和平均数 加权调和平均数 3、简单调和平均数 、
第五章 平均指标与变异指标
主 要 内 容
一、 概 述 → 二、数值平均数→ 、 、 、 平均数→ → →
一、概述 概念
平均指标反映同质总体内某一数量标志在一定历 史条件下的一般水平。 史条件下的一般水平 。 它是总体内各单位参差不 齐的标志值的代表值, 齐的标志值的代表值 , 也是对变量分布集中趋势 的测定。 的测定。 数据集中区 变量x 变量
xG = n πxi
加权: 加权:
xG = Σfi πxi
fi
优点: 优点: ①灵敏度高 ②受极端值影响小 ③适宜于各比率之 积为总比率的变量 求平均 缺点: 缺点 ①有“ 0”或负值时 或负值时 不能计算 ②偶数项数列只能 用正根
① G = 3 95%×93%×90% = 3 0.79515 = 92.64% x
1 ②ln xG = (ln 0.95 + ln 0.93+ ln 0.90) 3 1 = (− 0.05129 − 0.07257 − 0.10536) = −0.07641 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
x
x
例 (1)
=4.75
频率分布变了,均值也变因此,严格地说, 权数应指频率。 调和平均数与算术平均数的区别 凡是掌握被平均指标的分母资料时,用算术平均法。 凡是掌握被平均指标的分子资料时,用调和平均法。 分子:标志总量 平均指标 = 分母:总体单位总数 几何平均等于对数的算术平均 组矩数列求中位数 是用插值法对中位数组分割的结果。
元294.2 9.92 21
i
30 2.494 12.03
各种平均数之间的关系
f
位置平均数与算术平均数的关系 f f
X
2 1
x Me Mo
Mo x Me
x Me Mo
(对称分布)
Mo x Me
X
12
x Me Mo
负偏态分布(左)
Mo Me
x
X
正偏态分布(右)
1 164 3 165 5 166 9 167 10 168 12 169 14 170 26 171 33 172 41 174 45 总计
3 8 5 3 7 1 5 2 3 1 83
48 56 61 64 71 72 77 79 82 83
中位数的确定方法
某年级83名女生身高资料 d M L 2
统计学原理
第一章绪论
第二章统计调查 第三章统计资料的整理 第四章总量指标与相对指标 第五章平均指标和变异指标 第六章时间数列
统计学原理
第七章统计指数
第八章抽样调查
第九章回归与相关分析
第十章统计预测
第十一章统计分析综述
第十二章我国国民经济核算体系
第五章 平均指标和变易指标
一、平均指标概述
主 要 内 容
• 位置平均数: 中位数,众数。
第二节 数值 平均数
一. 算术平均数
二. 调和平均数 三.几何平均数
算术平均数
算术平均数的计算
数据集 xi ( x1 , x2 , xN 1 , xN )
算术平均数= 总体标志总量 总体单位总数
x
数据个数 N
x x N
简单算术平均数
变量值 次数 频率 某年级83名女生身高资料 x f f/Σf
xG n xi
加权:
xG xi
f i
fi
就用途而言,几何平均方法直 接用于个体数量相乘等于总数量的 第一道工序 第二道工序 全工序 现象的平均。
投入制品 1000个 900个 1000个 某产品的总合格率 合格产品 900个 810个 810个 合格率% 90 90 81 =各连续作业工序合格率之积 81%=90%90%
中位数
中位数(median):位于变 量值序列中点的数值
152 156 159 160 160 161 162 163 165 165 166 168 170 171 154 156 159 160 160 161 162 163 165 165 167 168 170 172 154 156 160 160 161 161 162 163 165 166 167 168 170 172 155 157 160 160 161 162 162 164 165 166 167 168 170 172 155 158 160 160 161 162 162 164 165 166 168 168 170 174 156 158 160 160 161 162 163 164 165 166 168 169 171
e
f S
fm
m 1
身高
(CM) 150-155 Me 155-160 160-165 165-170 170以上
3 160 2 11
累计 83 (人) 14人数
34 24 11 83
人数
34
48 72 83
3 5 164.04 14
总计
中位数的作用及用法
中位数一定存在; 中位数与算术平均数相近; 中位数不受极端值影响; 变量值与中位数离差绝对值之和最小。
众数
众数(mode):出现次数最多 即出现频率最高的变量值。
152 156 159 160 160 161 162 163 165 165 166 168 170 171 154 156 159 160 160 161 162 163 165 165 167 168 170 172 154 156 160 160 161 161 162 163 165 166 167 168 170 172 155 157 160 160 161 162 162 164 165 166 167 168 170 172 155 158 160 160 161 162 162 164 165 166 168 168 170 174 156 158 160 160 161 162 163 164 165 166 168 169 171
加权算 组距数列 术平均 数
权数与加权
1
2
3
4
5
6
7
8
9
x
算术平均数的计算取决于 变量值和权数的共同作用: 1 2 2 2 3 4 4 5 5 3 6 2 7 1 8 1 9 1
变量值决定平均数的范围;
权数则决定平均数的位置
21
4.24
关于权数的选择
必须是标志值的直接承担者; 与标志值相乘具有标志总量的意义; 组的权数必须不尽相同。
算术平均数的性质
• 各标志值与算术平均数离差之和等于零; • 各标志值与算术平均数离差平方之和最小; • 各标志值同时减去一个常数一 (不等于零),计算的平 均数再加上一与原平均数相等; • 将每个标志值同时除以常数 D(D 不等于零) 之后,计 算的平均数乘以 D,等于原来的平均数; • 将每个标志值同时减去常数一再除以常数 D(A,D 不等 于零) 得新变量值,新变量值的平均数乘以 D 再加上 一之后与原变量平均值相等。 • 注意 A,D 的选择: • A:最接近变量平均数的值, • D:最大公约数。
调和平均数
xf x f
苹果 单价 购买量 总金额 品种 为已知 x、f (元)(公斤) (元) 红富士 6 青香蕉 1.8 5 9 和xf ,而f 未知,则不能使用
x 2
f 3
xf
若只知 x 加权算术平均方式,只能使用其变形即 2 3 1 .8 5 加权调和平均方式。 x 1.875
平均指标及其特点
一、平均指标
平均指标反映同类现象的一般水平,是总体内各 单位参差不齐的标志值的代表值,也是对变量分 布集中趋势的测定。 数据集中区
变量 x
x
平均指标的作用和种类
• 作用:
对现象进行对比分析 用来综合测定工作质量和工作效率 分析现象之间的依存关系 可以进行数量上的估算和推算
• 常用的平均指标: • 数值平均数: 算术平均数,几何平均数,调和平均 数.
众数的确定方法
某年级83名女生身高资料
身高 人数
身高 人数
(CM) (人) 164 3 165 8 166 5 167 3 168 7 169 1 170 5 171 2 172 3 174 1 总计 83 (CM) (人) 152 1 154 2 155 2 156 4 157 1 158 2 159 2 160 12 161 7 162 8 163 4
组距数列求众数 是以频数之差计算的比例分割众数组组距的结果。
求某种商品三种零售价格的平均价格 价格(元) 销售量(斤) 价格(元) 销售额(元) 3.3 3 3.3 10 2.5 4 2.5 10 2.0 2.0 5 10 12 合计 合计 30
算术平均
调和平均
10 10 10 xi f i 3.3 3 2.5 4 2.0 5 xH mi x 1 1 1 1 mi 10 10 10 f i 3 45 x 3.3 2.5 2.0
xf x 1 xf x
35 69 x 1.875 6 9 2 1.8
调和平均数
概念 调和平均数 标志值倒 () xH 数平均数 的倒数 计算公式 简单: 特点 优点:①灵敏度高 ②在某种不能计算 的条件下,可以代 替 缺点:①不易理解 ②易受极值影响 ③有“ 0 ”值时不能 计算
身高
(cm) 150-155 155-160 160-165 165-170 170以上
组中值
(cm ) 152.5 157.5 162.5 167.5 172.5
人数
(人) 3 11 34 24 11 83
比重
(%) 3.61 13.25 40.96 28.92 13.25 100
总计
f f x x x x f f
中位数
中位数的确定方法
某年级83名女生身高资料 对于未分组数据: 身高 人数 累计
累计 (CM) (人) 人数 (CM) (人) 人数 中位数位置为 身高
152 154 155 156 157 158 159 160 161 162 163
人数
1 2 2 4 1 2 2 12 7 8 4
N 1 83 1 42 2 2
向银行借款1000元,年利率(复利) 为10%,则:第一年利息额100元,第二 年利息额 110元,两年合计210元。两年后 若干年间总的1+利率(复利) 还款本利和与借款额的比例为1.21。 =各年度1+利率之积 1.21=1.11.1
第三节 位置平均数
