4.5.1梯形(1)
五年级数学期末试卷(整理10篇)

五年级数学期末试卷(整理10篇)篇1:五年级数学期末试卷最新五年级数学期末试卷首先,填空。
(每个空格1分,共35分)1、最小的质数与最小的合数加起来是( )2、在分数中,当a( )7时,是一个真分数;当a( )7时,是一个假分数;当a是( )时,的分数值等于1.3、14和21的最大公因数是( ),最小公倍数是( )4、3620平方厘米=( )平方分米=( )平方米;7400平方米=( )公顷5、一个平行四边形的面积的底和高都扩大3倍,面积扩大( )倍。
6、的分子加上4,要是原分数大小不变,分母应加上( )。
7、分母是9的最大真分数是( ),分子是9的最大假分数是( )8、有一个两位数5□,如果它是5的倍数,□里最大可以填( ),如果它是3的倍数,□里最小可以填( );如果同时是2、5的倍数,□里可以填( )。
9、口袋里有大小相同的8个红球和4个黄球,从中任意摸出1个球,摸出红球的可能性是( ),摸出黄球的可能性是( ),摸出( )球的可能性大。
10、( )÷( )= = = =11、5个是( ),24千克的是( )12,1包含(),加上()是最小的素数。
13、一个三角形的面积是6平方米,高是5米,它的底是( )14.五(1)班45人,其中男生25人,占班级人数的()和班级人数的()。
15、一个三角形和一个平行四边形等底等高,三角形的面积是10平方厘米,那么平行四边形的面积是( ).16、8.4965保留整数约(),保留小数点后一位约(),保留小数点后两位约()。
二、判断题。
(对的打“√”,错的打“×”)(5分)1、分数的分子和分母同时乘或除以相同的数,分数的大小不变。
( )2、把一个长方形拉成平行四边形,它的'周长不变,面积变大。
( )3、假分数一定比真分数大。
( )4、将变成,分数大小扩大了10倍。
( )5、献爱心活动中,笑笑捐了自己零花钱的,淘气捐了自己零花钱的,淘气捐的钱比笑笑捐的多。
4.5.1梯形

实物梯形 梯形定义 特殊梯形 性质定理 课堂练习 课堂小结
等腰梯形的性质
性质1:等腰梯形在同一底上的两角相等 性质2:等腰梯形的对角线相等
在梯形ABCD中,AD//BC, ∵ AB=DC ∴ ∠ ABC= ∠ DCB (等腰梯形在同一底上的两角相
A
D
等)
AC=DB(等腰梯形的对角线
相等)
B
C
小 结:
一、等腰梯形的性质: 1. 等腰梯形 2. 等腰梯形 3. 等腰梯形 4. 等腰梯形是
相等 相等 相等 图形
二、解决梯形问题的基本思路和 方法:通过添加适当的辅助线,把 梯形问题转化为 与 问 题来解决。
三、等腰梯形常用辅助线的作法:
A D A D
1
B
E
C
B
E
F
C
数学梯形试题答案及解析

数学梯形试题答案及解析1.一个梯形的上下底之和是40.5厘米,高是1.2厘米,它的面积是平方厘米.【答案】24.3【解析】梯形的面积=(a+b)h÷2,将数据代入公式即可求解.解:40.5×1.2÷2=24.3(平方厘米);答:这个梯形的面积是24.3平方厘米.故答案为:24.3.点评:此题主要考查梯形的面积的计算方法.2.写出计算如图直角梯形的面积的算式.【答案】(5+7)×5÷2【解析】根据梯形各边的名称及梯形的面积公式即可求解.注意本题梯形的高为5.解:梯形面积=(5+7)×5÷2.故答案为:(5+7)×5÷2.点评:此题主要考查梯形的面积公式:梯形的面积=(上底+下底)×高÷2.3.有一个梯形,它的上底是7厘米,下底是12厘米,高是6厘米,这梯形的面积是立方厘米.【答案】57【解析】根据梯形的面积公式=(上底+下底)×高÷2进行计算即可得到答案.解:(7+12)×6÷2=19×6÷2,=57(立方厘米),答:这个梯形的面积是57立方厘米.故答案为:57.点评:此题主要考查的是梯形的面积公式的灵活应用.4.一个面积是20平方分米的梯形,当上底是12分米,下底是8分米时,高一定是1分米.….【答案】错误【解析】根据梯形的面积=(上底+下底)×高÷2进行计算,看面积是否等于20平方分米,然后再进行判断即可得到答案.解:(12+8)×1÷2=20×1÷2,=10(平方分米),答:上底12分米,下底8分米,高是1分米的梯形的面积是10平方分米.故答案为:错误.点评:此题主要考查的是梯形的面积公式的灵活应用.5.一个梯形的面积是34平方米,高是4米,下底长10米,上底长米.【答案】7【解析】根据梯形的面积公式可得:梯形的上底=面积×2÷高﹣下底,代入数据即可解答.解:34×2÷4﹣10,=17﹣10,=7(米),答:上底是7米.故答案为:7.点评:此题考查了梯形的面积公式的灵活应用.6.(如图)(1)在图中梯形内加一条线段,使它成为一个平形四边形和一个三角形.(2)量出相关数据(取整厘米)算出梯形面积是平方厘米.【答案】,4.5【解析】(1)利用过直线外一点作已知直线的平行线的方法即可作图;(2)量得梯形的上底是1厘米,下底是2厘米,高是3厘米,代入梯形面积公式即可求其面积.解:(1)如下图所示,即为所要求的作图,;(2)梯形的面积:(1+2)×3÷2,=3×3÷2,=4.5(平方厘米);答:梯形的面积是4.5平方厘米.故答案为:4.5.点评:此题主要考查过直线外一点作已知直线的平行线的方法及梯形面积公式.7.一个梯形的上底是5m,下底是12m,高是8m,它的面积是m2.【答案】68【解析】梯形的面积公式:S=(a+b)h÷2,上底是5,下底是12,高是8,代入公式进行计算.解:S=(a+b)h÷2,=(5+12)×8÷2,=17×8÷2,=68(平方米);答:它的面积是68平方米.故答案为:68.点评:本题主要考查了学生对梯形面积公式的掌握情况.8.用一根长56厘米的铁丝围成一个等腰梯形,两条腰长之和是36厘米,高是7厘米.它的面积是平方厘米.【答案】70【解析】根据题意,可用56减去36得到等腰梯形上、下底的和,然后再按照梯形的面积=(上底+下底)×高÷2进行计算即可.解:(56﹣36)×7÷2=20×7÷2,=140÷2,=70(平方厘米),答;这个等腰梯形的面积是70平方厘米.故答案为:70.点评:解答此题的关键是根据等腰梯形的周长确定等腰梯形上、下底的和,最后再利用梯形的面积公式进行计算即可.9.三角形面积用字母表示为,梯形面积用字母表示为.【答案】s=ah,s=【解析】(1)根据“三角形的面积=底×高÷2”进行解答即可;(2)根据“梯形的面积=(上底+下底)×高÷2”进行解答即可.解:(1)s=ah;(2)s=;故答案为:s=ah,s=.点评:解答此题的关键是根据三角形的面积计算公式和梯形的面积计算公式进行性解答即可.10.一堆钢管,最底层有18根,最高层有6根,每相邻的两层相差一根,这堆钢管共有.【答案】156根【解析】根据题意,最上层有6根,最下层有18根,相邻两层相差1根,这堆钢管的层数是(18﹣6+1)层,根据梯形的面积计算方法进行解答.解:(6+18)×(18﹣6+1)÷2=24×13÷2=156(根);答:这堆钢管一共有 156根.故答案为:156根.点评:此题主要考查梯形的面积计算方法,能够根据梯形的面积计算方法解决有关的实际问题.11.一个梯形的上底是7厘米,下底是5厘米,高是4厘米,它的面积是平方厘米.【答案】24【解析】将数据代入梯形面积公式即可求解.解:(7+5)×4÷2,=12×4÷2,=24(平方厘米);答:梯形面积是24平方厘米.故答案为:24.点评:此题主要考查梯形面积的计算.12.平行四边形的面积或梯形面积的大小分别与它们的底和高有关,与它们的形状和位置无关..【答案】√【解析】根据平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2,可以看出平行四边形的面积与梯形的面积的大小与它们的底和高有关系,与它们的形状和位置无关.解:平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2,所以平行四边形的面积与梯形的面积的大小与它们的底和高有关系,与它们的形状和位置无关.故答案为:√.点评:此题主要考查的是平行四边形的面积公式和梯形的面积公式的应用.13.(2011•杭州模拟)有一个等腰梯形,底角为450,上底为8厘米,下底为12厘米,这个梯形的面积应是平方厘米.【答案】20【解析】根据等腰图形的面积公式可得,只要求出梯形的高就可以解决问题,作出梯形的两条高,根据等腰梯形的性质,可将这个底角为450的梯形分成了两个等腰直角三角形,由此可以得出梯形的高为2厘米.解:梯形的高:(12﹣8)÷2,=4÷2,=2(厘米),梯形的面积:(8+12)×2÷2,=20×2÷2,=20(平方厘米),答:梯形的面积为20平方厘米.故答案为:20.点评:画出梯形的两条高将梯形分成两个直角三角形和长方形,是解决此类问题到的关键.14. (2012•德江县模拟)有一块梯形木板,上底比下底多0.6米,上底是1.8米,高比下底少0.9米,这块木板的面积是 . 【答案】0.45平方米【解析】先求出梯形的下底和高,再根据梯形的面积公式求出这个梯形的面积即可.解:1.8﹣0.6=1.2(米),1.2﹣0.9=0.3(米),(1.8+1.2)×0.3÷2=3×0.3÷2,=0.45(平方米);答:这块木板的面积是0.45平方米.故答案为:0.45平方米.点评:考查了梯形的面积公式:梯形的面积=(上底+下底)×高÷2,本题要先求出梯形的下底和高.15. 在梯形ABCD 中,BE=2EC ,CF=2AF ,阴影部分的面积为3平方厘米,则梯形的面积为 平方厘米.【答案】20.25【解析】在三角形BFE 、三角形EFC 中高相等,BE=2EC ,可以求出三角形BEF 的面积,在三角形BFC 与三角形AFB 中,高相等,CF=2AF ,可以求出三角形AFB 的面积,而三角形AFB 的面积等于三角形DFC 的面积,在三角形DFC 与三角形AFD 中高相等,CF=2AF ,可以求出三角形ADF 的面积,进而求出梯形的面积.解:在三角形BFE 、三角形EFC 中高相等,BE=2EC ,S △BEF :S △EFC =BE :EC=2:1,S △BEF =2S △EFC =2×3=6(平方厘米),在三角形BFC 与三角形AFB 中,高相等,CF=2AF ,S △ABF :S △BFC =AF :FC=1:2,所以S △ABF =S △BFC =(6+3)=4.5(平方厘米),S △ABF =S △DFC =4.5平方厘米,在三角形DFC 与三角形AFD 中高相等,CF=2AF ,S △AFD :S △DFC =AF :FC=1:2,所以S △AFD =S △DFC =×4.5=2.25(平方厘米),梯形的面积是:2S △DFC +S △BEF +S △EFC +S △AFD =4.5×2+6+3+2.25=20.25(平方厘米),故答案为:20.25.点评:题考查了三角形的高相等时,面积与底成正比的性质的灵活应用.16. 把一个平行四边形的底增加2.4厘米后,就变成了一个梯形,面积增加6平方厘米,则梯形的高是 厘米.【答案】5【解析】如图所示,增加部分为一个三角形,这个三角形的面积是6平方厘米,底为2.4厘米,则可以求出三角形的高,也就是梯形的高.解:6×2÷2.4,=5(厘米);答:梯形的高是5厘米.故答案为:5.点评:解答此题的关键是利用直观画图,求出三角形的高,也就等于求出了梯形的高.17.一个梯形上底和下底同时扩大到原来的6倍,高缩小为原来的一半,面积会(填“扩大”或“缩小”)到原来的倍.【答案】扩大、3【解析】梯形的面积=(上底+下底)×高÷2,若上底和下底同时扩大到原来的6倍,则上底和下底的和也扩大到原来的6倍,即面积扩大6倍;高缩小为原来的一半,则面积会缩小原来的一半,这时面积应该是扩大到原来的6×=3倍.解:因为梯形的面积=(上底+下底)×高÷2,若上底和下底同时扩大到原来的6倍,则上底和下底的和也扩大到原来的6倍,即面积扩大6倍;高缩小为原来的一半,则面积会缩小原来的一半,这时面积应该是扩大到原来的6×=3倍.故答案为:扩大、3.点评:此题主要考查梯形面积公式的灵活应用.18.如图,平行四边形面积是54cm2,则阴影部分面积是 cm2.【答案】6【解析】要求阴影部分面积,需要求出三角形的底边,可以通过求平行四边形的底边得到,再根据三角形的面积公式即可求解.解:54÷6=9(cm),(9﹣7)×6÷2=2×6÷2=6(cm2).答:则阴影部分面积是 6cm2.故答案为:6.点评:考查了平行四边形的面积和三角形的面积,本题关键是求得三角形的底边,这是本题的难点.19.一个梯形的上底、下底和高都是另外一个梯形的3倍,那么这个梯形的面积是另一个梯面积的()A.3倍B.6倍C.9倍【答案】C【解析】梯形的面积=(上底+下底)×高÷2,若一个梯形的上底、下底和高都是另外一个梯形的3倍,那么这个梯形的面积是另一个梯面积的9倍.解:因为梯形的面积=(上底+下底)×高÷2,若一个梯形的上底、下底和高都是另外一个梯形的3倍,那么这个梯形的面积是另一个梯面积的9倍.故答案为:C.点评:此题主要考查梯形的面积公式.20.一个梯形面积是64平方米,上底与下底的和是16米,高是()米.A.4B.8C.2【答案】B【解析】已知梯形的面积和上下底之和求高,由梯形的面积公式s=(a+b)h,可以推出h=2s÷(a+b);由此解答.解:64×2÷16,=8(米);答:高是8米.故选:B.点评:此题主要根据梯形面积的计算方法,以及求一个因数等于积除以另一个因数,由此解决问题.21.求图的梯形面积,列式正确的是()A.(4+6)×7÷2B.(5+7)×4÷2C.(5+7)×6÷2【答案】C【解析】根据梯形的面积=(上底+下底)×高÷2,上底、下底及高已知,从而代入公式即可求解.解:由梯形的面积公式可得,梯形面积为:(5+7)×6÷2.故选C.点评:此题主要考查梯形的面积计算.22.推导梯形面积的计算公式时,把两个完全一样的梯形转化成平行四边形,其方法是()A.旋转B.平移C.旋转和平移【答案】C【解析】将两个完全一样的梯形中的一个梯形沿上底或下底的一个端点进行旋转并且平移,即可拼成一个平行四边形,从而推导出梯形的面积公式.解:将两个完全一样的梯形中的一个梯形沿上底或下底的一个端点进行旋转并且平移,即可构成一个平行四边形,从而推导出梯形的面积公式.故选:C.点评:此题主要考查梯形面积公式的推导过程.23.下底是4分米,上底和高都是2分米的梯形面积是()A.8平方分米B.6平方分米C.12平方分米【答案】B【解析】梯形面积=(上底+下底)×高÷2,将已知数据代入公式即可求解.解:(2+4)×2÷2=6(平方分米);故选:B.点评:此题主要考查梯形的面积公式.24.小明用一张梯形纸做折纸游戏.先上下对折,使两底重合,可得图1,并测出未重叠部分的两个三角形面积和是20平方厘米.然后再将图1中两个小三角形部分向内翻折,得到图2.经测算,图2的面积相当于图1的.这张梯形纸的面积是()平方厘米.A.50B.60C.100D.120【答案】C【解析】在图1中左右两个三角形的面积相等,将图1中两个小三角形部分向内翻折后,减少了一个三角形的面积即20÷2=10(平方厘米);这10平方厘米就相当于图2的面积比图1的面积少了(1﹣)对应的分率,把图1的面积看作单位“1”,根据分数除法的意义,可以求出图1的面积,列式为:10÷(1﹣)=60(平方厘米);再求图2的面积是:60×=50(平方厘米);又因为图2的面积是这张梯形纸的面积的一半,所以可以求出这张梯形纸的面积,列式为:50×2=100(平方厘米);然后据此选择即可.解:每个三角形的面积是:20÷2=10(平方厘米);图1的面积是:10÷(1﹣),=10÷,=60(平方厘米);图2的面积是:60×=50(平方厘米);梯形纸的面积是:50×2=100(平方厘米);答:梯形纸的面积是100平方厘米.故选:C.点评:本题实质是考查了梯形面积推导的过程,同时揉合了分数除法的意义,本题关键是得出由图1到图2减少的面积对应的分率.25.如图,等腰梯形对角线互相垂直,且它的对角线长10厘米,求梯形的面积.【答案】50cm2【解析】梯形的面积=三角形ABC的面积+三角形ACD的面积=AC×BO÷2+AC×DO÷2=AC×(BO+DO)÷2=AC×BD÷2,即对角线互相垂直的四边形的面积可以用对角线×对角线÷2求出.解:10×10÷2=100÷2=50(cm2).答:梯形的面积为50cm2.点评:考查了对角线互相垂直的四边形的面积计算,直接用对角线×对角线÷2计算即可.26.张大伯靠一面墙用篱笆围成一个面积是72平方米的梯形养鸡场,至少需要多少米的篱笆?【答案】30米【解析】根据梯形的面积公式=(上底+下底)×高÷2,利用梯形的面积乘2再除以高即可得到梯形上下底的和,然后再加上梯形的高即可得到需要的篱笆长度,列式解答即可得到答案.解:72×2÷6+6=24+6,=30(米),答:至少需要30米篱笆.点评:解答此题的关键是根据梯形的面积公式确定梯形上下底的和,然后再加上梯形的高即可.27.一块梯形麦田的面积是1820平方米,已知上底是48米,下底是56米,求梯形的麦田的高?【答案】35米【解析】根据梯形的面积公式:(上底+下底)×高÷2=梯形的面积,可用梯形的面积1820平方米乘2再除以梯形上底与下底的和即可得到答案.解:1820×2÷(48+56),=3640÷104,=35(米).答:梯形的麦田的高是35米.点评:此题主要考查的是梯形的面积公式的应用.28.如图,用24米长的篱笆,在靠墙的地方围了一块菜地,这块菜地的占地面积是多少平方米?【答案】54平方米【解析】根据图和题意知道,梯形的上底+下底=24﹣6=18米,再根据梯形的面积公式S=(a+b)×h÷2,即可求出菜地的占地面积.解:(24﹣6)×6÷2,=18×6÷2,=108÷2,=54(平方米).答:这块菜地的占地面积是54平方米.点评:关键是求出上底与下底的和,再利用梯形的面积公式S=(a+b)×h÷2解决问题.29.计算下面每个梯形的面积.面积面积面积.【答案】30平方厘米;20平方米;36平方米【解析】根据梯形的面积=(上底+下底)×高÷2,代入数据即可解答.解:(2+8)×6÷2,=10×3,=30(平方厘米),(2+6)×5÷2,=8×5÷2,=20(平方米),(6+12)×4÷2,=18×2,=36(平方米),答:梯形的面积分别是30平方厘米、20平方米、36平方米.故答案为:30平方厘米;20平方米;36平方米.点评:此题主要考查梯形的面积公式的计算应用.30.用篱笆围成一个梯形养兔场(如图所示),一边利用房屋墙壁,篱笆全长80米,养兔场面积有多大?【答案】750平方米【解析】观察图形可知,篱笆长度是这个梯形的上下底之和与高的长度之和,又因为高是30米,可得出梯形的上下底之和是80﹣30=50(米),据此根据梯形的面积=上下底之和×高÷2计算即可.解:(80﹣30)×30÷2,=50×30÷2,=750(平方米),答:养兔场的面积是750平方米.点评:此题考查梯形的面积公式的计算应用,解答此题的关键是明确上下底之和.31.测量你所需的条件,并算出它们的面积.【答案】,5平方厘米,2平方厘米,5.25平方厘米【解析】平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,据此测量出它们对应的边长,代入公式即可解答.解:经过测量可知:(1)2×2.5=5(平方厘米),答:平行四边形的面积是5平方厘米.(2)4×1÷2=2(平方厘米),答:三角形的面积是2平方厘米.(3)(1.5+2)×3÷2,=3.5×3÷2,=5.25(平方厘米),答:梯形的面积是5.25平方厘米.点评:此题主要考查梯形、三角形、平行四边形的面积公式的计算应用.32.用篱笆围成一个梯形养鸡场(如图所示),一边利用房屋的墙壁,篱笆的总长度是65米,求养鸡场的面积.【答案】375平方米【解析】“一边利用房屋的墙壁,篱笆的总长度是65米”,所以这个梯形的上下底的和就是65﹣15=50米.然后再根据梯形的面积公式可求出这个养鸡场的面积.解:(65﹣15)×15÷2,=50×15÷2,=375(平方米).答:养鸡场的面积是375平方米.点评:本题的关键是求出这个梯形上下底的和,再根据梯形的面积公式进行计算.33.利用一面墙,用篱笆围一块梯形菜地,已知篱笆全长35米,求菜地的面积是多少平方米?【答案】108平方米【解析】根据题意,可利用梯形的面积公式(上底+下底)×高÷2计算梯形菜地的面积,可用篱笆的全长35米减去8米就是这个梯形菜地的上底与下底的和,然后再用上底与下底的和乘高8米再除以2即可得到答案.解:(35﹣8)×8÷2=27×8÷2,=216÷2,=108(平方米),答:菜地的面积是108平方米.点评:解答此题的关键是确定这个梯形菜地的上底与下底的和,然后再利用梯形的面积公式进行解答.34.一条下水道的横截面是梯形,下水道的宽是2.8米,下水道的底宽是1.2米,下水道的深是1.6米,它的横截面面积是多少平方米?【答案】3.2平方米【解析】要求它的横截面面积是多少平方米,因为下水道的横截面是梯形,根据“梯形的面积=(上底+下底)×高÷2”,代入数值,解答即可.解:(2.8+1.2)×1.6÷2,=4×1.6÷2,=3.2(平方米);答:它的横截面面积是3.2平方米.点评:此题考查的是梯形的面积的计算方法,应灵活运用.35.寻找合适的条件,求出各图形的面积.(单位:米)【答案】29.75平方米,12.8平方米,20.58平方米【解析】将各图形求面积所用线段的数值,代入各自的面积计算公式即可求解.解:(1)三角形的面积:7×8.5÷2,=59.5÷2,=29.75(平方米);(2)梯形的面积:(3+5)×3.2÷2,=8×3.2÷2,=25.6÷2,=12.8(平方米);(3)平行四边形的面积:9.8×2.1=20.58(平方米);答:三角形的面积是29.75平方米,梯形的面积是12.8平方米,平行四边形的面积是20.58平方米.点评:解答此题的关键是,找准各图形计算面积所用的线段的值,要注意底和高的对应.36.找准所需条件,计算下列图形的面积.(单位:米)【答案】24平方米;190平方米【解析】(1)根据三角形的面积公式S=ah÷2,把底6米,高8米代入公式即可;(2)根据梯形的面积公式S=(a+b)×h÷2,把数据代入公式,列式解答即可.解:(1)6×8÷2=24(平方米);(2)(14+24)×10÷2,=38×10÷2,=190(平方米);答:三角形的面积是24平方米;梯形的面积是190平方米.点评:本题主要考查了三角形的面积公式S=ah÷2与梯形的面积公式S=(a+b)×h÷2的实际应用.37.一个等腰直角三角形最长边是14厘米,如图折成一个梯形,梯形的面积是多少?【答案】18.375平方厘米【解析】由图意可知:折成的梯形的上底和高都是14÷4=3.5厘米,再据等腰直角三角形的斜边上的高就是斜边的一半,于是可得:梯形的下底等于14÷2=7厘米,从而利用梯形的面积公式即可求解.解:梯形的上底和高都是14÷4=3.5厘米,梯形的下底等于14÷2=7厘米,所以图形的面积是:(3.5+7)×3.5÷2,=10.5×3.5÷2,=18.375(平方厘米);答:梯形的面积是18.375平方厘米.点评:此题主要考查梯形的面积的计算方法,关键是求出计算面积所需要的线段的长度.38.王伯伯用篱笆靠墙圈出一块菜地(如图),篱笆长100米,求这块菜地的面积?【答案】962平方米【解析】根据题意可知,用100米减去梯形菜地的高26米即可得到梯形菜地的上底与下底的和,然后再利用梯形的面积公式(上底+下底)×高÷2进行计算即可得到答案.解:(100﹣26)×26÷2=74×26÷2,=1924÷2,=962(平方米),答:这块菜地的面积是962平方米.点评:解答此题的关键是用篱笆长减去梯形的高得到梯形上底与下底的和,最后再利用梯形的面积公式进行计算即可.39.一块梯形的土地,上底为8米,下底为12米,高是上底与下底和的50%,现在这块地的30%用来种花生,剩下的部分按2:3种玉米和大豆,请问玉米种多大的面积?【答案】28平方米【解析】要求玉米种多大的面积,需先求出剩下土地的面积,要求剩下土地面积,就要求出种花生的土地面积,因这块地的30%用来种花生,首先要求根据梯形的面积公式求出出这块地的面积,据此来解答.解:这块地的面积:(8+12)×(8+12)×50%÷2,=20×20×0.5÷2,=100(平方米);种花生的面积:100×30%=30(平方米);乘下地的面积:100﹣30=70(平方米);种玉米的面积:70×=70×=28(平方米).答:玉米种了28平方米.点评:本题综合考查了学生对于梯形的面积以及分数乘法和按比例分配的知识.40.一块梯形的宣传牌,上底8米,下底10米,高5米.油漆这块宣传牌的正反两面共需油漆多少千克?(每平方米需用油漆1千克)【答案】90千克【解析】此题实际上是求这块梯形广告牌两面的面积,梯形的上底、下底和高已知,则面积可求;每平方米的用漆量已知,从而能求出两面的用漆量.解:(8+10)×5÷2×2×1,=18×5÷2×2×1,=90÷2×2×1,=90×1,=90(千克);答:油漆这块宣传牌的正反两面共需油漆90千克.点评:解答此题的关键是明白:先求出这块梯形广告牌两面的面积,进而可以求出总的用漆量.41.用篱笆围成一个养鸡场(如图),其中一边利用房屋的墙壁.已知篱笆长65米,求养鸡场的面积.【答案】318平方米【解析】由题意可知:这个梯形的上底与下底的和为(65﹣12)=53米,高为12米,代入梯形的面积公式即可求解.解:(65﹣12)×12÷2,=53×12÷2,=318(平方米);答:养鸡场的面积是318平方米.点评:此题主要考查梯形的面积的计算方法的灵活应用.42.有一块菜地为梯形,上底是13米,比下底短8米,高是50米,这个梯形菜地的面积是多少?【答案】850平方米【解析】梯形的面积=(上底+下底)×高÷2,梯形的上底和高已知,先利用上底与下底的关系求出下底,再将已知数据代入梯形的面积公式即可求出菜地的面积.解:[13+(13+8)]×50÷2,=(13+21)×50÷2,=34×50÷2,=1700÷2,=850(平方米);答:这个梯形菜地的面积是850平方米.点评:解答此题的关键是先求出下底,再利用梯形的面积公式计算即可.43.(1)画出上面各图形底边上的高,并量出它的长度(测量结果保留整厘米数).(2)计算各图形的面积.【答案】,10平方厘米,7平方厘米,6.5平方厘米【解析】(1)根据平行四边形的高,梯形的高,三角形的高的定义,分别画出这三个图形的已知底上的高线,再利用刻度尺分别测量出它们的高度;(2)根据平行四边形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,代入数据即可解答.解:(1)根据根据平行四边形的高,梯形的高,三角形的高的定义,分别画出这三个图形的已知底上的高线,并测量出它们的高分别如图所示:(2)平行四边形的面积是:5×2=10(平方厘米),梯形的面积是:(2.2+4.8)×2÷2=7(平方厘米),三角形的面积是:13×1÷2=6.5(平方厘米),答:平行四边形的面积是10平方厘米,梯形的面积是7平方厘米,三角形的面积是6.5平方厘米.点评:此题考查了平行四边形、梯形、三角形的高的画法以及面积公式的计算应用.44.有一块梯形果园,下底80米,比上底长20米,高50米,平均每7平方米栽一棵果树,这块地共可栽多少棵果树?【答案】1000棵【解析】根据题意,可用80减去20计算上底的长,然后再利用梯形的面积公式计算出梯形果园的面积,然后再用果园的面积除以7进行计算即可.解:(80﹣20+80)×50÷7=140×50÷7,=1000(棵),答:这块地可栽1000棵果树.点评:解答此题的关键是确定梯形果园的上底,然后再利用梯形的面积公式进行计算即可.45.某林场砍伐树木,运到家具厂将其逐层堆放,每层比下一层少一根,最上层堆放了4根,一共堆放了7层,林场一共砍伐了多少根树木?【答案】49根【解析】根据堆成梯形的物品的计算方法:根数=(上层根数+下层根数)×层数÷2,代入数据进行解答.解:[4+(7﹣1+4)]×7÷2,=[4+10]×7÷2,=14×7÷2,=49(根).答:林场一共砍伐了49根树木.点评:本题主要考查了学生对根数=(上层根数+下层根数)×层数÷2,这一数量关系的掌握情况.46.一块菜地面积共2000平方米,阴影部分种白菜,空白部分种土豆,种白菜和种土豆的面积各是多少平方米?【答案】1200平方米,800平方米【解析】先根据梯形的面积=(上底+下底)×高÷2进行计算可求梯形的高,即两个三角形的高,再根据三角形的面积=底×高÷2进行计算可求种白菜和种土豆的面积.解:2000×2÷(40+60),=2000×2÷100,=40(米),60×40÷2=1200(平方米),40×40÷2=800(平方米).答:种白菜的面积是1200平方米,种土豆的面积是800平方米.点评:此题主要考查的是梯形面积公式和三角形的面积公式的灵活应用.47.①如图中梯形的面积是多少?②如果把这个梯形的上底增加1cm,下底减少1cm,得到的新梯形与原梯形的面积之间有什么关系?③如果梯形的上底增加2cm,下底减少2cm呢?④你发现了什么?请说明理由.【答案】40平方厘米,得到的新梯形与原梯形的面积相等,得到的新梯形与原梯形的面积相等,上底+下底的和不变,高不变,那么梯形的面积也不变【解析】①梯形的面积=(上底+下底)×高÷2,代入公式计算即可.②梯形的上底增加1cm,下底减少1cm,高不变,那么梯形的面积也不变.③梯形的上底增加2cm,下底减少2cm,高不变,那么梯形的面积也不变.④上底+下底的和不变,高不变,那么梯形的面积也不变.解:①(16+30)×15÷2,=46×15÷2,=345(平方厘米).答:梯形的面积是40平方厘米.②(16+1+30﹣1)×15÷2,=46×15÷2,=345(平方厘米).答:得到的新梯形与原梯形的面积相等.③(16+2+30﹣2)×15÷2,=46×15÷2,=345(平方厘米).答:得到的新梯形与原梯形的面积相等.④上底+下底的和不变,高不变,那么梯形的面积也不变.点评:此题主要考查梯形的面积公式及其计算,并通过计算能得出规律.48.梯形面积是36平方厘米,求阴影部分的面积.【答案】28平方厘米【解析】梯形的面积=(上底+下底)×高÷2,则下底=梯形的面积×2÷高﹣上底,下底即阴影部分三角形的底,再根据三角形的面积=底×高÷2,代入公式即可求解.解:(36×2÷8﹣2)×8÷2,=(9﹣2)×8÷2,=7×8÷2,=28(平方厘米).答:阴影部分的面积是28平方厘米.点评:此题主要考查梯形的面积和三角形面积的灵活计算.49.一条新挖的水渠,横截面是梯形.渠口宽2.8m,渠底宽1.4m,渠深1.2m.它的横截面的面积是多少?【答案】2.52平方米【解析】根据梯形的面积公式:S=(a+b)h÷2,上底就是2.8米,下底是1.4米,高是1.2。
五年级上数学一课一练4.5梯形的面积 北师大版含答案

五年级上册数学一课一练-4.5梯形的面积一、单选题1.下图中,平行线间梯形A,B的面积相等,梯形B的下底是()cm。
A. 5B. 3C. 3.3D. 无法确定2.一个梯形面积是24平方米,上底与下底的和是8米,那么高是()米。
A. 2B. 4C. 6D. 83.梯形的面积是96平方厘米,高是8厘米,则上、下底的和是()厘米.A. 12B. 24C. 484.一块梯形土地的面积是1300平方米,已知梯形的上底是20米,下底是上底的4倍.梯形土地的高是()A. 13米B. 26米C. 28米D. 76米二、判断题5.判断,正确的填“正确”,错误的填“错误”.只有一组对边平行的四边形叫做梯形.6.判断,正确的填“正确”,错误的填“错误”.两个完全一样的梯形能拼成一个长方形.7.两个面积相等的梯形可以拼成一个平行四边形。
()三、填空题8.下面梯形的面积________.上底4米,下底6米,高5米9.计算下面图形的面积是________cm2(单位:cm)10.一个梯形的面积是168平方米,上底长10米,是下底的一半,高是________厘米。
11.一个梯形的面积是48m2,上下底之和是12m,高是________m。
12.梯形的面积是18平方分米,下底长5分米,高是4分米,上底是________分米四、解答题13.(1)一个梯形各顶点在方格图中的位置分别是(3,1)、(11,1)(6,8)、(9,8).请在方格纸上画出这个梯形.(2)方格纸中每个小正方形的边长看作1厘米,求出这个梯形的面积.14.在上底为4厘米,下底为6厘米的梯形中画一条线段,把梯形分成面积相等的两部分(画出三种分法)五、综合题15.挖一条长180米的流水道,流水道的横截面是一个梯形,这个梯形的上底是80厘米,下底是60厘米,高是45厘米。
(1)已经挖了80米长,挖出多少方土?(2)挖完这条流水道要挖出多少方土?六、应用题16.有一堆堆成横截面是梯形的钢管上层有12根,下层有18根,一共有6层.这堆钢管共有多少根?17.计算如图梯形的面积.参考答案一、单选题1.【答案】C2.【答案】C3.【答案】B4.【答案】B二、判断题5.【答案】正确6.【答案】错误7.【答案】错误三、填空题8.【答案】25平方米9.【答案】35010.【答案】11.211.【答案】812.【答案】4四、解答题13.【答案】(1)解:(2)解:这个梯形的上底是3厘米,下底是8厘米,高是7厘米(3+8)×7÷2=11×7÷2=38.5(平方厘米)答:这个梯形的面积是38.5平方厘米。
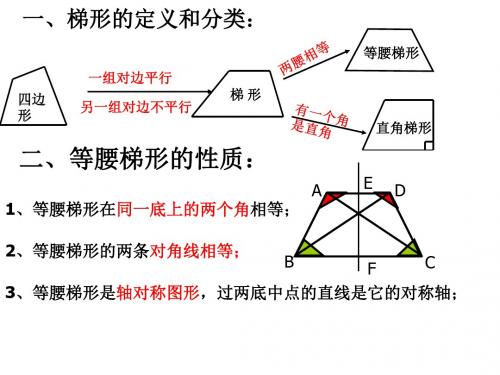
4.5.1梯形的定义和分类
等腰梯形.
(√)
(4) 一组对边平行,另一组对边相等的四边形一定
是等腰梯形. (5)对角互补的梯形一定是等腰梯形.
(×) (√)
2.有两个内角是70度的梯形一定是等腰
梯形. ( √ )
例题分析
例 1:如图,在梯形ABCD中, BAD,
∠A=100°, 求梯形ABCD的各个内角
A
D
BE F C
• 等腰梯形的判定方法 1、两腰相等的梯形是等腰梯形; 2、同一底上的两个角相等的梯形是等腰梯形; 3、对角线相等的梯形是等腰梯形;
A
D
B
C
达标训练:
1、抢答题 判断正误:
(1)有两个角相等的梯形一定是等腰梯形.
(×)
(2)两条对角线相等的梯形一定是等腰梯形. (√)
(3)如果一个梯形是轴对称图形,则它一定是
G
A
D
A
D
A
D
B
E
CB M
NC
B
C
定义法:
1、两腰相等的梯形是等腰梯形;
2、同一底上两个角相等的梯形是等腰梯形;
猜想:
3、对角线相等的梯形是等腰梯形;
命题2:对角线相等的梯形是等腰梯形。
已知:在梯形ABCD中,AD∥BC,AC=BD.
证明:四边形ABCD是等腰梯形.
A
D
2
1
B
C
E
证法二:过点A作AE⊥BC,过点D作DF⊥BC.
2 C
又∵ M是AD的中点,
∴AM=DM ∴ △ABM ≌△DCM
∴AB=DC
即:四边形ABCD是等腰梯形。
例2:画一个等腰梯形,使它的上、下底分别 为4cm,和12cm,高为3cm。并计算这个等 腰梯形的周长和面积.
2022-2023学年江西省南昌市湾里区数学六年级第一学期期末达标测试试题含解析

2022-2023学年六上数学期末模拟试卷一、认真审题,细心计算1.直接写出得数。
49×18= 78÷354= 512×20%= 4×0.375= 2116415⨯= 167×0.75= 25501339÷= 0.6+0.4= 15117()938⨯+⨯= 1111112481632+++++=2.计算下面各题。
311432⨯÷ 7573107105⎡⎤⎛⎫⨯÷- ⎪⎢⎥⎝⎭⎣⎦3.解方程.25x =5 3.7x +x =23.5 0.2+2.8x =2.16二、认真读题,准确填写4.2÷5=8 = 15()=________(填小数) 5.一块三角形菜地底长40米,高60米.如果平均每平方米收白菜9千克,这块菜地一共能收白菜________千克6.比30千克多15的是(______)千克;(______)米比60米少14。
7.求比值:15分钟∶13小时=(______)。
8.配制一种药水,0.35克药需加水700克,x 克药需加水2000克。
根据比例关系列出等式:________=________9.用自然数中最小的素数、最小的奇数、最小的合数,组成一个最小的三位数是__。
10.一个数的25%与35的20%相等,这个数是(______)。
11.下图是在电脑上下载一份文件的过程示意图,下载的这份文件已用了8分钟,那么还要等(______)分钟才能下载完。
12.( )÷( )=== =0.6513.已知,那么A:B=(______):(______),A 与B 成(_______)比例。
14.一个粮店有粮食m 吨,又运来2车,每车a 吨.粮店现在有粮食________吨,如果m=8,a=5,那么粮店现在有粮食________吨.三、反复比较,精心选择15.右边的分数中:、、、、、,比大的有( )个. A .3个B .4个C .2个 16.能够与13∶15组成比例的是( )。
钢结构图集(最新2010[1].4.5)
![钢结构图集(最新2010[1].4.5)](https://img.taocdn.com/s3/m/b05539ccbb4cf7ec4afed06a.png)
细分招聘专家,精准求职首选:钢构就业网01(04)SG519多、高层民用建筑钢结构节点构造详图(2004年局部修改版).pdf 01SG519多、高层民用建筑钢结构节点构造详图.pdf02(04)SG518-1门式刚架轻型房屋钢结构(2004年局部修改版).pdf02SG518-1门式刚架轻型房屋钢结构.pdf02SG614框架结构填充小型空心砌块墙体结构构造.pdf02ZG710发泡水泥复合板.pdf03G101-1混凝土结构施工图平面整体表示方法制图规则和构造详图(现浇混凝土框架、剪力墙、框架-剪力墙、框支剪力墙结构).pdf03G101-2混凝土结构施工图平面整体表示方法制图规则和构造详图(现浇混凝土板式楼梯).pdf03G322-1钢筋混凝土过梁.pdf03G322-2钢筋混凝土过梁(烧结多孔砖砌体).pdf03G322-3钢筋混凝土过梁(混凝土小型空心砌块砌体).pdf03G329-1建筑物抗震构造详图(民用框架、框架-剪力墙、剪力墙、部分框支剪力墙、框架-核心筒、筒中筒、板柱-剪力墙结构).pdf03G329-2建筑物抗震构造详图(单层砌体房屋).pdf03G363多层砖房钢筋混凝土构造柱抗震节点详图.pdf03G372钢筋混凝土雨棚.pdf03SG409预应力混凝土管桩.pdf03SG435-1预应力混凝土圆孔板(预应力钢筋为螺旋肋钢丝,跨度2.1m~4.8m).pdf 03SG435-2预应力混凝土圆孔板(预应力钢筋为螺旋肋钢丝,跨度4.8m~7.2m).pdf 03SG519-1多、高层建筑钢结构节点连接(次梁与主梁的简支螺栓连接;主梁的栓焊拼接).pdf03SG520-1实腹式钢吊车梁(中轻级工作制A1~A5 Q235钢跨度6.0m、7.5m、9.0m).pdf03SG520-2实腹式钢吊车梁(中轻级工作制A1~A5 Q345钢跨度6.0m、7.5m、9.0m).pdf03SG610-1建筑结构隔震构造详图.pdf03SG611砖混结构加固与修复.pdf03SG615配筋混凝土砌块砌体建筑结构构造.pdf 03SG715-1蒸压轻质加气混凝土板(NACL)构造详图.pdf04G101-3混凝土结构施工图平面整体表示方法制图规则和构造详图(筏形基础).pdf04G101-4混凝土结构施工图平面整体表示方法制图规则和构造详图(现浇混凝土楼面与屋面板:适用于主体结构为混凝土结构及砌体结构).pdf04G211砖烟囱.pdf04G314钢筋混凝土折线型屋架.pdf04G320钢筋混凝土基础梁.pdf04G321钢筋混凝土连系梁.pdf04G322-4钢筋混凝土过梁(混凝土小型空心砌块夹心墙).pdf04G323-1钢筋混凝土吊车梁(工作级别A6).pdf04G323-2钢筋混凝土吊车梁(工作级别A4、A5).pdf04G325吊车轨道联结及车挡.pdf04G329-1建筑物抗震构造详图(民用框架、框架-剪力墙、剪力墙、部分框支剪力墙、筒中筒和板柱-剪力墙).pdf04G329-2建筑物抗震构造详图(单层砌体房屋).pdf04G329-3建筑物抗震构造详图(砖墙楼房).pdf04G329-4建筑物抗震构造详图(小砌块墙楼房).pdf04G329-5建筑物抗震构造详图(配筋砖砌体楼房).pdf04G329-6建筑物抗震构造详图(局部框架房屋).pdf04G329-7建筑物抗震构造详图(砖排架房屋).pdf04G329-8建筑物抗震构造详图(钢筋混凝土柱单层厂房).pdf04G337吊车梁走道板.pdf04G353-1钢筋混凝土屋面梁(6m单坡).pdf04G353-2钢筋混凝土屋面梁(9m单坡).pdf04G353-3钢筋混凝土屋面梁(12m单坡).pdf04G353-4钢筋混凝土屋面梁(9m双坡).pdf04G353-5钢筋混凝土屋面梁(12m双坡).pdf04G353-6钢筋混凝土屋面梁(15m双坡).pdf04G361预制钢筋混凝土方桩.pdf细分招聘专家,精准求职首选:钢构就业网04G362钢筋混凝土结构预埋件.pdf04G410-1 1.5mX6.0m预应力混凝土屋面板(预应力混凝土部分).pdf04G410-2 1.5mX6.0m预应力混凝土屋面板(钢筋混凝土部分).pdf04G415-1预应力混凝土折线型屋架(预应力钢筋为钢绞线跨度18m~30m).pdf 04G426 6m后张法预应力混凝土吊车梁.pdf04G612砖墙结构构造(烧结多孔砖与普通砖、蒸压砖).pdf04J008_挡土墙.pdf04SG307现浇钢筋混凝土板式楼梯.pdf04SG308混凝土后锚固连接构造.pdf04SG309钢筋焊接网混凝土楼板与剪力墙构造详图.pdf04SG330混凝土结构剪力墙边缘构件和框架柱构造钢筋选用.pdf04SG518-2门式刚架轻型房屋钢结构(有悬挂吊车).pdf04SG518-3门式刚架轻型房屋钢结构(有吊车).pdf04SG519-2多、高层建筑钢结构节点连接(主梁的全栓拼接).pdf04SG523型钢混凝土组合结构构造.pdf05G212钢筋混凝土烟囱(高度60m、80m、100m).pdf05G335单层工业厂房钢筋混凝土柱.pdf05G336柱间支撑.pdf05G359-1悬挂运输设备轨道(适用于钢筋混凝土和预应力混凝土折线型屋架).pdf 05G359-2悬挂运输设备轨道(适用于钢筋混凝土屋面梁和预应力混凝土工字形屋面梁).pdf05G359-3悬挂运输设备轨道(适用于一般混凝土梁).pdf05G359-4悬挂运输设备轨道(适用于梯形钢屋架).pdf05G414-1~5预应力混凝土工字形屋面梁.pdf05G511梯形钢屋架.pdf05G512钢天窗架.pdf05G513钢托架.pdf05G514-1 12m实腹式钢吊车梁轻级工作制(A1~A3)Q235钢.pdf05G514-2 12m实腹式钢吊车梁中级工作制(A4、A5)Q235钢.pdf05G514-3 12m实腹式钢吊车梁中级工作制(A4、A5)Q345钢.pdf 05G514-4 12m实腹式钢吊车梁重级工作制(A6、A7)Q345钢.pdf05G515轻型屋面梯形钢屋架.pdf05G516轻型屋面钢天窗架.pdf05G517轻型屋面三角形钢屋架.pdf05G525吊车轨道联结及车挡(适用于钢吊车梁).pdf05SG105民用建筑工程互提资料深度及图样结构专业.pdf05SG110建筑结构实践教学及见习工程师图册.pdf05SG332小城镇住宅结构构件与构造.pdf05SG343现浇混凝土空心楼盖.pdf05SG408 SP预应力空心板.pdf05SG521-1钢檩条钢墙梁(冷弯薄壁卷边槽钢檩条).pdf05SG521-2钢檩条钢墙梁(冷弯薄壁斜卷边Z形钢檩条).pdf05SG521-3钢檩条钢墙梁(高频焊接薄壁H型钢檩条).pdf05SG521-4钢檩条钢墙梁(冷弯薄壁卷边槽钢、高频焊接薄壁H型钢墙梁).pdf 05SG522钢与混凝土组合楼(屋)盖结构构造.pdf05SG616混凝土砌块系列块型.pdf05SG811条形基础.pdf06CG01蒸压轻质砂加气混凝土(AAC)砌块和板材结构构造.pdf06CG08悬挂运输设备轨道设计计算(附计算软件).pdf06G101-6混凝土结构施工图平面整体表示方法制图规则和构造详图(独立基础、条形基础、桩基承台).pdf06G112_建筑结构设计常用数据.pdf06G901-1钢筋混凝土结构施工钢筋排布规则与构造详图.PDF06SG331-1混凝土异形柱结构构造(一).pdf06SG429后张预应力混凝土结构施工图表示方法及构造详图.pdf06SG432-1预应力混凝土双T板(坡板宽度2.4m).pdf06SG501民用建筑钢结构防火构造.pdf06SG515-1轻型屋面梯形钢屋架(圆钢管、方钢管).pdf06SG515-2轻型屋面梯形钢屋架(部分T型钢).pdf06SG517-1轻型屋面三角形钢屋架(圆钢管、方钢管).pdf细分招聘专家,精准求职首选:钢构就业网06SG517-2轻型屋面三角形钢屋架(部分T型钢).pdf06SG524钢管混凝土结构构造.pdf06SG529-1单层房屋钢结构节点构造详图(工字型截面钢柱柱脚连接).pdf 06SG614-1砌体填充墙结构构造.pdf06SG812桩基承台.pdf07G120工程做法(自重计算).pdf07FG05人防窗井.pdf07FG03人防楼梯.pdf07FG01人防荷载及构造.pdf07SG359-5悬挂运输设备管道(适用于门式刚架轻型房屋钢结构).pdf07SG518-4多跨门式刚架轻型房屋钢结构(无吊车).pdf07SG526户外钢结构独立柱广告牌.pdf07SG531钢网架结构设计.pdf93G436(一)预应力混凝土空心板.pdf93G436(二)预应力混凝土空心板.pdf94G316Π型钢筋混凝土天窗架.pdf95G358-1钢筋混凝土V形折板(总说明和结构构造).pdf95G358-2钢筋混凝土V形折板(折板构件).pdf95G358-3钢筋混凝土V形折板(悬挑构件).pdf95G358-4钢筋混凝土V形折板(悬挂集中荷载折板).pdf95G358-5钢筋混凝土V形折板(托梁和三脚架).pdf95G425先张法预应力混凝土吊车梁.pdf95G428 12m预应力混凝土鱼腹式吊车梁.pdf95G437-1预应力V形折板(总说明和结构构造).pdf95G437-2预应力V形折板(冷拔低碳钢丝折板构件).pdf95G437-3预应力V形折板(碳素钢丝折板构件).pdf95G437-4预应力V形折板(悬挂集中荷载折板).pdf95G437-5预应力V形折板(悬挑折板).pdf95G437-6预应力V形折板(托梁和三脚架).pdf96G370(一)混凝土空腹屋架(12m跨).pdf 96G370(三)混凝土空腹屋架(18m跨).pdf96G370(二)混凝土空腹屋架(15m跨).pdf96G433-1预应力混凝土折线形托架.pdf96G433-2预应力混凝土三角形托架.pdf96G443(一)预应力混凝土空腹屋架(12m).pdf96G443(三)预应力混凝土空腹屋架(18m).pdf96G443(二)预应力混凝土空腹屋架(15m).pdf96J333-1建筑防腐蚀构造.pdf99ZG408(附册一)SP预应力空心板技术手册.pdf99ZG408(附册二)SP板/砌块居住建筑设计指南.pdf 2003全国民用建筑工程设计技术措施-结构.pdf。
【分层作业】4.5 探索活动:梯形的面积(同步练习) 五年级上册数学同步课时练 (北师大版,含答案)

第四单元多边形的面积4.5 探索活动:梯形的面积【基础巩固】一、选择题1.如图,平行线间三个阴影图形的面积关系是()。
(单位:cm)A.平等四边形的面积最大B.梯形的面积最大C.面积都相等2.一个梯形的下底是18厘米,上底是下底的一半,高是10厘米,这个梯形的面积是()平方厘米。
A.135 B.270 C.1803.把一个梯形分割成两个三角形,这两个三角形的()总是相等。
A.高B.底C.周长D.面积4.一堆钢管堆成梯形,顶层有2根,底层有6根,共5层,这堆钢管共有()根.A.40 B.60 C.20 D.无法确定5.如果一个梯形的面积是90平方厘米,高是30厘米,则它的上下底之和是()A.3厘米B.60厘米C.6厘米二、填空题6.一个梯形的面积是80cm2,如果梯形的上底增加l0cm,下底减少10cm,高不变,面积是( )cm2。
7.如图,淘气用两个完全相同梯形推导面积计算公式,他把两个梯形转化成平行四边形,平行四边形的底相当于梯形( ),平行四边形的高相当于梯形的高,平行四边形的面积相当于( ),因为平行四边形的面积=底×高,也就相当于梯形( )×( ),因此一个梯形的面积=( )。
8.如图,与平行四边形面积相等的图形有( )个;③号长方形最多可以剪出( )个①号三角形。
9.如图,梯形的上底增加2cm,高不变。
要使这个梯形的面积不变,下底应该是( )cm。
10.一条水渠横截面是梯形,渠口宽4.2米,渠底宽3.8米,渠深2.6米,这个水渠的横截面的面积是平方米.三、图形计算题11.求下面图形中阴影部分的面积(单位:m)【能力提升】四、作图题12.在下面的方格纸上画出一个平行四边形和一个梯形,使它们的面积都与所给出的三角形面积相等。
五、解答题13.在城固县南沙湖风景区入口处有一个上底为24m、下底为37m、高为16m的梯形宣传栏。
宣传栏中间留出一个宽为1m,长为16m的长方形刷黄色油漆,其余的刷白色油漆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一组对边平行,另一组对边不平行的四边形,叫做梯形
两腰相等的梯形叫做等腰梯形. B A 底角 腰 上底 腰 B C D
一腰与底垂直的梯形叫做直角梯形.
C AB=CD
高
C
C
下底
底角
二、性质探究
请你画一画、量一量,猜想等腰梯形的性质
等腰梯形的性质: ⑴对称性: 轴对称图形.对称轴—两底中点所在直线
A D
A 分析2:分别过点A、D作AF⊥BC、
A
D
E
D
C
DE⊥BC ,垂足为点E、F.
F 已知:在梯形ABCD中,AD∥BC,AB=DC. A 求证:AC=DB B B 例2.求证:等腰梯形的两条对角线相等.
E
C D
C
四、达标测试
1.填 图 平行四 ( ) 边形
等腰梯形 四边形
梯形 ( 有一组对边平行 ) 另一组对边不平行
五、对自己说,你有什么收获!
(直角梯形和等腰梯形,主要研究了等腰梯形)
1.我们今天学习了哪几种特殊的梯形?主要研究了哪种梯形?
2.等腰梯形性质 1)等腰梯形的一组对边平行,两腰相等。 2)等腰梯形同一底上的两个底角相等,对角线相等。 3)等腰梯形为轴对称图形,对称轴是连接两底中心的直线。 3. 在研究梯形问题时,用哪些方法将问题转化为其他图形问题?
⑵边: 两底边平行,两腰相等. ⑶角: 同一底上的两个内角相等.
∵在等腰梯形ABCD中,AD∥BC
B
A
D
C
∴∠A=∠D, ∠B=∠C.
B ⑷对角线:等腰梯形的两条对角线相等. ∵在等腰梯形ABCD中,AD∥BC ∴AC=BD.
C
三、例题欣赏
例1.已知:在梯形ABCD中, AD∥BC, AB=DC.求证:∠B=∠C,∠A=∠D. 分析1:过点D作DE∥AB, 交BC于点E . B
方法有平移一腰、作两高线、延长两腰。
对教师说,你有什么疑惑! 对同学说,你有什么提示!
直角 ( 梯形
)
2.判断正误
(1)等腰梯形的对称轴是连结上、下底中点的线段。( × ) (2)若等腰梯形有一底角是50°,则其余各角分别为50°、 130°、130°。( ) √
3.选择题
(1)对于等腰梯形,下列结论错误的是(
A.只有一组相等的对边
C)
B.只有一条对称轴
C.只有一对相等的内角 D.两条对角线相等 (2)有两个角相等的梯形是( C )
课件编性质,能用于解决问题; 2.探索梯形概念、性质的过程中培养探究习惯和说理能力 ; 3.体会平移 轴对称有关知识在研究等腰梯形性质中的运用; 教学重点:探索梯形的有关概念、性质及其应用。 教学难点:探索等腰梯形的性质。
一、概念理解
A AD∥BC D
A.等腰梯形 B.直角梯形 C.等腰或直角梯形 D.一般梯形
4.已知:等腰梯形ABCD的腰长是10㎝,∠B=60º , D 上底是8㎝,求梯形的周长。 A
解:过点A作AE∥DC交BC于点E.
在梯形ABCD中, DC=AB=10.
∴∠C=∠B=60˚ ,
B
C
∴∠AEB=∠C=60˚
即△ABE为等边三角形, BE=AB=10.
由AD∥BC, AE∥DC 得 ∴EC=AD=8
AECD ,
梯形周长为:10+10+8+18=46(㎝).
5.已知梯形的上底为8cm,下底为15cm,一腰长为
6cm, 求另一腰x的取值范围.
8
A
6 6 15 E
D
X
B
7
C
6.已知等腰梯形的上、下底边长分别是2㎝, 8㎝, 腰长是5㎝, 求这个梯形的高及面积.
