D4.1
d-对羟基本甘氨酸甲酯盐酸盐生产工艺规程

1 目的规范D-对羟基苯甘氨酸甲酯盐酸盐生产工艺规程,使本产品生产操作过程具有一致性和保证产品质量的均一性,为该产品的生产提供技术标准。
2 范围适用于402车间D-对羟基苯甘氨酸甲酯盐酸盐生产的全过程。
3 责任生产部组织制订,生产车间按要求严格执行,质管部、生产部监督实施。
4 内容4.1 产品概述4.1.1 产品名称:D-对羟基苯甘氨酸甲酯盐酸盐4.1.2 产品概述:4.1.2.1 分子式:C9H11NO3· HCl4.1.2.2 分子量:217.654.1.2.3 结构式:4.1.2.4 用途是制备羟氨苄青霉素、阿莫西林、羟氨苄头孢菌素和羟氨唑头孢菌素等β-内酰胺类抗生素的重要中间体, 同时它也用于多种多肽类激素及农药的合成。
4.2 主要原辅料质量标准4.2.1 原辅料质量标准物料名称质量标准甲醇外观无色透明易挥发的液体,无可见杂质。
鉴别相同条件在色谱图中,供试品主峰保留时间与对照品主峰保留时间一致。
水分≤0.15%含量≥99.5%D-对羟基苯甘氨酸外观白色结晶性粉末溶解度用1mol/L氨水制成5%的溶液,应为无色或淡黄色澄清液体。
比旋度-156.0~-161.0吸光值用1mol/L HCl 制成浓度5%的溶液吸光值应:≤0.040用1mol/L NaOH 制成浓度为5%的溶液吸光值应:≤0.100含 量≥99.0% 水 分 ≤0.30%氯化亚砜外 观无色至淡黄色透明有刺激性臭味的液体。
密度(20℃) 1.630~1.650 色度,(K 2CrO 4)≤1#沸程,75-80℃%(V/V ) ≥99.0 %水质符合饮用水标准。
4.3 化学反应过程及生产工艺流程图 4.3.1 化学反应式:+ CH 3OH4.3.2 工艺流程图(见附表)温度D-对羟基苯甘氨酸甲醇氯化亚砜合成罐D-对羟基苯甘氨酸甲酯盐酸盐4.4 生产工艺过程往合成反应罐中加入D-对羟基苯甘氨酸450kg、750Kg、825Kg、900Kg、1000Kg、1500Kg, 甲醇1600L、2800L、3000L、3300L、3700L、5600L。
4.1 切线方程(精讲)(提升版)(原卷版)
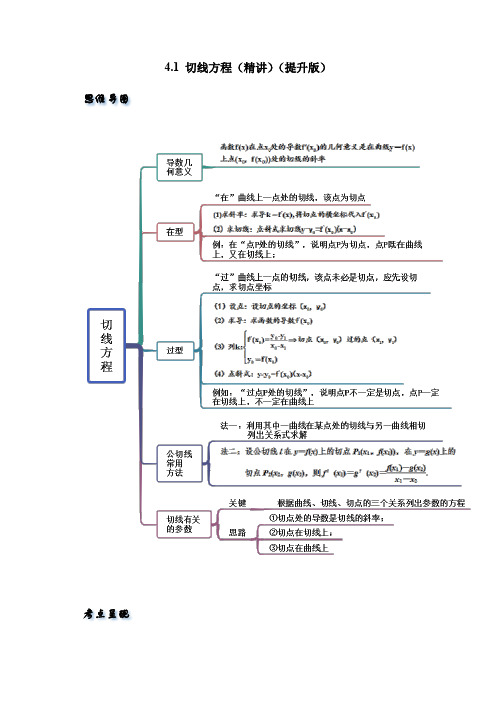
4.1 切线方程(精讲)(提升版)思维导图考点呈现考点一 斜率和倾斜角【例1-1】(2022·江苏淮安)已知函数()cos2(0,πf x x x =∈,)在0x x =处的切线斜率为85,则00co sin s x x -=( ) A .35 B .35C .355-D .355【例1-2】(2022·重庆一中)已知偶函数()f x ,当0x >时,()()212f x x f x '=-+,则()f x 的图象在点()()2,2f --处的切线的斜率为( ) A .3- B .3 C .5- D .5【一隅三反】1.(2022·辽宁)已知曲线()3cos1f x x =-在点()()1,1f 处的切线与直线:30l ax y --=垂直,则实数a 的值为______.2.(2022·湖南·长沙县第一中学模拟预测)函数()2ln 1sin y x x =++的图象在0x =处的切线对应的倾斜角为α,则sin2α=( ) A .310B .±310 C .35D .±35例题剖析3.(2022·湖南)已知P 是曲线)2:ln C y x x a x =++上的一动点,曲线C 在P 点处的切线的倾斜角为θ,若32ππθ≤<,则实数a 的取值范围是( )A .)⎡⎣B .)⎡⎣C .(,-∞ D .(-∞考点二 “在型”的切线方程【例2-1】(2022·广西)曲线31y x =+在点()1,a -处的切线方程为( ) A .33y x =+ B .31y x C .31y x =-- D .33y x =--【例2-2】(2022·广西·贵港市)已知曲线e ln x y ax x =+在点()1,e a 处的切线方程为3y x b =+,则( ) A .e a =,2b =- B .e a =,2b = C .1e a -=,2b =- D .1e a -=,2b =【一隅三反】1.(2022·河南)已知函数()()423f x x m =++的图象经过坐标原点,则曲线()y f x =在点()()1,1f --处的切线方程是( )A .872y x =-B .476y x =-C .872y x =+D .476y x =+2.(2022·安徽)已知()f x 为奇函数,且当0x >时()211e xf x x-=+,则曲线()y f x =在点11,22f ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭处的切线方程为( ) A .240x y ++= B .240x y -+= C .220x y -+= D .220x y ++=3.(2022·安徽·巢湖市)曲线22x ay x +=+在点()1,b 处的切线方程为60kx y -+=,则k 的值为( ) A .1- B .23-C .12D .14.(2022·湖北·武汉二中模拟预测)已知函数()1ln f x x x=-,直线y mx n =+是曲线()y f x =的一条切线,则2m n +的取值范围是( ) A .[)3,∞-+ B .2e 3,e -⎛⎤-∞ ⎥⎝⎦C .[)2ln 24,--+∞D .5ln 2,4⎡⎫-+∞⎪⎢⎣⎭考点三 “过型”的切线方程【例3】(2022·河南洛阳)已知函数()3221f x x x x =-++,则曲线()y f x =过坐标原点的切线方程为( ) A .y x = B .2y x =C .3y x =D .4y x =【一隅三反】1.(2022·广东·新会陈经纶中学)(多选)已知曲线3()21f x x =+.则曲线过点P (1,3)的切线方程为.( ) A .630x y --= B .3230x y -+=C .690x y +-=D .3290x y +-=2(2022·北京·汇文中学)228y x =+过点()12P ,的切线方程是__________.3.(2022·四川·广安二中)函数()2e x f x x =过点()0,0的切线方程为考点四 切线或切点数量问题【例4-1】(2022·河南洛阳)若过点()1,0P 作曲线3y x =的切线,则这样的切线共有( ) A .0条 B .1条C .2条D .3条【例4-2】(2022·全国·高三专题练习)若过点(,)a b 可以作曲线ln y x =的两条切线,则( ) A .ln a b < B .ln b a <C .ln b a <D .ln a b <【一隅三反】1.(2022·河南洛阳)若过点()1,0P 作曲线3y x =的切线,则这样的切线共有( ) A .0条 B .1条 C .2条 D .3条2.(2022·湖北·宜城市第一中学)若过点(),a b 可以作曲线()10y x x x=->的两条切线,则( ) A .0b a >> B .10a b a a-<<< C .10a b a a<-<< D .1a b a a>>-且0a >3.(2022·河南洛阳)若过点()1,P t 可作出曲线3y x =的三条切线,则实数t 的取值范围是( ) A .(),1-∞ B .()0,∞+ C .()0,1 D .{}0,14.(2022·全国·高考真题)若曲线()e x y x a =+有两条过坐标原点的切线,则a 的取值范围是________________.考点五 公切线【例5-1】(2022·安徽省舒城中学)已知直线l 是曲线e 1x y =-与ln 1y x =+的公共切线,则l 的方程为_____.【例5-2】(2022·江苏·南京外国语学校模拟预测)若两曲线y =x 2-1与y =a ln x -1存在公切线,则正实数a 的取值范围为( ) A .(]0,2e B .(]0,e C .[)2,e +∞ D .(],2e e【一隅三反】1.(2022·全国·模拟预测)若直线l 与曲线2y x 和2249x y +=都相切,则l 的斜率为______.2.(2022·河北保定·二模)(多选)若直线3y x m =+是曲线()30y x x =>与曲线()260y x nx x =-+->的公切线,则( ) A .2m =-B .1m =-C .6n =D .7n =3.(2022·安徽·合肥一六八中学)若直线y kx m =+是曲线ln(1)y x =-的切线,也是曲线3e x y -=的切线,则k =__________.考点六 切线与其他知识的运用【例6-1】(2022·湖北·黄冈中学)已知a ,b 为正实数,直线y x a =-与曲线ln()y x b =+相切,则14a b+的最小值为( )A .8B .9C .10D .13【例6-2】(2022·广东·深圳市光明区高级中学)已知函数()()2ln f x x x ax x a =-+∈R ,则曲线()y f x =在点()()1,1f 处的切线l 恒过定点_____________.【一隅三反】1.(2022·河北衡水)已知函数2ln ()2xf x x x=-在1x =处的切线为l ,第一象限内的点(,)P a b 在切线l 上,则1111a b +++的最小值为( )A B C D 2.(2022·安徽)对于三次函数()f x ,若曲线()y f x =在点(0,0)处的切线与曲线()y xf x =在点(1,2)处点的切线重合,则(2)f '=( )A .34-B .14-C .4-D .143.(2022·黑龙江·哈尔滨三中)若曲线e x y =过点(2,0)-的切线恒在函数212()e 31e e x f x a x x ⎛⎫=-+-+- ⎪⎝⎭的图象的上方,则实数a 的取值范围是__________.考点七 切线方程的运用【例7-1】(2022·全国·高三专题练习)设点P 在曲线y x =上,点Q 在曲线()ln 2y x =上,则PQ 的最小值为( )A .1ln 22- B )1ln 2- C .1ln 22+ D .)1ln 22+【例7-2】(2022·山东烟台·三模)已知函数()2ln ,021,0x x f x x x x ⎧>=⎨+-≤⎩,若方程()1f x ax =-有且仅有三个实数解,则实数a 的取值范围为( ) A .01a << B .02a << C .1a > D .2a >【一隅三反】1.(2022·江苏徐州)过平面内一点P 作曲线|ln |y x =的两条互相垂直的切线12,l l ,切点分别为12,P P (12,P P 不重合),设直线12,l l 分别与y 轴交于点A ,B ,则ABP △面积的取值范围为( ) A .10,2⎛⎤⎥⎝⎦B .()0,1C .1,12⎡⎫⎪⎢⎣⎭D .(0,2]2.(2022·全国·高三专题练习)已知函数()()e ln xf x x a x x =-+有两个零点,则实数a 的取值范围是______.3.(2022·云南曲靖·二模)设()'f x 是函数()f x 的导函数,()f x ''是函数()'f x 的导函数,若对任意R ()0,()0x f x f x '''∈><,恒成立,则下列选项正确的是( ) A .0(3)(3)(2)(2)f f f f ''<<-< B .0(3)(2)(2)(3)f f f f ''<-<< C .0(3)(2)(3)(2)f f f f ''<<<- D .0(2)(3)(3)(2)f f f f ''<<<-4.(2022·江西·新余市)若点A 在曲线ln 1y x =-上运动,点B 在直线2y x =+上运动,,A B 两点距离的最小值为______。
七年级地理上册4.1《天气和天气预报》2

(běifāng)
都表示北风。 风力是风的__强__弱,级数
越大,风力越__强。
2.在卫星云图上绿色(lǜ sè)表示陆__地__,蓝 色表示__海__洋,白色表示 ___云_ 区。不同地 区,云层厚度是不同的。云的顔色越 白,表示云层____。越云厚层厚的地方一 般是____ 。 阴雨区第三十八页,共四十四页。
第十七页,共四十四页。
明天(míngtiān)的天气怎么样?
天气预报(tiānqìyùbào)的内容
第十八页,共四十四页。
收听广播
观看电视 阅读报纸
拨打(bō dǎ)12121电话查 询
上网(shànɡ wǎnɡ) 查询
手机(shǒu jī)短信息查 询
第十九页,共四十四页。
假如没有播报
(bō bào)员的说明,电 视上出现了卫星云 图和符号,你能明 白其中的含义吗? 你能做一个天气预 报员吗?
大雨到
青蛙叫
天气晴
泥鳅静
出门带雨衣
乌龟背冒汗
天放晴
知了鸣
出门带雨伞
第十六页,共四十四页。
天气(tiānqì)的影响(“漫谈天地人” )
材料A:天气(tiānqì)
与交通的关系;
材料B:天气与生 活的关系;
材料C:天气与农 业的关系;
材料D:天气与军
事活动的关系。
想一想:天气影响(yǐngxiǎng)人们的哪些活动?
1、天气(tiānqì)(weather)
指一个地方短时间内风雨、冷热、 阴晴等大气状况。
特 点: 时间短
变化快 不稳定
第九页,共四十四页。
天气的特点(tèdiǎn)(小结)
1. 时间短,变化快 例如: “太阳雨”、“雷阵雨”。
4.1 整 式 同步练习人教版(2024新教材)七年级数学上册(含答案)

4.1 整式第 1 课时用字母表示数A层知识点一含字母式子的书写及意义1.下列各式符合书写要求的是 ( )a B. n ·2 C.a÷b D.2πr²A.1232.下列表述中,不能表示“4a”的意义的是( )A.4与a的积B. a 的4 倍C.4 个a 相加D.4 个 a 相乘3.式子3(y—1)的正确含义是 ( )A.3乘 y 减1B.3 与 y 的积减去 1C. y 与1的差的3倍D. y 的 3 倍减去 1知识点二用含字母的式子表示数量关系4.用式子表示“a 的平方与b的和”,正确的是( )A.a+b²B.a²+bC.a²+b²D.(a+b)²5.原产量n 吨,增产30%之后的产量应为( )A.(1-30%)n 吨B.(1+30%)n 吨C.(n+30%)吨D.30%n 吨6.某品种苹果的市场价格为15元/千克,买 a 千克该苹果需要元.7.用含字母的式子表示:大2,则乙数为多少?(1)甲数为x,乙数比甲数的13(2)每本练习本m元,甲买了6本,乙买了a本,两人共花了多少元?甲比乙多花了多少元?B层8.一个两位数,它的十位数字是x,个位数字是y,那么这个两位数是 ( )A. x+yB.10xyC.10(x+y)D.10x+y9.已知轮船在静水中的速度为x 千米/时,水流速度为a 千米/时,则轮船在顺水中航行3小时的路程是千米.10.一根长80cm的弹簧,一端固定.如果另一端挂上物体,那么在正常情况下物体的质量每增加1 kg可使弹簧增长 2cm.正常情况下,当挂着xkg的物体时,弹簧的长度是 cm.11.如图,已知长方形的长为a、宽为 2,两个半圆的直径都为 2,用含 a 的式子表示出阴影部分的面积.12.电影院里座位的总排数是m,若第一排的座位数是a,并且从第二排起,每排总比前一排的座位数多1个,则该电影院里第m 排有多少个座位?第 2 课时单项式A层知识点一单项式的相关概念1.下列各式: 124,4xy,4a+b,a,2009,¹/₂a²bc中,单项式的个数是( )A.3B.4C.5D.62.单项式−3xy²的系数是( )A.-3B.3C.-3xD.3x3.关于单项式−5xy n8的说法,正确的是 ( )A.系数是5,次数是nB.系数是−58,次数是n+1C.系数是−58,次数是nD.系数是-5,次数是n+14.已知一个单项式的系数是3,次数是5,则这个单项式可能是 ( )A.5x²yB.−3x⁵C.3x²y⁵D.3x²y³5.若单项式 25x"y 是四次单项式,则 n 的值为【变式题】(1)若单项式−58a2b m与−117x3y4是次数相同的单项式,则m 的值为;(2)若单项式−x³yⁿ⁺⁵的系数是m,次数是9,则m+n的值为 .知识点二单项式的应用7.已知一个长方体的长、宽、高分别为a,b,c,则这个长方体的体积为,这个式子的系数为,次数为 .8.如图是一个长方形活动窗,窗高 1.5 米,当活动窗扇拉开长度为b米时,长方形窗框的通风面积为平方米.B层9.下列说法中,正确的是 ( )A.单项式一定是含字母的式子B.单项式a 没有系数C.-y 的次数是0D.单项式−π²x²y的系数是-π²,次数是310.已知( (a−1)x²yᵃ⁺¹是关于x,y的五次单项式,则这个单项式的系数是 ( )A.1B.2C.3D.011.小英对单项式3a 给出了这样的解释:西瓜每千克 3元,那么买 a 千克西瓜共需 3a 元.请你对该单项式做出另外的解释:12.若3x"y" 是含有字母x 和y 的五次单项式,m,n 均为正整数,则 m"的最大值为 .13.观察下列各式:−x,12x2,−13x3,14x1,−15x5,⋯.(1)请你写出第2020个和第2021个单项式;(2)★请你写出第n个单项式.第 3 课时多项式A层知识点一多项式及其相关概念1.下列式子中不是多项式的是 ( )A.4s+3tB.2abC.a+b3D. x+12.在下列给出的四个多项式中,为三次二项式的多项式是 ( )A.a²−3B.a³+2ab−1C.4a³−bD.4a²−3b+23.对于多项式3x²−y+3x²y³+x⁴−1,下列说法正确的是 ( )A.次数为 12B.常数项为 1C.项数为5D.最高次项为x⁴4.如果多项式xⁿ⁻²−3x+2是关于x 的三次三项式,那么n等于 ( )A.3B.4C.5D.6.【变式题】关注次数→关注项数若关于 x 的多项式(a−4)x³−x²+x−2是二次三项式,则a= .5.指出下列多项式的项和次数:(1)2m4−12m2+23;(2)a³−2a²b+ab²+3b³.知识点二 整式及其应用6.下列各式中是整式的有 ( )1—3x²,— 12x, 2x ,- 24,π+ 12a,0,-x²+y²—1.A.7个B.6 个C.5个D.4 个7.农民张大伯因病住院,手术费为a 元,其他费用为b 元,由于参加农村合作医疗,手术费报销85%,其他费用报销 60%,则张大伯此次住 院可报销 元.8.有一块长为 x m 、宽为 y m 的长方形草坪,在草坪中间有一条宽为2m 的人行道,形状如图所示,则 这 块 草 坪 的 实 际 绿 化 面 积 是 m². 9. 已知多项式 a 3+12ab 4−a m+1b −6是六次四项式,单项式2xy³n.与该多项式的次数相同,求 m²+n²的值.B 层10.已知关于 x 的多项式 3x⁴−(m +5)x³+ (n −1)x²−5x +3不含 x³ 和x²,则 ( )A. m=-5,n=-1B. m=5,n=1C. m=-5,n=1D. m=5,n=-111若2a ⁴b+a"b² 是五次多项式,则指数 m 的值不可能是( )A.4B.3C.2D.112.随着计算机技术的迅猛发展,电脑价格不断降低.某品牌电脑按原售价降低m 元后,又降低20%,现售价为n 元,那么该电脑的原售价为 ( )A.(45n +m)元B.(54n +m)元C.(5m+n)元D.(5n+m)元13.有一个关于x ,y 的多项式,每项的次数都是3.(1)这个多项式最多有 项;(2)在上述条件下,若此时这个多项式各项系数和为0,则这个多项式可能为 .(写出一个即可)14.如图是一个工件的横断面(上半部分为半圆,下半部分为两个长方形)及其尺寸(单位:cm).(1)用含a ,b 的式子表示它的面积S ;(2)当a=15,b=8时,求 S 的值(π取3.14,结果保留两位小数).15.已知关于x的整式( (|k|−3)x³+(k−3)x²−k.(1)若此整式是单项式,求 k 的值;(2)若此整式是二次多项式,求k 的值;(3)若此整式是二项式,求k 的值.C层16.用同样大小的黑色棋子按如图所示的规律摆放:(1)第5 个图形有多少颗黑色棋子?第n 个图形有多少颗黑色棋子?(2)第几个图形有2022 颗黑色棋子?请说明理由.第1 课时 用字母表示数1. D2. D3. C4. B5. B6.15a7.解:(1)乙数为 13x +2.(2)两人共花了(6m+am)元,甲比乙多花了(6m-am)元.8. D 9.3(x+a) 10.(80+2x)11.解:阴影部分的面积为 2a-π.12.解:因为共有 m 排座位,且从第二排起,每排总比前一排的座位数多1个,所以第一排有a 个座位,第二排有(a+1)个座位,第三排有(a+2)个座位……第m 排有(a+m-1)个座位.第 2 课时 单项式1. B2. A3. B4. D5.3 【变式题】(1)5 (2)06.解:(1)从左到右,从上到下分别填入 0.2,一 27 35π,-2°,1,5,2,5.7. abc 1 3 8.1.5b 9. D 10. A11.作业本每个3元,买 a 个作业本共需要 3a 元(答案不唯一)12.913.解:(1)第2020个单项式是 12020x 2020,第 2021个单项式是 −12021x 2021.(2)第n 个单项式是 (−1)n ⋅1n x n . 第 3 课时 多项式1. B2. C3. C4. C 【变式题】45.解:(1)各项分别是 2m 4,−12m 2,23,次数是4.(2)各项分别是a³,-2a²b,ab²,3b³,次数是3.6. B7.(85%a+60%b)8.(xy-2y)9.解:依题意得 m+1+1=6,1+3n=6,则 m =4,n =53.所以 m 2+n 2=42+(53)2= 1879.10. C 11. A 12. B13.(1)四 (2)x³+x²y −xy²−y³(答案不唯一)14.解: (1)S =23ab +12π×(a 2)2=(23ab +) π8a 2)(cm 2).(2)当a=15,b=8时, S =23×15×8+ 3.148×152≈168.31(cm 2).15.解:(1)因为关于 x 的整式是单项式,所以|k|-3=0且k-3=0.解得k=3.所以k 的值是3.(2)因为关于x 的整式是二次多项式,所以|k|--3=0且k--3≠0.解得k=--3.所以k 的值是-3.(3)当关于x 的整式是二项式时,分以下两种情况:①三次项系数为0,即|k|—3=0且k--3≠0,解得k=--3;②常数项为0,则k=0.综上可知,k 的值是-3或0.16.解:(1)第1 个图形有6颗黑色棋子,第 2 个图形有 9 颗黑色棋子,第 3 个图形有 12 颗黑色棋子,第4个图形有15颗黑色棋子,所以第5个图形有 18 颗黑色棋子,第n 个图形有3(n+1)颗黑色棋子.(2)第673 个图形有2022颗黑色棋子.理由如下:因为 2022÷3—1=673,所以第 673个图形有 2022 颗黑色棋子.。
人教版高中数学精讲精练必修一4.1 指数运算(精练)(解析版)

4.1指数运算(精练)1.(2023·全国·=()A.34a B.78a C.1112a D.2728a 【答案】C11111111112236322221212[()]()a a a a a a a a a=⋅=⋅⋅=⋅⋅=.故选:C2.(2023·全国·(a,b为正数)的结果是()A.22baB.22abC.22a b D.ab【答案】C()()178333112233123322222ab a b a ba ba bb a b===⎡⎤⎣⎦.故选:C.3.(2023·全国·高一课堂例题)若321x x x++=-,则2827211227281x x x x x x x x----++⋅⋅⋅++++++⋅⋅⋅++的值是()A.2B.0C.1-D.1【答案】D【解析】由321x x x++=-,得()2110x x x+++=,即()()2110x x++=,解得=1x-.∴28272112272811x x x x x x x x----++⋅⋅⋅++++++⋅⋅⋅+=+.故选:D4.(2023·全国·高一专题练习)下列根式与分数指数幂的互化正确的是()A.()12x=-B13(0)y y=<C.130)x x-=>D.1234x=【答案】C【解析】对于A选项:由1122(0),()0)x x x x=-≥-=≤,故该项等号两侧不相等,所以A错误;对于B13(0)y y=-<,所以B错误;对于C 选项:由指数幂的运算性质,可得130)xx -=>,所以C 正确;对于D 选项:当0x >时,2333144423()x x ===,当0x <时,2333144423)(()x x ==-=,显然当0x <时,该项的等量关系不成立,所以D 错误.故选:C.5.(2023·全国·高一专题练习)计算1022-)A .1B .CD .122-【答案】B【解析】1022(1)12-+-=故选:B6.(2023·全国·高一专题练习)方程135108x x x -⋅=的解集是()A .{}1,4B .14⎧⎫⎨⎬⎩⎭C .11,4⎧⎫⎨⎬⎩⎭D .14,4⎧⎫⎨⎩⎭【答案】B【解析】原方程可化为:13335522x x x x -⋅⋅=,即4151x -=,解得:14x =.故选:B .7.(2023秋·内蒙古阿拉善盟·高一阿拉善盟第一中学校考期末)已知正数m ,n 满足242m n ⨯=,则12m n+的最小值为()A .3B .5C .8D .9【答案】D【解析】由正数m ,n 满足242m n ⨯=,即222222m n m n +⨯==,所以21m n +=,所以()12122225529n m m n m n m n m n ⎛⎫+=+=++≥+ ⎪⎝⎭,当且仅当n m m n =,即13m n ==时,取得等号.故选:D.8.(2023秋·高一课时练习)计算下列各式.(1=;(2=;(3=.【答案】a-π3-12【解析】(1a =-.(23ππ3=-=-.(353112222==--=.故答案为:(1)a -;(2)π3-;(3)129.(2023·全国·.【答案】=33-22⎡⎤=⎢⎥⎣⎦(515=++-=====.故答案为:10.(2022·江苏·高一专题练习)()1⎫+⋅⋅⋅=⎪.【答案】8【解析】原式()112132438180⎛=⨯+++⋅⋅⋅+ ----⎝⎭(11=+()11==()818=+.故答案为:8.11.(2023·全国·高三专题练习)()2031.82-⎛⎫-+= ⎪⎭⎝.【答案】19【解析】()222330232711.8192380.12-⎛⎫⎛⎫⎛⎫-+=+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⨯2333224349110311027199294⨯⎛⎫=+⨯-+=+⨯-+= ⎪⎝⎭.故答案为:1912.(2023春·上海宝山)若实数x y 、满足21x y +=,则24x y +的最小值为.【答案】【解析】24y x ≥==+=当且仅当2x y =,即11,24x y ==时取到等号.故答案:.13.(2022·高一课时练习)方程41217480x x +-⨯+=,x =.【答案】12-或32.【解析】】因为()22417480x x ⋅-⨯+=,所以142x=或8,解得12x =-或32.故答案为:12-或32.14.(2023·安徽)已知()2311a a --=,则a 的取值可能是.【答案】2或23或0【解析】因为()2311a a --=,当311a -=,即23a =时,()4233111a a ---==,满足要求,当311a -=-,即0a =时,()()223111a a ---=-=,满足要求,当311a -≠且311a -≠-时,由()2311a a --=可得20a -=,所以2a =,所以a 的取值可能是2或23或0,故答案为:2或23或0.15.(2023·全国·0=,则()2020yx =.【答案】10=,0130x y =⇒+++=,所以13x y =-=-,.所以()2020202031)]1[(yx -=-=.故答案为:116.(2023·全国·高三专题练习)若27,16a b==-⨯-=【答案】6(-⨯-()()()()11253211272564164ab a ba b a b ⋅⋅=⋅⋅25113322171536244a b a b a b a b ⎛⎫⎛⎫⋅ ⎪⎪⎝⎭⎝⎭=⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭12111575233223644ab +--+--=11344a -=,因为27,16a b ==,所以原式1134427166-=⨯⨯=.故答案为:6.17.(2023·全国·高三专题练习)()()()()()3333241441121a a a a a a a a aa a a ------+-+-+=-++-【答案】2a【解析】原式()()66212144121a a a a a a a a a a a a --------⋅+=+-++-()()()()()222441114411a a a a a a a aa a a a -------++-=+--++()()1111112a a a a a a a a a a a a a------+-=-=++-=-.故答案为:2a .18.(2023·全国·高三专题练习)132111333311111x x x xx x x x -+-+-+++-=【答案】13x -【解析】132111333311111x x x xx x x x -+-+-+++-12112111133333333321113333111111111x x x x x x x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫-++++ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭=+⎛⎫⎛⎫--+ ⎪⎝+⎪⎭⎭-++-⎝12121133333311x x x x x x =-+-+--=-.故答案为:13x -19(2022秋·内蒙古阿拉善盟)(1)计算())24233330.12328-⎛⎫⎛⎫-+⋅-⎪ ⎪⎝⎭⎝⎭(2)化简:121121332a b a b ---⎛⎫⋅⋅⋅ ⎪.(3)已知11222a a -+=,求22112a a a a --++++的值.【答案】2-;(2)1a -;(3)34【解析】(1)())24233330.12328-⎛⎫⎛⎫-+⋅- ⎪ ⎪⎝⎭⎝⎭431322491((3))194=+⨯--1131=+--2=(2)121121332a b a b ---⎛⎫⋅⋅⋅⎪111132231566=aba b --+⋅⋅55661566aba b -⋅=⋅1a -=(3)因为11222a a -+=,两边同时平方可得:12a a -+=,再将12a a -+=两边同时平方可得:222a a -+=,所以22112132224a a a a --+++==+++.20.(2023秋·高一课时练习)求下列各式的值.(1)若32,35a b ==,求23a b -;(2)已知312ab +=a b 的值;(3)若13,2a b -==122a -⋅;(4)若,2.520a b ==111332338234a b a b ---⎛⎫⋅⋅⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭.【答案】(1)45(2)3(3)14(4)4【解析】(1)利用指数运算法则可知()22233333a ab a b b--=⋅=,将32,35ab==代入可得2224355a b-==.(2()3322112222333333333a a b a ba ba b ba a +⋅⋅====⋅,又312ab +=,3233a bb +==(3)化简得()()211111123231132222222aab aba ab a b ---+++⎛⎫==⋅⋅⋅= ⎪⎝⋅⎭,将13,2a b -=3211232321112224a a b --⎛⎫⋅===⨯= ⎪⎝⎭(411133231138283412226923339a b a b a b a b a b b -------=⎛⎫⋅⋅⎛⎫ ⎪⎛⎫ ⎪=⋅ ⎪ ⎪⎝⎭ ⎪⎝⎭=又,2.520a b ==,所以34222311133238233320842.5a b a b b a ---⎛⎫⋅⎛⎫⎫ ⎪⎛⎛⎫=== ⎪ ⎪⎝⎭ ⎝⎪= ⎪⎪⎭⎝⎭21.(2023秋·高一课时练习)已知817,2771a b =-=,求(2112133334133327a a b a a a b++-的值.【答案】94【解析】因为0,270a a b ≠-≠,133327aa a b-21121133333341133339327a a b b a b a a ba++-=⨯-2112211233333333523339392727a a b a b a b a b ba a b++---=-2222333271119248()(27)()327a b a a b a-=====---.22.(2022秋·高一单元测试)计算下列各式的值:(1))()1004623.251648229004-⎛⎫+-⨯-- ⎪⎝⎭;(2)41332233814a a bb a ⎛-÷- ⎝++【答案】(1)100(2)a【解析】(1))()1004623.251648229004-⎛⎫+-⨯-- ⎪⎝⎭()()46310.25331114224234272122--⎫⎛⎫=+-⨯⨯-- ⎪⎝⎭⨯⨯⎭⎝4131113113242622224463324272122⎛⎫⎛⎫⨯--⨯- ⎪ ⎪⎝⎭⎝⎭⎡⎤⎛⎫⎢⎥=+-⨯⨯-- ⎢⨯⨯⎪⎢⎥⎝⎭⎥⎣⎦1332442324272122-=⨯⨯+-⨯⨯--2727211004+---=⨯=(2)41332233814a a bb a ⎛-÷- ⎝++()()11113333221133338422aa b a ab ab a b a-=÷⨯+-+()()11133322111333338422aa b aab ab a ba -=⨯⨯++-()88a b aa a b-==-23(2023·全国·高一课堂例题)化简下列各式:(1)())21132330.0021028---⎛⎫-+--+⎪⎝⎭;0a >,0b >);(3)112111222111aa a a a----+--+(0a >且1a ≠).【答案】(1)1679-(2)7188a -(3)0【解析】(1)原式())121232322312715001021 53138008----⎛=⎫⎛⎫=+-+⎪ ⎪⎝⎭⎝⎛⎫-⋅+⎭⎪⎝⎭416720199=+-+=-.(2)方法一(由内向外化)==13122241324a b ab a b⎛⎫⎪=⋅⋅⎪⎪⎝⎭1171113371222188422444a b a a b-+----⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭.方法二(由外向内化)11122232a bb a⎡⎤⎛⎫⎢⎥==⎢⎥⎝⎢⎥⎣⎦11213111127123238424288811333248a b a a b a a b a a bb a b b a b b a b-⎧⎫⎡⎤⎪⎪⎛⎫⎛⎫⎪⎪⎛⎫⎛⎫⎢⎥==⋅=⋅⋅=⎨⎬ ⎪ ⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎪⎪⎣⎦⎪⎪⎩⎭⋅.(3)方法一原式()()11221111111122222111112222211111a aa aa a a a a a a aa a a a a a----------⎛⎫+⎪--+⎝⎭=-=-=-=-+-+.方法二原式()112111111222221111011a aa a a aa a-----+=-=-=⎛⎫-+⎪⎝⎭.24.(2023·全国·高三专题练习)解下列方程:342956x x x⨯+⨯=⨯;【答案】0x=或1x=;【解析】由342956x x x⨯+⨯=⨯,可得()()2232502323x x x x⨯-⨯+⨯=⨯,所以()()2203233x x x x-⨯⨯-=,所以230x x-=或20323x x-⨯=⨯,由230x x -=,可得213x⎛⎫= ⎪⎝⎭,故0x =,由20323x x -⨯=⨯,可得1123x x --=,即1213-⎛⎫ ⎪⎝⎭=x ,所以10x -=,即1x =,所以0x =或1x =;1.(2023·河南开封)已知0a >,0b >,且1a b +=,a b ¹,则下列不等式成立的是()A 1122a b <<+B 1122a b <+<C .1122a b +<<D .1122a b+<<【答案】A【解析】2112a b a b =++=+≤++=,∵a b ¹;1122a b +≥==∵a b ¹,∴等号不成立,故1122a b +>1122a b <<+.故选:A.2.(2022秋·高一课时练习)化简1111132168421212121212-----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的结果为()A .1321122-⎛⎫- ⎪⎝⎭B .11321122--⎛⎫- ⎪⎝⎭C .113212--⎛⎫+ ⎪⎝⎭D .12【答案】B 【解析】1111132168421212121212-----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=11111113232168324212121212121212-------⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+++++÷- ⎪⎪⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=111111161683242121212121212------⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-++++÷- ⎪⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=111118832421212121212-----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+++÷- ⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=11113244212121212----⎛⎫⎛⎫⎛⎫⎛⎫-++÷- ⎪ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭=1113222121212---⎛⎫⎛⎫⎛⎫-+÷- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭=()11321212--⎛⎫-÷- ⎪⎝⎭=11321122--⎛⎫- ⎪⎝⎭故选:B3.(2023·全国·高三专题练习)已知0a b >>,224a b ab +=,则22-a b ab 的值为.【答案】【解析】由0a b >>,224a b ab +=,可得224,4a b a b ab b a+=∴+=,设a t b =,则1t >,则214,410t t t t +=∴-+=,解得2t =(2t =,故2212222a b a b t ab b a t -=-=-=+++,故答案为:。
人教版七上地理4.1《人口与人种》习题精选(含答案)

第一节人口与人种基础巩固1.人口的自然增长率是由________决定的()。
A.人口出生率B.人口死亡率C.经济发展水平D.人口出生率与人口死亡率读漫画“灾难深重的‘母亲’”,完成第2~3 题。
2.该漫画反映的人口问题是()。
A.人口增长过快B.人口增长过慢C.人口分布不均D.人口城市化太高3.该漫画反映的人口问题最严重的地区是()。
A.大洋洲B.非洲C.欧洲D.北美洲4.关于人口密度的叙述,正确的是()。
A.人口的疏密程度可用人口密度来表示B.人口越多的国家,人口密度越大C.人口自然增长率高的国家,人口密度大D.经济发达的国家人口密度大,发展中国家人口密度小5.世界人口稀少的地区是()。
A.寒带气候分布的地区B.热带季风气候分布的地区C.温带海洋性气候分布的地区D.地势低平的平原地区6.由于人口增长过快而带来的问题不包括()。
A.人口老龄化、劳动力短缺B.过度开发资源,造成环境问题C.就业困难,教育、医疗紧张D.住房紧张、交通拥堵7.下列叙述正确的是()。
A.人种的分布都是小范围的集中分布B.黄种人多分布在较为寒冷的地区C.黑种人多分布在气温较高的热带地区D.白种人分布在低纬度地区8.下列叙述符合黄种人特征的是()。
A.肤色黝黑,头发卷曲,嘴唇较厚B.肤色、眼色、发色浅,鼻梁高C.皮肤淡黄色,头发黑直,面庞扁平D.肤色浅,嘴唇较厚,头发卷曲9.同学们在观看体育节目时,经常可以看见美国的篮球体育明星,如乔丹(下图),你知道他的祖先来自哪里吗?()A.南美洲B.大洋洲C.非洲D.欧洲10.亚洲东部的居民主要是()。
A.白种人B.黑种人C.黄种人D.各种人都有能力提升11.亮亮同学学习了本节内容后,对世界人口的增长、分布、人口问题、密度等方面作了如下归纳,其中错误的一项是()。
A.非洲人口自然增长率最高B.人口的增长要与社会、经济发展相适应,与资源、环境相协调C.中纬度近海地区的人口分布多,高寒地区人口分布少D.人口越少的国家,人口密度越小12.大量乡村人口涌入城市带来的问题是()。
D4.1原子的构成【丰田初中导学案】

第四单元物质构成的奥秘4.1原子的构成一、学习目标:1.知道原子是由质子、中子和电子构成的。
2.理解原子不显电性的原因。
3.初步了解相对原子质量的概念,学会查相对原子质量表。
重点:原子的构成,相对原子质量难点:核电荷数、核内质子数和核外电子数的关系,相对原子质量概念的形成。
【课前预习】1.分子与原子的本质区别是什么?2.原子是不是在任何情况下都是不可分割的实心小球呢?如果不是,那你想象中的原子是什么样的呢?【情境导入】中国第一颗原子弹爆炸成功(1964.10.16新疆罗布泊),原子弹的巨大威力是如何产生的呢?二、自主探究:【阅读】课本第70页原子的构成一段文字,观察图4-11.同桌互相描述一下原子的结构。
(提示:可从位置、电性、所占体积等不同角度描述。
)2.分子、原子都在不断地运动着,想象一下,构成原子的原子核和电子是如何运动的呢?【观察】教师播放的动画:原子内部的运动,概括原子的结构。
【分析思考】分析教材第70页表4—1、4—2,思考并回答下列问题:1.构成原子的三种粒子的电性、质量如何?整个原子的质量主要集中在哪部分?2.原子中有带电的粒子,那么整个原子是否带电?为什么?3.是否所有原子核内都有中子?4.同种原子核内的质子数和中子数有何特点?5.不同种类原子的内部结构有何不同?【阅读】课本第71页第一段,体会原子的体积之小。
表1【阅读】教材第71页的相关内容。
1.结合表1体会为什么采用相对原子质量。
2.请用公式的形式表示出原子的实际质量与相对原子质量的关系。
3.运用这个式子,计算一下表1中任意两种原子的相对原子质量。
【交流讨论】1.相对原子质量有没有单位?2.两种原子的质量之比与其相对原子质量之比是何关系?3.分析表2,思考各原子相对原子质量的近似值,与该原子的质子数、中子数有何关系?表2【交流讨论】同桌互相提问,从附录中查出一些原子的相对原子质量。
【课堂小结】通过本节课的学习,你收获了什么?【我的收获】【小结】一、原子的构成个单位)———1.1个单位)2.原子为什么不显电性?3.不同种类的原子,核内的质子数,核外的电子数。
五步拳4.1d

妙招名称
武术—五步拳
妙招针对的重难点问题
学段
学科
教材版本
章节
针对的
重难点问题名称
小学
体育
人教版
第五章
武术基本动作的舒展、大方
妙招的描述
要达到快、准、稳、狠。(出拳要快、目标要准、步伐要稳、对准目标要狠)
妙招的修改
我要修改两个妙招:
第一、动作名称要记牢,学生一般都记不住每个动作名称,上动下不停,、协调、连贯最关键。
妙招的使用
通过上述的改变,学生做的时候就知道照猫画虎、不知道怎样记动作名称要领,记住了动作名称也就不难了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4. 段寄存器 •新增 、GS两个新的 位段寄存器 :CS、DS、SS、 新增FS、 两个新的 两个新的16位段寄存器 新增 、 、 、 ES 、FS、GS 、 •保护模式下: 保护模式下: 保护模式下 每一个存储段定义了一个8字节长的数据结构 字节长的数据结构, 每一个存储段定义了一个 字节长的数据结构,用来说明 段的基址 段的界限长度 大小)和段的访问控制属性 基址, 界限长度( 访问控制属性, 段的基址,段的界限长度(大小)和段的访问控制属性, 该数据结构称为段描述符。 有关的段描述符放在一起并构成一个系统表, 有关的段描述符放在一起并构成一个系统表,称为段描述 符表。 为了标识一个段描述符在哪一个段描述符表中,其索引号 为了标识一个段描述符在哪一个段描述符表中, 是多少,它的特权级如何, 为每个段定义了一个16 是多少,它的特权级如何,80486为每个段定义了一个 为每个段定义了一个 位的段选择符 (段选择子)
每一种描述符表在存储器中的段基地址、界限和段属性信 每一种描述符表在存储器中的段基地址、 息由系统地址寄存器保存
47 GDTR IDTR 15 TR LDTR 15 0 0 段选择符 段选择符 47 63 32位段基址 位段基址 63 32位段基址 位段基址 20位段界限 位段界限 20位段界限 位段界限 16 15 16 15 0 0 0 12位段属性 位段属性 0 12位段属性 位段属性 32位段基址 位段基址 32位段基址 位段基址 16位段界限 位段界限 16位段界限 位段界限
8086内部寄存器 8086内部寄存器 8014个 16位的寄存器 , 其寄存器结构 中有14 位的寄存器, 如图2 所示。 如图2.3所示。
4.1.2 80486内部寄存器 80486内部寄存器
基 本 结 构 寄 存 器 组 浮 点 寄 存 器 组 寄存器 标 寄存器 指令 指针 通用寄存器 指令指针寄存器 标志寄存器 段寄存器 系 统 级 寄 存 器 组
1. 总线接口部件 通过数据总线、地址总线和控制总线负责与外部联系, 通过数据总线、地址总线和控制总线负责与外部联系, 包括访问存储器和访问I/O端口以及完成其它控制功能 包括访问存储器和访问 端口以及完成其它控制功能 2. 高速缓存部件 芯片内部集成8KB,存放 最近要使用的指令和数据, 芯片内部集成 ,存放CPU最近要使用的指令和数据 最近要使用的指令和数据 分为4组 每组2KB,称为 路成组相联 路成组相联Cache 分为 组,每组 ,称为4路成组相联 3. 指令预取部件 从高速缓冲存储器中取出指令并放入指令队列, 从高速缓冲存储器中取出指令并放入指令队列, 128位内 位内 部总线,一次可预取16字节 容量为32字节 字节, 部总线,一次可预取 字节,容量为 字节 4. 指令译码部件 从指令预取队列缓冲区中取出指令进行译码, 从指令预取队列缓冲区中取出指令进行译码,产生指令 的微码入口地址和寻址信息,放入译码部件队列, 的微码入口地址和寻址信息,放入译码部件队列,可同 时存放三条指令的译码信息
31…19 18 17 16 15 14 13 12 11 10 9 A V R C M F N IOP T L 8 7 6 5 4 A F 3 2 P F 1 0 C F
O D I T S Z F F F F F F
FLAGS
位的含义与8086的FLAGES基本相同 低16位的含义与 位的含义与 的 基本相同 AC—对准标志位。若AC=1,且CR0中AM=1时,则进行字、 对准标志位。 对准标志位 , 中 时 则进行字、 双字、 字的对准检查 字的对准检查, 双字、4字的对准检查,发现访问存储器操作数未按边界对 异常中断17错误 错误; 准,则产生 异常中断 错误;AC=0时,不进行对准检查 时 VM—虚拟 虚拟8086方式标志位。保护模式下 方式标志位。 虚拟 方式标志位 保护模式下VM为1时,转换到 为 时 虚拟8086工作方式;当VM为0时,80486返回保护方式。在 工作方式; 返回保护方式。 虚拟 工作方式 为 时 返回保护方式 实地址方式下, 实地址方式下,VM位无效 位无效 RF—恢复标志位。与调试寄存器的代码断点结合使用,以 恢复标志位。与调试寄存器的代码断点结合使用, 恢复标志位 保证不重复使用断点。用于DEBUG调试,每执行完一条指 调试, 保证不重复使用断点。用于 调试 复位; 令,使RF复位;而RF置1时,即便遇到断点或调试故障均被 复位 置 时 忽略 NT—任务嵌套标志位。表示当前任务是否嵌套在另一任务 任务嵌套标志位。 任务嵌套标志位 有嵌套时NT=1;否则 。只用于保护模式 内。有嵌套时 ;否则=0。 IOPL—I/O特权级标志位。只用于保护模式,规定I/O操作 特权级标志位。只用于保护模式,规定 操作 特权级标志位 的级别( 的级别(0~3) )
80486微处理器 第4章 Intel 80486微处理器
简单地说: 简单地说:80486=80386+cache+80387
80486主要特点 : 主要特点
•采用 采用RISC(精简指令系统计算机)技术,部分微码控制改为硬件逻 采用 (精简指令系统计算机)技术, 辑直接控制。 辑直接控制。 •微处理器内部为全 位, CPU和FPU之间的数据通道是 位, CPU 微处理器内部为全32位 之间的数据通道是64位 微处理器内部为全 和 之间的数据通道是 之间以及Cache和Cache之间的数据通道均为 位。 之间的数据通道均为128位 和Cache之间以及 之间以及 和 之间的数据通道均为 •片内集成了浮点运算部件,可支持32、64和80位的浮点算术运算。 片内集成了浮点运算部件,可支持 、 和 位的浮点算术运算 位的浮点算术运算。 片内集成了浮点运算部件 •片内具有 片内具有8KB的数据 指令高速缓存 的数据/指令高速缓存 片内具有 的数据 指令高速缓存Cache。 。 •片内具有存储管理部件 片内具有存储管理部件MMU,可支持对存储器地址实施管理和对存 片内具有存储管理部件 , 储器空间进行保护。 储器空间进行保护。 •采用了突发式总线周期操作 。 采用了突发式总线周期操作 •具有实地址方式、虚拟地址保护方式(保护方式)和虚拟8086方式 。 具有实地址方式、虚拟地址保护方式(保护方式)和虚拟 具有实地址方式 方式
15 CS DS SS ES FS GS 段寄存器 段描述符寄存器 0 63 0
•段描述符的装入过程对程序员是透明的 段描述符的装入过程对程序员是透明的 •实地址和虚拟 实地址和虚拟8086方式下与 方式下与8086相同 实地址和虚拟 方式下与 相同
5. 系统地址寄存器 系统地址寄存器——保护方式寄存器 保护方式寄存器 在保护方式中, 共设计了四种描述符表: 在保护方式中,80486共设计了四种描述符表: 共设计了四种描述符表 •全局描述符表 全局描述符表GDT(Global Descriptor Table) 全局描述符表 ( ) 存放操作系统和各任务公用的描述符 (1个) 个 •局部描述符表 局部描述符表LDT(Local Descriptor Table) 局部描述符表 ( ) 每任务1个 存放各个任务私有的描述符 (每任务 个) •中断描述符表 中断描述符表IDT(Interrupt Descriptor Table) 中断描述符表 ( ) 存放系统的中断描述符 (1个) 个 •任务状态段 任务状态段TSS(Task State Segment) 任务状态段 ( ) 每任务1个 存放多个任务的私有运行状态信息描述符 (每任务 个)
段描述符表 段寄存器( 位 段寄存器(16位) 物理存储器 段描述符( 位 段描述符(64位)
段选择符 段描述符 段描述符
索引值
访问控制 界限 段基址 存储段
•CS、DS、SS、ES、FS和GS寄存器存放每个当前段的选择符 、 、 、 、 和 寄存器存放每个当前段的选择符
硬件自动根据段选择符中的索引值,从描述符表中取出 字 硬件自动根据段选择符中的索引值,从描述符表中取出8字 节的描述符, 节的描述符,装入相应段描述符寄存器。以后再访问该段 存储器时, 存储器时,可以直接使用相应的段描述符寄存器中的段基 址作为线性地址计算的一个元素,无需再次查表, 址作为线性地址计算的一个元素,无需再次查表,可加快 存储器物理地址的形成
5. 控制器部件 从指令译码器队列中取出指令微码入口地址, 从指令译码器队列中取出指令微码入口地址,用来产生 对个部件操作所需的一系列信号,其内部控制ROM中存 对个部件操作所需的一系列信号,其内部控制 中存 放着微处理器指令的微码 6. 算术逻辑运算部件 执行控制器所规定的算术与逻辑运算 •算术逻辑单元 ALU——内部 位数据总线 内部64位数据总线 算术逻辑单元 内部 •8个通用寄存器 个通用寄存器 •若干专用寄存器 若干专用寄存器 •1个桶型移位寄存器 个桶型移位寄存器——加快移位、乘除指令的执行 加快移位、 个桶型移位寄存器 加快移位 7. 浮点运算部件 专门用来完成实数和复杂运算 8. 存储器管理部件 存储器管理部件MMU •分段部件:将指令给出的逻辑地址转化为线性地址 分段部件: 分段部件 •分页部件:将线性地址换算为物理地址 分页部件: 分页部件
8086基本组成 8086基本组成 8086CPU由总线接口部件 8086CPU由总线接口部件BIU(Bus 由总线接口部件BIU( Interface Unit)和指令执行部件EU(Execution Unit)和指令执行部件EU( Unit)两个独立的功能部件组成。 Unit)两个独立的功能部件组成。其内部结构框 图如图2.1所示 所示。 图如图2.1所示。
EU 控制 系统 执行部件 EU) (EU)
Q总线 16位 16位
指令队列
1 2 3 4 5 6
总线接口部件 BIU) (BIU)
标志
4.1 80486内部结构
80486基本组成 4.1.1 80486基本组成
•总线接口部件 总线接口部件 •高速缓存部件 高速缓存部件
八 个 部 份
•指令预取部件 指令预取部件 •指令 指令 • • • •存 存 部件 部件 部件 部件 部件MMU 部件 指令预取 部件 指令 存
