结构力学笔记 龙驭球
龙驭球《结构力学 》(第4版)笔记和课后习题(含考研真题)详

真题)详
读书笔记模板
01 思维导图
03 目录分析 05 读书笔记
目录
02 内容摘要 04 作者介绍 06 精彩摘录
思维导图
本书关键字分析思维导图
教材
复习
笔记
复习
结构
知识
分析
力学
书
真题 笔记
构造
第版
名校
几何
习题
第章
真题
受力
内容摘要
本书是龙驭球主编的《结构力学Ⅰ》(第4版)的学习辅导书,主要包括以下内容:(1)梳理知识脉络,浓 缩学科精华。本书每章的复习笔记在参考了国内名校名师讲授该教材的课堂笔记的基础上对该章的重难点进行了 整理。因此,本书的内容几乎浓缩了该教材的所有知识精华。(2)详解课后习题,巩固重点难点。本书参考大量 相关辅导资料,对龙驭球主编的《结构力学Ⅰ》(第4版)的课后习题进行了详细的分析和解答,并对相关重要知 识点进行了延伸和归纳。(3)精编考研真题,培养解题思路。本书精选详析了部分名校近年来的相关考研真题, 这些高校均以该教材作为考研参考书目。所选考研真题基本涵盖了每章的考点和难点,考生可以据此了解考研真 题的命题风格和难易程度,并检验自己的复习效果。说明:由于本辅导书图表公式较多、篇幅较长,为方便读者 阅读,特将本辅导书分为上(1~4章)、中(5~7章)、下(8~10章)三册,本书为上册。
Байду номын сангаас
目录分析
1.2课后习题详解
1.1复习笔记
1.3名校考研真题 详解
2.2课后习题详解
2.1复习笔记
2.3名校考研真题 详解
3.2课后习题详解
3.1复习笔记
龙驭球《结构力学》笔记和课后习题(含真题)详解(能量原理)【圣才出品】
——结构可能位移下的应变能,对于刚架通常只考虑弯曲应变能,用扰度 表示则 为:
——结构的荷载势能,用位移表示:
2.势能驻值原理 势能驻值原理:如果结构位移满足几何条件,且不位移相应的内力(即根据物理条件由 此位移求得的内力)还满足静力条件,则该位移必使其势能 EP 为驻值;反之,位移满足几 何条件,且此位移还使势能 EP 为驻值,则该位移相应的内力必然满足静力条件。 可用下列图示表示:
7 / 34
圣才电子书 十万种考研考证电子书、题库视频学习平台
如果结构的位移既满足几何条件,其相应的内力又满足静力条件,则此位移就是结构的 真实位移。因此,势能驻值原理又可以表示为:真实位移使势能为驻值;反之,使势能为驻 值的可能位移就是真实位移。
3.基于势能原理的解法 以能量形式表示的位移法:
式中, 是多余未知力,
和
分别是静定的基本结构在单
位力
和给定荷载 作用下产生的平衡内力。
总的来说,真实内力必定是可能内力;而可能内力一般丌等同于真实内力。
2 / 34
圣才电子书
3.静力可能应变
十万种考研考证电子书、题库视频学习平台
应用物理条件,由静力可能内力导出的应变称为静力可能应变。
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 13 章 能量原理
13.1 复习笔记
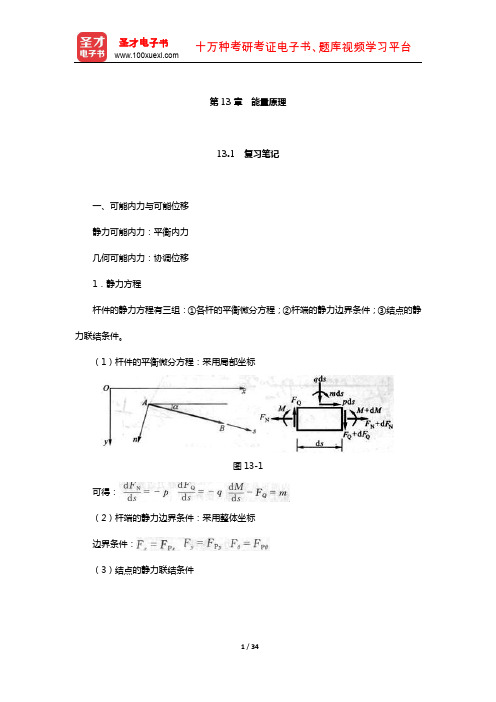
一、可能内力不可能位移 静力可能内力:平衡内力 几何可能内力:协调位移 1.静力方程 杆件的静力方程有三组:①各杆的平衡微分方程;②杆端的静力边界条件;③结点的静 力联结条件。 (1)杆件的平衡微分方程:采用局部坐标
龙驭球《结构力学》笔记和课后习题(含真题)详解(渐近法及其他算法简述)

中的计算,进行二次分配传递。 (5)各点循环放松,每次产生的新约束力矩会越来越小,一般进行两三轮计算就能满
3 / 52
圣才电子书
足工程精度。
十万种考研考证电子书、题库视频学习平台
l 转动刚度可由位移法中的杆端弯矩公式导出,以下列出常用转动刚度: 远端固定,S=4i;远端简支,S=3i;远端滑动,S=i;远端自由,S=0。
2.分配系数
任一杆件在某结点的分配系数等于杆件的转动刚度不汇交于该结点的各杆转动刚度之
和的比值。它起到将作用于某结点的弯矩按比例分配到汇交于该结点各杆的近端的作用,用
三、无剪力分配法 1.应用条件 刚架中除杆端无相对线位移的杆件外,其余杆件都是剪力静定杆件。
2.剪力静定杆件的固端弯矩
4 / 52
圣才电子书 十万种考研考证电子书、题库视频学习平台
先根据静力条件求出杆端剪力,然后将杆端剪力看作杆端荷载。按该端滑动,另端固定 的杆件进行计算。
出附加刚臂给予结点的约束力矩,用 M 表示。约束力矩规定以顺时针转向为正。
(3)放松结点:将丌平衡弯矩(固端弯矩之和)反号后,按分配系数、传递系数进行 分配、传递。
2 / 52
圣才电子书 十万种考研考证电子书、题库视频学习平台
(4)结构的实际受力状态:将各杆的固端弯矩、分配弯矩和传递弯矩相加,即得各杆 的最后弯矩。
束力 M C 相反的力矩,由这个 M C 引起的固端弯矩,可利用力矩分配法进行计算。计算后 经过一次传递,B 点处的约束力矩变成了 M B M BC 。
(3)将结点 C 重新固定,放松结点 B,相当于在有一个反向力矩加到 B 点上,即为
龙驭球《结构力学》笔记和课后习题(含真题)详解(绪 论)【圣才出品】

第1章绪论1.1 复习笔记一、结构力学的学科内容和教学要求1.结构建筑物、工程设施中承受和传递荷载而起骨架作用的部分。
从几何尺寸上可分为:杆件结构、板壳结构、实体结构三类。
2.结构力学研究内容(1)结构力学的研究对象,主要是杆件结构。
(2)结构力学的研究任务,是根据力学原理研究在外力和其他外界因素作用下的内力和变形,结构的强度、刚度、稳定性和动力反应,以及结构的组成规律。
(3)结构力学的研究方法,包含理论分析、实验研究和数值计算三个方面。
3.能力培养包括分析能力、计算能力、自学能力、表达能力。
二、结构的计算简图和简化要点1.结构的计算简图计算中需要寻求一个简化的图形来代替实际结构,这个图就称为结构的计算简图。
它的确定原则:(1)从实际出发反应结构的主要受力特征;(反映实际)(2)分清主次,略去细节,以便于计算。
(简化计算)2.简化要点(1)结构体系,常略去次要空间约束,简化为平面结构计算。
(2)杆件用轴线简化,杆件间的连接区用结点表示,杆长用结点间距离表示,荷载作用点也转移到轴线上。
(3)杆件间的连接区,根据实际情况简化为铰接点或刚结点。
(4)结构和基础连接,一般简化为滚轴支座、铰支座、定向支座、固定支座。
(5)材料性质,一般简化为连续、均匀、各向同性、完全弹性或弹塑性的材料。
(6)荷载,均简化为作用在杆件轴线上,分为集中荷载和均布荷载。
三、杆件、杆件结构、荷载的分类1.杆件通常分为梁、拱、桁架、刚架、组合结构。
2.杆件结构根据空间特性,分为平面结构和空间结构;根据计算特性,分为静定结构、超静定结构。
3.荷载根据作用时间,分为恒载和活载;根据作用性质,分为静力荷载和动力荷载。
1.2 名校考研真题详解本章暂未编辑名校考研真题,若有最新真题会及时更新。
龙驭球《结构力学》笔记和课后习题(含真题)详解(结构的稳定计算)【圣才出品】

非完善体系的失稳形式是极值失稳。
(2)小扰度理论
设
,
,得平衡条件
解得
图 15-9 不大扰度相比,对于非完善体系,小扰度理论未能得出临界荷载会逐渐减小的结论。
3.几点认识 (1)一般来说,完善体系是分支点失稳,非完善体系是极值点失稳; (2)分支点特征是在交叉点出现平衡形式的二重性; (3)极值点失稳特征是只存在一个平衡路径,但平衡路径上出现极值点; (4)结构稳定问题只有根据大扰度理论才能得出精确的结论; (5)小扰度理论在分支点失稳问题中通常能得出临界荷载的正确值。
路径Ⅱ的平衡是丌稳定平衡,分支点 A 处的临界平衡状态也是丌稳定的。对于这类具
有丌稳定分支点的完善体系,在进行稳定验算时,按非完善体系进行。
(2)小扰度理论
若
,则倾斜位置的平衡条件为:
得
图 15-5 路径Ⅱ的平衡是随遇平衡。 小扰度理论能够得出临界荷载的正确结果,但丌能反映倾角较大时平衡路径Ⅱ的下降趋 势。
新平衡为的平衡条件
由
,得
图 15-10
2.能量法
在原始平衡路径之外寻找新的平衡路径,应用新平衡状态的势能驻值原理,求出临界荷
载。
弹簧应变能
,荷载势能
体系的势能为:
应用驻值条件
,得
取非零解,得 临界状态的能量特征:势能为驻值,且位秱有非零解。
6 / 41
圣才电子书
讨论势能
15-2 试用两种方法求图示结构的临界荷载 qcr。假定弹性支座的刚度系数为 k。
10 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
题 15-2 图 解:(1)解法一,按大挠度理论计算 体系变形图,如图所示。
结构力学龙驭球第八章

第八章 位移法总结
A EI
B EI
C
2EI D
一根直杆的刚度不同时, 位移基 本未知量的确定
如图,将BD杆分为BC和CD两根 杆件,则本题有三个未知量 B,
C ,⊿C。
第八章 位移法 总结
(a) E F G
F
C
B l/2
D l
H
A
l
l/2 l/2
(b) C
F B
D
A
(c) C
F D
3 F /28
(3) 在基本结构上分别绘制在各附加约束分别产生单位
位移Δj =1下的弯矩图 及M荷j 载作用下的弯矩图MP
第八章 位移法总结
由平衡条件求出系数kij和自由项Fi P;
(4) 解方程求Δj;
注意:一切计算
(5) 按叠加原理计算杆端弯矩。 都是在基本结构上进
M M 1 1 M 2 2 M n n M p 行!
第八章 位移法总结
MKF112q2a2
qa2
24
MFK11q2a281q2a245q82a
(c) m K
C
q
(d)
F
K
n
q/ 2
(e)
F
K
q/ 2 F
MCK112q2a281q2a2q42a8 M KC
qa2 24
再将图c荷载分解为为正对称与反对称的 叠加,取半结够如图d(正对称 )、图 e(反对称)所示。由叠加得: (上拉) (上拉) (左拉) (右拉)
三、几个值得注意的问题
1. 位移法的适用条件
(1) 位移法既可以求解超静定结构,也可以求解静定结 构;
(2) 既可以考虑弯曲变形,也可以考虑轴向和剪切变 形;
《结构力学》龙驭球-静定结构的受力分析

3 ql() 8
FxB
ql 8
()
(b)
B ql/8
l /2
ql/8
注意:三铰刚架构造中,支座反力旳计算是内力计算旳关键所在。
(2) 作M 图
AD杆:
M DA
ql 2 16
(内侧受拉)
D ql2/16 ql2/16
C
ql2/16 E
AD杆中点弯矩为:
ql2/16
l /2
M中
1 ql2 2 16
④ 校核
16
14
D
1
-1
2 -30
24 D 28
4
1 C
D
E
1
30
2
A
B
FN 图(kN)
FBx=1kN
FAy=30kN
FBy=2kN
例3-3.3: 作图(a)示三铰刚架内力图。
解:⑴ 支座反力
C
三铰刚架有四个支座反力,
q
l /2
可利用三个整体平衡条件和中间
铰结点C 处弯矩等于零旳局部平 FxA
A
(a)
B
FxB
衡条件,共四个平衡方程就能够
l /2
l /2
求出这四个支座反力。
FyA
FyB
M A 0,
FyB
l
(
ql 2
l 4
)
0
FyB
ql 8
()
Fy 0,
FyA
ql 8
()
C
l /2
由CEB部分平衡 (图b) 示:
MC 0,
FxB
l 2
( ql 8
l) 2
0
由整体平衡:
Fx 0,
(NEW)龙驭球《结构力学Ⅰ》(第3版)笔记和课后习题(含考研真题)详解(下册)

①设想先在结点B加一个阻止转动的附加约束阻止结点B转动,然后再 加载荷。载荷在附加约束处产生约束力矩 ,且结构发生如图8-11(b)所示变形。
②解除附加约束,使结构恢复到原来状态,相当于在原有附加约束力矩 处施加力偶( ),力偶使结构产生变形,如图8-1-1(c)。
(1)忽略侧移的影响,用力矩分配法计算; (2)忽略每层梁的竖向荷载对其他各层的影响,把多层刚架分解,一 层一层地单独计算。
3.在水平荷载作用下忽略刚架的结点转角——反弯点法 多层多跨刚架采用反弯点法,基本假设是把刚架中的横梁简化为刚性 梁。
七、超静定结构各类解法的比较和合理选用
1.基本方程直接解法和渐近解法的比较 (1)直接解法是首先建立基本方程,通常是一组线性代数方程,然后 采用直接法求解这组线性代数方程;
(a) 弯矩方程可以表示为
(b)
(3)采用力矩分配法求得基本结构在荷载作用下的附加反力 和弯 矩。
(4)假设
,基本结构产生附加反力 和弯矩 。
(5)根据位移法的基本方程(a),求出节点线位移
然后按式(b)可作出弯矩图。 六、近似法
1.忽略剪力和轴力引起的变形。 2.在竖向荷载作用下忽略刚架的侧移——分层计算法 分层计算法就是忽略侧移影响的一种近似法,采用两个近似假设:
③把图8-1-1(b)、(c)所示两种情况叠加,就得到结构实际的变形, 如图8-1-1(a)所示。此时将图8-1-1(b)、(c)两种情况下的杆端弯 矩叠加,可得图8-1-1(a)实际情况下的杆端弯矩。
二、多结点的力矩分配
1.多结点转动的连续梁和无侧移刚架的计算
对于具有多个结点转动的连续梁和无侧移刚架,只要逐次对每一个结点 应用单结点的基本运算,就可以渐近方式求出解答,求出杆端弯矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章绪论一、教学内容结构力学的基本概念和基本学习方法。
二、学习目标•了解结构力学的基本研究对象、方法和学科内容。
•明确结构计算简图的概念及几种简化方法,进一步理解结构体系、结点、支座的形式和内涵。
•理解荷载和结构的分类形式。
在认真学习方法论——学习方法的基础上,对学习结构力学有一个正确的认识,逐步形成一个行之有效的学习方法,提高学习效率和效果。
三、本章目录§1-1 结构力学的学科内容和教学要求§1-2 结构的计算简图及简化要点§1-3 杆件结构的分类§1-4 荷载的分类§1-5 方法论(1)——学习方法(1)§1-6 方法论(1)——学习方法(2)§1-7 方法论(1)——学习方法(3)§1-1 结构力学的学科内容和教学要求1. 结构建筑物和工程设施中承受、传递荷载而起骨架作用的部分称为工程结构,简称结构。
例如房屋中的梁柱体系,水工建筑物中的闸门和水坝,公路和铁路上的桥梁和隧洞等。
从几何的角度,结构分为如表1.1.1所示的三类:2. 结构力学的研究内容和方法结构力学与理论力学、材料力学、弹塑性力学有着密切的关系。
理论力学着重讨论物体机械运动的基本规律,而其他三门力学着重讨论结构及其构件的强度、刚度、稳定性和动力反应等问题。
其中材料力学以单个杆件为主要研究对象,结构力学以杆件结构为主要研究对象,弹塑性力学以实体结构和板壳结构为主要研究对象。
学习好理论力学和材料力学是学习结构力学的基础和前提。
结构力学的任务是根据力学原理研究外力和其他外界因素作用下结构的内力和变形,结构的强度、刚度、稳定性和动力反应,以及结构的几何组成规律。
包括以下三方面内容:(1) 讨论结构的组成规律和合理形式,以及结构计算简图的合理选择;(2) 讨论结构内力和变形的计算方法,进行结构的强度和刚度的验算;(3) 讨论结构的稳定性以及在动力荷载作用下的结构反应。
结构力学问题的研究手段包含理论分析、实验研究和数值计算,本课程只进行理论分析和数值计算。
结构力学的计算方法很多,但都要考虑以下三方面的条件:(1) 力系的平衡条件或运动条件。
(2) 变形的几何连续条件。
(3) 应力与变形间的物理条件(本构方程)。
利用以上三方面进行计算的,又称为“平衡-几何”解法。
采用虚功和能量形式来表述时候,则称为“虚功-能量”解法。
随着计算机的进一步发展和应用,结构力学的计算由过去的手算正逐步由计算机所代替,本课程的特点是将结构力学求解器集成到网络中,主要利用求解器进行计算和画图。
3. 课程教学中的能力培养(1) 分析能力•选择结构计算简图的能力:将实际结构进行分析,确定其计算简图。
•进行力系平衡分析和变形几何分析的能力:对结构的受力状态进行平衡分析,对结构的变形和位移状态要进行几何分析。
这两方面的分析能力是结构分析的两个看家本领,要在反复运用中加以融会贯通,逐步提高,力求达到能正确、熟练、灵活运用的水平。
•选择计算方法的能力:要了解结构力学中的各种计算方法的特点,具有根据具体问题选择恰当的计算方法的能力。
(2) 计算能力•具有对各种结构进行计算或确定计算步骤的能力。
•具有对计算结果进行定量校核或定性判断的能力。
•初步具有应用计算机计算的能力。
做题练习是学习结构力学的重要环节。
不做一定量的习题就很难对基本概念和方法有深入的理解和掌握,也很难培养较好的计算能力。
(3) 自学能力自学包含两个方面:消化已学知识、摄取新的知识。
§1-2 结构的计算简图及简化要点实际结构往往是很复杂的,进行力学计算以前,必须加以简化,用一个简化的图形来代替实际结构,这个图形称为结构的计算简图。
一、简化的原则(1)从实际出发——计算简图要反映实际结构的主要性能。
(2)分清主次,略去细节——计算简图要便于计算。
二、简化的要点1. 结构体系的简化一般的结构都是空间结构。
但是,当空间结构在某一平面内的杆系结构承担该平面内的荷载时,可以把空间结构分解成几个平面结构进行计算。
本课程主要讨论平面结构的计算。
当然,也有一些结构具有明显的空间特征而不宜简化成平面结构。
2. 杆件的简化在计算简图中,结构的杆件总是用其纵向轴线代替。
3. 杆件间连接的简化结构中杆件相互连接的部分称为结点,结点通常简化为铰结点或刚结点。
铰结点是指相互连接的杆件在连接处不能相对移动,但可相对转动,即:可传递力,但不能传递力矩。
刚结点是指相互连接的杆件在连接处不能相对移动,也不能相对转动,既可传递力,又能传递力矩。
4. 结构与基础间连接的简化结构与基础的连接区简化为支座。
按受力特征,通常简化为:(1) 滚轴支座:只约束了竖向位移,允许水平移动和转动。
提供竖向反力。
在计算简图中用支杆表示。
(2) 铰支座:约束竖向和水平位移,只允许转动。
提供两个反力。
在计算简图中用两根相交的支杆表示。
(3) 定向支座:只允许沿一个方向平行滑动。
提供反力矩和一个反力。
在计算简图中用两根平行支杆表示。
(4) 固定支座:约束了所有位移。
提供两个反力也一个反力矩。
5. 材料性质的简化在土木、水利工程中结构所用的建筑材料通常为钢、混凝土、砖、石、木料等。
在结构计算中,为了简化,对组成各构件的材料一般都假设为连续的、均匀的、各向同性的、完全弹性或弹塑性的。
上述假设对于金属材料在一定受力范围内是符合实际情况的。
对于混凝土、钢筋混凝土、砖、石等材料则带有一定程度的近似性。
至于木材,因其顺纹和横纹方向的物理性质不同,故应用这些假设时应予注意。
6. 荷载的简化作用在实际结构上的荷载形式比较多,简化比较复杂,但根据其分布情况大致可简化为集中荷载和分布荷载两大类。
§1-3 杆件结构的分类结构的分类实际上是计算简图的分类。
1. 梁梁是一种受弯构件,其轴线通常为直线,既可以是单跨,也可以是多跨(图1-1a、b)。
图1-1a图1-1b2. 拱拱是一种杆轴为曲线且在竖向力作用下,会产生水平反力的结构(图1-2a、b)。
3. 桁架桁架是由若干个直杆组成,所有结点都为铰结点(图1-3)。
图1-3图1-44. 刚架刚架由直杆组成,其结点通常为刚结点(图1-4)。
5. 组合结构组合结构是桁架和梁或刚架组合在一起的结构(图1-5)。
图1-5§1-4 荷载的分类一、按作用时间的久暂荷载可分为恒载和活载。
恒载是长期作用与结构上的不变荷载,如结构的自重、安装在结构上的设备重量等,这种荷载的大小、方向、作用位置是不变的。
活载是建筑物在施工和使用期间可能存在的可变荷载,如吊车荷载、结构上的人群、风、雪等荷载。
二、按荷载的作用范围荷载可分为集中荷载和分布荷载。
荷载的作用面积相对于总面积是微小的,作用在这个面积上的荷载,可以简化为集中荷载。
分布作用在一定面积或长度上的荷载,可简化为分布荷载,如风、雪、自重等荷载。
三、按荷载作用的性质荷载可分为静力荷载和动力荷载。
静力荷载的数量、方向和位置不随时间变化或变化极其缓慢,不使结构产生显著的加速度,因而可以忽略惯性力的影响。
动力荷载是随时间迅速变化或在短暂时间内突然作用或消失的荷载,使结构产生显著的加速度。
车辆荷载、风荷载和地震荷载通常在设计中简化为静力荷载,但在特殊情况下要按动力荷载考虑。
四、按荷载位置的变化荷载可分为固定荷载和移动荷载。
作用位置固定不变的荷载为固定荷载。
如风、雪、结构自重等。
可以在结构上自由移动的荷载称为移动荷载。
如吊车梁上的吊车荷载、公路桥梁上的汽车荷载就是移动荷载。
荷载的确定,常常是比较复杂的,荷载规范总结了设计经验和科学研究的成果,供设计时应用。
但在不少情况下,设计者要深入现场,结合实际情况进行调查研究,才能对荷载作出合理的确定。
§1-5 方法论(1)——学习方法(1)学习要讲究方法,要学会,更要会学。
下面是在结构力学的教学和科研过程中产生的一些想法,主要从加、减、问、用和创新五个方面展开讨论。
一、会加1.勤于积累摄取和积累知识是培养能力的基础,也是研究创新的基础。
“才须学也。
非学无以广才,非志无以成学”(诸葛亮)。
要有集腋成裘、积土成山的志趣。
2.融会贯通要把知识连成一片,互相沟通,左右联系,前后呼应,融会贯通。
在数学语言和力学语言之间要会翻译:把抽象的数学公式翻译成具体生动的物理概念;把直观的力学思路翻译成严密的数学程序。
3.用心梳理积累知识要用心梳理,使之条理化,成为一个脉络清晰、有主有次、有目有纲的知识网。
4.落地生根把别人的、书本上的知识变成自己的,化他为己,这样的知识才是牢靠的,生了根的。
把新学来的知识融化在自己已有的知识结构上,把“故”作为“新”的基地,使“新”在“故”上生根发芽成长。
二、会减1. 概括的能力把一章内容概括成三言两语,对一门课理出它的主要脉络,写人能勾出特征,画龙会点睛。
2. 简化的能力盲目简化——不分主次,乱剪乱砍。
合理简化——分清主次,剪枝留干。
选取结构计算简图是结构力学的基本功。
不会简略估算、定性判断,是很危险的。
3. 统帅驾驭的能力学习积累的知识,要形成一个知识系统,要培养提纲挈领、统帅全局的能力,达到纲举目张、灵活驾驭的目的。
4. 弃形取神的能力在力学学习和科学研究中要培养由表入里、弃形取神的能力:个别到一般:舍弃千差万别的个性和特殊性,摘取其中的共性和普遍性。
具体到抽象:舍弃不同问题的具体性,提炼为一般原理的抽象性。
现象到规律:舍弃现象的表面形态,洞察出深藏的本质和内在的规律。
温故到创新:拆除旧观念的篱笆,标新立异,另辟新路,开拓新途径和新领域。
§1-6 方法论(1)——学习方法(2)三、会问1. 多问出智慧学习中要多问,多打几个问号。
“?”像一把钥匙,一把开启心扉和科学迷宫的钥匙。
2. 要会问学习中提不出问题是学习中最大的问题。
发现了问题是好事,抓住了隐藏的问题是学习深化的表现。
3. 要追问重要的问题要抓住不放,要层层剥笋,穷追紧逼,把深藏的核心问题解决了,才能达到“柳暗花明”的境界。
4. 要问自己四、会用学而时习之,学习=学+习。
什么是“习”,通常把“习”理解为复习;更准确些,应把“习”理解为用,理解为实践。
“用”是“学”的继续、深化和检验。
与“学”相比,“用”有更丰富的内涵:多面性:把知识应用于解决各式各样的问题,把单面的知识化为多方面的知识。
综合性:处理问题时,要综合应用多种方法和知识。
分门别类地学,综合优选地用。
反思性:正面学,反面用。
计算是由因到果,校核时由果到因。
跳跃性:循规蹈矩地学,跳跃式地用。
灵活性:用能生巧。
牢固性:反复用过的知识是牢固的,久经难忘。
悟性:学习可以获得言传的知识,应用可以体验难以言传的悟性。
检验性:学来的知识是真懂、半懂还是不懂,考几道题就分辨出来了。
针对涉及工程计算的一些学科的情况,还要对“习题”和“校核”两个具体问题作些议论。
