第四章 网络定理
合集下载
网 络 定 理

(2) 当网络中有多个激励同 时作用时, 时作用时,总响应等于每个激 励单独作用(其余激励置零 时所 励单独作用 其余激励置零)时所 其余激励置零 产生的响应分量的代数和, 产生的响应分量的代数和,符 合可加性(Additivity)。 。 合可加性
线性网络的线性及叠加定理反映了 线性网络的基本性质, 线性网络的基本性质,在线性网络理论 和分析中占有重要地位。 和分析中占有重要地位。在应用叠加定 理时应注意以下几点。 理时应注意以下几点。 (1) 叠加定理适用于所有线性网络, 叠加定理适用于所有线性网络, 而非线性网络一般不适用; 而非线性网络一般不适用; (2)叠加定理只能用于计算线性网络 叠加定理只能用于计算线性网络 的电压和电流, 的电压和电流,而不能用于计算功率和 能量,因为功率和能量是电压或电流的 能量, 二次函数; 二次函数;
图4-20 互易定理形式三
在应用互易定理时应注意以下几点。 在应用互易定理时应注意以下几点。 (1)该定理的使用范围较窄,只能用于 该定理的使用范围较窄, 该定理的使用范围较窄 不含受控源的单个独立源激励的线性网络, 不含受控源的单个独立源激励的线性网络, 对其他的网络一般不适用。 对其他的网络一般不适用。
(3)不仅可以用电压源或电流源替代已 不仅可以用电压源或电流源替代已 知电压或电流的支路, 知电压或电流的支路,而且可以替代已知 端口电压或端口电流的二端网络。 端口电压或端口电流的二端网络。因此应 用替代定理和电源转移,如图4-5所示可将 用替代定理和电源转移,如图4-5所示可将 一个大网络撕裂成若干个小网络, 一个大网络撕裂成若干个小网络,用于大 网络的分析。 网络的分析。
定理中的独立电流源与电阻并联的电 路通常称为二端网络N的诺顿等效电路。 路通常称为二端网络 的诺顿等效电路。 的诺顿等效电路
第四章 网络定理

a
-
1K 0.5 i1 u (b)
i b+
列方程:
2.5i1 i u 1Ki1
解得: Ro 0.4K 41
如果要用开短路法,求短路电流。
i1 1K
a
+
10V 1K 0.5 i1
iSC
(c)
-
列方程:1.5i1 iSC
i1
10 1K
解得: iSC 15mA 42
例:图(a)电路中,N为有源线性二端
25
端口电压电流关联
u Roi uoc
26
证明如下:。
端口支路用电流源i 替代,如图(a),根
据叠加定理,电流源单独作用产生
u’=Roi [图(b)],网络内部全部独立电
源共同作用产生u”=uoc [图(c)]。由此
得到
u u' u" Roi uoc
27
例6 求图(a)网络的戴维南等效电路。
isc
i2
i3
iS2
R1 R1 R2
iS1
uS R3
iS2
求Ro,图(b)求得
Ro
(R1 R2 )R3 R1 R2 R3
画出诺顿等效电路,如图(c)所示。
33
含源线性电阻单口网络的等效电路 只要确定uoc,isc或Ro 就能求得两种等 效电路。
34
戴维南定理和诺顿定理注意几点:
1. 被等效的有源二端网络是线性
2.求电阻Ro 图b网络的独立
电压源置零,
得图c,设端口 电压为u',端 上电流为 i '
1 2 - 6 i1’ +
i’ +
4
u’
i1’
第四章 网络定理
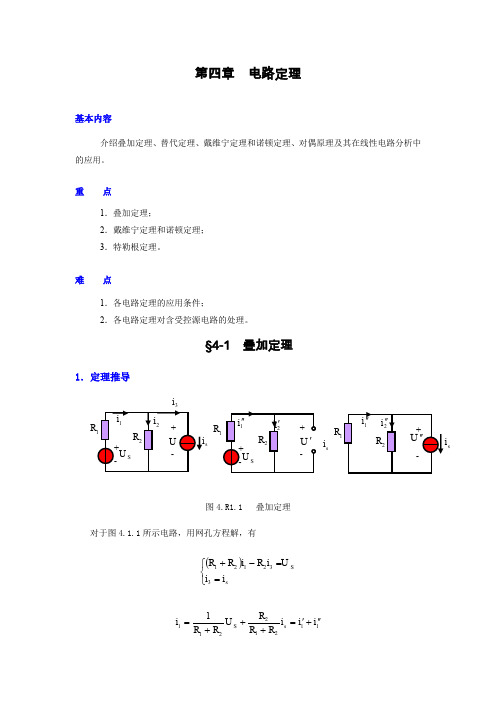
第四章 电路定理基本内容介绍叠加定理、替代定理、戴维宁定理和诺顿定理、对偶原理及其在线性电路分析中的应用。
重 点1.叠加定理;2.戴维宁定理和诺顿定理; 3.特勒根定理。
难 点1.各电路定理的应用条件;2.各电路定理对含受控源电路的处理。
§4-1叠加定理1.定理推导图4.R1.1 叠加定理对于图4.1.1所示电路,用网孔方程解,有()⎩⎨⎧==-+sSi i U i R i R R 332121 112122111i i i R R R U R R i s S ''+'=+++=R ss iR s i22211212i i i R R R R R U i s S ''+'=+-+=U U i R R RR U R R R U s S ''+'=+++-=2121212可见,由于电阻都是线性的,故支路电流21,i i 和支路电压U 都是电流源s i和电压源sU 的一次函数。
当ss U i ,0时=总能作用,有sssU R R R U U R R i U R R i 21221221111+-='+='+='当=s U 时,s i单独作用,有sssi R R R U i R R i i R R i 21221221111+-=''+="+="而U U U i i i i i i ''+'="+'="+'=2221112.定理描述叠加定理:在线性电路中,由n 个独立电源共同作用产生的各支路电流或支路电压,等于各个独立电源分别单独作用时在相应支路中产生的电流或电压的叠加。
所谓独立电源不作用,指独立电压源短路,独立电流源开路,受控源则保留。
注意:1)叠加定理适用于非线性电路;2)叠加时,电路的连接以及电路中所有电路和受控源都不要变动。
戴维宁定理

在电子设备中,输入信号被放大处理后最终被传输到负载, 负载不同,负载上获得的功率就不同。那么在什么条件下,负 载能获得最大功率呢?这就是最大功率传输问题。
RO +
UOC
-
I
PL
I
2 RL
( Uoc RO RL
)2 RL
RL
dPL dRL
U
OC
2
(
RO
RL )2 2(RO (RO RL )4
求解最大功率传输问题的关键是求电路的戴维宁 等效电路。
I 2Ω
+
6V -
- 2I
+ 4Ω
a
2Ω
R
4I
b
(a)
I 2Ω
+
6V -
-+ 2I
4Ω
a
2Ω
4I
b
(b)
a
I
-+ 2I
4Ω
+
2Ω
2Ω
4I
U
IS
-
(c)
b
解:先将a、b端断开,求a、b端的戴维宁等效电路:
Uab 2I 2I 6 6V
外加电流源,求a、b端的戴维南等效电阻:
U 4IS 2I 2I 4IS
§4-3 诺顿定理和含源单口的等效电路
一、诺顿定理
诺顿定理:含独立源的线性电阻单口网络N,就端口特 性而言,可以等效为一个电流源和电阻的并联[图(a)]。
isc称为短路电流。Ro称为诺顿电阻,也称为输入电阻 或输出电阻。电流源isc和电阻Ro的并联单口,称为单口网 络的诺顿等效电路。
在端口电压电流采用关联参考方向时,单口的 VCR方
RO
U IS
4
解:先将a、b端断开,求a、b端的戴维南等效电路:
第4章 网络定理

1 R2 i1 uS iS R1 R2 R1 R2
1 R1 ' '' i2 i1 i S uS iS i 2 i2 R1 R2 R1 R2
其中
i i2 i
' 2 " 2
S 0
1 uS R1 R2 R1 iS R1 R2
i i2 u
例4
封装好的电路如图,已知下 + 列实验数据:
uS
-
当 uS 1V , i S 1 A 时, 响应 i 2 A 当 uS 1V , i S 2 A 时, 响应 i 1 A
iS
无源 线性 网络
i
研 究 激 励 和 响 应 关 系 的 实
求 uS - 3V , i S 5 A 时, 响应 i ?
几点说明:
(1) 叠加定理只适用于线性电路。 (2)某独立源单独作用时,其它独立源应置零(电压源 短路,电流源开路); (3)叠加定理不适用于功率叠加。 (4)u,i叠加时要注意各分量的参考方向。 (5)受控源不能单独作用,也不能随意置零。
例1
电路如图所示,试用 叠加定理求u0。
3Ω
6Ω
+
6V
_
6Ω
S 0
i1 + us _
' i1
R1 i2 R2 R1
' i2 + ' R2 u2 _
电流i2的叠加 + u2 _ is
1 R1 i2 uS iS R1 R2 R1 R2
' '' i2 i2
+ us _
'' i1
i i2 i
1 R1 ' '' i2 i1 i S uS iS i 2 i2 R1 R2 R1 R2
其中
i i2 i
' 2 " 2
S 0
1 uS R1 R2 R1 iS R1 R2
i i2 u
例4
封装好的电路如图,已知下 + 列实验数据:
uS
-
当 uS 1V , i S 1 A 时, 响应 i 2 A 当 uS 1V , i S 2 A 时, 响应 i 1 A
iS
无源 线性 网络
i
研 究 激 励 和 响 应 关 系 的 实
求 uS - 3V , i S 5 A 时, 响应 i ?
几点说明:
(1) 叠加定理只适用于线性电路。 (2)某独立源单独作用时,其它独立源应置零(电压源 短路,电流源开路); (3)叠加定理不适用于功率叠加。 (4)u,i叠加时要注意各分量的参考方向。 (5)受控源不能单独作用,也不能随意置零。
例1
电路如图所示,试用 叠加定理求u0。
3Ω
6Ω
+
6V
_
6Ω
S 0
i1 + us _
' i1
R1 i2 R2 R1
' i2 + ' R2 u2 _
电流i2的叠加 + u2 _ is
1 R1 i2 uS iS R1 R2 R1 R2
' '' i2 i2
+ us _
'' i1
i i2 i
第四章 线性网络定理 电路理论 教学课件-精品文档

例3
求电压Us 。
+ 10V –
I1 6
4
10 I1 + –
Us
+ – 4A
解: (1) 10V电压源单独作用: (2) 4A电流源单独作用:
I1'
+ 10V –
6
4
10 I1' + –
I1'' 6
4
10 I1'' + –
Us '
–
+
+ Us' ' –
4A
Us'= -10 I1'+U1'
2.5A
10V
2
1A
不满足
2.5A
5 10V
2
?
5V
5V
1.5A
1A
满足
?
A +
5V
1A
A + 1V B
+ _1V
A + 1V B
1
1A
不满足
?
B
1A
2) 被替代的支路和电路其它部分应无耦合关系。
§4—2 叠加定理 (Superposition Theorem)
概念:在多个电源同时作用的线性电路(由线 性元件组成的电路)中,任何支路的电流或 任意两点间的电压,都是各个电源单独作用 时所得结果的代数和。
I1 R1
+ I2
I3
I1 R1
I2
I3
+
R2
R3
8V 4// 4 R2 // R3 = 4V × 8 = U= 8 4// 4) R1 +R2 // R3 ( 2+
第四章线性网络的基本定理

除去独立电源,有 u 6I 6(i I)
Ro
u i
=6
画出等效电路,有 R=Ro =6
⊥
Pm =3/8W
3/ 6 6I / 6
6
1/ 6 1/ 31/ 6s
I
0.5V
IsUc oc 3V
3
i 5 A PL 30%
12
Ps
24
Uoc Io Uo
Ro Isc
-
(1)等效变换法(除源) u
(2)外加电源法
Ro
(除源)
i
(3) 开路短路法( Uoc 、 Isc
)(注不意除:电源R压o )与 U电Isocc流方向关联
3、含受控源有源单口网络不一定同时存在两种等效电源
4、含源单口网络与外电路应无耦合; 线 性
5、含源单口网络应为线性网络;
20
练习: 图示电路分别求R=2、6 、18 时的电流I和R
所吸收的功率P。
解:U oc
144 6 36
144 2
24V
Ro
36 36
8 2
6
I 当R=2时: I=3A ,P=18W; 当R=6时: I=2A ,P=24W; 当R=18时:I=1A ,P=18W.
+ Uoc -
21
4-4 最大功率传输定理
Uoc=-1V Ro
Ro= 1
13
例2:已知图示网络的伏安关系为:
含
U=2000I+10
源
并且 Is=2mA.求网络N的戴维南等效电路。
Is
网 络
解: 设网络N 的戴维南等效电路参
N
数为Uoc和Ro,则有
U Uoc (I Is )Ro
电路理论4电路定理

2V 3
R1 图(a) R2 b
I3
a
Us1
rI3
+
Eo
求 等效内阻(求短路电流),图(c):
I0 I3 I1 I2,
I1
US1 R1
1A ,
I2
rI3 R2
1 I3 2
0.5I3 2
I3 1 0.5I3 , I3 3 A
I0
2 3
A
,
R0
E0 I0
1
R1图(b +
R1
Is
R2
Uoc
I1
图(b)
_ b
2)求等效内阻,方法1:外加电压源,图(c):
I2
US R2
US 3
I1
2I2 US R1
2I2 US
1 3
U
S
2 I0 I2 I1 3 US
R0
US I0
3 2
2I2
a
I2 Io
R1
R2
I1 图(c)
Us
b
2)求等效内阻方法2:直接求等效电阻
4.1.2 叠加定理 (Superposition Theorem) 定理内容:
在任一线性电路中,任一支路电流(或电压)都等于电路中各个独立电源单 独作用于网络时,在该支路产生的电流(或电压)的叠加(代数和)。
定理特点:
将多电源电路转化为单电源电路进行计算。
例1:
R1
i2
+
Us
R2
-
两个独立源分别单独作用
若替代后电路仍具有唯一解,则整个电路的各支路电压和电流保持不变。
例子:
i
u=3V
i=1A +
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《电路分析基础》
P61-9 第4章 网络定理
u i
k 1
b
k k
' 0
和
u
k 1
b
ቤተ መጻሕፍቲ ባይዱ
k
' ik 0
特勒根定理适用于任意集总参数电路。 特勒根定理可以用KCL和KVL来证明。
4.5 互易定理
互易性——线性不含独立源、受控源的电路,在单一 激励情况下,激励和响应的位置互换,相同激励的响 应不变。 互易网络:具有互易性的网络。
《电路分析基础》
P61-6 第4章 网络定理
戴维南定理和诺顿定理注意几点: 1.被等效的有源二端网络是线性的,且与外电路之间 不能有耦合关系 2.求等效电路的Ro时,应将网络中的所有独立源置零 ,而受控源保留 3.当Ro≠0和∞时,有源二端网络既有戴维南等效电 路又有诺顿等效电路,并且 uoc、isc和Ro存在关系:
《电路分析基础》
P61-5 第4章 网络定理
任一线性有源二端网络N,就其两个输出端而言总可与 一个独立电压源和线性电阻串联的电路等效,其中独立电压 源的电压等于该二端网络N输出端的开路电压 uOC ,电阻 Ro等于N内所有独立源置零时从输出端看入的等效电阻。
求Ro方法小结: 1.串、并联法;2.加压求流法,或加流求压法; 3.开短路法;4.两点法。 4.3.2 诺顿定理 任一线性有源网络N,就端口而言,可以等效为一个电 流源和电阻的并联。电流源的电流等于网络外部短路时的 端口电流isc;电阻Ro是网络内全部独立源置零时从输出端 看入的等效电阻。
4.2 替代定理
在具有唯一解的任意集总参数网络中,若某条支路k 与网络中的其他支路无耦合,如果已知该支路的支路电 压 u k (支路电流 i k ),则该支路可以用一个电压 为 u k 的独立电压源(电流为 i k 的独立电流源)替代 ,替代前后电路中各支路电压和电流保持不变。
《电路分析基础》
P61-4 第4章 网络定理
注意: 1. 适用于任意集总参数网络(线性的、非线性的,时 不变的、时变的)
2. 所替代的支路与其它支路无耦合 3. “替代”与“等效变换”是不同的概念。“替代” 是特定条件下支路电压或电流已知时,用相应元件替代支 路。等效变换是两个具有相同端口伏安特性的电路间的相 互转换,与变换以外电路无关。 4. 已知支路可推广为已知二端网络(有源、无源)。大 网络成小网络 4.3 戴维南定理和诺顿定理 4.3.1 戴维南定理
电路分析基础
刘 陈
沈元隆
第四章
《电路分析基础》
P13-1
第4章 网络定理
第4章 网络定理 4.l 4.2 4.3 4.4 4.5 线性和叠加定理 替代定理 戴维南定理和诺顿定理 特勒根定理 互易定理
习题
《电路分析基础》
P61-2
第4章 网络定理
4.l 线性和叠加定理 线性网络:由独立电源和线性元件组成。 具有线性性质: 1.齐次性:单个激励(独立源)作用时,响应与激励成正比。 2.可加性:多个激励同时作用时,总响应等于每个激励单独 作用(其余激励置零)时所产生的响应分量的代数和。 由n个独立电源共同产生的响应,等于每个独立电源单独 作用所产生响应之和。 叠加定理: 由全部独立电源在线性电阻电路中产生的任一响应(电压 或电流),等于每一个独立电源单独作用所产生的相应响应(电 压或电流)的代数和。 注意: 1. 适用于线性网络。非线性网络不适用。
Ro uoc isc uoc Ro isc isc uoc Ro
4.作为定理,一个电路可以应用多次。
5.一般端电压与开路电压不相等。
4.3.3 最大功率传输条件
《电路分析基础》
P61-7 第4章 网络定理
负载电阻吸收的功率
uoc p i RL R R L o
2
RL
互易定理有三种形式:
《电路分析基础》
P61-10 第4章 网络定理
形式一:NR 仅由电阻组成,激励电压源uS与响应电流 可以互换位置,即互易前后的响应电流相同。
形式二:NR 仅由电阻组成,激励电流源iS 与响应电压 可以互换位置,即互易前后的响应电压相同。
形式三:NR仅由电阻组成,激励电压源uS与响应开路电 压u互换位置后,将此激励换为相同数值的电流源is,产 生的响应短路电流i在数值上与互易前响应电压u相等。
互易定理可以用特勒根定理来证明。 由特勒根定理,得
u1i1 'u2i2 ' u1 ' i1 u2 ' i2
《电路分析基础》
P61-11 第4章 网络定理
对于形式一: u1 =uS, u2 =0,u1‘=0, u2 ’=uS,代 入特勒根定理,可得 uS i1 '=uS i2 ' 故 i2 = i1 ' 因此形式一成立。 同样,可以证明其余两种形式。 互易定理的形式一也可表示为:互易前的激励电压源比响 应电流等于互易后的激励电压源比响应电流。 互易定理的形式二也可表示为:互易前的激励电流源比响 应电压等于互易后的激励电流源比响应电压。 互易定理的形式三也可表示为:互易前的激励电压源比响 应电压流等于互易后的激励电流源比响应电流。
《电路分析基础》
P61-12 第4章 网络定理
注意: 1.NR不含独立源、受控源,外部只有单个激励和响应; 2.若互易前后激励和响应的参考方向关系一致(都相同或 都相反),则对形式一和二有:相同的激励产生 相同 的 响应;对形式三则相同激励产生的响应相差一个负号。
《电路分析基础》
P61-13
第4章 网络定理
2
欲获得最大功率,有
dp dRL
RL Ro
2
2 RL RL Ro
L
R
uoc 4 Ro
2
Ro
4
uoc 0
2
可得最大功率传输条件:RL=Ro 此时,负载获最大功率为:
pmax
此时对于等效电路而言:效率为50% 。
《电路分析基础》
P61-8 第4章 网络定理
4.4 特勒根定理
《电路分析基础》
P61-3 第4章 网络定理
2.某一激励单独作用时,其他激励置零,即独立电压源 短路,独立电流源开路;电路其余结构都不改变。 3.任一激励单独作用时,该电源的内阻、受控源均应保 留。 4.受控源不能单独作用。 5.叠加的结果为代数和,注意电压或电流的参考方向 。 6.只适用于电压和电流,不能用于功率和能量的计算, 它们是电压或电流的二次函数。
任意一个具有b条支路、n个节点的集总参数网络,设它 的各支路电压和电流分别为u k 和 i k (k=1、2、3、…b), 且各支路电压和电流取关联参考方向,则有
u
k 1
b
k k
i 0
特勒根第一定理(功率守恒)。 特勒根第二定理(似功率守恒)表述如下: 任意两个同样具有b条支路、n个节点的集总参数网 络N和N’,设它们的各支路电压和电流分别为 u k 和 i k ' ;u k 和 ik ' (k=1、2、3、…b),且各支路电压和电流取 相同的关联参考方向,则有
P61-9 第4章 网络定理
u i
k 1
b
k k
' 0
和
u
k 1
b
ቤተ መጻሕፍቲ ባይዱ
k
' ik 0
特勒根定理适用于任意集总参数电路。 特勒根定理可以用KCL和KVL来证明。
4.5 互易定理
互易性——线性不含独立源、受控源的电路,在单一 激励情况下,激励和响应的位置互换,相同激励的响 应不变。 互易网络:具有互易性的网络。
《电路分析基础》
P61-6 第4章 网络定理
戴维南定理和诺顿定理注意几点: 1.被等效的有源二端网络是线性的,且与外电路之间 不能有耦合关系 2.求等效电路的Ro时,应将网络中的所有独立源置零 ,而受控源保留 3.当Ro≠0和∞时,有源二端网络既有戴维南等效电 路又有诺顿等效电路,并且 uoc、isc和Ro存在关系:
《电路分析基础》
P61-5 第4章 网络定理
任一线性有源二端网络N,就其两个输出端而言总可与 一个独立电压源和线性电阻串联的电路等效,其中独立电压 源的电压等于该二端网络N输出端的开路电压 uOC ,电阻 Ro等于N内所有独立源置零时从输出端看入的等效电阻。
求Ro方法小结: 1.串、并联法;2.加压求流法,或加流求压法; 3.开短路法;4.两点法。 4.3.2 诺顿定理 任一线性有源网络N,就端口而言,可以等效为一个电 流源和电阻的并联。电流源的电流等于网络外部短路时的 端口电流isc;电阻Ro是网络内全部独立源置零时从输出端 看入的等效电阻。
4.2 替代定理
在具有唯一解的任意集总参数网络中,若某条支路k 与网络中的其他支路无耦合,如果已知该支路的支路电 压 u k (支路电流 i k ),则该支路可以用一个电压 为 u k 的独立电压源(电流为 i k 的独立电流源)替代 ,替代前后电路中各支路电压和电流保持不变。
《电路分析基础》
P61-4 第4章 网络定理
注意: 1. 适用于任意集总参数网络(线性的、非线性的,时 不变的、时变的)
2. 所替代的支路与其它支路无耦合 3. “替代”与“等效变换”是不同的概念。“替代” 是特定条件下支路电压或电流已知时,用相应元件替代支 路。等效变换是两个具有相同端口伏安特性的电路间的相 互转换,与变换以外电路无关。 4. 已知支路可推广为已知二端网络(有源、无源)。大 网络成小网络 4.3 戴维南定理和诺顿定理 4.3.1 戴维南定理
电路分析基础
刘 陈
沈元隆
第四章
《电路分析基础》
P13-1
第4章 网络定理
第4章 网络定理 4.l 4.2 4.3 4.4 4.5 线性和叠加定理 替代定理 戴维南定理和诺顿定理 特勒根定理 互易定理
习题
《电路分析基础》
P61-2
第4章 网络定理
4.l 线性和叠加定理 线性网络:由独立电源和线性元件组成。 具有线性性质: 1.齐次性:单个激励(独立源)作用时,响应与激励成正比。 2.可加性:多个激励同时作用时,总响应等于每个激励单独 作用(其余激励置零)时所产生的响应分量的代数和。 由n个独立电源共同产生的响应,等于每个独立电源单独 作用所产生响应之和。 叠加定理: 由全部独立电源在线性电阻电路中产生的任一响应(电压 或电流),等于每一个独立电源单独作用所产生的相应响应(电 压或电流)的代数和。 注意: 1. 适用于线性网络。非线性网络不适用。
Ro uoc isc uoc Ro isc isc uoc Ro
4.作为定理,一个电路可以应用多次。
5.一般端电压与开路电压不相等。
4.3.3 最大功率传输条件
《电路分析基础》
P61-7 第4章 网络定理
负载电阻吸收的功率
uoc p i RL R R L o
2
RL
互易定理有三种形式:
《电路分析基础》
P61-10 第4章 网络定理
形式一:NR 仅由电阻组成,激励电压源uS与响应电流 可以互换位置,即互易前后的响应电流相同。
形式二:NR 仅由电阻组成,激励电流源iS 与响应电压 可以互换位置,即互易前后的响应电压相同。
形式三:NR仅由电阻组成,激励电压源uS与响应开路电 压u互换位置后,将此激励换为相同数值的电流源is,产 生的响应短路电流i在数值上与互易前响应电压u相等。
互易定理可以用特勒根定理来证明。 由特勒根定理,得
u1i1 'u2i2 ' u1 ' i1 u2 ' i2
《电路分析基础》
P61-11 第4章 网络定理
对于形式一: u1 =uS, u2 =0,u1‘=0, u2 ’=uS,代 入特勒根定理,可得 uS i1 '=uS i2 ' 故 i2 = i1 ' 因此形式一成立。 同样,可以证明其余两种形式。 互易定理的形式一也可表示为:互易前的激励电压源比响 应电流等于互易后的激励电压源比响应电流。 互易定理的形式二也可表示为:互易前的激励电流源比响 应电压等于互易后的激励电流源比响应电压。 互易定理的形式三也可表示为:互易前的激励电压源比响 应电压流等于互易后的激励电流源比响应电流。
《电路分析基础》
P61-12 第4章 网络定理
注意: 1.NR不含独立源、受控源,外部只有单个激励和响应; 2.若互易前后激励和响应的参考方向关系一致(都相同或 都相反),则对形式一和二有:相同的激励产生 相同 的 响应;对形式三则相同激励产生的响应相差一个负号。
《电路分析基础》
P61-13
第4章 网络定理
2
欲获得最大功率,有
dp dRL
RL Ro
2
2 RL RL Ro
L
R
uoc 4 Ro
2
Ro
4
uoc 0
2
可得最大功率传输条件:RL=Ro 此时,负载获最大功率为:
pmax
此时对于等效电路而言:效率为50% 。
《电路分析基础》
P61-8 第4章 网络定理
4.4 特勒根定理
《电路分析基础》
P61-3 第4章 网络定理
2.某一激励单独作用时,其他激励置零,即独立电压源 短路,独立电流源开路;电路其余结构都不改变。 3.任一激励单独作用时,该电源的内阻、受控源均应保 留。 4.受控源不能单独作用。 5.叠加的结果为代数和,注意电压或电流的参考方向 。 6.只适用于电压和电流,不能用于功率和能量的计算, 它们是电压或电流的二次函数。
任意一个具有b条支路、n个节点的集总参数网络,设它 的各支路电压和电流分别为u k 和 i k (k=1、2、3、…b), 且各支路电压和电流取关联参考方向,则有
u
k 1
b
k k
i 0
特勒根第一定理(功率守恒)。 特勒根第二定理(似功率守恒)表述如下: 任意两个同样具有b条支路、n个节点的集总参数网 络N和N’,设它们的各支路电压和电流分别为 u k 和 i k ' ;u k 和 ik ' (k=1、2、3、…b),且各支路电压和电流取 相同的关联参考方向,则有
