第一章(图论的基本概念)
第一章(图论的基本概念)
第二节 图的顶点度和图的同构(4)
图序列:简单图的度序列. (d1, d 2 , , d p )(d1 d 2 d p ) 定理4 非负整数序列 是图序列当 p 且仅当 d i 是偶数,并且对一切整数k, 1 k p 1, 有
i 1
第二节 图的顶点度和图的同构(1)
定义1 设G是任意图,x为G的任意结点,与结点x关联的 边数(一条环计算两次)称为x的度数.记作deg(x)或d(x). 定义2 设G为无向图,对于G的每个结点x,若d(x)=K,则 称G为K正则的无向图.设G为有向图,对于G的每个结点 x,若d+(x)=d-(x), 则称G为平衡有向图.在有向图G中, 若 (G) (G) (G) (G) K , 则称G为K正则有向图. 定理1(握手定理,图论基本定理)每个图中,结点度数的 总和等于边数的二倍,即 deg(x) 2 E .
•
A
N
S
B
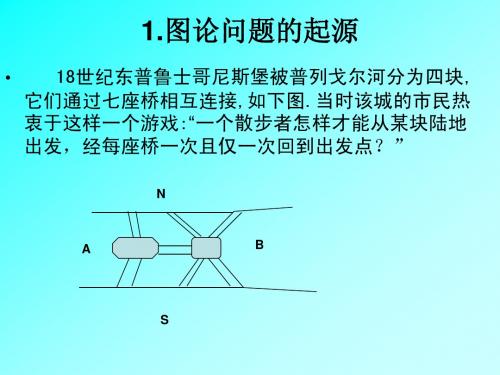
欧拉的结论 • 欧拉指出:一个线图中存在通过每边一次仅一次 回到出发点的路线的充要条件是: • 1)图是连通的,即任意两点可由图中的一些边连 接起来; • 2)与图中每一顶点相连的边必须是偶数. • 由此得出结论:七桥问题无解. 欧拉由七桥问题所引发的研究论文是图论的开 篇之作,因此称欧拉为图论之父.
xV
定理2 每个图中,度数为奇数的结点必定是偶数个.
第二节 图的顶点度和图的同构(2)
• 定理3 在任何有向图中,所有结点入度之和等于所有结 点出度之和. • 证明 因为每条有向边必对应一个入度和出度,若一个结 点具有一个入度或出度,则必关联一条有向边,因此,有向 图中各结点的入度之和等于边数,各结点出度之和也等 于边数. • 定义 度序列,若V(G)={v1,v2,…,vp},称非负整数序列 (d(v1),d(v2),…,d(vp))为图G的度序列.
图论讲义-图的基本概念

有向图(Digraph)、无向图(Undigraph)
若边e对应的无序点对为u,v,则记e=(u,v)或<u,v>,
其中点u与v均称为边e的端点。 若e=<u,v>,则<u,v>表示从u到v的一条弧(Arc),且 称u为弧尾(Tail)或初点(Initial node),称v为弧头 (Head)或终点(Terminal node),此时的图称为有 向图(Digraph)。
v1
5
v4
v1
v4
e1 v2
e2 e3
e4
v3
v2
v3
上两例中,同一条边的两个端点称为相邻;若两条边有一个共同的端点,则这
两条边也称为相邻;若点u是边e的端点,则称u与e相关联。称两个端点相同的 边为环,不与任何边相关联的点称为孤立点。若图中n条不同的边e1,e2,…,en, (n≥2)中的每一条边的两个端点均为u和v,则这些边称为n重边,简称为重边。 不是重边的边称为单边。图中顶点的个数称为该图的阶。 例3、对例1所示的图,点v1与v2相邻,v1与v3不相邻;边e1与e2相邻,e1与e4 不相邻;点v1与边e1相关联。边e5为环。边e2与e3为二重边。这是一个4阶图。 例2中v4是孤立点。
六、路与图的连通性
v1 v2 v5
图G中,取Γ1=v1v2v3,
v3
v4
G
Γ2=v1v2v3v4v2, Γ3=v1v2v3v2v3v4 则 Γ1,Γ2,Γ3依次为长为2,4,5的 通路,其中Γ1与Γ2为简单通路, Γ1为基本通路。 由定义可看出,G中v1v2v5v1为 长为3的圈,v1v2v3v4v2v5v1为 长为6的简单回路。
对于有向图G,如果略去G中各个有向边的方向后所得
图论第01讲

•
两个问题:
(1)经过每个顶点一次且仅一次; (2)代价最小的Hamilton回路。
(目前无有效的方法求解)
•
货郎问题(Traveling Salesman Problem)
一个货郎到各村去卖货,要求每个村子 至少去一次,最后返回出发点,为其设计一 种销售路线,使总耗时最短。
求解方法:把路线全排列,求其中最小的。
1930年,波兰数学家库拉托父斯基 (Kuratowski)证明了平面图可以画在平面上;
•
里程碑:1936年,匈牙利数学家寇尼希 (D.Konig)发表名著《有限图和无限图理论》 ,使得图论成为一门独立的数学学科;
蓬勃发展:1946年,随着世界上第一台计算机 的问世,使图论的发展突飞猛进。 其后,图论在现代数学、计算机科学、工程技 术、优化管理等领域有大用而得以大力发展。
图论第01讲
•
课程简介
▪ 《图论》是计算机科学与技术专业、信息 安全专业的选修课程。 通过本课程的学习,使学生对图论的 历史背景、研究内容、相关技术及其发展 有一个较为全面地了解,从而将所学知识 和技术运用于实际应用领域奠定基础。
•
▪ 本课程所介绍的内容包括:
图论的发展历程和经典问题; 图的基本概念; 有关树和图的算法; 网络流问题; 匹配问题、色数问题;
•如何才能在所有桥都恰巧只走一遍的前提下,回到原出发点?
•
不少数学家都尝试去解析这个事例。而 这些解析,最后发展成为了数学中的图论。
莱昂哈德·欧拉(Leonhard Euler)在1736 年圆满地解决了这一问题,证明这种方法并 不存在。他在圣彼得堡科学院发表了图论史 上第一篇重要文献。欧拉把实际的问题抽象 简化为平面上的点与线组合,每一座桥视为 一条线,桥所连接的地区视为点。这样若从 某点出发后最后再回到这点,则这一点的线 数必须是偶数。
(图论)图的基本概念--第一章

证明 设G=<V,E>为任意一图,令
V1={v|v∈V∧d(v)为奇数} V2={v|v∈V∧d(v)为偶数} 则V1∪V2=V,V1∩V2= ,由握手定理可知
2m d (v) d (v) d (v)
vV
vV1
vV2
由于2m和 d (v) ,所以 d (v) 为偶数,
举例
NG(v1) = {v2,v5} NG(v1) = {v1,v2,v5} IG(v1) = {e1,e2,e3}
Г+D(d ) = {c} Г-D(d ) = {a,c} ND(d ) = {a,c} ND(d ) = {a,c,d}
简单图与多重图
定义1.3 在无向图中,关联一对顶点的无向边如果多于1条,则 称这些边为平行边,平行边的条数称为重数。 在有向图中,关联一对顶点的有向边如果多于1条,并且这些 边的始点和终点相同(也就是它们的方向相同),则称这些边 为平行边。 含平行边的图称为多重图。 既不含平行边也不含环的图称为简单图。
无向图和有向图
定义1 一个无向图是一个有序的二元组<V,E>,记作G,其中 (1)V≠称为顶点集,其元素称为顶点或结点。 (2)E称为边集,它是无序积V&V的多重子集,其元素称为无向 边,简称边。
定义2 一个有向图是一个有序的二元组<V,E>,记作D,其中 (1)V≠称为顶点集,其元素称为顶点或结点。 (2)E为边集,它是笛卡儿积V×V的多重子集,其元素称为有向 边,简称边。
vV2
vV1
但因V1中顶点度数为奇数, 所以|V1|必为偶数。
问题研究
问题:在一个部门的25个人中间,由于意见不同,是否可能每 个人恰好与其他5个人意见一致?
图论期末考试整理复习资料

目录第一章图的基本概念 (1)二路和连通性 (3)第二章树 (3)第三章图的连通度 (4)第四章欧拉图与哈密尔顿图 (5)一,欧拉图 (5)二.哈密尔顿图 (6)第五章匹配与因子分解 (9)一.匹配 (9)二.偶图的覆盖于匹配 (10)三.因子分解 (11)第六章平面图 (14)二.对偶图 (16)三.平面图的判定 (17)四.平面性算法 (20)第七章图的着色 (24)一.边着色 (24)二.顶点着色 (25)第九章有向图 (30)二有向树 (30)第一章图的基本概念1.点集与边集均为有限集合的图称为有限图。
2.只有一个顶点而无边的图称为平凡图。
3.边集为空的图称为空图。
4.既没有环也没有重边的图称为简单图。
5.其他所有的图都称为复合图。
6.具有二分类(X, Y)的偶图(或二部图):是指该图的点集可以分解为两个(非空)子集X 和Y ,使得每条边的一个端点在X 中,另一个端点在Y 中。
7.完全偶图:是指具有二分类(X, Y)的简单偶图,其中X的每个顶点与Y 的每个顶点相连,若|X|=m,|Y|=n,则这样的偶图记为Km,n8. 定理1 若n 阶图G 是自补的(即),则n = 0, 1(mod 4)9. 图G 的顶点的最小度。
10. 图G 的顶点的最大度。
11. k-正则图: 每个点的度均为 k 的简单图。
例如,完全图和完全偶图Kn,n 均是正则图。
12. 推论1 任意图中,奇点的个数为偶数。
13.14. 频序列:定理4 一个简单图G 的n 个点的度数不能互不相同。
15. 定理5 一个n 阶图G 相和它的补图有相同的频序列。
16.17.18. 对称差:G1△G2 = (G1∪G2) - (G1∩G2) = (G1-G2)∪(G2-G1)19. 定义: 联图 在不相交的G1和G2的并图G1+G2中,把G1的每个顶点和G2的每个顶点连接起来所得到的图称为G1和G2的联图,记为G1∨G220. 积图:积图 设G1= (V1, E1),G2 = (V2, E2),对点集V = V1×V2中的任意两个点u =(u1,u2)和v = (v1,v2),当(u1 = v1和 u2 adj v2) 或 (u2 = v2 和 u1 adj v1) 时就把 u 和 v 连接起来所得到的图G 称为G1和G2积图。
图论与代数结构

假如 G1 G2 ,则必须满足: (1) | V (G1) || V (G2 ) |, | E(G1 ) || E(G2 ) | . (2) G1 和 G2 结点度的非增序列相同. (3)存在同构的导出子图.
图的概念
性质1.1.5 非空简单图G中一定存在度相同的结点. 证明:设在G中不存在孤立结点,则对n个结 点的简单图,每个结点度d(v)的取值范围是 1~(n-1),由抽屉原理,一定存在两个度相同的 结点.若存在一个孤立的结点,亦类似可证.
图的概念
定义1.1.4 如果图G=(V,E)的每条边 ek (vi , v j ) 都赋以一 个实数wk 作为该边的权,则称G是赋权图.特别 地,如果这些权都是正实数,就称G是正权图. 图1.5就是一个正权图.权可以表示该边的长度, 时间,费用或者容量等.
图的概念
性质1.1.1 设G=(V,E)有n个结点,m条边,则
v V (G )
d (v) 2m
证明:由于每条边e=(u,v)对结点u和v度的贡献 各为1,因此m条边对全部结点的总贡献率为 2m.
图的概念
性质1.1.2 G中度为奇数的结点必为偶数个. 证明: G中任一结点的度或为偶数或为奇数,设 Ve是度为偶 的结点集,Vo 是度为奇的结点集,于是有
vVe
d (v) d (v) 2m
vV0
因此上式左边第二项也为偶数,也即度为奇数的结点 必为偶数个
图的概念
性质1.1.3 有向图G中正度之和等于负度之和.这是因 为每条边对结点的正,负度贡献各为1. 性质1.1.4 K n 的边数是n(n-1)/2. 证明:K n 中各结点的度都是(n-1),由性质 1.1.1就可以得到
图论概念定理知识点梳理

图论基本知识点梳理第一部分(基本概念)1.G连通的充分必要条件是(G) = 1 o或若|V(G) |=2k,且对—v V(G),有d(v) _ k,则G是连通图。
4•图G为二分图当且仅当G中无奇圈。
5•在仅两个奇次顶点的图中,此二奇次顶点连通。
6•设G为简单图,若、;(G) _ 2,则G中有圈。
7.设G为简单图,若「.(G) 一3,则G中有偶圈。
具体地,(1)单星妖怪中有偶圈。
⑵在k -正则图G中,若k _3,则G中有偶圈。
8•简单图G与其补图G c不能都不连通。
29•在."■:的三角剖分中,正常三角形为奇数个。
10•以下等价(1) G是树(无圈连通图)° (2) G中任两顶点间恰有一条轨。
⑶G 无圈,=■…1。
(4) G是连通图,;-、•-1 ° (5) G是连通图,且对G的任意边e, G -e不连通。
(树每边皆割边)(6) G无圈,且对任一不在E(G)的边e, G e恰含一个圈。
11. 若G连通,则;(G) (G)-1。
G的生成树是G最小的连通生成子图。
12. G是连通图的充分必要条件是G有生成树。
13. > - 2的树T至少有两个叶。
14. 完全图K n的生成树个数・(K n)二n n°。
15. 图G可平面嵌入的充分必要条件是G可以球面嵌入。
(染地球上各国等价于染地图上各国)16. (Euler公式) G是连通平面图,贝X - ;「- 2.17. 证明:若G是、-3的连通平面图,则;乞3 -6。
18. 证明:平面图G的最小顶点次数5。
19 -3平面图G是极大平面图的充要条件是G的平面嵌入的每个面皆三角形。
' -3平面图G是极大平面图的充要条件是;=3二-6。
20 G是平面图当且仅当G中不含与K5和K3,3同胚的子图。
21 M是图G的最大匹配当且仅当G中无M的可增广轨。
22婚配定理:设G是具有二分类(X,Y)的偶图,存在把X中顶点皆许配的匹配的充要条件是-s X,|N(S)|」S|,其中N(S)是S中每个顶点的邻点组成的所谓S的邻集推论:k -正则二分图有完美匹配,k .0。
图论-图的基本概念

证明:按每个顶点的度来计数边,每条边恰数了两次。 推论 1.1.1 任何图中,奇度顶点的个数总是偶数(包括 0)。 4. 子图
子图(subgraph):如果 V (H ) ⊆ V (G) 且 E(H ) ⊆ E(G) ,则称图 H 是 G 的子图,记为 H ⊆G。
生成子图(spanning subgraph): 若 H 是 G 的子图且V (H ) = V (G) ,则称 H 是 G 的生成子图。
这便定义出一个图。
2. 图的图示
通常,图的顶点可用平面上的一个点来表示,边可用平面上的线段来表示(直的或曲的)。 这样画出的平面图形称为图的图示。
例如,例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注:(1)由于表示顶点的平面点的位置的任意性,同一个图可以画出形状迥异的很多图示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
过 k 年的旧设备的决策
(k ) (2)弧集 E={ ( X ib , X i 1,b ),( X ir , X i 1,b ), i=1,2,3,4; k=1,2,…,i-1} 1) (k ) ( k 1) ∪{ ( X ib , X i( , =1,2,3,4,5} ∪ { ) ( X , X 1,r ir i 1,r ) ,i=1,2,3,4,5 ;k=1,2,i -1}
deg( x) 2 E .
xV
定理2 每个图中,度数为奇数的结点必定是偶数个.
第二节 图的顶点度和图的同构(2)
定理3 在任何有向图中,所有结点入度之和等于所有结 点出度之和. 证明 因为每条有向边必对应一个入度和出度,若一个结 点具有一个入度或出度,则必关联一条有向边.因此,有向 图中各结点的入度之和等于边数,各结点出度之和也等 于边数. 定义度序列 若V(G)={v1,v2,…,vp},称非负整数序列 (d(v1),d(v2),…,d(vp))为图G的度序列.
第二节 图的顶点度和图的同构(3) 推论1 非负整数序列 (d1, d 2 ,..., d p ) 是某个图的度序 p d i 是偶数. 列当且仅当
证明:由定理1知必要性成立.对于充分性取p各相异顶点 v1,v2,…,vp,若di是偶数,就在vi处作di/2个环; 若di是奇数,在vi处作(di-1)/2个环,由于 d i是偶数,
5.图的广泛应用
图的应用是非常广泛的,在工农业生产、交 通运输、通讯和电力领域经常都能看到许多网络, 如河道网、灌溉网、管道网、公路网、铁路网、 电话线网、计算机通讯网、输电线网等等.还有 许多看不见的网络,如各种关系网,像状态转移关 系、事物的相互冲突关系、工序的时间先后次序 关系等等,这些网络都可以归结为图论的研究对 象—图.其中存在大量的网络优化问题需要我们 解决.还有象生产计划、投资计划、设备更新等 问题也可以转化为网络优化的问题.
一个有向图D,称D为G的一个定向图.
例 证明:在任意六个人的聚会上,要么三个曾相识, 要么三个不曾相识.
证明:用A,B,C,D,E,F代表这六个人,若两人曾相识,则在代 表该两人的顶点间连一条红边;否则连一条蓝边.于是, 原问题等价于证明所得图中必含有同色三角形.考察某 一顶点,设为F.与F关联的边中必有三条同色,不妨设它 们是三条红边FA, FB, FC.再看三角形ABC.若它有一条 红边,设为AB,则FAB是红边三角形;若三角形ABC没有 红边,则其本身就是蓝边三角欧拉指出:一个线图中存在通过每边一次仅 一次回到出发点的路线的充要条件是: 1)图是连通的,即任意两点可由图中的一些 边连接起来; 2)与图中每一顶点相连的边必须是偶数. 由此得出结论:七桥问题无解. 欧拉由七桥问题所引发的研究论文是图论 的开篇之作,因此称欧拉为图论之父.
2 n(n 1)条边. (3) n个结点的完全图记为Kn,完全图Kn有 Cn
完全图的对称有向图称为完全有向图,记作 K * . n (4) 图G的顶点个数 称为图G的阶. (5) 对于有向图D,去掉边上的方向得到的无向图G称为D的
基础图.反之,任一个无向图G,将G的边指定一个方向得到
1 2
第二节 图的顶点度和图的同构(1)
定义1 设G是任意图,x为G的任意结点,与结点x 关联的边数(一条环计算两次)称为x的度数.记 作deg(x)或d(x). 设D是任意有向图,x为G的任一结点,以x为 终点的边的条数称为x的入度,记作deg+(x)或 d+(x). 以x为始点的边的条数称为x的出度,记作 deg-(x)或d-(x).
任课教师:陈六新
chenliux@
答疑时间:星期三下午2:30-3:30;
地点:数理学院3楼 应用数学教学部
建议参考书: 图论及其算法 殷剑宏 吴开亚 中科大出版社
图论及其应用 张清华等编 清华大学出版社
图论与网络流理论,高随祥,高教社 通信网图论及应用, 刘焕淋, 陈勇 ,人民邮电 电网络理论(图论,方程 综合)周庭阳,张红岩;械工业出版社 图论导引,(美)Douglas B. West 社 译 李建中 ,机械工业出版
内容:关系与函数.
第一章 图的基本概念(1)
定义1 图G是一个三元组,记作 (1) V (G) {v1, v2 ,, vn } (2) E(G) {e1, e2 ,, em}
G V (G ), E (G ), (G )
其中
V (G ) ,
称为图G的结点集.
是G的边集合,其中 ei 或 {v j , vt } 或
若第 i 年初作了决策 X i 后,第 i+1 年初可以作决策 X i 1 ,则顶点 X i 与 X i 1 之间有弧( X i , X i 1 ),其权 W( X i , X i 1 )代表第 i 年初到第 i+1
(1) 年初之间的费用.例如,弧 ( X 3b , X 4 r ) 代表第三年初买新设备,第四 年初决定用第三年买的用过一年的旧设备,其权则为第三年初的购 臵费与第三、第四年间的维修费之和,即为 12+5=17.
v j , vt 为边。
{v j , vt }, 称 ei 为以 v j , vt 为端点的无向边。 若 ei 为 v j , vt , 称 ei 为以 v j 为起点, vt 为终点的有向边。
若 ei 为
(G) : E V V
称为关联函数.
第一章 图的基本概念(2)
定义2. 邻接结点:关联于同一条边的两个结点. 孤立结点:不与任何结点相连接的结点. 邻接边:关联于同一顶点的两条边. 环:两端点相同的边称为环或自回路. 平行边:两个结点间方向相同的若干条边称为平 行边或重边. 对称边:两端点相同但方向相反的两条有向边.
4.图的作用
图是一种表示工具,改变问题的描述方式,往往 是创造性的启发式解决问题的手段. 一种描述方式就好比我们站在一个位臵和角度 观察目标,有的东西被遮挡住了,但如果换一个位臵和 角度,原来隐藏着的东西就可能被发现.采用一种新的 描述方式,可能会产生新思想. 图论中的图提供了一种直观,清晰表达已知信息 的方式.它有时就像小学数学应用题中的线段图一样, 能使我们用语言描述时未显示的或不易观察到的特 征、关系,直观地呈现在我们面前,帮助我们分析和思 考问题,激发我们的灵感.
(1) ( 2) (1) ( 2) X 1b X 2 X X X X r 3r 4b 5r 6r ; (1) (1) ( 2) ( 3) X 1b X 2 X X X X r 3b 4r 5r 6r 因此,计划为第一、第三年初购臵新设备,或第一、第四年初购臵 新设备,五年费用均最省,为 53.
(k ) (3)问题转化为顶点 X 1b 到 X 6 的最短路问题.五年的最优购臵 r 费为
k 1,2 ,3,4 ,5
min {d ( X
1b
(k ) , X6 r )}
(k ) (k ) X X 其中 d( X 1b , X 6 ) 为顶点 到 1b r 6r 的最短路的权. 求得最短路的权为 53,而两条最短路分别为
可化为最短路问题的多阶段决策问题
例 1 设备更新问题:企业使用一台设备,每年年初,企业领导 就要确定是购臵新的,还是继续使用旧的.若购臵新设备,就要支 付一定的购臵费用;若继续使用,则需支付一定的维修费用.现要 制定一个五年之内的设备更新计划,使得五年内总的支付费用最 少. 已知该种设备在每年年初的价格为: 第一年 第二年 第三年 第四年 11 11 12 12 使用不同时间设备所需维修费为: 使用年限 维修费 0-1 5 1-2 6 2-3 8 3-4 11 第五年 13 4-5 18
δ+(G)=min{d+G(x)|x∈V(G)}.
Δ-(G)=max{d-G(x)|x∈V(G)};
δ-(G)=min{d-G(x)|x∈V(G)}.
第二节 图的顶点度和图的同构(1) 定义2 设G为无向图,对于G的每个结点x,若d(x)=K, 则称G为K正则的无向图.设G为有向图,对于G的 每个结点x,若d+(x)=d-(x), 则称G为平衡有向图. ( G ) ( G ) ( G ) (G) K , 在有向图G中,若 则称G为K正则有向图. 定理1(握手定理,图论基本定理) 每个图中,结点 度数的总和等于边数的二倍,即
第一章 图的基本概念(4)
说明:(1)在简单图G V (G ), E (G ), (G ) 中,以x为起点y为终
点的边至多有一条,因此,图中的边可直接用顶点对表
示,而关联函数 就可以直接表示在其边集中,故可简
记为G=<V(G),E(G)>.
(2)对无向图G,将G中的每条边用两条与e有相同端点对 称边e和e’来代替后得到一个有向图D,这样得到的有 向图D称为G的对称有向图.由此可见,无向图可视为 特殊的有向图.
i 1 p
i 1
故 (d1, d 2 ,..., d p )中由偶数个奇数顶点,从而将所有与奇数di 相对应的顶点vi两两配对并连上一条边.最后所得的序列 就是 d1, d 2 ,..., d.p
构造加权有向图 G1(V,E)
(k ) ( 1 ) 顶 点 集 V = { X ib , i=1,2,3,4,5}∪{ X ir , i=2,3,4,5,6; k =1,2,…,i-1}, 每个顶点代表年初的一种决策, 其中顶点 X ib 代 (k ) 表第 i 年初购臵新设备的决策, 顶点 X ir 代表第 i 年初修理用
1.图论问题的起源
18世纪东普鲁士哥尼斯堡被普列戈尔河分为四块,它 们通过七座桥相互连接,如下图.当时该城的市民热衷于 这样一个游戏:“一个散步者怎样才能从某块陆地出发, 经每座桥一次且仅一次回到出发点?”
