8cq工程力学第12章答案
大学《工程力学》课后习题解答-精品
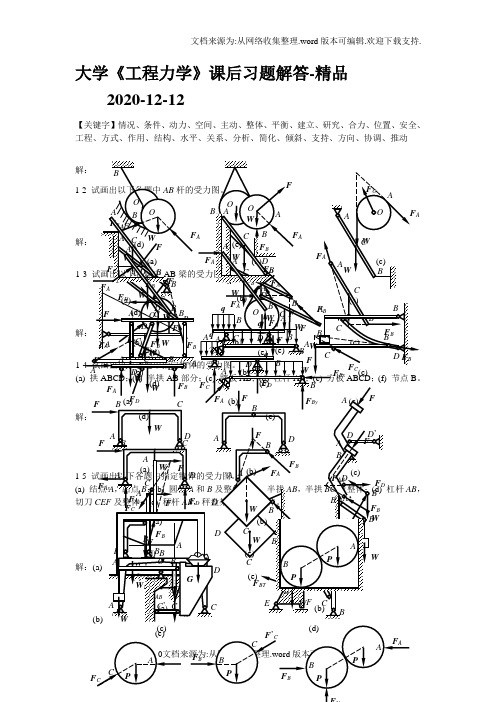
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解:(1) 取整体(2) 2-4 在简支梁,力的大小等于20KN ,如图所示。
若解:(1)(2)求出约束反力:2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F =200 N ,试求支座A 和E 的约束力。
解:(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解:(1)取铰链B (2) 取铰链C 由前二式可得:F FF ADF2-9 三根不计重量的杆AB,AC,AD在A点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与O D平行的力F作用下,各杆所受的力。
已知F=0.6 kN。
解:(1)间汇交力系;(2)解得:AB、AC3-1 已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) (b) (c) 3-2 M ,试求A 和C解:(1) 取 (2) 取 3-3 Nm ,M 2解:(1)(2) 3-5 大小为AB 。
各杆 解:(1)(2)可知:(3) 研究OA 杆,受力分析,画受力图:列平衡方程:AB A3-7 O1和O2圆盘与水平轴AB固连,O1盘垂直z轴,O2盘垂直x轴,盘面上分别作用力偶(F1,F’1),(F2,F’2)如题图所示。
第十二章动能定理习题解答

第十二章动能定理习题解答习题12–1一刚度系数为k的弹簧,放在倾角为的斜面上。
弹簧的上端固定,下端与质量为m的物块A相连,图12-23所示为其平衡位置。
如使重物A从平衡位置向下沿斜面移动了距离,不计摩擦力,试求作用于重物A上所有力的功的总和。
图12-23Wmgink2(t(t)2)2kmginkt22k2212–2如图12-24所示,在半径为r的卷筒上,作用一力偶矩M=a+b2,其中为转角,a和b为常数。
卷筒上的绳索拉动水平面上的重物B。
设重物B的质量为m,它与水平面之间的滑动摩擦因数为不计绳索质量。
当卷筒转过两圈时,试求作用于系统上所有力的功的总和。
图12-244π0WMMd(a+b2)d8aπ2643bπ3WFmg4πr4πmgr644W8aπ2bπ34πmgrπ(6πa16π2b3mgr)3312–3均质杆OA长l,质量为m,绕着球形铰链O的铅垂轴以匀角速度转动,如图12-25所示。
如杆与铅垂轴的夹角为,试求杆的动能。
图12-2511mmdEk(dm)v2(d某)(某in)2(in2)某2d某22l2llm1Ek(2in2)某2d某ml22in202l612–4质量为m1的滑块A沿水平面以速度v移动,质量为m2的物块B沿滑块A以相对速度u滑下,如图12-26所示。
试求系统的动能。
图12-26Ek11m1v2m2[(uco30v)2(uin30)2]22-1-11m1v2m2(u2v22uvco30)2211m1v2m2(u2v23uv)2212–5如图12-27所示,滑块A质量为m1,在滑道内滑动,其上铰接一均质直杆AB,杆AB长为l,质量为m2。
当AB杆与铅垂线的夹角为时,滑块A的速度为vA,杆AB的角速度为试求在该瞬时系统的动能。
图12-27EkEkAEkAB11ll112m1vAm2[(vAco)2(in)2](m2l2)22222212111122m1vAm2(vAl22l vAcol22)2241211122m1vAm2(vAl22lvAco)22312–6椭圆规尺在水平面内由曲柄带动,设曲柄和椭圆规尺都是均质细杆,其质量分别为m1和2m1,且OC=AC=BC=l,如图12-28所示。
(完整版)工程力学课后详细答案
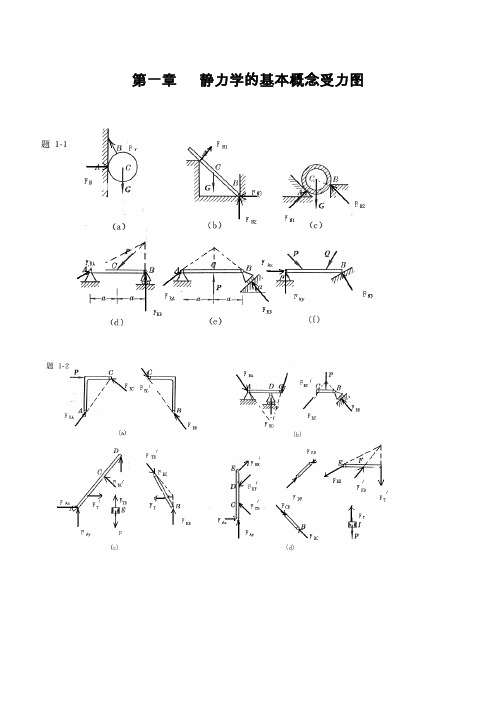
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
工程力学第12章答案供参习
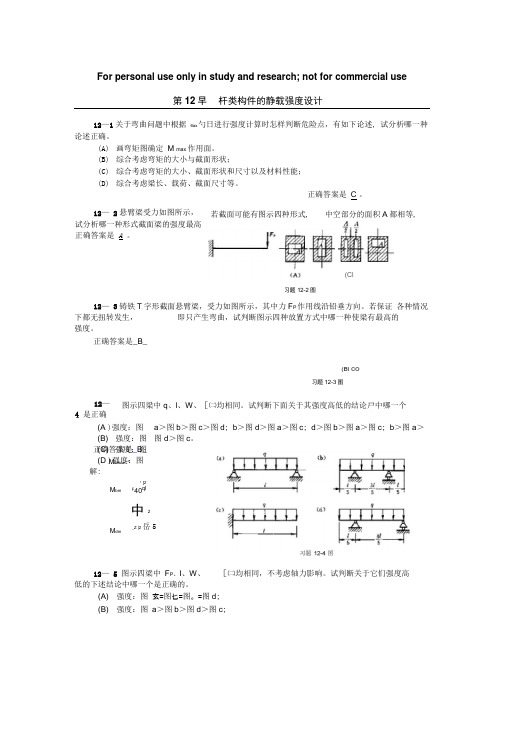
For personal use only in study and research; not for commercial use第12早 杆类构件的静载强度设计12—1关于弯曲问题中根据 6ax 勺日进行强度计算时怎样判断危险点,有如下论述, 试分析哪一种论述正确。
(A) 画弯矩图确定 M max 作用面。
(B) 综合考虑弯矩的大小与截面形状;(C) 综合考虑弯矩的大小、截面形状和尺寸以及材料性能; (D) 综合考虑梁长、载荷、截面尺寸等。
正确答案是 C 。
12— 3铸铁T 字形截面悬臂梁,受力如图所示,其中力F P 作用线沿铅垂方向。
若保证 各种情况下都无扭转发生, 即只产生弯曲,试判断图示四种放置方式中哪一种使梁有最高的 强度。
正确答案是_B _(Bl CO习题12-3图图示四梁中q 、l 、W 、[㈡均相同。
试判断下面关于其强度高低的结论戸中哪一个 a >图b >图c >图d ; b >图d >图a >图c ; d >图b >图a >图c ; b >图a >图d >图c 。
12— 5 图示四梁中 F P 、I 、W 、 低的下述结论中哪一个是正确的。
(A) 强度:图 玄=图匕=图。
=图d ; (B) 强度:图 a >图b >图d >图c ;12— 2悬臂梁受力如图所示, 试分析哪一种形式截面梁的强度最高 正确答案是 A 。
中空部分的面积A 都相等,12— 4 是正确的。
(A )强度:图 (B) 强度:图 (C) 强度:图(D )强度:图 正确答案是_B_ 解:M amax *2M bm1[2F40qlM dm中2_Z |2岳5[㈡均相同,不考虑轴力影响。
试判断关于它们强度高若截面可能有图示四种形式, 习题12-2图(Cl仅供参考 a a匚5M /F p lA2/习题12-5题1 3AA B(b-1) (c-1)2/M AB(a)C?=5o](N/tnI Mi20FRB1 21 3 3 (d-1)习题12-6题习题12-7图a m 4 (a-1)FRA--D max :-Cmax M /F P Io )铸铁,其抗拉许用应力【二】=30MPa (C) 强度: (D) 强度: 正确答案是 解: M故选(B)M /F P l 2■3抗压许用应力【门■= 60MPa 。
工程力学第十二章全解

E E
M
y
r
这表明,直梁的横截面上的正应力
沿垂直于中性轴的方向按线性规律变化
(3)静力学关系━━ 应力与内力。
梁的横截面上与正应力相应的法 向内力元素dA(图d )不可能组成轴 力( FN A d A 0 ),也不可能组成对 (d) 于与中性轴垂直的y 轴(弯曲平面内的
只是绕垂直于弯曲平面(纵向平面)的某一轴转动,转动后
的横截面与梁弯曲后的轴线保持正交。
此假设已为弹性力学的理论分析结果所证实。
〈3〉纵向线应变在横截面范围内的变化规律 图c为由相距d x的两横截面取出的梁段在梁弯曲后的情况, 两个原来平行的横截面绕中性轴相对转动了角d。梁的横截
面上距中性轴 z为任意距离 y 处的纵向线应变由图c可知为
第十二章 弯曲应力
§12-1 梁弯曲时的正应力 §12-2 惯性矩的计算 §12-3 梁弯曲时的强度计算 §12-4 梁弯曲时的切应力 §12-5 提高弯曲强度的措施
M
FQ
梁横截面上 与弯矩M对应, 与剪力F对应。
F
FQ
M
C F
C
M
F
A
12-1 梁弯曲时的正应力
一、弯曲分类
轴)的内力偶矩( M y AzdA 0 ),只
能组成对于中性轴 z 的内力偶矩,即
M z y d A M
A
将 E
r 代入上述三个静力学条件,有
y
FN d A
A
E
r
E
A
yd A
ESz
r
0
(a)
M y z d A
A
r
E
清华出版社工程力学答案-第12章 简单的静不定问题

①
②
③ l
(a)
A a FP A
B a
C
FN1
FN2 B a
FN3 C
(b) a
FP A1 (c) A Δl1 A′
习题 12-4 图
B1 B B′
Δl2
C′ Δl3 C
即
Δl1 − Δl3 = 2Δl2
3. 物理方程
(b)
Δl1 =
FN1l , EA 5FP , 6
Δl2 =
FN 2l , EA
Δl3 =
FP 铜,Ec=105GPa 铝,Ea=70GPa
300
25 60
FP
习题 12-2 图
ε=
0.24 = 8 × 10 − 4 300
轴向载荷等于二者受力之和:
FP = σ cu Acu + σ al Aal = Ecu εAcu + Eal εAal
π π = 105 × 109 × 8 × 10−4 × × 252 × 10 −6 +70 × 109 × 8 × 10−4 × ( 602 − 252 ) × 10−6 4 4 = 172.1 kN
4. 联立求解 将(a) 、 (b) 、 (c)三式联立,求得:
F1 =
(16 + 2 ) l
2 Eδ
2 EAδ
, F2 =
1
(16 + 2 ) l
4 EAδ
1
据此求得二杆横截面上的正应力分别为:
F1杆 = F2杆 =
(16 + 2 ) l
4 Eδ
=
2 × 200 ×109 × 1. 5 × 10−3
7
FA =
7F 4
工程力学(天津大学)第12章答案

第十二章 用能量法计算弹性位移习 题12−1 两根杆拉伸刚度均为EA ,长度相同,承受荷载如图所示,分布荷载集度q =F/l ,试求这两根杆的应变能,并作比较。
解:EAl F V 221=,EA l F dx EA l )qx (dx EA l F V l l N622202022===⎰⎰ 213V V =12−2 试求图示受扭圆轴内所积蓄的应变能,杆长为l ,直径为d ,材料的剪变模量为G 。
解:4320420232163222Gdl m dx d πGl )mx (dx GI l T V l lP ===⎰⎰ 12−3 试计算下列梁内所积蓄的应变能,略去剪力的影响。
习题12−2图解:(a )先求支座反力: ql F ,ql F RB RA 8381==以A 为坐标原点,x 1以向右为正,AC 段的弯矩方程为:118x qlM = 以B 为坐标原点,x 2以向左为正,BC 段的弯矩方程为:22222183qx x ql M -= 梁的变形能为:EIl q dx EI )qx qlx (dx EI )qlx (dx EIMdx EI M V l l l l 153601722183282252202222202120222021=-+=+=⎰⎰⎰⎰(b) 以B 为坐标原点,x 以向左为正,AB 段的弯矩方程为:306x lq M =梁的变形能为:EIl q dx EI )l x q (dx EI M V l l 504262520023002===⎰⎰ (c) 以B 为坐标原点,x 以向左为正,AB 段的弯矩方程为:Fx M )x (M +=梁的变形能为:EIl F EI MFl EI l M dx EI )Fx M (dx EI M V l l6222232220202++=+==⎰⎰ (d) 先求支座反力: ,ql F RA 83=以A 为坐标原点,x 1以向右为正,AB 段的弯矩方程为:21112183qx x ql M -= (0≤x 1≤l )以C 为坐标原点,x 2以向左为正,BC 段的弯矩方程为:22221qx M -=(0≤x 2≤l /2) 梁的变形能为:EIl q dx EI )qx (dx EI )qx qlx (dx EIMdx EI M V l ll l12803221221832252220222102211202221=-+-=+=⎰⎰⎰⎰12−4 试求图示结构中的弹性变形能。
工程力学课后习题答案

6-7空心圆截面轴,外径 ,内径 ,扭矩 ,试计算距轴心 处的扭转切应力,以及横截面上的最大与最小扭转切应力。
2-24平面桁架的支座和载荷如图所示,求杆1,2和3的内力。(提示:先截断AD、3、2杆,用截面法分析;再取C节点)
2-25两根相同的均质杆AB和BC,在端点B用光滑铰链连接,A,C端放在不光滑的水平面上,如图所示。当ABC成等边三角形时,系统在铅直面内处于平衡状态。求杆端与水平面间的摩擦因数。
题2-25图
题5-9图
题5-9图
5-10图示外伸梁,承受集度为 的均布载荷作用。试问当 为何值时梁内的最大弯矩之值(即 )最小。
题5-10图
为保证梁的最大弯矩值最小,即最大正弯矩等于最大负弯矩
第六章杆件的应力
6-1图示的杆件,若该杆的横截面面积 ,试计算杆内的最大拉应力与最大压应力。
题6-1图
6-2图示阶梯形圆截面杆,承受轴向载荷 与 作用, 与 段的直径分别为 与 ,如欲使 与 段横截面上的正应力相同,试求载荷 之值。
4-3材料力学的基本假设是什么?均匀性假设与各向同性假设有何区别?能否说“均匀性材料一定是各向同性材料”?
4-4杆件的轴线与横截面之间有何关系?
4-5试列举五种以上不是各向同性的固体。
4-6杆件的基本变形形式有几种?请举出相应变形的工程实例。
第五章杆件的内力
5-1试求图示各杆1-1、2-2、3-3截面上的轴力,并作轴力图。
5-5某传动轴,转速 ,轮1为主动轮,输入功率 ,轮2、轮3与轮4为从动轮,输出功率分别为 , 。
(1)试画轴的扭矩图,并求轴的最大扭矩;
(2)若将轮1和轮3的位置对调,轴的最大扭矩变为何值,对轴的受力是否有利。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题12-3图 习题12-2图习题12-4图 第12章 杆类构件的静载强度设计12-1 关于弯曲问题中根据][max σσ≤进行强度计算时怎样判断危险点,有如下论述,试分析哪一种论述正确。
(A )画弯矩图确定M max 作用面。
(B )综合考虑弯矩的大小与截面形状;(C )综合考虑弯矩的大小、截面形状和尺寸以及材料性能; (D )综合考虑梁长、载荷、截面尺寸等。
正确答案是 C 。
12-2 悬臂梁受力如图所示,若截面可能有图示四种形式,中空部分的面积A 都相等,试分析哪一种形式截面梁的强度最高。
正确答案是 A 。
12-3 铸铁T 字形截面悬臂梁,受力如图所示,其中力F P 作用线沿铅垂方向。
若保证各种情况下都无扭转发生,即只产生弯曲,试判断图示四种放置方式中哪一种使梁有最高的强度。
正确答案是 B 。
12-4 图示四梁中q 、l 、W 、][σ均相同。
试判断下面关于其强度高低的结论中哪一个是正确的。
(A )强度:图a >图b >图c >图d ; (B )强度:图b >图d >图a >图c ; (C )强度:图d >图b >图a >图c ; (D )强度:图b >图a >图d >图c 。
正确答案是 B 。
解:2amax 81ql M =2bmax 401ql M =2cmax 21ql M = 2dmax 1007ql M =12-5 图示四梁中F P 、l 、W 、][σ均相同,不考虑轴力影响。
试判断关于它们强度高低的下述结论中哪一个是正确的。
(A )强度:图a =图b =图c =图d ; (B )强度:图a >图b >图d >图c ; (C )强度:图b >图a >图c >图d ; (D )强度:图b >图a >图d >图c 。
l q PF=3231ABM )(o M(a)习题12-5题习题12-6题3l M P /F 1(d-1)lM P /F 21AB(c-1)lM P /F 10351BA 351 (b-1) l M P /F 41AB 1 (a-1) 正确答案是 B 。
解:cmax dmax bmax amax M M M M <<< 故选 (B)。
12-6 铸铁制简支梁承受集中力偶M 0如图所示。
试判断四种截面(截面面积均为A )形状中,哪一种可使许可外力偶矩M 0最大。
正确答案是 C 。
解:截面面积相同时D C B A I I I I =<<yI M =σ 2C 0max C 34y I M =σ-, 2C 0max C 32y I M =σ+2D 0max D 32y I M =σ-, 2D 0max D 34y I M =σ+由于铸铁抗压强度高于其抗拉强度,故正确答案选:C 。
12-7 T 形截面外伸梁,受力与截面尺寸如图所示,其中C 为截面形心,710136.2⨯=z I mm 4。
梁的材料为铸铁,其抗拉许用应力+][σ= 30MPa ,抗压许用应力-][σ= 60MPa 。
试校核该梁是否安全。
解:1.0=∑B M ,F R A = 37.5kN (↑)习题12-7图F R BF R AA CDB(kN.m)25zM14.1(a)习题12-8图25150212-=⨯⨯-=BMkN·mRQ=-=qxFFA75.0505.37R===qFx Am1.14212R=-⋅=qxxFM AC kN·m2.C截面8.85130.01036.21101.14130.053max=⨯⨯⨯=⨯=-+zCIMσMPa+>][σ不安全3.B截面5.581036.2105.01025050.063max=⨯⨯⨯=⨯=-+zBIMσMPa+>][σ152130.0max=⨯=-zBIMσMPa->][σ,不安全。
12-8加固后的吊车主梁如图所示。
梁的跨度l = 8m,许用应力][σ= 100MPa。
试分析当小车行走到什么位置时,梁内弯矩最大,并计算许可载荷(小车对梁的作用可视为集中力)。
解:1.小车行至梁中间时,梁内弯矩最大。
PP1242FFM=⨯=82381103467.1)16367512675(21010755.1⨯=⨯⨯+⨯+⨯=zImm44351110113.8mm10113.8166-⨯=⨯==zzIWm3][11σ≤zWM,即64P1010010113.82⨯≤⨯-F56.40P≤F kN (1)2.小车行至离两端1.4 m处PP2155.14.18)4.18(FFM=⨯-=4110922.6-⨯=zW m3][22σ≤zWM,即64P1010010922.6155.1+-⨯≤⨯F9.59P≤F kN (2)比较(1)、(2),得[F P] = 40.56 kN习题12-9图习题12-10图αα12-9 为了起吊重W = 300kN 的大型设备,采用一台150kN 和一台200kN 的吊车及一根辅助梁AB ,如图所示。
已知钢材的][σ= 160MPa ,l = 4m 。
试分析和计算: 1.设备吊在辅助梁的什么位置(以至150kN 吊车的间距a 表示),才能保证两台吊车都不会超载?2.若以普通热轧工字型钢作为辅助梁,确定工字型钢型号。
解:1.0=∑A M )(1501a l W l -= )(30041501a l -=⨯ a 1 = 2m 0=∑B M 2200Wa l =667.230042002002=⨯==W l a m667.2m 2≤≤a m 2. a 1 = 2m 时3002150max 1=⨯=M kN ·m][1max1σσ≤=W M63max 111016010300][⨯⨯==σM W 411075.18-⨯≥W m 3a 2 = 2.667m 时6.266)667.24(200max 2=-⨯=M kN ·m max 1M <故由W 1值选工字钢型号为:No.50a ,其W = 1860cm 3%8.0187515||11==-W W W ,误差不大,故取No.50a 工字钢。
12-10 支承楼板的木梁如图所示,其两端支承可视为简支,楼板受均布面载荷p = 3.5kN/m 2的作用。
已知木梁跨度l = 6m ,楼板间距a = 1m ;木材的][σ= 10MPa ,木梁截面尺寸b /h = 2/3。
试求b 和h 各为多少。
解:木梁受力图(a )pal ql F A 212R ==22R max 81)2(212pal l q l F M A =-⋅= ][89632813222max max σσ≤=⋅==h pal hh pal W M242.010********.39][89362332=⨯⨯⨯⨯⨯⨯=≥σpal h m = 242 mm取h = 242 mm16132==h b mm12-11 简支梁受力如图所示。
采用普通热轧工字型钢,且已知][σ= 160MPa 。
试确定工字paq =B BR F lAR F(a)型钢型号,并按最大切应力准则对梁的强度作全面校核。
解:1.F R A = F R B = 180kN (↑)75.885.010215.01802=⨯⨯-⨯==D C M M kN ·m100210215.116021802max =⨯⨯-⨯-⨯==M M E kN ·m175105.0180Q =⨯-=C F kN][maxmax σσ≤=W M463max 1025.61016010100][-⨯=⨯⨯=≥σM W m 3查型钢表,选工字钢No.32a :W = 692.2 cm 2,I z = 11075.5 cm 446.27=z zS I cmE 截面:5.144max max==W MσMPa5.144313r =-=σσσMPa ][σ< 2. A +、B -截面:691026.27105.910180233Q max =⨯⨯⨯⨯==--zz dI S F τMPa13824max 2max 3r ===ττσMPa ][σ<3.C -、D +截面:2.1161010755.1101451075.88833=⨯⨯⨯⨯=--x σMPaMPa46.491010755.1105.9105.15215130101758393*Q =⨯⨯⨯⨯⨯⨯⨯⨯=⋅=---zzC xy dI S F τ6.1524223r =+=xy x τσσMPa ][σ<选No.32a 工字钢安全。
12-12 图示4.5m 长的四根小梁,一端支承在长10.5m 的大梁AB 上,另一端支承于混凝土墙上。
每根小梁上承受集度为q = 16 kN/m 的均布载荷。
已知材料的][σ= 165 MPa ,且大、小梁均采用普通热轧工字型钢。
试选择用于大梁和小梁的最小型号,并应用形状改变比能准则对大梁AB 的强度作全面校核。
解:1.小梁CE ,图(a )2max 81)2(ql l M M G ==,][1max σ≤W M6623max 110245101655.4101681][-⨯=⨯⨯⨯⨯=≥σM W m 3选工字钢No.20b ,其W = 250 cm 32. 大梁AB ,图(b )2525.35.4max =⨯===q M M M D C kN ·m F Q C = 4.5q = 72 kN先按C 截面上最大正应力粗选:l = 4500qCEG·(a)180175)k N (Q F AC1515BD175E ACE D B88.7588.75100Mm-kN(a)习题12-12图180习题12-13图][2maxσσ≤=W M363max 2105273.11016510252][-⨯=⨯⨯=≥σM W m 3(1) 初选No.45c 工字钢W = 1570 cm 3,I z = 35280 cm 4C 截面上翼缘与腹板交界点上应力: 86.1471035280102071025210)18225(8333=⨯⨯⨯⨯=⨯-=---z C I M σMPa88.71035280105.15102161815410728393*Q =⨯⨯⨯⨯⨯⨯⨯⨯=⋅=---zzC I S F δτMPa5.1483224r =+=τσσMPa ][σ<(2)若选用No.45b 工字钢,其W = 1500 cm 3, I z = 33760 cm 41681015001025263max max=⨯⨯==-W M σMPa%5%8.1%1001653][][max <=⨯=-σσσ,工程上是允许的。
此时C 截面翼缘和腹板交界点的应力: 5.1541033760207.010252207.083max =⨯⨯⨯=⨯=-z I M σMPa336.91033760105.13102161815210728333*Q =⨯⨯⨯⨯⨯⨯⨯⨯=⋅=---zzC I S F δτMPa1553224r =+=τσσMPa ][σ< 故可选No.45b 工字钢。
