第2章习题参考-答案~(精品文档)

合集下载

同济大学版高等数学课后习题答案第2章

习题2-11. 设物体绕定轴旋转, 在时间间隔[0, t ]内转过的角度为θ, 从而转角θ是t 的函数: θ=θ(t ). 如果旋转是匀速的, 那么称t θω=为该物体旋转的角速度, 如果旋转是非匀速的, 应怎样确定该物体在时刻t 0的角速度？解在时间间隔[t 0, t 0+∆t ]内的平均角速度ω为tt t t t ∆-∆+=∆∆=)()(00θθθω,故t 0时刻的角速度为)()()(lim lim lim 000000t tt t t t t t t θθθθωω'=∆-∆+=∆∆==→∆→∆→∆.2. 当物体的温度高于周围介质的温度时, 物体就不断冷却, 若物体的温度T与时间t 的函数关系为T =T (t ), 应怎样确定该物体在时刻t 的冷却速度？解物体在时间间隔[t 0, t 0+∆t ]内, 温度的改变量为 ∆T =T (t +∆t )-T (t ),平均冷却速度为tt T t t T t T ∆-∆+=∆∆)()(,故物体在时刻t 的冷却速度为)()()(lim lim 00t T tt T t t T t T t t '=∆-∆+=∆∆→∆→∆.3. 设某工厂生产x 单位产品所花费的成本是f (x )元, 此函数f (x )称为成本函数, 成本函数f (x )的导数f '(x )在经济学中称为边际成本. 试说明边际成本f '(x )的实际意义.解 f (x +∆x )-f (x )表示当产量由x 改变到x +∆x 时成本的改变量.xx f x x f ∆-∆+)()(表示当产量由x 改变到x +∆x 时单位产量的成本.xx f x x f x f x ∆-∆+='→∆)()(lim )(0表示当产量为x 时单位产量的成本.4. 设f (x )=10x 2, 试按定义, 求f '(-1).解 xx x f x f f x x ∆--∆+-=∆--∆+-=-'→∆→∆2200)1(10)1(10lim)1()1(lim )1( 20)2(lim 102lim 10020-=∆+-=∆∆+∆-=→∆→∆x xx x x x .5. 证明(cos x )'=-sin x .解 xxx x x x ∆-∆+='→∆cos )cos(lim )(cos 0xxx x x ∆∆∆+-=→∆2sin )2sin(2lim0 x x xx x x sin ]22sin )2sin([lim 0-=∆∆∆+-=→∆. 6. 下列各题中均假定f '(x 0)存在, 按照导数定义观察下列极限, 指出A 表示什么:(1)A xx f x x f x =∆-∆-→∆)()(lim000;解 xx f x x f A x ∆-∆-=→∆)()(lim 000)()()(lim 0000x f x x f x x f x '-=∆--∆--=→∆-.(2)A xx f x =→)(lim 0, 其中f (0)=0, 且f '(0)存在;解 )0()0()0(lim )(lim 00f x f x f x x f A x x '=-+==→→.(3)A hh x f h x f h =--+→)()(lim 000.解 hh x f h x f A h )()(lim 000--+=→hx f h x f x f h x f h )]()([)]()([lim 00000----+=→hx f h x f h x f h x f h h )()(lim)()(lim 000000----+=→→ =f '(x 0)-[-f '(x 0)]=2f '(x 0). 7. 求下列函数的导数: (1)y =x 4; (2)32x y =; (3)y =x 1. 6;(4)xy 1=;(5)21x y =;(6)53x x y =;(7)5322x x x y =; 解 (1)y '=(x 4)'=4x 4-1=4x 3 . (2)3113232323232)()(--=='='='x x x xy . (3)y '=(x 1. 6)'=1.6x 1. 6-1=1.6x 0. 6.(4)23121212121)()1(-----=-='='='x x x xy .(5)3222)()1(---='='='x x x y . (6)511151651653516516)()(x x x x xy =='='='-.(7)651616153226161)()(--=='='='x x x x x x y .8. 已知物体的运动规律为s =t 3(m). 求这物体在t =2秒(s )时的速度. 解v =(s )'=3t 2, v |t =2=12(米/秒).9. 如果f (x )为偶函数, 且f (0)存在, 证明f (0)=0. 证明当f (x )为偶函数时, f (-x )=f (x ), 所以)0(0)0()(lim 0)0()(lim 0)0()(lim)0(000f x f x f x f x f x f x f f x x x '-=-----=---=--='→-→→,从而有2f '(0)=0, 即f '(0)=0. 10. 求曲线y =sin x 在具有下列横坐标的各点处切线的斜率: π32=x , x =π.解因为y '=cos x , 所以斜率分别为 2132cos 1-==πk , 1cos 2-==πk .11. 求曲线y =cos x 上点)21 ,3(π处的切线方程和法线方程式.解y '=-sin x , 233sin 3-=-='=ππx y ,故在点)21 ,3(π处, 切线方程为)3(2321π--=-x y , 法线方程为)3(3221π--=-x y .12. 求曲线y =e x 在点(0,1)处的切线方程. 解y '=e x , y '|x =0=1, 故在(0, 1)处的切线方程为 y -1=1⋅(x -0), 即y =x +1.13. 在抛物线y =x 2上取横坐标为x 1=1及x 2=3的两点, 作过这两点的割线, 问该抛物线上哪一点的切线平行于这条割线？解 y '=2x , 割线斜率为421913)1()3(=-=--=y y k . 令2x =4, 得x =2.因此抛物线y =x 2上点(2, 4)处的切线平行于这条割线. 14. 讨论下列函数在x =0处的连续性与可导性: (1)y =|sin x |;(2)⎪⎩⎪⎨⎧=≠=0001sin 2x x xx y . 解 (1)因为y (0)=0, 0)sin (lim |sin |lim lim 0=-==---→→→x x y x x x ,0sin lim |sin |lim lim 00===+++→→→x x y x x x ,所以函数在x =0处连续. 又因为1sin lim 0|0sin ||sin |lim 0)0()(lim )0(000-=-=--=--='---→→→-xx x x x y x y y x x x ,1sin lim 0|0sin ||sin |lim 0)0()(lim )0(000==--=--='+++→→→+xx x x x y x y y x x x , 而y '-(0)≠y '+(0), 所以函数在x =0处不可导.解因为01sin lim )(lim 200==→→xx x y x x , 又y (0)=0, 所以函数在x =0处连续.又因为01sin lim 01sin lim 0)0()(lim0200==-=--→→→xx x x x x y x y x x x , 所以函数在点x =0处可导, 且y '(0)=0.15. 设函数⎩⎨⎧>+≤=1 1)(2x b ax x x x f 为了使函数f (x )在x =1处连续且可导, a , b 应取什么值？解因为1lim )(lim 211==--→→x x f x x , b a b ax x f x x +=+=++→→)(lim )(lim 11, f (1)=a +b ,所以要使函数在x =1处连续, 必须a +b =1 . 又因为当a +b =1时211lim )1(21=--='-→-x x f x , a x x a x b a x a x b ax f x x x =--=--++-=--+='+++→→→+1)1(lim 11)1(lim 11lim )1(111,所以要使函数在x =1处可导, 必须a =2, 此时b =-1.16. 已知⎩⎨⎧<-≥=0 0)(2x x x x x f 求f +'(0)及f -'(0), 又f '(0)是否存在？解因为f -'(0)=10lim )0()(lim 00-=--=---→→xx x f x f x x ,f +'(0)=00lim )0()(lim 200=-=-++→→xx x f x f x x ,而f -'(0)≠f +'(0), 所以f '(0)不存在. 17. 已知f (x )=⎩⎨⎧≥<0 0sin x x x x , 求f '(x ) .解当x <0时, f (x )=sin x , f '(x )=cos x ; 当x >0时, f (x )=x , f '(x )=1;因为 f -'(0)=10sin lim )0()(lim 00=-=---→→xx x f x f x x ,f +'(0)=10lim )0()(lim 00=-=-++→→x x x f x f x x , 所以f '(0)=1, 从而f '(x )=⎩⎨⎧≥<0 10cos x x x .18. 证明: 双曲线xy =a 2上任一点处的切线与两坐标轴构成的三角形的面积都等于2a 2 .解由xy =a 2得x a y 2=, 22xa y k -='=. 设(x 0, y 0)为曲线上任一点, 则过该点的切线方程为)(02020x x x a y y --=-.令y =0, 并注意x 0y 0=a 2, 解得0022002x x ax y x =+=, 为切线在x 轴上的距.令x =0, 并注意x 0y 0=a 2, 解得00022y y x a y =+=, 为切线在y 轴上的距. 此切线与二坐标轴构成的三角形的面积为 200002||2|2||2|21a y x y x S ===.习题 2-21. 推导余切函数及余割函数的导数公式: (cot x )'=-csc 2x ; (csc x )'=-csc x cot x .解 x x x x x x x x 2sin cos cos sin sin )sin cos ()(cot ⋅-⋅-='=' x xx x x 22222csc sin 1sin cos sin -=-=+-=. x x xx x x cot csc sin cos)sin 1()(csc 2⋅-=-='='. 2. 求下列函数的导数: (1)1227445+-+=xx x y ;(2) y =5x 3-2x +3e x ; (3) y =2tan x +sec x -1; (4) y =sin x ⋅cos x ; (5) y =x 2ln x ; (6) y =3e x cos x ; (7)x x y ln =;(8)3ln 2+=xe y x ; (9) y =x 2ln x cos x ;(10)tt s cos 1sin 1++=;解 (1))12274()12274(14545'+-+='+-+='---x x x xx x y 2562562282022820x x x x x x +--=+--=---. (2) y '=(5x 3-2x +3e x )'=15x 2-2x ln2+3e x .(3) y '=(2tan x +sec x -1)'=2sec 2x +sec x ⋅tan x =sec x (2sec x +tan x ). (4) y '=(sin x ⋅cos x )'=(sin x )'⋅cos x +sin x ⋅(cos x )' =cos x ⋅cos x +sin x ⋅(-sin x )=cos 2x . (5) y '=(x 2ln x )'=2x ⋅ln x +x 2⋅x1=x (2ln x +1) .(6) y '=(3e x cos x )'=3e x ⋅cos x +3e x ⋅(-sin x )=3e x (cos x -sin x ).(7)22ln 1ln 1)ln (x x x xx x x x y -=-⋅='='. (8)3422)2(2)3ln (x x e x x e x e x e y x x x x -=⋅-⋅='+='. (9) y '=(x 2ln x cos x )'=2x ⋅ln x cos x +x 2⋅x1⋅cos x +x 2 ln x ⋅(-sin x )2x ln x cos x +x cos x -x 2 ln x sin x . (10)22)cos 1(cos sin 1)cos 1()sin )(sin 1()cos 1(cos )cos 1sin 1(t tt t t t t t t t s +++=+-+-+='++='.3. 求下列函数在给定点处的导数: (1) y =sin x -cos x , 求6π='x y 和4π='x y .(2)θθθρcos 21sin +=,求4πθθρ=d d .(3)553)(2x x x f +-=, 求f '(0)和f '(2) . 解 (1)y '=cos x +sin x ,21321236sin 6cos 6+=+=+='=πππx y ,222224sin 4cos 4=+=+='=πππx y . (2)θθθθθθθθρcos sin 21sin 21cos sin +=-+=d d ,)21(4222422214cos 44sin 214πππππθρπθ+=⋅+⋅=+==d d . (3)x x x f 52)5(3)(2+-=', 253)0(='f , 1517)2(='f . 4. 以初速v 0竖直上抛的物体, 其上升高度s 与时间t 的关系是2021gt t v s -=.求:(1)该物体的速度v (t ); (2)该物体达到最高点的时刻. 解 (1)v (t )=s '(t )=v 0-gt . (2)令v (t )=0, 即v 0-gt =0, 得gv t 0=, 这就是物体达到最高点的时刻. 5. 求曲线y =2sin x +x 2上横坐标为x =0的点处的切线方程和法线方程. 解因为y '=2cos x +2x , y '|x =0=2, 又当x =0时, y =0, 所以所求的切线方程为 y =2x , 所求的法线方程为x y 21-=, 即x +2y =0.6. 求下列函数的导数: (1) y =(2x +5)4 (2) y =cos(4-3x ); (3)23x e y -=; (4) y =ln(1+x 2); (5) y =sin 2x ; (6)22x a y -=; (7) y =tan(x 2); (8) y =arctan(e x ); (9) y =(arcsin x )2; (10) y =lncos x .解 (1) y '=4(2x +5)4-1⋅(2x +5)'=4(2x +5)3⋅2=8(2x +5)3. (2) y '=-sin(4-3x )⋅(4-3x )'=-sin(4-3x )⋅(-3)=3sin(4-3x ). (3)22233236)6()3(x x x xe x e x e y ----=-⋅='-⋅='. (4)222212211)1(11xx x x x x y +=⋅+='+⋅+='.(5) y '=2sin x ⋅(sin x )'=2sin x ⋅cos x =sin 2x . (6))()(21])[(22121222122'-⋅-='-='-x a x a x a y222122)2()(21xa x x x a --=-⋅-=-.(7) y '=sec 2(x 2)⋅(x 2)'=2x sec 2(x 2). (8)xx x x e e e e y 221)()(11+='⋅+='.(9) y '21arcsin 2)(arcsin arcsin 2x x x x -='⋅=.(10)x x xx x y tan )sin (cos 1)(cos cos 1-=-='⋅='.7. 求下列函数的导数: (1) y =arcsin(1-2x ); (2)211x y -=; (3)x e y x 3cos 2-=;(4)xy 1arccos =;(5)xx y ln 1ln 1+-=;(6)x x y 2sin =;(7)x y arcsin =; (8))ln(22x a x y ++=; (9) y =ln(sec x +tan x ); (10) y =ln(csc x -cot x ). 解 (1)2221)21(12)21()21(11xx x x x y --=---='-⋅--='.(2))1()1(21])1[(21212212'-⋅--='-='---x x x y222321)1()2()1(21xx x x x --=-⋅--=-.(3))3)(3sin (3cos )2()3(cos 3cos )(2222'-+'-='+'='----x x e x x e x e x e y xxx x )3sin 63(cos 213sin 33cos 21222x x e x e x e xxx +-=--=---.(4)1||)1()1(11)1()1(1122222-=---='--='x x x x x x x y . (5)22)ln 1(2)ln 1(1)ln 1()ln 1(1x x x x x x x y +-=+--+-='. (6)222sin 2cos 212sin 22cos x x x x x x x x y -=⋅-⋅⋅='. (7)2222121)(11)()(11x x x x x x y -=⋅-='⋅-='. (8)])(211[1)(12222222222'+++⋅++='++⋅++='x a x a x a x x a x x a x y 2222221)]2(211[1xa x x a x a x +=++⋅++=. (9) x xx x x x x x x x y sec tan sec sec tan sec )tan (sec tan sec 12=++='+⋅+='. (10) x xx x x x x x x x y csc cot csc csc cot csc )cot (csc cot csc 12=-+-='-⋅-='.8. 求下列函数的导数: (1)2)2(arcsin x y =;(2)2tan ln x y =;(3)x y 2ln 1+=; (4)xe y arctan=;(5)y =sin n x cos nx ;(6)11arctan -+=x x y ;(7)x x y arccos arcsin =;(8) y =ln[ln(ln x )] ; (9)x x x x y -++--+1111;(10)xx y +-=11arcsin .解 (1)'⋅=')2(arcsin )2(arcsin 2x x y)2()2(11)2(arcsin 22'⋅-⋅=x x x 21)2(11)2(arcsin 22⋅-⋅=x x . 242arcsin 2x x-=(2))2(2sec 2tan 1)2(tan 2tan 12'⋅⋅='⋅='x x x x x yx x x csc 212sec 2tan 12=⋅⋅=.(3))ln 1(ln 121ln 1222'+⋅+=+='x x x y )(ln ln 2ln 1212'⋅⋅+=x x x x x x1ln 2ln 1212⋅⋅+=x x x 2ln 1ln +=.(4))(arctan arctan '⋅='x e y x )()(112arctan '⋅+⋅=x x e x)1(221)(11arctan 2arctan x x e x x exx+=⋅+⋅=.(5) y '=n sin n -1x ⋅(sin x )'⋅cos nx +sin n x ⋅(-sin nx )⋅(nx )' =n sin n -1x ⋅cos x ⋅cos nx +sin n x ⋅(-sin nx )⋅n=n sin n -1x ⋅(cos x ⋅cos nx -sin x ⋅sin nx )= n sin n -1x cos(n +1)x . (6)222211)1()1()1()11(11)11()11(11x x x x x x x x x x y +-=-+--⋅-++='-+⋅-++='. (7)222)(arccos arcsin 11arccos 11x x x x x y -+-=' 22)(arccos arcsin arccos 11x x x x +⋅-=22)(arccos 12x x -=π.(8))(ln ln 1)ln(ln 1])[ln(ln )ln(ln 1'⋅⋅='⋅='x xx x x y)ln(ln ln 11ln 1)ln(ln 1x x x x x x ⋅=⋅⋅=.(9)2)11()121121)(11()11)(121121(x x x x x x x x xx y -++--+--+--++-++=' 22111xx -+-=. (10)2)1()1()1(1111)11(1111x x x xx x x x x y +--+-⋅+--='+-⋅+--=' )1(2)1(1x x x -+-=. 9. 设函数f (x )和g (x )可导, 且f 2(x )+g 2(x )≠0, 试求函数)()(22x g x f y +=的导数.解 ])()([)()(212222'+⋅+='x g x f x g x f y )]()(2)()(2[)()(2122x g x g x f x f x g x f '+'⋅+=)()()()()()(22x g x f x g x g x f x f +'+'=.10. 设f (x )可导, 求下列函数y 的导数dxdy : (1) y =f (x 2);(2) y =f (sin 2x )+f (cos 2x ).解 (1) y '=f '(x 2)⋅(x 2)'= f '(x 2)⋅2x =2x ⋅f '(x 2). (2) y '=f '(sin 2x )⋅(sin 2x )'+f '(cos 2x )⋅(cos 2x )'= f '(sin 2x )⋅2sin x ⋅cos x +f '(cos 2x )⋅2cos x ⋅(-sin x ) =sin 2x [f '(sin 2x )- f '(cos 2x )]. 11. 求下列函数的导数: (1) y =ch(sh x ); (2) y =sh x ⋅e ch x ; (3) y =th(ln x ); (4) y =sh 3x +ch 2x ; (5) y =th(1-x 2); (6) y =arch(x 2+1); (7) y =arch(e 2x ); (8) y =arctan(th x ); (9)xx y 2ch 21ch ln +=;(10))11(ch 2+-=x x y解 (1) y '=sh(sh x )⋅(sh x )'=sh(sh x )⋅ch x . (2) y '=ch x ⋅e ch x +sh x ⋅e ch x ⋅sh x =e ch x (ch x +sh 2x ) .(3))(ln ch 1)(ln )(ln ch 122x x x x y ⋅='⋅='.(4) y '=3sh 2x ⋅ch x +2ch x ⋅sh x =sh x ⋅ch x ⋅(3sh x +2) . (5))1(ch 2)1()1(ch 122222x x x x y --=-⋅-='.(6)222)1()1(112422++='+⋅++='x x x x x y .(7)12)(1)(142222-='⋅-='x xx x e e e e y . (8)xxx x x x x y 222222ch 1ch sh 11ch 1th 11)th ()th (11⋅+=⋅+='⋅+=' xx x 222sh 211sh ch 1+=+=.(9))ch (ch 21)ch (ch 124'⋅-'⋅='x xx x yx x xx x sh ch 2ch 21ch sh 4⋅⋅-=x x x x x x x x 323ch sh ch sh ch sh ch sh -⋅=-= x xxx x x 33332th ch sh ch )1ch (sh ==-⋅=. (10)'+-⋅+-⋅+-='+-⋅+-=')11()11(sh )11(ch 2])11(ch [)11(ch 2x x x x x x x x x x y)112(sh )1(2)1()1()1()112(sh 22+-⋅+=+--+⋅+-⋅=x x x x x x x x . 12. 求下列函数的导数: (1) y =e -x (x 2-2x +3); (2) y =sin 2x ⋅sin(x 2); (3)2)2(arctan x y =;(4)n x x y ln =;(5)t t t t ee e e y --+-=; (6)xy 1cos ln =;(7)x ey 1sin 2-=;(8)x x y +=;(9) 242arcsin x x x y -+=;(10)212arcsin tt y +=.解 (1) y '=-e -x (x 2-2x +3)+e -x (2x -2) =e -x (-x 2+4x -5).(2) y '=2sin x ⋅cos x ⋅sin(x 2)+sin 2x ⋅cos(x 2)⋅2x =sin2x ⋅sin(x 2)+2x ⋅sin 2x ⋅cos(x 2). (3)2arctan 44214112arctan 222x x x x y +=⋅+⋅='.(4)121ln 1ln 1+--=⋅-⋅='n n n n x x n x nx x x xy . (5)2222)1(4)())(())((+=+---++='-----t t t t t t t t t t t t e e e e e e e e e e e e y .(6)x x x x x x x y 1tan 1)1()1sin (1sec )1(cos 1sec 22=-⋅-⋅='⋅='. (7))1(1cos )1sin 2()1sin (21sin 21sin 22x x x e x ey x x -⋅⋅-⋅='-⋅='--x e x x1sin 222sin 1-⋅⋅=. (8))211(21)(21x xx x x x x y +⋅+='+⋅+='xx x x +⋅+=412.(9)2arcsin )2(421214112arcsin 22x x x x x x y =-⋅-+⋅-⋅+='.(10)22222222)1()2(2)1(2)12(11)12()12(11t t t t tt t t t t y +⋅-+⋅⋅+-='+⋅+-=' )1(|1|)1(2)1()1(2)1(1222222222t t t t t t t +--=+-⋅-+=.习题 2-31. 求函数的二阶导数: (1) y =2x 2+ln x ; (2) y =e 2x -1; (3) y =x cos x ; (4) y =e -t sin t ; (5)22x a y -=; (6) y =ln(1-x 2) (7) y =tan x ;(8)113+=x y ;(9) y =(1+x 2)arctan x ;(10)xe y x =; (11)2x xe y =;(12))1ln(2x x y ++=. 解 (1)x x y 14+=', 214xy -=''.(2) y '=e 2x -1 ⋅2=2e 2x -1, y ''=2e 2x -1 ⋅2=4e 2x -1. (3) y =x cos x ; y '=cos x -x sin x ,y ''=-sin x -sin x -x cos x =-2sin x -x cos x . (4) y '=-e -t sin t +e -t cos t =e -t (cos t -sin t )y ''=-e -t (cos t -sin t )+e -t (-sin t -cos t )=-2e -t cos t .(5)222222)(21xa x x a x a y --='-⋅-=', 22222222222)(xa x a a xa x a xx x a y ---=---⋅---=''.(6) 22212)1(11x x x x y --='-⋅-=',222222)1()1(2)1()2(2)1(2x x x x x x y -+-=--⋅---=''.(7) y '=sec 2 x ,y ''=2sec x ⋅(sec x )'=2sec x ⋅sec x ⋅tan x =2sec 2x ⋅tan x .(8)232233)1(3)1()1(+-=+'+-='x x x x y ,333433223)1()12(6)1(3)1(23)1(6+-=+⋅+⋅-+⋅-=''x x x x x x x x x y . (9)1arctan 211)1(arctan 222+=+⋅++='x x xx x x y ,212arctan 2xx x y ++=''.(10)22)1(1x x e x e x e y x x x -=⋅-⋅=', 3242)22(2)1(])1([x x x e x x x e x e x e y x x x x +-=⋅--⋅+-=''. (11))21()2(2222x e x e x e y x x x +=⋅⋅+=',)23(24)21(222222x xe x e x x e y x x x +=⋅++⋅⋅=''. (12)2222211)1221(11)1(11x x x x x x x x x y +=++⋅++='++⋅++=',xx x x x x x x y ++-=+⋅+-='⋅+⋅+-=''1)1()12211)1(1122222.2. 设f (x )=(x +10)6, f '''(2)=?解f '(x )=6(x +10)5, f ''(x )=30(x +10)4, f '''(x )=120(x +10)3, f '''(2)=120(2+10)3=207360.3. 若f ''(x )存在, 求下列函数y 的二阶导数22dxyd :(1) y =f (x 2);(2) y =ln[f (x )] .解 (1)y '= f '(x 2)⋅(x 2)'=2xf '(x 2),y ''=2f '(x 2)+2x ⋅2xf ''(x 2)=2f '(x 2)+4x 2f ''(x 2). (2))()(1x f x f y '=',2)]([)()()()(x f x f x f x f x f y ''-''=''22)]([)]([)()(x f x f x f x f '-''=.4. 试从y dy dx '=1导出:(1)322)(y y dy x d '''-=; (2)5233)()(3y y y y dy x d '''''-''=. 解 (1)()()()3222)(1)(11y y y y y dy dx y dx d y dy d dy dx dy d dy xd '''-='⋅'''-=⋅'='==. (2)(())(())dy dx y y dx d y y dy d dy xd ⋅'''-='''-=3333 52623)()(31)()(3)(y y y y y y y y y y y '''''-''='⋅''''⋅''-''''-=.5. 已知物体的运动规律为s =A sin ωt (A 、ω是常数), 求物体运动的加速度, 并验证:0222=+s dts d ω.解 t A dt ds ωωcos =,t A dts d ωωsin 222-=. 22dt s d 就是物体运动的加速度. 0sin sin 22222=+-=+t A t A s dts d ωωωωω. 6. 验证函数y =C 1e λx +C 2e -λx (λ,C 1, C 2是常数)满足关系式: y ''-λ2y =0 . 解 y '=C 1λe λx -C 2λe -λx , y ''=C 1λ2e λx +C 2λ2e -λx .y ''-λ2y =(C 1λ2e λx +C 2λ2e -λx )-λ2(C 1e λx +C 2e -λx ) =(C 1λ2e λx +C 2λ2e -λx )-(C 1λ2e λx +C 2λ2e -λx )=0 . 7. 验证函数y =e x sin x 满足关系式: y ''-2y '+2y =0 .解 y '=e x sin x +e x cos x =e x (sin x +cos x ),y ''=e x (sin x +cos x )+e x (cos x -sin x )=2e x cos x . y ''-2y '+2y =2e x cos x -2e x (sin x +cos x )+2e x sin x =2e x cos x -2e x sin x -2e x cos x +2e x sin x =0 . 8. 求下列函数的n 阶导数的一般表达式:(1) y =x n +a 1x n -1+a 2x n -2+ ⋅ ⋅ ⋅ +a n -1x +a n (a 1, a 2, ⋅ ⋅ ⋅, a n 都是常数); (2) y =sin 2x ; (3) y =x ln x ; (4) y =xe x .解 (1) y '=nx n -1+(n -1)a 1x n -2+(n -2)a 2x n -3+ ⋅ ⋅ ⋅ +a n -1,y ''=n (n -1)x n -2+(n -1)(n -2)a 1x n -3+(n -2)(n -3)a 2x n -4+ ⋅ ⋅ ⋅ +a n -2, ⋅ ⋅ ⋅,y (n )=n (n -1)(n -2)⋅ ⋅ ⋅2⋅1x 0=n ! . (2) y '=2sin x cos x =sin2x , )22sin(22cos 2π+==''x x y ,)222sin(2)22cos(222ππ⋅+=+='''x x y ,)232sin(2)222cos(233)4(ππ⋅+=⋅+=x x y ,⋅ ⋅ ⋅,]2)1(2sin[21)(π⋅-+=-n x y n n .(3) 1ln +='x y , 11-==''x x y ,y '''=(-1)x -2, y (4)=(-1)(-2)x -3, ⋅ ⋅ ⋅,y (n )=(-1)(-2)(-3)⋅ ⋅ ⋅(-n +2)x -n +1112)!2()1()!2()1(-----=--=n n n n x n x n . (4) y '=e x +xe x ,y ''=e x +e x +xe x =2e x +xe x , y '''=2e x +e x +xe x =3e x +xe x , ⋅ ⋅ ⋅,y (n )=ne x +xe x =e x (n +x ) . 9. 求下列函数所指定的阶的导数: (1) y =e x cos x , 求y (4) ; (2) y =x sh x , 求y (100) ; (3) y =x 2sin 2x , 求y (50) . 解 (1)令u =e x , v =cos x , 有 u '=u ''=u '''=u (4)=e x ;v '=-sin x , v ''=-cos x , v '''=sin x , v (4)=cos x , 所以 y (4)=u (4)⋅v +4u '''⋅v '+6u ''⋅v ''+4u '⋅v '''+u ⋅v (4)=e x [cos x +4(-sin x )+6(-cos x )+4sin x +cos x ]=-4e x cos x . (2)令u =x , v =sh x , 则有 u '=1, u ''=0;v '=ch x , v ''=sh x , ⋅ ⋅ ⋅ , v (99)=ch x , v (100)=sh x ,所以)100()99(99100)98(98100)98(2100)99(1100)100()100( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅==100ch x +x sh x . (3)令u =x 2 , v =sin 2x , 则有 u '=2x , u ''=2, u '''=0;x x v 2sin 2)2482sin(24848)48(=⋅+=π,v (49)=249cos 2x , v (50)=-250sin 2x ,所以 )50()49(4950)48(4850)48(250)49(1150)50()50( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅= )50()49(4950)48(4850v u v u C v u C ⋅+⋅'+⋅''= )2sin 2(2cos 22502sin 22249505024928x x x x x -⋅+⋅⋅+⋅⋅⋅= )2sin 212252cos 502sin (2250x x x x x ++-=.习题 2-31. 求函数的二阶导数: (1) y =2x 2+ln x ; (2) y =e 2x -1; (3) y =x cos x ; (4) y =e -t sin t ; (5)22x a y -=; (6) y =ln(1-x 2) (7) y =tan x ; (8)113+=x y ;(9) y =(1+x 2)arctan x ;(10)xe y x =;(11)2x xe y =;(12))1ln(2x x y ++=. 解 (1)x x y 14+=', 214xy -=''.(2) y '=e 2x -1 ⋅2=2e 2x -1, y ''=2e 2x -1 ⋅2=4e 2x -1. (3) y =x cos x ; y '=cos x -x sin x ,y ''=-sin x -sin x -x cos x =-2sin x -x cos x . (4) y '=-e -t sin t +e -t cos t =e -t (cos t -sin t )y ''=-e -t (cos t -sin t )+e -t (-sin t -cos t )=-2e -t cos t . (5)222222)(21xa x x a x a y --='-⋅-=', 22222222222)(xa x a a xa x a xx x a y ---=---⋅---=''.(6) 22212)1(11xx x x y --='-⋅-=',222222)1()1(2)1()2(2)1(2x x x x x x y -+-=--⋅---=''. (7) y '=sec 2 x ,y ''=2sec x ⋅(sec x )'=2sec x ⋅sec x ⋅tan x =2sec 2x ⋅tan x .(8)232233)1(3)1()1(+-=+'+-='x x x x y , 333433223)1()12(6)1(3)1(23)1(6+-=+⋅+⋅-+⋅-=''x x x x x x x x x y .(9)1arctan 211)1(arctan 222+=+⋅++='x x xx x x y ,212arctan 2xx x y ++=''.(10)22)1(1x x e x e x e y x x x -=⋅-⋅=',3242)22(2)1(])1([x x x e x x x e x e x e y x x x x +-=⋅--⋅+-=''. (11))21()2(2222x e x e x e y x x x +=⋅⋅+=',)23(24)21(222222x xe x e x x e y x x x +=⋅++⋅⋅=''. (12)2222211)1221(11)1(11x x x x x x x x x y +=++⋅++='++⋅++=',xx x x x x x x y ++-=+⋅+-='⋅+⋅+-=''1)1()12211)1(1122222. 2. 设f (x )=(x +10)6, f '''(2)=?解f '(x )=6(x +10)5, f ''(x )=30(x +10)4, f '''(x )=120(x +10)3, f '''(2)=120(2+10)3=207360.3. 若f ''(x )存在, 求下列函数y 的二阶导数22dxyd :(1) y =f (x 2);(2) y =ln[f (x )] .解 (1)y '= f '(x 2)⋅(x 2)'=2xf '(x 2),y ''=2f '(x 2)+2x ⋅2xf ''(x 2)=2f '(x 2)+4x 2f ''(x 2). (2))()(1x f x f y '=',2)]([)()()()(x f x f x f x f x f y ''-''=''22)]([)]([)()(x f x f x f x f '-''=.4. 试从y dy dx '=1导出:(1)322)(y y dy x d '''-=; (2)5233)()(3y y y y dy x d '''''-''=. 解 (1)()()()3222)(1)(11y y y y y dy dx y dx d y dy d dy dx dy d dy xd '''-='⋅'''-=⋅'='==.(2)(())(())dy dx y y dx d y y dy d dy xd ⋅'''-='''-=3333 52623)()(31)()(3)(y y y y y y y y y y y '''''-''='⋅''''⋅''-''''-=.5. 已知物体的运动规律为s =A sin ωt (A 、ω是常数), 求物体运动的加速度, 并验证:0222=+s dts d ω. 解 t A dt ds ωωcos =,t A dts d ωωsin 222-=. 22dt s d 就是物体运动的加速度. 0sin sin 22222=+-=+t A t A s dts d ωωωωω. 6. 验证函数y =C 1e λx +C 2e -λx (λ,C 1, C 2是常数)满足关系式:y ''-λ2y =0 . 解 y '=C 1λe λx -C 2λe -λx , y ''=C 1λ2e λx +C 2λ2e -λx .y ''-λ2y =(C 1λ2e λx +C 2λ2e -λx )-λ2(C 1e λx +C 2e -λx ) =(C 1λ2e λx +C 2λ2e -λx )-(C 1λ2e λx +C 2λ2e -λx )=0 . 7. 验证函数y =e x sin x 满足关系式: y ''-2y '+2y =0 .解 y '=e x sin x +e x cos x =e x (sin x +cos x ),y ''=e x (sin x +cos x )+e x (cos x -sin x )=2e x cos x . y ''-2y '+2y =2e x cos x -2e x (sin x +cos x )+2e x sin x =2e x cos x -2e x sin x -2e x cos x +2e x sin x =0 . 8. 求下列函数的n 阶导数的一般表达式:(1) y =x n +a 1x n -1+a 2x n -2+ ⋅ ⋅ ⋅ +a n -1x +a n (a 1, a 2, ⋅ ⋅ ⋅, a n 都是常数); (2) y =sin 2x ;(3) y =x ln x ; (4) y =xe x .解 (1) y '=nx n -1+(n -1)a 1x n -2+(n -2)a 2x n -3+ ⋅ ⋅ ⋅ +a n -1,y ''=n (n -1)x n -2+(n -1)(n -2)a 1x n -3+(n -2)(n -3)a 2x n -4+ ⋅ ⋅ ⋅ +a n -2, ⋅ ⋅ ⋅,y (n )=n (n -1)(n -2)⋅ ⋅ ⋅2⋅1x 0=n ! . (2) y '=2sin x cos x =sin2x , )22sin(22cos 2π+==''x x y ,)222sin(2)22cos(222ππ⋅+=+='''x x y ,)232sin(2)222cos(233)4(ππ⋅+=⋅+=x x y ,⋅ ⋅ ⋅,]2)1(2sin[21)(π⋅-+=-n x y n n .(3) 1ln +='x y , 11-==''x x y ,y '''=(-1)x -2, y (4)=(-1)(-2)x -3, ⋅ ⋅ ⋅,y (n )=(-1)(-2)(-3)⋅ ⋅ ⋅(-n +2)x -n +1112)!2()1()!2()1(-----=--=n n n n x n x n . (4) y '=e x +xe x ,y ''=e x +e x +xe x =2e x +xe x , y '''=2e x +e x +xe x =3e x +xe x , ⋅ ⋅ ⋅,y (n )=ne x +xe x =e x (n +x ) . 9. 求下列函数所指定的阶的导数: (1) y =e x cos x , 求y (4) ; (2) y =x sh x , 求y (100) ; (3) y =x 2sin 2x , 求y (50) .解 (1)令u =e x , v =cos x , 有 u '=u ''=u '''=u (4)=e x ;v '=-sin x , v ''=-cos x , v '''=sin x , v (4)=cos x , 所以 y (4)=u (4)⋅v +4u '''⋅v '+6u ''⋅v ''+4u '⋅v '''+u ⋅v (4)=e x [cos x +4(-sin x )+6(-cos x )+4sin x +cos x ]=-4e x cos x . (2)令u =x , v =sh x , 则有 u '=1, u ''=0;v '=ch x , v ''=sh x , ⋅ ⋅ ⋅ , v (99)=ch x , v (100)=sh x , 所以)100()99(99100)98(98100)98(2100)99(1100)100()100( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅==100ch x +x sh x . (3)令u =x 2 , v =sin 2x , 则有 u '=2x , u ''=2, u '''=0;x x v 2sin 2)2482sin(24848)48(=⋅+=π,v (49)=249cos 2x , v (50)=-250sin 2x ,所以 )50()49(4950)48(4850)48(250)49(1150)50()50( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅= )50()49(4950)48(4850v u v u C v u C ⋅+⋅'+⋅''= )2sin 2(2cos 22502sin 22249505024928x x x x x -⋅+⋅⋅+⋅⋅⋅= )2sin 212252cos 502sin (2250x x x x x ++-=.习题2-41. 求由下列方程所确定的隐函数y 的导数dxdy : (1) y 2-2x y +9=0; (2) x 3+y 3-3axy =0; (3) xy =e x +y ; (4) y =1-xe y .解 (1)方程两边求导数得2y y '-2y -2x y ' =0 , 于是 (y -x )y '=y , xy y y -='. (2)方程两边求导数得3x 2+3y 2y '-2ay -3axy '=0, 于是 (y 2-ax )y '=ay -x 2 ,axy x ay y --='22.(3)方程两边求导数得 y +xy '=e x +y (1+y '), 于是 (x -e x +y )y '=e x +y -y ,yx y x e x ye y ++--='.(4)方程两边求导数得 y '=-e y -xe y y ', 于是 (1+xe y )y '=-e y ,yy xe e y +-='1. 2.求曲线323232a y x =+在点)42 ,42(a a 处的切线方程和法线方程.解方程两边求导数得 032323131='+--y y x ,于是 3131---='y x y ,在点)42 ,42(a a 处y '=-1.所求切线方程为)42(42a x a y --=-, 即a y x 22=+.所求法线方程为)42(42a x a y -=-, 即x -y =0.3. 求由下列方程所确定的隐函数y 的二阶导数22dxyd :(1) x 2-y 2=1;(2) b 2x 2+a 2y 2=a 2b 2; (3) y =tan(x +y ); (4) y =1+xe y .解 (1)方程两边求导数得 2x -2yy '=0, y '=y x ,3322221)(y y x y y y xx y y y x y y x y -=-=-='-='=''. (2)方程两边求导数得2b 2x +2a 2yy '=0,yx a b y ⋅-='22, 22222222)(y yx a b x y a b y y x y a b y ⋅--⋅-='-⋅-=''32432222222ya b y a x b y a a b -=+⋅-=. (3)方程两边求导数得y '=sec 2(x +y )⋅(1+y '),1)(cos 1)(sec 1)(sec 222-+=+-+='y x y x y x y 222211)(sin )(cos )(sin y y x y x y x --=+-+++=, 52233)1(2)11(22yy y y y y y +-=--='=''. (4)方程两边求导数得y '=e y +xe y y ',ye y e xe e y y y y y -=--=-='2)1(11, 3222)2()3()2()3()2()()2(y y e y y y e y y e y y e y y y y y --=-'-=-'---'=''.4. 用对数求导法求下列函数的导数:(1) x xx y )1(+=;(2)55225+-=x x y ;(3)54)1()3(2+-+=x x x y ;(4)x e x x y -=1sin . 解 (1)两边取对数得ln y =x ln|x |-x ln|1+x |，两边求导得xx x x x x y y +⋅-+-⋅+='11)1ln(1ln 1,于是 ]111[ln )1(xx x x x y x ++++='.(2)两边取对数得)2ln(251|5|ln 51ln 2+--=x x y ,两边求导得22251515112+⋅--⋅='x x x y y , 于是 ]225151[25512552+⋅--=+-='x x x x x y .(3)两边取对数得)1ln(5)3ln(4)2ln(21ln +--++=x x x y ,两边求导得1534)2(211+---+='x x x y y ,于是 ]1534)2(21[)1()3(254+--+++-+='x x x x x x y。

第二章变动成本法练习题及答案

第二章变动成本法练习题及答案一、单选1、混合成本的分解方法中，主观性最强的方法是A、账户分析法B、高低点法C、散布图法D、回归直线法2、下列费用中属于酌量性固定成本的是A、房屋及设备租金B、技术开发费C、行政管理人员的薪金D、不动产税3、下列费用中属于约束性固定成本的是A、照明费B、广告费C、职工教育培训费D、业务招待费4、下列各种混合成本可以用模型y＝a＋bx表示的是A、半固定成本 B延伸变动成本 C半变动成本 D阶梯式变动成本5、采用散布图法分解混合成本时，通过目测在各成本点之间画出一条反映成本变动趋势的直线，这条直线与纵轴的交点就是固定成本，斜率则是变动成本。

理论上这条直线距各成本点之间的最小。

A距离之和 B离差之和 C离差平方和 D标准差6、是分解混合成本诸方法中最为简便的一种，同时也是相关决策分析中应用比较广泛的一种。

A高低点法 B账户分析法 C回归直线法 D工程分析法7、管理会计将成本区分为固定成本、变动成本和混合成本三大类，这种分类的标志是A成本的可辨认性 B成本的可盘存性 C成本的性态D成本的时态8、成本在决策中属于无关成本A边际 B沉没C专属 D机会9、造成“某期按变动成本法与按完全成本法确定的营业净利润不相等”的根本原因是A两种方法对固定性制造费用的处理方式不同B两种方法计入当期损益表的固定生产成本的水平不同C两种方法计算销售收入的方法不同D两种方法将营业费用计入当期损益表的方式不同10、造成某期按变动成本法与完全成本法确定的营业净利润不相等的根本原因是A、两法对固定性制造费用的处理方式不同。

B、两法计入当期损益表的固定生产成本的水平不同。

C、两法即使销售收入和生产成本之间的水平不同D、两法对期间成本和生产成本之间的区分不同11、在变动成本法下，构成产品成本的是A、单位变动成本B、生产成本C、变动成本总额D、变动成本与固定成本之和12、某企业只生产一种产品，本月份生产并销售产品100件，单位产品售价1000元；发生的变动成本30000元，变动管理费用和变动销售费用2080元，固定性制造费用10000元，固定成本40000元。

kxx第2章铸造成形习题及参考答案

kxx第2章铸造成形习题及参考答案习题第2章铸造成形填空题：1、铸造⽅法从总体上可分为普通铸造和特种铸造两⼤类，普通铸造是指砂型铸造⽅法，不同于砂型铸造的其他铸造⽅法统称为特种铸造，常⽤的特种铸造⽅法有：（）、（）、（）、（）、（）等。

2、凝固过程中所造成的体积缩减如得不到液态⾦属的补充，将产⽣（）或（）。

3、对砂型铸件进⾏结构设计时，必须考虑合⾦的（）和铸造（）对铸件结构提出的要求。

4、（）是铸造合⾦本⾝的物理性质，是铸件许多缺陷（）产⽣的基本原因。

5、浇注位置是指造型时（）在铸型中所处的位置，它影响铸件的质量。

6、铸造应⼒按产⽣的原因不同，主要可分为（）和（）两种。

7、铸件上各部分壁厚相差较⼤，冷却到室温，厚壁部分的残余应⼒为（）应⼒，⽽薄壁部分的残余应⼒为（）应⼒。

8、任何⼀种液态⾦属注⼊铸型以后，从浇注温度冷却⾄室温都要经过三个联系的收缩阶段，即（）、（）和（）。

9、在低压铸造、压⼒铸造和离⼼铸造时，因⼈为加⼤了充型压⼒，故（）较强。

提⾼浇铸温度是改善合⾦（）的重要措施。

10、铸件浇铸位置的选择必须正确，如重要加⼯⾯、⼤平⾯和薄壁部分在浇铸时应尽量（），⽽厚⼤部位应尽量（），以便安放冒⼝进⾏（）。

单项选择题：1、下列合⾦流动性最好的是：（）①普通灰铸铁；②球墨铸铁；③可锻铸铁；④蠕墨铸铁。

2、摩托车活塞应具有良好的耐热性、热膨胀系数⼩，导热性好、耐磨、耐蚀、重量轻等性能。

在下列材料中，⼀般选⽤：（）①铸造黄铜；②合⾦结构钢；③铸造铝硅合⾦；④铸造碳钢。

3、在下列铸造合⾦中，⾃由收缩率最⼩的是：（）①铸钢；②灰铸铁；③铸造铝合⾦；④⽩⼝铸铁4、图⽰圆锥齿轮铸件，齿⾯质量要求较⾼。

材料HT350，⼩批⽣产。

最佳浇5①采⽤在热节处加明、暗冒⼝或冷铁以实现顺序凝固②尽量使铸件壁厚均匀以实现同时凝固③提⾼浇注温度④采⽤颗粒⼤⽽均匀的原砂以改善填充条件多项选择题：1、液态合⾦浇注温度冷却到室温所经历的收缩阶段有：（）①⾼温收缩；②液态收缩；③凝固收缩④低温收缩；⑤固态收缩2、挖沙或假箱造型时候，分型⾯：（）①⼀定是曲⾯；②⼀定是圆锥⾯；③可以是平；④⼀定是平⾯；⑤可以是曲⾯3、影响液态合⾦充型能⼒的主要因素是：（）①合⾦的结晶特性；②浇注温度；③合⾦的收缩率；④铸造⼯艺凝固原则；⑤铸件壁厚和铸型条件4、影响液态合⾦充型能⼒的主要因素是：（）①合⾦的结晶特性；②浇注温度；③合⾦的收缩率；④铸造⼯艺凝固原则；⑤铸件壁厚和铸型条件5、产⽣缩孔、缩松的基本原因：（）①液态收缩；②固态收缩；③凝固收缩；④线收缩；⑤等温收缩结构改错题：1、如下图所⽰，浇铸位置是否合理？若不合理请改为合理。

数字设计-原理与实践（第四版）课后习题答案

数字设计-原理与实践（第四版）课后习题答案第1 章习题参考答案:1-6 一个电路含有一个2 输入与门（AND2），其每个输入/输出端上都连接了一个反相器；画出该电路的逻辑图，写出其真值表；能否将该电路简化？解：电路图和真值表如下：由真值表可以看出，该电路与一个2 输入或门（OR2）相同。

第2 章习题参考答案:2.2 将下面的八进制数转换成二进制数和十六进制数。

(a) 12348=1 010 011 1002=29C16(b) 1746378=1 111 100 110 011 1112=F99F16(c) 3655178=11 110 101 101 001 1112=1EB4F16(d) 25353218=10 101 011 101 011 010 0012=ABAD116(e) 7436.118=111 100 011 110.001 0012=F1E.2416(f) 45316.74748=100 101 011 001 110.111 100 111 12=4ACE.F2C162.3 将下面的十六进制数转换为二进制数和八进制数。

(a) 102316=1 0000 0010 00112=100438(b) 7E6A16=111 1110 0110 10102=771528(c) ABCD16=1010 1011 1100 11012=1257158(d) C35016=1100 0011 0101 00002=1415208(e)9E36.7A16=1001 1110 00110110.0111 10102=117066.3648(f)DEAD.BEEF16=1101 1110 1010 1101.1011 1110 1110 11112 =157255.57567482.5 将下面的数转换成十进制数。

(a) 11010112=107 (b) 1740038=63491 (c) 101101112=183 (d)67.248=55.3125 (e)10100.11012=20.8125 (f)F3A516= 62373(g) 120103=138 (h) AB3D16=43837 (i) 71568=3694(j) 15C.3816=348.218752.6 完成下面的数制转换。

有机化学问题及习题参考答案

CH 3(CH 2)4C CH 2CH 2CH(CH 3)2C 2H 5C(CH 3)2C(CH 3)2CH 2CH 3CH 3CH 2CH CHCH 2CH 2CH 3CH 3CH(CH 3)CH(CH 3)2CH 3CH 2CHCH 2CHCH 2CH 3CH 3CCH 2CH 3CH 3CH 3CH 2CHCH 2CHCH 2CH 2CHCH 2CHCH 2CH 3CH 2CHCH 2CHCH 2CH 3CH 3CH 3CH 3CH 2CH 3第2章问题及习题参考答案问题2-1 写出下列化合物的CCS 和IUPAC 名称。

1.CCS 名称为：2-甲基-5,5-二(1,1-二甲基丙基)癸烷或2-甲基-5,5-二-1/,1/-二甲基丙基癸烷。

IUPAC 名称为：5,5-di(1,1-dimethylpropyl)decane or 5,5-di-1/,1/- dimethylpropyl-2-methyldecane 。

2.CCS 名称为：2,3,5-三甲基-4-丙基庚烷；IUPAC 名称为：4-propyl-2,3,5-trimethylheptane 。

3.CCS 名称为：3,9-二甲基-5,11-二乙基-7,7-二(2,4-二甲基己基)十三烷；IUPAC 名称为：7,7- di(2,4-dimethylhexyl)- 3,9-diethyl-5,11-dimethyltridecane 。

4.HC CC=CCH=CH 2CH 2CH 2CH 3CH 2CH 2CH 3CCS 名称为： 3,4-二丙基-1,3-己二烯-5-炔。

IUPAC 名称为：3,4-dipropyl-1,3-hexadiene-5-yne 。

问题2-2 写出下列化合物的CCS 和IUPAC 名称。

1.C CH 3CHCO 2H CH 3(Z )- 2-甲基-2-丁烯酸（(Z )- 2-methyl-2-butenic acid ）2.CC H 3CHH CH 3(E )- 2-丁烯（(E )- 2-butene ）。

1编译原理第三版陈火旺课后习题及答案

第2章习题参考答案P36-6 (1)L G ()1是0~9组成的数字串(2) 最左推导:N ND NDD NDDD DDDD DDD DD D N ND DD D N ND NDD DDD DD D ⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒0010120127334556568最右推导:N ND N ND N ND N D N ND N D N ND N ND N D ⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒77272712712701274434886868568P36-7 G(S)O N O D N S O AO A AD N→→→→→1357924680|||||||||||P36-8文法：E T E T E T TF T F T F F E i→+-→→|||*|/()| 最左推导:E E T T TF T i T i T F i F F i i F i i i E T T F F F i F i E i E T i T T i F T i i T i i F i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+********()*()*()*()*()*()*()最右推导:E E T E TF E T i E F i E i i T i i F i i i i i E T F T F F F E F E T F E F F E i F T i F F i F i i i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+⇒+**********()*()*()*()*()*()*()*()语法树：/********************************EE FTE +T F F T +iiiEEFTE-T F F T -iiiEEFT+T F FTiii*i+i+ii-i-ii+i*i*****************/P36-9句子iiiei 有两个语法树：S iSeS iSei iiSei iiiei S iS iiSeS iiSei iiiei ⇒⇒⇒⇒⇒⇒⇒⇒P36-10/**************)(|)(|S T TTS S →→***************/P36-11/*************** L1:ε||cC C ab aAb A AC S →→→ L2:bcbBc B aA A AB S ||→→→εL3:εε||aBb B aAb A AB S →→→ L4:AB B A A B A S |01|10|→→→ε ***************/第2章习题参考答案P64–7(1)101101(|)*1 ε ε 1 0 11 确定化：0 1 {X} φ {1,2,3} φ φ φ {1,2,3} {2,3} {2,3,4} {2,3} {2,3} {2,3,4} {2,3,4} {2,3,5} {2,3,4}{2,3,5} {2,3} {2,3,4,Y} {2,3,4,Y}{2,3,5}{2,3,4,}1 00 0 1 1 0X 1 2 3 4 Y5 XY0 12 30 10 1 1 1 最小化：{,,,,,},{}{,,,,,}{,,}{,,,,,}{,,,}{,,,,},{},{}{,,,,}{,,}{,,,},{},{},{}{,,,}{,012345601234513501234512460123456012341350123456012310100==== 3012312401234560110112233234012345610101}{,,,}{,,}{,},{,}{},{},{}{,}{}{,}{,}{,}{}{,}{}{},{},{,},{},{},{}===== 010 0 1 00 1 0 1 1 1P64–8(1)01)0|1(*(2))5|0(|)5|0()9|8|7|6|5|4|3|2|1|0)(9|8|7|6|5|4|3|2|1(*(3)******)110|0(01|)110|0(10P64–12(a)aa,b a65 4 5 01 2 4 3 01确定化：a b {0} {0,1} {1} {0,1} {0,1} {1} {1} {0} φ φφφ给状态编号：a b 0 1 2 1 1 2 2 0 3 333aaa b b bba最小化：{,},{,}{,}{}{,}{}{,}{,}{,}{}{,},{},{}012301101223032330123a ba b ====a ab bab (b)b b aa ba0 1 2 3 01 2 0 2 3a bb aa a已经确定化了,进行最小化最小化：{{,}, {,,,}}012345011012423451305234523452410243535353524012435011012424{,}{}{,}{,}{,,,}{,,,}{,,,}{,,,}{,}{,}{,}{,}{,}{,}{,}{,}{{,},{,},{,}}{,}{}{,}{,}{,}a b a b a b a b a b a =============={,}{,}{,}{,}{,}{,}{,}10243535353524 b a bb b aa baP64–14(1) 01 0 (2):(|)*0100 1 ε ε14 5 0 1 2 01YX YX2 1确定化：0 1 {X,1,Y} {1,Y} {2} {1,Y} {1,Y} {2} {2} {1,Y} φ φφφ给状态编号：0 1 0 1 2 1 1 2 2 1 3 3330 1 01 1 10 最小化：{,},{,}{,}{}{,}{}{,}{,}{,}{}{,},{},{}0123011012231323301230101====1 1 1 0第4章课后习题答案P81–1(1) 按照T,S 的顺序消除左递归ε|,)(||^)(T S T T S T T a S S G '→''→→'递归子程序：0 2 13 01 3procedure S; beginif sym='a' or sym='^' then abvance else if sym='(' then begin advance;T;if sym=')' then advance; else error; end else error end;procedure T; begin S;'T end;procedure 'T ; beginif sym=',' then begin advance; S;'T end end; 其中:sym:是输入串指针IP 所指的符号 advance:是把IP 调至下一个输入符号 error:是出错诊察程序 (2)FIRST(S)={a,^,(} FIRST(T)={a,^,(} FIRST('T )={,,ε} FOLLOW(S)={),,,#} FOLLOW(T)={)} FOLLOW('T )={)} 预测分析表a^() , # S S a →S →^S T →()TT ST →' T ST →' T ST →''T'→T ε '→'T ST ,是LL(1)文法P81–2文法：|^||)(|*||b a E P F F F P F T T T F T E E E T E →'→''→→''→+→''→εεε(1)FIRST(E)={(,a,b,^} FIRST(E')={+,ε} FIRST(T)={(,a,b,^} FIRST(T')={(,a,b,^,ε} FIRST(F)={(,a,b,^} FIRST(F')={*,ε} FIRST(P)={(,a,b,^} FOLLOW(E)={#,)} FOLLOW(E')={#,)} FOLLOW(T)={+,),#} FOLLOW(T')={+,),#}FOLLOW(F)={(,a,b,^,+,),#} FOLLOW(F')={(,a,b,^,+,),#} FOLLOW(P)={*,(,a,b,^,+,),#} (2)考虑下列产生式:'→+'→'→'→E E T T F F P E a b ||*|()|^||εεεFIRST(+E)∩FIRST(ε)={+}∩{ε}=φ FIRST(+E)∩FOLLOW(E')={+}∩{#,)}=φ FIRST(T)∩FIRST(ε)={(,a,b,^}∩{ε}=φ FIRST(T)∩FOLLOW(T')={(,a,b,^}∩{+,),#}=φ FIRST(*F')∩FIRST(ε)={*}∩{ε}=φFIRST(*F')∩FOLLOW(F')={*}∩{(,a,b,^,+,),#}=φ FIRST((E))∩FIRST(a) ∩FIRST(b) ∩FIRST(^)=φ 所以,该文法式LL(1)文法. (3)+ * ( ) a b ^ # EE TE →'E TE →' E TE →' E TE →'E' '→+E E'→E ε'→E εTT F T →'T F T →' T F T →' T F T →'T''→T ε'→T T '→T ε '→T T '→T T '→T T '→T εFF P F →' F P F →' F P F →' F P F →'F' '→F ε '→'F F * '→F ε '→F ε '→F ε '→F ε '→F ε '→F εPP E →() P a → P b → P →^(4)procedure E; beginif sym='(' or sym='a' or sym='b' or sym='^' then begin T; E' end else error endprocedure E'; beginif sym='+'then begin advance; E endelse if sym<>')' and sym<>'#' then error endprocedure T; beginif sym='(' or sym='a' or sym='b' or sym='^' then begin F; T' end else error endprocedure T'; beginif sym='(' or sym='a' or sym='b' or sym='^' then Telse if sym='*' then error endprocedure F; beginif sym='(' or sym='a' or sym='b' or sym='^' then begin P; F' end else error endprocedure F'; beginif sym='*'then begin advance; F' end endprocedure P; beginif sym='a' or sym='b' or sym='^' then advanceelse if sym='(' thenbeginadvance; E;if sym=')' then advance else error endelse errorend;P81–3/***************(1) 是，满足三个条件。

工程力学(静力学答案)

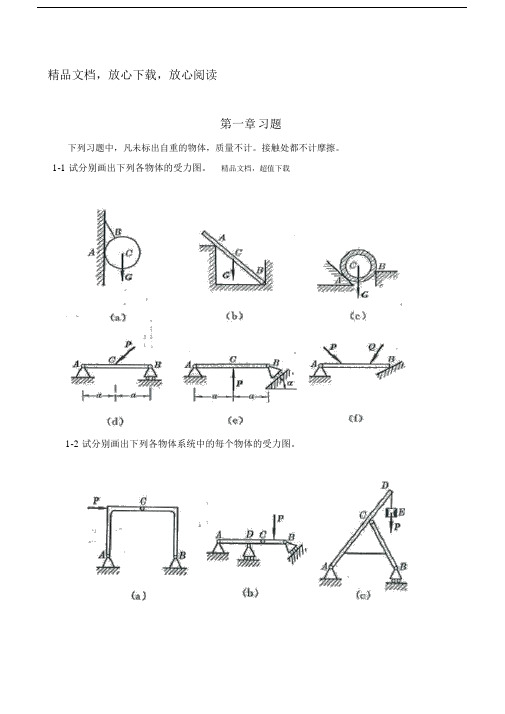
精品文档，放心下载，放心阅读第一章习题下列习题中，凡未标出自重的物体，质量不计。

接触处都不计摩擦。

1-1 试分别画出下列各物体的受力图。

精品文档，超值下载1-2 试分别画出下列各物体系统中的每个物体的受力图。

1-3 试分别画出整个系统以及杆BD ，AD ，AB（带滑轮 C，重物 E 和一段绳索）的受力图。

1-4 构架如图所示，试分别画出杆HED ，杆 BDC 及杆 AEC 的受力图。

1-5 构架如图所示，试分别画出杆BDH ，杆 AB ，销钉 A 及整个系统的受力图。

1-6 构架如图所示，试分别画出杆AEB ，销钉 A 及整个系统的受力图。

1-7 构架如图所示，试分别画出杆AEB ，销钉 C，销钉 A 及整个系统的受力图。

1-8 结构如图所示，力 P 作用在销钉 C 上，试分别画出 AC ，BCE 及 DEH 部分的受力图。

参考答案1-1 解：1-2 解：1-3 解：1-4 解：1-5 解：1-6 解：1-7 解：1-8 解：第二章习题参考答案2-1 解：由解析法， F RX X P 2 cos P 3 80NF RYY P 1 P 2 sin 140NF R F 2 F 2 161.2N故： RX RY(F R , P 1) arccos F RY 29 44F R2-2 解：即求此力系的合力，沿OB建立 x 坐标，由解析法，有F RX X P1 cos45 P2P3 cos453KNF RY Y P1 sin45 P3 sin 450故：F R F RX2F RY23KN 方向沿OB。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a）由平衡方程有：X 0 F AC sin 30F AB0Y 0 F AC cos30W0联立上二式，解得：F AB0.577W （拉力）FAC 1.155W（压力）（b）由平衡方程有：X 0 F AC F AB cos700Y 0 F AB sin 70W0联立上二式，解得：FAB 1.064W（拉力）F AC0.364W （压力）（c）由平衡方程有：X 0 F AC cos60F AB cos300Y 0 F AB sin 30F AC sin 60 W0联立上二式，解得：FAB 0.5W(拉力)FAC 0.866W（压力）（d）由平衡方程有：X 0 F AB sin 30F AC sin 300Y 0 F AB cos30F AC cos30 W0联立上二式，解得：FAB 0.577W(拉力)FAC 0.577W(拉力)2-4 解：（ a）受力分析如图所示：x 0 F RA4P cos 45 0 42由22F RA15.8 KNF RA2F RB P sin 45 042由Y 022F RB7.1KN(b)解：受力分析如图所示：由x 0 F RA 3F RB cos45 P cos45 0 10FRA 1F RB sin 45 P sin 45 0Y 010联立上二式，得：F RA22.4KNF RB10KN2-5 解：几何法：系统受力如图所示三力汇交于点 D，其封闭的力三角形如图示所以：FRA5KN（压力）F RB 5KN（与X轴正向夹150度）2-6 解：受力如图所示：已知， F R G1，F AC G2x 0F r 0由F AC coscos G1 G2由Y 0 F AC sinF N W 0F N W G2 sin W G22G122-7 解：受力分析如图所示，取左半部分为研究对象x 0由P F RA cos 45 F CB cos45 0 Y 0 F CB sin 45F RA sin 450联立后，解得：FRA0.707 PF RB0.707 P由二力平衡定理FRBFCBFCB0.707 P2-8 解：杆 AB，AC均为二力杆，取 A 点平衡x 0由F AC cos 60 F AB cos30 W 0Y 0 F AB sin 30F AC sin 60 W0联立上二式，解得：F AB7.32KN （受压）FAC 27.3KN（受压）2-9 解：各处全为柔索约束，故反力全为拉力，以D， B 点分别列平衡方程（1）取 D 点，列平衡方程x 0T DB sinW cos0由T DB Wctg0（2）取 B 点列平衡方程由Y 0 T sinT BD cos0T T BD ctg Wctg 230KN 2-10 解：取 B 为研究对象：FBC由Y 0 F BC sinP 0Psin取 C 为研究对象：x 0F DC sin F CE sin0由F BC cos由Y 0F BC sin F DC cos F CE cos0联立上二式，且有FBCFBC解得：P cos1 FCEsin2cos2取 E 为研究对象：由 Y 0 F NH F CE cos0F CE F CE 故有：F NH P cos 1 P2 sin 2 cos cos22sin 2-11 解：取 A 点平衡：x 0F AB sin 75 F AD sin 75 0Y 0 F AB cos75 F AD cos75 P 0PF AD F AB联立后可得： 2cos 75取 D 点平衡，取如图坐标系：x 0F AD cos5 F ND cos80 0cos5F ND F ADcos80由对称性及F AD F ADF N2F ND2 cos5FAD2 cos5P166.2KNcos80cos802cos 75 2-12 解：整体受力交于O点，列 O点平衡x 0由F RA cosF DC P cos30 0Y 0 F RA sin P sin 300联立上二式得：F RA 2.92 KNFDC 1.33KN（压力）列 C点平衡4x0FDC FAC53Y0FBCFAC5联立上二式得：FAC1.67KN（拉力）F BC 1.0KN （压力）2-13 解：（1）取 DEH部分，对 H点列平衡x 0 F RD 2F RE 0 5Y0FRD1Q 05联立方程后解得：FRD5QF RE2Q（2）取 ABCE部分，对 C 点列平衡x0F RE F RA cos 450Y 0 F RB F RA sin 45 P0且F RE F RE联立上面各式得：FRA2 2QF RB 2Q P（3）取 BCE 部分。

第2章地图数学基础习题及参考答案

第二章地图的数学基础习题及参考答案习题　一、判断题（对的打“√”，错的打“×”）　1.地球体的数学表面，也是对地球形体的二级逼近，用于测量计算的基准面。

　2.在地图学中，以大地经纬度定义地理坐标。

　3.1：100万的地形图，是按经差2o，纬差3o划分。

　4.1987年国家测绘局公布：启用《1985国家高程基准》取代《黄海平均海水面》，其比《黄海平均海水面》下降29毫米。

5.球面是个不可展的曲面，要把球面直接展成平面，必然要发生断裂或褶皱。

　6.长度比是一个常量，它既不随着点的位置不同而变化，也不随着方向的变化而变化。

　7.长度变形没有正负之分，长度变形恒为正。

　8.面积变形有正有负，面积变形为零，表示投影后面积无变形，面积变形为正，表示投影后面积增加；面积变形为负，表示投影后面积缩小。

　9.制1：100万地图，首先将地球缩小100万倍，而后将其投影到平面上，那么1：100万就是地图的主比例尺。

　10.在等积圆锥投影上中央经线上纬线间隔自投影中心向外逐渐增大。

　11.J—50—5—Ｅ表示1：５万地形图。

　12.地形图通常是指比例尺小于1：100万，按照统一的数学基础，图式图例，统一的测量和编图规范要求，经过实地测绘或根据遥感资料，配合其他有关资料编绘而成的一种普通地图。

　13.等积投影的面积变形接近零。

　14.等角投影能保持制图区域较大面积的形状与实地相似。

　15.水准面有无数个，而大地水准面只有一个。

　16.地球面上点的位置是用地理坐标和高程来确定的。

　17.正轴圆锥投影的各种变形都是经度的函数，与纬度无关。

　18.磁坐偏角指磁子午线与坐标纵线之间的夹角。

以坐标纵线为准，磁子午线东偏为负，西偏为正。

）19.一般情况下真方位角（A）、磁偏角（δ）、磁方位角（Am）三者之间的关系是A=Am+δ。

　20.不同地点的磁偏角是不相同的，同一地点的磁偏角是相同的。

　二、名词解释　1.大地体2.水准面3.大地水准面4.椭球体　5.天文经度6.天文纬度7.大地经度8.大地纬度9.1956年黄海高程系10.地图投影11.长度比12.长度变形13.面积比14.面积变形15.角度变形16.等变形线17.方位投影18.圆住投影19.圆锥投影20.高斯-克吕格投影21.直线定向　22.真子午线23.磁子午线24.磁偏角25.子午线收敛角26.磁坐偏角27.方位角28.象限角　29.三北方向　三、问答题　1.简述地球仪上经纬网的特点。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章行列式1. 求以下9级排列的逆序数,从而决定它们的奇偶性1) 1 3 4 7 8 2 6 9 5; 2) 2 1 7 9 8 6 3 5 4; 3)9 8 7 6 5 4 3 2 1;解:1) 所求排列的逆序数为:()1011033110134782695=+++++++=τ，所以此排列为偶排列。

2) 所求排列的逆序数为:()1810345401217986354=+++++++=τ，所以此排列为偶排列。

4) 所求排列的逆序数为:()()36219912345678987654321=-=+++++++=τ，所以此排列为偶排列。

2.选择i 与k 使1) 1274i 56k 9成偶排列； 2) 1i 25k 4897成奇排列。

解: 1) 当3,8==k i 时, 所求排列的逆序数为:()()12745691274856390041311010i k ττ==+++++++=，故当3,8==k i 时的排列为偶排列.。

2)当6,3==k i 时, 所求排列的逆序数为:()()1254897132564897010110115i k ττ==+++++++=，故当6,3==k i 时的排列为奇排列。

3.写出把排列12345变成排列25341的那些对换。

解: 12345()()()2534125431214354,35,22,1−−→−−−→−−−→−。

4.决定排列()211 -n n 的逆序数,并讨论它的奇偶性。

解: 因为1与其它数构成1-n 个逆序,2与其它数构成2-n 个逆序, ……n n 与1-构成1个逆序,所以排列()211 -n n 的逆序数为 ()()()()112112212n n n n n n τ--=-+-+++=⎡⎤⎣⎦ 4,4142,43n k k n k k =+=++故当时，排列为偶排列；当时排列为奇排列。

5.如果排列n n x x x x 121- 的逆序数为k ,排列121x x x x n n -的逆序数是多少? 解: 因为比i x 大的数有i x n -个,所以在121x x x x n n -与n n x x x x 121- 这两个排列中,由i x 与比它的各数构成的逆序数的和为i x n -.因而,由i x 构成的逆序总数恰为 ()()21121-=-+++n n n 。

而排列n n x x x x 121- 的逆序数为k ,故排列121x x x x n n -的逆序数为()k n n --21。

6.在6阶行列式中,651456423123a a a a a a , 256651144332a a a a a a 这两项应带有什么符号?解:()()()11)1(44312645234516=-=-++ττ，故项256651144332a a a a a a 前面的符号为正； ()()()()11146234165341562=-=-++ττ ，故项256651144332a a a a a a 带正号。

7．写出4阶行列式中所有带有负号并且因子23a 的项。

解：所求的各项应是44322311a a a a - ， 41342312a a a a - ， 42312314a a a a - 。

8．按定义计算行列式：1）000001002001000 n n - 2）.000100002000010n n -3）nn 000000100200100- 。

解：1）所给行列式的展开式中只含有一个非零项11,21n n n a a a -，它前面的符号应为()[]()2)1(21)1(11---=-n n n n τ ，所以原行列式=()()!121n n n --。

2）所给行列式的展开式中只含有一个非零项1,12312n n n a a a a - ，它前面的符号应为()()()112311--=-n n τ ，所以原行列式=()n n 11--！。

3）所给行列式的展开式中只含有一个非零项nn n n n a a a a 1,12,21,1--- ，它前面的符号应为()()()[]()()()221212111-----=-n n n n n τ ，所以原行列式=()()()n n n 2211---！。

9．由行列式定义证明：00000000002121215432154321=e e d d c c b b b b b a a a a a 解：行列式展开的一般项可表示为5432154321j j j j j a a a a a ，列标543j j j 只可以在1，2，3，4，5中取不同的值，故三个下标中至少有一个要取3，4，5列中之一数，从而任何一个展开式中至少要包含一个0元素，故所给行列式展开式中每一项的乘积必为0，因此原行列式值为0。

10．由行列式定义计算()xxx x xx f 111123111212-=中4x 与3x 的系数，并说明理由。

解：含有4x 的展开项只能是44332211a a a a ，所以4x 的系数为2；同理，含有3x 的展开项只能是44332112a a a a ，所以3x 的系数为-1。

11.由0111111111= ，证明：奇偶排列各半。

证：由题设，所给行列式的展开式中的每一项的绝对值等于1。

而行列式的值为0，这说明带正号与带负号的项的项数相等.根据行列式的定义，其展开式中的每一项的符号是由该乘积中各因子下标排列的逆序数所决定的，即当该乘积中各因子的第一个下标排成自然顺序，且第二个下标所成排列为偶排列时，该项前面所带的符号为正，否则为负号，所以，由带正号的项与带负号的项数相等即说明奇偶排列各半。

12．设 ()112111222211211121111-------=n n n n n n n a a a a a a a a a x x x x P，其中121,,,-n a a a 是互不相同的数。

1）由行列式定义，说明()x P 是一个1-n 次多项式； 2）由行列式性质，求()x P 的根。

解：1）因为所给行列式的展开式中只有第一行含有x ，所以若行列式的第一行展开时，含有1-n x 的对应项的系数恰为()11+-n 乘一个范德蒙行列式212112323322222212111111-------n n n n n n n a a a a a a a a a a a a于是，由121,,,-n a a a 为互不相同的的数即知含有1-n x 的对应项的系数不为0，因而()x P 为一个1-n 次的多项式。

2）若用121,,,-n a a a 分代替x 时，则由行列式的性质知所给行列式的值为0，即()0=i a P .故()x P 至少有1-n 个根121,,,-n a a a .又因为()x P 是一个1-n 次的多项式，所以121,,-n a a a 必是()x P 的全部根。

13．计算下面的行列式：1）6217213424435431014327427246- 2）yx yx x y x yy x y x+++ 3）31111311113111134）32142143143243215）y y x x-+-+1111111111111111 6）()()()()()()()()()()()()2222222222222222321321321321++++++++++++d d d d c c c c b b b b a a a a解：1）原式=621114431232711106217211000443543200032742710005==550132710114432941001621=-⨯2）原式=xyx y xyx y y x y xyx x y x yx y x y yx ---++=+++++001)(2222222 =()332x y -+3）原式=4886200002000020111163116131611361116=⨯==。

4）原式=1110222031143211032110214101431043210------==20113022160004--=- 。

5）原式=2200000111111000000111111x x xx x x y yy y yy--==--6）原式=221222122212221252321252321252321252321222222222++++=++++++++++++d d c cb b a a d d d dc c c cb b b b a a a a =0 。

14.证明 2221112222221111112c b a c b a cb a b a ac c b b a a c c b b a a c cb =+++++++++。

证明：由行列式的性质，有左边=222222221111111b a a c c b a b a a c c b a b a a c cb a ++++++++++++ =22222211111c b c b a c b c b a cb cb a --++--++--++=2=222111c b a c b a cb a右边。

15．算出下列行列式的全部代数余子式：1）300120012104121- 2）410123211- 解：1）611-=A ，012=A ，013=A ，014=A ，1221-=A ，622=A ，023=A ，024=A ，313233344142434415,6,3,0,7,0,1,2A A A A A A A A ==-=-=====- 。

2）3,12,7131211=-==A A A ，1,4,6232221-===A A A ， 5,5,5333231==-=A A A 。

16．计算下面的行列式：1）1234522131121111- 2）210112111311213111211----3）531212133215311210241210-- 4）2103122101102112321102110211--- 解：1）原式=210010051101111321041151101111---=------ =1100210051101111=-- 。

2）原式=1023*********341211023112122212113121--=---=433133311131641324121212321001---=-=-- 3）原式=1422115531041112121420211550310411121241210------=-------=-3860312*******866151396138661501396011212=--=--=3483163019-=4）原式=13621621011430410211022201281106242101101246211022201281---=---=172120303125022*******6216211143410221281--=--=-251270121333300108881221710017-=-= 17．计算下列n 阶行列式：1）xyx y x y x 00000000000000002）nn n n nnb a b a b a b a b a b a b a b a b a --------- 2122212121113）mx x x x m x x x x mx n nn ---212121 4）n2222322222222215）nn nn n ------110200000220000111321解：1）按第一列展开，原式=()n n n y x 11+-+。