中考数学总复习几何部分经典题型

合集下载

中考数学几何专题复习

专题几何专题题型一考察概念基础知识点型例1如图1,等腰△ABC 的周长为21,底边BC ＝ 5,AB 的垂直平分线是DE ,则△BEC 的周长为 ; 例2 如图2,菱形ABCD 中,60A ∠=°,E 、F 是AB 、AD 的中点,若2EF=,菱形边长是______．图1 图2 图3 例3 已知AB 是⊙O 的直径,PB 是⊙O 的切线,AB ＝3cm,PB ＝4cm,则BC ＝．题型二折叠题型：折叠题要从中找到对就相等的关系,然后利用勾股定理即可求解; 沿DE 折叠,若48CDE ∠=°,则APD ∠等例4 D E ，分别为AC ,BC 边的中点,于 ;例5如图4.矩形纸片ABCD 的边长AB =4,AD =2．将矩形纸片沿 EF 折叠, 使点A 与点C 重合,折叠后在其一面着色图,则着色部分的面积为A ． 8B ．112C ． 4D ．52EDBC A P图4图5 图6题型三涉及计算题型：常见的有应用勾股定理求线段长度,求弧长,扇形面积及圆锥体积,侧面积,三角函数计算等;例6如图3,P 为⊙O 外一点,PA 切⊙O 于A,AB 是⊙O 的直径,PB 交⊙O 于C,PA ＝2cm,PC ＝1cm,则图中阴影部分的面积S 是A.2235cm π- B 2435cm π- C 24235cm π- D 2232cm π- 图3 题型四证明题型：第二轮复习之几何一——三角形全等判定方法1：SAS例1如图,AC 是菱形ABCD 的对角线,点E 、F 分别在边AB 、AD 上,且 AE=AF; 求证：△ACE ≌△ACF例2 在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED ． 1求证：△BEC ≌△DEC ；2延长BE 交AD 于F ,当∠BED =120°时,求∠EFD 的度数．BD GFF ADFEBCDCBA EFG判定方法2：AASASA例3 如图,ABCD 是正方形,点G 是BC 上的任意一点,DE AG ⊥于 E ,BF DE ∥,交 AG 于F ,求证：AFBF EF =+．例4如图,在□ABCD 中,分别延长BA,DC 到点E,使得AE=AB, CH=CD 连接EH,分别交AD,BC 于点F,G;求证：△AEF ≌△CHG.判定方法3：HL 专用于直角三角形例5在△ABC 中,AB=CB,∠ABC=90o,F 为AB 延长线上一点,点E在BC上, 且AE=CF. 1求证:Rt △AB E ≌Rt △CBF; 2若∠CAE=30o,求∠ACF 度数.对应练习1.如图,在平行四边形ABCD 中,E 为BC 中点,AE 的延长线与DC 的延长线相交于点F.1证明：∠DFA = ∠FAB； 2证明: △ABE≌△FCE.2.如图,点E 是正方形ABCD 内一点,CDE ∆是等边三角形,连接EB 、EA ,延长BE 交边AD 于点F . 1求证:BCE ADE ∆≅∆；5分2求AFB ∠的度数.5分3．如图,已知∠ACB ＝90°,AC ＝BC ,BE ⊥CE 于E ,AD ⊥CE 于D ,CE 与AB 相交于F ．1求证：△CEB ≌△ADC ；2若AD ＝9cm,DE ＝6cm,求BE 及EF 的长．第二轮复习之几何二——三角形相似Ⅰ.三角形相似的判定例1如图,在平行四边形ABCD 中,过点A 作AE ⊥BC,垂足为E,连接DE,F 为线段DE 上一点,且∠AFE ＝∠B. 1求证：△ADF ∽△DEC2若AB ＝4,AD ＝33,AE ＝3,求AF 的长. 例2如图9,点P 是正方形ABCD 边AB 上一点不与点A ．B重合,连接PD 并将线段PD 绕点P 顺时针方向旋转90°得到线段PE, PE 交边BC 于点F ．连接BE 、DF;E B D A CF AF DEB CABCEFABCDF EF ED CBA 1求证：∠ADP=∠EPB ； 2求∠CBE 的度数； 3当APAB的值等于多少时．△PFD ∽△BFP 并说明理由．2.相似与圆结合,注意求证线段乘积,一般是转化证它所在的三角形相似;将乘积式转化为比例式→比例式边长定位到哪个三角形→找条件证明所在的三角形相似例3 如图,在△ABC 中,AB=AC,以AB 为直径的⊙O 交AC 与E,交BC 与D ．求证：1D 是BC 的中点；2△BEC∽△ADC； 3BC 2=2AB CE ．3.相似与三角函数结合,①若题目给出三角函数值一般会将给出的三角函数值用等角进行转化,然后求线段的长度②求某个角的三角函数值,一般会先将这个角用等角转化,间接求三角函数值例4如图,点E 是矩形ABCD 中CD 边上一点,⊿BCE 沿BE 折叠为⊿BFE,点F 落在AD 上.1求证：⊿ABE∽⊿DFE ;2若sin∠DFE=31,求tan∠EBC 的值. 练习一、选择题1、如图1,将非等腰ABC △的纸片沿DE 折叠后,使点A 落在BC 边上的点F 处．若点D 为AB 边的中点,则下列结论：①BDF △是等腰三角形；②DFE CFE ∠=∠；③DE 是ABC △的中位线,成立的有 A ．①②B ．①③C ．②③D ．①②③图1 图22.如图,等边△ABC 中,BD=CE,AD 与BE 相交于点P,则∠APE 的度数是A ．45° B．55° C．60° D．75° 3.如图3,在ABC △中,13AB AC ==,10BC =,点D 为BC 的中点,DE DE AB ⊥,垂足为点E ,则DE等于A ．1013 B ．1513 C ．6013 D ．7513MEDCBA图3 图4 图5GFE CBADAO BCXY4.如图4,⊿ABC 和⊿CDE 均为等腰直角三角形,点B,C,D 在一条直线上,点M 是AE 的中点,下列结论：①tan∠AEC=CDBC;②S ⊿ABC +S ⊿CDE ≧S ⊿ACE ;③BM⊥DM;④BM=DM.正确结论的个数是 A1个 B2个 C3个 D4个5.如图5,等边三角形ABC 中,D 、E 分别为AB 、BC 边上的两个动点,且总使AD=BE ,AE 与CD 交于点F ,AG ⊥CD 于点G,则FGAF= ． 6.如图6,已知点A 、B 、C 、D 均在已知圆上,AD ∥BC ,AC 平分∠BCD ,∠ADC = 120°,四边形ABCD 的周长为10cm ．图中阴影部分的面积为 A. 32B.3C. 23D. 43图6 图7对折,使点A 落在点1A 处;已知7.如图7,在直角坐标系中,将矩形OABC 沿OB3=OA ,1=AB ,则点1A 的坐标是 ; A 、23,23 B 、23,3 C 、23,23 D 、21,23 三、解答题1如图,矩形ABCD 中,点E 是BC 上一点,AE ＝AD,DF⊥AE 于F,连结DE.求证：DF ＝DC ．2.如图,四边形ABCD 是矩形,△PBC 和△QCD 都是等边三角形,且点P 在矩形上方,点Q 在矩形内．求证：1∠PBA =∠PCQ =30°；2PA =PQ ．3.如图9,已知点D 为等腰直角△ABC 内一点,∠CAD ＝∠CBD ＝15°,E 为AD 延长线上的一点,且CE ＝CA ．1求证：DE 平分∠BDC ；2若点M 在DE 上,且DC=DM ,求证： ME=BD ． 4.如图5AB 是⊙O 的直径,AC 是弦,CD 是⊙O 的切线,C 为切点,AD ⊥CD 于点D ．求证：1∠AOC =2∠ACD ； 2AC 2＝AB ·AD ．、5．把一张矩形ABCD 纸片按如图方式折叠,使点A 与点E 重合,点C 与点F 重合E 、F 两点均在BD 上,折痕分别为BH 、DG;1求证：△BHE ≌△DGF ；2若AB ＝6cm,BC ＝8cm,求线段FG 的长;6．如图8,在Rt △ABC 中,∠BAC=90°,AC=2AB,点D 是AC 的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A 、D 重合, 连结BE 、EC ．试猜想线段BE 和EC 的数量及位置关系,并证明你的猜想．ABCDEAC B DPQABCDEF 第二轮复习之几何三——四边形例1 如图,分别以Rt△ABC 的直角边AC 及斜边AB 向外作等边△ACD、等边△ABE;已知∠BAC=30o,EF⊥AB,垂足为F,连结DF;1试说明AC=EF ；2求证：四边形ADFE 是平行四边形;例2如图,AD ∥FE,点B 、C 在AD 上,∠1＝∠2,BF ＝BC⑴求证：四边形BCEF 是菱形⑵若AB ＝BC ＝CD,求证：△ACF ≌△BDE例3如图,四边形ABCD 是边长为2的正方形,点G 是BC 延长线上一点,连结AG,点E 、F 分别在AG 上,连接BE 、DF,∠1=∠2 ,∠3=∠4.1证明：△ABE≌△DAF； 2若∠AGB=30°,求EF 的长.例4如图,在等腰梯形ABCD 中,已知AD BC ∥,AB DC =,2AD =, 4BC =延长BC 到E ,使CE AD =．1证明：BAD DCE △≌△；2如果AC BD ⊥,求等腰梯形ABCD 的高DF 的值．对应练习1.如图,在菱形ABCD 中,∠A=60°,点P 、Q 分别在边AB 、BC 上,且AP=BQ ． 1求证：△BDQ ≌△ADP ；2已知AD=3,AP=2,求cos ∠BPQ 的值结果保留根号．2、如图,E F ，是四边形ABCD 的对角线AC 上两点,AF CE DF BE DFBE ==，，∥．求证：1AFD CEB △≌△．2四边形ABCD 是平行四边形．3．如罔7,在一方形ABCD 中．E 为对角线AC 上一点,连接EB 、ED,1求证：△BEC ≌△DEC ：2延长BE 交AD 于点F,若∠DEB=140°．求∠AFE 的度数．4.如图,在梯形ABCD 中,AD ∥BC ,延长CB 到点E ,使BE =AD ,连接DE 交AB 于点M .1求证：△AMD ≌△BM E ；2若N 是CD 的中点,且M N=5,BE =2,求BC 的长.第二轮复习之几何四——圆Ⅰ、证线段相等例1：如图,AB 是⊙O 的直径,C 是的中点,CE ⊥AB 于 E ,BD 交CE 于点F ．1求证：CF=BF ；2若CD =6, AC =8,则⊙O 的半径为 ___ ,CE 的长是 ___ ．ABDEFCDAB EC F ACBDEFO2、证角度相等例2如图,AB 是⊙O 的直径,C 为圆周上一点,30ABC ∠=︒,过点B 的切线与CO 的延长线交于点D ．:求证：1CAB BOD ∠=∠；2ABC ∆≌ODB ∆． 3、证切线点拨：证明切线的方法——连半径,证垂直;根据：过半径的外端且垂直于半径的直线是圆的切线例3如图,四边形ABCD 内接于⊙O,BD 是⊙O 的直径, AE⊥CD 于点E,DA 平分∠BDE;1求证：AE 是⊙O 的切线;2若∠DBC=30°,DE=1cm,求BD 的长;例4如图,点A 、B 、C 、D 都在⊙O 上,OC⊥AB,∠ADC=30°． 1求∠BOC 的度数；2求证：四边形AOBC 是菱形．对应练习1．如图,已知⊙O 的直径AB 与弦CD 互相垂直,垂足为点E . ⊙O 的切线BF 与弦AD的延长线相交于点F ,且AD =3,cos ∠BCD= . 1求证：CD ∥BF ； 2求⊙O 的半径； 3求弦CD 的长.2.如图,点D 是⊙O 的直径CA 延长线上一点,点B 在⊙O 上,且AB ＝AD ＝AO ．1求证：BD 是⊙O 的切线．2若点E 是劣弧BC 上一点,AE 与BC 相交于点F,且△BEF 的面积为8,cos∠BFA＝32,求△ACF 的面积．1.一副三角板,如图所示叠放在一起,则图中∠α的度数是A ．75B ．60C ．65D ．55图1 图22．如图2,在边长为4的等边三角形ABC 中,AD 是BC 边上的高,点E 、F 是AD 上的两点,则图中阴影部分的面积是A ．43B ．33C ．23D ．33.如图3,△ABC 中,∠C =90°,AC =3,∠B =30°,点P 是BC 边上的动点,则AP 长不可能是DCBOADOBCA E 例7图43DOEC O图 8OFE BCADCB A O P D图3 图4 A B C D74. 如图4,直角三角形纸片的两直角边长分别为6,8,现将ABC △如图那样折叠,使点A 与点B 重合,折痕为DE ,则tan CBE ∠的值是 A ．247B ．73C ．724D ．135.如图5,ABC △是等腰直角三角形,BC 是斜边,将ABP △绕点A 逆时针旋转后,能与ACP '△重合,如果3AP =,那么PP '的长等于 A ．32B ．23C ．42 D ．336. 图6,已知等边△ABC 中,点D,E 分别在边AB,BC 上,把△BDE 沿直线DE 翻折,使点B 落在点B ˊ处,DB ˊ,EB ˊ分别交边AC 于点F,G,若∠ADF=80o ,则∠EGC 的度数为图5 图67．如图,已知：在平行四边形ABCD 中,AB=4cm,AD=7cm,∠ABC 的平分线交AD•于点E,交CD 的延长线于点F,则DF=______cm ．8．如图,矩形ABCD 中,AB ＝2,BC ＝3,对角线AC 的垂直平分线分别交AD,BC 于点E 、F,连接CE,则CE 的长________.9.如图,BD 是⊙O 的直径,OA ⊥OB,M 是劣弧错误!上一点,过点M 作⊙O 的切线MP 交OA 的延长线于P 点,MD 与OA 交于点N; 1求证：PM=PN ； 2若BD=4,PA=32AO,过B 点作BC ∥MP 交⊙O 于C 点,求BC 的长． 10．如图,在△ABC 中,以AB 为直径的⊙O 交BC 于点P,PD ⊥AC 于点D,且PD 与⊙O 相切．1求证：AB ＝AC ；2若BC ＝6,AB ＝4,求CD 的值．11．一副直角三角板如图放置,点C 在FD 的延长线上,AB ∥CF,∠F=∠ACB=90°, ∠ E=45°,∠A=60°,AC=10,试求CD 的长．12．如图,四边形ABCD 是边长为a 的正方形,点G ,E 分别是边AB ,BC 的中点,∠AEF =90o,且EF 交正方形外角的平分线CF 于点F ． 1证明：∠BAE =∠FEC ； 2证明：△AGE ≌△ECF ； 3求△AEF 的面积．13．如图,矩形ABCD 中,53AB AD ==，．点E 是CD 上的动点,以AE 为直径的O ⊙与AB 交于点F ,过点F 作FG BE ⊥于点G ．1当E 是CD 的中点时：①tan EAB ∠的值为______________； ② 证明：FG 是O ⊙的68CEABD切线；2试探究：BE 能否与O ⊙相切若能,求出此时DE 的长；若不能,请说明理由．几何之——解直角三角形1在△ABC 中,∠C＝90°,sinA＝45,则tanB ＝A ．43B ．34C ．35D ．452、在 ABC 中,若｜sinA-22 |+23-cosB 2=0, ∠A.∠B 都是锐角,则∠C 的度数是A. 750B. 9003、如下左图,在△ABC 中,∠C=90°,AB=13,BC=5,则sinA 的值是A 、513B 、1213 C 、512D 、1354如上右图,在四边形ABCD 中,E 、F 分别是AB 、AD 的中点,若EF=2, BC=5,CD=3,则tanC 等于A 、34B 、43C 、35D 、455、如,在矩形ABCD 中,DE⊥AC 于E,设∠ADE=α,且53cos =α, AB = 4, 则AD 的长为． A3 B316 C 320 D 516 6在锐角△ABC 中,∠BAC=60°,BD、CE 为高,F 为BC 的中点,连接DE 、DF 、EF,则结论：①DF=EF；②AD：AB=AE ：AC ；③△DEF 是等边三角形；④BE+CD=BC；⑤当∠ABC=45°时,BE=√2DE 中,一定正确的有A 、2个B 、3个C 、4个D 、5个7.084sin 45(3)4-︒+-π+-=为528.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离米,则这个破面的坡度为 . 9.如图,已知直线1l∥2l ∥3l ∥4l ,相邻两条平行直线间的距离都是1,如果正方形ABCD 的四个顶点分别在四条直线上,则sin α= ．直角三角形常见模型1 张华同学在学校某建筑物的C 点处测得旗杆顶部A 点的仰角为30°,旗杆底部B 点的俯角为45°．若旗杆底部B 点到建筑物的水平距离BE=9米,旗杆台阶高1米,试求旗杆AB 的高度;2．海船以5海里/小时的速度向正东方向行驶,在A 处看见灯塔B 在海船的北偏东DE OCBG FAABC DαAABCDEADBE图6i =1:3C60°方向,2小时后船行驶到C 处,发现此时灯塔B 在海船的北偏西45方向,求此时灯塔B 到C 处的距离; 3某年入夏以来,松花江哈尔滨段水位不断下降,一条船在松花江某段自西向东沿直线航行,在A 处测得航标C 在北偏东60°方向上;前进100m 到达B 处,又测得航标C 在北偏东45°方向上如图,在以航标C 为圆心,120m 为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险4如图6,梯形ABCD 是拦水坝的横断面图,图中3:1=i 是指坡面的铅直高度DE 与水平宽度CE 的比,∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD 的面积．结果保留三位有效数字.参考数据：3≈,2≈3 1.73≈。

初中数学经典几何题及答案

初中数学经典几何题及答案1.题目：已知直角三角形的两条直角边分别为3cm和4cm，求斜边的长度。

解答：根据勾股定理，直角三角形中斜边的平方等于两直角边的平方和。

所以斜边的长度为√(3^2 + 4^2) = √(9 + 16) = √25 = 5cm。

2.题目：已知一个正方形的边长为6cm，求其对角线的长度。

解答：正方形的对角线可以看作是两个相等的直角三角形的斜边，所以可以使用勾股定理来计算对角线的长度。

正方形的边长为6cm，所以直角三角形的直角边为6cm，斜边即为对角线的长度。

所以对角线的长度为√(6^2+ 6^2) = √(36 + 36) = √72 ≈ 8.49cm。

3.题目：已知一个梯形的上底长为8cm，下底长为12cm，高为5cm，求梯形的面积。

解答：梯形的面积可以通过上底和下底的平均值乘以高来计算。

所以梯形的面积为(8 + 12) × 5 ÷ 2 = 20cm²。

4.题目：已知一个等边三角形的边长为10cm，求其面积。

解答：等边三角形的面积可以通过边长的平方乘以根号3再除以4来计算。

所以等边三角形的面积为(10^2 × √3) ÷ 4 = (100 × √3) ÷ 4 ≈ 43.30cm²。

5.题目：已知一个长方形的长为8cm，宽为5cm，求其周长。

解答：长方形的周长可以通过将长和宽分别乘以2再相加来计算。

所以长方形的周长为(8 × 2) + (5 × 2) = 16 + 10 = 26cm。

6.题目：已知一个圆的半径为6cm，求其面积。

解答：圆的面积可以通过半径的平方乘以π（约等于3.14）来计算。

所以圆的面积为6^2 × 3.14 ≈ 113.04cm²。

7.题目：已知一个正五边形的边长为4cm，求其周长。

解答：正五边形的周长可以通过边长乘以5来计算。

所以正五边形的周长为4 × 5 = 20cm。

中考数学几何证明题经典题型分析【范本模板】

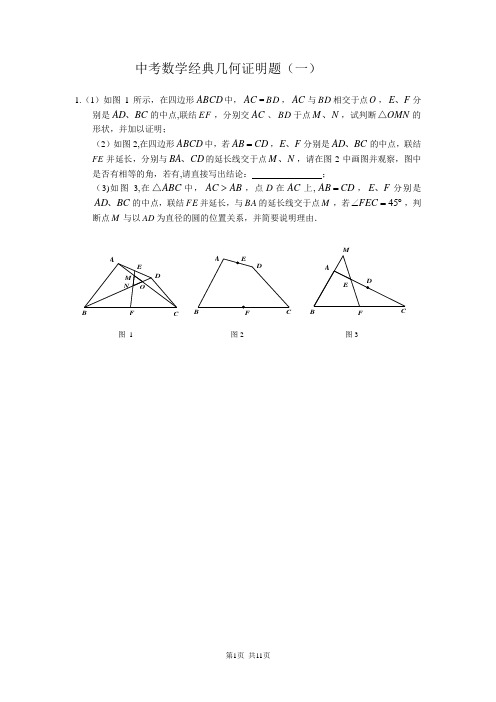
中考数学经典几何证明题（一）1.（1）如图1所示，在四边形ABCD 中，AC =BD ，AC 与BD 相交于点O ，E F 、分别是AD BC 、的中点,联结EF ，分别交AC 、BD 于点M N 、，试判断OMN △的形状，并加以证明；（2）如图2,在四边形ABCD 中，若AB CD =，E F 、分别是AD BC 、的中点，联结FE 并延长，分别与BA CD 、的延长线交于点M N 、，请在图2中画图并观察，图中是否有相等的角，若有,请直接写出结论：；（3)如图3,在ABC △中，AC AB >，点D 在AC 上,AB CD =，E F 、分别是AD BC 、的中点，联结FE 并延长，与BA 的延长线交于点M ，若45FEC ∠=︒，判断点M 与以AD 为直径的圆的位置关系，并简要说明理由．图 1 图2 图3FB ACD EFM NOD 2．(1）如图1，已知矩形ABCD中，点E是BC上的一动点，过点E作EF⊥BD于点F，EG⊥AC于点G，CH⊥BD于点H，试证明CH=EF+EG;图1D（2) 若点E在ＢＣ的延长线上，如图2，过点E作EF⊥BD于点F,EG⊥AC的延长线于点G，CH⊥BD于点H, 则EF、EG、ＣH三者之间具有怎样的数量关系，直接写出你的猜想；（3）如图3,BD是正方形ABCD的对角线，L在BD上，且BL=BC, 连结CL，点E是CL上任一点，EF⊥BD于点F，EG⊥BC于点G，猜想EF、EG、BD之间具有怎样的数量关系,直接写出你的猜想；(4) 观察图1、图2、图3的特性,请你根据这一特性构造一个图形，使它仍然具有EF、EG、ＣH这样的线段，并满足（1)或（2）的结论，写出相关题设的条件和结论.BGAFDECH3。

如图，△ABC 是等边三角形，F 是AC 的中点,D 在线段BC 上，连接DF ，以DF 为边在DF 的右侧作等边△DFE ,ED 的延长线交AB 于H ,连接EC ，则以下结论:①∠AHE +∠AFD =180°;②AF =21BC ;③当D 在线段BC 上（不与B ,C 重合）运动，其他条件不变时BD BH 是定值;④当D 在线段BC 上（不与B ，C 重合)运动，其他条件不变时DCECBC 21是定值；（1)其中正确的是——-----—------————-；（2）对于（1)中的结论加以说明;4. 在ABC △中，AC=BC ，90ACB ∠=︒,点D 为AC 的中点．（1)如图1,E 为线段DC 上任意一点，将线段DE 绕点D 逆时针旋转90°得到线段DF ，连结CF ，过点F 作FH FC ⊥，交直线AB 于点H ．判断FH 与FC 的数量关系并加以证明． (2)如图2,若E 为线段DC 的延长线上任意一点，（1）中的其他条件不变，你在(1）中得出的结论是否发生改变，直接写出你的结论,不必证明．5。

中考复习初中数学几何证明经典试题(含答案)

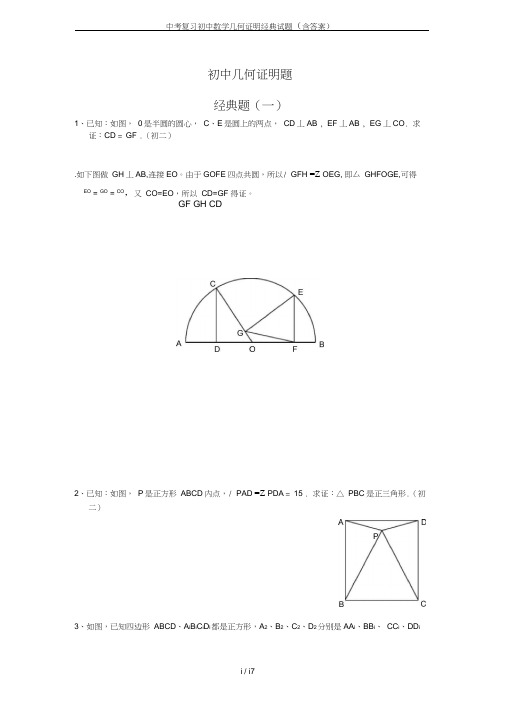
初中几何证明题经典题（一）1、已知：如图，0是半圆的圆心，C、E是圆上的两点，CD丄AB , EF丄AB , EG丄CO. 求证：CD = GF .（初二）.如下图做GH丄AB,连接EO。

由于GOFE四点共圆，所以/ GFH =Z OEG, 即厶GHFOGE,可得EO = GO = CO，又CO=EO，所以CD=GF 得证。

GF GH CD2、已知：如图，P是正方形ABCD内点，/ PAD =Z PDA = 15°. 求证：△ PBC是正三角形.（初二）3、如图，已知四边形ABCD、A i B i C i D i都是正方形，A2、B2、C2、D2分别是AA i、BB i、CC i、DD i的中点.及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证：AP = AQ .（初二）3、如果上题把直线 MN 由圆外平移至圆内，则由此可得以下命题:设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN P 、Q .4、 1、求证：四边形 A 2B 2C 2D 2是正方形.（初二）已知: 求证: 如图，在四边形的延长线交 / DEN = Z△ ABC 中, MN F .ABCD 中，AD = BC , M 、N 分别是 AB 、CD 的中点，AD 、BC 于E 、F .经典题（二）已知： (1) 求证：AH = 20M ;(2) 若/ BAC = 60°,求证:H 为垂心（各边高线的交点），0为外心，且 0M 丄BC 于M . AH = A0 .(初二)2、设MN 是圆O 外一直线，过O 作OA 丄MN 于A ，自A 引圆的两条直线，交圆于DCGN求证：AP = AQ .（初二）ECAM NP4、如图，分别以厶 ABC 的AC 和BC 为一边，在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ，点P 是EF 的中点.求证：点P 到边AB 的距离等于 AB 的一半.（初二）经典题（二）1、如图，四边形 ABCD 为正方形, 求证：CE = CF .（初二）2、如图，四边形 ABCD 为正方形，DE // AC ,且CE = CA ，直线EC 交DA 延长线于F . 求证：AE = AF .（初二）DE // AC , AE = AC , AE 与 CD 相交于 F .FEAD1、设P 是边长为1的正△ ABC 内任一点,4、如图，PC 切圆0于C , AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于3、设ABCD 为圆内接凸四边形，求证： AB • CD + AD • BC = AC • BD .（初三）B 、D .求证: AB = DC , BC = AD .（初三）1、已知：△ ABC 是正三角形，P 是三角形内一点求：/ APB 的度数.（初二）2、设P 是平行四边形 ABCD 内部的一点，且/求证：/ PAB = Z PCB .（初二）4、平行四边形 ABCD 中，设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证：/ DPA =Z DPC .（初二）AO DB EFC求证:4、如图，△ ABC 中，/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点，/ DCA = 30°, / EBA = 20°，求/ BED 的度数. LiB C经典题（一）1•如下图做GH丄AB,连接E0。

中考总复习数学04- 第二部分专题四几何最值问题(精练册)

∵∠BCF=∠EDF=75°-30°=45°,BC=DE,
∴△BCF≌△EDF(SAS),∴BF=EF,
专题四几何最值问题— 两点之间线段最短问题
∵AB=AE=6,AF=AF,∴△BAF≌△EAF(SSS),
∵∠BAE=120°-30°=90°,∴∠BAF=∠EAF=45°,
∵∠AKF=∠BKF=90°,∴∠KAF=∠KFA=45°,∴AK=FK,
三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最
小值和最大值之和是( B )
A.5
B.6
C.7
D.8
1
2
3
4
5
6
7
专题四几何最值问题— 点圆求最值问题
返回类型清单
2.如图,半径为1的☉M经过平面直角坐标系的原点O,与x轴交于点A,点A
的坐标为( ,0),点B是直角坐标系平面内一动点,且∠ABO=30°,则BM
M,N分别是BD,BC上的动点,则CM+MN的最小值为( B )
A.4
B.5
C.4.5
D.6
专题四几何最值问题— 垂线段最短问题
4.如图,正方形ABCD的边长为3,E是BC上一点且CE=1,F
是线段DE上的动点.连接CF,将线段CF绕点C逆时针旋

转90°得到CG,连接EG,则EG的最小值是
.
(1)连接PC,AC,求∠PCA的度数;
解:连接OP,如图1,
由题意得,∠AOP=120°.

∵∠PCA= ∠AOP,

∴∠PCA=60°;
返回类型清单
专题四几何最值问题— 两点之间线段最短问题
(2)连接AP,PB,求证:△DAO≌△APB;

中考数学常见题型几何动点问题

中考数学压轴题型研究（一）——动点几何问题例1：在△ABC 中，∠B=60°,BA=24CM,BC=16CM, (1)求△ABC 的面积；(2)现有动点P 从A 点出发，沿射线AB 向点B 方向运动，动点Q 从C 点出发，沿射线CB 也向点B 方向运动。

如果点P 的速度是4CM/秒，点Q 的速度是2CM/秒，它们同时出发，几秒钟后，△PBQ的面积是△ABC 的面积的一半？(3)在第（2）问题前提下，P ,Q 两点之间的距离是多少？例2: ()已知正方形ABCD 的边长是1，E 为CD 边的中点， P 为正方形ABCD 边上的一个动点，动点P 从A 点出发，沿A →B → C →E 运动，到达点E.若点P 经过的路程为自变量x ，△APE 的面积为函数y ，（1）写出y 与x 的关系式 (2)求当y ＝13时，x 的值等于多少？例3：如图1 ，在直角梯形ABCD 中，∠B=90°，DC ∥AB ，动点P 从B 点出发，沿梯形的边由B →C → D → A 运动，设点P 运动的路程为x ,△ABP 的面积为y , 如果关于x 的函数y 的图象如图2所示，那么△ABC 的面积为（）A ．32B ．18C ．16D ．10ACB By例4：直线364y x =-+与坐标轴分别交于A B 、两点，动点P Q 、同时从O 点出发，同时到达A 点，运动停止．点Q 沿线段OA 运动，速度为每秒1个单位长度，点P 沿路线O →B →A 运动．（1）直接写出A B 、两点的坐标；（2）设点Q 的运动时间为t 秒，OPQ △的面积为S ，求出S 与t 之间的函数关系式；（3）当485S =时，求出点P 的坐标，并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标．例5：已知：等边三角形ABC 的边长为4厘米，长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动（运动开始时，点M 与点A 重合，点N 到达点B 时运动终止），过点M N 、分别作AB 边的垂线，与ABC △的其它边交于P Q 、两点，线段MN 运动的时间为t 秒．（1）线段MN 在运动的过程中，t 为何值时，四边形MNQP 恰为矩形？并求出该矩形的面积；（2）线段MN 在运动的过程中，四边形MNQP 的面积为S ，运动的时间为t ．求四边形MNQP 的面积S 随运动时间t 变化的函数关系式，并写出自变量t 的取值范围．例6：如图（3），在梯形ABCD 中，906DC AB A AD ∠==∥，°，厘米，4DC =厘米，BC 的坡度34i =∶，动点P 从A 出发以2厘米/秒的速度沿AB 方向向点B 运动，动点Q 从点B 出发以3厘米/秒的速度沿B C D →→方向向点D 运动，两个动点同时出发，当其中一个动点到达终点时，另一个动点也随之停止．设动点运动的时间为t秒．（1）求边BC 的长；（2）当t 为何值时，PC 与BQ 相互平分；图（3）BC PQBA MN（3）连结PQ ，设PBQ △的面积为y ，探求y 与t 的函数关系式，求t 为何值时，y 有最大值？最大值是多少？二、利用函数与方程的思想和方法将所解决图形的性质（或所求图形面积）直接转化为函数或方程。

中考数学之平面几何最全总结+经典习题

平面几何知识要点（一)【线段、角、直线】1.过两点有且只有一条直线.2.两点之间线段最短。

3.过一点有且只有一条直线和已知直线垂直。

4.直线外一点与直线上各点连接的所有线段中，垂直线段最短。

垂直平分线，简称“中垂线”。

定义:经过某一条线段的中点，并且垂直于这条线段的直线,叫做这条线段的垂直平分线（中垂线）。

线段的垂直平分线可看作和线段两端点距离相等的所有点的集合。

中垂线性质：垂直平分线垂直且平分其所在线段。

垂直平分线定理:垂直平分线上任意一点，到线段两端点的距离相等。

逆定理：到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。

三角形三条边的垂直平分线相交于一点，该点叫外心,并且这一点到三个顶点的距离相等。

角1.同角或等角的余角相等。

2.同角或等角的补角相等.3.对顶角相等。

角的平分线性质角的平分线是到角的两边距离相等的所有点的集合定理1：角的平分线上的点到这个角的两边的距离相等.定理2：到一个角的两边距离相等的点，在这个角的平分线上.三角形各内角平分线的交点,该点叫内心，它到三角形三边距离相等。

【平行线】平行线性质1:两直线平行，同位角相等。

平行线性质2：两直线平行，内错角相等。

平行线性质3:两直线平行，同旁内角互补。

平行线判定1:同位角相等,两直线平行。

平行线判定2：内错角相等，两直线平行。

平行线判定3：同旁内角互补,两直线平行。

平行线判定4：如果两条直线都和第三条直线平行,这两条直线也互相平行.平行公理：经过直线外一点,有且只有一条直线与这条直线平行。

平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例。

推论:平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例。

平面几何知识要点（二)【三角形】面积公式：1．已知三角形底a ，高h ，12S ah =2．正三角形面积 S=24(a 为边长正三角形）3．已知三角形三边a ，b,c ，则S =（海伦公式) 其中:()2a b c p ++= （周长的一半） 4．已知三角形两边a ，b 及这两边夹角C ，则1sin 2S ab C =. 5．设三角形三边分别为a 、b 、c,内切圆半径为r ，则()2a b c r S ++= 6．设三角形三边分别为a 、b 、c,外接圆半径为R ，则4abc S R =记住★:已知正三角形边长为a ,其外接圆半径为R ，内切圆半径为r ，则有：R = ,r = ， 2R r = 内角和定理：三角形三个内角的和等于180°推论1 :直角三角形的两个锐角互余推论2 ：三角形的一个外角等于和它不相邻的两个内角的和推论3 ：三角形的一个外角大于任何一个和它不相邻的内角全等三角形性质：如果两三角形全等，那么其对应边，对应角相等.其中对应边除了三角形的边长外，还包括对应高,对应中线，对角平分线.全等三角形判定定理：边边边公理：有三边对应相等的两个三角形全等.（SSS ）边角边公理：有两边和它们的夹角对应相等的两个三角形全等。

10道中考数学几何典型题型

解决几何最值问题的通常思路两点之间线段最短；直线外一点与直线上所有点的连线段中，垂线段最短；三角形两边之和大于第三边或三角形两边之差小于第三边（重合时取到最值）是解决几何最值问题的理论依据，根据不同特征转化是解决最值问题的关键．通过转化减少变量，向三个定理靠拢进而解决问题；直接调用基本模型也是解决几何最值问题的高效手段。

几何最值问题中的基本模型举例：二、典型题型1．如图：点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=，则△PMN的周长的最小值为．【分析】作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN 的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．【解答】解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵PC关于OA对称，∴∠COP=2∠AOP，OC=OP同理，∠DOP=2∠BOP，OP=OD∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．∴△COD是等腰直角三角形．则CD=OC=×3=6．【题后思考】本题考查了对称的性质，正确作出图形，理解△PMN周长最小的条件是解题的关键．2．如图，当四边形PABN的周长最小时，a=．【分析】因为AB，PN的长度都是固定的，所以求出PA+NB的长度就行了．问题就是PA+NB什么时候最短．把B点向左平移2个单位到B′点；作B′关于x轴的对称点B″，连接AB″，交x轴于P，从而确定N 点位置，此时PA+NB最短．设直线AB″的解析式为y=kx+b，待定系数法求直线解析式．即可求得a的值．【解答】解：将N点向左平移2单位与P重合，点B 向左平移2单位到B′（2，﹣1），作B′关于x轴的对称点B″，根据作法知点B″（2，1），设直线AB″的解析式为y=kx+b，则，解得k=4，b=﹣7．∴y=4x﹣7．当y=0时，x=，即P（，0），a=．故答案填：．【题后思考】考查关于X轴的对称点，两点之间线段最短等知识．3．如图，A、B两点在直线的两侧，点A到直线的距离AM=4，点B到直线的距离BN=1，且MN=4，P为直线上的动点，|PA﹣PB|的最大值为．【分析】作点B于直线l的对称点B′，则PB=PB′因而|PA﹣PB|=|PA﹣PB′|，则当A，B′、P在一条直线上时，|PA﹣PB|的值最大．根据平行线分线段定理即可求得PN和PM的值然后根据勾股定理求得PA、PB′的值，进而求得|PA﹣PB|的最大值．【解答】解：作点B于直线l的对称点B′，连AB′并延长交直线l于P．∴B′N=BN=1，过D点作B′D⊥AM，利用勾股定理求出AB′=5∴|PA﹣PB|的最大值=5．【题后思考】本题考查了作图﹣轴对称变换，勾股定理等，熟知“两点之间线段最短”是解答此题的关键．4．动手操作：在矩形纸片ABCD中，AB=3，AD=5．如图所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为．【分析】本题关键在于找到两个极端，即BA′取最大或最小值时，点P或Q的位置．经实验不难发现，分别求出点P与B重合时，BA′取最大值3和当点Q 与D重合时，BA′的最小值1．所以可求点A′在BC 边上移动的最大距离为2．【解答】解：当点P与B重合时，BA′取最大值是3，当点Q与D重合时（如图），由勾股定理得A′C=4，此时BA′取最小值为1．则点A′在BC边上移动的最大距离为3﹣1=2．故答案为：2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．5．如图，直角梯形纸片ABCD，AD⊥AB，AB=8，AD=CD=4，点E、F分别在线段AB、AD上，将△AEF 沿EF翻折，点A的落点记为P．当P落在直角梯形ABCD内部时，PD的最小值等于．【分析】如图，经分析、探究，只有当直径EF最大，且点A落在BD上时，PD最小；根据勾股定理求出BD的长度，问题即可解决．【解答】解：如图，∵当点P落在梯形的内部时，∠P=∠A=90°，∴四边形PFAE是以EF为直径的圆内接四边形，∴只有当直径EF最大，且点A落在BD上时，PD最小，此时E与点B重合；由题意得：PE=AB=8，由勾股定理得：BD2=82+62=80，∴BD=，∴PD=．【题后思考】该命题以直角梯形为载体，以翻折变换为方法，以考查全等三角形的判定及其性质的应用为核心构造而成；解题的关键是抓住图形在运动过程中的某一瞬间，动中求静，以静制动．。

中考数学复习专题：几何综合题(含答案解析)

几何综合题1.已知△ABC 中，AD 是的平分线，且AD =AB ，过点C 作AD 的垂线，交 AD 的延长线于点H ．（1）如图1，若①直接写出B ∠和ACB ∠的度数； ②若AB =2，求AC 和AH 的长；（2）如图2，用等式表示线段AH 与AB +AC 之间的数量关系，并证明．答案：（1）①75B ∠=︒，45ACB ∠=︒；②作DE ⊥AC 交AC 于点E .Rt △ADE 中，由30DAC ∠=︒，AD =2可得DE =1，AE 3. Rt △CDE 中，由45ACD ∠=︒，DE=1，可得EC =1. ∴AC 31.Rt △ACH 中，由30DAC ∠=︒，可得AH 33+=；（2）线段AH 与AB +AC 之间的数量关系：2AH =AB +AC证明：延长AB 和CH 交于点F ，取BF 中点G ，连接GH .易证△ACH ≌△AFH .∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =，∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =.∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==.2.正方形ABCD 的边长为2，将射线AB 绕点A 顺时针旋转α，所得射线与线段BD 交于点M ，作CE AM ⊥于点E ，点N 与点M 关于直线CE 对称，连接CN ．（1）如图1，当045α︒<<︒时， ①依题意补全图1．②用等式表示NCE ∠与BAM ∠之间的数量关系：__________．BAC ∠60BAC ∠=︒（2）当4590α︒<<︒时，探究NCE ∠与BAM ∠之间的数量关系并加以证明．（3）当090α︒<<︒时，若边AD 的中点为F ，直接写出线段EF 长的最大值．答案：（1）①补全的图形如图7所示．② ∠NCE =2∠BAM ．（2）当45°<α<90°时，=1802NCE BAM ∠︒-∠．证明：如图8，连接CM ，设射线AM 与CD 的交点为H ．∵ 四边形ABCD 为正方形， ∴ ∠BAD=∠ADC=∠BCD=90°，直线BD 为正方形ABCD 的对称轴，点A 与点C 关于直线BD 对称． ∵ 射线AM 与线段BD 交于点M ， ∴ ∠BAM=∠BCM=α． ∴ ∠1=∠2=90α︒-． ∵ CE ⊥AM ， ∴ ∠CEH=90°，∠3+∠5=90°．又∵∠1+∠4=90°，∠4=∠5， ∴ ∠1=∠3．∴ ∠3=∠2=90α︒-．∵ 点N 与点M 关于直线CE 对称，∴ ∠NCE=∠MCE=∠2+∠3=1802BAM ︒-∠．（31CDBA图1备用图C DBAM3. 如图，已知60AOB ∠=︒，点P 为射线OA内，且满足DPA OPE ∠=∠，6DP PE +=. （1）当DP PE =时，求DE 的长；（2）在点P 的运动过程中，请判断是否存在一个定点M答案：（1）作PF ⊥DE 交DE 于F . ∵PE ⊥BO ，60AOB ∠=， ∴30OPE ∠=.∴30DPA OPE ∠=∠=. ∴120EPD ∠=. ∵DP PE =,6DP PE +=,∴30PDE ∠=,3PD PE ==. ∴cos30DF PD =⋅︒=∴2DE DF ==（2）当M 点在射线OA 上且满足OM =DMME的值不变，始终为1.理由如下：当点P 与点M 不重合时，延长EP 到K 使得PK PD =. ∵,DPA OPE OPE KPA ∠=∠∠=∠, ∴KPA DPA ∠=∠. ∴KPM DPM ∠=∠.∵PK PD =,PM 是公共边, ∴KPM △≌DPM △.∴MK MD =.作ML ⊥OE 于L ,MN ⊥EK 于N . ∵60MO MOL =∠=，∴sin 603ML MO =⋅=.∵PE ⊥BO ,ML ⊥OE ,MN ⊥EK ， ∴四边形MNEL 为矩形. ∴3EN ML ==.∵6EK PE PK PE PD =+=+=, ∴EN NK =. ∵MN ⊥EK ,∴MK ME =.∴ME MK MD ==,即1DMME=. 当点P 与点M 重合时，由上过程可知结论成立.4. 如图，在菱形ABCD 中，∠DAB =60°，点E 为AB 边上一动点（与点A ，B 不重合），连接CE ，将∠ACE 的两边所在射线CE ，CA 以点C 为中心，顺时针旋转120°，分别交射线AD 于点F ，G. （1）依题意补全图形；（2）若∠ACE=α，求∠AFC 的大小（用含α的式子表示）；（3）用等式表示线段AE 、AF 与CG 之间的数量关系，并证明．答案：（1）补全的图形如图所示.（2）解：由题意可知，∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD 是菱形，∠DAB=60°， ∴∠DAC=∠BAC= 30°. ∴∠AGC=30°. ∴∠AFC =α+30°.（3）用等式表示线段AE 、AF 与CG 之间的数量关系为CG AF AE 3=+.证明：作CH ⊥AG 于点H.由（2）可知∠BAC=∠DAC=∠AGC=30°. ∴CA=CG. ∴HG =21AG. ∵∠ACE =∠GCF ，∠CAE =∠CGF ， ∴△ACE ≌△GCF. ∴AE =FG .在Rt △HCG 中， .23cos CG CGH CG HG =∠⋅= ∴AG =3CG .即AF+AE =3CG .5.如图，Rt △ABC 中，∠ACB = 90°，CA = CB ，过点C 在△ABC 外作射线CE ，且∠BCE = α，点B 关于CE 的对称点为点D ，连接AD ，BD ，CD ，其中AD ，BD 分别交射线CE 于点M ，N . （1）依题意补全图形；（2）当α= 30°时，直接写出∠CMA 的度数；（3）当0°<α< 45°时，用等式表示线段AM ，CN 之间的数量关系，并证明．答案：（1）如图；（2）45°；（3）结论：AM 2CN ．A BC E证明：作AG ⊥EC 的延长线于点G ．∵点B 与点D 关于CE 对称， ∴CE 是BD 的垂直平分线． ∴CB =CD ．∴∠1=∠2=α．∵CA =CB ，∴CA =CD ．∴∠3=∠CAD ． ∵∠4=90°，∴∠3=（180°∠ACD ）=（180°90°αα）=45°．∴∠5=∠2+∠3=α+45°-=45°． ∵∠4=90°，CE 是BD 的垂直平分线， ∴∠1+∠7=90°，∠1+∠6=90°． ∴∠6=∠7． ∵AG ⊥EC ，∴∠G =90°=∠8． ∴在△BCN 和△CAG 中，∠8=∠G ， ∠7=∠6， BC =CA ，BCN ≌△CAG ．∴CN =AG ． ∵Rt △AMG 中，∠G =90°，∠5=45°，∴AM AG ．∴AM CN ．答案：（1）补全图形略（2）①证明：连接BD ，如图2，∵线段AP 绕点A 顺时针旋转90°得到线段AQ ， ∴AQ AP =，90QAP ∠=°． ∵四边形ABCD 是正方形， ∴AD AB =，90DAB ∠=°． ∴12∠=∠．∴△ADQ ≌△ABP ． ∴DQ BP =，3Q ∠=∠．∵在Rt QAP ∆中，90Q QPA ∠+∠=°， ∴390BPD QPA ∠=∠+∠=°． ∵在Rt BPD ∆中，222DP BP BD +=，12-12----αα又∵DQ BP =，222BD AB =，∴2222DP DQ AB +=． ②BP AB =．7.如图，在等腰直角△ABC 中，∠CAB=90°，F 是AB 边上一点，作射线CF ，过点B 作BG ⊥C F 于点G ，连接AG ．（1）求证：∠ABG =∠ACF ；（2）用等式表示线段C G ，AG ，BG 之间的等量关系，并证明．答案：（1）证明 :∵ ∠CAB=90°. ∵ BG ⊥CF 于点G ， ∴ ∠BGF =∠CAB =90°. ∵∠GFB =∠CFA . ∴ ∠ABG =∠ACF .（2）CG =2AG +BG .证明：在CG 上截取CH =BG ，连接AH ， ∵ △ABC 是等腰直角三角形， ∴ ∠CAB =90°，AB =AC . ∵ ∠ABG =∠ACH . ∴ △ABG ≌△ACH . ∴ AG =AH ,∠GAB =∠HAC . ∴ ∠GAH =90°. ∴ 222AG AH GH +=. ∴ GH =2AG . ∴ CG =CH +GH =2AG +BG .8.如图，在正方形ABCD 中，E 是BC 边上一点，连接AE ，延长CB 至点F ，使BF=BE ，过点F 作FH ⊥AE 于点H ，射线FH 分别交AB 、CD 于点M 、N ，交对角线AC 于点P ，连接AF ．（1）依题意补全图形；（2）求证：∠FAC =∠APF ；（3）判断线段FM 与PN 的数量关系，并加以证明．答案：（1）补全图如图所示．（2）证明∵正方形ABCD ，∴∠BAC =∠BCA =45°，∠ABC =90°， ∴∠PAH =45°-∠BAE ． ∵FH ⊥AE ．∴∠APF =45°+∠BAE ．EDCBAM H PDAC∵BF=BE ，∴AF=AE ，∠BAF =∠BAE ． ∴∠FAC =45°+∠BAF ． ∴∠FAC =∠APF ．（3）判断：FM =PN ．证明：过B 作BQ ∥MN 交CD 于点Q ，∴MN =BQ ，BQ ⊥AE ． ∵正方形ABCD ，∴AB =BC ，∠ABC =∠BCD=90°． ∴∠BAE =∠CBQ ． ∴△ABE ≌△BCQ ． ∴AE =BQ ． ∴AE =MN ．∵∠FAC =∠APF ， ∴AF =FP ． ∵AF=AE ， ∴AE =FP ． ∴FP =MN ． ∴FM =PN ．9.如图所示，点P 位于等边ABC △的内部，且∠ACP =∠CBP ．(1) ∠BPC 的度数为________°；(2) 延长BP 至点D ，使得PD =PC ，连接AD ，CD ．①依题意，补全图形； ②证明：AD +CD =BD ；(3) 在(2)的条件下，若BD 的长为2，求四边形ABCD 的面积．解：(1)120°. ----------------------------2分(2)①∵如图1所示.②在等边ABC △中，60ACB ∠=︒， ∴60.ACP BCP ∠+∠=︒ ∵=ACP CBP ∠∠，∴60.CBP BCP ∠+∠=︒ ()180120.BPC CBP BCP ∠=︒-∠+∠=︒∴∴18060.CPD BPC ∠=︒-∠=︒ ∵=PD PC ，∴CDP △为等边三角形.∵60ACD ACP ACP BCP ∠+∠=∠+∠=︒， ∴.ACD BCP ∠=∠ 在ACD △和BCP △中，M H PDA CDAC BC ACD BCP CD CP =⎧⎪∠=∠⎨⎪=⎩，，， ∴()SAS ACD BCP △≌△.∴.AD BP =∴.AD CD BP PD BD +=+=-----------------------------------------4分（3）如图2，作BM AD ⊥于点M ，BN DC ⊥延长线于点N . ∵=60ADB ADC PDC ∠∠-∠=︒， ∴=60.ADB CDB ∠∠=︒ ∴=60.ADB CDB ∠∠=︒∴3= 3.BM BN BD == 又由（2）得，=2AD CD BD +=，ABD BCD ABCD S S S ∴△△四边形=+1122AD BM CD BN =+()32AD CD =+ 32=3.=-----------------------------------7分10.如图1，在等边三角形ABC 中，CD 为中线，点Q 在线段CD 上运动，将线段QA 绕点Q 顺时针旋转，使得点A的对应点E 落在射线BC 上，连接BQ ，设∠DAQ =α（0°＜α＜60°且α≠30°）. （1）当0°＜α＜30°时，①在图1中依题意画出图形，并求∠BQE （用含α的式子表示）； ②探究线段CE ，AC ，CQ 之间的数量关系，并加以证明；（2）当30°＜α＜60°时，直接写出线段CE ，AC ，CQ 之间的数量关系.解：（1）①． ………………………………………………………………………… 1分3-图1 备用图② 0≤QL2分（2）设直线+3y =与x 轴，y 轴的交点分别为点A ，点B ，可得A ，(0,3)B ．∴ OA =，3OB =，30OAB ∠=︒．由0≤QL y =．①如图13，当⊙D 与x 轴相切时，相应的圆心1D 满足题意，其横坐标取到最大值．作11D E x ⊥轴于点1E ，可得11D E ∥OB ，111D E AE BO AO=． ∵ ⊙D 的半径为1， ∴ 111D E =．∴ 1AE =11OE OA AE =-=． ∴1D x =②如图14，当⊙D 与直线y =相切时，相应的圆心2D 满足题意，其横坐标取到最小值．作22D E x ⊥轴于点2E ，则22D E ⊥OA ．设直线y =与直线+33y x =的交点为F 可得60AOF ∠=︒，OF ⊥AB ．则9cos2AF OA OAF =⋅∠==．∵ ⊙D 的半径为1， ∴ 21D F =．∴2272AD AF D F =-=．∴ 22cos AE AD OAF=⋅∠72==，224OE OA AE =-=．图13∴2D x =．由①②可得，D x≤D x≤． ………………………………………… 5分（3）画图见图15．．……………………………… 7分11.如图，在等边ABC △中， ,D E 分别是边,AC BC 上的点，且CD CE = ,30DBC ∠<︒ ，点C 与点F 关于BD对称，连接,AF FE ，FE 交BD 于G .（1）连接,DE DF ，则,DE DF 之间的数量关系是；（2）若DBC α∠=，求FEC ∠的大小; （用α的式子表示）（3）用等式表示线段,BG GF 和FA 之间的数量关系，并证明.（1）DE DF =；（2）解：连接DE ，DF ， ∵△ABC 是等边三角形， ∴60C ∠=︒. ∵DBC α∠=， ∴120BDC α∠=︒-.∵点C 与点F 关于BD 对称，∴120BDF BDC α∠=∠=︒-，DF DC =. ∴1202FDC α∠=︒+. 由（1）知DE DF =.∴F ，E ，C 在以D 为圆心，DC 为半径的圆上.∴1602FEC FDC ∠=∠=︒+α.（3）BG GF FA =+.理由如下：GFE DCBA图15GFEDCBA连接BF ，延长AF ，BD 交于点H ， ∵△ABC 是等边三角形，∴60ABC BAC ∠=∠=︒，AB BC CA ==. ∵点C 与点F 关于BD 对称， ∴BF BC =，FBD CBD ∠=∠. ∴BF BA =. ∴BAF BFA ∠=∠. 设CBD α∠=，则602ABF α∠=︒-. ∴60BAF α∠=︒+. ∴FAD α∠=.∴FAD DBC ∠=∠. 由（2）知60FEC α∠=︒+. ∴60BGE FEC DBC ∠=∠-∠=︒. ∴120FGB ∠=︒，60FGD ∠=︒.四边形AFGB 中，360120AFE FAB ABG FGB ∠=︒-∠-∠-∠=︒. ∴60HFG ∠=︒.∴△FGH 是等边三角形. ∴FH FG =，60H ∠=︒. ∵CD CE =， ∴DA EB =.在△AHD 与△BGE 中，,,.AHD BGE HAD GBE AD BE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△△AHD BGE ≅. ∴BG AH =.∵AH HF FA GF FA =+=+，∴BG GF FA =+．12.如图，在△ABC 中，AB=AC ，∠BAC =90°，M 是BC 的中点，延长AM 到点D ，AE = AD ，∠EAD =90°，CE 交AB 于点F ，CD =DF .（1）∠CAD = 度；（2）求∠CDF 的度数；（3）用等式表示线段CD 和CE 之间的数量关系，并证明.HGFEDCBA解：（1）45 ……………………………………………………………1分（2）解：如图，连接DB.∵90 AB AC BAC =∠=，°，M 是BC 的中点，∴∠BAD=∠CAD=45°.∴△BAD ≌△CAD . ………………………………2分 ∴∠DBA =∠DCA ，BD = CD . ∵CD =DF ,∴B D =DF . ………………………………………3分 ∴∠DBA =∠DFB =∠DCA . ∵∠DFB +∠DFA =180°, ∴∠DCA +∠DFA =180°. ∴∠BAC +∠CDF =180°.∴∠CDF =90°. ………………………………………4分（3）CE =)21CD . ……………………………………5分证明：∵90 EAD ∠=°，∴∠EAF =∠DAF =45°. ∵AD =AE ，∴△EAF ≌△DAF . …………………………………6分 ∴DF =EF .由②可知，CF 2CD . …………………………7分 ∴CE =()21C D .13.如图，正方形ABCD 中，点E 是BC 边上的一个动点，连接AE ，将线段AE 绕点A 逆时针旋转90°，得到AF ，连接EF ，交对角线BD 于点G ，连接AG ．（1）根据题意补全图形；（2）判定AG 与EF 的位置关系并证明；（3）当AB = 3，BE = 2时，求线段BG 的长．解：（1）图形补全后如图…………………1分（2）结论：AG ⊥EF ． …………………2分证明：连接FD ，过F 点FM ∥BC ，交BD 的延长线于点M ．GFAB DCAB CE D∵四边形ABCD 是正方形，∴AB=DA=DC=BC ，∠DAB =∠ABE =∠ADC =90°， ∠ADB =∠5=45°．∵线段AE 绕点A 逆时针旋转90°，得到AF ， ∴AE=AF ，∠FAE =90°． ∴∠1=∠2．∴△FDA ≌△EBA ． …………………3分 ∴∠FDA =∠EBA =90°，FD=BE ． ∵∠ADC =90°，∴∠FDA +∠ADC =180°。

2024年中考数学重难点《几何最值问题》题型及答案解析

重难点几何最值问题中考数学中《几何最值问题》部分主要考向分为五类：一、将军饮马类最值二、动点辅助圆类最值三、四点共圆类最值四、瓜豆原理类最值五、胡不归类最值几何最值问题虽然在中考数学中经常考察的是将军饮马类和辅助圆类，剩余几种虽然不经常考察，但是考到的时候难度都比较大，所以也需要理解并掌握不同类型的几何最值问题的处理办法，这样到考到的时候才能有捷径应对。

考向一：将军饮马类最值一动”“两定异侧普通一动”“两定同侧普通动”两定“一动”两定“两两动”“两定同侧两动”“两定异侧满分技巧将军饮马：。

1．（2023•绥化）如图，△ABC是边长为6的等边三角形，点E为高BD上的动点．连接CE，将CE绕点C 顺时针旋转60°得到CF．连接AF，EF，DF，则△CDF周长的最小值是3+3．【分析】分析已知，可证明△BCE≌△ACF，得∠CAF＝∠CBE＝30°，可知点F在△ABC外，使∠CAF ＝30°的射线AF上，根据将军饮马型，求得DF+CF的最小值便可求得本题结果．【解答】解：∵△ABC是等边三角形，∴AC＝BC＝6，∠ABC＝∠BCA＝60°，∵∠ECF＝60°，∴∠BCE＝60°﹣∠ECA＝∠ACF，∵CE＝CF，∴△BCE≌△ACF（SAS），∴∠CAF＝∠CBE，∵△ABC是等边三角形，BD是高，∴∠CBE＝∠ABC＝30°，CD＝AC＝3，过C点作CG⊥AF，交AF的延长线于点G，延长CG到H，使得GH＝CG，连接AH，DH，DH与AG 交于点I，连接CI，FH，则∠ACG＝60°，CG＝GH＝AC＝3，∴CH＝AC＝6，∴△ACH为等边三角形，∴DH＝CD•tan60°＝，AG垂直平分CH，∴CI＝HI，CF＝FH，∴CI+DI＝HI+DI＝DH＝3，CF+DF＝HF+DF≥DH，∴当F与I重合时，即D、F、H三点共线时，CF+DF的值最小为：CF+DF＝DH＝3，∴△CDF的周长的最小值为3+3．故答案为：3+3．2．（2023•德州）如图，在四边形ABCD中，∠A＝90°，AD∥BC，AB＝3，BC＝4，点E在AB上，且AE＝1．F，G为边AD上的两个动点，且FG＝1．当四边形CGFE的周长最小时，CG的长为．【分析】先确定FG和EC的长为确定的值，得到四边形CGFE的周长最小时，即为CG+EF最小时，平移CG到C'F，作点E关于AD对称点E'，连接E'C'交AD于点G'，得到CG+EF最小时，点G与G'重合，再利用平行线分线段成比例求出C'G'长即可．【解答】解：∵∠A＝90°，AD∥BC，∴∠B＝90°，∵AB＝3，BC＝4，AE＝1，∴BE＝AB﹣AE＝3﹣1＝2，在Rt△EBC中，由勾股定理，得EC＝＝＝，∵FG＝1，∴四边形CGFE的周长＝CG+FG+EF+EC＝CG+EF+1+，∴四边形CGFE的周长最小时，只要CG+EF最小即可．过点F作FC'∥GC交BC于点C'，延长BA到E'，使AE'＝AE＝1，连接E'F，E'C'，E'C'交AD于点G'，可得AD垂直平分E'E，∴E'F＝EF，∵AD∥BC，∴C'F＝CG，CC'＝FG＝1，∴CG+EF＝C'F+E'F≥E'C'，即CG+EF最小时，CG＝C'G'，∵E'B＝AB+AE'＝3+1＝4，BC'＝BC﹣CC'＝4﹣1＝3，由勾股定理，得E'C'＝＝＝5，∵AG'∥BC'，∴＝，即＝，解得C'G'＝，即四边形CGFE的周长最小时，CG的长为．故答案为：．考向二：动点辅助圆类最值满分技巧动点运动轨迹为辅助圆的三种类型：一．定义法——若一动点到定点的距离恒等于固定长，则该点的运动轨迹为以定点为圆心，定长为半径的圆（或圆弧）二.定边对直角模型原理：直径所对的圆周角是直角思路构造：若一条定边所对的“动角”始终为直角，则直角顶点运动轨迹是以该定边为直径的圆（或圆弧）三．定边对定角模型原理：在同圆或等圆中，同弧所对的圆周角相等思路构造：若一条定边所对的“动角”始终为定角，则该定角顶点运动轨迹是以该定角为圆周角，该定边为弦的圆（或圆弧）1．（2023•徐州）如图，在Rt△ABC中，∠C＝90°，CA＝CB＝3，点D在边BC上．将△ACD沿AD折叠，使点C落在点C′处，连接BC′，则BC′的最小值为．【分析】由折叠性质可知AC＝AC'＝3，然后根据三角形的三边不等关系可进行求解．【解答】解：∵∠C＝90°，CA＝CB＝3，∴，由折叠的性质可知AC＝AC'＝3，∵BC'≥AB﹣AC'，∴当A、C′、B三点在同一条直线时，BC'取最小值，最小值即为，故答案为．2．（2023•黑龙江）如图，在Rt△ACB中，∠BAC＝30°，CB＝2，点E是斜边AB的中点，把Rt△ABC绕点A顺时针旋转，得Rt△AFD，点C，点B旋转后的对应点分别是点D，点F，连接CF，EF，CE，在旋转的过程中，△CEF面积的最大值是4+．【分析】线段CE为定值，点F到CE距离最大时，△CEF的面积最大，画出图形，即可求出答案．【解答】解：∵线段CE为定值，∴点F到CE的距离最大时，△CEF的面积有最大值．在Rt△ACB中，∠BAC＝30°，E是AB的中点，∴AB＝2BC＝4，CE＝AE＝AB＝2，AC＝AB•cos30°＝2，∴∠ECA＝∠BAC＝30°，过点A作AG⊥CE交CE的延长线于点G，∴AG＝AC＝，∵点F在以A为圆心，AB长为半径的圆上，∴AF＝AB＝4，∴点F到CE的距离最大值为4+，∴，故答案为：．3．（2023•大庆模拟）如图，AB是⊙O的直径，AB＝4，C为的三等分点（更靠近A点），点P是⊙O上个动点，取弦AP的中点D，则线段CD的最大值为（）A．2B．C．D．【分析】如图，连接OD，OC，首先证明点D的运动轨迹为以AO为直径的⊙K，连接CK，当点D在CK的延长线上时，CD的值最大，利用勾股定理求出CK即可解决问题．【解答】解：如图，连接OD，OC，∵AD＝DP，∴OD⊥P A，∴∠ADO＝90°，∴点D的运动轨迹为以AO为直径的⊙K，连接CK，AC，当点D在CK的延长线上时，CD的值最大，∵C为的三等分点，∴∠AOC＝60°，∴△AOC是等边三角形，∴CK⊥OA，在Rt△OCK中，∵∠COA＝60°，OC＝2，OK＝1，∴CK＝＝，∵DK＝OA＝1，∴CD＝+1，∴CD的最大值为+1，故选：D．考向三：四点共圆类最值满分技巧对角互补的四边形必有四点共圆，即辅助圆产生模型原理：圆内接四边形对角互补∴FD＝，在四边形ACBF中，∠ACB＝∠AFB＝90°，∴A、C、B、F四点共圆，∴∠ACF＝∠ABF＝45°，∠CAB＝∠CFB，∵∠PCD＝45°∴∠ACP＝∠FCD，又∵△ABE∽△FBD，∴∠BAE＝∠BFD，∴∠CAP＝∠CFD，∴△CAP∽△CFD，∴，在四边形ACBF中，由对角互补模型得AC+CB＝，∴CF＝∴，∴AP＝1，∴PE＝2，故答案为：2考向四：瓜豆原理类最值满分技巧瓜豆原理的特征和结论：∴AB＝CD＝6，∠B＝∠BCD＝90°，∵∠BET＝∠FEG＝45°，∴∠BEF＝∠TEG，∵EB＝ET，EF＝EG，∴△EBF≌△ETG（SAS），∴∠B＝∠ETG＝90°，∴点G在射线TG上运动，∴当CG⊥TG时，CG的值最小，∵BC＝，BE＝，CD＝6，∴CE＝CD＝6，∴∠CED＝∠BET＝45°，∴∠TEJ＝90°＝∠ETG＝∠JGT＝90°，∴四边形ETGJ是矩形，∴DE∥GT，GJ＝TE＝BE＝，∴CJ⊥DE，∴JE＝JD，∴CJ＝DE＝3，∴CG＝CJ+GJ＝+3，∴CG的最小值为+3，故答案为：+3．2．（2023•宿城区二模）如图，矩形ABCD中，AD＝6，DC＝8，点E为对角线AC上一动点，BE⊥BF，，BG⊥EF于点G，连接CG，当CG最小时，CE的长为．【分析】过点B作BP⊥AC于点P，连接PG，则可得△ABE∽△PBG，进而可知∠BPG为定值，因此CG⊥PG时，CG最小，通过设元利用三角函数和相似比可表示出PG、CP，即可求出结果．【解答】解：如图，过点B作BP⊥AC于点P，连接PG，∵，∠ABC＝∠EBF，∴△ABC∽△EBF，∴∠CAB＝∠FEB，∵∠APB＝∠EGB＝90°，∴△ABP∽△EBG，∴＝，∠ABP＝∠EBG，∴∠ABE＝∠PBG，∴△ABE∽△PBG，∴∠BPG＝∠BAE，即在点E的运动过程中，∠BPG的大小不变且等于∠BAC，∴当CG⊥PG时，CG最小，设此时AE＝x，∵，∴PG＝，∵CG⊥PG，∴∠PCG＝∠BPG＝∠BAC，∴，代入PG＝，解得CP＝x，∵CP＝BC•sin∠CBP＝BC•sin∠BAC＝，∴x＝，∴AE＝∴CE＝，故答案为：．考向五：胡不归类最值满分技巧胡不归模型解决步骤：模型具体化：如图，已知两定点A、B，在定直线BC上找一点P，使从B走道P，再从P走到A的总时间最小解决步骤：由系数k·PB确定分割线为PBPA在分割线一侧，在分割线PB另一侧依定点B构α角，使sinα=k，α角另一边为BD过点P作PQ⊥BD，转化kPB=PQ过定点A作AH⊥BD，转化（PA+k·PB）min=AH，再依“勾股法”求AH的长即可。

初三数学几何综合大题

初三数学几何综合大题1.如图1，在△ACB中，∠ACB=90°，CA=CB，点D，E分别在边CA，CB上，CD=CE，连接DE，AE，BD，过点C作CF⊥AE, 垂足为H，直线CF交直线BD于F.（1）求证：DF=BF；（2）将图1中的△CDE绕点C逆时针旋转，其他条件不变，如图2，（1）的结论是否成立？如果成立，请证明；如果不成立，请说明理由；（3）若CD=2，CB=4，将△CDE绕点C逆时针旋转一周，当A，E，D三点共线时，直接写出CF的长。

2.如图1，在△ABE和△ACD中，AE=AB，AD=AC,且∠BAE=∠CAD，则可证明得到△AEC≌△ABD.【初步探究】（1）如图2，△ABC为等边三角形，过A点作AC的垂线l，点P为l上一动点（不与点A重合），连接CP，把线段CP绕点C逆时针方向旋转60°得到CQ，连接QB.请写出AP与BQ的数量关系并说明理由；【深入探究】（2）如图3，在（1）的条件下，连接PB并延长PB交直线CQ于点D.当点P运动到PD⊥CQ时，若AC=√(2)，求PB的长；【拓展探究】（3）如图4，在△ABC中，∠ACB=45°，以AB为直角边，A为直角顶点向外作等腰直角△ABD，连接CD，若AC=1，BC=3，则CD长为____.3.已知△ABC和△ADE都是等腰三角形，AB=AC，AD=AE，∠DAE=∠BAC.【初步感知】（1）特殊情形：如图1，若点D，E分别在边AB，AC上，则DB____EC.(填>、<、=)（2）发现证明：如图2，将图1中△ADE绕点A旋转，当点D在△ABC外部，点E在△ABC 内部时，求证：DB=EC.【深入研究】（3）如图3，△ABC和△ADE都是等边三角形，点C,E,D在同一条直线上，则∠CDB的度数为_____; 线段CE,BD之间的数量关系为_____。

（4）如图4，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°,点C、D、E在同一条直线上，AM为△ADE中DE边上的高，则∠CDB的度数为______; 线段AM,BD,CD之间的数量关系为______.。

中考数学几何题总汇经典

三角形知识考点：理解三角形三边的关系及三角形的主要线段（中线、高线、角平分线）和三角形的内角和定理。

关键是正确理解有关概念，学会概念和定理的运用。

应用方程知识求解几何题是这部分知识常用的方法。

精典例题：【例1】已知一个三角形中两条边的长分别是a 、b ，且b a >，那么这个三角形的周长L 的取值范围是（） A 、b L a 33>> B 、a L b a 2)(2>>+C 、a b L b a +>>+262D 、b a L b a 23+>>-分析：涉及构成三角形三边关系问题时，一定要同时考虑第三边大于两边之差且小于两边之和。

答案：B变式与思考：在△ABC 中，AC ＝5，中线AD ＝7，则AB 边的取值范围是（）A 、1＜AB ＜29 B 、4＜AB ＜24C 、5＜AB ＜19D 、9＜AB ＜19评注：在解三角形的有关中线问题时，如果不能直接求解，则常将中线延长一倍，借助全等三角形知识求解，这也是一种常见的作辅助线的方法。

【例2】如图，已知△ABC 中，∠ABC ＝450，∠ACB ＝610，延长BC 至E ，使CE ＝AC ，延长CB 至D ，使DB ＝AB ，求∠DAE 的度数。

分析：用三角形内角和定理和外角定理，等腰三角形性质，求出∠D ＋∠E 的度数，即可求得∠DAE 的度数。

略解：∵AB ＝DB ，AC ＝CE∴∠D ＝21∠ABC ，∠E ＝21∠ACB ∴∠D ＋∠E ＝21（∠ABC ＋∠ACB ）＝530∴∠DAE ＝1800－（∠D ＋∠E ）＝1270探索与创新：【问题一】如图，已知点A 在直线l 外，点B 、C 在直线l 上。

（1）点P 是△ABC 内任一点，求证：∠P ＞∠A ；（2）试判断在△ABC 外，又和点A 在直线l 的同侧，是否存在一点Q ，使∠BQC ＞∠A ，并证明你的结论。

nm•ll问题一图CBACA分析与结论：（1）连结AP ，易证明∠P ＞∠A ；（2）存在，怎样的角与∠A 相等呢？利用同弧上的圆周角相等，可考虑构造△ABC 的外接⊙O ，易知弦BC 所对且顶点在弧A m B ，和弧A n C 上的圆周角都与∠A 相等，因此点Q 应在弓形A m B 和A n C 内，利用圆的有关性质易证明（证明略）。

初中数学经典题型【中考数学几何集锦】(含详细答案)

初中数学几何中考经典试题集【编著】黄勇权【第一组题型】1、在平行四边形ABCD中，∠A=30°，AD =8 3，BD =8，则平行四边形ABCD的面积等于。

2、如图，在矩形ABCD中，E是边AB的中点，连接DE交对角线AC于点F，且AF⊥DE,若AB=8，AD=6，则CF的长为。

3、如图，在矩形ABCD中，AB=5，AD=12，以BC为斜边在矩形外部作直角三角形BEC，F为CD的中点，则EF的最大值为（）4、如图，∠PAC=30°，在射线AC上顺次截取AD=3cm，DB=10cm，以DB为直径作⊙O交射线AP于E、F两点，求圆心O到AP的距离及EF的长．【答案】1、在平行四边形ABCD中，∠A=30°，AD=8 3，BD=8，则平行四边形ABCD的面积等于。

解：（1）过D作DE⊥AB，在直角△ADE中，因为∠A=30°，AD=8 3，故：DE= 4 3----------------------①AE=12------------------②（2）在直角△BDE中，因为BD=8, DE= 4 3由勾股定理，解得BE= 4---------③（3）由②、③知：AB=AE + BE =12+4=16（4）平行四边形ABCD的面积= 2 S△ADB=2* 12*AB*DE=16*4 3 =64 3 答：平行四边形ABCD的面积等于64 32、如图，在矩形ABCD 中，E 是边AB 的中点，连接DE 交对角线AC 于点F ，且AF ⊥DE,若AB=8，AD=6，则CF 的长为。

解：（1）因为ABCD 是矩形，由勾股定理，解得对角线AC= AD ²+DC ² = 6²+8²= 10----① （2）E 是边AB 的中点，且AB=8，所以：AE=4-------------② （3）在直角△ADE 中，由勾股定理，解得 DE= AD ²+AE ² = 6²+4²= 2 13------------③（4）在直角△ADE 中,△ADE 的面积= 12AD*AE又因为AF ⊥DE ，△ADE 的面积= 12DE*AF故：AD*AE=DE*AF 分别将 AD 、AE 、DE 的值代入，即：6 * 4= 2 13 *AF解得：AF= 121313（5）CF=AC-AF= 10- 121313答：CF的长为10- 1213133、如图，在矩形ABCD中，AB=5，AD=12，以BC为斜边在矩形外部作直角三角形BEC，F为CD的中点，则EF的最大值为（）4、如图，∠PAC=30°，在射线AC 上顺次截取AD=3cm ，DB=10cm ，以DB 为直径作⊙O 交射线AP 于E 、F 两点，求圆心O 到AP 的距离及EF 的长．解：（1）过O 作AP 的垂线，连接OE 、OF 。

中考数学专题复习：几何综合题

【考点总结】四、全等三角形的性质与判定
1．概念：能够完全重合的两个三角形叫做全等三角形． 2．性质：全等三角形的对应边、对应角分别相等． 3．判定：(1)有三边对应相等的两个三角形全等，简记为(SSS)； (2)有两边和它们的夹角对应相等的两个三角形全等，简记为(SAS)； (3)有两角和它们的夹边对应相等的两个三角形全等，简记为(ASA)； (4)有两角和其中一角的对边对应相等的两个三角形全等，简记为(AAS)； (5)有斜边和一条直角边对应相等的两个直角三角形全等，简记为(HL)．
三角形专题
1，掌握三角形相关基础知识（2课时）
目标
2，掌握三角形有关模型的全等或相似证明（3课时） 3，完成三角形有关模型的全等或相似证明（3课时）
三角形
模型
手拉手模型
三垂直模型
相似模型
三角形有关的知识
【考点总结】一、三角形中的重要线段 1．三角形的高线：从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫做三角形的高线，简称高．特性：三角形的三条高线相交于一点． 2．三角形的中线：在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线．特性：三角形的三条中线交于一点． 3．三角形的中位线：连接三角形两边中点的线段叫做三角形的中位线．定理：三角形的中位线平行于第三边，且等于它的一半 4．三角形的角平分线：三角形一个角的平分线和这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线．特性：三角形的三条角平分线交于一点，这点叫做三角形的内心．性质：角平分线上的点到角的两边的距离相等．
小组合作
1.在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．
（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段

中考数学：初中数学几何模型大全+经典题型含答案

初中数学几何模型大全+经典题型（含答案）全等变换平移：平行等线段（平行四边形）对称：角平分线或垂直或半角旋转：相邻等线段绕公共顶点旋转说明：以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

对称半角模型说明：上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

旋转全等模型半角：有一个角含1/2角及相邻线段自旋转：有一对相邻等线段，需要构造旋转全等共旋转：有两对相邻等线段，直接寻找旋转全等中点旋转：倍长中点相关线段转换成旋转全等问题说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

自旋转模型构造方法：遇60度旋60度，造等边三角形遇90度旋90度，造等腰直角遇等腰旋顶点，造旋转全等遇中点旋180度，造中心对称共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个经常考察的内容。

通过“8”字模型可以证明。

模型变形说明：模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

说明：两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点，证明另外两个顶点与中点所成图形为等腰直角三角形。

证明方法是倍长所要证等腰直角三角形的一直角边，转化成要证明的等腰直角三角形和已知的等腰直角三角形（或者正方形）公旋转顶点，通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。

几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明：通过对称进行等量代换，转换成两点间距离及点到直线距离。

几何图形中求线段,线段和,面积等最值问题(4题型)—2024年中考数学压轴题(全国通用)(解析版)

几何图形中求线段，线段和，面积等最值问题（压轴通关）目录【中考预测】预测考向，总结常考点及应对的策略【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题，讲解通关策略（含新考法、新情境等）几何图形中求线段、线段和、面积最值题是全国中考的热点内容，更是全国中考的必考内容。

每年都有一些考生因为知识残缺、基础不牢、技能不熟、答欠规范等原因导致失分。

1．从考点频率看，几何图形中的性质综合问题，是高频考点、也是必考点。

2．从题型角度看，以解答题的最后一题或最后二题为主，分值12分左右，着实不少！题型一线段最值问题【例1】（2024·四川成都·一模）如图1，在四边形ABFE 中，90F ∠=︒，点C 为线段EF 上一点，使得AC BC ⊥，24AC BC ==，此时BF CF =，连接BE ，BE AE ⊥，且AE BE =．(1)求CE 的长度；(2)如图2，点D 为线段AC 上一动点（点D 不与A ，C 重合），连接BD ，以BD 为斜边向右侧作等腰直角三角形BGD ．①当DG AB ∥时，试求AD 的长度；②如图3，点H 为AB 的中点，连接H G ，试问H G 是否存在最小值，如果存在，请求出最小值；如果不存在，请说明理由．【答案】(2)①103；②2【分析】（1）取AB 的中点H ，连接,EH HC ，证明FEB CAB ∠=∠，得出1tan tan 2FB FEB CAB EF ∠==∠=则12BF EF =，进而根据CE EF CF =−（2）①如图所示，过点D 作DM EF ⊥于点M ，过点D 作DN AB ⊥于点N ，证明DBC GBF ∽得出DC ，即可得出DM GF =，证明DMG GFB ≌，进而证明G 在EF 上，根据已知条件证明D 在EB上，然后解直角三角形，即可求解；②如图所示，过点H 作HP EF ⊥于点P ，连接EH ，由①可得G 在EF 上运动，当HG EF ⊥时，H G 取得最小值，即,G P 重合时，HP 的长即为HG 的最小值，由①可得103AT =，求得sin ETA ∠=45HEF ETA α∠=+︒=∠，即可求解．【详解】（1）解：如图所示，取AB 的中点H ，连接,EH HC ，∵BF CF =，90F ∠=︒，∴45BCF ∠=︒，BC ，又∵AC BC ⊥ ∴45ECA ∠=︒ ∵AE BE =，BE AE ⊥ ∴45EBA ∠=︒ ∴45ECA ABE ∠=∠=︒ ∴FEB CAB ∠=∠ ∵24AC BC ==， ∴2BC =∴BF CF = ∴1tan 2CB CAB AC ∠== ∴1tan tan 2FB FEB CAB EF ∠==∠= ∴12BF EF =∴EF =∴CE EF CF =−（2）①如图所示，过点D 作DM EF ⊥于点M ，过点D 作DN AB ⊥于点N ，由（1）可得45ACE ABE ∠=∠=︒ ∴CDM V 是等腰直角三角形，∴CD ，∵,CBF DBG 都是等腰直角三角形，∴CB DBBF BG==∴BD BGBC BF= 又∵DBG CBF ∠=∠ ∴DBC GBF ∠=∠ ∴DBC GBF ∽∴DC DBGF GB==∴DC ∴DM GF = 在,DMG GFB 中，DM GF DMG F DG BG =⎧⎪∠=∠⎨⎪=⎩∴DMG GFB ≌ ∴MGD FBG ∠=∠ ∵90FBG FGB ∠+∠=︒∴90MGD FGB ∠+∠=︒ 又∵90DGB ∠=︒ ∴180MGF ∠=︒ ∴G 在EF 上，∵DG AB ∥，90DGB ∠=︒ ∴90GBA ∠=︒∵45,45ABE DBG ABD ∠=︒∠=︒=∠ ∴D 在EB 上， ∵1tan 2CAB ∠=，∴12DN AN =，则AD ∵,45DN AB ABE ⊥∠=︒ ∴DN DB = ∴3AB DN =， ∵4AC =，2CB =∴AB ==∴13DN AB ==∴103AD ==， ②如图所示，过点H 作HP EF ⊥于点P ，连接EH ，由①可得G 在EF 上运动，∴当HG EF ⊥时，HG 取得最小值，即,G P 重合时，HP 的长即为H G 的最小值，设,AC EB 交于点T ，即与①中点D 重合，由①可得103AT =∵AB =∴AE 12EH AB ==∴sin 3AE ETA AT ∠=== 设FEB CAB α∠=∠= 则45HEF ETA α∠=+︒=∠，在Rt PEH △中，sin sin 102PH HEF EH ETA EH =∠⨯=∠⨯= 【点睛】证明G 点在EF 上是解题的关键．【例2】（2024·天津红桥·一模）在平面直角坐标系中，点()0,0O ，()2,0A ， (2,B )，C ，D 分别为OA ，OB 的中点．以点O 为中心，逆时针旋转OCD ，得OC D ''，点C ，D 的对应点分别为点C '，D ¢．(1)填空∶如图①，当点D ¢落在y 轴上时，点D ¢的坐标为_____，点C '的坐标为______； (2)如图②，当点C '落在OB 上时，求点D ¢的坐标和 BD '的长； (3)若M 为C D ''的中点，求BM 的最大值和最小值(直接写出结果即可)．逆时针旋转OCD ，得OC D ''，知为中心，逆时针旋转OCD，得OC D''，可得(2,23B为中心，逆时针旋转OCD，得OC D''，()A，2,0()A2,0,(2,23 B是AOB的中位线，为中心，逆时针旋转OCD，得OC D''，'==，D CD3M是C'(2,23B1．（2024·山东济宁·模拟预测）已知，四边形ABCD 是正方形，DEF 绕点D 旋转（DE AB <），90EDF ∠=︒，DE DF =，连接AE CF ，．(1)如图1，求证：ADE CDF ≅； (2)直线AE 与CF 相交于点G ．①如图2，BM AG ⊥于点M ，⊥BN CF 于点N ，求证：四边形BMGN 是正方形；②如图3，连接BG ，若6AB =，3DE =，直接写出在DEF 旋转的过程中，线段BG 长度的最小值为．再证明AMB CNB ≅可得MB ，证明BGM 是等腰直角三角形，然后求出【详解】（1）证明：四边形ABCD 是正方形，AD DC ∴=，90ADC ∠=︒，DE DF =，90EDF ∠=︒，ADC EDF ∴∠=∠，ADE CDF \Ð=Ð，在ADE V 和CDF 中，DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩， SAS ADE CDF ∴（）≌．（2）解：①证明：如图2中，设AG 与CD 相交于点P ，90ADP ∠=︒， 90DAP DPA ∴∠+∠=︒，ADE CDF ≅，DAE DCF ∴∠=∠，DPA GPC ∠∠=，90DAE DPA GPC GCP ∠∠∠∠∴+=+=︒， 90PGN ∠∴=︒，BM AG ⊥，BN GN ⊥，∴四边形BMGN 是矩形，90MBN ∴∠=︒，四边形ABCD 是正方形，AB BC ∴=，90ABC MBN∠∠==︒，ABM CBN ∴∠=∠，又90AMB BNC ∠∠==︒，AMB CNB ∴≅，MB NB ∴=，∴矩形BMGN 是正方形；∵DAH BAM ABM ∠+∠=∠∴DAH ABM ∠=∠，又∵AD BA =，DHA ∠∴AMB DHA ≌△△， BM AH ∴=，2AH AD =DH ∴最大时，可知，BGM 是等腰直角三角形，23⨯=(1)若AC AB AD BC >⊥，，当点E 在线段AC 上时，AD BE ，交于点F ，点F 为BE 中点．①如图1，若37BF BD AD ===，，求AE 的长度；②如图2，点G 为线段AF 上一点，连接GE 并延长交BC 的延长线于点H ．若点E 为GH 中点，602BAC DAC EBC ∠=︒∠=∠，，求证：12AG DF AB +=． (2)如图3，若360AC AB BAC ︒==∠=，．当点E 在线段AC 的延长线上时，连接DE ，将DCE △沿DC 所在直线翻折至ABC 所在平面内得到DCM △，连接AM ，当AM 取得最小值时，ABC 内存在点K ，使得ABK CAK ∠=∠，当KE 取得最小值时，请直接写出2AK 的值．的长，证明(AAS)FDB FGE ≌AD BC EG AD ⊥⊥，， 90BDF ∴∠=︒，EGF ∠=BDF EGF ∴∠=∠，在Rt BDF △中，90BDF ∠=点(AAS)FDB FGE ∴≌3BD GE ∴==DFAD=，7∴=AG ADRt AGE中，2⊥，AD BC90∴∠=︒，ADC点E为GH的中点，∴=，GE HE在AGE和KHE△中，=AE KE∴≌(SAS) AGE KHE∴∠=∠34∠=DAC∴设EBC∠点和KEF中，(SAS)AFB KEF ∴≌89AB FK ∴=∠=∠，BAC ∠=Rt FDM 中，1由题意可知：160∠=︒，AC 30CAM ∴∠=︒，1322CM AC ∴==， ABK ∠=ABK ∴∠+∠EKQ EOA ∴∽，KE KQ QE（1）如图①，在ABC 中，点M ，N 分别是AB ，AC 的中点，若BC =MN 的长为__________．问题探究：（2）如图②，在正方形ABCD 中，6AD =，点E 为AD 上的靠近点A 的三等分点，点F 为AB 上的动点，将AEF △折叠，点A 的对应点为点G ，求CG 的最小值．问题解决：（3）如图③，某地要规划一个五边形艺术中心ABCDE ，已知120ABC ∠=︒，60BCD ∠=︒，40m AB AE ==，80m BC CD ==，点C 处为参观入口，DE 的中点P 处规划为“优秀”作品展台，求点C 与点P 之间的最小距离．是ABC 的中位线，由中位线的性质，即可求解，Rt EDC 中，根据勾股定理，求出∵点E为AD上的靠近点∴11633AE AD==⨯=在Rt EDC中，EC 根据折叠的性质，【问题提出】（1）如图1，点D 为ABC 的边BC 上一点，连接2,,3BD AD BDA BAC AB ∠=∠=，若ABD △的面积为4，则ACD 的面积为______；【问题探究】（2）如图2，在矩形ABCD 中，6,5AB BC ==，在射线BC 和射线CD 上分别取点E F 、，使得65BE CF =，连接AE BF 、相交于点P ，连接CP ，求CP 的最小值；【问题解决】（3）如图3，菱形ABCD 是某社区的一块空地，经测量，120AB =米，60ABC ∠=︒．社区管委会计划对该空地进行重新规划利用，在射线AD 上取一点E ，沿BE CE 、修两条小路，并在小路BE 上取点H ，将CH 段铺设成某种具有较高观赏价值的休闲通道（通道宽度忽略不计），根据设计要求，BHC BCE ∠=∠，为了节省铺设成本，要求休闲通道CH 的长度尽可能小，问CH 的长度是否存在最小值？若存在，求出CH 长度的最小值；若不存在，请说明理由．994CBAABDSS ==，即可得到ACD 的面积；为直径的O 上交O 于点P ）证明,CBH EBC ∽得到，再证明,ABH EBA ∽得到在O 的劣弧与O 相交于点ABDCBAS S=994CBAABDSS ==，∴ACD 的面积为9CBAABDS S−=故答案为：为直径的O 上运动，交O 于点P，作ABH 的外接圆O ，连接∴,CBH EBC ∽ BC BH∴,ABH EBA ∽ 120AHB EAB ∠=∠=在O 的劣弧120=︒在AOB 中，则1602BM AM AB ===米，与O 相交于点题型二线段和的最小值问题【例1】（2024·四川达州·模拟预测）【问题发现】（1）如图1，在OAB 中，3OB =，若将OAB 绕点O 逆时针旋转120︒得OA B ''，连接BB '，则BB '=________．【问题探究】（2）如图2，已知ABC 是边长为BC 为边向外作等边BCD △，P 为ABC 内一点，连接AP BP CP ，，，将BPC △绕点C 逆时针旋转60︒，得DQC △，求PA PB PC ++的最小值；【实际应用】（3）如图3，在长方形ABCD 中，边1020AB AD ==，，P 是BC 边上一动点，Q 为ADP △内的任意一点，是否存在一点P 和一点Q ，使得AQ DQ PQ ++有最小值？若存在，请求出此时PQ 的长，若不存在，请说明理由．将AQD 绕点BC ⊥在OAB 中，3OB =，将OAB 绕点120BOB '∴∠=︒，3OB OB '==，OBB OB B ''∴∠=∠，OBB '∠+OC BB ⊥OCB '∴∠将∴++=+PA PB PC PA∴当点D、Q、P、A⊥连接AD，作DE AC∠=，ABC边长为DCBDCE BCA∴∠=∠=60）如图所示，将AQD绕点，90EA︒=【例2】（2024·贵州毕节·一模）在学习了《图形的平移与旋转》后，数学兴趣小组用一个等边三角形继续进行探究．已知ABC 是边长为2的等边三角形．(1)【动手操作】如图1，若D 为线段BC 上靠近点B 的三等分点，将线段AD 绕点A 逆时针旋转60︒得到线段AE ，连接CE ，则CE 的长为________；(2)【探究应用】如图2,D 为ABC 内一点，将线段AD 绕点A 逆时针旋转60︒得到线段AE ，连接CE ，若,,B D E本题主要考查了等边三角形的性质与判定，矩形的性质与判定，旋转的性质，勾股定理，含度角的直角三角形的性质，解题的关键在于利用旋转构造等边三角形，从而把三条不在一条直线的线段之和的问题，转换成几点共线求线段的最值问题是解题的关键．三点共线，求证：EB 平分AEC ∠；(3)【拓展提升】如图3，若D 是线段BC 上的动点，将线段AD 绕点D 顺时针旋转60︒得到线段DE ，连接CE ．请求出点D 在运动过程中，DEC 的周长的最小值．证明BAD CAE ≌，的三等分点和ABC 是边长为ADB AEC =∠60BEC ∠=︒EB（3）由ABD ACE ≌△△，得CE BD =，可得DEC 的周长BC DE =+，而DE AD =，知AD 的最小时，DEC的周长最小，此时AD BC ⊥，即可求得答案．∵ABC 是等边三角形，AB AC =，∴SAS ABD ACE ≌（）BD CE =；的三等分点，且ABC 是边长为∵ABC 是等边三角形，AB AC =，∴SAS ABD ACE≌（），120ADB AEC ∠=∠=上时，DEC 的周长存在最小值，如图：∵ABD ACE ≌△△， ∴CE BD =，∴DEC 的周长DE CE =++∴当点D 在线段BC 上时，DEC 的周长∵DEC 为等边三角形，DE AD =，的最小时，DEC 的周长最小，此时∴DEC 的周长的最小值为【点睛】本题考查几何变换综合应用，旋转性质、涉及等边三角形的性质，全等三角形的判定和性质，垂1．（2024·陕西·二模）在平面直角坐标系中，A 为y 轴正半轴上一点，B 为x 轴正半轴上一点，且4OA OB ==，连接AB ．(1)如图1，C 为线段AB 上一点，连接OC ，将OC 绕点O 逆时针旋转90︒得到OD ，连接AD ，求AC AD +的值．(2)如图2，当点C 在x 轴上，点D 位于第二象限时，90ADC ∠=︒，且AD CD =，E 为AB 的中点，连接DE ，试探究线段AD DE +是否存在最小值？若存在，求出AD DE +的最小值；若不存在，请说明理由．≌，可得出点，证明AND CMDAOC的平分线对称，由∴AND CMD≌，DN DM=，P大值和最小值分别是______和______；（2）如图2，在矩形ABCD中，4AB=，6AD=，点P在AD上，点Q在BC上，且AP CQ=，连接CP、QD，求PC QD+最小时AP的长；（3）如图3，在ABCDY中，10AB=，20AD=，点D到AB的距离为动点E、F在AD边上运动，始终保持3EF=，在BC边上有一个直径为BM的半圆O，连接AM与半圆O交于点N，连接CE、FN，求CE EF FN++的最小值．()SASABP CDQ≌=的O 外有一点在O 上，如图，当点P 在AO 的延长线上时，此时PA 的最大值为：PO OA +故答案为：11；3；（2）延长BA 至点B '，使AB ∵在矩形ABCD 中，4AB =，∴DAB BAP CBA DCQ '∠=∠=∠=∠在ABP 和CDQ 中，AB CD =∴()SAS ABP CDQ ≌Rt B BC '中，AB P BB ''=∠ （3）如图，过点F 作FG EC ∥，交BC OG '，NO ，∵在ABCD Y 中，10AB =，20AD =，点∴AD BC ∥，即EF CG ∥，BC AD =EFGC【点睛】本题考查圆的基本性质，全等三角形的判定和性质，相似三角形的判定和性质，矩形的性质，平行四边形的判定和性质，对称的性质，勾股定理，三角形三边关系定理，两点之间线段最短等知识点．灵活运用所学知识、弄清题意并作出适当辅助线是解题的关键．3．（2024·陕西西安·三模）【问题提出】（1）如图①，AB 为半圆O 的直径，点P 为半圆O 的AB 上一点，BC 切半圆O 于点B ，若10AB =，12BC =，则CP 的最小值为；【问题探究】（2）如图②，在矩形ABCD 中，3AB =，5BC =，点P 为矩形ABCD 内一点，连接PB 、PC ，若矩形ABCD 的面积是PBC 面积的3倍，求PB PC +的最小值；【问题解决】（3）如图③，平面图形ABCDEF 为某校园内的一片空地，经测量，AB BC ==米，=60B ∠︒，150BAF BCD ∠=∠=︒，DE DC ⊥，20CD =米，劣弧E F 所对的圆心角为90︒，E F 所在圆的圆心在AF 的延长线上，10AF =米．某天活动课上，九（1）班的同学准备在这块空地上玩游戏，每位同学在游戏开始前，在BC 上选取一点P ，在弧E F 上选取一点Q ，并在点P 和点Q 处各插上一面小旗，从点A 出发，先到点P 处拔下小旗，再到点Q 处拔下小旗，用时最短者获胜．已知晓雯和晓静的跑步速度相同，要使用时最短，则所跑的总路程()AP PQ +应最短，问AP PQ +是否存在最小值？若存在，请你求出AP PQ +的最小值；若不存在，请说明理由．交O于点P⊥PH BC交O于点P点P为半圆O的AB上一点，∴当点P与点P不重合时，1当点P与点P重合时，BC切半圆∴∠=ABC=OB OP矩形ABCD 的面积是PBC 面积的13553PBCS∴=⨯⨯=CF PH =又5BC =，60ABC ∠=︒，AB BC ==ABC ∴是等边三角形， 60BAC BCA ∴∠=∠=︒，150BAF BCD ∠=∠=︒，DE AA M '∴和CMN ∴∠=点'A Q OQ+∴的最小值为A Q'ABC为等边三角形，点∴点为BC△,E G分别作,,⊥⊥与EF交于点F，连接CF．EF AD FG AB FG特例感知（1）以下结论中正确的序号有______；ED CF BG为边围成的三角形不是直①四边形AGFE是矩形；②矩形ABCD与四边形AGFE位似；③以,,角三角形；类比发现（2）如图2，将图1中的四边形AGFE绕着点A旋转，连接BG，观察CF与BG之间的数量关系和位置关系，并证明你的发现；拓展应用（3）连接CE ，当CE 的长度最大时， ①求BG 的长度；②连接,,AC AF CF ，若在ACF △内存在一点P ，使CP AP ++的值最小，求CP AP ++的最小值．先证明APF AKL ∽，得到∴HF DE =，CH BG =，∴CHF 是直角三角形，∵四边形ABCD 是矩形，∴43AB CD ==，AD =∴228AC AB BC =+=，则由（2）知，90CEF ∠=︒，∵2247CF CE EF =+=，根据旋转，可得30PAF KAL ∠=∠=，根据两边对应成比例且夹角相等可得APF AKL ∽， ∴3KL PF =，过P 作PS AK ⊥于S ，则12PS AP =题型三面积的最小值问题【例1】（新考法，拓视野）（2024·陕西西安·一模）【问题提出】（1）如图1，已知在边长为5的等边ABC 中，点D 在边BC 上，3BD =，连接AD ，则ACD 的面积为；【问题探究】（2）如图2，已知在边长为6的正方形ABCD 中，点E 在边BC 上，点F 在边CD 上，且45EAF ∠=︒，若5EF =，求AEF △的面积；【问题解决】（3）如图3是某座城市廷康大道的一部分，因自来水抢修在4AB =米，AD =ABCD 区域内开挖一个AEF △的工作面，其中B 、F 分别在BC CD 、边上（不与B 、C 、D 重合），且60EAF ∠=︒，为了减少对该路段的拥堵影响，要求AEF △面积最小，那么是否存在一个面积最小的AEF △？若存在，请求出AEF △面积的最小值；若不存在，请说明理由．，证明()SAS ABG ADF ≌，再证明()SAS AEF AEG ≌，得到ABG ，则)()33AEF AEG SS==最小值最小值∵ABC 是边长为 ∴()SAS ABG ADF ≌∴()SAS AEF AEG ≌，得到ABG ， )()33AEF AEG SS==最小值最小值【例2】（2024·陕西西安·二模）图形旋转是解决几何问题的一种重要方法．如图1，正方形ABCD 中，E F 、分别在边AB BC 、上，且45EDF ∠=︒，连接EF ，试探究AE CF EF 、、之间的数量关系．解决这个问题可将ADE V 绕点D 逆时针旋转90︒到CDH △的位置（易得出点H 在BC 的延长线上），进一步证明DEF 与DHF △全等，即可解决问题．(1)如图1，正方形ABCD 中，45,3,2EDF AE CF ∠=︒==，则EF =______；(2)如图2，正方形ABCD 中，若30EDF ∠=︒，过点E 作EM BC ∥交DF 于M 点，请计算AE CF +与EM 的比值，写出解答过程；(3)如图3，若60EDF ∠=︒，正方形ABCD 的边长8AB =，试探究DEF 面积的最小值．进一步证明DEF,,,D F H G 四点共圆；进而可得30FHG ∠=，根据1tan 30AE CF CH CF FH EM GH GH ++====︒（3）过点E 作EK CD ⊥于K ，交DF 于M ，作FT EK ⊥于T ，得出 4DEFS EM =，进而根据（2）的方法得出EM GH =，根据FC AE CH ==时，面积最小，得出32OF =− 【详解】（1）解：∵将ADE V 绕点D 逆时针旋转90︒， ∴90DCH A DCB ∠=∠=︒=∠，DH DE HDC EDA =∠=∠， ∴点H 在BC 的延长线上， ∵四边形ABCD 是正方形 ∴90ADC ∠=︒， ∵45EDF ∠=︒，∴45HDF CDH FDC ADE FDC EDF ∠=∠+∠=∠+∠=︒=∠ 又∵DF DF =，∴DEF ()SAS DHF ≌，∴235EF FH FC CH FC AE ==+=+=+=，故答案为：5．（2）解：将ADE V ，DEM △绕点D 逆时针旋转90︒，得,DCH DHG∴,AED CHD DEM DHG ∠=∠∠=∠， ∵EM BC ∥，则EM AB ⊥， ∴90AEM ∠=︒，∴90CHG CHD DHG AED DEM AEM ∠=∠+∠=∠+∠=∠=︒， ∵30EDF ∠=︒，EM BC ∥则EM AD ∥， ∴ADE CDH ∠=∠，30GDH MDE ∠=∠=︒， ∵EM BC ∥， ∴EMF DFC ∠=∠，∴180EMD EMF EMD DFC ∠+∠=∠+∠=︒，即180DFC DGH ∠+∠=︒， ∴,,,D F H G 四点共圆； ∴30GFH GDH ∠=∠=︒，又30FHG ∠=︒∴1tan 30AE CF CH CF FH EM GH GH ++====︒（3）如图，过点E 作EK CD ⊥于K ，交DF 于M ，作FT EK ⊥于T ，90FTK TKC BCD ∠=∠=∠=︒∴四边形CFTK 是矩形， FT CK ∴=8DK CK DK FT ∴+=+= 111()4222DEFEMDEMFSSSEM DK EM FT EM DK FH EM ∴=+=⋅+⋅=+=同（2）将ADE V ，DEM △绕点D 逆时针旋转90︒，得,DCH DHG ，可得60GFH EDM ∠=∠=︒，EM GH = 取得最小值时，DEF 的面积最小，∵2220−=≥，∴FH x y =+≥ 当且仅当x y =时取得等于号，此时FC AE CH ==，设,,,D F H G 的圆心为O ， ∵DC FH ⊥，FC CH =， ∴DC 经过点O ，∴OF OD =，sin 602OC OF =︒= ∵8OD OC +=8OF +=解得：32OF =−∴232FH FC OF ===−∴48GH =，∴()44448192DEFSEM GH ====，即DEF 面积的最小为192．【点睛】本题考查了旋转的性质，正方形的性质、全等三角形的判定与性质、四点共圆等知识，解直角三角形，熟练掌握旋转的性质是解题的关键．1．（2023·陕西西安·一模）问题发现（1）在ABC 中，2AB =，60C ∠=︒，则ABC 面积的最大值为；（2）如图1，在四边形ABCD 中，6AB AD ==，90BCD BAD ∠=∠=︒，8AC =，求BC CD +的值．问题解决（3）有一个直径为60cm 的圆形配件O ，如图2所示．现需在该配件上切割出一个四边形孔洞OABC ，要求60O B ∠=∠=︒，OA OC =OABC 的面积尽可能小．试问，是否存在符合要求的面积最小的四边形OABC ？若存在，请求出四边形OABC 面积的最小值及此时OA 的长；若不存在，请说明理由．为弦的确定的圆上，作ABC 的外接圆，可得当点时，ABC 的面积最大，求出，再根据三角形的面积公式计算即可；将ABC 绕点A 逆时针旋转、D 、E 在同一条直线上，求出BCES，可得要使四边形面积最小，就要使BCE 的面积最大，然后由（时，BCE 的面积最）的方法求出BCE 面积的最大值，可得四边形，根据OA 如图，作ABC 的外接圆，∴当点C 在C '的位置，即时，ABC 的面积最大，∴C A C B ''=，BD =∴ABC '△是等边三角形，∴ABC 面积的最大值为）如图，将ABC 绕点∴B ADE ∠=∠，BAC ∠∵6AB AD ==，BCD ∠∴180B ADC ∠+∠=︒，∵60AOC ∠=︒，OA OC =∴将AOB 绕O 点顺时针旋转至COE ，连接∴60BOE ∠=︒，OE OB =∴BOE △是等边三角形，AOBBCOSS+COEBCOSS+ BOE BCES S− BCESBCES，的面积最小，就要使BCE 的面积最大，作BCE 的外接圆I ，点F 是I 上一点，CF 交由（1）可知，当CF 是直径，且CF BE ⊥时，BCE 的面积最大，∴BCE 面积的最大值为150BCES=（1）如图①，已知ABC 是面积为AD 是BAC ∠的平分线，则AB 的长为______．问题探究：（2）如图②，在ABC 中，90C ∠=︒，AC BC =，4AB =，点D 为AB 的中点，点E ，F 分别在边AC ，BC 上，且90EDF ∠=︒．证明：DE DF =．问题解决：（3）如图③，李叔叔准备在一块空地上修建一个矩形花园ABCD ，然后将其分割种植三种不同的花卉．按照他的分割方案，点P ，Q 分别在AD ，BC 上，连接PQ 、PB 、PC ，60BPC ∠=︒，E 、F 分别在PB 、PC 上，连接QE 、QF ，QE QF =，120EQF ∠=︒，其中四边形PEQF 种植玫瑰，ABP 和PCD 种植郁金香，剩下的区域种植康乃馨，根据实际需要，要求种植玫瑰的四边形PEQF 的面积为2，为了节约成本，矩形花园ABCD 的面积是否存在最小值？若存在，请求出矩形ABCD 的最小面积，若不存在，请说明理由．）设ABC 的边长为EQG ，根据四边形则当PQ BC ⊥时，矩形ABCD 的面积最小，根据2ABCD PEQF S S =四边形四边形，即可求解．【详解】解：（1）∵ABC 是面积为AD 是BAC ∠的平分线， ∴12BD CD AB ==设ABC 的边长为a∴AD ==∴2112224ABCS BC AD a =´=´´=∴24a =解得：4a =，故答案为：4．（2）如图所示，连接CD ，∵在ABC 中，90C ∠=︒，AC BC =，4AB =，点D 为AB 的中点， ∴CD AD =，90ADC ∠=︒，45A DCF ∠=∠=︒ 又∵90EDF ∠=︒∴ADE ADC CDE EDF EDC CDF ∠=∠−∠=∠−∠=∠ 在,ADE CDF △△中，45A DCF ADE CDF AD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴ADE CDF V V ≌ ∴DE DF =；（3）如图所示，∵60BPC ∠=︒，120EQF ∠=︒， ∴36060120180PFQ PEQ ∠+∠=︒−︒−︒=︒ 将QFP △绕点Q 逆时针旋转120︒，得到EQG ， ∴,,P E G 三点共线，∴四边形PEQF 的面积等于PQG ，又∵120,PQG PQ GQ ∠=︒=，∴30QPG QGP ∠=∠=︒过点Q 作QN PG ⊥于点N ，则12QN PQ =设PQ b =，则1,22NQ b PN ==∴2PG PN ==∴2111222PQGSPG NQ b =⨯=⨯=∵四边形PEQF 的面积为 ∴16b =，即16PQ =,如图所示，作QM PM ⊥于点M ，∵30EPQ FPQ ∠=∠=︒，QM PM ⊥，QN PG ⊥，则QN QM =，在,ENQ FMQ 中，QN QM EQ FQ =⎧⎨=⎩∴()HL ENQ FMQ ≌，同理可得PNQ PMQ ≌ 则2PNQPEQF S S=四边形∴PEQF PNQM S S =四边形四边形，作点Q 关于PE 的对称点T ，连接PT ，则PTQ 是等边三角形，则PTQS=如图所示，依题意，当PQ BC ⊥时，矩形ABCD 的面积最小，此时,E F 与,N M 重合，，∴22ABCD PEQF S S ==⨯四边形四边形∴矩形ABCD 的最小面积为2【点睛】本题考查了全等三角形的性质与判定，等边三角形的性质与判定，等腰三角形的性质与判定，勾股定理，旋转的性质，综合运用以上知识是解题的关键．3．（2024·陕西榆林·二模）（1）如图1，AB CD ∥，1,2AB CD ==，AD ，BC 交于点E ，若4=AD ，则AE = ；（2）如图2，矩形ABCD 内接于O ， 2,AB BC ==点 P 在AD 上运动，求 PBC 的面积的最大值；（3）为了提高居民的生活品质，市政部门计划把一块边长为 120米的正方形荒地 ABCD (如图3)改造成一个户外休闲区，计划在边AD ，BC 上分别取点P ，Q ，修建一条笔直的通道PQ ，要求 2CQ AP =，过点 B 作 BE PQ ⊥于点E ，在点E 处修建一个应急处理中心，再修建三条笔直的道路BE CE DE ，，，并计划在 CDE 内种植花卉， DEP 内修建老年活动区， BCE 内修建休息区，在四边形ABEP 内修建儿童游乐园．问种植花卉的 CDE 的面积是否存在最小值？若存在，求出最小值；若不存在，请说明理由．得ABE DCE ∽，得对应成比例的线段，于是得到结论；时，PBC 的面积有最大值，解直角三角形求出PBC 的高即可得到结论；于点M ，作BME 的外接圆O ，过点OF DC ⊥₂E CD ₂的面积最小．（）∥AB CD DCE ，是O的直径．₂的面积最大．P BC上任意另取一点P₁PBC的面积最大．Rt OBE中，．S=PBC。

2020年中考数学复习：几何专项练习题(含答案)

2020年中考数学复习：几何专项练习题一、选择题1.如图，直角三角板ABC 的斜边AB=12cm ，∠A=30°，将三角板ABC 绕C 顺时针旋转90°至三角板A ′B ′C ′的位置后，再沿CB 方向向左平移，使点B ′落在原三角板ABC 的斜边AB 上，则三角板A ′B ′C ′平移的距离为（）A.6cmB.4cmC.cmD.cm2.如图，△ABC 和△DEF 是等腰直角三角形，∠C=∠F=90°，AB=2，DE=4．点B 与点D 重合，点A ，B （D ），E 在同一条直线上，将△ABC 沿DE 方向平移，至点A 与点E 重合时停止．设点B ，D 之间的距离为x ，△ABC 与△DEF 重叠部分的面积为y ，则准确反映y 与x 之间对应关系的图象是（）A B C D 二、填空题3.如图，将两块直角三角板的斜边重合，E 是两直角三角形公共斜边AC 的中点．D 、B 分别为直角顶点，连接DE 、BE 、DB ，∠DAC=60°，∠BAC=45°．则∠EDB 的度数为_______．(6-()64.如图，一块直角三角形木板△ABC，将其在水平面上沿斜边AB所在直线按顺时针方向翻滚，使它滚动cm．三、解答题5.如图，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F.（1）EF+AC =AB；（2）点C1从点C出发，沿着线段CB向点B运动（不与点B重合），同时点A1从点A出发，沿着BA的延长线运动，点C1与点A1运动速度相同，当动点C1停止运动时，另一动点A1也随之停止运动.如图，AF1平分∠B A1C1，交BD于F1，过F1作F1E1⊥A1C1，垂足为E1，试猜想F1E1，A1C1与AB之间的数量关系，并证明你的猜想.（3）在（2）的条件下，当A1 E1=3，C1 E1=2时，求BD的长.21216.如图，等腰Rt△ABC 中，∠C=90°，AC=6，动点P 、Q 分别从A 、B 两点同时以每秒1个单位长的速度按顺时针方向沿△ABC 的边运动，当Q 运动到A 点时，P 、Q 停止运动.设Q 点运动时间为t 秒，点P 运动的轨迹与PQ 、AQ 围成图形的面积为S.求S 关于t 的函数解析式.7.正方形ABCD中，点F为正方形ABCD 内的点，△BFC 绕着点B 按逆时针方向旋转90°后与△BEA 重合．（1）如图1，若正方形ABCD 的边长为2，BE=1，FC=，求证：AE ∥BF ；（2）如图2，若点F 为正方形ABCD 对角线AC 上的点，且AF ：FC=3：1，BC=2，求BF 的长．8.将正方形ABCD 和正方形BEFG 如图1摆放，连DF ．∠DMC=_____；∠DMC 的值，并证明你的结论；3∠DMC=_________．请画出图形，并直接写出你的结论（不用证明）．9.已知△ABC≌△ADE，∠BAC=∠DAE=90°．（1）如图（1）当C、A、D在同一直线上时，连CE、BD，判断CE和BD位置关系，填空：CE_____BD．（2）如图（2）把△ADE绕点A旋转到如图所示的位置，试问（1）中的结论是否仍然成立，写出你的结论，并说明理由．（3）如图（3）在图2的基础上，将△ACE绕点A旋转一个角度到如图所示的△AC′E′的位置，连接BE′、DC′，过点A作AN⊥BE′于点N，反向延长AN交DC′于点M．求的值．10.将正方形ABCD和正方形CGEF如图1摆放，使D点在CF边上，M为AE中点，（1）连接MD、MF，则容易发现MD、MF间的关系是______________（2）操作：把正方形CGEF绕C点旋转，使对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M，探究线段MD、MF的关系，并加以说明；（3）将正方形CGEF绕点C旋转任意角度后（如图3），其他条件不变，（2）中的结论是否仍成立？直接写出猜想，不需要证明.DMDC交射线ON 于点B ，且使∠APB+∠MON=180°．（1）利用图1，求证：PA=PB ；（2）如图2，若点C 是AB 与OP 的交点，当S △POB =3S △PCB 时，求PB 与PC 的比值；（3）若∠MON=60°，OB=2，射线AP 交ON 于点D ，且满足且∠PBD=∠ABO ，请借助图3补全图形，并求OP 的长．12、在中，过点C 作CE ⊥CD 交AD 于点E,将线段EC 绕点E 逆时针旋转得到线段EF(如图1)（1）在图1中画图探究：①当P 为射线CD 上任意一点（P 1不与C 重合）时，连结EP 1绕点E 逆时针旋转得到线段EC 1.判断直线FC 1与直线CD 的位置关系，并加以证明；②当P 2为线段DC 的延长线上任意一点时，连结EP 2,将线段EP 2绕点E 逆时针旋转得到线段EC 2.判断直线C 1C 2与直线CD 的位置关系，画出图形并直接写出你的结论.（2）若AD=6,tanB=,AE=1,在①的条件下，设CP 1=，S =，求与之间的函数关系式，并写出自变量的取值范围.图1 备用图13、已知：如图，N 、M 是以O 为圆心，1为半径的圆上的两点，B 是上一动点（B 不与点M 、N 重合），ABCD Y 90o90o 90o43x 11P FC V y y xx ¼MN∠MON=90°，BA ⊥OM 于点A ，BC ⊥ON 于点C ，点D 、E 、F 、G 分别是线段OA 、AB 、BC 、CO 的中点，GF 与CE 相交于点P ，DE 与AG 相交于点Q ．（1）四边形EPGQ （填“是”或者“不是”）平行四边形；（2）若四边形EPGQ 是矩形，求OA 的值.14、已知如图，在梯形中，点是的中点，是等边三角形．（1）求证：梯形是等腰梯形；（2）动点、分别在线段和上运动，且保持不变．设求与的函数关系式；（3）在（2）中，当取最小值时，判断的形状，并说明理由．15、已知正方形ABCD 的边长为6cm ，点E 是射线BC 上的一个动点，连接AE 交射线DC 于点F ，将△ABE 沿直线AE 翻折，点B 落在点B′ 处．（1）当=1 时，CF=______cm ，（2）当=2 时，求sin∠DAB′ 的值；（3）当= x 时（点C 与点E 不重合），请写出△ABE 翻折后与正方形ABCD 公共部分的面积y 与x 的关系式，（只要写出结论，不要解题过程）．ABCD 24AD BC AD BC ==∥，，，M AD MBC △ABCD P Q BC MC 60MPQ =︒∠PC x MQ y ==，，y x y PQC△CEBECEBECEBE16、在△ABC 中，∠ACB=45º．点D （与点B 、C 不重合）为射线BC 上一动点，连接AD ，以AD 为一边且在AD 的右侧作正方形ADEF ．（1）如果AB=AC ．如图①，且点D 在线段BC 上运动．试判断线段CF 与BD 之间的位置关系，并证明你的结论．（2）如果AB ≠AC ，如图②，且点D 在线段BC 上运动．（1）中结论是否成立，为什么？（3）若正方形ADEF 的边DE 所在直线与线段CF 所在直线相交于点P ，设AC ＝，，CD=，求线段CP 的长．（用含的式子表示）17、已知：如图（1），射线射线，是它们的公垂线，点、分别在、上运动（点与点不重合、点与点不重合），是边上的动点（点与、不重合），在运动过程中始终保持，且．（1）求证：∽；（2）如图（2），当点为边的中点时，求证：；（3）设，请探究：的周长是否与值有关？若有关，请用含有的代数式表示的周长；若无关，请说明理由．3=BC xx //AM BN AB D C AM BN D A C B E AB E A B EC DE ⊥a AB DE AD ==+ADE ∆BEC ∆E AB CD BC AD =+m AE =BEC ∆m m BEC∆18、已知正方形中，为对角线上一点，过点作交于，连接，为中点，连接．（1）直接写出线段与的数量关系；（2）将图1中绕点逆时针旋转，如图2所示，取中点，连接，你在（1）中得到的结论是否发生变化？写出你的猜想并加以证明．（3）将图1中绕点旋转任意角度，如图3所示，再连接相应的线段，问（1）中的结论是否仍然成立？（不要求证明）参考答案一、选择题 1.【答案】C. 2.【答案】B. 二、填空题 3.【答案】15°.4.三、解答题5.【答案与解析】（1）证明：如图1，过点F 作FM ⊥AB 于点M ，在正方形ABCD 中，AC ⊥BD 于点E ． ∵AF 平分∠BAC ， ∴EF=MF ，又∵AF=AF ，ABCD E BD E EF BD ⊥BC F DF G DF EG CG ，EG CG BEF ∆B 45︒DF G EG CG ，BEF ∆B 图3图2图1FEABCDABC DEFGGFED C BA∴Rt △AMF ≌Rt △AEF ， ∴AE=AM ，∵∠MFB=∠ABF=45°， ∴MF=MB，MB=EF ， ∴EF+AC=MB+AE=MB+AM=AB ．（2）E 1F 1，A 1C 1与AB 三者之间的数量关系：E 1F 1+A 1C 1=AB 证明：如图2，连接F 1C 1，过点F 1作F 1P ⊥A 1B 于点P ，F 1Q ⊥BC 于点Q ， ∵A 1F 1平分∠BA 1C 1，∴E 1F 1=PF 1；同理QF 1=PF 1，∴E 1F 1=PF 1=QF 1，又∵A 1F 1=A 1F 1，∴Rt △A 1E 1F 1≌Rt △A 1PF 1， ∴A 1E 1=A 1P ，同理Rt △QF 1C 1≌Rt △E 1F 1C 1， ∴C 1Q=C 1E 1，由题意：A 1A=C 1C ，∴A 1B+BC 1=AB+A 1A+BC -C 1C=AB+BC=2AB ， ∵PB=PF 1=QF 1=QB ，∴A 1B+BC 1=A 1P+PB+QB+C 1Q=A 1P+C 1Q+2E 1F 1，即2AB=A 1E 1+C 1E 1+2E 1F 1=A 1C 1+2E 1F 1， ∴E 1F 1+A 1C 1=AB ．（3）解：设PB=x ，则QB=x ， ∵A 1E 1=3，QC 1=C 1E 1=2，Rt △A 1BC 1中，A 1B 2+BC 12=A 1C 12，即（3+x ）2+（2+x ）2=52， ∴x 1=1，x 2=-6（舍去）， ∴PB=1， ∴E 1F 1=1，又∵A 1C 1=5，121212126.【答案与解析】当P运动到C点时：t=6当Q运动到A点：t=∴分两种情况讨论(1)当0≤t≤6时，如图：作PH⊥AB于H，则△APH为等腰直角三角形此时AP=t，BQ=t，则AQ=-tPH=APsin45°=t∴S△AQP=AQ·PH=·(-t)·t=t2+3t(2)当6＜t≤时，如图：过P过PH⊥AB于H，此时△PBH为等腰直角三角形AC+CP=t，BQ=t∴BP=AC+CB-(AC+CP)=12-t∴PH=BPsin45°=(12-t)∴S四边形AQPC=S△ABC-S△BPQ=AC·BC-BQ·PH=·6·6-·t·(12-t)=18-t+t2=t2-t+18.综上，.7.【答案与解析】（1）证明：∵△BFC绕着点B按逆时针方向旋转90°后与△BEA重合∴BE=BF=1，∠EBF=∠ABC=90°，∠AEB=∠BFC在△BFC中，BC2=22=4∴BF2+FC2=BC2∴∠BFC=90°…（3分）∴∠AEB+∠EBF=180°∴AE ∥BF …（4分）（2）解：∵Rt △ABC 中，AB=BC=2，由勾股定理，得∵AF ：FC=3：1，∵△BFC 绕着点B 按逆时针方向旋转90°后与△BEA 重合∵四边形ABCD 是正方形∴∠ABC=90°∴∠BAC+∠ACB=90° ∴∠EAB+∠BAC=90°即∠EAF=90° 在Rt △EBF 中，EF 2=BE 2+BF 2∵BE=BF8.【答案与解析】（1）如图2，连接BF ，∵四边形ABCD 、四边形BEFG 是正方形，∴∠FBC=∠CBD=45°，∴∠CBD=∠GBC=90°，而BF=BG ，BD=BC ，∴△BFD ∽△BGC ，22而∠DMC=180°-∠BCG-∠BCD-∠CDF=180°-∠BDF-∠BCD-∠CDF=180-45°-90°=45°，（2）如图3，∵将图1中的正方形BEFG 绕B 点顺时针旋转45°，DF 的延长线交CG 于M ，∴B 、E 、D 三点在同一条直线上，而四边形ABCD 、四边形BEFG 是正方形，∴△BFD ∽△BGC ，而∠DMC=180°-∠BCG-∠BCD-∠CDF=180°-∠BDF-∠BCD-∠CDF=180-45°-90°=45°，即∠DMC=45°；9．【答案与解析】（1）CE ⊥BD ．（2）延长CE 交BD 于M ，设AB 与EM 交于点F ．∵∠BAC=∠DAE=90°， ∴∠CAE=∠BAD ．又∵△ABC ≌△ADE ，∴AC=AE ，AB=AD ， ∴∠ACE=，∠ABD=，∴∠ACE=∠ABD ．又∵∠AFC=∠BFM ，∠AFC+∠ACE=90°，∴∠ABD+∠BFM=90°，∴∠BMC=90°，∴CE ⊥BD ．（3）过C ′作C ′G ⊥AM 于G ，过D 作DH ⊥AM 交延长线于点H ．∵∠∠E ′NA=∠AGC ′=90°，∴∠NE ′A+∠NAE ′=90°，∠NAE ′+∠C ′AG=90°，∴∠NE ′A=∠C ′AG ，∵AE ′=AC ′∴△ANE ′≌△C ′GA （AAS ），∴AN=C ′G ．同理可证△BNA ≌△AHD ，AN=DH ．∴C ′G=DH ．在△C ′GM 与△DHM 中，∠C ′GM=∠DHM=90°，∠C ′MG=∠DMH ，C ′G=DH ，∴△C ′GM ≌△DHM ，∴C ′M=DM ，01802CAE -∠01802BAD -∠10．【答案与解析】如图1，延长DM交FE于N，图1∵正方形ABCD、CGEF，∴CF=EF，AD=DC，∠CFE=90°，AD∥FE，∴∠1=∠2，又∵MA=ME，∠3=∠4，∴△AMD≌△EMN，∴MD=MN，AD=EN．∵AD=DC，∴DC=NE．又∵FC=FE，∴FD=FN．又∵∠DFN=90°，∴FM⊥MD，MF=MD；（2）MD=MF，MD⊥MF．如图2，延长DM交CE于N，连接FD、FN．∵正方形ABCD，∴AD∥BE，AD=DC，∴∠1=∠2．又∵AM=EM，∠3=∠4，∴△ADM≌△ENM，∴AD=EN，MD=MN．∵AD=DC，∴DC=NE．又∵正方形CGEF，∴∠FCE=∠NEF=45°，FC=FE，∠CFE=90°．又∵正方形ABCD，∴∠BCD=90°，∴∠DCF=∠NEF=45°，∴△FDC≌△FNE，∴FD=FN，∠5=∠6，∠DFN=∠5+∠CFN=∠6+∠CFN=90°，∴△DFN为等腰直角三角形，且FM为斜边DN上的中线，∴MD=MF，MD⊥MF；（3）FM⊥MD，MF=MD．如图3，过点E作AD的平行线分别交DM、DC的延长线于N、H，连接DF、FN．∴∠ADC=∠H，AD∥EH，∴∠3=∠4．∵AM=ME，∠1=∠2，∴△AMD≌△EMN，∴DM=NM，AD=EN．∵正方形ABCD、CGEF，∴AD=DC，FC=FE，∠ADC=∠FCG=∠CFE=90°．∴∠H=90°，∠5=∠NEF，DC=NE．∴∠DCF+∠7=∠5+∠7=90°，∴∠DCF=∠5=∠NEF．∵FC=FE，∴△DCF≌△NEF．∴FD=FN，∠DFC=∠NFE．∵∠CFE=90°，∴∠DFN=90°．∴FM⊥MD，MF=MD．11、【答案】（1）作PE ⊥OM ，PF ⊥ON ，垂足为E 、F ∵四边形OEPF 中，∠OEP=∠OFP=90°， ∴∠EPF+∠MON=180°，已知∠APB+∠MON=180°，∴∠EPF=∠APB ，即∠EPA+∠APF=∠APF+∠FPB ，∴∠EPA=∠FPB ，由角平分线的性质，得PE=PF ，∴△EPA ≌△FPB ，即PA=PB ；（2）∵S △POB =3S △PCB ，∴PO=3PC ，由（1）可知△PAB 为等腰三角形，则∠PBC=（180°-∠APB ）=∠MON=∠BOP ，又∵∠BPC=∠OPB （公共角），∴△PBC ∽△POB ，∴，即PB 2=PO •PC=3PC 2，∴ （3）作BH ⊥OT ，垂足为H ，当∠MON=60°时，∠APB=120°，由PA=PB ，得∠PBA=∠PAB=（180°-∠APB ）=30°，又∵∠PBD=∠ABO ，∠PBD+∠PBA+∠ABO=180°，∴∠ABO=（180°-30°）=75°，则∠OBP=∠ABO+∠ABP=105°，在△OBP 中，∵∠BOP=30°，∴∠BPO=45°，在Rt △OBH 中，BH=OB=1，OH=， 1212PB PC PO PB=3PB PC=1212123在Rt △PBH 中，PH=BH=1，∴OP=OH+PH=+1．12、【答案与解析】（1）①直线与直线的位置关系为互相垂直．证明：如图1，设直线与直线的交点为．∵线段分别绕点逆时针旋转90°依次得到线段，∴．∵，， ∴． ∴． ∴． ∵，∴， ∴．31FG CD 1FG CD H 1EC EP 、E 1EF EG 、111190PEG CEF EG EP EF EC ∠=∠===°，，1190G EF PEF ∠=-∠°1190PEC PEF ∠=-∠°11G EF PEC ∠=∠11G EF PEC △≌△11G FE PCE ∠=∠EC CD ⊥190PCE ∠=°190G FE ∠=°FDC BAE 图1 G 2 G 1P 1 H P 2∴．∴．∴．②按题目要求所画图形见图1，直线与直线的位置关系为互相垂直．（2）∵四边形是平行四边形，∴．∵， ∴．可得．由（1）可得四边形为正方形．∴． ①如图2，当点在线段的延长线上时，∵， ∴． 90EFH ∠=°90FHC ∠=°1FG CD ⊥12G G CD ABCD B ADC ∠=∠461tan 3AD AE B ===，，45tan tan 3DE EBC B =∠==，4CE =EFCH 4CH CE ==1P CH 1114FG CP x PH x ===-，11111(4)22P FG x x S FG PH -=⨯⨯=△D G 1P 1 H C BAE F∴． ②如图3，当点在线段上（不与两点重合）时， ∵， ∴． ∴． ③当点与点重合时，即时，不存在．综上所述，与之间的函数关系式及自变量的取值范围是或． 13、【答案】（1）是．证明：连接OB ，如图①，212(4)2y x x x =->1P CH C H 、1114FG CP x PH x ===-，11111(4)22P FG x x S FG PH -=⨯=△212(04)2y x x x =-+<<1P H 4x =11PFG △y x x 212(4)2y x x x =->212(04)2y x x x =-+<<FG 1 P 1 CAB E D H∵BA ⊥OM ，BC ⊥ON ， ∴∠BAO=∠BCO=90°， ∵∠AOC=90°， ∴四边形OABC 是矩形．∴AB ∥OC ，AB=OC ，∵E 、G 分别是AB 、CO 的中点，∴AE ∥GC ，AE=GC ，∴四边形AECG 为平行四边形．∴CE ∥AG ，∵点D 、E 、F 、G 分别是线段OA 、AB 、BC 、CO 的中点，∴GF ∥OB ，DE ∥OB ，∴PG ∥EQ ，∴四边形EPGQ 是平行四边形；（2）解：如图②，∵口EPGQ 是矩形．∴∠AED+∠CEB=90°．又∵∠DAE=∠EBC=90°，∴∠AED=∠BCE ．∴△AED ∽△BCE ，∴， AD AE BE BC得y 2=2x 2，又∵OA 2+AB2=OB 2，即x 2+y 2=12．∴x 2+2x 2=1，14、【答案与解析】（1）证明：∵是等边三角形∴∵是中点∴∵∴∴∴∴梯形是等腰梯形．（2）解：在等边中， ∴ ∴ ∴∴ MBC △60MB MC MBC MCB ===︒，∠∠M AD AM MD =AD BC ∥60AMB MBC ==︒∠∠，60DMC MCB ==︒∠∠AMB DMC △≌△AB DC =ABCD MBC △4MB MC BC ===，60MBC MCB ==︒∠∠，60MPQ =︒∠120BMP BPM BPM QPC +=+=︒∠∠∠∠BMP QPC =∠∠BMP CQP △∽△PC CQ BM BP=∵∴∴∴（3）解：为直角三角形，∵∴当取最小值时，∴是的中点，而∴∴∴为直角三角形.15、【答案与解析】（1）CF=6cm；（2）①如图1，当点E在BC上时，延长AB′交DC于点M，PC x MQ y==，44BP x QC y=-=-，444x yx-=-2144y x x=-+PQC△()21234y x=-+y2x PC==P BC MP BC⊥，60MPQ=︒∠，30CPQ=︒∠，90PQC=︒∠PQC△图1∵ AB ∥CF ，∴ △ABE ∽△FCE ，∴ ． ∵ =2， ∴ CF=3． ∵ AB ∥CF，∴∠BAE=∠F ．又∠BAE=∠B ′ AE ， ∴ ∠B ′ AE=∠F ．∴ MA=MF ．设MA=MF=k ，则MC=k -3，DM=9-k ．在Rt △ADM 中，由勾股定理得：k 2=(9-k)2+62，解得 k=MA=． ∴ DM=． ∴ sin ∠DAB ′=； ②如图2，当点E 在BC 延长线上时，延长AD 交B ′ E 于点N ，同①可得NA=NE ．设NA=NE=m ，则B ′ N=12-m ．在Rt △AB ′ N 中，由勾股定理，得m 2=(12-m)2+62，解得 m=AN=． ∴ B ′N=． ∴ sin ∠DAB ′=．（3）①当点E 在BC 上时，y=； FCAB CE BE =CEBE 13252135=AM DM 1529253='AN N B 18x x 1+图2②当点E 在BC 延长线上时，y=． 16、【答案与解析】（1）结论：CF ⊥BD ；证明如下：AB=AC ，∠ACB =45º，∴∠ABC=45º．由正方形ADEF 得 AD=AF ，∵∠DAF=∠BAC =90º，∴∠DAB=∠FAC ，∴△DAB ≌△FAC ， ∴∠ACF=∠ABD ．∴∠BCF=∠ACB+∠ACF= 90º．即 CF ⊥BD ．（2）CF ⊥BD ．(1)中结论仍成立．理由是：过点A 作AG ⊥AC 交BC 于点G ，∴AC=AG可证：△GAD ≌△CAF ∴∠ACF=∠AGD=45º∠BCF=∠ACB+∠ACF= 90º．即CF ⊥BD（3）过点A 作AQ ⊥BC 交CB 的延长线于点Q ，①点D 在线段BC 上运动时，∵∠BCA=45º，可求出AQ= CQ=4．∴DQ=4-x ，易证△AQD ∽△DCP ，∴ ，∴，．18x 18x-ΘCP CD DQ AQ =44CP x x =-24x CP x ∴=-+②点D 在线段BC 延长线上运动时，∵∠BCA=45°，∴AQ=CQ=4，∴DQ=4+x ．过A 作AQ ⊥BC ， ∴∠Q=∠FQC=90°，∠ADQ=∠AFC ，则△AQD ∽△ACF ．∴CF ⊥BD ，∴△AQD ∽△DCP ，∴, ∴, ． 17、【答案】（1）证明：∵，∴．∴．又∵，∴．∴．∴∽．（2）证明：如图，过点作，交于点，∵是的中点，容易证明． CD DQ AQ 4+4x x =24x CP x ∴=+EC DE ⊥︒=∠90DEC ︒=∠+∠90BEC AED ︒=∠=∠90B A ︒=∠+∠90EDA AED EDA BEC ∠=∠ADE ∆BEC ∆E EF BC //CD F E AB )(21BC AD EF +=在中，∵ ，∴ ． ∴ ． ∴ ．（3）解：的周长，．设，则．∵ ，∴ ．即．∴ ．由（1）知∽，∴ ． ∴ 的周长的周长． ∴ 的周长与值无关．18、【答案与解析】（1）（2）（1）中结论没有发生变化，即．证明：连接，过点作于，与的延长线交于点．在与中，∵，∴．∴．DEC Rt ∆CF DF =CD EF 21=)(21BC AD +CD 21=CD BC AD =+AED ∆DE AD AE ++=m a +=m a BE -=x AD =x a DE -=︒=∠90A 222AD AE DE +=22222x m x ax a +=+-am a x 222-=ADE ∆BEC ∆的周长的周长BEC ∆∆ADE BEAD =m a a m a --=222a m a 2+=BEC ∆⋅+=m a a 2ADE ∆a 2=BEC ∆m CG EG =CG EG =AG G MN AD ⊥M EF N DAG ∆DCG ∆AD CD ADG CDG DG DG =∠=∠=，，DAG DCG ∆∆≌AG CG =在与中，∵， ∴．∴在矩形中，在与中，∵，∴．∴．∴（3）（1）中的结论仍然成立．DMG ∆FNG ∆DGM FGN FG DG MDG NFG ∠=∠=∠=∠，，DMG FNG ∆∆≌MG NG =AENM AM EN =Rt AMG ∆Rt ENG ∆AM EN MG NG ==，AMG ENG ∆∆≌AG EG =EG CG =M N图2A B CDE F GG图3FE A B CD。

二、解答重难题型突破+题型6 几何综合探究问题+课件+2025年九年级中考数学总复习人教版(山东)

∴OD⊥AB,
∵AC⊥AB,∴OD∥AC,
∵DE∥BC,∴四边形DOCE是平行四边形,
由(1)知,OD=OC,∴四边形DOCE为菱形;
20
(3)如图,
在OC上截取OE=1,连接DE,作AF⊥BC于F,
∵OD=OB=3,OC=BC-OB=9,

∴ = = ,

∴∠DOE=∠CDO,
∵△HCG是等腰直角三角形,∴CG= GH=8,∴GD=8-5=3;
16
当E在BC延长线上时,延长GH,使HQ=HF,连接FQ,
则△HFQ是等腰直角三角形,
∴∠Q=45°,FQ= FH,GQ=HG+HQ=HC+HF=CF,∠QGF=90°-∠GFH=∠CFE,
∴△QGF≌△CFE(ASA),
∴GF=EF=AE=
∠AOC=180°-30°-30°=120°,
∴∠OCN=∠OAN'=30°,
=
∵在△OCN和△OAN'中 ∠ = ∠′ ,
′ =
7
∴△OCN≌△OAN'(SAS),
∴ON=ON',∠CON=∠AON',
∴∠N'ON=∠COA=120°,
又∵∠MON=60°,
∴∠MON=∠MON'=60°,
法:有直角,作垂线,找全等或相似;有中点,作倍长,通过全等转移边和角;有平行,找
相似,转比例等.
3
类型1
动点、动线类探究
【例1】(2024·烟台招远市模拟)已知:等边△ABC中,点O是边AC,BC的垂直平分线
的交点,M,N分别在直线AC,BC上,且∠MON=60°.
(1)如图1,当CM=CN时,M,N分别在边AC,BC上时,请写出AM,CN,MN三者之间的数

初中必考几何题型归纳总结

初中必考几何题型归纳总结几何是数学中的重要分支，也是初中数学中的必考题型之一。

学好几何，对于初中生来说至关重要。

本文将对初中必考的几何题型进行归纳和总结，帮助同学们更好地备考。

一、平面几何题型1. 直线与角度直线和角度是平面几何中最基础的概念。

常见的直线与角度题型有以下几种：a. 直线的分类：根据两直线之间的关系，可以分为相交、平行和重合三种情况。

b. 角的分类：根据角的大小以及内部直线的关系，角可以分为锐角、直角、钝角和平角。

c. 角的性质：根据角的性质，可以解决一些直线和角度的计算问题，如余角、补角、同位角等。

2. 三角形三角形是平面几何中最基本的图形之一，也是初中必考的重点。

以下是几种常见的三角形题型：a. 三角形的分类：根据三角形的边长和角度，可以分为等边三角形、等腰三角形、直角三角形和一般三角形等。

b. 三角形的性质：三角形的内角和为180度，可以利用这一性质解决角度计算的问题。

c. 三角形的面积：三角形的面积计算可以通过底和高的乘积、海伦公式等方法求解。

3. 四边形四边形是平面几何中另一个重要的图形。

常见的四边形题型有以下几类：a. 平行四边形：平行四边形的性质包括对角线互相平分、对边相等、相邻角互补等。

b. 矩形和正方形：矩形和正方形是常见的特殊平行四边形，具有特殊的性质，如对角线相等、内角为直角等。

c. 梯形：梯形的面积计算可以通过底和高的乘积或者上底与下底的和乘以高的一半等方法求解。

4. 圆圆是平面几何中特殊的图形，也是初中必考题型之一。

以下是常见的圆题型：a. 圆的性质：圆的性质包括半径、直径、弧长、圆心角等，可以通过这些性质解决各种计算题。

b. 扇形和弓形：通过计算扇形或弓形的面积，可以运用圆的性质解决相关问题。

二、空间几何题型空间几何是初中数学中的另一个重要内容。

以下是空间几何中常见的题型：1. 空间图形的计算：如长方体、正方体、圆柱体、圆锥体和球体等的体积和表面积计算。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

图形认识初步经典题型1.（2007年）已知：∠A=40°，则∠A 的补角等于（）.（A ）50° （B ）90° （C ）140° （D ）180°说明：本题为2007年西藏中考题，下同。

2.（2006年）已知∠α与∠ß互补，且∠α=35°18′，则∠ß=（）.（A ）54°42′ （B ）54°32′ （C ）144°42′ （D ）144°32′3.（2005年）一个角比它的余角小8°，那么这个角的度数是（）.（A ）98° （B ）41° （C ）49° （D ）92°4.（2002年）如果一个角的补角是它的余角的3倍，那么这个角的度数是（）.（A ）30° （B ）45° （C ）60° （D ）90°5.下列说法正确的是（）.（A ）29.3°等于29°3′ （B ）角的两边越大，角就越大（C ）射线OP 可以写成射线PO （D ）一个锐角的补角比它的余角大90°6.如图，已知直线AB 、CD 相交于点O ，OE 平分∠COB ，若∠EOB=55°，则∠BOD 的度数是（）.（A ）35°（B ）55°（C ）70°（D ）110° 7.（2000年）如图，∠AOB=34°，OC 是∠AOB 的平分线，那么∠AOC 等于度.8.78.6°= 度= 分.9.如图，点B 是线段AC 的中点，则1210.如图，AB ⊥CD 于点B ，BE 是∠ABD 则∠CBE 的度数为 . 11.（2005年）如图，O 是直线EF 上的一点，∠AOB=90°，OC 平分∠AOF ，∠BOF=20°，那么∠BOC= 度.12.（选做）如图，将一副三角板叠放在一起，使直角顶点重合于O 点，则∠AOC+∠DOB= 度.E A B C DO A O B C ....DB C A A E B C F OA BC D O十四：相交线与平行线 1.（2000年）下面的命题正确的是（）.（A ）内错角互补，两直线平行（B ）同旁内角互补，两直线平行（C ）两直线平行，同位角互补（D ）两直线平行，同旁内角相等2.（2008年）已知：如图，直线a ∥b ，直线c 与直线a 、b 相交，∠1=120°，则∠2的度数是（）. （A ）120° （B ）60° （C ）30° （D ）80°(第2题图) (第3题图) (第4题图)3.（2009年）如图，已知直线a ∥b ，∠1=35°，则∠2的度数是（）.（A ）35° （B ）55° （C ）145° （D ）135°4.（2002年）如图，直线a ∥b ，直线l 与a 、b 相交，那么下面的结论不能肯定正确的是（）.（A ）∠1=∠5 （B ）∠1=∠3 （C ）∠2=∠6 （D ）∠2＋∠4=180°5.（2006年）如图，AB ∥CD ，∠1=140°，∠2=90°，则∠3的度数是（）. （A ）40° （B ）45°（C ）50° （D ）60°6.下列说法正确的是（）. （A ）两直线平行，同旁内角相等（B ）互补的两个角一定是邻补角（C ）同位角相等（D ）垂直于同一直线的两直线平行7.如图，AB 、CD 相交于点O ，∠1=80°，如果DE ∥AB ，那么∠D 的度数为（）. （A ）110° （B ）100°（C ）90° （D ）80° 8.如图，直线a ∥b ，点B 在直线b 上，且AB ⊥BC ，∠2=35°，则∠1的度数为（）.（A ）35° （B ）45° （C ）55° （D ）65°(第8题图) (第9题图)9.如图，已知AB ∥CD ，点E 在CD 上，BC 平分∠ABE ，若∠C=25°，则∠ABE 的度数是（）.（A ）12.5° （B ）25° （C ）50° （D ）60°10.如图，直线m ∥n ，∠1=55°，∠2=45°，则∠3的度数为（）.（A ）80° （B ）90° （C ）100° （D ）110°(第10题图) (第11题图) (第12题图) (第13题图)11.如图，已知∠1=∠2，∠3=80°，则∠4=（）.（A ）80° （B ）70° （C ）60° （D ）50°12.如图，直线l 1∥l 2，则∠α为（）.（A ）150° （B ）140° （C ）130° （D ）120°b a 1221a b 364512E A B C D123OA B C D E1A B C D E n m 312l 1l 270︒130︒αA B C 21a b b a 1234l 2l 113213.如图，直线l 1∥l 2，∠1=120°，∠2=100°，则∠3=（）.（A ）20° （B ）40° （C ）50° （D ）60°14.下列图形中，由AB ∥CD ，能得到∠1=∠2的是（）.（A ）（B ）（C ）（D ）15.如图，∠1=150°，则∠2= °，∠3= °，∠4= °. 16.如图，∠1=50°，∠2=30°，则∠3= °.(第16题图) (第17题图) (第18题图) (第19题图)17.（2007年）如图，已知直线a ∥b ，∠1=85°，则∠2= .18.如图，已知直线a ∥b ，∠1=130°，则∠2= .19.如图，如果∠2=∠3，那么 ∥ ；如果∠1=∠2，那么 ∥ .20.如图，OA ⊥OB ，OD ⊥OC ，∠AOC=30°，则∠BOD 的度数为 . 21.（2003年）如图，DH ∥EG ∥BC ，且DC ∥EF ，那么图中与∠BFE 相等的角（不包括∠BFE 本身）共有个.22.如图，AB ∥CD ，AD ⊥AC ，∠ADC=32°，则∠CAB 的度数是 .(第22题图) (第23题图)23.如图，AE ∥BD ，∠1=130°，∠2=30°，则∠C= .24.如图，AB ∥CD ，∠1=50°，∠(第24题图) (第25题图)25.如图，直线a ∥b ，l 与a 、b 交于E 、F 点，PF 平分∠EFD 交a 于P 点，若∠1=70°，则 ∠2= .12B D C A 12B D C A 2341213c a b 12a b c12B A D CH FG E A B C D A B C D 132A B C D 12A C D B 21132E A C D B A B C DE A D B C12a b中考复习之十五：三角形1.下列长度的三条线段，能组成三角形的是（）.（A ）1cm ，2cm ，3cm （B ）2cm ，3cm ，6cm （C ）4cm ，6cm ，8cm （D ）5cm ，6cm ，12cm2.已知三角形的两条边长分别为3cm 和8cm ，则此三角形的第三边的长可能是（）.（A ）4cm （B ）5cm （C ）6cm （D ）13cm3.已知等腰三角形的一条边长等于6，另一条边长等于3，则此等腰三角形的周长是（）.（A ）9 （B ）12 （C ）15 （D ）12或154.若一个多边形的内角和为1080°，则这个多边形的边数为（）.（A ）5 （B ）6 （C ）7 （D ）85.若一个多边形的内角和为n180°，则这个多边形的边数为（）.（A ）n （B ）n+1 （C ）n+2 （D ）n+36.（2006年）七边形的外角和是（）.（A ）360° （B ）720° （C ）900° （D ）1260°7.若一个多边形的内角和等于它的外角和，则这个多边形的边数是（）.（A ）4 （B ）5 （C ）6 （D ）78.（2003年）四边形ABCD 中，∠A 、∠B 、∠C 、∠D 的度数之比是2：3：4：3，那么∠D 的度数是（）.（A ）60° （B ）75° （C ）90° （D ）120°9.如图，△ABC 中，∠A=70°，∠B=60°，点D 在BC 的延长线上，则∠ACD 等于（）.（A ）100° （B ）120° （C ）130° （D ）150°10.（2008年）等腰三角形的一内角的度数为50°，那么它的底角的度数为（）.（A ）50° （B ）65° （C ）130° （D ）50°或65° 11.如图，在△ABC 中，∠C=90°，若沿图中虚线剪去∠C ，则∠1＋∠2等于（）. （A ）315° （B ）270° （C ）180° （D ）135° 12.如图，AB=AC ，BD=BC ，若∠A=40°，则∠ABD 的度数是（）.（A ）20° （B ）30° （C ）35° （D ）40° 13.（2000年）如图，CD 是Rt △ABC 斜边AB 上的中线，∠A=58°，那么∠BCD 等于（）. （A ）58° （B ）32°（C ）45° （D ）26° 14.（2003年）如图，△ABC 中，D 、E 分别是边BC 、AC 的中点，如果DE=3，那么AB 等于（）.（A ）23 （B ）6（C ）9 （D ）94 15.（2007年）如图，在△ABC 中，D 、E 分别是AB 、AC 的中点，BC=12，则DE 的长是（）. （A ）4 （B ）5（C ）6 （D ）7B ACD A BC D B A D E CAB DC E AA B C 12AB CD16.已知：如图，△ABC 中，AD ⊥BC ，BE ⊥AC ，AD=8，BC=12，BE=10，则AC=（）.（A ）9.2 （B ）9.4（C ）9.6 （D ）9.817.六边形的对角线共有（）.（A ）7条（B ）8条（C ）9条（D ）10条18.如图，△ABC 是等边三角形，点D 是AC 的中点，DE ⊥BC ，CE=3，则AB 等于（）.（A ）11 （B ）12（C ）13 （D ）14 19.以线段a ，b ，c 为三边，能构成直角三角形的是（）.（A ）a=6，b=3，c=2 （B ）a=5，b=6，c=8（C ）a=8，b=17，c=15 （D ）a=3，b=4，c=620.如图，中间是一个直角三角形，外面三个正方形的面积分别为 S 1、S 2、S 3，则（）. （A ）S 1＋S 2=S 3 （B ）S 21＋S 22=S 23（C ）123S S S （D ）以上都不对 21.（2001年）下面四组条件下，不能确定两个三角形全等的是（）.（A ）两个三角形的两边一角对应相等（B ）两个三角形的两角一边对应相等（C ）两个三角形的三边对应相等（D ）两个三角形的两边及夹角对应相等22.下列说法中，正确的是（）.（A ）面积相等的两个三角形全等（B ）两边一角对应相等的两个三角形全等（C ）三角对应相等的两个三角形全等（D ）两角一边对应相等的两个三角形全等 23.（2003年）如图，某同学把一块三角形的玻璃打碎成了三块，现在要把玻璃带到店里去配一块与原来完全一样的玻璃，那么最省事的方法是（）.（A ）带①去（B ）带②去（C ）带③去（D ）带①②去24.（2004年）如图，P 是∠AOB 的平分线OC 上一点（不与O 重合），过P 分别向角的两边作垂线PD 、PE ，垂足是D 、E ，连接DE ，那么图中全等的直角三角形共有（）. （A ）3对（B ）2对（C ）1对（D ）没有25.一个三角形的周长是36cm ，以这个三角形各边中点为顶点的三角形的周长是（）.（A ）8cm （B ）12cm （C ）15cm （D ）18cm26.如图，在Rt △ABC 中，∠B=90°，ED 是AC 的垂直平分线，交AC 于点D ，交BC 于点E.已知∠BAE=10°，则∠C 的度数为（）.（A ）30° （B ）40° （C ）50° （D ）60° 27.（选做）如图，在Rt △ABC 中，∠A=90°，AB=AC=86，点E 为AC 的中点，点F 在底边BC 上，且FE ⊥BE ，则△CEF 的面积是（）. （A ）16 （B ）18（C ）66 （D ）76 A B C D E S 2S 3S 1O P F A B D C E A B CDA BE CF28.（2000年）等腰三角形的两边分别为5和2，那么第三边长为 .29.（2007年）等腰三角形一边为5cm ，另一边长为11cm ，则它的周长是 cm.30.若等腰三角形的一边长为7，另一边长为5，则这个等腰三角形的周长为 .31.（2006年）在△ABC 中，∠A=72°，AB=AC ，则∠B 的度数是 .32.在△ABC 中，∠A ：∠B ：∠C=1：1：2，则这个三角形是三角形.33.如图，AC ⊥BD ，∠A=40°，∠D=25°，则∠BFD= °.(第33题图) (第34题图)34.已知：如图，∠B=50°，∠C=30°，AD 是△ABC 的角平分线，则∠ADC= °. 35.已知：如图，AD 、CE 分别是△ABC 的高和角平分线， ∠BAC=80°，∠B=40°，则∠COD= °. 36.正八边形的每个内角等于度. 37.一个多边形的每个外角都等于18°，则这个多边形的内角和等于度.38.一个多边形的内角和是外角和的3倍，则这个多边形的边数是 .39.等腰三角形的一个内角是100°，则它的底角的度数是 .40.等腰三角形的一个外角是110°，则它的顶角的度数是 .41.已知等腰三角形的一个底角等于顶角的2倍，则底角为度.42.已知：如图，∠E=70°，BD 垂直平分AE ，则∠ABC= °.(第42题图) (第43题图)43.如图，△ABC 中，∠C=90°，BD 平分∠ABC 交AC 于点D ，若CD=6，则点D 到AB 的距离为 .44.等腰三角形的顶角为120°，腰长为8cm ，则底边上的高为 cm.45.如图，△ABC 中，∠ACB=90°，CD 是AB 边上的高，∠A=30°，BC=12，则AD= .(第45题图) (第46题图)46.如图，∠1=∠C ，△ABC 的周长为27，AC=6，则△ABD 的周长为 .47.如图，AB=AD=DC ，∠C=35°，则∠B= 度.48.在Rt △ABC 中，∠C=90°，∠B=60°，BC=2，则AC= .49.在Rt △ABC 中，∠C=90°，∠A=30°，AC=10，则BC= .50.直角三角形的两边长分别为3和5，则第三边长为 . 51.如图，在△ABC 中，AD ⊥BC 于D ，AB=AC=5，BC=8，则AD= . 52.（2001年）等腰直角三角形一条直角边长为1cm ，那么它斜边上的高为 cm.A B E CD F A B D C O A B C DE E A DC B A B CD A B C D A B D C AB C D A B C D 153.等腰三角形一腰上的高与另一腰的夹角为30°，腰长为4cm ，则其腰上的高为 cm.54.（2002年）如果等边三角形的边长是3cm ，那么它的一条高为 cm.55.如图，在Rt △ABC 中，∠ACB=90°，CD ⊥AB 于D ，BC=6，AC=8，则CD= .(第55题图) (第56题图)56.如图，△ABC 中，AB=5cm ，BC=12cm ，AC=13cm ，那么AC 边上的中线BD 的长为 cm.57.放学了，扎西和卓玛从学校同时回家，扎西以每分钟40米的速度向南走，卓玛以每分钟30米的速度向东走，4分钟后他们相距米.58.（选做）如图，△ABC 中，∠ABC 的平分线交AC 于E ，BE ⊥AC ，DE ∥BC 交AB 于D ，若BC=4，则DE= .(第58题图) (第59题图)59.（选做）把两块含有30°的相同的三角板按如图所示摆放，连结AE ，若AC=6cm ，则△ADE 的面积是 . 60.（2007年）如图，AC 和BD 相交于点E ，AB ∥CD ，BE=DE.求证：AB=CD.61.已知：AB ∥DC ，AE ⊥BD ，CF ⊥BD ，BF=DE. 求证：△ABE ≌△CDF.B ACD B C A DA B C D E A B D C E A B C D E F E A CD B中考复习之十六：四边形中考集训1.在ABCD 中，∠A ：∠B=5：7，则∠D 为（）.（A ）105° （B ）95° （C ）75° （D ）55°2.在ABCD 中，AB ＋BC=8，则ABCD 周长为（）.（A ）8 （B ）12 （C ）16 （D ）203.如图，在ABCD 中，AB=8，AC=10，BO=7，则△CDO 的周长为（）.（A ）19 （B ）20 （C ）21 （D ）22（第3题图）（第4题图）4.如图，在ABCD 中，AE ⊥BC ，AF ⊥CD ，∠B=40°，则∠EAF 等于（）.（A ）50° （B ）45° （C ）40° （D ）135°5.如图，在ABCD 中，已知AD=8cm ，AB=6cm ，DE 平分∠ADC 交BC 边于点E ，则BE 等于（）. （A ）2cm （B ）4cm（C ）6cm （D ）8cm 6.（2001年）菱形一个内角是120°，一边长是8，那么它较短的对角线是（）.（A ）3 （B ）4 （C ）8 （D ）7.（2009年）已知菱形的边长为4，一个内角为60°，则菱形较短的对角线长为（）. （A （B ）（C ）2 （D ）48.（2004年）菱形的两条对角线长分别为6和8，那么这个菱形的面积为（）.（A ）14 （B ）48 （C ）24 （D ）129.（2007年）正方形的边长是5，则其面积为（）.（A ）5 （B ）10 （C ）15 （D ）2510.如图，在正方形ABCD 的外侧，作等边三角形ADE ，则∠AEB 等于（）.（A ）10° （B ）15° （C ）20° （D ）25° 11.下列说法中，错误的是（）. （A ）对角线垂直且平分的四边形是菱形（B ）对角线平分且相等的四边形是矩形（C ）对角线互相平分的四边形是平行四边形（D ）对角线垂直且相等的四边形是正方形12.菱形的两条对角线的长分别是6和8，则这个菱形的周长是（）.（A ）24 （B ）20 （C ）10 （D ）5AB CDE AB C DEFA BC DE O A B C D13.如图，矩形ABCD 的两条对角线相交于点O ，∠AOB=60°，AB=2，则矩形的对角线AC 的长是（）. （A ）2 （B ）4（C ）23 （D ）43 14.已知菱形的边长和一条对角线的长都为2cm ，则菱形的面积为（）. （A ）3cm 2 （B ）4cm 2 （C ）3cm 2 （D ）23cm 215.如图，要使ABCD 成为矩形，需添加的条件是（）. （A ）AB=BC （B ）AC ⊥BD（C ）∠ABC=90° （D ）∠1=∠2 16.在四边形ABCD 中，∠A ：∠B ：∠C ：∠D=1：2：2：1，则这个四边形是（）. （A ）平行四边形（B ）菱形（C ）等腰梯形（D ）直角梯形17.连结等腰梯形各边中点的四边形一定是（）.（A ）等腰梯形（B ）矩形（C ）正方形（D ）菱形18.在梯形ABCD 中，AB ∥CD ，∠A=60°，∠B=30°，AD=CD=6，则AB 的长度为（）.（A ）9 （B ）12 （C ）18 （D ）6＋3319.如图，在梯形ABCD 中，AB ∥DC ，∠D=90°，AD=DC=4，AB=1，F 为AD 的中点，则点F 到BC 的距离是（）. （A ）2 （B ）4 （C ）8 （D ）120.（选做）如图，四边形ABCD 中，AB=BC ，∠ABC=∠CDA=90°，BE ⊥AD 于点E ，且四边形ABCD的面积为8，则BE=（）.（A ）2 （B ）3 （C ）22 （D ）2321.（选做）如图，在ABCD 中，AB=6，AD=9，∠BAD 的平分线交BC 于点E ，交DC 的延长线于点F ，BG ⊥AE ，垂足为G ，若BG=42，则△CEF 的周长为（）. （A ）8 （B ）9.5 （C ）10 （D ）11.5 22.在ABCD 中，∠B ＋∠D=170°，则∠A= °.23.在ABCD 中，AB=4，AD=6，∠B=30°，则ABCD 的面积= . 24.如图，在ABCD 中，AC 、BD 相交于点O ，S △ABO =3，则S △BCD = .25.（2002年）已知菱形的两条对角线长分别是5cm 和8cm ，它的面积是 .26.如图，矩形ABCD 的两条对角线相交于O ，∠AOD=120°，AB=4，则AD= . 27.一个正方形的对角线的长为6，则这个正方形的边长为 .28.菱形的一个内角是60°，较短的对角线的长为3，则菱形的周长为 .29.如图，四边形ABCD 是菱形，对角线AC=8，DB=6，DH ⊥AB 于点H ，则DH= .D CB A OA B C D O 12F A BC D .A B C D E G FE AB DC O AB C D D CB A OH OA BC D（第29题图）（第30题图）30.（2005年）如图，7个大小完全相同的小矩形正好拼成一个大矩形，如果大矩形的周长是17cm ，那么小矩形的较短的边长是 cm.31.矩形ABCD 中，对角线AC 、BD 交于点O ，AE ⊥BD 于E ，若OE ：ED=1：3，，则BD= .32.如图，一活动菱形衣架中，菱形的边长都为16cm ，若墙上钉子间的距离AB=BC=16cm ，则∠1= 度.33.如图，矩形的对角线相交于点O ，过点O 的直线交AD 、BC 于点E 、F ，AB=2，BC=3，则图中阴影部分的面积为 .（第33题图）（第34题图） 34.如图，正方形ABCD 的边长为1cm ，E 、F 分别是BC 、CD 的中点，连结BF 、DE ，则图中阴影部分的面积是 cm 2.35.（2004年）等腰梯形的腰长为5cm ，上、下底的长分别为6cm 和12cm ，那么它的高等于 cm.36.如图，在等腰梯形ABCD 中，∠B=60°，AD=DC=4，则这个梯形的周长为 .（第36题图）（第37题图）37.如图，等腰梯形ABCD 中，AD ∥BC ，AD=3，AB=4，BC=7，则∠B 的度数= .38.如图，在直角梯形ABCD 中，∠B=90°，∠C=45°，AD=3，BC=6，则梯形ABCD 的面积为 .（第38题图）（第39题图）39.如图，在等腰梯形ABCD 中，AD ∥BC ，AB=DC ，∠1=∠2，∠C=60°，BC=6，则等腰梯形ABCD 的周长为 .40.如图，在梯形ABCD 中，AD ∥BC ，AB=AD=2，∠A=60°，BC=4，则CD= .（第40题图）（第41题图）41.（选做）如图，在梯形ABCD 中，AB ∥CD ，∠A ＋∠B=90°，CD=5，AB=11，点M 、N 分别为AB 、CD 的中点，则线段MN= .42.（选做）如图，在菱形ABCD 中，∠ADC=72°，AD 的垂直平分线交对角线BD 于点P ，垂足为E ，连接CP ，则∠CPB= 度.A B C1A B C D E A C A B C D D C B A A B C D 12DC B A AD C B N M A B C DE P A CD43.（2001年）已知：如图，BD 是ABCD 的对角线，AE ⊥BD ，CF ⊥BD ，垂足分别是E 、F. 求证：BE=DF.44.（2008年）如图，已知ABCD ，按要求完成下列各题. (1)过点A 作AE ⊥BD 交BD 于点E ，过点C 作CF ⊥BD 交BD 于点F ；(2)证明：△ABE ≌△CDF.45.（2009年）如图，E ，F 是平行四边形ABCD 的对角线AC 上的点，CE=AF.求证：(1)BE=DF ；(2)BE ∥DF.46.（2005年）已知：如图，D 是△ABC 的AB 边的中点，E 是AC 边上不与A 重合的一点，BF ∥AC ，且与ED 的延长线交于点F. 求证：四边形AEBF 是平行四边形.A B CD E F DC B A E F A B CDEF AB C D中考复习之十七：相似1.（2000年）如图，等腰梯形ABCD的两条对角线AC和BD相交于点O，图中相似三角形共有（）.（A）2对（B）3对（C）4对（D）5对2.（2004年）两个相似三角形的相似比是1：4，那么它们的面积比是（）.（A）1：2 （B）1：4 （C）1：16 （D）13.（2003年）两个相似三角形的面积比是1：4，那么它们的相似比是（）.（A）1：2 （B）1：16 （C）4：1 （D）1：44.（2005年）如图，DE∥BC，且AD=2，BD=5，则△ADE与△ABC的相似比为（）.（A）2：5 （B）5：2 （C）2：7 （D）7：2（第4题图）（第5题图）5.（2002年）如图，D、E分别是△ABC中AB、AC边上的点，且AD：DB=AE：EC=1：2，那么△ADE与△ABC面积的比是（）.（A）1：2 （B）1（C）1：3 （D）1：96.下列说法中，错误的是（）.（A）任意两个等边三角形相似（B）有一个锐角对应相等的两个直角三角形相似（C）两个全等三角形一定相似（D）有一个角为30°的两个等腰三角形相似7.如图，Rt△ABC中，CD是斜边上的高，∠A=30°，则S△CBD：S△ABC=（）.（A）1：5 （B）1：4 （C）1：3 （D）1：28.如图，正方形ABCD边长是4，P是CD中点，Q是BC上的一点（不能取B点），要使△ADP与△PCQ相似，则CQ为（）.（A）1 （B）1.5 （C）2 （D）2.5（第8题图（第9题图） (第10题图) (第11题图) (第12题图) 9.如图，在△ABC中，DE∥BC，AD=2，AE=3，BD=4，则AC=（）.（A）7 （B）8 （C）9 （D）1010.如图，在△ABC中，∠C=90°，∠B=60°，D是AC上一点，DE⊥AB于E，且CD=2，DE=1，则BC的长为（）.（A）2 （B）43（C）（D）11.点E、F分别是△ABC中AC、AB边的中点，BE、CF相交于点G，FG=2，则CF的长为（）.（A）4 （B）4.5 （C）5 （D）6A BOD CEADCBB CDAEA BCD QPA DB CAB CD EABCDEGCFABE22m8m12.如图，用3.2m 的竹竿测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时，竹竿与这一点相距8m ，与旗杆相距22m ，则旗杆的高为（）.（A ）12m （B ）10m （C ）8m （D ）7m13.△ABC ∽△DEF ，AB=8,DE=6，则△ABC 与△DEF 周长的比为，面积的比为 . 14.（2009年）已知△ABC ∽△DEF ，且它们的周长之比为1：2，那么它们的面积之比为 .15.一个五边形的各边扩大为原来的3倍，则这个五边形的面积扩大为原来的倍.16.△ABC 的三边分别为3、4、5，与它相似的△DEF 的最大边长为10，则△DEF 的周长为，面积为 .17.中午12点，身高为165cm 的扎西的影长为55cm ，同学格桑的影长为60cm ，则格桑的身高为 cm.18.已知：如图，AB 、CD 相交于点O ，AC ∥BD.求证：BO ·CO=DO ·AO.19.已知：如图，∠C=∠ABD. 求证：AB 2=AD ·AC.20.如图，在矩形ABCD 中，点E 、F 分别在边AD 、DC 上，△ABE ∽△DEF ，AB=6，AE=9，DE=2，求EF 的长.21.如图，PS ⊥a ，PS ⊥b ，测得QS=45米，ST=90米，QR=60米，求河宽PQ.22.如图，已知：EF ∥BC ，FD ∥AB ，AE=1.8，BE=1.2，CD=1.4，求BD.A B C D O A C B DF A C B DE D A B C E F。