出租车上的数学问题
五年级数学分段收费应用题

五年级数学分段收费应用题一、出租车问题一)基本公式:总价=(总路程-起步路程)×单价+起步价总路程=(总价-起步价)÷单价+起步路程二)、例题:1、兴化城区出租车起步路程是3千米,起步价是6元。
每超出1千米单价是1.6元。
(1)XXX乘车到28千米的乡下,他应付多少元?2)小红有22元,最多可以乘车多少千米?3)XXX乘车到33.2千米的乡下,他应付多少元?2、某市出租车计费方法如下表:起步路程起步价3~5千米5千米以外3千米8元每千米2元每千米1.5元(1)XXX乘出租车到18.5千米的地方办事,要付车费多少元?2)小红有车费27元,最多可以行多少千米?三)练:1.某市出租车收费标准是:路程收费标准3千米7元之内3千米每增加1千米多增收以上1.8元⑴乘出租车行9.3千米要付费多少元?⑵16元最多可以乘坐多远的路程?2.某城区出租车计费标准如下表起步路程起步价3~5千米5千米以外3千米9元每千米2.5元每千米2元(1)XXX乘车到22.5千米的乡下,他应付多少元?(2)小红有50元,最多可以乘车多少千米?13.XXX住在幸运小区,春游结束后,他一小我坐出租车从学校回家,起步价6元(2.5千米内含2.5千米),超过2.5千米每增加500米加1元.1)XXX家离学校4300米.到家时,他该付车费多少元?2)XXX从学校坐出租车回家付车资14元,XXX家离学校最多多少千米?2、其它阶段免费基本公式:总价=基准付费+(总时间-基准时间)×第二阶段单价总时间=基准时间+(总价-基准付费)÷第二阶段单价电话费某XXX有两种手机卡,采用的收费标准见下表:种类牢固月租每分钟通话费XXX每月的通话工夫累积不超过80分钟。
XXX每月的通话工夫累积在200分钟左右。
请A卡30元0.3元你帮她们分别选一种比较划算的手机卡,并通过XXX0.6元计算申明缘由。
电费某地的电费收取办法规定如下:每月用电在200千瓦时(含200千瓦时)以内的,每千瓦时收费0.55元;每月用电超过200千瓦时的,超过部分每千瓦时电多加0.10元。
1.12 分段计费的实际问题-人教版数学五年级上册

总用电量
1235 1592 1月1日 2月1日
200千瓦时以内按每 千瓦时0.55元收费
超过部分按每千 瓦时0.65元收费
变式训练
1.每月用电在200千瓦时(含200千瓦时)以内的, 每千瓦时收费0.55元;每月用电超过200千瓦时的, 超过部分每千瓦时电多加0.10元。奶奶家用电情况 如下图,1月份应付电费多少元?
前段
后段
方法二:先假设后调整。
应付车费=单价×总里程 +(起步价-单价×起步里程)
假设
调整
课堂练习
1 五(1)班35名师生照合影。每人一张合影照片,
一共需付多少钱?
合影价格表
照相的钱+加印照片的钱=
照相:27.5元
一共需要付的钱。
(含5张照片)
27.5+2.5 ×(35-5)
加印一张2.5元
=27.5+75
阅读与理解
① 总行驶里程 6.3 公里;
从题目中你知道 ② 3km以内的里程固定价 7 元; 了哪些数学信息? ③ 超过3km的部分,每公里1.5元;
④ 不足1km按1km计算。
探究新知
9 右面是某地出租车的计
价标准。李叔叔乘坐出 租车行驶了6.3km,他应 付出租车费多少钱?
计价标准 3km及以内7元; 超过3km的部分,每千米1.5元 (不足1km,按1km计算)。
阅读与理解
要解决的问题 是什么?
应付出租车总 费用是多少?
行驶的里程是6.3km, 超过3km了,需要 分段计费。
小组合作 该怎么计算李叔叔应付的车费呢?
合作要求 1.各人先尝试解答,然后组内交流。 2.说说你是怎么想的,你有几种解决方法。 3.准备全班汇报。
线段方法解答:出租车分段收费问题,一共要多少钱(四年级数学下册)

题目:出租车3千米以内收费8元,超过3千米后,每千米加收1.70元; 李老师乘坐12千米,要花多少钱?
思路1:理解每段收费是不同的,用线段分别进行表示
思路2:理解分段收费是按照每公里收,还是总路程收
出租车3千米以内收费8元,就是3公里共收8
元
8元
画出3千米线ቤተ መጻሕፍቲ ባይዱ,共收费8元
1.7元
3千米后,每千米1.70元
画出每千米线段,1.70元 画出总里程12千米 每千米1.7元共行程了12-3=9(千米) 总费用,3公里的钱加上每千米1.7元共行驶的钱
8 + 1.7 X 9 = 23.3(元)
3千米
1千米 12千米
小学五年级数学出租车计算应用题
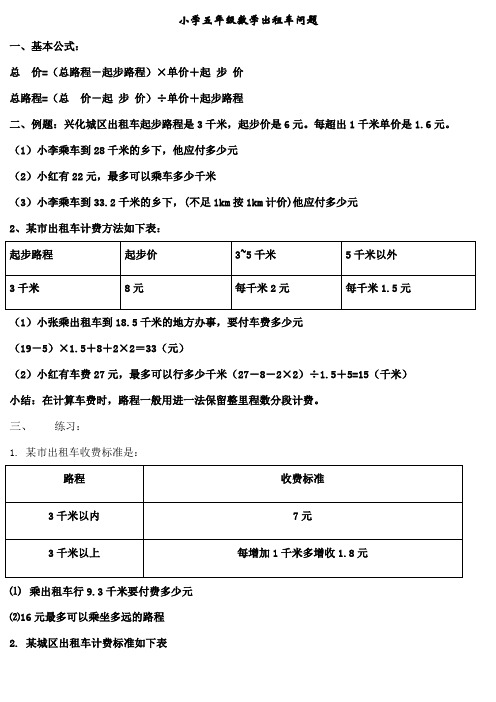
小学五年级数学出租车问题一、基本公式:总价=(总路程-起步路程)×单价+起步价总路程=(总价-起步价)÷单价+起步路程二、例题:兴化城区出租车起步路程是3千米,起步价是6元。
每超出1千米单价是1.6元。
(1)小李乘车到28千米的乡下,他应付多少元(2)小红有22元,最多可以乘车多少千米(3)小李乘车到33.2千米的乡下,(不足1km按1km计价)他应付多少元2、某市出租车计费方法如下表:(1)小张乘出租车到18.5千米的地方办事,要付车费多少元(19-5)×1.5+8+2×2=33(元)(2)小红有车费27元,最多可以行多少千米(27―8―2×2)÷1.5+5=15(千米)小结:在计算车费时,路程一般用进一法保留整里程数分段计费。
三、练习:1. 某市出租车收费标准是:⑴乘出租车行9.3千米要付费多少元⑵16元最多可以乘坐多远的路程2. 某城区出租车计费标准如下表(1)小李乘车到22.5千米的乡下,他应付多少元(2)小红有50元,最多可以乘车多少千米3.在一个停车场停车一次至少要交费8元。
如果停车超过3小时,每多停1小时车要多交2.5元。
一辆汽车在离开时交了23元,这辆车停了多长时间4、在一个停车停车一次至少要交费6元。
如果停车超过3小时,每多停1小时车要多交2.5元。
一辆汽车停了6.5小时,在离开时应交费多少元5、小红和伙伴们16人一起拍照片,7元拍一次有1张底片和6张照片。
每加洗1张0.5元。
如果每人有1张照片,每人要多少元钱6.陈叔叔选择的手机话费收费标准是:30元包打220分钟,超过的按每分钟0.3元计算,陈叔叔8月份打了280分钟,陈叔叔至少应该付多少元电话费7.乐至到石湍有21千米,秦老师从乐至坐出租车回石湍,已知出租车的起步价是4元,2千米后按每千米1.4元计费,秦老师至少需要付多少元8.某停车场收费标准是:(1)1小时内收2.5元。
机场的出租车问题数学建模题目

机场的出租车问题数学建模题目机场出租车问题是指在机场附近出租车的数量有限,而需求却很大,导致乘客等待时间过长的问题。
为了解决这个问题,我们可以通过数学建模来优化出租车的分配和调度,使得乘客的等待时间最小化。
首先,我们需要确定机场出租车的数量和位置。
假设机场周围有n 辆出租车,我们可以将它们的位置表示为(x1, y1), (x2, y2), ..., (xn, yn)。
这些位置可以通过GPS系统获取,我们可以将其转换为平面上的坐标,方便后续的计算。
其次,我们需要确定乘客的需求分布。
假设在机场附近有m个乘客需要出租车,我们可以将他们的位置表示为(x1', y1'), (x2',y2'), ..., (xm', ym')。
乘客的需求分布可能受到时间、天气等因素的影响,我们可以通过历史数据和统计分析来确定乘客的出现概率和位置分布。
接着,我们需要确定出租车的调度规则。
一般来说,我们希望出租车能够以最短的时间到达乘客的位置,并且尽量减少乘客的等待时间。
为了实现这一目标,我们可以采用最短路径算法来确定每辆出租车的调度顺序和路径规划,以便最大程度地满足乘客的需求。
另外,我们还可以考虑出租车的容量和载客规则。
为了提高出租车的利用率,我们可以考虑将多个乘客的需求合并,让一辆出租车同时满足多位乘客的需求。
这就涉及到了乘客需求的匹配问题,我们可以通过数学建模和算法设计来实现这一目标。
在实际应用中,我们还需要考虑一些约束条件。
比如,每辆出租车的最大载客量、路况和交通限制、乘客等待时间的最大限制等。
这些约束条件可以通过线性规划或整数规划来描述,并且我们可以通过求解优化问题来获得最优的出租车调度方案。
除了以上提到的问题,我们还可以考虑一些扩展问题。
比如,机场出租车的调度问题可能会受到节假日或活动等因素的影响,我们可以通过实时数据和预测分析来进行调整;另外,我们还可以考虑解决出租车的分配问题,比如在机场附近的不同区域分别安排不同数量的出租车,以适应不同区域的需求特点。
2019数学建模c题出租车c

2019数学建模c题出租车c
对于这个出租车问题,我们可以使用数学建模来解决。
以下是一个可能的建模过程:
1. 定义问题:我们需要找到最优的出租车调度方案,使得所有乘客的需求都能得到满足,并且最小化出租车的总行驶里程。
2. 建立数学模型:设想我们有n辆出租车和m个乘客。
我们需要确定每个乘客的出发地和目的地,以及每辆出租车的行驶路线。
我们可以将每个乘客的起始点和目的地表示为坐标点(x1, y1)和(x2, y2),每辆出租车的位置也可以表示为坐标点(x, y)。
3. 求解过程:我们可以使用最优化算法来找到最佳的出租车调度方案。
一种常用的方法是线性规划。
我们可以将出租车的总行驶里程作为目标函数,并设置一些约束条件。
例如,每个乘客只能被一辆出租车接送,出租车的行驶里程不能超过一定的限制等等。
4. 实施方案:根据求解结果,我们可以获得每个乘客的出租车选择和行驶路径。
然后,我们可以将乘客指派给出租车,并通知出租车司机按照指定路径行驶。
5. 评估结果:我们可以通过比较实际行驶里程和最优解计算得到的行驶里程,来评估方案的效果。
如果实际行驶里程较接近最优解,说明我们的模型和算法是有效的。
总之,数学建模可以帮助我们解决出租车调度问题,优化出租车的行驶路径,提高运输效率。
当然,具体的建模过程还需要根据实际情况进行调整和扩展。
出租车中的数学问题教学设计

课题名称:出租车中的数学问题设计者:王立华单位:平谷区山东庄中学教材版本:北京市义务教育课程改革实验教材教学年级:初一年级一、教学内容分析1、单元主要内容:本章先介绍了字母表示数和列代数式及代数式的值、合并同类项的知识,然后学习等式的概念和等式的两个基本性质,以及方程、方程的解、解方程等概念;接着学习运用等式的基本性质和移项法则解一元一次方程,归纳出一元一次方程的概念,以及解一元一次方程的一般步骤;最后结合实际举例说明如何列出一元一次方程解应用题,从中渗透“未知”可以转化为“已知”的思想方法以及用方程的方法处理某些问题的优越性。
课时安排:字母表示数2课时同类项与合并同类项1课时等式与方程1课时等式的基本性质1课时一元一次方程和它的解法7课时一元一次方程的应用10课时小节与复习3课时2、教材编写意图通过学习应用一元一次方程解决简单的实际问题,初步学会用方程表示实际问题中的数量关系,进而使学生初步体验:方程是刻画现实世界数量关系的一个有效的数学模型,而本节课则是通过现实生活中的出租车收费问题使学生经历研究问题过程学习建立数学模型的一般过程,从而培养学生应用数学的意识体会数学地价值,为此课前简单的了解学生对出租车问题知识的认识,让学生从现实生活中的出租车收费问题具体到用数学方法求车费,亲身体会现实生活中的问题可以用数学知识解决,体会了数学的实用价值,提高学习数学的兴趣。
3、教材所处的地位及前后联系解方程是数学中的主要内容之一,而解一元一次方程不仅有很多直接应用而且它也是学习解其他方程和方程组的基础。
一元一次方程的应用,小学只知道列方程解应用题,现在则进一步强调实际应用,不仅是解决数学中的应用题,更是解决实际生活问题的一种手段。
不光让学生感受列方程解应用题的优越性,另一方面也体现数学知识可以解决实际问题。
列方程解决实际问题体现了现实世界中事物的相互联系,学生从中体会对应的关系,为今后学习函数奠定了基础。
案例:出租车上的数学问题

案例:出租车上的数学问题师:同学们都乘过出租车吧?坐出租车的时候你有没有想过——出租车上有哪些数学问题呢?师:今天这节课我们就一起来研究研究出租车上的数学问题。
当我们乘坐出租车之后,会得到这样的专用发票——(出示3张出租车专用发票)师:你能看懂出租车发票吗?从发票上我们能够获得哪些信息呢?拿出自己带的发票,小组内交流,不懂的地方讨论讨论。
(小组讨论之后请一组汇报)生1:我们组发现出租车票上有车牌号、电话号码这样一些信息,我们想这些信息是为了便于顾客电话联系到这辆车,寻找丢失物品或者投诉的。
生2:我们还发现有乘车听日期、上车时间、下车时间、单价、里程这些信息。
而且我们知道用单价乘以里程的结果就是最后的车费,也就是小票上的金额。
生3:我们还发现发票上的单位都是四位数,我们认为因为出租车公司有的单位名称会比较长,市交通管理局为了便于管理就给公司都编了号,所以发票上就都是数字了。
生4:最后我们组有个问题没有解决,我们发现发票上写着一个“状态:0”,这是什么意思?哪位同学能够解答?生5:我也有一样的疑问,我也观察到这一点,而且看过很多发票的“状态”一栏要么是“1”,要么是“0”,没有“2”以上的数字出现,这是为什么?(同学们十分热情,纷纷举手要作答)生6:我了解,在这里“1”代表往返乘车,“0”代表单程。
生7:我的理解恰好相反,我认为“1”是单程,0是返程。
因为我也看了很多人的发票,大多数都是“1”,而我们生活中毕竟乘坐往返车的是少数人,所以我认为“1”是单程,0是往返。
(同学们纷纷赞同)师:看来大家都认为“1”和“0”代表的分别是单程和往返乘车。
华老师以前也不知道这个问题,为此专程到交管局了解了一下,1代表往返,0代表单程。
生7的见解很有道理,可为什么错了呢?课后再研究,好吗?师:还有什么问题吗?生1:我还发现了有一栏写的是“等候”时间,我也知道等时间是要花出租费的,但我不知道等候与正常速度行驶在计价上有什么区别呢?生2:等候时间累计5分钟就按照1公里来计价。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 1
2
3 4
5 6 7
8
9 10 11 12 13 14 15 16 17 18
10元
1.60元/千米
2.40元/千米
1.60元/千米的收费标准:
(1) (2) (3) (4) 3千米以内含3千米收费10元; 3千米以上至15千米(含15千米 ) ,每千米1.60元; 15千米以上每千米2.40元; 等候每累计5分钟加收1公里租价的费用。
从家到图书馆大约行驶 多少千米? 请你选择正确的算式, 并说明理由。
按里程计价
图书馆1.20元/千米,来自用16元。(× ) (1) 16÷1.2≈14(千米) (2) (16-10)÷1.2=5(千米) (× ) (3)(16-10)÷1.2+4=9(千米) ( √)
王迪与周蕾合打一辆1.60元/千米的出租车。 行驶到4千米处,王迪下车,周蕾继续乘 车又行驶了2千米。两人可以怎样分摊车费?
基价
按里程计价
思 考 题
4千米
2千米
“阶梯式水价”将居民生活用水中的 供水价格划分为3个级别。其中, 第一级的供水价格是1.09元/立方米; 第二级的供水价格是1.635元/立方米; 第三级的供水价格是2.18元/立方米。
孙老师要乘出租车到距学校7千米的教委 领一份紧急通知,取通知需要10分钟,然后乘 出租车按原路回校。如果孙老师只乘坐1.20元 的出租车,在一路畅通的情况下孙老师怎样打 车更省钱?
1.20元/千米的收费标准: (1)4千米以内含4千米收费10元; (2)4千米以上至15千米(含15千米)每千米1.20元; (3)15千米以上每千米1.80元。 (4)等候每累计5分钟加收1公里租价的费用。
我叫张洁
乘坐1.60元/千米的出租车。
汽车行驶如果一路畅通。到
达时应付给司机多少元 ?
家
00:01:12 00:10:04
14 22
我 叫 玲 玲
从家到图书馆大约行驶 多少千米? 请你选择正确的算式, 并说明理由。
图书馆
家 1.20元/千米,共用16元。 (1) 16÷1.2≈14(千米) (2) (16-10)÷1.2=5(千米) (3)(16-10)÷1.2+4=9(千米)
我 叫 玲 玲 基价 家
a b 让出租车等候继续乘坐 换乘另一辆出租车
10+(14-4)×1.2+2.4≈24(元)
10+(7-4)×1.2≈14(元) 14×2=28(元)
动物园 6千米
我叫张洁
乘坐1.60元/千米的出租车。
汽车行驶如果一路畅通。到
达时应付给司机多少元 ?
基价
家
按里程计价 动物园
6千米 10+1.6×(6-3)
下车时,我特意要了发票, 可怎样算也不对,这到底 是怎么回事?同学们能帮 我解决吗?
请你试试看:
单价 里程(千米) 等候时间 金额(元) 1.60元/千米 1.60元/千米 5 8
1.20元/公里
1.60元/公里
2.00元/公里
单 基
价 价
1.20元/公里 10.00元
1.60元/公里 10.00元
里 程 金 额 等候时间 其 他
1.60元/公里
北京市物价局监制
1、本车每公里租价1.60元,基价公里为 敬 3公里,起价10.00元。 告 2、单程行驶15公里以上部分加收50%空 乘 驶费。 (每公里2.40元) 客 3、等候每累计5分钟加收1公里租价的费用。 1.60元/公里
