8421BCD—余3码转换
8421转换法 -回复

8421转换法-回复8421转换法,也被称为8421BCD码,是一种用来将十进制数字转换成二进制码的方法。
在这种转换法中,我们将每一个十进制数字转换成相应的BCD码。
BCD码是一种用4位二进制数表示一个十进制数的编码方式。
8421转换法的名字源自其权重分配,这种分配方式为8-4-2-1。
具体来说,每一个十进制数字都被转换成4位二进制数,其中最高位的权重为8,其次为4,然后是2,最低位的权重为1。
通过这种方式,我们可以方便地将十进制数字转换成二进制码。
在进行8421转换时,我们需要遵循以下几个步骤:Step 1:将十进制数字分解成各位数值。
Step 2:将每个各位数值分别转换成4位的BCD码。
为此,我们可以使用真值表或者逻辑运算方法进行转换。
Step 3:将每个各位数值的BCD码连接在一起,得到最终的BCD码。
让我们以一个具体的例子来说明上述步骤。
假设我们要将十进制数字123转换成BCD码。
Step 1:将数字123分解成各位数值1、2和3。
Step 2:将每个各位数值分别转换成4位的BCD码。
- 数字1转换成BCD码:0001- 数字2转换成BCD码:0010- 数字3转换成BCD码:0011Step 3:将每个各位数值的BCD码连接在一起,得到最终的BCD码:000100100011通过以上步骤,我们成功地将十进制数字123转换成了BCD码000100100011。
8421转换法的应用非常广泛。
在数字电路设计中,我们常常需要将十进制数字转换成二进制码。
这种转换法具有简单、直观、可行的特点。
通过8421转换法,我们可以将数字信号传输到不同的逻辑电路中,如七段数码管、计数器、显示设备等。
8421转换法也为数字化系统的实现提供了一种有效的方式,可以将模拟信号转换成数字信号,提高了信息处理的精度和准确性。
以电子计算机为例,计算机内部采用二进制系统进行运算和存储。
因此,我们需要将输入的十进制数字转换成二进制码,以便计算机进行处理。
数字逻辑课后习题答案(科学出版社_第五版)

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B)+AB(C+C)=AB+AC=右边(3)EDCCDACBAA)(++++=A+CD+E 证明:左边=EDCCDACBAA)(++++=A+CD+A B C+CD E=A+CD+CD E=A+CD+E=右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) = Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
EDA实验三组合逻辑电路设计(一)--编译码器设计

西安邮电学院实验中心实验报告院系电子工程学院班级学号姓名成绩教师签字实验日期实验名称组合逻辑电路设计(一)--编译码器设计_______________________________________________________一、实验目的二、实验所用仪表及主要器材三、实验原理简述四、实验测量记录:(如数据、表格、曲线、计算等)五、实验遇到的问题及解决办法:(余留问题,体会等)一、实验目的(1)熟悉组合逻辑电路的VHDL描述方法。
(2)掌握利用CPL器件实现组合逻辑数字电路的方法和过程。
(3)熟练掌握“case”语句与“if…else…”语句的用法。
二、实验所用仪表及主要器材PC,可编程逻辑实验电路板,下载线,USB电源线,双踪示波器,数字万用表,导线若干。
三、实验原理简述应用VHDL设计简单的逻辑电路四、实验内容在MAX+PULSII环境下,用VHDL语言按照输入—>编译—>仿真。
(1)8421BCD码转换为余3码转换表.在MAX+plusII 环境下,用VHDL 语言描述下列逻辑电路,并编译,仿真。
程序仿真结果:(2)设计一个优先编码器。
程序实现如下:仿真结果:五、实验结果见上述内容。
六、实验心得在本次实验中我学会了使用MAX+PLUSII软件的文本编程的方式设计电路。
在本次实验的文本编译环节中出现不少问题:(1)保存时文件名与实体名不一致,导致程序编译结果不正确。
(2)写程序时没有按照语法规则编写,使得文件编译频繁报错,标点的错误也会导致整个程序无法编译。
经过本次实验,加深了我对VHDL的文本编译设计的理解,今后我应该多练习MAX+PLUSII软件以减少错误。
数字逻辑(第2版)习题答案

毛法尧第二版习题一1.1 把下列不同进制数写成按权展开式:⑴(4517.239)10= 4×103+5×102+1×101+7×100+2×10-1+3×10-2+9×10-3⑵(10110.0101)2=1×24+0×23+1×22+1×21+0×20+0×2-1+1×2-2+0×2-3+1×2-4⑶(325.744)8=3×82+2×81+5×80+7×8-1+4×8-2+4×8-3⑷(785.4AF)16=7×162+8×161+5×160+4×16-1+A×16-2+F×16-31.2 完成下列二进制表达式的运算:1.3 将下列二进制数转换成十进制数、八进制数和十六进制数:⑴(1110101)2=(165)8=(75)16=7×16+5=(117)10⑵(0.110101)2=(0.65)8=(0.D4)16=13×16-1+4×16-2=(0.828125)10⑶(10111.01)2=(27.2)8=(17.4)16=1×16+7+4×16-1=(23.25)101.4 将下列十进制数转换成二进制数、八进制数和十六进制数,精确到小数点后5位:⑴(29)10=(1D)16=(11101)2=(35)8⑵(0.207)10=(0.34FDF)16=(0.00111)2=(0.15176)8采用0舍1入规则⑶(33.333)10=(21.553F7)16=(100001.01011)2=(41.25237)81.5 如何判断一个二进制正整数B=b6b5b4b3b2b1b0能否被(4)10整除?解: 一个二进制正整数被(2)10除时,小数点向左移动一位, 被(4)10除时,小数点向左移动两位,能被整除时,应无余数,故当b1=0和b0=0时, 二进制正整数B=b6b5b4b3b2b1b0能被(4)10整除.1.6 写出下列各数的原码、反码和补码:⑴0.1011[0.1011]原=0.1011; [0.1011]反=0.1011; [0.1011]补=0.1011⑵0.0000[0.000]原=0.0000; [0.0000]反=0.0000; [0.0000]补=0.0000⑶-10110[-10110]原=110110; [-10110]反=101001; [-10110]补=1010101.7 已知[N]补=1.0110,求[N]原,[N]反和N.解:由[N]补=1.0110得: [N]反=[N]补-1=1.0101, [N]原=1.1010,N=-0.10101.8 用原码、反码和补码完成如下运算:⑴0000101-0011010[0000101-0011010]原=10010101;∴0000101-0011010=-0010101。
数字逻辑课后答案第二章
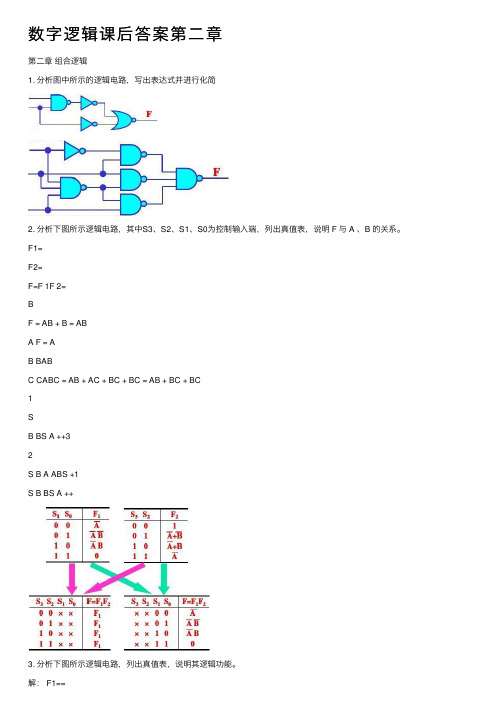
数字逻辑课后答案第⼆章第⼆章组合逻辑1. 分析图中所⽰的逻辑电路,写出表达式并进⾏化简2. 分析下图所⽰逻辑电路,其中S3、S2、S1、S0为控制输⼊端,列出真值表,说明 F 与 A 、B 的关系。
F1=F2=F=F 1F 2=BF = AB + B = ABA F = AB BABC CABC = AB + AC + BC + BC = AB + BC + BC1SB BS A ++32S B A ABS +1S B BS A ++3. 分析下图所⽰逻辑电路,列出真值表,说明其逻辑功能。
解: F1==真值表如下:当B ≠C 时, F1=A 当B=C=1时, F1=A 当B=C=0时, F1=0裁判判决电路,A 为主裁判,在A 同意的前提下,只要有⼀位副裁判(B ,C )同意,成绩就有效。
F2=真值表如下:CB BC A C AB C B A +++ABCC B A ABC C B A C B A +⊕=++)(A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 100000111AC BC AB C A C B B A ++=++当A 、B 、C 三个变量中有两个及两个以上同时为“1”时,F2 = 1 。
4.图所⽰为数据总线上的⼀种判零电路,写出F 的逻辑表达式,说明该电路的逻辑功能。
解:F=只有当变量A0~A15全为0时,F = 1;否则,F = 0。
因此,电路的功能是判断变量是否全部为逻辑“0”。
5. 分析下图所⽰逻辑电路,列出真值表,说明其逻辑功能解:因此,这是⼀个四选⼀的选择器。
6. 下图所⽰为两种⼗进制数代码转换器,输⼊为余三码,输出为什么代码?解:A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1000011111514131211109876543210A A A A A A A A A A A A A A A A +++301201101001X A A X A A X A A X A A F +++=这是⼀个余三码⾄8421 BCD 码转换的电路7. 下图是⼀个受 M 控制的4位⼆进制码和格雷码的相互转换电路。
数字电子技术基础习题没答案

20.试说明下列各种门电路中哪些可以将输出端并联使用(输入端的状态不一定相同)。
(1)具有推拉式输出级的TTL电路;
(2)TTL电路的OC门;
(3)TTL电路的三态输出门;
(4)普通的CMOS门;
(5)漏极开路输出的CMOS门;
(6)CMOS电路的三态输出门;
第三章 逻辑代数基础、逻辑函数化简
⒍将下列数转换为十进制数:1101B4FBH110.11B
⒎将下列数转换为二进制数:7.85D3DF.2BH256D
⒐将下列数转换为十六进制数:256D1101.11B110.11B
⒑将下列十进制数转换为对应的八进刺数:
211302725048101295100.625
⒒分别用842lBCD码、余3码表示下列各数:
(3)A接10V,B悬空.用万用表测B端电压,VB为多少伏?
(4)A接0.3V,B悬空,测VB时应为多少伏?
(5)A接5kΩ电阻,B悬空,测VB电压时,应为多少伏?
15.在图2-5所示电路中,(1)设RK=3kΩ,RB=20kΩ,试问晶体管的β值最小应为多少才能满足饱和条件?(2)设β=30,RB=30kΩ,试问RK的阻值最大应该是多少才能满足饱和条件?
图5-9
11.时序逻辑电路与组合逻辑电路的主要区别是什么;
描述时序电路逻辑功能的方法有哪几种?它们之间有何种关系?
12.已知状态图如图5-10所示,试作出它的状态表。
图5-10
13.已知某时序电路的状态表如表5-1所示,试画出它的状态图。如果电路的初始状态在S2,输入信号依次为0,1,0,1,1,1,试求出相应的输出。
图4-3
5.用三个异或门和三个与门实现下列逻辑关系
6.分析图4-4所示各电路的逻辑功能。写出电路输出信号的逻辑表达式。
8421bcd码转换十进制方法小数点

8421bcd码转换十进制方法小数点8421BCD码是一种二进制编码方式,常用于将十进制数字转换为二进制数字,它可以将一个十进制数表示为四位二进制码。
8421BCD码中的每个十进制数表示为4位二进制码,其中8、4、2、1代表二进制码的权重。
例如,十进制数3可以用8421BCD码表示为:0011。
这里的0是0000, 1是0001, 2是0010, 3是0011, 4是0100, 5是0101, 6是0110, 7是0111, 8是1000, 9是1001。
那么如果给定一个8421BCD码,我们如何将其转换为十进制数字呢?下面是一种简单的方法:1.将给定的8421BCD码从左到右依次分割成四位一组,每一组代表一个十进制数。
2.将每一组的权重与相应的二进制位进行相乘,然后将结果相加,即得到对应的十进制数。
举一个例子,假设给定的8421BCD码为1001 0100 0001。
我们可以按照上面的方法进行转换:-第一组:1001,权重为8、4、2、1。
计算方式为:1*8 + 0*4 + 0*2 + 1*1 = 9。
-第二组:0100,权重为8、4、2、1。
计算方式为:0*8 + 1*4 + 0*2 + 0*1 = 4。
-第三组:0001,权重为8、4、2、1。
计算方式为:0*8 + 0*4 + 0*2 + 1*1 = 1。
将每一组的计算结果相加,即得到最终的十进制数:9 + 4 + 1 = 14。
通过以上的步骤,我们可以将给定的8421BCD码转换为十进制数14。
需要注意的是,上述方法适用于8421BCD码的转换,如果使用其他二进制编码方式,可能需要不同的转换方法。
在实际应用中,我们可以利用计算机编程语言中提供的函数或算法来进行8421BCD码到十进制数的转换。
例如,我们可以使用C语言中的位操作来进行转换:```c#include <stdio.h>int BCDToDecimal(int bcd) {int decimal = 0;int weight = 1;while(bcd > 0) {decimal += (bcd % 10) * weight; bcd /= 10;weight *= 2;}return decimal;}int main() {int bcd = 1001;int decimal = BCDToDecimal(bcd);printf("Decimal: %d\n", decimal);return 0;}```以上的C语言代码中定义了一个BCDToDecimal函数,用于将给定的BCD码转换为十进制数。
数字电子技术第4章组合逻辑电路习题解答
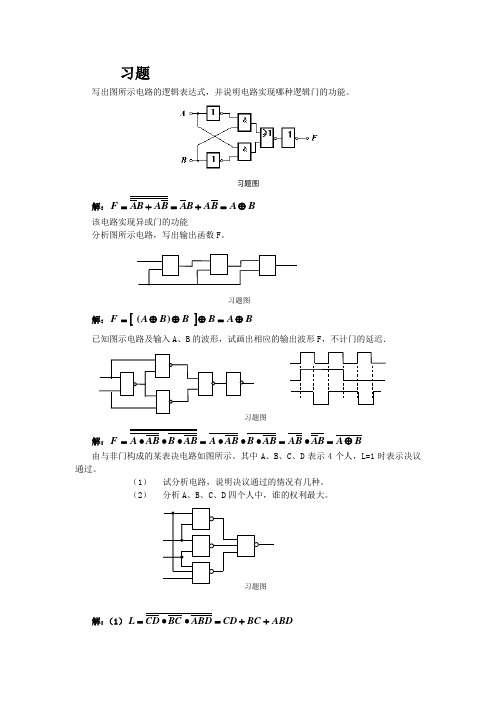
、已知8421BCD可用7段译码器,驱动日字LED管,显示出十进制数字。指出下列变换真值表中哪一行是正确的。(注:逻辑“1”表示灯亮)
D
C
B
A
a
b
c
d
e
f
g *
0
0
0
0
0
0
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
1
1
7
0
1
1
(1)试分析电路,说明决议通过的情况有几种。
(2)分析A、B、C、D四个人中,谁的权利最大。
习题图
解:(1)
(2)
ABCD
L
ABCD
L
0000
0001
0010
0011
0100
0101
0110
0111
0
0
0
1
0
0
1
1
1000
1001
1010
1011
1100
1101
1110
1111
0
0
0
1
0
1
1
1
(3)根据真值表可知,四个人当中C的权利最大。
3) 用与或非门实现。
解:(1)将逻辑函数化成最简与或式并转换成最简与非式。
根据最简与非式画出用与非门实现的最简逻辑电路:电路略。
(2 )由上述卡偌图还可得到最简或与表达式:
即可用或非门实现。
(3)由上步可继续做变换:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
VHDL程序并行语句的应用
一、实训目的
1.巩固编译、仿真VHDL文件的方法。
2.掌握VHDL程序并行语句的应用。
二、实训器材
计算机与Quartus Ⅱ工具软件。
三、实训指导
(一) 实训原理
8421BCD-余3码转换电路的真值表如表3-1所示。
表3-1 8421BCD-余3码转换电路的真值表
输入 输出
a3 a2 a1 a0 y3 y2 y1 y0
0 0 0 0 0 0 1 1
0 0 0 1 0 1 0 0
0 0 1 0 0 1 0 1
0 0 1 1 0 1 1 0
0 1 0 0 0 1 1 1
0 1 0 1 1 0 0 0
0 1 1 0 1 0 0 1
0 1 1 1 1 0 1 0
1 0 0 0 1 0 1 1
1 0 0 1 1 1 0 0
(二)实训步骤
1.设计输入VHDL文件
(1)建立工程项目。
(2)建立VHDL文件。
(3)用条件信号赋语句或选择信号赋值语句等并行语句设计VHDL文件。
VHDL代码如下:
LIBRARY ieee;
USE ieee.std_logic_1164.ALL;
ENTITY ysmzh IS
PORT(a:IN STD_LOGIC_VECTOR(3 DOWNTO 0);
y:OUT STD_LOGIC_VECTOR(3 DOWNTO 0));
END ysmzh;
ARCHITECTURE a OF ysmzh IS
BEGIN
PROCESS(a)
BEGIN
CASE a IS
WHEN "0000"=>y<="0011";
WHEN "0001"=>y<="0100";
WHEN "0010"=>y<="0101";
WHEN "0011"=>y<="0110";
WHEN "0100"=>y<="0111";
WHEN "0101"=>y<="1000";
WHEN "0110"=>y<="1001";
WHEN "0111"=>y<="1010";
WHEN "1000"=>y<="1011";
WHEN "1001"=>y<="1100";
WHEN OTHERS=>NULL;
END CASE;
END PROCESS;
END a;
2.编译仿真VHDL文件
(1)编译VHDL文件。
如果有错误,检查并纠正错误,直至最后通过。
(2)仿真VHDL文件。
认真核对输入/输出波形,检查设计的功能是否正确。
8421BCD-余3码转换的仿真波形图如图3-1所示。
图3-1 8421BCD-余3码转换仿真波形图
四、实训总结
通过本次试验我掌握了VHDL文件的编译与仿真,同时巩固了VHDL程序并行
语句的应用。
