一元二次讲义 打印一份
一元二次方程教材分析讲义

高次方程
新课程标准
• 能够根据具体问题中的数量关系,列出方程,体会方程 是刻画现实世界的一个有效的数学模型;
• 经历用观察、画图或计算器等手段估计方程解的过程; • 理解配方法,会用因式分解法、公式法、配方法解简单
的数字系数的一元二次方程; • 能根据具体问题的实际意义,检验结果是否合理.
课程学习目标
以 做
x m2 2m2
一
些
铺
如果(1)和(2)中的条件
垫
m>-1和m>0去掉又如何解?
设计让推导公式成为一种需要 求根公式使我们省略了每次重复的配方过程.(机器) 求根公式包含初中所学的六种运算,最美的公式 解方程本身就是变形的过程.
b b2 4ac x
2a
解一元二次方程(公式法)
用配方法解方程
程之间的联系,体会
试求 a 2 2007a 等20式0变8 的形的值一。般方法 a2 1
降次,解一元二次方程
从一元二次方程解法的发展历史来看, 我们在教学的安排顺序如下:
1.直接开平方法 2.配方法 3.公式法 4.因式分解法
一元二次方程(配方法)
①用配方法解二次项系数为1的一元二次方程.
一元二次方程ax2 bx c 0a 0
题
(y+1)2与2y的
差.
3y2 =0 ⑥
例1(补).判断下列方程是否为一元二次方程?
(1) 3x 2 5y 3 (2) x2 4
1 x2
x2
2
(3) x 2 1 x 整式方程 x 1
x2 4 1
(4) 7 x 5 x 2 x
3
2
(5) x 2 4 (x 2)2 整理化简
这样由基本到一般再到特殊的过程是十分切合学生的认
一元二次方程及其应用讲义

《一元二次方程及其应用》讲义一、一元二次方程的定义【例题】1、关于x 的方程023)1()1(2=++++-m x m x m ,当m 时为一元一次方程;当m 时为一元二次方程。
2、下列方程中,是关于x 的一元二次方程的有________.(1)2y 2+y -1=0;(2)x (2x -1)=2x 2;(3)21x-2x=1;(4)ax 2+bx+c=0;(5)12x 2=0. 3、关于x 的方程(m 2-1)x 2+(m -1)x+2m -1=0是一元二次方程的条件是________.【习题】1、下列方程中是一元二次方程的是( ).A.xy +2=1B. 09212=-+xx C. x 2=0 D.02=++c bx ax 2、下列方程中,不是一元二次方程的是( ) A.2x 2+7=0 B.2x 2+23x +1=0 C.5x 2+x 1+4=0 D.3x 2+(1+x ) 2+1=03、关于x 的方程(m -4)x 2+(m +4)x +2m +3=0,当m __________时,是一元二次方程,当m __________时,是一元一次方程.4、下列说法正确的是( )A .一元二次方程的一般形式是20ax bx c ++= B .一元二次方程20ax bx c ++=的根是242b b ac x a -±-= C .方程2x x =的解是x =1D .方程(3)(2)0x x x +-=的根有三个 二、一元二次方程的根【例题】1、若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n的值是( )A 、1B 、2C 、-1D 、-22、若x =1是方程ax 2+bx +c =0的解,则( )A.a +b +c =1B.a -b +c =0C.a +b +c =0D.a -b -c =03、已知0和1-都是某个方程的解,此方程是( )A. 012=-xB. 0)1(=+x xC. 02=-x xD. 1+=x x4、如果21x -2x -8=0,则1x 的值是________.5、已知一元二次方程02=++c bx ax ,若0=++c b a ,则该方程一定有一个根是( )A. 0B. 1C. -1D. 2【习题】1、若x =-1是方程ax 2+bx +c =0的解,则( )A.a +b +c =1B.a -b +c =0C.a +b +c =0D.a -b -c =02、已知(x 2+y 2+1)(x 2+y 2+3)=8,则x 2+y 2的值为( ).A .-5或1B .1C .5D .5或-13、已知m 是一元二次方程x 2–2005x +1=0的解,求代数式22200520041m m m -++的值.4、已知x = –5是方程x 2+mx –10=0的一个根,求x =3时,x 2+mx –10的值.三、一元二次方程的解法【例题】1、填写解方程3x (x +5)=5(x +5)的过程解:3x (x +5)__________=0(x +5)(__________)=0x +5=__________或__________=0∴x 1=__________,x 2=__________2、用配方法解方程x 2+2x -1=0时①移项得__________________②配方得__________________即(x +__________)2=__________③x +__________=__________或x +__________=__________④x 1=__________,x 2=__________3、方程2(x+2)2-8=0的根是 。
一元二次方程解法讲义(全4讲)

一元二次方程解法讲义(全四讲)第一讲 直接开平一、学习目标了解形如()()20x h k k +=≥的一元二次方程的解法——直接开平方法;能够熟练而准确的运用开平方法求一元二次方程的解.二、知识回顾1.什么叫做平方根?平方根有哪些性质?平方根的定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根.用式子表示:若x 2=a ,则x 叫做a 的平方根.记作x=如:9的平方根是3±;425的平方根是25±.平方根的性质:(1)一个正数有两个平方根,这两个平方根是互为相反数的; (2)0的平方根是0; (3)负数没有平方根.2.x 2=4,则x=±2.想一想:求x 2=4的解的过程,就相当于求什么的过程?三、新知讲解四、典例探究1.用直接开平方法求一元二次方程的解【例1】解方程:(1)2x 2﹣8=0;(2)(2x ﹣3)2=25.分析:(1)先变形得到x 2=4,然后利用直接开平方法求解;(2)首先两边直接开平方可得2x ﹣3=±5,再解一元一次方程即可.解答:解:(1)x 2=4,两边直接开平方,得x1=2,x2=﹣2.(2)两边直接开平方,得2x﹣3=±5,则2x﹣3=5,2x﹣3=﹣5,所以x=4,x=﹣1.点评:本题考查了解一元二次方程﹣直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法求解.总结:运用直接开平方法解一元二次方程,首先要将一元二次方程的左边化为含有未知数的完全平方式,右边化为非负数的形式,然后直接用开平方的方法求解.练1.(2015•东西湖区校级模拟)解方程:(2x+3)2﹣25=0分析:先移项,写成(x+a)2=b的形式,然后利用数的开方解答.解答:解:移项得,(2x+3)2=25,开方得,2x+3=±5,解得x1=1,x2=﹣4.点评:(1)用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.(2)运用整体思想,会把被开方数看成整体.(3)用直接开方法求一元二次方程的解,要仔细观察方程的特点.练2.(2014秋•昆明校级期中)解方程:9(x+1)2=4(x﹣2)2.分析:两边开方,即可得出两个一元一次方程,求出方程的解即可.解答:解:两边开方得:3(x+1)=±2(x﹣2),即3(x+1)=2(x﹣2),3(x+1)=﹣2(x﹣2),解得:x1=﹣7,x2=.点评:本题考查了解一元二次方程和解一元一次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程.2.用直接开平方法判断方程中字母参数的取值范围【例2】(2015春•南长区期末)若关于x的一元二次方程x2﹣k=0有实数根,则()A.k<0 B.k>0 C.k≥0 D.k≤0分析:根据直接开平方法的步骤得出x2=k,再根据非负数的性质得出k≥0即可.解答:解:∵x2﹣k=0,∴x2=k,∵一元二次方程x2﹣k=0有实数根,∴k≥0,故选:C..点评:此题考查了直接开平方法解一元二次方程,用直接开方法求一元二次方程的解的类型有:x2=a (a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”总结:先把方程化为“左平方,右常数”的形式,且把系数化为1,再根据一元二次方程有无解来求方程中字母参数的取值范围.练3.(2015春•利辛县校级月考)已知一元二次方程mx2+n=0(m≠0,n≠0),若方程有解,则必须()A.n=0 B.m,n同号 C.n是m的整数倍 D.m,n异号分析:首先求出x2的值为﹣,再根据x2≥0确定m、n的符号即可.解答:解:mx2+n=0,x2=﹣,∵x2≥0,∴﹣≥0,∴≤0,∵n≠0,∴mn异号,故选:D.点评:此题主要考查了直接开平方法解一元二次方程,关键是表示出x2的值,根据x2的取值范围确定m、n的符号.练4.(2015•岳阳模拟)如果关于x的方程mx2=3有两个实数根,那么m的取值范围是.解:∵关于x的方程mx2=3有两个实数根,∴m>0.故答案为:m>0.五、课后小测一、选择题1.(2015•石城县模拟)方程x2﹣9=0的解是()A.x=3 B.x=9 C.x=±3 D.x=±92.(2015•河北模拟)已知一元二次方程x2﹣4=0,则该方程的解为()A.x1=x2=2 B.x1=x2=﹣2 C.x1=﹣4,x2=4 D.x1=﹣2,x2=23.(2015•杭州模拟)关于x的方程a(x+m)2+n=0(a,m,n均为常数,m≠0)的解是x1=﹣2,x2=3,则方程a(x+m﹣5)2+n=0的解是()A.x1=﹣2,x2=3 B.x1=﹣7,x2=﹣2 C.x1=3,x2=﹣2 D.x1=3,x2=84.(2015•江岸区校级模拟)如果x=﹣3是一元二次方程ax2=c的一个根,那么该方程的另一个根是()A.3 B.﹣3 C.0 D.15.(2014•枣庄)x1、x2是一元二次方程3(x﹣1)2=15的两个解,且x1<x2,下列说法正确的是()A.x1小于﹣1,x2大于3 B.x1小于﹣2,x2大于3C.x1,x2在﹣1和3之间 D.x1,x2都小于36.(2014春•淮阴区校级月考)方程(1﹣x)2=2的根是()A.﹣1,3 B.1,﹣3 C., D.,7.(2012秋•内江期末)已知a2﹣2ab+b2=6,则a﹣b的值是()A. B.或 C.3 D.8.方程x2=0的实数根有()A.1个 B.2个 C.无数个 D.0个9.方程5y2﹣3=y2+3的实数根的个数是()A.0个 B.1个 C.2个 D.3个二、填空题10.(2015•泉州)方程x2=2的解是.11.(2014•怀化模拟)方程8x2﹣72=0解为.三、解答题12.(2014•祁阳县校级模拟)解方程:(x ﹣2)2﹣16=0.13.(2014秋•青海校级月考)解方程:.14.已知一元二次方程x 2﹣4x+1+m=5请你选取一个适当的m 的值,使方程能用直接开平方法求解,并解这个方程.(1)你选的m 的值是 ;(2)解这个方程.第二讲 配方法一、 学习目标1.掌握用配方法解一元二次方程的一般步骤; 2.学会利用配方法解一元二次方程. 二、知识回顾1.形如2()x m n +=(n ≥0)的一元二次方程,利用求平方根的方法,立即可得而解出方程的根,这种解一元二次方程的方法叫“直接开平方法”.2.如果方程能化成x 2=p 或(mx +n )2=p (p ≥0)的形式,那么利用直接开平方法可得xmx+n三、新知讲解 1.配方法的依据配方法解一元二次方程的依据是完全平方公式2222()a ab b a b ±+=±及直接开平方法.2.配方法的步骤(1)化—— 化二次项系数为1如果一元二次方程的二次项系数不是1,那么在方程的两边同时除以二次项系数,把二次项系数化为1. (2)移——移项通过移项使方程左边为 二次项 和 一次项 ,右边为 常数项 . (3)配——配方1.形如2()x m n +=(n ≥0)的一元二次方程,利用求平方根的方法,立即可得而解出方程的根,这种解一元二次方程的方法叫“直接开平方法”.在方程两边都加上 一次项系数一半的平方 ,根据完全平方公式把原方程变为2()x m n +=(n ≥0)的形式.(4)解——用直接开平方法解方程. 四、典例探究1.配方法解一元二次方程 【例1】(2015•科左中旗校级一模)用配方法解下列方程时,配方有错误的是( )A .x 2﹣2x ﹣99=0化为(x ﹣1)2=100B .x 2+8x+9=0化为(x+4)2=25 C .2t 2﹣7t ﹣4=0化为(t﹣)2=D .3x 2﹣4x ﹣2=0化为(x ﹣)2=【解析】配方法的一般步骤: (1)把常数项移到等号的右边; (2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.根据以上步骤进行变形即可.解:A 、∵x 2﹣2x ﹣99=0,∴x 2﹣2x=99,∴x 2﹣2x+1=99+1,∴(x ﹣1)2=100,故A 选项正确.B 、∵x 2+8x+9=0,∴x 2+8x=﹣9,∴x 2+8x+16=﹣9+16,∴(x+4)2=7,故B 选项错误. C 、∵2t 2﹣7t ﹣4=0,∴2t 2﹣7t=4,∴t 2﹣t=2,∴t 2﹣t+=2+,∴(t ﹣)2=,故C 选项正确. D 、∵3x 2﹣4x ﹣2=0,∴3x 2﹣4x=2,∴x 2﹣x=,∴x 2﹣x+=+,∴(x ﹣)2=.故D 选项正确.故选:B .点评:此题考查了配方法解一元二次方程,选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.练1用配方法解方程: x 2﹣2x ﹣24=0;(2)3x 2+8x-3=0;(3)x (x+2)=120.【解析】(1)移项,得x 2﹣2x=24,配方,得:x 2﹣2x+1=24+1,即:(x ﹣1)2=25, 开方,得:x ﹣1=±5, ∴x 1=6,x 2=﹣4.(2)两边除以3,得: 28103x x +-=, 移项,得:2813x x +=, 配方,得:222844()1()333x x ++=+,即:2245(x )()33+=,开方,得:4533x +=± ∴121,33x x ==- (3)整理,得:22120x x +=, 配方,得:2211201x x ++=+,即:2(1)121x +=,开方,得:111x +=±∴1210,12x x ==-点评:本题考查了解一元二次方程﹣﹣配方法.2.用配方法求多项式的最值【例2】(2015春•龙泉驿区校级月考)当x ,y 取何值时,多项式x 2+4x+4y 2﹣4y+1取得最小值,并求出最小值. 【解析】把所给代数式整理为两个完全平方式子与一个常数的和,最小值应为那个常数,从而确定最小值.解:x 2+4x+4y 2﹣4y+1=x 2+4x+4+4y 2﹣4y+1﹣4=(x+2)2+(2y ﹣1)2﹣4,又∵(x+2)2+(2y ﹣1)2的最小值是0,∴x 2+4x+4y 2﹣4y+1的最小值为﹣4. ∴当x=﹣2,y=时有最小值为﹣4.点评:本题考查配方法的应用;根据﹣4y ,4x 把所给代数式整理为两个完全平方式子的和是解决本题的关键.总结:配方法是求代数式的最值问题中最常用的方法.基本思路是:把代数式配方成完全平方式与常数项的和,根据完全平方式的非负性求代数式的最值.练2(2014•甘肃模拟)用配方法证明:二次三项式﹣8x 2+12x ﹣5的值一定小于0.【解析】将﹣8x 2+12x ﹣5配方,先把二次项系数化为1,然后再加上一次项系数一半的平方,然后根据配方后的形式,再根据a 2≥0这一性质即可证得.解:﹣8x 2+12x ﹣5=﹣8(x 2﹣x )﹣5=﹣8[x 2﹣x+()2]﹣5+8×()2=﹣8(x ﹣)2﹣, ∵(x ﹣)2≥0, ∴﹣8(x ﹣)2≤0, ∴﹣8(x ﹣)2﹣<0,即﹣8x 2+12﹣5的值一定小于0. 点评:此题考查了学生的应用能力,解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.练3(2014秋•崇州市期末)已知a 、b 、c 为△ABC 三边的长.(1)求证:a2﹣b2+c2﹣2ac<0.(2)当a2+2b2+c2=2b(a+c)时,试判断△ABC的形状.【解析】(1)将不等式的左边因式分解后根据三角形三边关系判断代数式的符号即可;(2)将等式右边的项移至左边,然后配方即可.解:(1)a2﹣b2+c2﹣2ac=(a﹣c)2﹣b2=(a﹣c+b)(a﹣c﹣b)∵a、b、c为△ABC三边的长,∴(a﹣c+b)>0,(a﹣c﹣b)<0,∴a2﹣b2+c2﹣2ac<0.(2)由a2+2b2+c2=2b(a+c)得:a2﹣2ab+b2+b2﹣2bc+c2=0配方得:(a﹣b)2+(b﹣c)2=0∴a=b=c∴△ABC为等边三角形.点评:本题考查了配方法的应用,解题的关键是对原式正确的配方.五、课后小测一、选择题1.(2015•延庆县一模)若把代数式x2﹣2x+3化为(x﹣m)2+k形式,其中m,k为常数,结果为()A.(x+1)2+4 B.(x﹣1)2+2C.(x﹣1)2+4 D.(x+1)2+22.(2015•东西湖区校级模拟)一元二次方程x2﹣8x﹣1=0配方后为()A.(x﹣4)2=17 B.(x+4)2=15C.(x+4)2=17 D.(x﹣4)2=17或(x+4)2=17二、填空题3.(2015春•盐城校级期中)一元二次方程x2﹣6x+a=0,配方后为(x﹣3)2=1,则a= .4.(2014秋•营山县校级月考)当x= 时,代数式3x2﹣6x的值等于12.三、解答题5.(2015•东西湖区校级模拟)用配方法解方程:x2﹣2x﹣4=0.6.(2013秋•安龙县校级期末)试说明:不论x,y取何值,代数式x2+4y2﹣2x+4y+5的值总是正数.你能求出当x,y取何值时,这个代数式的值最小吗?7.(2014秋•蓟县期末)阅读下面的材料并解答后面的问题:小李:能求出x2+4x﹣3的最小值吗?如果能,其最小值是多少?小华:能.求解过程如下:因为x2+4x﹣3=x2+4x+4﹣4﹣3=(x2+4x+4)﹣(4+3)=(x+2)2﹣7而(x+2)2≥0,所以x2+4x﹣3的最小值是﹣7.问题:(1)小华的求解过程正确吗?(2)你能否求出x2﹣3x+4的最小值?如果能,写出你的求解过程.8.(2014秋•安陆市期末)阅读下面的解答过程,求y2+4y+8的最小值.解:y2+4y+8=y2+4y+4+4﹣(y+2)2+4∵(y+2)2≥0∴(y+2)2+4≥4∴y2+4y+8的最小值为4仿照上面的解答过程,求m2+m+4的最小值和4﹣2x﹣x2的最大值.9.(2014春•乳山市期末)已知代数式x2﹣2mx﹣m2+5m﹣5的最小值是﹣23,求m的值.10.(2014秋•江阴市期中)配方法可以用来解一元二次方程,还可以用它来解决很多问题.例如:因为3a2≥0,所以3a2+1≥1,即:3a2+1有最小值1,此时a=0;同样,因为﹣3(a+1)2≤0,所以﹣3(a+1)2+6≤6,即﹣3(a+1)2+6有最大值6,此时 a=﹣1.①当x= 时,代数式﹣2(x﹣1)2+3有最(填写大或小)值为.②当x= 时,代数式﹣x2+4x+3有最(填写大或小)值为.③矩形花园的一面靠墙,另外三面的栅栏所围成的总长度是16m,当花园与墙相邻的边长为多少时,花园的面积最大?最大面积是多少?第三讲公式法一、学习目标了解掌握一元二次方程根的判别式,不解方程能判定一元二次方程根的情况;理解一元二次方程求根公式的推导过程;掌握公式结构,知道使用公式前先将方程化为一般形式,通过判别式判断根的情况;学会利用求根公式解简单数字系数的一元二次方程.二、知识回顾1.什么是配方法?配方法解一元二次方程的一般步骤是什么?配方法:通过配方,先把方程的左边配成一个含有未知数的完全平方式,右边是一个非负数,然后运用直接开平方法求解,这种解一元二次方程的方法叫做配方法.配方法解一元二次方程的一般步骤:(1)移常数项到方程右边; (2)化二次项系数为1;(3)方程两边同时加上一次项系数一半的平方; (4)化方程左边为完全平方式;(5)若方程右边为非负数,则利用直接开平方法解得方程的根.2.怎样用配方法解形如一般形式ax 2+bx +c =0(a ≠0)的一元二次方程? 解:移项,得2,ax bx c +=-二次项系数化为1,得2,b c x x a a +=-配方,得222()(),22b b c bx x a a a a++=-+ 即:222424b b ac x a a -⎛⎫+= ⎪⎝⎭, 因为0,a ≠所以当240b ac ->时,2b x a-=;当240;2b b ac a -==-12时,x =x240b ac -=当时,原方程无解.三、新知讲解一元二次方程根的判别式24b ac -叫做一元二次方程ax 2+bx +c =0(a ≠0)根的判别式,通常用希腊字母∆表示它,即24b ac ∆=-.一元二次方程根的情况与判别式的关系(1)240b ac ∆=->⇔方程有两个不相等的实数根; (2)240b ac ∆=-=⇔方程有两个相等的实数根; (3)240b ac ∆=-<⇔方程没有实数根. 公式法解一元二次方程一般地,对于一般形式的一元二次方程ax 2+bx +c =0(a ≠0),当240b ac -≥时,它的两个根分别是1x =,2x =,这里,()2402b x b ac a-±=-≥叫做一元二次方程的求根公式,利用它解一元二次方程的方法叫做公式法.公式法解一元二次方程的一般步骤把方程化成一般形式:ax 2+bx +c =0(a ≠0);确定a ,b ,c 的值;求出24b ac -的值,并判断方程根的情况:当240b ac ->时,方程有两个不相等的实数根; 当240b ac -=时,方程有两个相等的实数根; 当240b ac -<时,方程没有实数根.当240b ac -≥时,将a ,b ,c 和24b ac -的值代入公式2b x a-=(注意符号).四、典例探究1.根据根的判别式判断一元二次方程根的情况【例1】(2015•重庆)已知一元二次方程2x 2﹣5x+3=0,则该方程根的情况是( ) A .有两个不相等的实数根 B .有两个相等的实数根 两个根都是自然数 D .无实数根分析:判断方程的根的情况,只要看根的判别式△=b 2﹣4ac 的值的符号就可以了. 解答:解:∵a=2,b=﹣5,c=3,∴△=b 2﹣4ac=(﹣5)2﹣4×2×3=1>0, ∴方程有两个不相等的实数根. 故选:A .点评:此题主要考查了一元二次方程根的判别式,要熟练掌握一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.总结:求根的判别式时,应该先将方程化为一般形式,正确找出a ,b ,c 的值.根的判别式与一元二次方程根的情况的关系如下:当240b ac ->时,方程有两个不相等的实数根;当240b ac -=时,方程有两个相等的实数根;当240b ac -<时,方程没有实数根.练1.(2015•铜仁市)已知关于x 的一元二次方程3x 2+4x ﹣5=0,下列说法不正确的是( ) A .方程有两个相等的实数根 B .方程有两个不相等的实数根 C .没有实数根 D .无法确定 分析:先求出△的值,再判断出其符号即可.解答:解:∵△=42﹣4×3×(﹣5)=76>0, ∴方程有两个不相等的实数根. 故选B .点评:本题考查的是根的判别式,熟知一元二次方程ax 2+bx+c=0(a≠0)的根与△的关系是解答此题的关键.练2.(2015•泰州)已知:关于x 的方程x 2+2mx+m 2﹣1=0 (1)不解方程,判别方程根的情况; (2)若方程有一个根为3,求m 的值. 分析:(1)找出方程a ,b 及c 的值,计算出根的判别式的值,根据其值的正负即可作出判断; (2)将x=3代入已知方程中,列出关于系数m 的新方程,通过解新方程即可求得m 的值.解答:解:(1)∵a=1,b=2m ,c=m 2﹣1,∵△=b 2﹣4ac=(2m )2﹣4×1×(m 2﹣1)=4>0,∴方程x2+2mx+m2﹣1=0有两个不相等的实数根;(2)∵x2+2mx+m2﹣1=0有一个根是3,∴32+2m×3+m2﹣1=0,解得,m=﹣4或m=﹣2.点评:此题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.也考查了一元二次方程的解的定义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.即用这个数代替未知数所得式子仍然成立.2.根据一元二次方程根的情况求参数的值或取值范围【例2】(2015•温州)若关于x的一元二次方程4x2﹣4x+c=0有两个相等实数根,则c的值是()A.﹣1 B.1 C.﹣4 D.4分析:根据方程根的情况与判别式的关系知△=42﹣4×4c=0,然后解一次方程即可.解答:解:∵一元二次方程4x2﹣4x+c=0有两个相等实数根,∴△=42﹣4×4c=0,∴c=1,故选B.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.总结:已知方程根的情况求字母的值或取值范围时:先计算根的判别式;再根据方程根的情况列出关于根的判别式的等式或不等式求解;若二次项系数出现了字母,应注意“二次项系数不为0”.练3.(2015•凉山州)关于x的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是()A.m≤3 B.m<3 C.m<3且m≠2 D.m≤3且m≠2分析:根据一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac的意义得到m-2≠0且△≥0,即22-4×(m-2)×1≥0,然后解不等式组即可得到m的取值范围.解答:解:∵关于x的一元二次方程(m-2)x2+2x+1=0有实数根,∴m-2≠0且△≥0,即22-4×(m-2)×1≥0,解得m≤3,∴m的取值范围是 m≤3且m≠2.故选:D.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.3.用公式法解一元二次方程【例3】用公式法解下列方程:(1)x2+2x﹣2=0;(2)y2﹣3y+1=0;(3)x2+3=2x.分析:(1)求出b2﹣4ac的值,代入公式x=求出即可;(2)求出b2﹣4ac的值,代入公式y=求出即可;(3)求出b2﹣4ac的值是负数,即可得出原方程无解.解答:解:(1)这里a=1,b=2,c=﹣2,∵b2﹣4ac=22﹣4×1×(﹣2)=12>0,∴x==﹣1,∴x1=﹣1+,x2=﹣1﹣;(2)这里a=1,b=﹣3,c=1.∵b2﹣4ac=(﹣3)2﹣4×1×1=5>0,y=,∴y1=,y2=;(3)移项,得x2﹣2x+3=0,这里a=1,b=﹣2,c=3.∵b2﹣4ac=(﹣2)2﹣4×1×3=﹣4<0.∴原方程没有实数根.点评:本题主要考查学生运用公式法正确解方程的能力,前提是先判断判别式的符号,再根据情况代入求根公式求解.总结:公式法的实质是配方法,只不过省去了配方的过程,而直接利用了配方的结论;运用公式法求解一元二次方程要注意两个前提:(1)先将一元二次方程化为一般形式,即确定a,b,c的值;(2)必须保证b2-4ac≥0.练4.(2014•锦江区模拟)解方程:x(x﹣2)=3x+1.分析:整理后求出b2﹣4ac的值,再代入公式求出即可.解答:解:x(x﹣2)=3x+1,整理得:x2﹣5x﹣1=0,b2﹣4ac=(﹣5)2﹣4×1×(﹣1)=29,x=,x1=,x2=.点评:本题考查了解一元二次方程的应用,能正确运用公式法解一元二次方程是解此题的关键,难度适中.练5.当x是何值时,3x2+4x﹣8的值和2x2﹣1的值相等?分析:根据3x2+4x﹣8的值和2x2﹣1的值相等,即可列出方程,然后利用公式法即可求解.解答:解:根据题意得:3x2+4x﹣8=2x2﹣1,即x2+4x﹣7=0,a=1,b=4,c=﹣7,△=b2﹣4ac=16+28=44>0,则x==﹣2.点评:本题考查了公式法解一元二次方程,注意公式运用的条件:判别式△≥0.五、课后小测一、选择题1.(2015•云南)下列一元二次方程中,没有实数根的是()A.4x2﹣5x+2=0 B.x2﹣6x+9=0 C.5x2﹣4x﹣1=0 D.3x2﹣4x+1=02.(2015•贵港)若关于x的一元二次方程(a﹣1)x2﹣2x+2=0有实数根,则整数a的最大值为()A.﹣1 B.0 C.1 D.23.(2015•烟台)等腰直角三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根,则n的值为()A.9 B.10 C.9或10 D.8或104.(2015•株洲)有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中a•c≠0,a≠c.下列四个结论中,错误的是()A.如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根B.如果方程M的两根符号相同,那么方程N的两根符号也相同C.如果5是方程M的一个根,那么是方程N的一个根D.如果方程M和方程N有一个相同的根,那么这个根必是x=15.(2013•日照)已知一元二次方程x2﹣x﹣3=0的较小根为x1,则下面对x1的估计正确的是()A.﹣2<x1<﹣1 B.﹣3<x1<﹣2 C.2<x1<3 D.﹣1<x1<0二、填空题6.(2011秋•册亨县校级月考)用公式法解方程2x2﹣7x+1=0,其中b2﹣4ac= ,x1= ,x2= .三、解答题7.(2014秋•通山县期中)用公式法解方程:2x2﹣4x=5.8.(2014秋•金溪县校级月考)解方程:2x2﹣2x﹣5=0.9.(2013春•石景山区期末)用公式法解方程:x(x)=4.10.(2015•梅州)已知关于x的方程x2+2x+a﹣2=0.(1)若该方程有两个不相等的实数根,求实数a的取值范围;(2)当该方程的一个根为1时,求a的值及方程的另一根.11.(2015•咸宁)已知关于x的一元二次方程mx2﹣(m+2)x+2=0.(1)证明:不论m为何值时,方程总有实数根;(2)m为何整数时,方程有两个不相等的正整数根.12.(2015•昆山市一模)已知关于x的一元二次方程x2+(m+3)x+m+1=0.(1)求证:无论m取何值,原方程总有两个不相等的实数根;(2)若x1、x2是原方程的两根,且|x1﹣x2|=2,求m的值.13.(2015•南充一模)已知关于x的一元二次方程kx2﹣2(k﹣1)x+k﹣2=0(k≠0)(1)小明考查后说,它总有两个不相等的实数根.(2)小华补充说,其中一个根与k无关.请你说说其中的道理.第四讲因式分解法一、学习目标1.会用因式分解法解一元二次方程;2.会用换元法解一元二次方程;3.灵活选用简便的方法解一元二次方程.二、知识回顾1.分解因式的常用方法有哪些?(1)提取公因式法:am+bm+cm= m(a+b+c)(2)公式法:22()()-2(-)++=+222a ab b a b+=,a b a b a ba ab b a b-=+-,2222()(3)十字相乘法:2()()()+++=++x a b x ab x a x b三、新知讲解1.因式分解法把一个多项式分解成几个整式乘积的形式叫做分解因式.当一元二次方程的一边是0,而另一边易于分解成两个一次因式的乘积时,我们可以使两个一次式分别等于0,从而实现降次. 这种解一元二次方程的方法称为因式分解法.2.因式分解法解一元二次方程的步骤:①把方程的右边化为0;②用提公因式法、公式法(这里指因式分解中的公式法)或十字相乘法把方程左边化成两个一次因式乘积的形式;③令每一个因式分别等于0,得到两个一元一次方程;④解这两个一元一次方程,它们的解就是原方程的解.3.因式分解法的条件、理论依据因式分解法解一元二次方程的条件是:方程右边等于0,而左边易于分解;理论依据是:如果两个因式的积等于零,那么至少有一个因式等于零.四、典例探究1.用因式分解法解一元二次方程【例1】用因式分解法解方程:(1)2(2x -1)2=(1-2x );(2)4(y +2)2=(y -3)2. 【解析】(1)移项,提取公因式;(2)移项并利用平方差公式分解因式求解.解:(1)2(2x -1)2=(1-2x )移项,得2(2x -1)2-(1-2x )=0,即:2(2x -1)2+(2x -1)=0,因式分解,得(2x-1)[2(2x-1)+1]=0, 整理,得(2x-1)(4x-1)=0, 解得x 1=12,x 2=14;(2)4(y +2)2=(y -3)2移项,得4(y +2)2-(y -3)2=0因式分解,得[2(y+2)+(y-3)][2(y+2)-(y-3)]=0 整理,得(3y+1)(y+7)=0 解得y 1=-13,y 2=-7.总结:用因式分解法解一元二次方程,是利用了“当ab=0时,必有a=0或者b=0”的结论. 因式分解法解一元二次方程的步骤: (1)把方程的右边化为0;(2)用提公因式法、公式法(这里指因式分解中的公式法)或十字相乘法把方程左边化成两个一次因式乘积的形式;(3)令每一个因式分别等于0,得到两个一元一次方程; (4)解这两个一元一次方程,它们的解就是原方程的解.练1(2014秋•赵县期末)用因式分解法解方程:x 2﹣6x+9=(5﹣2x )2解:x 2﹣6x+9=(5﹣2x )2,(x ﹣3)2﹣(5﹣2x )2=0, 因式分解得:(x ﹣3+5﹣2x )(x ﹣3﹣5+2x )=0, 整理得:(2﹣x )(3x ﹣8)=0, 解得:x 1=2,x 2=.点评:此题主要考查了因式分解法解一元二次方程,正确分解因式是解题关键.2.用换元法解一元二次方程【例2】(2014•山西校级模拟)解方程(x ﹣1)2﹣5(x ﹣1)+4=0时,我们可以将x ﹣1看成一个整体,设x ﹣1=y ,则原方程可化为y 2﹣5y+4=0,解得y 1=1,y 2=4.当y=1时,即x ﹣1=1,解得x=2;当y=4时,即x ﹣1=4,解得x=5,所以原方程的解为x 1=2,x 2=5.利用这种方法求方程(2x+5)2﹣4(2x+5)+3=0的解.【解析】先设2x+5=y ,则方程即可变形为y 2﹣4y+3=0,解方程即可求得y (即2x+5)的值,进一步可求出x 的值.解:设x ﹣1=y ,则原方程可化为y 2﹣4y+3=0, 所以(y ﹣1)(y ﹣3)=0 解得y 1=1,y 2=3.当y=1时,即2x+5=1, 解得x=﹣2;当y=3时,即2x+5=3, 解得x=﹣1,所以原方程的解为:x1=﹣2,x2=﹣1.点评:本题运用换元法解一元二次方程.总结:换元法在解特殊一元二次方程的时候用的较多,运用了整体思想.在一元二次方程中,某个代数式几次出现,用一个字母来代替它可以简化问题时,我们可以考虑用换元法来解.解高次方程时,通过换元的方法达到降次的目的.练2(2015•呼和浩特)若实数a、b满足(4a+4b)(4a+4b﹣2)﹣8=0,则a+b=_______.【解析】设a+b=x,则原方程转化为关于x的一元二次方程,通过解该一元二次方程来求x(即a+b)的值.解:设a+b=x,则由原方程,得4x(4x﹣2)﹣8=0,整理,得(2x+1)(x﹣1)=0,解得x1=﹣,x2=1.则a+b 的值是﹣或1.故答案是:﹣或1.点评:本题主要考查了换元法,即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.练3解方程:(x2-3)2-5(3-x2)+4=0.【解析】设x2-3=y,则原方程转化为关于y的一元二次方程,通过解该一元二次方程来求y(即x2-3)的值.解:设x2-3=y,则原方程可化为y2-5(-y)+4=0,即:y2+5y+4=0,因式分解得:(y+1)(y+4)=0,解得y1=-1,y2=-4.当y1=-1时,x2-3=-1,即x2=2,解得x=当y2=-4时,x2-3=-4,即x2-3=-1,方程无实数根.综上,x=3.灵活选用方法解一元二次方程【例3】(2014秋•漳县校级期中)选择适当方法解下列方程:(1)x2﹣5x+1=0;(2)3(x﹣2)2=x(x﹣2);(3)2x2﹣2x﹣5=0;(4)(y+2)2=(3y﹣1)2.【解析】(1)利用配方法得到(x ﹣)2=,然后根据直接开平方法求解;(2)先变形得到3(x﹣2)2﹣x(x﹣2)=0,然后利用因式分解法解方程;(3)先计算判别式的值,然后利用求根公式法求解;(4)先变形得到(y+2)2﹣(3y﹣1)2=0,然后利用因式分解法解方程.解:(1)x2﹣5x=﹣1,x2﹣5x+()2=﹣1+()2,(x﹣)2=,x﹣=±,所以x1=,x2=;(2)3(x﹣2)2﹣x(x﹣2)=0,(x﹣2)(3x﹣6﹣x)=0,所以x1=2,x2=3;(3)△=(﹣2)2﹣4×2×(﹣5)=48x===,所以x1=,x2=;(4)(y+2)2﹣(3y﹣1)2=0,(y+2+3y﹣1)(y+2﹣3y+1)=0,y+2+3y﹣1=0或y+2﹣3y+1=0,所以y1=﹣,y2=.点评:本题考查了一元二次方程的四种常见解法.总结:解一元二次方程常用的方法有直接开平方法、配方法、公式法和因式分解法,根据一元二次方程的特征,灵活选用解方程的方法,可以起到事半功倍的作用.(1)一般地,当一元二次方程一次项系数为0时,即形如ax2+c=0形式的一元二次方程,应选用直接开平方法.(2)若常数项为0,即形如ax2+bx=0的形式,应选用因式分解法.(3)若一次项系数和常数项都不为0,即形如ax2+bx+c=0的形式,看左边的整式是否能够因式分解,如果能,则宜选用因式分解法;不然选用公式法;不过当二次项系数是1,且一次项系数是偶数时,用配方法也较简单.(4)公式法虽然是万能的,对任何一元二次方程都适用,但不一定是最简单的. 因此在解方程时,我们首先考虑能否应用直接开平方法、因式分解法等简单方法,若不行,则再考虑公式法(适当也可考虑配方法).练4(2015春•无锡校级期中)选择合适的方法解下列方程.(1)x2﹣5x﹣6=0;(2)3x2﹣4x﹣1=0;(3)x(x﹣1)=3﹣3x;【解析】(1)根据因式分解法,可得方程的解;(2)根据公式法,可得方程的解;(3)根据因式分解法,可得方程的解;(4)根据公式法,可得方程的解.解:(1)因式分解,得 (x ﹣1)(x ﹣6)=0,解得x 1=6,x 2=﹣1; (2)a=3,b=﹣4,c=﹣1,x 1=,x 2=;(3)方程化简得x 2+2x ﹣3=0, 因式分解,得(x+3)(x ﹣1)=0, 解得x 1=1,x 2=﹣3;(4)a=1,b=﹣2,c=1,x 1=1+,x 2=﹣1+.点评:本题考查了解一元二次方程,根据方程的特点选择适当的方法是解题关键.五、课后小测 一、选择题1.方程(x-16)(x+8)=0的根是( )A. x 1=-16,x 2=8B. x 1=16,x 2=-8C. x 1=16,x 2=8D. x 1=-16,x 2=-8 2. 方程5x(x+3)=3(x+3)的解为( ) A.123,35x x == B.35x = C.123,35x x =-=- D.123,35x x ==-3.(2015•滕州市校级模拟)方程x 2﹣2x=3可以化简为( )A .(x ﹣3)(x+1)=0B .(x+3)(x ﹣1)=0C .(x ﹣1)2=2D .(x ﹣1)2+4=0 二、填空题4.(2015•丽水)解一元二次方程x 2+2x ﹣3=0时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程 . 5.(2014•杭州模拟)方程x (x+1)=2(x+1)的解是 .6.(2013秋•苏州期末)已知(x 2+y 2+1)(x 2+y 2+2)=6,则x 2+y 2的值为 . 三、解答题 7.(2014秋•静宁县期末)解下列方程:(1)x 2﹣2x+1=0(2)x 2﹣2x ﹣2=0(3)(x ﹣3)2+2(x ﹣3)=0. 8.(2014秋•沧浪区校级期末)解下列方程:(1)x 2﹣4x ﹣3=0(2)(x ﹣2)2=3(x ﹣2) (3)2(﹣x )2﹣(x ﹣)﹣1=0.9.(2014秋•宛城区校级期中)为了解方程(x 2﹣1)2﹣5(x 2﹣1)+4=0,我们可以将x 2﹣1看作一个整体,然后设x 2﹣1=y ,则(x 2﹣1)2=y 2,那么原方程可化为y 2﹣5y+4=0,解得y 1=1,y 2=4.当y=1时,x 2﹣1=1,x 2=2,x=±.。
一元二次方程讲义

一元二次方程讲义1.解方程2(2)9x -=. 2(3x ﹣1)2=8.例题3:配方法1.已知方程260xx q +=-可以配方成27x p =(-)的形式,那么262x x q +=-可以配方成下列的( ) A. 25x p =(-) B. 29x p =(-) C. 229x p +=(-) D. 225x p +=(-) 2.用配方法解方程:2420x x ++=练习:1. 用配方法解方程:x 2﹣7x+5=0. 2x 2﹣3x+1=0.x 2﹣6x ﹣7=0.例题4.公式法1.一元二次方程4x 2﹣2x+=0的根的情况是( )A. 有两个不相等的实数根B. 有两个相等的实数根C. 没有实数根D. 无法判断2.用公式法解方程:03822=+-x x.练习:1.用公式法解方程:3x 2+5(2x+1)=0.练习:1.“在线教育”指的是通过应用信息科技和互联网技术进行内容传播和快速学习的方法.”互联网+”时代,中国的在线教育得到迅猛发展.根据中国产业信息网数据统计分析,2015年中国在线教育市场产值约为1600亿元,2017年中国在线教育市场产值在2015年的基础上增加了900亿元.(1)求2015年到2017年中国在线教育市场产值的年平均增长率;(2)若增长率保持不变,预计2018年中国在线教育市场产值约为多少亿元?例题2:利润问题1.某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个.因受库存的影响,每批次进货个数不得超过180个,商店若将准备获利2000元,则应进货多少个?定价为多少元?练习:1.今年本市蜜桔大丰收,某水果商销售一种蜜桔,成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:(1)求y与x之间的函数关系式;(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?(销售利润=销售价﹣成本价)例题3:面积问题1.某中学标准化建设规划在校园内的一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草(如图所示),若使每一块草坪的面积都为96平方米.求人行道的宽。
一元二次方程专题 讲义

1 =0 2
(3)2x2+1=3x
(4)3x2-6x+4=0
5
整理人:王子明
九年级上第一章 一元二次方程专题讲义
知识点 3:公式法 (1) 解一元二次方程时, 可以先将方程化为一般形式 ax2+bx+c=0, 当 b2-4ac≥0 时, 将 a、 b、c 代入式子 x=
b b 2 4ac 就得到方程的根. 2a b b 2 4ac 叫做一元二次方程的求根公式. 2a
知识点 4:因式分解法 依据 A.B=0 则 A=0 或 B=0 因式分解法要使方程一边为两个一次因式相乘,另一边为 0, 再分别使各一次因式等于 0 ※方程特点:左边可以分解为两个一次因式的积,右边为“0” , ※ 方 程 形 式 : 如
ax m 2 bx n 2
,
x a x b x a x c
2
公式: x
b b 2 4ac 2 , a 0, 且b 4ac 0 2a
考点:用公式法解方程 例 1 用公式法解下列方程. (1)2x2-x-1=0 (2)x2+1.5=-3x (3) x2- 2 x+
ห้องสมุดไป่ตู้
1 =0 2
(4)4x2-3x+2=0
6
整理人:王子明
九年级上第一章 一元二次方程专题讲义
2
9
整理人:王子明
九年级上第一章 一元二次方程专题讲义
1.4 根的判别式及应用 课标知识与能力目标 4.不解方程判断方程根的情况 5.根据方程根的情况确定字母参数的取值范围 6.应用根的判别式证明方程根的情况 7.构造一元二次方程,应用根的判别式解决相关的存在性问题 考点 1:不解方程判断方程根的情况 例 1 下列四个结论中,正确的是 ( )
初一数学一元二次方程全章精品讲义

当 <0,方程无实数解。
典例分析:
题型1:根据判别式判断根的情况
例1:方程 的根的情况()
A、该方程有两个相等的实数根B、该方程有两个不相等的实数根
C、该方程没有实数根D、无法确定
例2:不解方程判断下列方程根的情况
(1) (2) (3)
(4) (5)
题型2:利用跟的判别式求方程中某个字母的值或取值范围
d=====( ̄▽ ̄*)b_____________________________________
例2:已知 是完全平方式,则 的值为______。
例3:若 是完全平方公式,则 的值为_______。
例4:根据完全平方式填空
(1) (2)
(3) (4)
题型2:用配方法解一元二次方程
例1:用配方法解下列方程:
例3:已知一元二次方程 的两个根分别为 ,则二次三项式 可分解为_________________。
例4:在实数范围为定义一种运算“*”,其规则为 ,根据这个规矩,方程 的解为______________。
例5:若关于 的方程 与 有相同的实数根,则 的值为_______。
例6:已知 为非负数,方程
(2)如果方程有两个相等的实数根,是判断△ABC的形状,并说明理由。
(3)如果△ABC是等边三角形,试求出这个一元二次方程的根。
例3:已知 的两边AB、AD的长是关于x的方程 的两个实数根。
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长?
(2)若AB的长为2,那么平行四边形ABCD的周长为多少?
6、求证:关于 的一元二次方程 恒有两个实数根.
7、已知关于 的方程
(1)当该方程的一个根为1时,求 的值及该方程的另一个根
一元二次不等式及其解法教学讲义
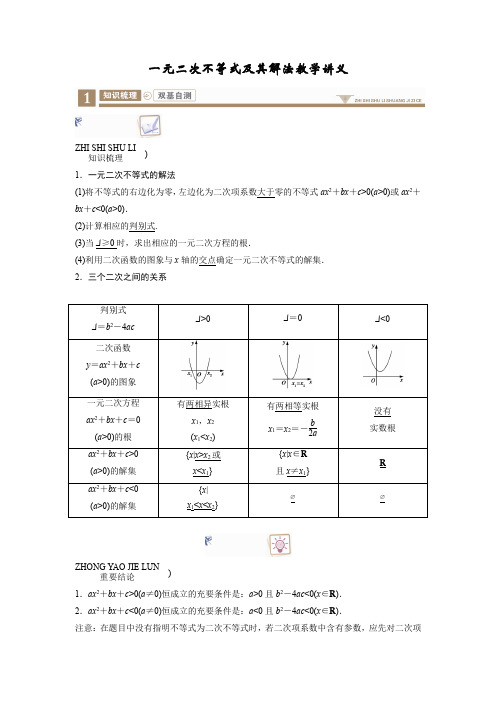
一元二次不等式及其解法教学讲义ZHI SHI SHU LI知识梳理)1.一元二次不等式的解法(1)将不等式的右边化为零,左边化为二次项系数大于零的不等式ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0).(2)计算相应的判别式.(3)当Δ≥0时,求出相应的一元二次方程的根.(4)利用二次函数的图象与x轴的交点确定一元二次不等式的解集.2.三个二次之间的关系判别式Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象一元二次方程ax2+bx+c=0 (a>0)的根有两相异实根x1,x2(x1<x2)有两相等实根x1=x2=-b2a没有实数根ax2+bx+c>0 (a>0)的解集{x|x>x2或x<x1}{x|x∈R且x≠x1}Rax2+bx+c<0 (a>0)的解集{x|x1<x<x2}∅∅ZHONG YAO JIE LUN重要结论)1.ax2+bx+c>0(a≠0)恒成立的充要条件是:a>0且b2-4ac<0(x∈R).2.ax2+bx+c<0(a≠0)恒成立的充要条件是:a<0且b2-4ac<0(x∈R).注意:在题目中没有指明不等式为二次不等式时,若二次项系数中含有参数,应先对二次项系数为0的情况进行分析,检验此时是否符合条件. 3.二次不等式解集的“边界值”是相应二次方程的根. 4.简单分式不等式的解法 (1)f (x )g (x )>0(<0)⇔f (x )g (x )>0(<0); (2)f (x )g (x )≥0(≤0)⇔⎩⎪⎨⎪⎧f (x )·g (x )≥0(≤0)g (x )≠0. 5.简单的指数与对数不等式的解法 (1)若a >1,a f (x )>a g (x )⇔f (x )>g (x ); 若0<a <1,a f (x )>a g (x )⇔f (x )<g (x ).(2)若a >1,log a f (x )>log a g (x )⇔f (x )>g (x )>0; 若0<a <1,log a f (x )>log a g (x )⇔0<f (x )<g (x ).SHUANG JI ZI CE双基自测 )1.不等式(x -1)(2-x )≥0的解集为( A ) A .{x |1≤x ≤2} B .{x |x ≤1或x ≥2} C .{x |1<x <2}D .{x |x <1或x >2}[解析] 由(x -1)(2-x )≥0可知(x -2)(x -1)≤0,所以不等式的解集为{x |1≤x ≤2}.故选A . 2.不等式1-x2+x ≥0的解集为( B )A .[-2,1]B .(-2,1]C .(-∞,-2)∪(1,+∞)D .(-∞,-2]∪(1,+∞)[解析] 原不等式化为⎩⎪⎨⎪⎧(1-x )(2+x )≥0,2+x ≠0,即⎩⎪⎨⎪⎧(x -1)(x +2)≤0x +2≠0,所以-2<x ≤1.故选B . 3.(教材改编)不等式ax 2+bx +2>0的解集是(-12,13),则a +b 的值是( D )A .10B .-10C .14D .-14[解析] 由题意知-12,13是ax 2+bx +2=0的两根,则a =-12,b =-2,所以a +b =-14.4.(2018·山东烟台期中)若集合M ={x |x 2+x -12≤0},N ={y |y =3x ,x ≤1},则集合{x |x ∈M 且x ∉N }等于( D ) A .(0,3] B .[-4,3] C .[-4,0)D .[-4,0][解析] M =[-4,3],N =(0,3], ∴{x |x ∈M 且x ∉N }=[-4,0],故选D .5.若不等式(a -3)x 2+2(a -3)x -4<0对一切x ∈R 恒成立,则实数a 取值的集合为( D ) A .(-∞,3) B .(-1,3) C .[-1,3]D .(-1,3] [解析] 当a =3时,-4<0恒成立;当a ≠3时,⎩⎪⎨⎪⎧a <3,Δ=4(a -3)2+16(a -3)<0,解得-1<a <3.所以-1<a ≤3.6.(2018·山东烟台联考)不等式x >1x的解集为(-1,0)∪(1,+∞).[解析] 当x >0时,原不等式等价于x 2>1,解得x >1;当x <0时,原不等式等价于x 2<1,解得-1<x <0.所以不等式x >1x 的解集为(-1,0)∪(1,+∞).考点1 一元二次不等式的解法——多维探究角度1 不含参数的不等式例1 解下列不等式 (1)-2x 2+x +3<0; (2)x 2-2x +2>0; (3)2x -13-4x≥1. [分析] (1)将二次项系数化为正数,变为2x 2-x -3>0,求方程2x 2-x -3=0的根,若无根,则解集为R ,若有根,则按“小于取中间,大于取两边”写出解集; (3)移项通分化为f (x )g (x )>0的形式,进而化为f (x )·g (x )>0求解.[解析] (1)化-2x 2+x +3<0为2x 2-x -3>0,∴(x +1)(2x -3)>0,即(x +1)(x -32)>0,∴x >32或x <-1,∴原不等式的解集为(-∞,-1)∪(32,+∞).(2)因为Δ<0,所以方程x 2-2x +2=0无实数解,而y =x 2-2x +2的图象开口向上,可得原不等式x 2-2x +2>0的解集为R .(3)化2x -13-4x ≥1为6x -43-4x ≥0,即3x -24x -3≤0,∴(3x -2)(4x -3)≤0,且x ≠34,即(x -23)(x -34)≤0(且x ≠34)∴原不等式的解集为{x |23≤x <34}.名师点拨 ☞解一元二次不等式的一般步骤(1)化:把不等式变形为二次项系数大于零的标准形式. (2)判:计算对应方程的判别式.(3)求:求出对应的一元二次方程的根,或根据判别式说明方程有没有实根. (4)写:利用“大于取两边,小于取中间”写出不等式的解集. 角度2 含参数的不等式例2 解下列关于x 的不等式: (1)ax 2-(a +1)x +1<0(a ∈R ); (2)x 2-2ax +2≤0(a ∈R );[分析] (1)因二次项系数含有字母,故需对其符号分类求解,即讨论a 与0的关系,并注意根的大小关系,即讨论1a 与1的关系,故需分a <0,a =0,0<a <1,a =1,a >1五种情况求解;(2)由于系数中含有字母,故需考虑对应的方程有无实根,以及有根时根的大小关系; [解析] (1)若a =0,原不等式等价于-x +1<0,解得x >1. 若a <0,则原不等式等价于(x -1a )(x -1)>0,解得x <1a 或x >1.若a >0,原不等式等价于(x -1a)(x -1)<0.①当a =1时,1a =1,(x -1a )(x -1)<0无解;②当a >1时,1a <1,解(x -1a )(x -1)<0得1a <x <1;③当0<a <1时,1a >1,解(x -1a )(x -1)<0得1<x <1a.综上所述:当a <0时,解集为{x |x <1a 或x >1};当a =0时,解集为{x |x >1};当0<a <1时,解集为{x |1<x <1a };当a =1时,解集为∅;当a >1时,解集为{x |1a <x <1}.(2)对于方程x 2-2ax +2=0,因为Δ=4a 2-8,所以当Δ<0,即-2<a <2时,x 2-2ax +2=0无实根.又二次函数y =x 2-2ax +2的图象开口向上,所以原不等式的解集为∅; 当Δ=0,即a =±2时,x 2-2ax +2=0有两个相等的实根, 当a =2时,原不等式的解集为{x |x =2}, 当a =-2时,原不等式的解集为{x |x =-2};当Δ>0,即a >2或a <-2时,x 2-2ax +2=0有两个不相等的实根,分别为x 1=a -a 2-2,x 2=a +a 2-2,且x 1<x 2,所以原不等式的解集为{x |a -a 2-2≤x ≤a +a 2-2}.综上,当a >2或a <-2时,解集为{x |a -a 2-2≤x ≤a +a 2-2};当a =2时,解集为{x |x =2};当a =-2时,解集为{x |x =-2};当-2<a <2时,解集为∅.名师点拨 ☞含参数的不等式的求解往往需要分类讨论(1)若二次项系数为常数,可先考虑分解因式,再对根的大小分类讨论(分点由x 1=x 2确定);若不易分解因式,且判别式符号确定,可考虑求根公式,以便写出解集,若判别式符号不能确定,则需对判别式分类讨论(分点由Δ=0确定).(2)若二次项系数为参数,则应先考虑二次项系数是否为零,然后讨论二次项系数大于零、小于零,以便确定解集形式.(3)解简单分式不等式是通过移项、通分化为整式不等式求解,要注意分母不能为零. (4)解简单的指数、对数不等式时,若底含有参数,则需对其是否大于1分类求解,注意对数的真数必须为正.〔变式训练1〕(1)(角度1)(2018·陕西部分学校摸底检测)已知集合U =Z ,集合A ={x ∈Z |3≤x <7},B ={x ∈Z |x 2-7x +10>0},则A ∩(∁U B )=( A ) A .{3,4,5} B .{2,3,4,5} C .{4,5}D .{2,3,4}(2)(角度1)不等式x -12x +1≤1的解集为{x |x >-12或x ≤-2}.(3)(角度2)解不等式x 2-(a +1)x +a <0(a ∈R )[解析] (1)∵A ={3,4,5,6},B ={x ∈Z |x >5或x <2},∴∁U B ={2,3,4,5},∴A ∩(∁U B )={3,4,5},故选A .(2)x -12x +1≤1⇔x -12x +1-1≤0⇔-x -22x +1≤0⇔x +22x +1≥0. x +22x +1≥0⇔⎩⎪⎨⎪⎧(x +2)(2x +1)≥0,2x +1≠0,解得{x |x >-12或x ≤-2}.(3)由x 2-(a +1)x +a =0,得(x -a )(x -1)=0, ∴x 1=a ,x 2=1,①当a >1时,x 2-(a +1)x +a <0的解集为{x |1<x <a }, ②当a =1时,x 2-(a +1)x +a <0的解集为∅, ③当a <1时,x 2-(a +1)x +a <0的解集为{x |a <x <1}.考点2 三个二次间的关系——师生共研例3 (1)(2018·重庆模拟)关于x 的不等式x 2-2ax -8a 2<0(a >0)的解集为(x 1,x 2),且x 2-x 1=15,则a =( A ) A .52B .72C .154D .152(2)若不等式x 2+ax -2>0在区间[1,5]上有解,则a 的取值范围是( A ) A .(-235,+∞)B .(-235,1]C .(1,+∞)D .(-∞,-235][分析] (1)思路一:利用根与系数的关系求解.思路二:因为a >0,可解方程x 2-2ax -8a 2=0,得两根x 1,x 2,代入x 2-x 1=15求解;(2)令f (x )=x 2+ax -2,Δ=a 2+8>0恒成立,又两根之积为负值,所以只要f (1)≥0或f (1)<0且f (5)>0,于是得解;思路二:“正难则反”,求x 2+ax -2≤0在区间[1,5]上恒成立的a 的取值集合,只需f (5)≤0,再求其补集即可;思路三:分离参数.[解析] (1)解法一:由题意知x 1,x 2是方程x 2-2ax -8a 2=0的两根,则x 1+x 2=2a ,x 1x 2=-8a 2.又x 2-x 1=15,∴(x 2-x 1)2=(x 1+x 2)2-4x 1x 2=4a 2+32a 2=36a 2=152.∵a >0,∴a =156=52,故选A . 解法二:由x 2-2ax -8a 2=(x +2a )(x -4a )<0,∵a >0,∴不等式的解集为(-2a,4a ). 又不等式的解集为(x 1,x 2),∴x 1=-2a ,x 2=4a .∴x 2-x 1=4a -(-2a )=6a =15,∴a =52,故选A .(2)令f (x )=x 2+ax -2,则Δ=a 2+8>0,∴方程f (x )=0,有两个不等实根,又两根之积为负,∴方程有一正根和一负根. 解法一:不等式x 2+ax -2>0在区间[1,5]上有解,只要f (1)≥0或⎩⎨⎧f (1)<0,f (5)>0.解得a ≥1或-235<a <1. ∴a 的取值范围是(-235,+∞),故选A .解法二:不等式x 2+ax -2≤0在[1,5]上恒成立,只要f (5)≤0,即25+5a -2≤0,解得a ≤-235,∴不等式x 2+ax -2>0在区间(1,5]上有解的a 的取值范围是(-235,+∞). [引申]若不等式x 2+ax -2<0在区间[1,5]上有解,则a 的取值范围是(-∞,1).[解析] 由例3(2)的解析知,不等式x 2+ax -2<0在区间[1,5]上有解,a <2x -x ,x ∈[1,5]有解,显然g (x )=2x -x 在[1,5]上递减,g max (x )=g (1)=1,∴a <1.名师点拨 ☞已知不等式的解集,等于知道了与之对应方程的根,此时利用韦达定理或判别式即可求出参数的值或范围,为简化讨论注意数形结合,如本例(2)中对应的二次函数图象过点(0,-2). 〔变式训练2〕(1)已知不等式ax 2-bx -1≥0的解集是[-12,-13],则不等式x 2-bx -a <0的解集是( A )A .(2,3)B .(-∞,2)∪(3,+∞)C .(13,12)D .(-∞,13)∪(12,+∞)(2)(2018·九江模拟)若关于x 的不等式x 2-4x -2-a >0在区间(1,4)内有解,则实数a 的取值范围是( A ) A .(-∞,-2) B .(-2,+∞) C .(-6,+∞)D .(-∞,-6)[解析] (1)依题意,-12与-13是方程ax 2-bx -1=0的两根,则⎩⎨⎧b a =-12-13,-1a =-12×(-13),即⎩⎨⎧b a =-56,1a =-16,又a <0,不等式x 2-bx -a <0可化为1a x 2-ba x -1>0,即-16x 2+56x -1>0,即x 2-5x +6<0,解得2<x <3.故选A .(2)解法一:由函数f (x )=x 2-4x -2-a 图象的对称轴为x =2.∴不等式x 2-4x -2-a >0在区间(1,4)内有解⇔f (4)>0,即a <-2,故选A .解法二:(分离参数法)不等式x 2-4x -2-a >0在区间(1,4)内有解等价于a <(x 2-4x -2)max ,令g (x )=x 2-4x -2,x ∈(1,4),∴g (x )<g (4)=-2,∴a <-2.故选A .考点3 一元二次不等式恒成立问题——师生共研例4 已知f (x )=mx 2-mx -1.(1)若对于x ∈R ,f (x )<0恒成立,求实数m 的取值范围; (2)若对于x ∈[1,3],f (x )<-m +5恒成立,求实数m 的取值范围; (3)若对于|m |≤1,f (x )<0恒成立,求实数x 的取值范围.[分析] (1)二次项系数含有字母m ,应分m =0和m ≠0讨论求解;(2)数形结合,分类讨论;(3)把二次不等式转化为含m 的一次不等式,根据一次函数的性质求解. [解析] (1)要使mx 2-mx -1<0恒成立, 若m =0,显然-1<0;若m ≠0,则⎩⎪⎨⎪⎧m <0,Δ=m 2+4m <0⇒-4<m <0.所以m 的取值范围为(-4,0]. (2)要使f (x )<-m +5在[1,3]上恒成立, 只需mx 2-mx +m <6恒成立(x ∈[1,3]), 又因为x 2-x +1=(x -12)2+34>0,所以m <6x 2-x +1.令y =6x 2-x +1=6(x -12)2+34.因为t =(x -12)2+34在[1,3]上是增函数,所以y =6x 2-x +1在[1,3]上是减函数.因此函数的最小值y min =67.所以m 的取值范围是(-∞,67).(3)将不等式f (x )<0整理成关于m 的不等式为(x 2-x )m -1<0. 令g (m )=(x 2-x )m -1,m ∈[-1,1].则⎩⎨⎧g (-1)<0,g (1)<0即⎩⎪⎨⎪⎧-x 2+x -1<0,x 2-x -1<0,解得1-52<x <1+52,即x 的取值范围为(1-52,1+52).名师点拨 ☞一元二次不等式恒成立问题1.在R 上恒成立(1)一元二次不等式ax 2+bx +c >0(或≥0)对于一切x ∈R 恒成立的条件是⎩⎪⎨⎪⎧a >0,Δ=b 2-4ac <0(或≤0). (2)一元二次不等式ax 2+bx +c <0(或≤0)对于一切x ∈R 恒成立的条件是⎩⎪⎨⎪⎧a <0,Δ=b 2-4ac <0(或≤0). 2.在给定某区间上恒成立(1)当x ∈[m ,n ],f (x )=ax 2+bx +c ≥0恒成立,结合图象,只需f (x )min ≥0即可; (2)当x ∈[m ,n ],f (x )=ax 2+bx +c ≤0恒成立,只需f (x )max ≤0即可.3.解决恒成立问题一定要搞清谁是自变量,谁是参数.一般地,知道谁的范围,谁就是自变量,求谁的范围,谁就是参数.4.“不等式f (x )≥0有解(或解集不空)的参数m 的取值集合”是“f (x )<0恒成立的参数m 取值集合”的补集;“f (x )>0的解集为∅”即“f (x )≤0恒成立.” 注意:ax 2+bx +c >0恒成立⇔⎩⎨⎧ a =b =0c >0或⎩⎨⎧a >0Δ=b 2-4ac <0; ax 2+bx +c <0恒成立⇔⎩⎨⎧ a =b =0c <0或⎩⎨⎧a <0Δ=b 2-4ac <0.〔变式训练3〕(1)(2018·甘肃天水月考)若不等式ax 2+2ax -4<2x 2+4x 对任意实数x 均成立,则实数a 的取值范围是( B ) A .(-2,2)B .(-2,2]C .(-∞,-2)∪[2,+∞)D .(-∞,2](2)(2018·山西忻州第一中学模拟)已知关于x 的不等式x 2-4x ≥m 对任意的x ∈(0,1]恒成立,则有( A ) A .m ≤-3 B .m ≥-3 C .-3≤m <0D .m ≥-4(3)已知对于任意的a ∈[-1,1],函数f (x )=x 2+(a -4)x +4-2a 的值总大于0,则x 的取值范围是( B ) A .{x |1<x <3} B .{x |x <1或x >3} C .{x |1<x <2}D .{x |x <1或x >2}[解析] (1)不等式ax 2+2ax -4<2x 2+4x ,可化为(a -2)x 2+2(a -2)x -4<0,当a -2=0,即a =2时,不等式恒成立,符合题意;当a -2≠0时,要使不等式恒成立,需⎩⎪⎨⎪⎧a -2<0,Δ<0,解得-2<a <2.所以a 的取值范围为(-2,2].故选B .(2)令f (x )=x 2-4x ,x ∈(0,1],∵f (x )图象的对称轴为直线x =2,∴f (x )在(0,1]上单调递减,∴当x =1时,f (x )取得最小值-3,∴m ≤-3,故选A .(3)记g (a )=(x -2)a +x 2-4x +4,a ∈[-1,1],依题意,只须⎩⎪⎨⎪⎧ g (1)>0,g (-1)>0⇒⎩⎪⎨⎪⎧x 2-3x +2>0,x 2-5x +6>0⇒x <1或x >3,故选B .。
第二章 一元二次方程复习 讲义

龙文教育学科教师辅导讲义学员姓名: 辅导课目:数学 年级:八年级 学科教师:汪老师 授课日期及时段课 题第二章 一元二次方程复习重点、难点、考点1、一元二次方程的基本概念2、一元二次方程的解法及应用学习目标1、理解一元二次方程的基本概念及其相应的应用2、一元二次方程的解法及其应用教学内容一、知识回顾:1.一元二次方程:在整式方程中,只含 个未知数,并且未知数的最高次数是 的方程叫做一元二次方程.一元二次方程的一般形式是 .其中 叫做二次项, 叫做一次项, 叫做常数项; 叫做二次项的系数, 叫做一次项的系数。
2. 一元二次方程的常用解法:(1)直接开平方法:形如)0(2≥=a a x 或)0()(2≥=-a a b x 的一元二次方程,就可用直接开平方的方法. (注意:用直接开平方的方法时要记得取正、负.)(2)配方法:关键化原方程为2()x m n +=的形式 (警告: 用配方法时二次项系数要化1.)(3)公式法:一元二次方程20(0)ax bx c a ++=≠的求根公式是221,24(40)2b b ac x b ac a-±-=-≥.(注意:方程要先化成一般形式.)(4)因式分解法(主要有提取公因式、运用平方差公式、运用完全平方公式、十字相乘法):因式分解法的一般步骤是:①将方程的右边化为 ;②将方程的左边化成两个一次因式的乘积; ③令每个因式都等于0,得到两个一元一次方程,解这两个一元一次方程,它们的解就是原一元二次方程的解.(注意:方程要先化成一般形式.)3.一元二次方程根的判别式: 24b ac ∆=-(1)一元二次方程20(0)ax bx c a ++=≠根的情况:①当0∆>时,方程有两个不相等的实数根;②当0∆=时,方程有两个相等的实数根; ③当0∆<时,方程无实数根. (2)判定一元二次方程根的情况; (3)确定字母的值或取值范围。
知识点练习知识一:一元二次方程的概念1、一元二次方程(1-3x)(x+3)=2x 2+1的一般形式是 它的二次项系数是 ; 一次项系数是 ;常数项是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知12,x x 是方程24440a x a x a -++=的两实根,是否能适当选取a 的值,使得
1221(2)(2)
x x x x --的值等于
54
________________。
已知2007())()0()a b b c c a a b -+-+-=≠,求2
()()()
c b c a a b ---的值.
已知m ,n 是有理数,并且方程20x mx n ++=2,那么m n +=_______.
已知a b ,为正整数,关于x 的方程220x ax b -+=的两个实数根为12x x ,,关于y 的方程
2
20y ay b ++=的两个实数根为12y y ,,且满足11222008x y x y ⋅-⋅=.求b 的最小值.
已知α,β是一元二次方程210x x +-=的两个根,求5325αβ+的值
设实数,s t 分别满足2199910s s ++=,299190t t ++=并且1st ≠,求41
st s t
++的值.
已知b ,c 为整数,方程250x bx c ++=的两根都大于1-且小于0,求b 和c 的值.
设p 是大于2的质数,k 为正整数.若4)1(02-+++=p k px x 有整根,求k 的值.
已知:PA =4PB =,以AB 为一边作正方形ABC D ,使P ,D 两点落在直线AB 的两侧如图,当45APB ∠=︒时,求AB 及PD 的长;当APB ∠变化,且其它条件不变时,求PD 的最大值,及相应的APB ∠的大小。
通州区2009一模第25题)请阅读下列材料:
已知:如图1在R t A B C ∆中,90B A C ∠=︒,AB AC =,点D 、E 分别为线段B C 上两动点,若45D AE ∠=︒.探究线段BD 、D E 、E C 三条线段之间的数量关系.
小明的思路是:把A E C ∆绕点A 顺时针旋转90︒,得到ABE '∆,连结E D ', 使问题得到解决.请你参考小明的思路探究并解决下列问题: ⑴ 猜想BD 、D E 、E C 三条线段之间存在的数量关系式,并对你的猜想给予证明; ⑵ 当动点E 在线段B C 上,动点D 运动在线段C B 延长线上时,如图2,其它条件不变,⑴中探究的结论是否发生改变?请说明你的猜想并给予证明.
图1
A
B
C
D
E
图2
A
B C
D
E
如图,B ,C ,E 三点共线,且A B C ∆与D C E ∆是等边三角形,连结BD ,AE 分别交A C ,
D C 于M ,N 点.求证:C M C N =.
N
M
E
D
C
B
A。
