九年级数学下册 第一章 直角三角形的边角关系 1.6 利用三角函数测高同步练习 北师大版
九年级数学下册第1章直角三角形的边角关系1.6利用三角函数测高同步练习
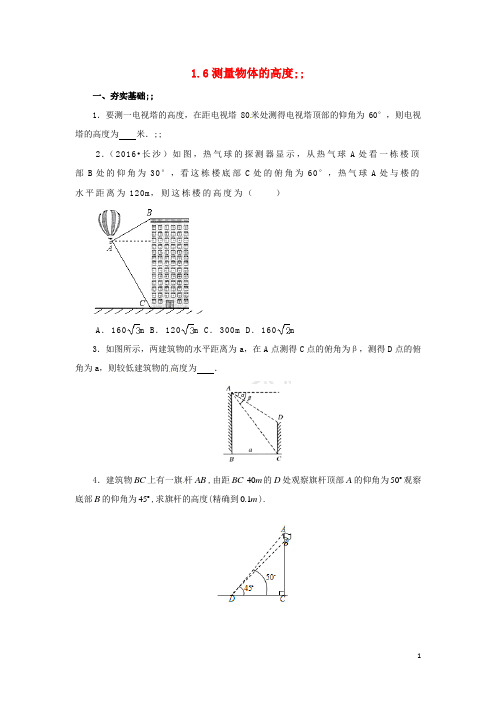
1.6测量物体的高度;;一、夯实基础;;1.要测一电视塔的高度,在距电视塔80米处测得电视塔顶部的仰角为60°,则电视塔的高度为米.;;2.(2016•长沙)如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为()A.160m B.120m C.300m D.160m3.如图所示,两建筑物的水平距离为a,在A点测得C点的俯角为β,测得D点的俯角为a,则较低建筑物的高度为.4.建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为50观察底部B的仰角为45,求旗杆的高度(精确到0.1m).5. (2016·重庆市A卷·4分)某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)()A.8.1米B.17.2米C.19.7米D.25.5米二、能力提升6.如图所示,在测量塔高AB时,选择与塔底同一水平面的同一直线上的C,D两处,用测角仪测得塔顶A的仰角分别是30°和60°,已知测角仪的高CE=1.5米CD=30米,求塔高AB.(精确到0.1 1.732)7.如图所示,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B点测得C点的仰角为60°.已知AB=20 m,点C和直线AB在同一平面上,求气球离地面的高度.(结果保留整数 1.73)8.如图所示,一位同学用一个有30°角的直角三角板估测学校的旗杆AB的高度.他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D,B的距离为15米.(1)求旗杆的高度;(精确到0.1 1.73)(2)请你设计出一种更简便的估测方法.三、课外拓展9.某商场门前的台阶截面如图1—9l所示,已知每级台阶的宽度(如CD)均为0.3 m,高度(如BE)均为0.2 m,现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A 为9°,计算从斜坡的起点(A点)到台阶前(B点)的距离.(精确到0.1 m,参考数据:sin 9°≈0.16,cos 9°≈0.99,tan 9°≈0.16)10.如图所示,甲、乙两栋高楼的水平距离BD为90米,从甲楼顶部C点测得乙楼顶部A点的仰角a为30°,测得乙楼底部B点的俯角B为60°,求甲、乙两栋高楼各有多高.(计算过程和结果都不取近似值)11.如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30.两人相距28m且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据 1.4≈ 1.7,结果保留整数)四、中考链接1.(2016·四川宜宾)如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)2.(2016·湖北黄石·8分)如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(1)求AB段山坡的高度EF;(2)求山峰的高度CF.( 1.414,CF结果精确到米)3. (2016·云南省昆明市)如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B ,C ,E 在同一水平直线上),已知AB=80m ,DE=10m ,求障碍物B ,C 两点间的距离(结果精确到0.1m )(参考数据:≈1.414,≈1.732)答案1. 2.故选A . 3.a(tan β-tan a) 4.20tan a +1.5 5.故选A .解:∵90C ∠=,45BDC ∠= ∴45DBC BDC ∠=∠= ∴40DC BC ==在Rt ADC ∆中,tan AC ADC ∠=∴tan 40tan5047.7AC DC ADC =⋅∠=⨯≈ ∴47.7407.7AB AC BC =-≈-= 答:旗杆的高度约为7.7m .6.解:在Rt △AGE 中,∠AEG=30°,tan30°=AG EG ,∴EG=tan 303AG ==在Rt △AFG 中∠AFG =60°,tan60°=AGFG,∴FG=.,30,tan60AGAG EF EG GF AG AG==-=∴== (米),∴AB=AG+GB=1.5≈27.5(米),即塔高AB约为27.5米.7.解:作CD⊥AB,垂足为D.设气球离地面的高度是x m,在Rt△ACD中,∠CAD=45°,∴AD=CD=x m.在Rt△CBD中,∠CBD=60°,∴tan 60°=CDBD,∴BD=tan603CD==x(m).∵AB=AD-BD,∴20=x,∴47(m).答:气球离地面的高度大约是47 m.8.解:(1)作CE⊥AB于E,在Rt△AEC中,AE=CE tan 30°=15米),∴AB=AE+BE= 1.3≈10.0(米).(2)∵旗杆底部可以到达,∴使用含45°角的直角三角板估测更简便.9.解:过C点作CF⊥AB交AB的延长线于F.由已知条件,得CF=0.6 m.在Rt△AFC中,tan A=CFAF,AF≈0.60.16=3.75(m),∴AB=AF-BF≈3.75-0.6=3.15(m).答:从斜坡起点(A点)到台阶前(B点)的距离约为3.15 m.10.解:作CE⊥AB于E.∵CE∥DB,CD∥AB,且∠CDB=90°,∴四边形BECD是矩形,∴CD=BE,CE=BD.在Rt△BEC中,β=60°,CE=BD=90米.∵tan β=BECE,∴BE=CEtanβ=90tan 60°=米),∴CD=BE=Rt△AEC中,a=30°,CE=90米.∵tan a=AECE,∴AE=CEtan a=90tan 30°=90(米),∴AB=AE+BE=米).答:甲楼高为乙楼高为米.11.解:分别过点A ,C 作AE M N ⊥于点E ,CF MN ⊥于点F 则 1.7 1.50.2EF AB CD =-=-= ∵90AEM ∠=,45MAE ∠= ∴AE M E =设AE ME x ==,则0.2MF x =+,28CF x =- 在Rt MFC ∆中,tan MF MCF FC ∠=∴tan 30MF FC =⋅∴0.2(28)x x +=- 解得10.0x ≈∴10.0 1.712MN ME EN ME AB =+=+≈+≈ 答:旗杆高约为12米. 中考链接:1.解:作CF⊥AB 于点F ,设AF=x 米,在Rt△ACF 中,tan∠ACF=,则CF====x ,在直角△ABE 中,AB=x+BF=4+x (米),在直角△ABF 中,tan∠AEB=,则BE===(x+4)米.∵CF﹣BE=DE ,即x ﹣(x+4)=3.解得:x=,则AB=+4=(米).答:树高AB 是米.2.解:(1)作BH⊥AF 于H ,如图,在Rt△ABF中,∵sin∠BAH=,∴BH=800•sin30°=400,∴EF=BH=400m;(2)在Rt△CBE中,∵sin∠CBE=,∴CE=200•sin45°=100≈141.4,∴CF=CE+EF=141.4+400≈541(m).答:AB段山坡高度为400米,山CF的高度约为541米.3.解:如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.则DE=BF=CH=10m,在直角△ADF中,∵AF=80m﹣10m=70m,∠ADF=45°,∴DF=AF=70m.在直角△CDE中,∵DE=10m,∠DCE=30°,∴CE===10(m),∴B C=BE﹣CE=70﹣10≈70﹣17.32≈52.7(m).答:障碍物B,C两点间的距离约为52.7m.。
九年级数学下册 第一章 直角三角形的边角关系 1.5 三角函数的应用1.6 利用三角函数测高

第十一页,共四十四页。
3.从高处甲看低处乙的俯角为30°,那么(nà me)从乙处看甲 处的仰角为_____3_0_°__.
第十二页,共四十四页。
知识点一 与方位角有关的问题(P21习题1.6T4变式)
【典例1】如图,在一条东西方向笔直的沿湖道路l上有A、
B两个游船码头,观光岛屿C在码头A的北偏东60°方向、 在码头B的北偏西45°方向,AC =4 km.求码头A,B之间的距离. (结果(jiē guǒ)保留根号)
≈0.86,tan 31°≈0.60.
第三十二页,共四十四页。
解:在Rt△CAD中,tan∠CAD= C D ,
AD
则AD= CD 5CD,
tan 31 3
在Rt△CBD中,∠CBD=45°,∴BD=CD, ∵AD=AB+BD,∴ 5 CD=CD+30,解得CD=45. 答:这座灯塔(dēngtǎ)的3 高度CD约为45 m.
第四十三页,共四十四页。
内容 总结 (nèiróng)
5 三角函数的应用。题目中点O是观测点,故点O为方向(fāngxiàng)坐标的原点.。B两个游船码头,观光岛
B.75·cos 55°米 D. 米 7 5
tan 5 5
第十八页,共四十四页。
★2.(2019·济宁市微山一模)如图,港口A在观测站O的正东
方向,OA=2km,某船从港口A出发,沿北偏东15°方向航行
一段距离后到达B处,此时从观测站O处测得该船位于北偏东
60°的方向,则该船航行的距离(即AB的长)为 世纪(shìjì)金榜导学
第四十一页,共四十四页。
解:设AD=x cm.由题意(tí yì)可得:AD=DC=x cm,
九年级数学北师大版初三下册--第一单元1.6《利用三角函数测高(第一课时)》习题课件

答:这架无人机的长度AB为5 m.
9. 【中考•内江】如图,某人为了测量小山顶上的塔ED的 高,他在山下的点A处测得塔尖点D的仰角为45°,再 沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角 为60°,塔底点E的仰角为30°,求塔ED的高度(结果 保留根号).
解:由题知,∠DBC=60°,∠EBC=30°, ∴∠DBE=∠DBC-∠EBC=60°-30°=30°. 又∵∠BCD=90°, ∴∠BDC=90°-∠DBC=90°-60°=30°. ∴∠DBE=∠BDE. ∴BE=DE. 设EC=x,则DE=BE=2EC=2x, DC=EC+DE=x+2x=3x, ∴BC= BE2-EC2=(2x)2-x2 3x.
第一章 直角三角形的边角关系
1.6 利用三角函数测高
第1课时 视角在测量中的应用
1 利用锐角三角函数解决测距问题 2 利用锐角三角函数解决不能到达底部的物高问题 3 利用锐角三角函数解决同一位置的视角问题 4 利用锐角三角函数测量有视线障碍的物高
8.【中考•株洲】如图,一架水平飞行的无人机AB的尾端点A测
结果精确到0.1 m,参考数据: 2 ≈1.41, 3 ≈1.73).
解:如图,过点C作CM⊥AB于点M,则四边形MEDC是矩形, ∴ME=DC=3,CM=ED. 在Rt△AEF中,∠AFE=60°, 设EF=x,则AF=2x,AE= 3 x. 在Rt△FCD中,CD=3,∠CFD=30°, ∴DF=3 3. 在Rt△AMC中,∠ACM=45°, ∴MA=MC.∵ED=MC,∴AM=ED.
得正前方的桥的左端点P的俯角为α,其中tan α=2 3 ,无 人机的飞行高度AH为500 3 m,桥的长度为1 255 m.
(1)求点H到桥左端点P的距离; (2)若无人机前端点B测得正前方的桥的右端点Q的俯角为
2018-2019学年九年级数学下册 第一章 直角三角形的边角关系 1.6 利用三角函数测高同步练习 (新版)北师大

课时作业(七)[第一章 6 利用三角函数测高]一、选择题1.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图K-7-1,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )链接听课例1归纳总结图K-7-1A.11-sinα米 B.11+sinα米C.11-cosα米 D.11+cosα米2.如图K-7-2,为了测量电视塔的高度AB,在D处用高为1米的测角仪CD测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB为链接听课例2归纳总结( )图K-7-2A.50 3米 B.51米C.(50 3+1)米 D.101米3.如图K-7-3,斜坡AB的坡度为1∶2.4,长度为52米,在坡顶B所在的平台上有一座高楼FH,已知在A处测得楼顶F的仰角为60°,在B处测得楼顶F的仰角为77°,则高楼FH的高度是(结果精确到1米,参考数据:sin77°≈0.97,tan77°≈4.33,3≈1.73)( )图K-7-3A.125米 B.105米C.85米 D.65米4.2017·深圳如图K-7-4,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°.已知斜坡CD的长度为20 m,DE的长度为10 m,则树AB的高度是( )A.20 3 m B.30 mC.30 3 m D.40 m图K-7-45.如图K-7-5,在两建筑物之间有一旗杆GE,高15米,从点A经过旗杆顶端恰好看到矮建筑物的墙脚点C,且俯角α为60°,又从点A测得点D的俯角β为30°,若旗杆底G为BC的中点,则矮建筑物的高CD为()图K-7-5A.20米 B.10 3米C.15 3米 D.5 6米二、填空题6.如图K-7-6,小亮在太阳光线与地面成35°角时,测得树AB在地面上的影长BC =18 m,则树高AB约为________m.(结果精确到0.1 m)图K-7-67.如图K-7-7(示意图),某学校组织学生到首钢西十冬奥广场开展综合实践活动,数学小组的同学们在距奥组委办公楼(原首钢老厂区的筒仓)20 m的点B处,用高为0.8 m 的测角仪测得筒仓顶点C的仰角为63°,则筒仓CD的高约为________m.(结果精确到0.1 m,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)链接听课例1归纳总结图K-7-78.如图K-7-8,两建筑物的水平距离BC为18 m,从点A测得点D的俯角α为30°,测得点C的俯角β为60°.则建筑物CD的高度为________m(结果不作近似计算).图K-7-8三、解答题9.2017·黄冈在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图K -7-9所示),已知标语牌的高AB=5 m,在地面的点E处,测得标语牌上点A的仰角为30°,在地面的点F处,测得标语牌上点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据:2≈1.41,3≈1.73)图K-7-910.2017·莱芜如图K-7-10,某学校教学楼(甲楼)的顶部E和大门A之间挂了一些彩旗.小颖测得大门A距甲楼的距离AB是31 m,在A处测得甲楼顶部E处的仰角是31°.(1)求甲楼的高度及彩旗的长度;(2)若小颖在甲楼楼底C处测得学校后面医院楼(乙楼)楼顶G处的仰角为40°,爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为19°,求乙楼的高度及甲、乙两楼之间的距离.(结果均精确到0.01 m,cos31°≈0.86,tan31°≈0.60,cos19°≈0.95,tan19°≈0.34,cos40°≈0.77,tan40°≈0.84)链接听课例2归纳总结图K-7-1011.学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:(1)如图K-7-11,在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;(2)在测点C与山脚B之间的D处安置测倾器(C,D与B在同一直线上,且C,D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;(3)测得测倾器的高度CF=DG=1.5米,并测得C,D之间的距离为288米.已知红军亭的高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB(3取1.732,结果保留整数).图K-7-11如图K-7-12,A,B是两幢地平面高度相等、隔岸相望的建筑物.由于建筑物密集,在A的周围没有开阔地带,为了测量B楼的高度只能利用A楼的空间,A的各层楼都可到达,且能看见B.现有的测量工具为皮尺和测角器(皮尺可用于测量长度,测角器可以测量仰角、俯角或两视线间的夹角).(1)请你设计一个测量B楼高度的方法,要求写出测量步骤和必要的测量数据(用字母表示),并画出测量图形;(2)用你测量的数据(用字母表示)写出计算B楼高度的表达式.图K-7-12详解详析【课时作业】 [课堂达标] 1.[答案] A2.[解析] C 设AG =x 米,在Rt △AEG 中, ∵tan ∠AEG =AG EG,∴EG =AG3=33x 米. 在Rt △ACG 中,∵tan ∠ACG =AG CG ,∴CG =x tan30°=3x 米,∴3x -33x =100,解得x =50 3,则AB =(50 3+1)米,故选C.3.[解析] B 如图,延长FH 交AC 于点.由题意知BG ⊥AC ,BH ⊥FH ,FE ⊥AC ,∴四边形BGEH 是矩形,∴BH =GE ,BG =HE .∵BG ∶AG =1∶2.4,∴设BG =x 米,AG =2.4x 米(x >0).在Rt △ABG 中,∵AB =52米,由勾股定理可得BG 2+AG 2=AB 2,即x 2+(2.4x )2=522,解得x =20,则BG =20米,AG =48米.在Rt △BHF 中,∵∠HBF =77°,∴tan77°=FH BH,∴FH =BH tan77°. 在Rt △AEF 中,∵∠EAF =60°,∴EF =3AE ,∴3(48+BH )=20+BH tan77°, 解得BH ≈24.25,∴FH =BH tan77°≈105米.故选B.4.[解析] B 先根据CD =20 m ,DE =10 m 得出∠DCE =30°,故可得出∠DCB =90°,再由∠BDF =30°可知∠DBF =60°,由DF ∥AE 可得出∠BGF =∠BCA =60°,故∠GBF =30°,所以∠DBC =30°,再由锐角三角函数的定义即可得出结论.5.[解析] A 如图,延长CD 交点A 所在的水平线于点F ,如图.由题意,知GE ∥AB∥CD ,BC =2GC ,GE =15米,∴AB =2GE =30米.∵AF =BC =AB tan ∠ACB =303=10 3(米),DF =AF ·tan30°=10 3×33=10(米),∴CD =AB -DF =30-10=20(米). 6.[答案] 12.6 7.[答案] 40.0[解析] 过点A 作AE ⊥CD 于点E . ∵AB ⊥BD ,CD ⊥BD , ∴四边形ABDE 是矩形,∴AE =BD =20 m ,DE =AB =0.8 m. 在Rt △ACE 中,∠CAE =63°,∴CE =AE ·tan63°≈20×1.96=39.2(m), ∴CD =CE +DE ≈39.2+0.8=40.0(m), 即筒仓CD 的高约为40.0 m.8.[答案] 12 3[解析] 过点D 作DE ⊥AB 于点E ,则四边形BCDE 是矩形.根据题意,得∠ACB =β=60°,∠ADE =α=30°,BC =18 m ,∴DE =BC =18 m ,CD =BE .在Rt △ABC 中,AB =BC ·tan∠ACB =18×tan60°=18 3(m). 在Rt △ADE 中,AE =DE ·tan∠ADE =18×tan30°=6 3(m),∴CD =BE =AB -AE =18 3-6 3=12 3(m).9.[解析] 如图,过点F 作FH ⊥AE 于点H .由题意可知∠HAF =∠HFA =45°,推出AH =HF .设AH =HF =x m ,则EF =2x m ,EH =3x m ,在Rt △AEB 中,由∠E =30°,AB =5 m ,推出AE =2AB =10 m ,可得x +3x =10,解方程即可.解:如图,过点F 作FH ⊥AE 于点H .由题意可知∠HAF =∠HFA =45°,∴AH =HF .设AH =HF =x m ,则EF =2x m ,EH =3x m. 在Rt △AEB 中,∵∠E =30°,AB =5 m , ∴AE =2AB =10 m ,∴x +3x =10,解得x =5 3-5,∴EF =2x =10 3-10≈7.3(m). 答:点E 与点F 之间的距离约为7.3 m.10.解:(1)在Rt △ABE 中,BE =AB ·tan31°=31×tan31°≈31×0.60=18.60(m),AE =ABcos31°=31cos31°≈310.86≈36.05(m),故甲楼的高度约为18.60 m ,彩旗的长度约为36.05 m. (2)过点F 作FM ⊥GD ,交GD 于点M , 在Rt △GMF 中,GM =FM ·tan19°. 在Rt △GDC 中,GD =CD ·tan40°.设甲、乙两楼之间的距离为x m ,则FM =CD =x m. 根据题意,得x tan40°-x tan19°=18.60,解得x =37.20.乙楼的高度GD =CD tan40°≈37.20×0.84≈31.25(m),故乙楼的高度约为31.25 m ,甲、乙两楼之间的距离约为37.20 m.11.解:设AH =x 米,在Rt △中, ∵∠EGH =45°,∴GH =EH =AE +AH =(x +12)米. ∵GF =CD =288米,∴HF =GH +GF =x +12+288=(x +300)米. 在Rt △AHF 中,∵∠AFH =30°, ∴AH =HF ·tan∠AFH ,即x =(x +300)·33, 解得x =150(3+1).∴AB =AH +BH =150(3+1)+1.5≈409.8+1.5≈411(米). 答:凤凰山与中心广场的相对高度AB 大约是411米. [素养提升][解析] 本题是一道开放性试题,解题方法很多,表达式也是多种多样的.测角器可以测得仰角和俯角,皮尺可以测得A 楼的高度,通过解直角三角形可得B 楼的高度.解:(1)答案不唯一.如图,设AC 表示A 楼,BD 表示B 楼.测量步骤如下:①用测角器在A 楼的顶端点A 测量B 楼楼底的俯角α; ②用测角器在点A 测量B 楼楼顶的仰角β;③用皮尺从A 楼楼顶放下,测量点A 到地面的高度为a . (2)在Rt △ACD 中,CD =atan ∠ADC =atan α.在Rt △AEB 中,BE =AE ·tan β. ∵AE =CD ,∴BE =a tan βtan α, ∴B 楼的高度BD =BE +ED =BE +AC =a tan βtan α+a =a ⎝ ⎛⎭⎪⎫1+tan βtan α.。
九年级数学下册第一章直角三角形的边角关系1.230°、45°、60°角的三角函数值练习北师大版(2

2018-2019学年九年级数学下册第一章直角三角形的边角关系1.2 30°、45°、60°角的三角函数值同步练习(新版)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年九年级数学下册第一章直角三角形的边角关系1.2 30°、45°、60°角的三角函数值同步练习(新版)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年九年级数学下册第一章直角三角形的边角关系1.2 30°、45°、60°角的三角函数值同步练习(新版)北师大版的全部内容。
课时作业(三)[第一章 2 30°,45 °,60°角的三角函数值]一、选择题1.2018·大庆2cos60°=()A.1 B。
错误! C.错误! D.错误!2.计算sin240°+cos240°的值为()A.0 B。
错误! C.1 D.23.在△ABC中,若∠C=90°,tan A=3,则sin B的值为()A.错误!B.错误!C。
错误!D。
错误!4.如图K-3-1,以点O为圆心,任意长为半径画弧,与射线OA交于点B,再以点B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则cos∠AOC的值为()图K-3-1A。
错误!B。
错误!C。
错误!D。
错误!5.如果在△ABC中,∠A,∠B为锐角,且sin A=cos B=错误!,那么下列对△ABC最确切的描述是()A.△ABC是直角三角形B.△ABC是等腰三角形C.△ABC是等腰直角三角形D.△ABC是锐角三角形6.在△ABC中,∠A,∠B是锐角,且有|tan B-3|+(2sin A-错误!)2=0,则△ABC的形状是()链接听课例2归纳总结A.等腰(非等边)三角形B.直角三角形C.等边三角形D.等腰直角三角形7.如图K-3-2,钓鱼竿AC长6 m,露在水面上的鱼线BC长3 错误!m,某钓者想看看鱼钩上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′长3 错误!m,则鱼竿转过的角度是()图K-3-2A.60°B.45°C.15°D.90°二、填空题8.点 M(-sin60°,cos60°)关于x轴对称的点的坐标是________.9.在Rt△ABC中,∠C=90°,BC=5 错误!,AC=5 错误!,则∠A=________°。
九年级数学下册第一章直角三角形的边角关系1.6利用三角函数测高初中九年级下册数学

下: ①测量数据尽可能少; ②在所给图形上,画出你设计的测量的平面图,并将应
测数据标记在图形上(如果测A、D间距离,用m表示; 如果测D、C间距离,用n表示;如果测角,用α、β、
γ等表示.测倾器高度不计)
(2)根据你测量的数据,计算塔顶到地面的高度HG(用 字母I表示)
2.已知测倾器的高CE=DF=1m,通过(tōngguò)计算求得, 该大厦的高为_8_3____m (精确到1m).
解:在Rt△AEG中,
EG= A G =1.732AG
ta n 3 0 °
在Rt△AFG中,FG= A G
EG-FG=C D
ta n 4 5 °
1.732AG-AG=60
AG=60÷0.732≈81.96
1.在测点A处安置(ānzhì)测倾器,测得M的仰角∠MCE=α. 2.在测点A与物体(wùtǐ)之间的B处安置测倾(A,B与N在一
条直线上),测得M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间 的距离AB=b.
根据测量数据, 你能求出物体 M MN的高度吗?说 说你的理由.
水平线
哈哈:同角 的余角相等
1
2
4
3
12/11/2021
第七页,共二十五页。
活动(huódòng测) 量底部可以到达的物体的高度 二所: 谓“底部可以到达”,就是(jiùshì)在地面上可以无障
碍地直接测得测点与被测物体底部之间的距离.
如图,要测量物体MN的高度(gāodù),需测量哪些数据?
可按下列步骤进行:
第十九页,共二十五页。
方案 一 (fāng àn)
九年级数学下册第一章直角三角形的边角关系1.6利用三角函数测高120

②[讲授效果反思]
在本节课的整个活动过程中,每个小组的成员都能积极地投入到活动中去,学生自始至终处于主体地位,积极想办法寻找解决问题的方案,克服困难,表现出极大的参与热情,尤其是平时数学成绩很一般的学生都充当了主角地位,他们出谋划策,测量、收集数据一马当先,对自己设计的方案感到非常自豪,大大提高了学生的动手、动脑能力,激发了学习热情.
2.进一步巩固用三角函数解决生活中的问题.如果学生掌握得好,进入下面的环节;如果学生掌握得不好,则可以再引导学生多加练习.
【拓展提升】
例1如图1-6-15,从地面C,D两处望山顶A,仰角分别为30°,45°.若C,D两处相距200 m,求山高AB.
例2如图1-6-16,大楼AD的高为图1-6-15
10米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D测得塔顶B处的仰角为30°,求塔BC的高度.
通过小组合作设计方案,培养学生科学的思维方式及归纳总结的能力.
这个活动的设计方案对于学生来说有一定的难度,所以在教学过程中要给学生留有充分的讨论时间,不可急于求成,也可各组间穿插讨论;同时教师要深入小组内讨论,帮助有困难的小组.这个活动的设计方案不唯一,学生说的只要合理,就应该给予肯定和鼓励.教师还要关注学生是否积极参与,是否真正理解.
图1-6-14
在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面的高度BE是1.4 m,求学校主楼的高度(精确到0.01 m).
(本题先让学生独立完成,找一名学生到黑板前板书解题过程,便于集体纠正出现的错误)
北师大版九年级数学下册第一章直角三角形的边角关系第6节利用三角函数测高课后练习
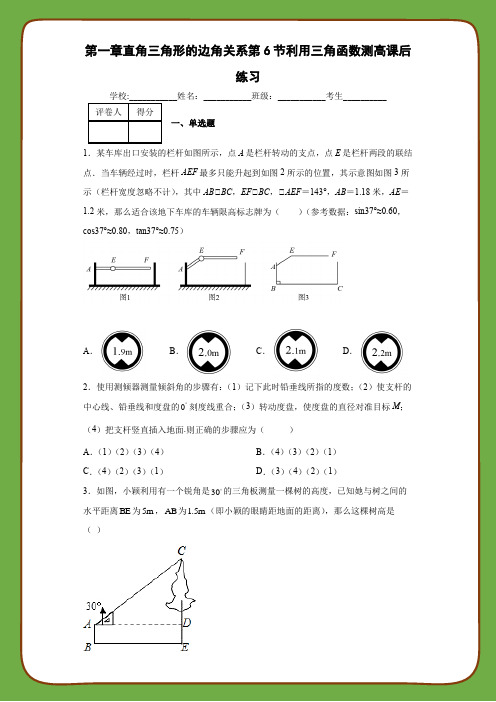
第一章直角三角形的边角关系第6节利用三角函数测高课后练习学校:___________姓名:___________班级:___________考生__________评卷人得分一、单选题1.某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF⊥BC,⊥AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为()(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)A.B.C.D.2.使用测倾器测量倾斜角的步骤有:(1)记下此时铅垂线所指的度数;(2)使支杆的中心线、铅垂线和度盘的0 刻度线重合;(3)转动度盘,使度盘的直径对准目标M;(4)把支杆竖直插入地面.则正确的步骤应为()A.(1)(2)(3)(4)B.(4)(3)(2)(1)C.(4)(2)(3)(1)D.(3)(4)(2)(1)3.如图,小颖利用有一个锐角是30的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是()A.(5√33+32)m B.(5√3+32)m C.5√33m D.4m4.如图,甲、乙两船同时从港口O出发,其中甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,已知两船的航行速度相同,如果1小时后甲、乙两船分别到达点A、B处,那么点B位于点A的()A.南偏西40°B.南偏西30°C.南偏西20°D.南偏西10°评卷人得分二、填空题5.如图,一辆小车沿着坡度为1:3i=的斜坡从点A向上行驶了50米到点B处,则此时该小车离水平面的垂直高度为_____________.6.如图,某同学用一个有60︒角的直角三角板估测学校旗杆AB的高度.他将与60︒角相邻的直角边水平放在1.5m高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得DB的距离为5m,则旗杆AB的高度约为________m.(结果精确到lm,3取1.73)7.如下图,建筑物AB和CD的水平距离为30m,从A点测得D点的俯角为30°,测得C 点的俯角为60°,则建筑物CD的高为________m.8.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼高_____m(结果保留根号).9.如图,一艘潜艇在海面下500m深的点A处,测得正前方俯角为31°方向上的海底有黑匣子发出信号,潜艇在同一深度保持直线航行500m,在点B处测得海底黑匣子位于正前方俯角36.9°的方向上,海底黑匣子C所在点距海面的深度为________m.(精确到1,m.参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31°≈0.51,cos31°≈0.87,tan31°≈0.60)10.如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC,若⊥B=56°,⊥C=45°,则游客中心A到观景长廊BC的距离AD的长约为_____米.(sin56°≈0.8,tan56°≈1.5)11.全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为________米(参考数据:tan78°12′≈4.8).12.某飞机如果在1200米的上空测得地面控制点的俯角为30°,那么此时飞机离控制点之间的距离是______________米.13.如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得8CD=,20BC=米,CD与地面成30角,且此时测得1米的影长为2米,则电线杆的高度为=__________米.14.如图,某公园入口处原有三级台阶,每级台阶高为20cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡的坡度i=1:5,则AC的长度是_____cm.评卷人得分三、解答题15.如图,光明中学九年级(2)班的同学用自己制作的侧倾器测量该校旗杆的高度,已知测倾器CD的高度为1.54米,测点D到旗杆的水平距离BD=20米,测得旗杆顶A的仰角α=35°,求旗杆AB的高度(精确到0.01米).16.如图,一游客在某城市旅游期间,沿街步行前往著名的电视塔观光,他在A处望塔顶C的仰角为30°,继续前行250m后到达B处,此时望塔顶的仰角为45°.已知这位游客的眼睛到地面的距离约为170cm,假若游客所走路线直达电视塔底.请你计算这座电视塔大约有多高?(结果保留整数. ≈1.7,≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)17.图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点B,E,D均为可转动点.现测得15AB BE ED CD====cm,经多次调试发现当点B,E所在直线垂直经过CD的中点F时(如图3所示)放置较平稳.(1)求平稳放置时灯座DC与灯杆DE的夹角的大小;(2)为保护视力,写字时眼离桌面的距离应保持在30cm,为防止台灯刺眼,点A离桌面的距离应不超过30cm,求台灯平稳放置时⊥ABE的最大值.(结果精确到0.01°,参考数据:3≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)图1图2图318.如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12米,求旗杆AB 的高度(结果精确到0.1米).参考数据:3≈1.73,2≈1.41.19.如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30º,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45º,请计算旗杆AB的高度(结果保留根号).20.在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为35°;(2)在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;(3)量出A,B两点间的距离为4.5米.请你根据以上数据求出大树CD的高度.(精确到0.1米)(可能用到的参考数据sin35°≈0.57cos35°≈0.82,tan35°≈0.70)21.某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB及两根与FG垂直且长均为1米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且⊥DAB=66°.(1)求点D与点C的高度差DH的长度;(2)求所用不锈钢材料的总长度l(即AD+AB+BC,结果精确到0.1米).(参考数据:sin66°≈0.91,cos66°≈0.41,tan66°≈2.25,cot66°≈0.45)22.某市某消防支队在一幢居民楼前进行消防演习,如图,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方D处又有一名求救者,消防官兵立即升高云梯将其求出,经测得点A与居民楼的水平距离AB是15米,且在点A测得第一次施救时云梯与水平线的夹角⊥CAB=45°,第二次施救时云梯与水平线的夹角⊥BAD=55°,求C、D两点间的距离(结果精确到0.1米).【参考数据:sin55°=0.82;cos 55°=0.57,tan55°=1.43】23.如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一老人坐在MN这层台阶上晒太阳.(3取1.73)(1)求楼房的高度约为多少米?(2)过了一会儿,当α=45°时,问老人能否还晒到太阳?请说明理由.24.小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为203米.(1)求出大厦的高度BD;(2)求出小敏家的高度AE.25.如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角⊥BAF=30°,⊥CBE=45°.(1)求AB段山坡的高度EF;(2)求山峰的高度CF.(2 1.414,CF结果精确到米)参考答案:1.A【解析】【分析】延长BA、FE,交于点D,根据AB⊥BC,EF⊥BC知⊥ADE=90°,由⊥AEF=143°知⊥AED=37°,根据sin⊥AEDADAE=,AE=1.2米求出AD的长,继而可得BD的值,从而得出答案.【详解】如图,延长BA、FE,交于点D.⊥AB⊥BC,EF⊥BC,⊥BD⊥DF,即⊥ADE=90°.⊥⊥AEF=143°,⊥⊥AED=37°.在Rt⊥ADE中,⊥sin⊥AEDADAE=,AE=1.2米,⊥AD=AE•sin⊥AED=1.2×sin37°≈0.72(米),则BD=AB+AD=1.18+0.72=1.9(米).故选:A.【点睛】本题考查了解直角三角形的应用,解题的关键是结合题意构建直角三角形,并熟练掌握正弦函数的概念.2.C【解析】【分析】根据基本测量理论知识,由测量的基本步骤顺序,即可得到答案.解:使用测倾器测量倾斜角的步骤有:把支杆竖直插入地面;使支杆的中心线、铅垂线和度盘的刻度线重合;转动度盘,使度盘的直径对准目标M;记下此时铅垂线所指的度数;所以正确的顺序是:(4)(2)(3)(1);故选择:C.【点睛】本题考查基本的测量理论,要求学生根据几何知识,结合实际操作,做出判断.3.A【解析】【详解】先根据题意得出AD=BE=5m,DE=AB=1.5m,在Rt⊥ACD中利用锐角三角函数的定义求出CD =AD•tan30°=5×33=533,由CE=CD+DE=533+1.5(m).故选A.点睛:本题考查的是解直角三角形在实际生活中的应用,熟知锐角三角函数的定义是解答此题的关键.4.C【解析】【详解】试题分析:由甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,得出⊥BOA的度数,由两船的航行速度相同,得出AO=BO,得出⊥BAO=50°,以及求出⊥BAD的度数,得出点B位于点A的方向,故本题选C.点睛:本题主要考查的就是方位角的问题,属于中等难度题型.解决这个问题的关键就是要能够根据已知的条件得出各个角的度数,从而求出问题中所要求的角的度数.在解决这种类型的题目时,我们还要注意参照物是那个物体,就要以参照物为标注建立方位图,从而得出答案.5.25【解析】【分析】设出垂直高度,表示出水平距离,利用勾股定理求解即可.设此时该小车离水平面的垂直高度为x米,则水平前进了3x米.根据勾股定理可得:x2+(3x)2=502.解得x=25.即此时该小车离水平面的垂直高度为25米.故答案为:25.【点睛】考查了解直角三角形的应用−坡度坡角问题,此题的关键是熟悉且会灵活应用公式:tan (坡度)=垂直高度÷水平宽度,综合利用了勾股定理.6.10【解析】【分析】在⊥ACE中,CE⊥AE,tan⊥ACE=AECE,由此可得AE,AB=AE+BE=AE+CD.【详解】解:由题意可知,在⊥ACE中,CE⊥AE,且⊥ACE=60°,BD=5,而tan⊥ACE=AE CE,⊥AE=CE×tan60°=53≈8.6.又⊥EB=1.5,⊥AB=AE+EB≈10(米).故答案为10.【点睛】解题的关键是把实际问题抽象到解直角三角形中,然后利用三角函数的定义解决问题.7.203m【解析】【分析】延长CD交AM于点E.在Rt⊥ACE中,可求出CE;在Rt⊥ADE中,可求出DE.CD=CE-DE.【详解】解:延长CD交AM于点E,则AE=30.⊥30103DE AE tan=⨯︒=.同理可得303CE.=⊥203CD CE DE=-=(米)故答案为203【点睛】考查利用解直角三角形知识解决实际问题的能力.8.1603【解析】【详解】试题分析:过A作AD⊥BC,垂足为D,如图所示:在Rt⊥ABD中,⊥⊥BAD=30°,AD=120m,⊥BD=ADtan30°=120×33=403m,在Rt⊥ACD中,⊥⊥CAD=60°,AD=120m,⊥CD=ADtan60°=120×3=1203m,BC=BD+CD=1603m.即这栋楼高为1603m.故答案为1603.考点:仰角与俯角的计算.9.2000.【解析】【详解】试题解析:作CD⊥AB于D,设CD=xm ,则AD=5tan 3CD DAC =∠xm , BD=4tan 3CD DBC =∠xm , 由题意得,AD-BD=500m ,即53x-43x=500, 解得,x=1500m ,1500+500=2000m.考点:解直角三角形的应用-仰角俯角问题.10.60【解析】【分析】 根据题意和图形可以分别表示出AD 和CD 的长,从而可以求得AD 的长,本题得以解决.【详解】⊥⊥B=56°,⊥C=45°,⊥ADB=⊥ADC=90°,BC=BD+CD=100米, ⊥BD=tan 56AD ︒,CD=tan 45AD ︒, ⊥tan 56AD ︒+tan 45AD ︒=100, 解得,AD≈60 考点:解直角三角形的应用.11.58【解析】【详解】试题分析:直接利用锐角三角函数关系得出EC 的长,进而得出AE 的长,进而得出答案.如图所示:由题意可得:CE⊥AB 于点E ,BE=DC , ⊥⊥ECB=18°48′, ⊥⊥EBC=78°12′, 则tan78°12′=10EC EC BE ==4.8, 解得:EC=48(m ), ⊥⊥AEC=45°,则AE=EC ,且BE=DC=10m ,⊥此塑像的高AB 约为:AE+EB=58(米).考点:解直角三角形的应用12.2400.【解析】【详解】试题解析:根据题意,飞机到控制点的距离是1200sin 30︒=2400(米). 考点:解直角三角形的应用-仰角俯角问题.13.(14+23)米【解析】【分析】过D 作DE ⊥BC 的延长线于E ,连接AD 并延长交BC 的延长线于F ,根据直角三角形30°角所对的直角边等于斜边的一半求出DE ,再根据勾股定理求出CE ,然后根据同时同地物高与影长成正比列式求出EF ,再求出BF ,再次利用同时同地物高与影长成正比列式求解即可.【详解】如图,过D 作DE ⊥BC 的延长线于E ,连接AD 并延长交BC 的延长线于F .⊥CD =8,CD 与地面成30°角,⊥DE =12CD =12×8=4,根据勾股定理得:CE =22CD DE -=2242-2284-=43.⊥1m 杆的影长为2m ,⊥DE EF =12, ⊥EF =2DE =2×4=8,⊥BF =BC +CE +EF =20+43+8=(28+43).⊥AB BF =12,⊥AB=12(28+43)=14+23.故答案为(14+23).【点睛】本题考查了相似三角形的应用,主要利用了同时同地物高与影长成正比的性质,作辅助线求出AB的影长若全在水平地面上的长BF是解题的关键.14.240【解析】【详解】试题分析:如图所示:所有台阶高度和为BD的长,所有台阶深度和为AD的长,即BD=60m,AD=60m.然后根据坡度比解答即可.解:由题可知BD=60cm,AD=60cm.⊥tan⊥BCA==⊥DC=300cm,⊥AC=DC﹣AD=300﹣60=240(cm).答:AC的长度是240cm,故答案为240.考点:解直角三角形的应用-坡度坡角问题.15.15.54米【解析】【分析】在Rt△ACE中,已知角的邻边求对边,可以用正切求AE,再加上BE即可.【详解】解:在Rt△ACE中,⊥ACE=α=35°,CE=BD=20,⊥tan⊥ACE=AE CE,⊥AE=CE•tan⊥ACE=20•tan35°14.004,⊥AB=AE+BE= 14.004+1.54≈15.54(米).【点睛】本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.16.电视塔大约高339米.【解析】【详解】试题分析:根据CG和⊥CFG、CG和⊥CEG可以求得FG、EG的长度,根据EF=EG﹣FG 可以求出CG的长度,即可解题.试题解析:延长EF交CD于G,在Rt⊥CGF中,FG==CG,Rt⊥CGE中,EG==CG,⊥EF=EG﹣FG,⊥CG==125(+1)≈337.5米170cm=1.7,337.5+1.7≈339米.答:电视塔大约高339米.考点:解直角三角形的应用-仰角俯角问题.17.(1)平稳放置时灯座DC与灯杆DE的夹角是60°(2)台灯平稳放置时⊥ABE的最大值是97.70°【解析】【分析】(1)由题意得:17.52DF CD==cm,EF CD⊥,根据1cos2DFDDE∠==,可求D∠;(2)如图3,过A作AH⊥BE交EB的延长线于H,求得31531522EF=⨯=,根据cos0.134BHABHAB∠=≈,可得ABH∠的值,进而可求ABE∠的值.(1)解:由题意得,17.52DF CD==cm,EF CD⊥,⊥1cos2DFDDE∠==⊥60D∠=︒⊥平稳放置时灯座DC与灯杆DE的夹角是60°.(2)解:如图3,过A作AH⊥BE交EB的延长线于H,⊥30HF=⊥31531522EF=⨯=⊥15330152BH BE EF=--=-⊥cos0.134BHABHAB∠=≈⊥82.30ABH∠≈︒⊥18097.70ABE ABH∠=︒-∠=︒⊥台灯平稳放置时⊥ABE的最大值是97.70°.【点睛】本题考查了解直角三角形的应用,特殊角的余弦值求角度.解题的关键在于找出线段的数量关系.18.约是5.3米.【解析】【分析】由条件易得BE =DE =20,在Rt △BCE 中,利用三角函数求得BC 的长,进而可求AB .【详解】解:⊥⊥BEC =⊥BDE +⊥DBE ,⊥⊥DBE =⊥BEC -⊥BDC =60°-30°=30°,⊥⊥BDE =⊥DBE ,⊥BE =DE =20,在Rt △BCE 中,⊥BCE =90°,sin⊥BEC =BC BE , ⊥3sin 2010310 1.7317.32BC BE BEC =⋅∠=⨯=≈⨯=(米), ⊥AB =BC -AC =17.3-12=5.3(米),答:旗杆AB 的高度约为5.3米.【点睛】 此题主要考查了解直角三角形的应用,关键是证明BE =DE ,掌握三角形函数定义. 19.旗杆AB 的高度是(83+8)米.【解析】【分析】根据锐角三角函数可得(CD+DB )×33=BD×1,解得BD ,从而可以求得AB 的高度. 【详解】,解:由题意可得,CD=16米,⊥AB=CB•tan30°,AB=BD•tan45°,⊥CB•tan30°=BD•tan45°,⊥(CD+DB )×33=BD×1, 解得BD=83+8,⊥AB=BD•tan45°=(83+8)米,即旗杆AB 的高度是(83+8)米.20.10.5米.【解析】【分析】设CD=x 米,由已知可得DB=CD=x ,AD=x+4.5,在Rt △ACD 中,利用⊥A 的正切求出x 的值即可.【详解】设CD=x 米,⊥⊥DBC=45°,⊥DB=CD=x ,AD=x+4.5,在Rt △ACD 中,tan⊥A=CD AD, ⊥tan35°=5.4+x x , 解得:x=10.5,所以大树的高为10.5米.【点睛】 本题考查了俯角、仰角的定义,借助俯角、仰角构造直角三角形,并结合图形利用三角函数解直角三角形是解题的关键.21.(1)1.2米;(2)约为4.9米.【解析】【分析】(1)根据“每级小台阶都为0.4米”即可求得高度差DH 的长度;(2)过点B 作BM ⊥AH ,垂足为M ,由题意得:MH =BC =AD = 1,66A ∠=,即可求得AM 的长,在Rt △AMB 中,根据⊥A 的余弦函数即可求得AB 的长,从而可以求得结果.(1)解:由题意得,DH =0.43⨯=1.2(米);答:点D 与点C 的高度差DH 为1.2米;(2)解:过点B作BM⊥AH,垂足为M,由题意得:⊥BCH=⊥CHM=⊥BMH=90°,⊥ 四边形BCHM是矩形,MH=BC=AD= 1,⊥ AM=AD+DH-MH=1+1.2-1=1.2,在Rt⊥AMB中,⊥A=66°,⊥cosAMAAB =,⊥AB=1.22.92cos660.41AM≈=︒(米),⊥ l =AD+AB+BC1 2.921 4.9≈++≈(米),答:所用不锈钢材料的总长度约为4.9米.【点睛】解直角三角形的应用是中考必考题,一般难度不大,正确作出辅助线构造直角三角形是解题关键.22.C、D两点间的距离约为6.5米.【解析】【详解】试题分析:要求线段CD的长,可以先求线段BC和BD的长. 根据已知条件易知⊥ABC是等腰直角三角形,根据线段AB的长可以求得线段BC的长. 根据已知条件可以利用Rt⊥ABD和⊥BAD 的正切值求得线段BD的长. 利用线段BC和BD的长即可求得线段CD的长.试题解析:⊥⊥ABC=90°,⊥CAB=45°,⊥在Rt⊥ABC中,⊥CAB=⊥BCA=45°,⊥AB =15(米),⊥在Rt⊥ABC 中,AB=BC =15(米).⊥⊥ABD =90°,⊥BAD =55°,tan55 1.43︒≈,⊥在Rt⊥ABD 中,tan tan5515 1.4321.45BD AB BAD AB =⋅∠=⋅︒≈⨯=(米),⊥BC =15(米),BD ≈21.45(米),⊥CD =BD -BC ≈21.45-15=6.45≈6.5(米).答:点C 与点D 之间的距离约为6.5米.点睛:本题考查了解直角三角形及其应用的相关知识. 本题的图形属于典型的“双直角三角形”,需要重点掌握. 该类型问题的关键在于利用两个直角三角形的公共边(如本题中的线段AB )将已知条件在两个直角三角形之间进行转换,最终求解出要求的线段和角度.23.(1)楼房的高度约为17.3米;(2)当α=45°时,老人仍可以晒到太阳.理由见解析【解析】【分析】(1)在Rt ⊥ABE 中,根据⊥α的正切值即可求得楼高;(2)当45α︒=时,从点B 射下的光线与地面AD 的交点为F ,与MC 的交点为点H .可求得AF =AB =17.3米,又因CF =CH =17.3-17.2=0.1米,CM =0.2,所以大楼的影子落在台阶MC 这个侧面上,即老人仍可晒到太阳.【详解】解:(1)当α=60°时,在Rt ⊥ABE 中,⊥tan 6010BA BA AE ︒==, ⊥BA =10tan 60°=10310 1.7317.3≈⨯=米.即楼房的高度约为17.3米;(2)当45α︒=时,老人仍可晒到太阳;理由如下:假设没有台阶,当45α︒=时,从点B 射下的光线与地面AD 的交点为F ,与MC 的交点为点H ,⊥⊥BF A =45°,⊥tan 451BA AF︒==,此时的影长AF =BA =17.3米, 所以CF =AF -AC =17.3-17.2=0.1,⊥CH =CF =0.1米,⊥大楼的影子落在台阶MC 这个侧面上.⊥老人仍可晒到太阳.【点睛】本题考查了解直角三角形的应用,属于常考题型,正确理解题意、熟练掌握三角函数的知识是解题的关键.24.(1)大厦的高度BD 为:(203+20)米;(2)小敏家的高度AE 为20米.【解析】【详解】试题分析:(1)易得四边形AEDC 是矩形,即可求得AC 的长,然后分别在Rt⊥ABC 与Rt⊥ACD 中,利用三角函数的知识求得BC 与CD 的长,继而求得答案;(2)结合(1),由四边形AEDC 是矩形,即可求得小敏家的高度AE .试题解析:(1)如图,⊥AC⊥BD ,⊥BD⊥DE ,AE⊥DE ,⊥四边形AEDC 是矩形,⊥AC=DE=203米,⊥在Rt⊥ABC 中,⊥BAC=45°,⊥BC=AC=203米,在Rt⊥ACD 中,tan30°=CD AC , ⊥CD=AC•tan30°=203×33=20(米), ⊥BD=BC+CD=203+20(米);⊥大厦的高度BD 为:(203+20)米;(2)⊥四边形AEDC 是矩形,⊥AE=CD=20米.⊥小敏家的高度AE为20米.考点:解直角三角形的应用-仰角俯角问题25.(1)山坡高度为400米;(2)山CF的高度约为541米.【解析】【详解】(1)作BH⊥AF于H,如图,在Rt△ABF中根据正弦的定义可计算出BH的长,从而得到EF的长;(2)先在Rt△CBE中利用⊥CBE的正弦计算出CE,然后计算CE和EF的和即可.试题解析:(1)作BH⊥AF于H,如图,在Rt△ABH中,⊥sin⊥BAH=BHAB,⊥BH=800•sin30°=400,⊥EF=BH=400米.答:AB段山坡的高度EF为400米;(2)在Rt△CBE中,⊥sin⊥CBE=CEBC,⊥CE=200•sin45°=1002,⊥CF=CE+EF=(1002+400)(米).答:山峰的高度CF为(1002+400)米.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业(七)[第一章 6 利用三角函数测高]一、选择题1.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图K-7-1,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )链接听课例1归纳总结图K-7-1A.11-sinα米 B.11+sinα米C.11-cosα米 D.11+cosα米2.如图K-7-2,为了测量电视塔的高度AB,在D处用高为1米的测角仪CD测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A 的仰角为60°,则这个电视塔的高度AB为链接听课例2归纳总结( )A.50 3米B.51米C.(50 3+1)米D.101米3.如图K-7-3,斜坡AB的坡度为1∶2.4,长度为52米,在坡顶B所在的平台上有一座高楼FH,已知在A处测得楼顶F的仰角为60°,在B处测得楼顶F的仰角为77°,则高楼FH的高度是(结果精确到1米,参考数据:sin77°≈0.97,tan77°≈4.33,3≈1.73)( )A.125米B.105米C.85米D.65米4.xx·深圳如图K-7-4,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°.已知斜坡CD的长度为20 m,DE的长度为10 m,则树AB的高度是( )A.20 3 m B.30 mC.30 3 m D.40 m图K-7-45.如图K-7-5,在两建筑物之间有一旗杆GE,高15米,从点A经过旗杆顶端恰好看到矮建筑物的墙脚点C,且俯角α为60°,又从点A测得点D的俯角β为30°,若旗杆底G为BC的中点,则矮建筑物的高CD为()图K-7-5A.20米B.10 3米C.15 3米D.5 6米二、填空题6.如图K-7-6,小亮在太阳光线与地面成35°角时,测得树AB在地面上的影长BC =18 m,则树高AB约为________m.(结果精确到0.1 m)图K-7-67.如图K-7-7(示意图),某学校组织学生到首钢西十冬奥广场开展综合实践活动,数学小组的同学们在距奥组委办公楼(原首钢老厂区的筒仓)20 m的点B处,用高为0.8 m的测角仪测得筒仓顶点C的仰角为63°,则筒仓CD的高约为________m.(结果精确到0.1 m,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)链接听课例1归纳总结图K-7-78.如图K-7-8,两建筑物的水平距离BC为18 m,从点A测得点D的俯角α为30°,测得点C的俯角β为60°.则建筑物CD的高度为________m(结果不作近似计算).图K-7-8三、解答题9.xx·黄冈在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图K-7-9所示),已知标语牌的高AB=5 m,在地面的点E处,测得标语牌上点A的仰角为30°,在地面的点F处,测得标语牌上点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据:2≈1.41,3≈1.73)图K-7-910.xx·莱芜如图K-7-10,某学校教学楼(甲楼)的顶部E和大门A之间挂了一些彩旗.小颖测得大门A距甲楼的距离AB是31 m,在A处测得甲楼顶部E处的仰角是31°.(1)求甲楼的高度及彩旗的长度;(2)若小颖在甲楼楼底C处测得学校后面医院楼(乙楼)楼顶G处的仰角为40°,爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为19°,求乙楼的高度及甲、乙两楼之间的距离.(结果均精确到0.01 m,cos31°≈0.86,tan31°≈0.60,cos19°≈0.95,tan19°≈0.34,cos40°≈0.77,tan40°≈0.84)链接听课例2归纳总结11.学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:(1)如图K-7-11,在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;(2)在测点C与山脚B之间的D处安置测倾器(C,D与B在同一直线上,且C,D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;(3)测得测倾器的高度CF=DG=1.5米,并测得C,D之间的距离为288米.已知红军亭的高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB(3取1.732,结果保留整数).如图K-7-12,A,B是两幢地平面高度相等、隔岸相望的建筑物.由于建筑物密集,在A的周围没有开阔地带,为了测量B楼的高度只能利用A楼的空间,A的各层楼都可到达,且能看见B.现有的测量工具为皮尺和测角器(皮尺可用于测量长度,测角器可以测量仰角、俯角或两视线间的夹角).(1)请你设计一个测量B楼高度的方法,要求写出测量步骤和必要的测量数据(用字母表示),并画出测量图形;(2)用你测量的数据(用字母表示)写出计算B楼高度的表达式.图K-7-12详解详析【课时作业】 [课堂达标] 1.[答案] A2.[解析] C 设AG =x 米,在Rt △AEG 中,∵tan ∠AEG =AG EG ,∴EG =AG 3=33x 米.在Rt △ACG 中,∵tan ∠ACG =AG CG ,∴CG =x tan30°=3x 米,∴3x -33x =100,解得x =503,则AB =(503+1)米,故选C.3.[解析] B 如图,延长FH 交AC BG ⊥AC ,BH ⊥FH ,FE ⊥AC ,∴四边形BGEH 是矩形,∴BH =GE ,BG =HE .∵BG ∶AG =1∶2.4,∴设BG =x 米,AG =2.4x 米(x >0).在Rt △ABG 中,∵AB =52米,由勾股定理可得BG 2+AG 2=AB 2,即x 2+(2.4x )2=522,解得x =20,则BG =20米,AG =48米.在Rt △BHF 中,∵∠HBF =77°,∴tan77°=FHBH,∴FH =BH tan77°. 在Rt △AEF 中,∵∠EAF =60°, ∴EF =3AE ,∴3(48+BH )=20+BH tan77°,解得BH ≈24.25,∴FH =BH tan77°≈105米.故选B. 4.[解析] B 先根据CD =20 m ,DE =10 m 得出∠DCE =30°,故可得出∠DCB =90°,再由∠BDF =30°可知∠DBF =60°,由DF ∥AE 可得出∠BGF =∠BCA =60°,故∠GBF =30°,所以∠DBC =30°,再由锐角三角函数的定义即可得出结论.5.[解析] A 如图,延长CD交点A所在的水平线于点F,如图.由题意,知GE∥AB∥CD,BC=2GC,GE=15米,∴AB=2GE=30米.∵AF=BC=ABtan∠ACB=303=10 3(米),DF=AF·tan30°=10 3×33=10(米),∴CD=AB-DF=30-10=20(米).6.[答案] 12.67.[答案] 40.0[解析] 过点A作AE⊥CD于点E.∵AB⊥BD,CD⊥BD,∴四边形ABDE是矩形,∴AE=BD=20 m,DE=AB=0.8 m.在Rt△ACE中,∠CAE=63°,∴CE=AE·tan63°≈20×1.96=39.2(m),∴CD=CE+DE≈39.2+0.8=40.0(m),即筒仓CD的高约为40.0 m.8.[答案] 12 3[解析] 过点D作DE⊥AB于点E,则四边形BCDE是矩形.根据题意,得∠ACB=β=60°,∠ADE=α=30°,BC=18 m,∴DE=BC=18 m,CD=BE.在Rt△ABC中,AB=BC·tan∠ACB=18×tan60°=18 3 (m).在Rt△ADE中,AE=DE·tan∠ADE=18×tan30°=6 3(m),∴CD=BE=AB-AE =18 3-6 3=12 3(m).9.[解析] 如图,过点F作FH⊥AE于点H.由题意可知∠HAF=∠HFA=45°,推出AH=HF.设AH=HF=x m,则EF=2x m,EH=3x m,在Rt△AEB中,由∠E=30°,AB=5 m,推出AE=2AB=10 m,可得x+3x=10,解方程即可.解:如图,过点F作FH⊥AE于点H.由题意可知∠HAF=∠HFA=45°,∴AH=HF.设AH=HF=x m,则EF=2x m,EH=3x m.在Rt△AEB中,∵∠E=30°,AB=5 m,∴AE =2AB =10 m , ∴x +3x =10,解得x =53-5,∴EF =2x =103-10≈7.3(m).答:点E 与点F 之间的距离约为7.3 m.10.解:(1)在Rt △ABE 中,BE =AB ·tan31°=31×tan31°≈31×0.60=18.60(m),AE =ABcos31°=31cos31°≈310.86≈36.05(m),故甲楼的高度约为18.60 m ,彩旗的长度约为36.05 m. (2)过点F 作FM ⊥GD ,交GD 于点M , 在Rt △GMF 中,GM =FM ·tan19°. 在Rt △GDC 中,GD =CD ·tan40°.设甲、乙两楼之间的距离为x m ,则FM =CD =x m. 根据题意,得x tan40°-x tan19°=18.60,解得x =37.20.乙楼的高度GD =CD tan40°≈37.20×0.84≈31.25(m),故乙楼的高度约为31.25 m ,甲、乙两楼之间的距离约为37.20 m.11.解:设AH =x 米,在∵∠EGH =45°,∴GH =EH =AE +AH =(x +12)米. ∵GF =CD =288米,∴HF =GH +GF =x +12+288=(x +300)米. 在Rt △AHF 中,∵∠AFH =30°,∴AH =HF ·tan∠AFH ,即x =(x +300)·33,解得x =150(3+1).∴AB =AH +BH =150(3+1)+1.5≈409.8+1.5≈411(米).答:凤凰山与中心广场的相对高度AB 大约是411米. [素养提升][解析] 本题是一道开放性试题,解题方法很多,表达式也是多种多样的.测角器可以测得仰角和俯角,皮尺可以测得A 楼的高度,通过解直角三角形可得B 楼的高度.解:(1)答案不唯一.如图,设AC 表示A 楼,BD 表示B 楼.测量步骤如下:①用测角器在A 楼的顶端点A 测量B 楼楼底的俯角α; ②用测角器在点A 测量B 楼楼顶的仰角β;③用皮尺从A 楼楼顶放下,测量点A 到地面的高度为a . (2)在Rt △ACD 中,CD =a tan ∠ADC =atan α.在Rt △AEB 中,BE =AE ·tan β.∵AE =CD ,∴BE =a tan βtan α,∴B 楼的高度BD =BE +ED =BE +AC =a tan βtan α+a =a ⎝ ⎛⎭⎪⎫1+tan βtan α.。
