人民币汇率研究 数学建模
大数据环境下的人民币汇率预测模型研究

大数据环境下的人民币汇率预测模型研究随着经济全球化的进程和金融市场的不断发展,人民币汇率的波动对国内外企业和个人产生了重要影响。
因此,准确而有效地预测人民币汇率变动成为了金融从业者和决策者的迫切需求。
在大数据时代的背景下,借助相关技术和工具,构建人民币汇率预测模型成为可能。
一、人民币汇率预测模型的重要性人民币汇率的波动会对外贸出口、国内经济政策、国际投资等产生深远的影响。
因此,通过建立准确的人民币汇率预测模型,可以为政府制定政策、企业制定战略、投资者进行风险管理等提供重要参考依据。
在大数据环境下,可以利用海量的数据和强大的计算能力,提高预测模型的准确度和稳定性。
二、大数据在人民币汇率预测中的应用1. 数据源的扩大:大数据时代的到来,使我们能够获取更多的数据源,包括经济指标、市场数据、新闻媒体、社交媒体等。
这些多源数据能够提供更全面、及时和准确的信息,有助于提高预测模型的精度和可靠性。
2. 数据解读的创新:大数据技术可以帮助识别和挖掘数据中的有用信息和规律。
例如,通过文本挖掘和情感分析技术,可以分析新闻媒体和社交媒体上对人民币汇率的讨论和预期,从而提取有关人民币汇率的市场情绪,作为预测模型的输入变量。
3. 模型的改进:利用大数据进行人民币汇率预测模型的研究,可以采用更复杂、更深入的模型。
例如,可以结合机器学习算法和神经网络模型,利用大规模样本训练模型,提高预测精度。
此外,还可以采用时间序列分析和异方差模型等方法,更好地捕捉人民币汇率的变动特征。
三、人民币汇率预测模型的构建1. 数据准备:首先需要收集和整理与人民币汇率相关的数据,包括经济指标(如GDP、CPI、汇率、利率)、市场数据(如股票指数、商品价格)以及新闻媒体和社交媒体上的舆情数据等。
同时,还需要考虑数据的质量、完整性和时效性。
2. 变量选择:通过相关性分析等方法,筛选出对人民币汇率影响较大的变量作为模型的输入。
这些变量可以包括经济指标、市场数据、舆情数据等。
货币汇率兑换数学模型

作为金融从业人员,在处理有关国际货币相互兑换结算时,会遇到这样的问题,每天将现有的欧元、人民币、英镑、美元四种货币按当天的兑算,按人民币结算价值最高。
当天汇率满如下表:欧元人民币英镑美元现有量需求量欧元 1 7.856 .787 1.235 80000 60000人民币.127 1 0.100 .157 10000 30000英镑 1.271 9.980 1 1.569 80000 10000美元0.810 6.360 .637 1 00000 100000(人民币结算价值=(兑入价值+兑出价值)/2;兑入1美元,结算价值=(6.360+1/.157)/2;那么这种情况应该怎么操作呢,下面就来探讨这个问题。
首先我们先来建立模型:欧元人民币英镑美元欧元e11 e12 e13 e14人民币e21 e22 e23 e24英镑e31 e32 e33 e34美元e41 e42 e43 e44上图中的eij(eij>=0)代表把eij单位个i种货币兑换为j种货币(i,j=1,2,3,4其中当1代表欧元,2代表人民币,3代表英镑,4代表美元)。
现在我们用数学建模来解决这一类问题接下来我们将上表的约束条件转化为数学表达式(建立约束条件);e11+e12+e13+e14=80000;e21+e22+e23+e24=10000;e31+e32+e33+e34=80000;e41+e42+e43+e44=0; (1)e11+0.127*e21+1.271*e31+0.810*e41>=60000;7.856*e12+e22+9.980*e32+6.360*e42>=30000;0.787*e13+0.100*e23+e33+0.637*43>=10000;1.235*e14+0.157*e24+1.569*e34+e44>=100000; (2)目标函数:Max=( e11+0.127*e21+1.271*e31+0.810*e41)*r1+(7.856*e12+e22+9.980*e32+6.360*e42)*r2+(0.787*e13+0.100*e23+e33+0.637*43)*r3+(1.235*e14+0.157*e24+1.569*e34+e44)*r4;为了后续解决问题的方便现取min=-max;(ri分别表示每种货币的人民币结算价值,r1=(7.856+1/0.127)/2;r2=(1+1/1)/2;r3=(9.980+1/0.100)/2;r4=(6.360+1/0.157)/2)这样上述问题已经完全转换为一个高维的线性规划问题,其中方程组(1)(2)是约束条件,Max 是目标函数。
人民币汇率对经济的影响模型

人民币汇率对经济的影响模型摘要:近年来,随着中国经济的发展,中国在世界上起着越来越重要的地位。
本文通过分析英镑汇率的变化对英国经济的影响,以及人民币与主要货币之间的关系,并在此基础上进一步讨论人民币汇率的变化对我国及世界经济的影响。
在问题一中,我们研究了英镑汇率的变化对英国贸易额的影响,建立了汇率x 与贸易额y 之间的线性回归方程:U bx a y ++=。
通过网络查找,得到1992年—2004年英镑汇率与英国贸易额数值,运用Mathematica 拟合出英镑汇率x 与英国贸易额y 之间的关系:x y 327.11279.3941-=。
用R 检验法检验回归结果,发现汇率与贸易额之间成负相关性。
在问题二中,我们采用数据拟合的方法对人民币汇率与美元、日元、欧元的汇率关系进行了分析。
人民币对日元的汇率变化没有相关性,因而未给出相关方程,对美元和欧元的汇率变化有一定相关性,我们对查找到的数据进行拟合,得到关系式如下:对美元:43210315.018133.32169.2747345.9325.376x x x x y +-+-=对欧元:23706.16928.73004.834x x y +-=在问题三中:我们用回归分析法与置信区间法来说明人民币汇率变化对我国及世界经济的影响,从而找到人民币汇率在(6.9812—9.6098)之间变动时,我国经济才可以持续、快速、稳定发展。
一、问题的提出近年来,有不少经济学家在探讨人民币汇率对我国及世界经济发展的影响。
一些学者希望提高人民币对一些主要货币的汇率,另一些学者希望稳定人民币的汇率。
试建立数学模型解决下列问题:1.以英镑汇率或日元汇率为例研究其变化对该国经济的影响;2.人民币汇率与主要货币(如英镑、日元、欧元等)的汇率关系;3.人民币汇率变化对我国及世界经济的影响。
二、问题的假设1、假设不考虑除汇率外其它因素对国家经济的影响,即模型中U=0。
2、在考虑人民币汇率对英国汇率影响时,不考虑英国经济对英国汇率的影响。
数学建模.人民币汇率对经济的影响论文

人民币汇率对经济的影响摘要近年来,随着中国经济的发展,中国经济对世界经济上起着越来越重要的作用。
引发不少经济学家探讨人民币汇率对我国及世界经济发展的影响。
一些学者希望提高人民币对一些主要货币的汇率,另一些学者希望稳定人民币的汇率。
对此,本文以英镑汇率为例研究其变化对该国经济的影响;并且联系人民币汇率与主要货币(本文选取英镑、日元、欧元为主要货币)的汇率关系;探讨人民币汇率变化对我国及世界经济的影响。
关键词人民币汇率贸易额我国经济世界经济一、问题的提出近年来,不少经济学家及学者都在探讨人民币汇率对我国及世界经济发展的影响。
众多经济学家和市场人士中,大多数都认为,目前升值不妥,贬值也可能得不偿失,在未来一年内,保持汇率稳定或是上策。
一些学者希望提高人民币对一些主要货币的汇率,主要出于以下几点理由:1.有利于进口成本的降低,对经济建设非常有利。
2.有利于推动外贸增长方式的转变,有助于我国外贸增长方式从原来的粗放型转向高质量和高效益的集约型,这会带来出口结构的改善,激励企业技术创新,实现可持续发展。
3.有利于改善贸易条件 4.有利于推动部分出口产业向中西部地区转移 5.有利于缓解贸易摩擦 6.有利于造就出中国真正具有国际竞争力的跨国公司。
而且,提高人民币对一些主要货币的汇率,会使国内市场得到更加便宜的进口,更大的国外投资和政府开支,而且能够遏制通货膨胀,减少政府对外债义务,升值将迫使中国经济变得更具生产力。
与此相反,其他大部分学者希望稳定人民币的汇率,中国如果持续贬值的政策,从中长期看,中国外汇储备大,等金融系统稳定之后,可能还会造成通胀压力和人民币升值的压力。
但是反之,如果人民币汇率升值有很大危害:人民币升值会给中国的通货紧缩带来更大的压力;人民币汇率升值将导致对外资吸引力的下降,减少外商对中国的直接投资;给中国的外贸出口造成极大的伤害;人民币汇率升值会降低中国企业的利润率,增大就业压力;财政赤字将由于人民币汇率的升值而增加,同时影响货币政策的稳定。
基于VAR模型的人民币汇率与通货膨胀关系研究

基于VAR模型的人民币汇率与通货膨胀关系研究人民币汇率与通货膨胀之间存在着复杂的关系。
通货膨胀是指一国商品和服务的整体价格水平的普遍上涨,而汇率则是一国货币与其他国家货币之间的兑换比率。
通常情况下,通货膨胀会对汇率产生影响,而汇率的变动也会影响通货膨胀。
VAR模型(向量自回归模型)是一种经济学中常用的时间序列模型,可以用来研究不同变量之间的关系。
在本文中,我们将利用VAR模型来研究人民币汇率与通货膨胀之间的关系。
我们需要确定要使用的变量。
人民币汇率通常由外汇市场的供求关系决定,可以使用人民币兑美元汇率作为衡量人民币汇率的变量。
而通货膨胀可以使用消费者价格指数(CPI)来衡量。
接下来,我们需要收集人民币兑美元汇率和CPI的时间序列数据,并进行预处理。
预处理包括对数据进行平稳性检验和差分处理,以确保数据满足VAR模型的基本假设。
然后,我们可以构建VAR模型。
VAR模型的核心是自回归方程,它用过去时刻的变量来预测当前时刻的变量。
在本文中,我们将建立一个二元VAR模型,其中包括人民币汇率和通货膨胀这两个变量。
在构建VAR模型之后,我们可以通过估计模型中的参数来分析人民币汇率和通货膨胀之间的关系。
参数估计可以使用最小二乘法或最大似然法进行。
我们可以通过VAR模型的脉冲响应函数和方差分解分析来得到更深入的结论。
脉冲响应函数用于分析一个变量的冲击对其他变量的影响,而方差分解分析可以衡量一个变量的变化对其他变量的解释度。
通过以上的研究方法,我们可以得出人民币汇率与通货膨胀之间的关系。
根据不同的数据和模型估计结果,结论可能有所不同。
但无论如何,利用VAR模型可以帮助我们更好地理解人民币汇率与通货膨胀之间的动态关系,有助于制定货币政策和外汇市场干预措施。
人民币兑美元汇率MS-ARCH模型的MCMC估计和分析

类。
一
果发 现 MS—A R模 型 比一 般 线 性 时 间 序 列模 型具
有更 强 的灵活性 , 能更 好 地 拟 合 具有 机 制 转 换 的 非
线性 时 间序列 。 另 一类 是 基 于 方 差项 建 立 Makv机 制 转 换 模 ro
类 是基 于均 值项建 立 Mak v 制转 换 模 型 。 ro 机
经 济 、 融数 据 呈现 出随机 性 、 金 时变性 和持 续性 的特点 , 不 同时 间段 可 能呈现 出不 同的波动状 态 。 在
为 了更 好 的 拟 合 这 种 变 化 规 律 , a l n 18 ) H mio ( 9 9 首 t
值都具有高 度 的持 续性。王建 军 ( 06 利用 M 20 ) S
( 0 0 利用 Makv模型 研究 黄金 价格 波动 特征 , 2 1) ro 结
用到 经济 、 金融 分析 的各个 领 域 , 显示 出许 多优 于 并 传统 的 非 线 性 时 间 序 列 模 型 的 特 性 。 目前 关 于 M ro 制 转 换 模 型 的应 用 研 究 大 致 可 以 分 成 两 akv机
[ 中图分类号 ] 80 9 F 3 . [ 文献标识码] A [ 文章编号 ]0 5— 4 0 2 1 )5—09 0 2 9 3 1 (0 2 0 02— 5
一
、
基于VAR模型的人民币汇率与通货膨胀关系研究

基于VAR模型的人民币汇率与通货膨胀关系研究
人民币汇率与通货膨胀之间的关系一直是国内外学术界和政策制定者关注的焦点之一。
通货膨胀率的变动可以对人民币汇率产生影响,而人民币汇率的变动也会对通货膨胀带来
影响。
为了深入理解这一关系,许多研究学者采用VAR模型(向量自回归模型)进行研究。
VAR模型是一种基于时间序列数据的多变量动态模型,能够捕捉变量之间的相互影响
和动态调整过程。
在研究人民币汇率与通货膨胀关系时,VAR模型可以帮助我们估计两者
之间的互动效应。
VAR模型可以用数学公式表示为:Y_t = A_1*Y_(t-1) + A_2*Y_(t-2) + ... +
A_p*Y_(t-p) + ε_t
Y_t是一个向量,表示多个变量在时间点t的取值;A_i是p阶自回归系数矩阵,用于描述变量之间的相互影响关系;ε_t是一个向量,表示扰动项(误差项)。
研究人民币汇率与通货膨胀关系时,我们可以选择人民币汇率与通胀率作为VAR模型
的两个变量,然后根据历史数据进行估计和分析。
通过对VAR模型的估计结果进行分析,
可以得出以下几个方面的结论:
VAR模型可以帮助我们研究人民币汇率和通胀率的长期均衡关系。
通过估计VAR模型
的系数矩阵,我们可以得到两者之间的长期关系。
如果人民币汇率对通胀率有显著的长期
作用,则说明人民币汇率对通胀具有重要影响。
基于VAR模型的人民币汇率与通货膨胀关系研究能够帮助我们深入理解两者之间的互
动效应,并对未来走势进行预测。
这不仅对于理论研究有重要意义,也对于政策制定和市
场参与者有重要指导意义。
数学建模论文模板
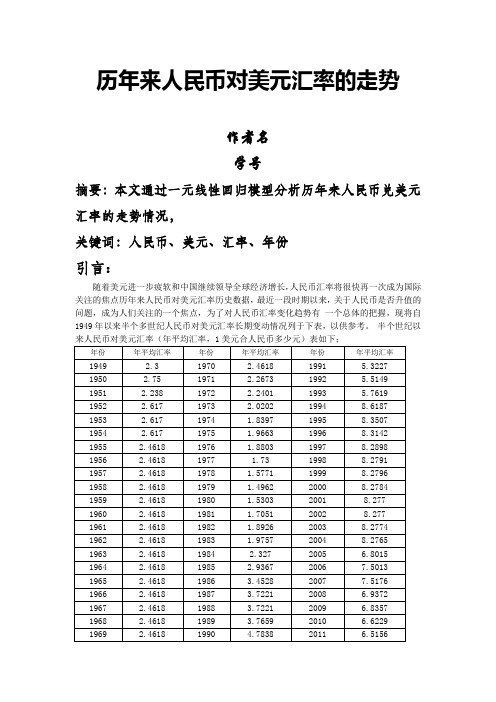
历年来人民币对美元汇率的走势作者名学号摘要:本文通过一元线性回归模型分析历年来人民币兑美元汇率的走势情况,关键词:人民币、美元、汇率、年份引言:随着美元进一步疲软和中国继续领导全球经济增长,人民币汇率将很快再一次成为国际关注的焦点历年来人民币对美元汇率历史数据,最近一段时期以来,关于人民币是否升值的问题,成为人们关注的一个焦点,为了对人民币汇率变化趋势有一个总体的把握,现将自1949年以来半个多世纪人民币对美元汇率长期变动情况列于下表,以供参考。
半个世纪以2、一元线性回归模型假设人人民币兑美元汇率与时间之间存在线性统计关系,为此构建一元线性回归模型,对它们的关系进行分析,另人民币兑美元的汇率的汇率为Y 作为模型中的响应量,时间为X 作为模型中的解释变量,回归模型如下Y i = a + bX i + εi其中Y i 表示因变量Y 第i 次试验下的观测值; a 与b 均为参数,称为回归系数;X i 为常数,表示因变量X 第i 次试验下的观测值;εi 为i 次试验的随机误差项,满足Gauss-Markov 假设,及均值为0,互不相关且方差相等。
3、最小乘法估计回归系数1. 最小二乘法估计回归系数对于给定直线Y = aX + b ,考虑第i 个观测值(X i , Y i ),当时间为X i 时,平均汇率为Y i ,如果用直线进行预测,预测平均汇率为aX i + b ,偏差为d i = Y i −a −bX i 。
作为预测或者说拟和实际数据用的回归直线,我们希望对每个实际观测数据的偏差尽可能的小,为此,引入偏差平方和来度量回归直线对所有样本数据的整体拟和的好坏。
Q =Q (a ,b )=(Y i -a -bX i )2i =1nå于是,所谓的回归直线,就是整体拟和的最好,即偏差平方和最小的直线。
因此寻找回归直线等价于:寻找一对数(a , b ),其中a , b 分别表示回归直线的截距与斜率,使对应的偏差平方和最小,即(ˆa ,ˆb )=argmin Q a ,b=(Y i -a -bX i)2i =1nå 通过求驻点的方式求Q (a ,b )的最小值点,令Q (a ,b )的偏导数为0,得方程组¶Q¶a =-2(Y i -a -bX i )=0i =1nå¶Q¶b =-2X i (Y i -a -bX i )=0i =1n åìíïïîïï解方程组得到回归直线截距与斜率的估计量ˆb =(X i -X )(Y i -Y )i =1n å(X i -X )2i =1nåˆa=Y -ˆbX ìíïïïîïïï 4、试验结果及讨论分别对1949~1969、1970~1993、1994~2011的数据作一元线性回归,结果如图1所说明了回归模型中,各时期人民币年平均汇率有着显著的直线相关关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人民币汇率研究问题提出:人民币汇率对经济的影响近年来成为人们议论的热点,有不少经济学家在探讨人民币汇率对我国及世界经济发展的影响。
一些学者希望提高人民币对一些主要货币的汇率,另一些学者则希望稳定人民币的汇率。
试建立数学模型解决下列问题:1、以英镑汇率或日元汇率为例研究其变化对该国经济的影响;2、人民币汇率与主要货币(如英镑、日元、欧元等)的汇率关系;3、人民币汇率变化对我国及世界经济的影响。
关键词:人民币汇率;数学模型;实证分析;因果关系;经济增长一、引言自东南亚金融危机爆发以来,人民币汇率的走势已成为人们关注的焦点之一。
由于中国出口产品与东南亚国家的出口产品具有较强的替代性,因而这些国家以竞争性货币贬值为主要特征的金融危机,严重地削弱了中国产品的国际竞争力。
虽然如此,中国政府出于对国际社会负责的考虑,多次向国际社会公开承诺并实现了金融危机爆发以来的人民币汇率的稳定。
这在目前东南亚金融危机日益深化和日元不断贬值的国际金融环境下实属不易。
从而引出了一个非常重要而敏感的问题:在此不利的国际经济环境下,人民币汇率能否继续保持稳定。
或者说,在什么样的条件下,管理浮动的人民币汇率能延续汇率并轨以来的稳定性。
由于汇率的变化取决于汇率制度和国内外宏观经济和金融环境,而给定汇制(管理浮动)的汇率变化主要取决于其基本的决定因素和中央银行的外汇干预。
因此,管理浮动汇制下的人民币汇率决定模型的界定以及模型的实证分析,既是一个重要的理论问题,又是一个非常重要的现实问题。
本文在下面首先讨论我国均衡汇率的确定模型。
通过对有关汇率的各种模型进行比较,建立了自己的模型,并且结合中国的实际数据作了实证分析,得出了一个汇率与各种相关经济变量的回归形式。
随后讨论了汇率与中国经济的关系,在这一部分中用到了因果关系理论。
结合实际数据通过因果分析得出它们的因果关系,并且根据这种关系提出了对今后中国汇率政策改革的建议。
本文论述结构如下:第一部分讨论我国均衡汇率的确定模型。
首先对有关汇率的各种模型作了简要介绍,针对各种模型的长短,本文建立了自己的模型,讨论了变量之间的动态关系。
第二部分讨论了汇率与中国经济的关系,在这一部分中用到了因果关系理论。
本部分不是通过论述性的文字讨论汇率与中国经济的关系,而是结合实际数据通过因果分析得出它们的因果关系,并且根据这种关系提出了对今后中国汇率政策改革的建议。
二、人民币汇率模型的建立及讨论Ⅰ、关于几种汇率模型正确确定一国汇率水平的重要性,早已为各国所认可。
作为世界经济中的一枝奇葩,中国受到了强烈的关注。
而有关人民币汇率的讨论正在逐渐升温,有关人民币汇率确定的理论也是纷繁复杂。
下面我们简要介绍一下各种理论的特点。
购买力平价理论无疑是20世纪最有影响的汇率决定理论和均衡汇率理论。
但是对人民币的实证分析,购买力平价理论不适用于1979年以来人民币汇率的实际变动,人民币汇率的变动可能受到某些非货币的实际因素影响。
同时,即使假定传统的购买力平价理论在超长期适用于人民币汇率,是一种确定超长期均衡汇率的有效方式,但是超长期有效对于选择合理的汇率政策是不够的。
当基本经济要素在中长期驱使均衡的实际汇率发生变化时,甚至会造成政策误导的严重后果。
目前在西方较有影响的均衡汇率理论,包括基本要素均衡汇率理论(FEER)、自然均衡汇率理论(NATREX)和ERER理论等。
FEER方法的突出特点是它强调外部均衡不是指国际收支的数量平衡或没有逆差,而是指经常项目具有可持续性,这样就排除了通过提高利率吸引大量外资流入来弥补大规模经常项目逆差的情况。
但它确定经常性项目目标时的随意性较强,同时运用不同计量模型测算出的结果相差较大。
而且FEER方法测算出来的均衡是一种流量均衡,没有考虑长期的存量均衡,因而在此意义上它是一种中期的均衡。
NA TREX是一个实证的而不是规范的均衡汇率概念,它是由实际经济要素和现行经济政策决定的。
在其理论中,这些经济政策不一定是社会最优的或福利最大化的,NA TREX也不是最优的实际汇率,而只是现行基本经济要素决定的汇率。
再比较行为均衡汇率(BEER)模型与ERER模型。
这两种模型得出的人民币高估、低估的起止时间、次数和失调程度都极为接近,它们对人民币汇的评估结果总体上是高度一致的。
但根据ERER模型的测算结果,1995年以来人民币均衡汇率基本保持稳定,而BEER模型却推出人民币均衡汇率持续贬值。
其理由是,1995年以来我国的广义货币供应量增长幅度较大。
但根据一般的判断,1995-1999年期间没有明显的理由导致人民币均衡汇率大幅度贬值,因此ERER模型的测算结果较为科学。
Ⅱ、模型的建立首先作出假设:⑴、市场上存在三类商品:出口品(X)、进口品(M)和非贸易品(N)。
本国生产出口品和非贸易品,消费进口品和非贸易品。
[2]、政府的收入来源于税收和举债水平。
本国私人部门(包括个人和公司)和政府部门消费进口品和非贸易品。
[3]、国内运行资本包括私人部门消费、政府部门支出及国内投资。
[4]、国家对贸易品采取关税控制,对进口征税,对出口退税。
[5]、存在完全预期。
基于如上假设,建立如下模型。
NM C C C += ①私人部门消费主要集中在进口品和非贸易品。
另外,政府支出体现在两方面,一方面是对非贸易品的消费,另一方面则体现为政府对基础建设、国防、科研等上面的花费,其直接效果是国际国内贸易环境转好,技术进步率提高(用g 表示)。
NG gY G += ②其中,Y 为国内生产总值,NN X X S P S P Y += ③在需求方面,需求函数满足如下性质:0<∂∂M M P D ,0>∂∂N M P D ,0>∂∂A D M ;0>∂M N P C ,0<∂∂N N P C ,0>∂A C N 。
而供给方面,有如下关系式:0>∂∂E S X ,0<∂∂N X P S ;0<∂∂E S N ,0>∂∂N N P S 。
要使汇率达到长期可持续均衡状态,就必须满足如下四个条件: ⒈国内经济处于稳定状态,非贸易品市场出清。
gYG C G C D P N N N N N -+=+= ④⒉外部经济实现均衡,即国际储备变动与经常项目差额均为0。
但中国近年来的外汇储备实际上已经超出了维持正常汇率水平所需标准,因此,在本模型中不予考虑。
⒊财政政策可持续,即政府不负债务,其收入完全来源于税收。
TD P Et D P t G M M M X X X ++-=*⑤其中T 为国内税收。
令*M P 、*X P 为进出口品的国际价格。
*+=MM M P t E P )1( ⑥10,)1(<<-=*ββX X X P t EP ⑦在出口品国际国内价格的等式中加入了一个β是基于如下事实:我国的出口产品基本上来自于劳动密集型产业。
这些产品的附加值低,价格定位也要略低于国际价格。
⒋贸易市场出清,即X X S D =,M M S D =。
最后定义实际汇率为,])1([**-+=M X NP P E P e αα,α体现出口量在对外贸易总量中所占比例。
Ⅲ、模型的结论通过简单的代入,我们得到,MM XX Nt P P t P e +-+-=1)1()1(αβα ⑧ 到这里,我们可以得到如下推论:推论1:若国内非贸易品相对于出口品价格上升,汇率将上升; 推论2:若国内非贸易品相对于进口品价格上升,汇率将上升;推论3:若β上升,即出口品中劳动密集型产品比重减小,汇率将上升;反之,若技术密集型或资本密集型产品比重减小,汇率将下降。
在理论上,我们得出了以上推论。
但实际上在汇率的相关问题上,远非我们所想得如此简单。
而且我们发现在模型中涉及到的某些变量并未出现,下面,我们更加深入地讨论这些问题。
利用公式④、⑤、⑥,我们得到,MM M X X N X M D t t T Y t g G t C t P )1]()1()1([+-++-+-=,XNX D C G Y g P --+=)1(,NN N D gYG C P -+=。
将以上三个式子代入⑨中,得到,MM N X X X XN X NN D t T C t Y g t G t D G C Y g t D gY G C e ])1()1)[(1(])1)[(1()(--++--+--+--+=αβα, 在这个式子中,我们发现了与我们更为熟悉的经济变量。
很明显,有如下推论: 推论4:若一国经济中出口份额小,则随着出口补贴税率上升,汇率下降;反之汇率上升;证明:我们对汇率求导,得到。
]1)11[(])1()1)[(1(])1)[(1()1(]1[])1()1)[(1(])1)[(1()1()])1)[(1(])1[((])1()1)[(1(])1)[(1(1MM MM XMM N X X X XN X N MM XMM N X X X XN X N MM N XN MM N X X X XN X XD t D t D D t T C t Y g t G t D G C Y g t GC Y g eD t D D t T C t Y g t G t D G C Y g t GC Y g eD t G C Y g D G C Y g D t T C t Y g t G t D G C Y g t et e -+--++--+--+---+=----++--+--+---+=--+-+--+---++--+--+--=∂∂αβαβααβααβααβααβα由上式,不难推出结论。
推论5:若对进口品征收税率升高,汇率将上升;推论6:若私人部门中对非贸易品的消费增加,汇率将上升。
令AgY G C N =-+,BT Y t g G t C t X X N X =-++-+-)1()1(,CC G Y g N =--+)1(。
其中,0>+=-+=N N N G C gY G C A ,,01)1(][)(])1([)1()1(>+=++-+--+-=-++-+-=-++-+-=MM M M MM M M X X X X X N N N N X N X X X N X t D P t t D P t D P t D P D P G C t T G Y g G C t T Y t g G t C t B0)1(>=--=--+=X X N N N D P C G Y C G Y g C 。
为求得G 、g 对汇率的作用,我们将e 分别对G 、g 求导,,])1)(1()1([])1()1)[(1(])1)[(1(1MM X XX MM N X X X XN X D t t D t D t T C t Y g t G t D G C Y g t eGe --+----++--+--+--=∂∂αβααβα 我们发现上式与对出口汇率求导式的形式一样,故影响也类似。
