三角形四边形看图形周长面积专项练习30题(有答案)ok
三角形四边形看图形周长面积专项练习30题(有答案)ok
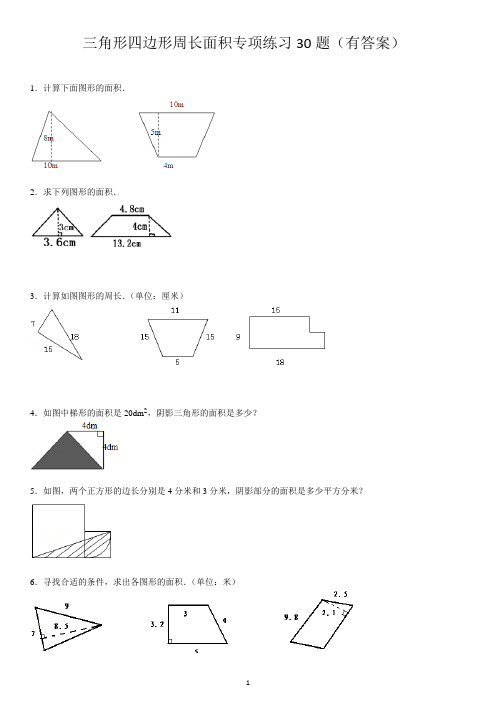
三角形四边形周长面积专项练习30题(有答案)1.计算下面图形的面积.2.求下列图形的面积.3.计算如图图形的周长.(单位:厘米)4.如图中梯形的面积是20dm2,阴影三角形的面积是多少?5.如图,两个正方形的边长分别是4分米和3分米,阴影部分的面积是多少平方分米?6.寻找合适的条件,求出各图形的面积.(单位:米)7.算出下面图形的面积.8.求阴影部分面积.单位:厘米.9.图形王国展风采.(求下面图形的周长,单位:厘米.)10.找准所需条件,计算下列图形的面积.(单位:米)11.求下面图形的面积.12.如图:三角形ABC的面积是6cm2,AB长4cm,求AB边上的高CD的长.13.如图所示,BC长为5,求画阴影线的两个三角形的面积之和.14.找准所需条件,计算下列图形的面积.(单位:米)15.如图,直角三角形的三条边分别长3cm、4cm、5cm,求最长边上的高为多少厘米.16.17.选择合适的数据计算下面图形的面积.18.求下面图形的面积.(单位:厘米)请同学们先写出每个图形的面积计算字母公式,然后再进行计算.19.计算下面图形或阴影部分的面积.(单位:cm)20.找出如图所需数据再求出面积.(单位:cm)21.一个三角形的底长是5m,如果底边延长1m,那么面积就增加1.5m2,请你求出原来三角形的面积是多少平方米?22.三角形ABC是一个正三角形,求这个图形的周长.23.求下面图形中阴影部分的面积.24.求下面各图形中涂色部分的面积25.如图,长方形的长是12cm,宽是5cm,三角形①的面积是24cm2,阴影部分面积是多少?26.求下面图形的面积.(单位:厘米)27.28.下面平行四边形中,涂色部分的面积是10平方分米求空白部分的面积.(单位:分米)29.30.如图数字分别表示两个长方形和一个直角三角形的面积,另一个三角形面积是_________.参考答案:1.三角形的面积:10×8÷2=80÷2,=40(m2);梯形的面积:(4+10)×5÷2=14×5÷2,=35(m2);答:三角形的面积为40(m2);梯形的面积为35(m2).2.(1)3.6×3÷2=5.4(平方厘米);(2)(4.8+13.2)×4÷2,=18×4÷2,=36(平方厘米);答:三角形的面积是5.4平方厘米,梯形的面积是36平方厘米3.①7+15+18=40(厘米);②5+11+15×2,=16+30,=46(厘米);③(18+9)×2=27×2,=54(厘米).答:三角形的周长是40厘米,等腰梯形的周长是46厘米,六边形的周长是54厘米.4.20﹣4×4÷2,=20﹣8,=12(平方分米),答:阴影三角形的面积是12平方分米.5.(4+3)×3÷2﹣(3×3﹣×3.14×32),=7×3÷2(9﹣7.065),=10.5﹣1.935,=8.565(平方分米);答:阴影部分的面积是8.565平方分米6.(1)三角形的面积:7×8.5÷2,=59.5÷2,=29.75(平方米);(2)梯形的面积:(3+5)×3.2÷2,=8×3.2÷2,=25.6÷2,=12.8(平方米);(3)平行四边形的面积:9.8×2.1=20.58(平方米);答:三角形的面积是29.75平方米,梯形的面积是12.8平方米,平行四边形的面积是20.58平方米7.(1)3.6×2.5÷2=4.5(平方厘米);(2)(1.4+4.6)×3.2÷2=6×3.2÷2=9.6(平方分米);(3)6.2×3.5=21.7(平方米);答:三角形的面积是4.5平方厘米;梯形的面积是9.6平方分米;平行四边形的面积是21.7平方米.8.12×12×=36(平方厘米);答:阴影部分的面积为36平方厘米.9.①6+7+9=22(厘米);②(13+24)×2=37×2,=74(厘米);③7+8+6+5+3+4=33(厘米);④32×4=128(厘米);答:三角形的周长是22厘米,长方形的周长是74厘米,六边形的周长是33厘米,正方形的周长是128厘米.10.(1)6×8÷2=24(平方米);(2)(14+24)×10÷2,=38×10÷2,=190(平方米);答:三角形的面积是24平方米;梯形的面积是190平方米11.(1)2.4×0.9÷2=1.08(平方厘米);(2)2.2×1.2+2.2×0.8÷2,=2.64+0.88,=3.52(平方分米);答:甲图形的面积是1.08平方厘米,乙图形的面积是3.52平方分米.12.6×2÷4,=12÷4,=3(cm);答:AB边上的高CD的长为3厘米.13.(5×5÷2﹣5×2÷2)×2,=(12.5﹣5)×2,=7.5×2,=15,答:阴影线的两个三角形的面积之和是15.14.三角形的面积:3×4÷2,=12÷2,=6(平方米);梯形的面积:(8+12)×10÷2,=20×10÷2,=200÷2,=100(平方米);组合图形的面积:6.3×4×2,=25.2×2,=50.4(平方米);答:三角形的面积是6平方米,梯形的面积是100平方米,组合图形的面积是50.4平方米15.3×4÷2×2÷5,=12÷5,=2.4(厘米),答:这个三角形最长边上的高2.4厘米,16.(27×2÷9)×5÷2,=(54÷9)×5÷2,=6×5÷2,=30÷2,=15(平方米);答:阴影部分的面积是15平方米.17.(1)30×40÷2,=1200÷2,=600(平方厘米),答:三角形的面积是600平方厘米;(2)15×8=120(平方分米),答:平行四边形的面积是120平方分米;(3)(8+15)×10÷2,=23×10÷2,=230÷2,=115(平方厘米),答:梯形的面积是115平方厘米.18.S△=ah÷2,=8×6÷2,=48÷2,=24(平方厘米);S▱=ah,=12×15,=180(平方厘米);S梯形=(a+b)h÷2,=(10+18)×12÷2,=28×12÷2,=336÷2,=168(平方厘米);答:三角形、平行四边形和梯形的面积分别是24平方厘米、180平方厘米和168平方厘米19.(1)12×4.5÷2,=4.5×6,=27(平方厘米),(2)8×8=64(平方厘米),(3)42×2÷15=5.6(厘米),(4.5+15)×5.6÷2,=19.5×5.6÷2,=54.6(平方厘米).20.(1)20×22÷2=220(平方厘米);答:三角形的面积是220平方厘米.(2)(18+12)×10÷2,=30×10÷2,=150(平方厘米);答:图形的面积是150平方厘米.(3)10×8=80(平方厘米);答:平行四边形的面积是80平方厘米21.原三角形的高:1.5×2÷1=3(米),原三角形的面积:5×3÷2=7.5(平方米);答:原来三角形的面积是7.5平方米.22.6×2+3.14×6×,=12+9.42,=21.42(厘米),答:这个图形的周长是21.42厘米.23.14×12÷2=84(平方厘米);答:阴影部分的面积是84平方厘米.24.(60+80)×30÷2﹣60×20÷2,=2100﹣600,=1500(平方厘米);答:图形中涂色部分的面积1500平方厘米25.阴影部分的面积:12×5﹣24=36(平方厘米);答:阴影部分的面积是36平方厘米.26.(1)8×6÷2,=48÷2,=24(平方厘米);(2)12×15=180(平方厘米);(3)(10+18)×12÷2,=28×12×,=28×6,=168(平方厘米),答:三角形的面积是24平方厘米,平行四边形的面积是180平方厘米,梯形的面积是168平方厘米.27.8×5÷2,=40÷2,=20,答:阴影部分是面积是20.28.因为空白部分的高=阴影部分的高,所以空白部分梯形的高为:10×2÷5=4(分米);空白部分的面积:(3+3+5)×4÷2,=11×4÷2,=44÷2,=22(平方分米);答:空白部分的面积是22平方分米.29.7×4﹣7×4÷2,=28﹣14,=14(平方厘米).答:阴影部分的面积是14平方厘米.30.因为AO×OD=15,OC×OE=12,所以AO×OD×OC×OE=15×12,而OD×OE=5×2=10,所以OA×OC=15×12÷10=18,所以另一个三角形面积是:18÷2=9,答:另一个三角形面积是9,故答案为:9。
小学-五年级-数学三角形的面积-练习题(含答案)

三角形的面积练习题一、填空题1、一个三角形的面积是25平方厘米,和它等底等高的平行四边形的面积是( 50 )平方厘米。
2、★在一个长9厘米,周长26厘米的长方形内画一个最大的三角形,这个三角形的面积是( 18 )平方厘米。
3、一个平行四边形的底是6厘米,高是14厘米,它的面积是(84 )平方厘米,与它等底等高的三角形面积是(42 )平方厘米。
4、沿着平行四边形的任一对角线剪开,分成两个完全一样的( 三角形),它们的底和平行四边形的底( 相等).它们的( 高)和平行四边形的高相等.每个三角形的面积是平行四边形面积的( 一半)。
5、一个三角形的面积是20平方厘米,它的高是8厘米,底是( 5 )厘米.6、一个三角形的底扩大2倍,高不变,这个三角形的面积扩大( 2 )倍7、直角三角形的两条直角边长分别为3厘米和4厘米,这个直角三角形面积是( 6 )平方厘米。
8、一个等腰直角三角形的直角边是10厘米,它的面积是(50 )平方厘米。
9、一个三角形的底和高分别扩大4倍,它的面积扩大(16 )倍。
10、一个等腰三角形,已知一个底角是55°,顶角是(70 )度。
11、一个直角三角形,其中一个锐角是另一个锐角的2倍,较小的锐角是(30 )度。
12、在一个面积是36平方米的长方形里剪一个最大的三角形,这个三角形的面积是(18 )平方厘米。
13、一个三角形和一个平行四边形的底相等,并且平行四边形的高是三角形高的2倍。
那么平行四边形的面积是三角形的(4 )倍。
14、270平方厘米=( 2.7 )平方分米 1.4公顷=( 14000)平方米15、一个三角形的面积比它等底等高的平行四边形的面积少12.5平方分米,平行四边形的面积是( 25)平方分米,三角形的面积是( 12.5)平方分米。
16、两个完全一样的三角形可以拼成一个( 平行四边形).每个三角形的面积等于所拼图形面积的( 一半),所以三角形的面积=( 底×高÷2 ),如果用S表示三角形的面积,用a表示三角形的底,h表示三角形的高,那么三角形的面积公式可以写成( S=0.5ah )17、一个等边三角形的周长是12厘米,高是3厘米,它的面积是( 6平方厘米).18、一个等腰三角形的周长是18分米,腰是7分米,底边上的高是3分米,它的面积是( 6平方分米).19、三角形一条边长是4分米,这条边上的高是6分米;另一条边长是3分米,则这条边上的高是( 8平方分米).20、一个等腰直角三角形,两条直角边的和是8分米,它的面积是( 8平方分米).21、一个直角三角形的面积是16平方厘米,一个直角边长是4厘米,另一个直角边长是( 8 )厘米.—1—22、一个平行四边形和一个三角形面积相等,底边一样长,如果三角形的高是6厘米,平行四边形的高是( 3 )厘米.二、判断题1、两个面积相等的三角形可以拼成平行四边形行(×)2、等底等高的三角形面积相等(√)3、三角形的面积等于平行四边形面积的一半(×)4、用两个直角三角形可以拼成一个长方形,也可以拼成一个平行四边形(√)5、三角形的底扩大到它的2倍,高也扩大到它的3倍,面积扩大到它的6倍(√)6、两个三角形面积相等,它们的形状也一定相同(×)7、平行四边形面积等于长方形面积。
三角形面积专项练习56题(有答案)ok

三角形面积专项训练56题(有答案)1、一个三角形的面积是25平方厘米,和它等底等高的平行四边形的面积是( )平方厘米。
2、在一个长9厘米,周长26厘米的长方形内画一个最大的三角形,这个三角形的面积是()平方厘米。
3、三角形的底扩大3倍,高扩大2倍,面积扩大()倍。
4、一个三角形与梯形的高相等,它们的面积也相等。
那梯形的上底与下底的和等于三角形()的长度。
5、一个平行四边形的底是6厘米,高是14厘米,它的面积是()平方厘米,与它等底等高的三角形面积是()平方厘米。
6、有一个长方形长15厘米,宽8厘米,另一直角梯形上底长6厘米,下底长7厘米,高8厘米,将它们拼成一个梯形,梯形的面积是()平方厘米。
7、三角形的底8厘米,高5厘米,面积( )平方厘米..8、沿着平行四边形的任一对角线剪开,分成两个完全一样的( ),它们的底和平行四边形的底( ).它们的( )和平行四边形的高相等.每个三角形的面积是平行四边形面积的( ).9、一个三角形的面积是20平方厘米,它的高是8厘米,底是( )厘米.10、一个三角形的底扩大2倍,高不变,这个三角形的面积扩大()倍11、在推导平行四边形面积计算公式时,可把平行四边形通过割补平移转化为( )形去推导,推导三角形面积计算公式时,可把两个完全一样的三角形拼成一个( )形去推导,推导梯形面积计算公式时,可把两个完全一样的梯形拼成一个( )形进行推导。
12、一个平行四边形的面积为S,则与它等底等高的三角形面积是( )。
13、直角三角形的两条直角边长分别为3厘米和4厘米,这个直角三角形面积是( )平方厘米。
14、三角形的面积是18平方分米,底边长是6分米,它的底边上的高是( )分米。
15、两个完全一样的三角形一定可以拼成一个( )。
16、一个三角形的面积是36平方厘米,高是8厘米,底是()厘米。
17、一个三角形与一个平行四边形的底和面积都相等,平行四边形的高是16厘米,三角形的高是()厘米。
面积周长练习题及答案

面积周长练习题及答案一、选择题1. 一个正方形的边长是4厘米,它的周长是多少厘米?A. 8厘米B. 12厘米C. 16厘米D. 20厘米答案:C2. 一个长方形的长是10厘米,宽是5厘米,它的面积是多少平方厘米?A. 30平方厘米B. 40平方厘米C. 50平方厘米D. 60平方厘米答案:C3. 一个圆的半径是3厘米,它的周长是多少厘米?(圆周率取3.14)A. 18.84厘米B. 21.98厘米C. 28.26厘米D. 36.5厘米答案:A二、填空题4. 如果一个三角形的底边长是6厘米,高是4厘米,那么它的面积是________平方厘米。
答案:12平方厘米5. 一个平行四边形的底边长是8厘米,高是3厘米,它的面积是________平方厘米。
答案:24平方厘米6. 如果一个圆的直径是14厘米,那么它的面积是多少平方厘米?(圆周率取3.14)答案:153.86平方厘米三、计算题7. 一个梯形的上底是5厘米,下底是10厘米,高是4厘米,求它的面积。
解:根据梯形面积公式 S = (a + b) * h / 2其中 a = 5厘米,b = 10厘米,h = 4厘米S = (5 + 10) * 4 / 2S = 15 * 4 / 2S = 60 / 2S = 30平方厘米8. 一个正六边形的边长是3厘米,求它的周长和面积。
解:正六边形的周长是边长的6倍,所以周长 P = 6 * 3 = 18厘米面积 A = 6 * (边长^2) / (4 * √3) = 6 * (3^2) / (4 * √3)A = 54 / (4 * √3)A = 27 / √3A ≈ 48.98平方厘米四、应用题9. 一个花坛是一个圆形,半径是5米。
如果沿着花坛的边缘铺设一圈小石子,小石子的总长度是多少?花坛的面积是多少?解:根据圆的周长公式C = 2πr,其中 r = 5米C = 2 * 3.14 * 5 = 31.4米根据圆的面积公式A = πr^2A = 3.14 * 5^2 = 3.14 * 25 = 78.5平方米10. 一块长方形的菜地,长是25米,宽是15米。
初中数学专题《四边形中的最值问题》专项训练30道含答案解析

专题18.8 四边形中的最值问题专项训练(30道)【人教版】考卷信息:本套训练卷共30题,选择10题,填空10题,解答10题,题型针对性较高,覆盖面广,选题有深度,可强化学生对四边形中最值问题模型的记忆与理解!一.选择题(共10小题)1.(2022春•重庆期末)如图,矩形ABCD中,AB=23,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )A.43+3B.221C.23+6D.45【分析】将△BPC绕点C逆时针旋转60°,得到△EFC,连接PF、AE、AC,则AE的长即为所求.【解答】解:将△BPC绕点C逆时针旋转60°,得到△EFC,连接PF、AE、AC,则AE 的长即为所求.由旋转的性质可知:△PFC是等边三角形,∴PC=PF,∵PB=EF,∴PA+PB+PC=PA+PF+EF,∴当A、P、F、E共线时,PA+PB+PC的值最小,∵四边形ABCD是矩形,∴∠ABC=90°,∴AC=AB2+BC2=43,∴AC=2AB,∴∠ACB=30°,AC=2AB=43,∵∠BCE=60°,∴∠ACE=90°,∴AE=(43)2+62=221,故选:B.2.(2022•灞桥区校级模拟)如图,平面内三点A、B、C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD的最大值是( )2 A.5B.7C.72D.72【分析】如图将△BDA绕点D顺时针旋转90°得到△CDM.由旋转不变性可知:AB=AM,CM=4,DA=DM.∠ADM=90°,推出△ADM是等腰直角三角形,推出AD=22推出当AM的值最大时,AD的值最大,利用三角形的三边关系求出AM的最大值即可解决问题;【解答】解:如图将△BDA绕点D顺时针旋转90°得到△CDM.由旋转不变性可知:AB=CM=4,DA=DM.∠ADM=90°,∴△ADM是等腰直角三角形,AM,∴AD=22∴当AM的值最大时,AD的值最大,∵AM≤AC+CM,∴AM≤7,∴AM的最大值为7,,∴AD的最大值为722故选:D .3.(2022春•中山市期末)如图,在边长为a 的正方形ABCD 中,E 是对角线BD 上一点,且BE =BC ,点P 是CE 上一动点,则点P 到边BD ,BC 的距离之和PM +PN 的值( )A .有最大值aB .有最小值22a C .是定值a D .是定值22a 【分析】连接BP ,作EF ⊥BC 于点F ,由正方形的性质可知△BEF 为等腰直角三角形,BE =a ,可求EF ,利用面积法得S △BPE +S △BPC =S △BEC ,将面积公式代入即可.【解答】解:如图,连接BP ,作EF ⊥BC 于点F ,则∠EFB =90°,∵正方形的性质可知∠EBF =45°,∴△BEF 为等腰直角三角形,∵正方形的边长为a ,∴BE =BC =a ,∴BF =EF =22BE =22a ,∵PM ⊥BD ,PN ⊥BC ,∴S △BPE +S △BPC =S △BEC ,∴12BE ×PM +12BC ×PN =12BC ×EF ,∵BE =BC ,∴PM +PN =EF =22a .则点P 到边BD ,BC 的距离之和PM +PN 的值是定值22a .故选:D .4.(2022春•三门峡期末)如图,在矩形ABCD 中,AB =2,AD =1,E 为AB 的中点,F 为EC 上一动点,P 为DF 中点,连接PB ,则PB 的最小值是( )A.2B.4C.2D.22【分析】根据中位线定理可得出点点P的运动轨迹是线段P1P2,再根据垂线段最短可得当BP⊥P1P2时,PB取得最小值;由矩形的性质以及已知的数据即可知BP1⊥P1P2,故BP 的最小值为BP1的长,由勾股定理求解即可.【解答】解:如图:当点F与点C重合时,点P在P1处,CP1=DP1,当点F与点E重合时,点P在P2处,EP2=DP2,CE.∴P1P2∥CE且P1P2=12当点F在EC上除点C、E的位置处时,有DP=FP.CF.由中位线定理可知:P1P∥CE且P1P=12∴点P的运动轨迹是线段P1P2,∴当BP⊥P1P2时,PB取得最小值.∵矩形ABCD中,AB=2,AD=1,E为AB的中点,∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=1.∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.∴∠DP2P1=90°.∴∠DP1P2=45°.∴∠P2P1B=90°,即BP1⊥P1P2,∴BP的最小值为BP1的长.在等腰直角BCP1中,CP1=BC=1.∴BP1=2.∴PB的最小值是2.故选:C.5.(2022春•滨湖区期末)如图,已知菱形ABCD的面积为20,边长为5,点P、Q分别是边BC、CD上的动点,且PC=CQ,连接PD、AQ,则PD+AQ的最小值为( )A.45B.89C.10D.72【分析】过点A作AM⊥BC于点M,延长AM到点A′,使A′M=AM,根据菱形的性质和勾股定理可得BM=3,以点B为原点,BC为x轴,垂直于BC方向为y轴,建立平面直角坐标系,可得B(0,0),A(3,4),C(5,0),D(8,4),A′(3,﹣4),然后证明△ABP≌△ADQ(SAS),可得AP=AQ=A′P,连接A′D,AP,A′P,由A′P+PD>A′D,可得A′,P,D三点共线时,PD+A′P取最小值,所以PD+AQ 的最小值=PD+A′P的最小值=A′D,利用勾股定理即可解决问题.【解答】解:如图,过点A作AM⊥BC于点M,延长AM到点A′,使A′M=AM,∵四边形ABCD是菱形,∴AB=BC=AD=5,∠ABC=∠ADC,∵菱形ABCD的面积为20,边长为5,∴AM=4,在Rt△ABM中,根据勾股定理得:BM=AB2−AM2=3,以点B为原点,BC为x轴,垂直于BC方向为y轴,建立平面直角坐标系,∴B(0,0),A(3,4),C(5,0),D(8,4),A′(3,﹣4),∵PC=CQ,BC=CD,∴BP=DQ,在△ABP和△ADQ中,AB=AD∠ABC=∠ADC,BP=DQ∴△ABP≌△ADQ(SAS),∴AP=AQ=A′P,连接A′D,AP,A′P,∵A′P+PD>A′D,∴A′,P,D三点共线时,PD+A′P取最小值,∴PD+AQ的最小值=PD+A′P的最小值=A′D=(8−3)2+(4+4)2=89.故选:B.6.(2022•泰山区一模)如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为2,则线段CF的最小值是( )A.2B.1C.5−1D.5−2【分析】根据正方形的性质可得AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,然后利用“HL”证明Rt△ADM和Rt△BCN全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△DCE和△BCE全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AFD=90°,取AD的中点O,连接OF、OC,根据直角AD=1,利用勾股定理列式求出OC,然三角形斜边上的中线等于斜边的一半可得OF=12后根据三角形的三边关系可知当O、F、C三点共线时,CF的长度最小.【解答】解:在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,在Rt△ADM和Rt△BCN中,AD=BCAM=BN,∴Rt△ADM≌Rt△BCN(HL),∴∠1=∠2,在△DCE和△BCE中,BC=CD∠DCE=∠BCE,CE=CE∴△DCE≌△BCE(SAS),∴∠2=∠3,∴∠1=∠3,∵∠ADF+∠3=∠ADC=90°,∴∠1+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,AD=1,则OF=DO=12在Rt△ODC中,OC=DO2+DC2=12+22=5,根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=5−1.故选:C.7.(2022•龙华区二模)如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为13−2.其中正确的有( )A.1个B.2个C.3个D.4个【分析】连接AE,过E作EH⊥AB于H,则EH=BC,根据全等三角形的判定和性质定理即可得到AF=EG,故①正确;根据平行线的性质和等腰三角形的判定和性质即可得到PE=PC;故②正确;连接EF,推出点E、P、F、C四点共圆,根据圆周角定理得到∠FEC=∠FPC=45°,于是得到BF=DE=1,同理当F运动到C点右侧时,此时∠FPC=45°,且EPCF四点共圆,EC=FC=3,故此时BF=BC+CF=4+3=7.因此BF=1或7,故③错误;取AE的中点O,连接PO,CO,根据直角三角形的性质得到AO=PO =1AE,推出点P在以O为圆心,AE为直径的圆上,当OC最小时,CP的值最小,根2据三角形的三边关系得到PC≥OC﹣OP,根据勾股定理即可得到结论.【解答】解:连接AE,过E作EH⊥AB于H,则EH=BC,∵AB=BC,∴EH=AB,∵EG⊥AF,∴∠BAF+∠AGP=∠BAF+∠AFB=90°,∴∠EGH=∠AFB,∵∠B=∠EHG=90°,∴△HEG≌△ABF(AAS),∴AF=EG,故①正确;∵AB∥CD,∴∠AGE=∠CEG,∵∠BAF+∠AGP=90°,∠PCF+∠PCE=90°,∵∠BAF=∠PCF,∴∠AGE=∠PCE,∴∠PEC=∠PCE,∴PE=PC;故②正确;连接EF,∵∠EPF=∠FCE=90°,∴点E、P、F、C四点共圆,∴∠FEC=∠FPC=45°,∴EC=FC,∴BF=DE=1,同理当F运动到C点右侧时,此时∠FPC=45°,且E、P、C、F四点共圆,EC=FC=3,故此时BF=BC+CF=4+3=7.因此BF=1或7,故③错误;取AE的中点O,连接PO,CO,AE,∴AO=PO=12∵∠APE=90°,∴点P在以O为圆心,AE为直径的圆上,∴当OC最小时,CP的值最小,∵PC ≥OC ﹣OP ,∴PC 的最小值=OC ﹣OP =OC −12AE ,∵OC =22+(72)2=652,在Rt △ADE 中,AE =42+12=17,∴PC 的最小值为652−172,故④错误,故选:B .8.(2022•南平校级自主招生)如图,在△ABC 中,AB =6,AC =8,BC =10,P 为边BC 上一动点(且点P 不与点B 、C 重合),PE ⊥AB 于E ,PF ⊥AC 于F .则EF 的最小值为( )A .4B .4.8C .5.2D .6【分析】先由矩形的判定定理推知四边形PEAF 是矩形;连接PA ,则PA =EF ,所以要使EF ,即PA 最短,只需PA ⊥CB 即可;然后根据三角形的等积转换即可求得PA 的值.【解答】解:如图,连接PA .∵在△ABC 中,AB =6,AC =8,BC =10,∴BC 2=AB 2+AC 2,∴∠A =90°.又∵PE ⊥AB 于点E ,PF ⊥AC 于点F .∴∠AEP =∠AFP =90°,∴四边形PEAF 是矩形.∴AP =EF .∴当PA 最小时,EF 也最小,即当AP ⊥CB 时,PA 最小,∵12AB •AC =12BC •AP ,即AP =AB ⋅AC BC =6×810=4.8,∴线段EF 长的最小值为4.8;故选:B .9.(2022春•崇川区期末)如图,正方形ABCD 边长为1,点E ,F 分别是边BC ,CD 上的两个动点,且BE =CF ,连接BF ,DE ,则BF +DE 的最小值为( )A .2B .3C .5D .6【分析】连接AE ,利用△ABE ≌△BCF 转化线段BF 得到BF +DE =AE +DE ,则通过作A 点关于BC 对称点H ,连接DH 交BC 于E 点,利用勾股定理求出DH 长即可.【解答】解:连接AE ,如图1,∵四边形ABCD 是正方形,∴AB =BC ,∠ABE =∠BCF =90°.又BE =CF ,∴△ABE ≌△BCF (SAS ).∴AE =BF .所以BF +DE 最小值等于AE +DE 最小值.作点A 关于BC 的对称点H 点,如图2,连接BH ,则A 、B 、H 三点共线,连接DH ,DH 与BC 的交点即为所求的E 点.根据对称性可知AE =HE ,所以AE +DE =DH .在Rt △ADH 中,AD =1,AH =2,∴DH =AH 2+AD 2=5,∴BF +DE 最小值为5.故选:C .10.(2022•泰州)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为( )A.2B.2C.22D.4【分析】连接AE,那么,AE=CG,所以这三个d的和就是AE+EF+FC,所以大于等于AC,故当AEFC四点共线有最小值,最后求解,即可求出答案.【解答】解:如图,连接AE,∵四边形DEFG是正方形,∴∠EDG=90°,EF=DE=DG,∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),∴AE=CG,∴d1+d2+d3=EF+CF+AE,∴点A,E,F,C在同一条线上时,EF+CF+AE最小,即d1+d2+d3最小,连接AC,∴d1+d2+d3最小值为AC,在Rt△ABC中,AC=2AB=22,∴d1+d2+d3最小=AC=22,故选:C.二.填空题(共10小题)11.(2022春•江城区期末)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=6,BC=2.运动过程中点D到点O的最大距离是 3+13 .【分析】取AB的中点E,连接OD、OE、DE,根据直角三角形斜边上的中线等于斜边AB,利用勾股定理列式求出DE,然后根据三角形任意两边之和大于的一半可得OE=12第三边可得OD过点E时最大.【解答】解:如图:取线段AB的中点E,连接OE,DE,OD,∵AB=6,点E是AB的中点,∠AOB=90°,∴AE=BE=3=OE,∵四边形ABCD是矩形,∴AD=BC=2,∠DAB=90°,∴DE=AE2+AD2=13,∵OD≤OE+DE,∴当点D,点E,点O共线时,OD的长度最大.∴点D到点O的最大距离=OE+DE=3+13,故答案为:3+13.12.(2022•东莞市校级一模)如图,在矩形ABCD中,AB=6,AD=5,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+DQ的最小值为 13 .【分析】连接BP,在BA的延长线上截取AE=AB=6,连接PE,CE,PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,在BA的延长线上截取AE=AB=6,则PC+QD=PC+PB=PC+PE≥CE,根据勾股定理可得结果.【解答】解:如图,连接BP,∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∵AP=CQ,∴AD﹣AP=BC﹣CQ,∴DP=QB,DP∥BQ,∴四边形DPBQ是平行四边形,∴PB∥DQ,PB=DQ,∴PC+QD=PC+PB,∴PC+QD的最小值转化为PC+PB的最小值,如图,在BA的延长线上截取AE=AB=6,连接PE,CE,∵PA⊥BE,∴PA是BE的垂直平分线,∴PB=PE,∴PC+PB=PC+PE,∴PC+QD=PC+PB=PC+PE≥CE,∵BE=2AB=12,BC=AD=5,∴CE=BE2+BC2=13.∴PC+DQ的最小值为13.故答案为:13.13.(2022•钱塘区一模)如图,在矩形ABCD中,线段EF在AB边上,以EF为边在矩形ABCD内部作正方形EFGH,连结AH,CG.若AB=10,AD=6,EF=4,则AH+CG的最小值为 62 .【分析】方法一:延长DA至A′,使A′A=EH=EF=4,连接A′E,EG,可得四边形AA′EH是平行四边形,所以A′E=AH,则AH+CG的最小值即为A′E+CG的最小值,根据勾股定理即可解决问题.方法二:过点G作GA′∥AH交AF于点A′,可得四边形AHGA′是平行四边形,进而可以解决问题.【解答】解:方法一:如图,延长DA至A′,使A′A=EH=EF=4,连接A′E,EG,∵HE⊥AB,AA′⊥AB,∴AA′∥EH,∵A′A=EH,∴四边形AA′EH是平行四边形,∴A′E=AH,则AH+CG的最小值即为A′E+CG的最小值,∵四边形EFGH是正方形,∴EF=FG=4,∴EG=42,∵A′D=AD+AA′=6+4=10,在Rt△A′DC中,DC=AB=10,∴A′C=A′D2+DC2=102,∴A′E+CG=A′C﹣EG=62.方法二:如图,过点G作GA′∥AH交AF于点A′,∴四边形AHGA′是平行四边形,∴AA′=HG=4,A′G=AH,∴A′B=AB﹣AA′=6,∵BC=6,∴A′C=62,∴AH+CG=A′G+CG≥A′C,则AH+CG的最小值为62.故答案为:62.14.(2022春•东城区期中)在正方形ABCD中,AB=5,点E、F分别为AD、AB上一点,且AE=AF,连接BE、CF,则BE+CF的最小值是 55 .【分析】连接DF,根据正方形的性质证明△ADF≌△ABE(SAS),可得DF=BE,作点D关于AB的对称点D′,连接CD′交AB于点F′,连接D′F,则DF=D′F,可得BE+CF=DF+CF=D′F+CF≥CD′,所以当点F与点F′重合时,D′F+CF最小,最小值为CD′的长,然后根据勾股定理即可解决问题.【解答】解:如图,连接DF,∵四边形ABCD是正方形,∴AD=AB,∠BAE=∠DAF=90°,在△ADF 和△ABE 中,AD =AB ∠FAD =∠EAB AF =AE,∴△ADF ≌△ABE (SAS ),∴DF =BE ,作点D 关于AB 的对称点D ′,连接CD ′交AB 于点F ′,连接D ′F ,则DF =D ′F ,∴BE +CF =DF +CF =D ′F +CF ≥CD ′,∴当点F 与点F ′重合时,D ′F +CF 最小,最小值为CD ′的长,在Rt △CDD ′中,根据勾股定理得:CD ′=CD 2+DD′2=52+102=55,∴BE +CF 的最小值是55.故答案为:55.15.(2022春•虎林市期末)如图,在Rt △ABC 中,∠BAC =90°,且BA =12,AC =16,点D 是斜边BC 上的一个动点,过点D 分别作DE ⊥AB 于点E ,DF ⊥AC 于点F ,点G 为四边形DEAF 对角线交点,则线段GF 的最小值为 245 .【分析】由勾股定理求出BC 的长,再证明四边形DEAF 是矩形,可得EF =AD ,根据垂线段最短和三角形面积即可解决问题.【解答】解:连接AD 、EF ,∵∠BAC =90°,且BA =9,AC =12,∴BC =AB 2+AC 2=122+162=20,∵DE ⊥AB ,DF ⊥AC ,∴∠DEA =∠DFA =∠BAC =90°,∴四边形DEAF 是矩形,∴EF =AD ,∴当AD ⊥BC 时,AD 的值最小,此时,△ABC 的面积=12AB ×AC =12BC ×AD ,∴12×16=20AD ,∴AD =485∴EF 的最小值为485,∵点G 为四边形DEAF 对角线交点,∴GF =12EF =245;故答案为:245.。
三角形、平行四边形、梯形的面积练习题

1、已知右图的上底是20厘米,下底是34厘米,其中阴影部分的面积是340平方厘米。
这个梯形的面积是多少?2、已知下图梯形的面积是252平方米,空白部分为平行四边形,求阴影部分的面积。
(单位:米)3、在一个底为6分米,高为15分米的直角三角形右侧对接上一个梯形(阴影部分)拼成了一个平行四边形,求这个梯形的面积。
4、一块直角梯形的地,它的下底是40米,如果上底增加38米,这块地就变成了正方形,原来梯形的面积是多少?5、如下图,一个平行四边形被分成甲、乙两部分,甲的面积比乙大32平方米,甲的上底是多少米?2、有一个梯形,如果它的上底增加2米,下底和高都不变,它的面积就增加4.8平方米;如果下底和上底都不变,高增加2米,它的面积就增加8.5平方米。
求原来梯形的面积。
7、一个长方形纸折成如下梯形的形状,AE=AD,AB边长10厘米,求梯形ABCD的面积。
8、一块三角形地的底是24米,高15米。
这块地的面积是多少平方米?9、一块平行四边形的麦地,底是230米,高是80米,每平方米收小麦5千克。
这块地共收小麦多少千克?一、填空20301.利用割补法,可以把一个平行四边形转化成一个(),它的面积与平行四边形的面积(),它的()与平行四边形的底相等,它的()与平行四边形的高相等。
因为它的面积等于(),所以平行四边形边的面积等于()。
2.平行四边形的面积公式用字母表示可以写作(),也可以写作()。
还可以写作()。
;三角形的面积的计算公式用字母表示是()。
3. 平行四边形的底是2分米5厘米,高是底的1.2倍,它的面积是()平方厘米。
4.一个三角形的底是4分米,高是30厘米,面积是()平方分米。
5.一个三角形的高是7分米,底是8分米,和它等底等高的平行四边形的面积是()平方分米。
6.一个三角形的面积是4.8平方米,与它等底等高的平行四边形的面积是()7.一个平行四边形的面积是280平方厘米,与它的等底等高的三角形的面积是()平方厘米。
三角形的面积与周长练习题

三角形的面积与周长练习题三角形是几何学中最基本的图形之一,了解三角形的面积和周长计算方法对于学习几何学以及解决实际问题都非常重要。
本文将为大家提供一些关于三角形面积和周长的练习题,帮助大家巩固相关知识。
题目一:已知一个三角形的底边长度为8cm,高为6cm,求其面积和周长。
解答一:首先计算三角形的面积。
由于已知三角形的底边长度和高,可以使用公式:面积 = 底边长度 ×高 ÷ 2,代入已知数据进行计算:面积 = 8cm × 6cm ÷ 2 = 24cm²接下来计算三角形的周长。
由于只知道底边的长度,无法直接计算周长,因此需要额外的信息。
但可以使用勾股定理求出三角形的两条边,再计算周长。
假设三角形的两条边分别为a和b,底边为c,则勾股定理可以表示为:c² = a² + b²。
根据已知底边和高,可以推导出一个直角三角形,其中底边是斜边,高作为一个直角边,可以计算另一条直角边。
即:a² + b² = c²8cm² + 6cm² = c²64cm² + 36cm² = c²100cm² = c²c = √100cmc = 10cm现在已知三角形的底边和两条边的长度,可以计算周长了:周长 = 底边长度 + a + b周长 = 8cm + 10cm + 6cm周长 = 24cm综上所述,该三角形的面积为24cm²,周长为24cm。
题目二:已知一个等边三角形的边长为10cm,求其面积和周长。
解答二:等边三角形的特点是三条边长度相等,因此只需要知道一个边长就可以计算出面积和周长。
首先计算三角形的面积。
由于等边三角形的高和底边相等,可以使用公式:面积 = 边长 ×高 ÷ 2,代入已知数据进行计算:面积= 10cm × 10cm × √3÷ 4 ≈ 43.3cm²接下来计算三角形的周长,由于三条边长度相等,周长等于三个边长的和:周长 = 边长 + 边长 + 边长周长 = 10cm + 10cm + 10cm周长 = 30cm综上所述,该等边三角形的面积约为43.3cm²,周长为30cm。
五年级数学必考题多边形的面积计算公式汇总+练习题(有答案解析)!

五年级数学必考题多边形的面积计算公式汇总+练习题(有答案解析)!面积计算公式1、长方形的面积=长×宽字母表示:S=ab长方形的长=面积÷宽 a=S÷b长方形的宽=面积÷长b=S÷a2、正方形的面积=边长×边长字母表示: S= a²3、平行四边形的面积=底×高字母表示:S=ah平行四边形的高=面积÷底 h=S÷a平行四边形的底=面积÷高 a=S÷h4、三角形的面积=底×高÷2字母表示:S=ah÷2三角形的高= 2×面积÷底h=2S÷a三角形的底= 2×面积÷高a=2S÷h5、梯形的面积=(上底+下底)×高÷2字母表示:S=(a+b)·h ÷2梯形的高=2×面积÷(上底+下底)h=2S÷(a+b)梯形的上底=2×面积÷高—下底a=2S÷h-b梯形的下底=2×面积÷高—上底b=2S÷h-a1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方米=10000平方厘米1米=10分米=100厘米多边形面积同步试题一、填空1.完成下表。
考查目的:平行四边形、三角形和梯形的面积计算及变式练习。
答案:解析:直接利用公式计算这三种图形的面积,对于学生来说完成的难度不大。
对于已知平行四边形的面积和高求底、已知三角形的面积和底求高这两个变式练习,可引导学生进行比较,理解并强化三角形和梯形的类似计算中需要先将“面积×2”这一知识点。
2.下图是一个平行四边形,它包含了三个三角形,其中两个空白三角形的面积分别是15 平方厘米和25 平方厘米。
中间涂色三角形的面积是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形四边形周长面积专项练习30题(有答案)1.计算下面图形的面积.2.求下列图形的面积.3.计算如图图形的周长.(单位:厘米)4.如图中梯形的面积是20dm2,阴影三角形的面积是多少?5.如图,两个正方形的边长分别是4分米和3分米,阴影部分的面积是多少平方分米?6.寻找合适的条件,求出各图形的面积.(单位:米)7.算出下面图形的面积.8.求阴影部分面积.单位:厘米.9.图形王国展风采.(求下面图形的周长,单位:厘米.)10.找准所需条件,计算下列图形的面积.(单位:米)11.求下面图形的面积.12.如图:三角形ABC的面积是6cm2,AB长4cm,求AB边上的高CD的长.13.如图所示,BC长为5,求画阴影线的两个三角形的面积之和.14.找准所需条件,计算下列图形的面积.(单位:米)15.如图,直角三角形的三条边分别长3cm、4cm、5cm,求最长边上的高为多少厘米.16.17.选择合适的数据计算下面图形的面积.18.求下面图形的面积.(单位:厘米)请同学们先写出每个图形的面积计算字母公式,然后再进行计算.19.计算下面图形或阴影部分的面积.(单位:cm)20.找出如图所需数据再求出面积.(单位:cm)21.一个三角形的底长是5m,如果底边延长1m,那么面积就增加1.5m2,请你求出原来三角形的面积是多少平方米?22.三角形ABC是一个正三角形,求这个图形的周长.23.求下面图形中阴影部分的面积.24.求下面各图形中涂色部分的面积25.如图,长方形的长是12cm,宽是5cm,三角形①的面积是24cm2,阴影部分面积是多少?26.求下面图形的面积.(单位:厘米)27.28.下面平行四边形中,涂色部分的面积是10平方分米求空白部分的面积.(单位:分米)29.30.如图数字分别表示两个长方形和一个直角三角形的面积,另一个三角形面积是_________.参考答案:1.三角形的面积:10×8÷2=80÷2,=40(m2);梯形的面积:(4+10)×5÷2=14×5÷2,=35(m2);答:三角形的面积为40(m2);梯形的面积为35(m2).2.(1)3.6×3÷2=5.4(平方厘米);(2)(4.8+13.2)×4÷2,=18×4÷2,=36(平方厘米);答:三角形的面积是5.4平方厘米,梯形的面积是36平方厘米3.①7+15+18=40(厘米);②5+11+15×2,=16+30,=46(厘米);③(18+9)×2=27×2,=54(厘米).答:三角形的周长是40厘米,等腰梯形的周长是46厘米,六边形的周长是54厘米.4.20﹣4×4÷2,=20﹣8,=12(平方分米),答:阴影三角形的面积是12平方分米.5.(4+3)×3÷2﹣(3×3﹣×3.14×32),=7×3÷2(9﹣7.065),=10.5﹣1.935,=8.565(平方分米);答:阴影部分的面积是8.565平方分米6.(1)三角形的面积:7×8.5÷2,=59.5÷2,=29.75(平方米);(2)梯形的面积:(3+5)×3.2÷2,=8×3.2÷2,=25.6÷2,=12.8(平方米);(3)平行四边形的面积:9.8×2.1=20.58(平方米);答:三角形的面积是29.75平方米,梯形的面积是12.8平方米,平行四边形的面积是20.58平方米7.(1)3.6×2.5÷2=4.5(平方厘米);(2)(1.4+4.6)×3.2÷2=6×3.2÷2=9.6(平方分米);(3)6.2×3.5=21.7(平方米);答:三角形的面积是4.5平方厘米;梯形的面积是9.6平方分米;平行四边形的面积是21.7平方米.8.12×12×=36(平方厘米);答:阴影部分的面积为36平方厘米.9.①6+7+9=22(厘米);②(13+24)×2=37×2,=74(厘米);③7+8+6+5+3+4=33(厘米);④32×4=128(厘米);答:三角形的周长是22厘米,长方形的周长是74厘米,六边形的周长是33厘米,正方形的周长是128厘米.10.(1)6×8÷2=24(平方米);(2)(14+24)×10÷2,=38×10÷2,=190(平方米);答:三角形的面积是24平方米;梯形的面积是190平方米11.(1)2.4×0.9÷2=1.08(平方厘米);(2)2.2×1.2+2.2×0.8÷2,=2.64+0.88,=3.52(平方分米);答:甲图形的面积是1.08平方厘米,乙图形的面积是3.52平方分米.12.6×2÷4,=12÷4,=3(cm);答:AB边上的高CD的长为3厘米.13.(5×5÷2﹣5×2÷2)×2,=(12.5﹣5)×2,=7.5×2,=15,答:阴影线的两个三角形的面积之和是15.14.三角形的面积:3×4÷2,=12÷2,=6(平方米);梯形的面积:(8+12)×10÷2,=20×10÷2,=200÷2,=100(平方米);组合图形的面积:6.3×4×2,=25.2×2,=50.4(平方米);答:三角形的面积是6平方米,梯形的面积是100平方米,组合图形的面积是50.4平方米15.3×4÷2×2÷5,=12÷5,=2.4(厘米),答:这个三角形最长边上的高2.4厘米,16.(27×2÷9)×5÷2,=(54÷9)×5÷2,=6×5÷2,=30÷2,=15(平方米);答:阴影部分的面积是15平方米.17.(1)30×40÷2,=1200÷2,=600(平方厘米),答:三角形的面积是600平方厘米;(2)15×8=120(平方分米),答:平行四边形的面积是120平方分米;(3)(8+15)×10÷2,=23×10÷2,=230÷2,=115(平方厘米),答:梯形的面积是115平方厘米.18.S△=ah÷2,=8×6÷2,=48÷2,=24(平方厘米);S▱=ah,=12×15,=180(平方厘米);S梯形=(a+b)h÷2,=(10+18)×12÷2,=28×12÷2,=336÷2,=168(平方厘米);答:三角形、平行四边形和梯形的面积分别是24平方厘米、180平方厘米和168平方厘米19.(1)12×4.5÷2,=4.5×6,=27(平方厘米),(2)8×8=64(平方厘米),(3)42×2÷15=5.6(厘米),(4.5+15)×5.6÷2,=19.5×5.6÷2,=54.6(平方厘米).20.(1)20×22÷2=220(平方厘米);答:三角形的面积是220平方厘米.(2)(18+12)×10÷2,=30×10÷2,=150(平方厘米);答:图形的面积是150平方厘米.(3)10×8=80(平方厘米);答:平行四边形的面积是80平方厘米21.原三角形的高:1.5×2÷1=3(米),原三角形的面积:5×3÷2=7.5(平方米);答:原来三角形的面积是7.5平方米.22.6×2+3.14×6×,=12+9.42,=21.42(厘米),答:这个图形的周长是21.42厘米.23.14×12÷2=84(平方厘米);答:阴影部分的面积是84平方厘米.24.(60+80)×30÷2﹣60×20÷2,=2100﹣600,=1500(平方厘米);答:图形中涂色部分的面积1500平方厘米25.阴影部分的面积:12×5﹣24=36(平方厘米);答:阴影部分的面积是36平方厘米.26.(1)8×6÷2,=48÷2,=24(平方厘米);(2)12×15=180(平方厘米);(3)(10+18)×12÷2,=28×12×,=28×6,=168(平方厘米),答:三角形的面积是24平方厘米,平行四边形的面积是180平方厘米,梯形的面积是168平方厘米.27.8×5÷2,=40÷2,=20,答:阴影部分是面积是20.28.因为空白部分的高=阴影部分的高,所以空白部分梯形的高为:10×2÷5=4(分米);空白部分的面积:(3+3+5)×4÷2,=11×4÷2,=44÷2,=22(平方分米);答:空白部分的面积是22平方分米.29.7×4﹣7×4÷2,=28﹣14,=14(平方厘米).答:阴影部分的面积是14平方厘米.30.因为AO×OD=15,OC×OE=12,所以AO×OD×OC×OE=15×12,而OD×OE=5×2=10,所以OA×OC=15×12÷10=18,所以另一个三角形面积是:18÷2=9,答:另一个三角形面积是9,故答案为:9。
