专题47 三角形中的旋转综合问题(解析版)
2020-2021备战中考数学——初中数学 旋转的综合压轴题专题复习附答案解析

2020-2021备战中考数学——初中数学旋转的综合压轴题专题复习附答案解析一、旋转1.操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.(1)连接AE,求证:△AEF是等腰三角形;猜想与发现:(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.结论1:DM、MN的数量关系是;结论2:DM、MN的位置关系是;拓展与探究:(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【答案】(1)证明参见解析;(2)相等,垂直;(3)成立,理由参见解析.【解析】试题分析:(1)根据正方形的性质以及等腰直角三角形的知识证明出CE=CF,继而证明出△ABE≌△ADF,得到AE=AF,从而证明出△AEF是等腰三角形;(2)DM、MN的数量关系是相等,利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直,利用三角形外角性质和等腰三角形两个底角相等性质,及全等三角形对应角相等即可得出结论;(3)成立,连接AE,交MD于点G,标记出各个角,首先证明出MN∥AE,MN=AE,利用三角形全等证出AE=AF,而DM=AF,从而得到DM,MN数量相等的结论,再利用三角形外角性质和三角形全等,等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°.从而得到DM、MN的位置关系是垂直.试题解析:(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠B=∠ADF=90°,∵△CEF 是等腰直角三角形,∠C=90°,∴CE=CF,∴BC﹣CE=CD﹣CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,∴△AEF是等腰三角形;(2)DM、MN的数量关系是相等,DM、MN的位置关系是垂直;∵在Rt△ADF中DM是斜边AF的中线,∴AF=2DM,∵MN 是△AEF的中位线,∴AE=2MN,∵AE=AF,∴DM=MN;∵∠DMF=∠DAF+∠ADM,AM=MD,∵∠FMN=∠FAE,∠DAF=∠BAE,∴∠ADM=∠DAF=∠BAE,∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°,∴DM⊥MN;(3)(2)中的两个结论还成立,连接AE,交MD于点G,∵点M为AF的中点,点N为EF的中点,∴MN∥AE,MN=AE,由已知得,AB=AD=BC=CD,∠B=∠ADF,CE=CF,又∵BC+CE=CD+CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,在Rt△ADF中,∵点M为AF的中点,∴DM=AF,∴DM=MN,∵△ABE≌△ADF,∴∠1=∠2,∵AB∥DF,∴∠1=∠3,同理可证:∠2=∠4,∴∠3=∠4,∵DM=AM,∴∠MAD=∠5,∴∠DGE=∠5+∠4=∠MAD+∠3=90°,∵MN∥AE,∴∠DMN=∠DGE=90°,∴DM⊥MN.所以(2)中的两个结论还成立.考点:1.正方形的性质;2.全等三角形的判定与性质;3.三角形中位线定理;4.旋转的性质.2.已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与BC、DC的延长线交于点E、F,连接EF,设CE=a,CF=b.(1)如图1,当a=42时,求b的值;(2)当a=4时,在图2中画出相应的图形并求出b的值;(3)如图3,请直接写出∠EAF绕点A旋转的过程中a、b满足的关系式.【答案】(1)422)b=8;(3)ab=32.【解析】试题分析:(1)由正方形ABCD的边长为4,可得AC=2,∠ACB=45°.再CE=a=2∠CAE=∠AEC,从而可得∠CAF的度数,既而可得 b=AC;(2)通过证明△ACF∽△ECA,即可得;(3)通过证明△ACF∽△ECA,即可得.试题解析:(1)∵正方形ABCD的边长为4,∴AC=42,∠ACB=45°.∵CE=a=42,∴∠CAE=∠AEC=452︒=22.5°,∴∠CAF=∠EAF-∠CAE=22.5°,∴∠AFC=∠ACD-∠CAF=22.5°,∴∠CAF=∠AFC,∴b=AC=CF=42;(2)∵∠FAE=45°,∠ACB=45°,∴∠FAC+∠CAE=45°,∠CAE+∠AEC=45°,∴∠FAC =∠AEC.又∵∠ACF=∠ECA=135°,∴△ACF∽△ECA,∴AC CFEC CA=,∴42442=,∴CF=8,即b=8.(3)ab=32.提示:由(2)知可证△ACF∽△ECA,∴∴AC CFEC CA=,∴4242a=,∴ab=32.3.已知正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF⊥BD 交BC 于F,连接DF,G 为DF 中点,连接EG,CG.(1) 求证:EG=CG;(2) 将图①中△BEF 绕B 点逆时针旋转 45∘,如图②所示,取DF 中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3) 将图①中△BEF 绕B 点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).【答案】解:(1)CG=EG(2)(1)中结论没有发生变化,即EG=CG.证明:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵ AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG.∴ AG=CG.在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG.∴ MG=NG在矩形AENM中,AM=EN.在Rt△AMG 与Rt△ENG中,∵ AM=EN, MG=NG,∴△AMG≌△ENG.∴ AG=EG∴ EG=CG.(3)(1)中的结论仍然成立.【解析】试题分析:(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.还知道EG⊥CG;试题解析:解:(1)证明:在Rt△FCD中,∵G为DF的中点,∴,同理,在Rt△DEF中,,∴CG=EG;(2)(1)中结论仍然成立,即EG=CG;连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点,如图所示:在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DC=DC,∴△DAG≌△DCG,∴AG=CG,在△DMG与△FNG中,∵∠DGM=∠FGN,DG=FG,∠MDG=∠NFG,∴△DMG≌△FNG,∴MG=NG,在矩形AENM中,AM=EN.,在Rt△AMG与Rt△ENG中,∵AM=EN,MG=NG,∴△AMG≌△ENG,∴AG=EG,∴EG=CG,(3)(1)中的结论仍然成立,即EG=CG且EG⊥CG。
几何综合(解析版)--中考数学抢分压轴题秘籍(全国通用)

几何综合--中考数学抢分秘籍(全国通用)几何综合问题在中考中以填空题和解答题的形式出现,考查难度较大.此类问题在中考中多考查面积平分、面积最值和几何变换的综合问题,一般要用到特殊三角形、特殊四边形、相似三角形、圆、锐角三角函数、勾股定理、图形变换的性质和二次函数的最值等相关知识,以及分类讨论、数形结合、转化与化归等数学思想.此类题型常涉及以下问题:①几何图形中的线段最值问题②探究图形面积的分割问题;③探究图形面积的最值问题.右图为几何综合问题中各题型的考查热度.题型1:线段最值问题①动点路径问题②“胡不归”问题③“将军饮马”问题④“造桥选址”问题解题模板:1.(2021秋•白云区校级月考)如图,正方形ABCD的边长为4,⊙O的半径为1.若⊙O在正方形ABCD内平移(⊙O可以与该正方形的边相切,则点A到⊙O上的点的距离的最大值为()A.B.C.D.【分析】由题意画出符合题意的图形,当⊙O与BC,CD相切时,点A到⊙O上的点的距离取得最大值,利用勾股定理即可求得结论.【解答】解:由题意,当⊙O与BC,CD相切时,点A到⊙O上的点的距离取得最大值,如图,由对称性可知:圆心O在AC上.AC==4.∵BC与⊙O相切于点E,∴OE⊥EC.∵四边形ABCD是正方形,∴∠ACB=45°.∴△OEC为等腰直角三角形.∴OC=OE=.∴CG=OC﹣OG=﹣1.∴AG=AC﹣CG=4﹣(﹣1)=3+1.故选:C.【点评】本题主要考查了切线的性质,正方形的性质,直线和圆的位置关系,勾股定理,连接OE,利用切线的性质得到OE⊥EC是解题的关键.【变式1-1】(2020•遵义)如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A、C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD、AB于点M、N,作射线DF交射线CA于点G.(1)求证:EF=DE;(2)当AF=2时,求GE的长.【分析】(1)要证明EF=DE,只要证明△DME≌△ENF即可,然后根据题目中的条件和正方形的性质,可以得到△DME≌△ENF的条件,从而可以证明结论成立;(2)根据勾股定理和三角形相似,可以得到AG和CG、CE的长,然后即可得到GE的长.【解答】(1)证明:∵四边形ABCD是正方形,AC是对角线,∴∠ECM=45°,∵MN∥BC,∠BCM=90°,∴∠NMC+∠BCM=180°,∠MNB+∠B=180°,∴∠NMC=90°,∠MNB=90°,∴∠MEC=∠MCE=45°,∠DME=∠ENF=90°,∴MC=ME,∵CD=MN,∴DM=EN,∵DE⊥EF,∠EDM+∠DEM=90°,∴∠DEF=90°,∴∠DEM+∠FEN=90°,∴∠EDM=∠FEN,在△DME和△ENF中,∴△DME≌△ENF(ASA),∴EF=DE;(2)解:如图1所示,由(1)知,△DME≌△ENF,∴ME=NF,∵四边形MNBC是矩形,∴MC=BN,又∵ME=MC,AB=4,AF=2,∴BN=MC=NF=1,∵∠EMC=90°,∴CE=,∵AF∥CD,∴△DGC∽△FGA,∴,∴,∵AB=BC=4,∠B=90°,∴AC=4,∵AC=AG+GC,∴AG=,CG=,∴GE=GC﹣CE==;如图2所示,同理可得,FN=BN,∵AF=2,AB=4,∴AN=1,∵AB=BC=4,∠B=90°,∴AC=4,∵AF∥CD,∴△GAF∽△GCD,∴,即,解得,AG=4,∵AN=NE=1,∠ENA=90°,∴AE=,∴GE=GA+AE=5.综上所述:GE的长为:,5.【点评】本题考查正方形的性质、全等三角形的判定与性质、三角形相似,解答本题的关键是明确题意,利用数形结合的思想解答.2.(2022春•广陵区期末)如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM=2,点P为线段BD上的一个动点,则MP+PB的最小值是4.【分析】过P点作PH⊥BC于H,过M点作MN⊥BC于N,如图,根据菱形的性质得到AB=BC,BO 平分∠ABC,AO⊥BD,再判断△ABC为等边三角形得到∠ABC=∠ACB=60°,则∠OBC=30°,所以PH=BP,则MP+PB=MP+PH,所以MP+PH的最小值为MN的长,然后利用含30度角的直角三角形三边的关系求出MN即可.【解答】解:过P点作PH⊥BC于H,过M点作MN⊥BC于N,如图,∵四边形ABCD为菱形,∴AB=BC,BO平分∠ABC,AO⊥BD,∵AB=AC=10,∴AB=AC=BC=10,∴△ABC为等边三角形,∴∠ABC=∠ACB=60°,∴∠OBC=30°,∴PH=BP,∴MP+PB=MP+PH,当M、P、H共线时,MP+PH的值最小,即MP+PH的最小值为MN的长,∵AM=2,∴CM=10﹣2=8,在Rt△MNC中,∵∠MCN=60°,∴CN=CM=4,∴MN=CN=4,即MP+PB的最小值为4.故答案为:.【点评】本题考查了胡不归问题:利用垂线段最短解决最短路径问题,把PB转化为PH是解决问题的关键.也考查了菱形的性质和等边三角形的性质.【变式2-1】(2021•郴州)如图,在△ABC中,AB=5,AC=4,sin A=,BD⊥AC交AC于点D.点P为线段BD上的动点,则PC+PB的最小值为.【分析】过点P作PE⊥AB于点E,过点C作CH⊥AB于点H,首先得出BD=4,AD=3,根据sin∠ABD=,得EP=,则PC+PB的最小值为PC+PE的最小值,即求CH的长,再通过等积法即可解决问题.【解答】解:过点P作PE⊥AB于点E,过点C作CH⊥AB于点H,∵BD⊥AC,∴∠ADB=90°,∵sin A==,AB=5,∴BD=4,由勾股定理得AD=,∴sin∠ABD=,∴EP=,∴PC+PB=PC+PE,即点C、P、E三点共线时,PC+PB最小,∴PC+PB的最小值为CH的长,=,∵S△ABC∴4×4=5×CH,∴CH=.∴PC+PB的最小值为.故答案为:.【点评】本题主要考查了锐角三角函数,垂线段最短、勾股定理等知识,将PC+PB的最小值转化为求CH的长,是解题的关键.3.(2022秋•朝阳区校级月考)如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且=,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的纵坐标为.【分析】根据已知条件得到AB=OB=4,∠AOB=45°,求得BC=3,OD=BD=2,得到D(2,0),C(4,3),作D关于直线OA的对称点E,连接EC交OA于P,则此时,四边形PDBC周长最小,E (0,2),求得直线EC的解析式为y=x+2,解方程组即可得到结论.【解答】解:∵∠OBA=90°,A(4,4),∴AB=OB=4,∠AOB=45°,∵=,点D为OB的中点,∴BC=3,OD=BD=2,∴D(2,0),C(4,3),作D关于直线OA的对称点E,连接EC交OA于P,则此时,四边形PDBC周长最小,E(0,2),∵直线OA的解析式为y=x,设直线EC的解析式为y=kx+b,则,解得:,∴直线EC的解析式为y=x+2,解,得,∴P(,),故答案为:.【点评】本题考查了轴对称﹣最短路线问题,等腰直角三角形的性质,正确的找到P点的位置是解题的关键.【变式3-1】(2021•聊城)如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x 轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为(﹣,0).【分析】在BC上截取BH=3,可证四边形BHEF是平行四边形,可得BF=EH,由对称性可得DE=D'E,则四边形BDEF的周长=EH+ED'+BD+EF,由EF和BD是定值,则当EH+D'E有最小值时,四边形BDEF 的周长有最小值,即当点E,点H,点D'共线时,EH+D'E有最小值,利用待定系数法可求HD'解析式,即可求解.【解答】解:在BC上截取BH=3,作点D关于x轴的对称点D',连接D'H交AO于点E,∴BH=EF=3,BC∥AO,∴四边形BHEF是平行四边形,∴BF=EH,∵点D与点D'关于x轴对称,∴DE=D'E,点D'坐标为(0,﹣4),∵四边形BDEF的周长=EF+BF+BD+DE,∴四边形BDEF的周长=EH+ED'+BD+EF,∵EF和BD是定值,∴当EH+D'E有最小值时,四边形BDEF的周长有最小值,∴当点E,点H,点D'共线时,EH+D'E有最小值,∵点B(﹣4,6),∴点H(﹣1,6),设直线D'H的解析式为y=kx+b,则,解得:,∴直线D'H的解析式为y=﹣10x﹣4,∴当y=0时,x=﹣,∴点E(﹣,0),故答案为:(﹣,0).【点评】本题考查了轴对称﹣最短路线问题,坐标与图形,平行四边形的判定和性质,一次函数的性质等知识,确定点E的位置是解题的关键.4.如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是.【分析】根据题意得出作EF∥AC且EF=,连接DF交AC于M,在AC上截取MN=,此时四边形BMNE的周长最小,进而利用相似三角形的判定与性质得出答案.【解答】解:作EF∥AC且EF=,连接DF交AC于M,在AC上截取MN=,延长DF交BC于P,作FQ⊥BC于Q,作出点E关于AC的对称点E′,则CE′=CE=1,将MN平移至E′F′处,则四边形MNE′F′为平行四边形,则当BM+EN=BM+FM=BF′时四边形BMNE的周长最小,由∠FEQ=∠ACB=45°,可求得FQ=EQ=1,∵∠DPC=∠FPQ,∠DCP=∠FQP,∴△PFQ∽△PDC,∴=,∴=,解得:PQ=,∴PC=,由对称性可求得tan∠MBC=tan∠PDC==.故答案为.【点评】此题主要考查了正方形的性质以及相似三角形的判定与性质,得出M,N的位置是解题关键.【变式4-1】如图,已知四边形ABCD四个顶点的坐标为A(1,3),B(m,0),C(m+2,0),D(5,1),当四边形ABCD的周长最小时,m的值为.【分析】因为AD,BC的长度都是固定的,所以求出AB+CD的长度就行了.问题就是AB+CD什么时候最短.把D点向左平移2个单位到D′点;作D′关于x轴的对称点D″,连接AD″,交x轴于P,从而确定C点位置,此时AB+CD最短.设直线AD″的解析式为y=kx+b,待定系数法求直线解析式.即可求得m的值.【解答】解:将C点向左平移2单位与B重合,点D向左平移2单位到D′(3,1),作D′关于x轴的对称点D″,根据作法知点D″(3,﹣1),设直线AD″的解析式为y=kx+b,则,解得k=﹣2,b=5.∴直线AD″的解析式为y=﹣2x+5.当y=0时,x=,即B(,0),m=.故答案为:.【点评】考查了轴对称﹣最短路线问题,关键是熟悉关于x轴的对称点,两点之间线段最短等知识.题型2:面积平分问题解题模板:技巧精讲1:利用中线平分图形面积的方法2.利用对称性平分图形面积的方法5.(1)问题提出:如图(1),在直角△ABC中,∠C=90°,AC=8,BC=6,点D为AC上一点且AD=2,过点D作直线DE交△ABC于点E,使得△ABC被分成面积相等的两部分,则DE的长为2.(2)类比发现:如图(2),五边形ABOCD,各顶点坐标为:A(3,4),B(0,2),O(0,0),C (4,0),D(4,2)请你找出一条经过顶点A的直线,将五边形ABOCD分为面积相等的两部分,求出该直线对应的函数表达式.(3)如图(3),王叔叔家有一块四边形菜地ABCD,他打算过D点修一条笔直的小路把四边形菜地ABCD 分成面积相等的两部分,分别种植不同的农作物,已知AB=AD=200米,BC=DC=200米,∠BAD =90°过点D是否存在一条直线将四边形ABCD的面积平分?若存在,求出平分该四边形面积的线段长:若不存在,请说明理由.【分析】(1)如图1中,取AC的中点F,连接BF,BD,作FE∥BD交BC于E,连接DE交BF于O.证明DE平分△ABC的面积,利用平行线分线段成比例定理求出CE即可解决问题.(2)如图2中,连接AO、AC,作BE∥AO交x轴于E,DF∥AC交x轴于F,EF的中点为M,则直线AM平分五边形ABCOD的面积,求出点M的坐标即可解决问题.(3)先求出四边形ABCD的面积,即可得出四边形ABQD的面积,从而求出QM,再用平行线分线段成比例定理求出BM,即可得出DM,最后用勾股定理即可.【解答】解:(1)如图1中,取AC的中点F,连接BF,BD,作FE∥BD交BC于E,连接DE交BF 于O.∵AF=FC,=S△BFC,∴S△AFB∵BD∥EF,=S△BDF,∴S△BDE=S△BOE,∴S△DFO=S四边形ABED,∴S△ECD∴DE平分△ABC的面积,∵AC=8,AD=2,∴AF=CF=4,DF=2,∵EF∥BD,∴=,∴=,∴CE=4,∴DE===2,故答案为2.(2)如图2中,连接AO、AC,作BE∥AO交x轴于E,DF∥AC交x轴于F,EF的中点为M,则直线AM平分五边形ABCOD的面积,∵直线AO的解析式为y=x,∴直线BE解析式为y=x+2,∴点E坐标(﹣,0),∵直线AC的解析式为y=﹣4x+16,∴直线DF的解析式为y=﹣4x+18,∴点F坐标为(,0)∴EF的中点M坐标为(,0),∴直线AM的解析式为:y=x﹣4.(3)如图3中,连接BD,AC交于点O.在BC上取一点Q,过Q作QM⊥BD,∵AB=AD=200、BC=CD=200,∴AC是BD的垂直平分线,在Rt△ABD中,BD=AB=200,∴DO=BO=OA=100,在Rt△BCO中,OC==300,=S△ABD+S△CBD=BD×(AO+CO)=×200×(100+300)=80000,∴S四边形ABCD∵在一条过点D的直线将筝形ABCD的面积二等分,=S四边形ABCD=40000,∴S四边形ABQD=×BD×OA=20000,∵S△ABD=BD×QM=×200×QM=100QM=S四边形ABQD﹣S△ABD=20000,∴S△QBD∴QM=100,∵QM∥CO.∴=,∴=,∴BM=,∴DM=BD﹣BM=,在Rt△MQD中,DQ===.【点评】此题是一次函数综合题,主要考查了等腰三角形的性质,三角形的中线,几何作图,勾股定理,等积问题等知识,解题的关键是把多边形转化为三角形是解决问题的关键,记住三角形的中线把三角形分成面积相等的两个三角形.【变式5-1】(2022•江北区模拟)新知学习:若一条线段把一个平面图形分成面积相等的两部分,我们把这条线段叫做该平面图形的二分线.解决问题:(1)①三角形的中线、高线、角平分线中,一定是三角形的二分线的是三角形的中线;②如图1,已知△ABC中,AD是BC边上的中线,点E,F分别在AB,DC上,连接EF,与AD交于=S△DGF,则EF是(填“是”或“不是”)△ABC的一条二分线.点G.若S△AEG(2)如图2,四边形ABCD中,CD平行于AB,点G是AD的中点,射线CG交射线BA于点E,取EB 的中点F,连接CF.求证:CF是四边形ABCD的二分线.(3)如图3,在△ABC中,AB=CB=CE=7,∠A=∠C,∠CBE=∠CEB,D,E分别是线段BC,AC上的点,且∠BED=∠A,EF是四边形ABDE的一条二分线,求DF的长.【分析】(1)①由平面图形的二分线定义可求解;②由面积的和差关系可得S△BEF=S△ABD=S△ABC,可得EF是△ABC的一条二分线;=S△CEF,由AB∥DC,G是AD的中点,证明△CDG≌△EAG,所(2)根据EB的中点F,所以S△CBF=S△CEF,所以S四边形AFCD=S△CBF,可得CF是四边形ABCD的二分线;以S四边形AFCD=S△DEC=S△ABE,可得S△HED=(3)延长CB使BH=CD,连接EH,通过全等三角形的判定可得S△BEHS四边形ABDE,即可得DF=DH=.【解答】解:(1)∵三角形的中线把三角形分成面积相等的两部分;∴三角形的中线是三角形的二分线,故答案为三角形的中线②∵AD是BC边上的中线=S△ACD=S△ABC,∴S△ABD=S△DGF,∵S△AEG+S△AEG=S四边形BDGE+S△DGF,∴S四边形BDGE=S△ABD=S△ABC,∴S△BEF∴EF是△ABC的一条二分线故答案为:是(2)∵EB的中点F,=S△CEF,∴S△CBF∵AB∥DC,∴∠E=∠DCG,∵G是AD的中点,∴DG=AG,在△CDG和△EAG中,∴△CDG≌△EAG(AAS),=S△DCG,∴S△AEG=S△CEF,∴S四边形AFCD=S△CBF,∴S四边形AFCD∴CF是四边形ABCD的二分线.(3)如图,延长CB使BH=CD,连接EH,AB=CB=CE=7,∠A=∠C,∠CBE=∠CEB,D,E分别是线段BC,AC上的点,且∠BED=∠A,∵BC=7∴BD+CD=7∴BD+BH=7=HD∵∠BED=∠A,∠BED+∠DEC=∠A+∠ABE∴∠ABE=∠CED,且AB=CE=7,∠A=∠C∴△ABE≌△CED(ASA)=S△EDC,∴AE=CD,BE=DE,∠AEB=∠EDC,S△ABE∴AE=BH,∵∠CBE=∠CEB∴∠AEB=∠EBH∴∠EBH=∠EDC,且BE=DE,BH=CD∴△BEH≌△DEC(SAS)、=S△DEC,∴S△BEH=S△DEC=S△ABE,∴S△BEH=S四边形ABDE,∴S△HED∵EF是四边形ABDE的一条二分线,=S四边形ABDE=S△HED,∴S△DEF∴DF=DH=【点评】本题是三角形综合题,考查了全等三角形的判定和性质,三角形中线的性质,平行线的性质,理解新定义是本题的关键.【变式5-2】(2021•西安一模)问题提出(1)如图①,在Rt△ABC中,∠A=90°,AB=3,AC=4,在BC上找一点D,使得AD将△ABC分成面积相等的两部分,作出线段AD,并求出AD的长度;问题探究(2)如图②,点A、B在直线a上,点M、N在直线b上,且a∥b,连接AN、BM交于点O,连接AM、BN,试判断△AOM与△BON的面积关系,并说明你的理由;解决问题(3)如图③,刘老伯有一个形状为筝形OACB的养鸡场,在平面直角坐标系中,O(0,0)、A(4,0)、B(0,4)、C(6,6),是否在边AC上存在一点P,使得过B、P两点修一道笔直的墙(墙的宽度不计),将这个养鸡场分成面积相等的两部分?若存在,请求出直线BP的表达式;若不存在,请说明理由.【分析】(1)当点D是BC的中点时,AD将△ABC分成面积相等的两部分,根据直角三角形斜边中线等于斜边的一般,可求出AD的长度;(2)根据同底等高的三角形面积相等,再减去相等的部分,就可以得出△AOM与△BON的面积相等;(3)连接AB,过点O作AB的平行线,交CA的延长线于点F,交OA于点G,则△OBG的面积等于△AFG的面积,则四边形OACB的面积转化为△BCF的面积,取CF的中点P,求出点P的坐标,即可求出直线BP的表达式.【解答】解:(1)如图①,取BC边的中点D,连接AD,则线段AD即为所求.在Rt△ABC中,∠BAC=90°,AB=3,AC=4,∴BC=,∵点D为BC的中点,∴AD=BC=.=S△BON,理由如下:(2)S△AOM=S△ABM﹣S△AOB,S△BON=S△ABN﹣S△AOB,由图可知,S△AOM如图②,过点M作MD⊥AB于点D,过点N作NE⊥AB于点E,∴MD∥NE,∠MDE=90°,又∵MN∥DE,∴四边形MDEN是矩形,∴MD=NE,=,S△ABN=,∵S△ABM=S△ABN,∴S△ABM=S△BON.∴S△AOM(3)存在,直线BP的表达式为:y=x+4.如图③,连接AB,过点O作OF∥AB,交CA的延长线于点F,交OA于点G,=S△AFG,由(2)的结论可知,S△OBG=S△BCF,∴S四边形OACB取CF的中点P,作直线BP,直线BP即为所求.∵A(4,0),B(0,4),C(6,6),∴线段AB所在直线表达式为:y=﹣x+4,线段AC所在直线的表达式为:y=3x﹣12,∴直线OF的表达式为:y=﹣x,联立,解得,∴F(3,﹣3),∵点P是CF的中点,∴P(,),∴直线BP的表达式为:y=x+4.【点评】主要考查了勾股定理,中点的性质,面积转化以及待定系数法求一次函数表达式等内容,熟练掌握勾股定理的内容,中点性质的应用,作出辅助线,进行面积的转化是解答本题的关键.题型3:面积最值问题6.(2019•无锡)如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为8.得到BM=CM=2,易证△AMB∽△CGB,求得GB=8,设BD=x,则DG=8﹣x,易证△EDH≌△DCG,EH=DG=8﹣x,所以S△BDE===,当x=4时,△BDE面积的最大值为8.【解答】解:过点C作CG⊥BA于点G,作EH⊥AB于点H,作AM⊥BC于点M.∵AB=AC=5,BC=4,∴△AMB∽△CGB,∴,∴GB=8,设BD=x,则DG=8﹣x,∵ED=DC,∠EHD=∠DGC,∠HED=∠GDC,∴△EDH≌△DCG(AAS),∴EH=DG=8﹣x,===,∴S△BDE当x=4时,△BDE面积的最大值为8.故答案为8.【点评】本题考查了正方形,熟练运用正方形的性质与相似三角形的判定与性质以及全等三角形的判定与性质是解题的关键.;【变式6-1】(1)如图①,若BC=6,AC=4,∠C=60°,求△ABC的面积S△ABC;(2)如图②,若BC=a,AC=b,∠C=α,求△ABC的面积S△ABC(3)如图③,四边形ABCD,AC=m,BD=n,对角线AC交于O点,他们所成锐角为β,求四边形ABCD .的面积S四边形ABCD【分析】(1)过A作AM⊥BC于M,解直角三角形求出AM,再根据三角形面积公式求出即可;(2)过A作AM⊥BC于M,解直角三角形求出AM,再根据三角形面积公式求出即可;(3)过A作AE⊥BD于E,过C作CF⊥BD于F,解直角三角形求出AE、CF,根据三角形面积公式求出即可.【解答】解:(1)如图①,过A作AM⊥BC于M,则∠AMC=90°,∵∠C=60°,AC=4,∴AM=AC×sin60°=4×=2,∵BC=6,=×BC×AM=×6×2=6;∴△ABC的面积S△ABC(2)如图②,过A作AM⊥BC于M,则∠AMC=90°,∵∠C=α,AC=b,∴AM=AC×sinα=b×sinα=b sinα,∵BC=a,=×BC×AM=×a×b sinα=ab sinα;∴△ABC的面积S△ABC(3)如图3,过A作AE⊥BD于E,过C作CF⊥BD于F,BD=n,OA+OC=m,∵AC、BD夹角为β,∴AE=OA•sinβ,CF=OC•sinβ,=S△ABD+S△BDC∴S四边形ABCD=BD•AE+BD•CF=BD•(AE+CF)=BD•(OA•sinβ+OC•sinβ)=BD•AC•sinβ=mn sinβ.=mn sinβ.即四边形ABCD的面积S四边形ABCD【点评】本题考查了解直角三角形,三角形的面积的应用,此题比较难,解题时关键要找对思路,即原四边形的高已经发生了变化,只要把高求出来,一切将迎刃而解.【变式6-2】如图,正方形ABCD的边长为2,动点E从点A出发,沿边AB﹣BC向终点C运动,以DE为边作正方形DEFG(点D、E、F、G按顺时针方向排列).设点E运动的速度为每秒1个单位,运动的时间为x秒.(1)如图1,当点E在AB上时,求证:点G在直线BC上;(2)设正方形ABCD与正方形DEFG重叠部分的面积为S,求S与x之间的函数关系式;(3)直接写出整个运动过程中,点F经过的路径长.【分析】(1)由正方形的性质得出AD=CD,DE=DG,∠ADE+∠EDC=∠EDC+∠CDG=90°,证出∠ADE=∠CDG,由SAS证明△ADE≌△CDG,得出∠DCG=∠DAE=90°,证出∠DCG+∠DCB=180°,即可得出结论;(2)分情况讨论:①当点E在AB边上时,过点E作EK∥AD,交CD于点K,则AC∥EK∥AD,证明△ADE∽△BEH,由相似三角形的性质得出=,求出BH=,S=正方形ABCD的面积﹣△ADE的面积﹣△BEH的面积,即可得出结果;②当点E在BC边上时,S=△DEC的面积=4﹣x;(3)由(1)知,当点E在AB上时,点G在直线BC上,当点E与B点重合时,点F的位置如图2所示:点F运动的路径为BF;同理,点E在BC上时,当点E与C点重合时,点F运动的路径为FG;由勾股定理求出BD,即可得出结果.【解答】(1)证明:∵四边形ABCD与四边形DEFG都是正方形,∴AD=CD,DE=DG,∠ADE+∠EDC=∠EDC+∠CDG=90°,∴∠ADE=∠CDG,在△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴∠DCG=∠DAE=90°,∵∠DCB=90°,∴∠DCG+∠DCB=180°,∴点G在直线BC上;(2)解:①当点E在AB边上时,过点E作EK∥AD,交CD于点K,如图1所示:则AC∥EK∥AD,∴∠HEK=∠EHB,∠DEK=∠EDA,∵∠EHB+∠BEH=90°,∠EDA+∠AED=90°,∠HEK+∠DEK=90°,∴∠EDA=∠BEH,∠AED=∠EHB,∴△ADE∽△BEH,∴=,即=,∴BH=,S=正方形ABCD的面积﹣△ADE的面积﹣△BEH的面积=2×2﹣×2×x﹣×(2﹣x)×=;②当点E在BC边上时,S=△DEC的面积=×2×(4﹣x)=4﹣x;(3)解:由(1)知,当点E在AB上时,点G在直线BC上,当点E与B点重合时,点F的位置如图2所示:点F运动的路径为BF;同理,点E在BC上时,当点E与C点重合时,点F运动的路径为FG;∵BD===2,∴BF+FG=2BD=4,∴点F运动的路径长为4.【点评】本题是四边形综合题目,考查了正方形的性质、平行线的判定与性质、三角形面积的计算、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识;熟练掌握正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质是解决问题的关键.1.如图,在边长为6的菱形ABCD中,∠BCD=60°,连接BD,点E、F分别是边AB、BC上的动点,且AE=BF,连接DE、DP、EF.(1)如图①,当点E是边AB的中点时,求∠EDF的度数;(2)如图②,当点E是边AB上任意一点时,∠EDF的度数是否发生改变?若不改变,请证明;若发生改变,请说明理由;(3)若点P是线段BD上一动点,求PF+DP的最小值.【分析】(1)由菱形的性质可得AB=BC=CD=AD=6,∠BCD=∠BAD=60°,可证△ABD,△BCD 是等边三角形,由等边三角形的性质可证DE=DF,∠EDF=60°,可得结论;(2)证明△ADE≌△BDF(SAS),根据全等三角形的性质得∠ADE=∠BDF,由角的和差即可得∠EDF =∠ADB=60°;(3)过点P作PG⊥AD于点G,连接PF,过点F作FG′⊥AD于点G′,交BD于点P′,可得GP=DP•sin60°=DP,则PF+DP=PF+GP,当点F、P、G三点共銭,且FG⊥AD时,PF+GP有最小值,最小值为FG′的长,过点D作DH⊥BC于点H,则DH=FG',PF+DP的最小值即为DH的长,由△BDC是等边三角形可得DH=CD•sin60°=3,即可求得PF+DP的最小值.【解答】解:(1)∵四边形ABCD是菱形,边长为6,∴AB=BC=CD=AD=6,∠BCD=∠BAD=60°,∴△ABD,△BCD是等边三角形,∵点E是边AB的中点,AE=BF,∴点F是边BC的中点,∴∠ADE=∠BDE=∠BDF=∠CDF=30°,∴∠EDF=∠BDE+∠BDF=60°;(2)∠EDF的度数不改变,证明:△ABD,△BCD是等边三角形,∴AD=BD,∠DAB=∠DBC=60°,∵AE=BF,∴△ADE≌△BDF(SAS),∴∠ADE=∠BDF,∴∠EDF=∠ADB=60°;(3)如图,过点P作PG⊥AD于点G,连接PF,过点F作FG′⊥AD于点G′,交BD于点P′,∵∠ADB=60°,∴GP=DP•sin60°=DP,∴PF+DP=PF+GP,∴当点F、P、G三点共銭,且FG⊥AD时,PF+GP有最小值,最小值为FG′的长,过点D作DH⊥BC于点H,∵四边形ABCD是菱形,∴DH=FG',∴PF+DP的最小值即为DH的长,∵DH⊥BC,△BDC是等边三角形,∴DH=CD•sin60°=3,∴PF+DP的最小值为3.【点评】本题考查了四边形的综合应用,掌握菱形的性质,等边三角形的判定和性质,全等三角形的判定和性质,最短路径等知识,添加恰当辅助线构造构造在直角三角形是解本题的关键.2.(2022•连云港)如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,且BE⊥DC.(1)求证:四边形DBCE为菱形;(2)若△DBC是边长为2的等边三角形,点P、M、N分别在线段BE、BC、CE上运动,求PM+PN的最小值.【分析】(1)先证明四边形DBCE是平行四边形,再由BE⊥DC,得四边形DBCE是菱形;(2)作N关于BE的对称点N',过D作DH⊥BC于H,由菱形的对称性知,点N关于BE的对称点N'在DE上,可得PM+PN=PM+PN',即知MN'的最小值为平行线间的距离DH的长,即PM+PN的最小值为DH的长,在Rt△DBH中,可得DH=DB•sin∠DBC=,即可得答案.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵DE=AD,∴DE=BC,∵E在AD的延长线上,∴DE∥BC,∴四边形DBCE是平行四边形,∵BE⊥DC,∴四边形DBCE是菱形;(2)解:作N关于BE的对称点N',过D作DH⊥BC于H,如图:由菱形的对称性知,点N关于BE的对称点N'在DE上,∴PM+PN=PM+PN',∴当P、M、N'共线时,PM+PN'=MN'=PM+PN,∵DE∥BC,∴MN'的最小值为平行线间的距离DH的长,即PM+PN的最小值为DH的长,在Rt△DBH中,∠DBC=60°,DB=2,∴DH=DB•sin∠DBC=2×=,∴PM+PN的最小值为.【点评】本题考查平行四边形性质及应用,涉及菱形的判定,等边三角形性质及应用,对称变换等,解题的关键是掌握解决“将军饮马”模型的方法.3.(2014•海南)如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.【分析】(1)利用待定系数法求出抛物线的解析式;(2)首先求出四边形MEFP面积的表达式,然后利用二次函数的性质求出最值及点P坐标;(3)四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.如答图3所示,将点M向右平移1个单位长度(EF的长度),得M1(1,1);作点M1关于x 轴的对称点M2,则M2(1,﹣1);连接PM2,与x轴交于F点,此时ME+PF=PM2最小.【解答】方法一:解:(1)∵对称轴为直线x=2,∴设抛物线解析式为y=a(x﹣2)2+k.将A(﹣1,0),C(0,5)代入得:,解得,∴y=﹣(x﹣2)2+9=﹣x2+4x+5.(2)当a=1时,E(1,0),F(2,0),OE=1,OF=2.设P(x,﹣x2+4x+5),如答图2,过点P作PN⊥y轴于点N,则PN=x,ON=﹣x2+4x+5,∴MN=ON﹣OM=﹣x2+4x+4.S四边形MEFP=S梯形OFPN﹣S△PMN﹣S△OME=(PN+OF)•ON﹣PN•MN﹣OM•OE=(x+2)(﹣x2+4x+5)﹣x•(﹣x2+4x+4)﹣×1×1=﹣x2+x+=﹣(x﹣)2+∴当x=时,四边形MEFP的面积有最大值为,把x=时,y=﹣(﹣2)2+9=.此时点P坐标为(,).(3)∵M(0,1),C(0,5),△PCM是以点P为顶点的等腰三角形,∴点P的纵坐标为3.令y=﹣x2+4x+5=3,解得x=2±.∵点P在第一象限,∴P(2+,3).四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.如答图3,将点M向右平移1个单位长度(EF的长度),得M1(1,1);作点M1关于x轴的对称点M2,则M2(1,﹣1);连接PM2,与x轴交于F点,此时ME+PF=PM2最小.设直线PM2的解析式为y=mx+n,将P(2+,3),M2(1,﹣1)代入得:,解得:m=,n=﹣,∴y=x﹣.当y=0时,解得x=.∴F(,0).∵a+1=,∴a=.∴a=时,四边形PMEF周长最小.方法二:(1)略.(2)连接MF,过点P作x轴垂线,交MF于点H,有最大值时,四边形MEFP面积最大.显然当S△PMF当a=1时,E(1,0),F(2,0),∵M(0,1),∴l MF:y=﹣x+1,设P(t,﹣t2+4t+5),H(t,﹣t+1),=(P Y﹣H Y)(F X﹣M X),∴S△PMF=(﹣t2+4t+5+t﹣1)(2﹣0)=﹣t2+t+4,∴S△PMF最大值为,∴当t=时,S△PMF=EF×MY=×1×1=,∵S△MEF的最大值为+=,∴S四边形MEFP∴P(,).(3)∵M(0,1),C(0,5),△PCM是以点P为顶点的等腰三角形,∴点P的纵坐标为3,∴﹣x2+4x+5=0,解得:x=2±,∵点P在第一象限,∴P(2+,3),PM、EF长度固定,当ME+PF最小时,PMEF的周长取得最小值,将点M向右平移1个单位长度(EF的长度),得M1(1,1),∵四边形MEFM1为平行四边形,∴ME=M1F,作点M1关于x轴的对称点M2,则M2(1,﹣1),∴M2F=M1F=ME,当且仅当P,F,M2三点共线时,此时ME+PF=PM2最小,∵P(2+,3),M2(1,﹣1),F(a+1,0),∴K PF=K M1F,∴,∴a=.【点评】本题是二次函数综合题,第(1)问考查了待定系数法;第(2)问考查了图形面积计算以及二次函数的最值;第(3)问主要考查了轴对称﹣最短路线的性质.试题计算量偏大,注意认真计算.4.(2021•靖江市校级一模)如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,若AE=2,则求EF的长.(请从“线段的长度或线段的位置关系”的方向设计条件及问题,并解答)【分析】过点A和点E作AG⊥BC,EH⊥BC于点G和H,可得矩形AGHE,再根据菱形ABCD中,AB=6,∠B=60°,可得BG=3,AG=3=EH,由题意可得,FH=FC﹣HC=2﹣1=1,进而根据勾股定理可得EF的长.【解答】若AE=2.则求EF的长.解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,在菱形ABCD中,AB=6,∠B=60°,∴BG=3,AG=3=EH,∴HC=BC﹣BG﹣GH=6﹣3﹣2=1,∵EF平分菱形面积,EF经过菱形对角线交点,∴FC=AE=2,∴FH=FC﹣HC=2﹣1=1,在Rt△EFH中,根据勾股定理,得:EF===2.【点评】本题考查了菱形的性质,勾股定理,矩形的性质,解决本题的关键是掌握菱形的性质.5.(2012•新密市自主招生)如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=4,则△DEF面积的最大值为.【分析】首先过点F作FG⊥AD,交AD的延长线于点G,由菱形ABCD的边长为4,∠BAD=60°,即=DE•FG)=﹣(x﹣2)2+,可求得AD=CD=4,∠FDG=60°,然后设AE=x,即可得S△DEF然后根据二次函数的性质,即可求得答案.【解答】解:过点F作FG⊥AD,交AD的延长线于点G,∵菱形ABCD边长为4,∠BAD=60°,∴AD=CD=4,∠ADC=180°﹣∠BAD=120°,∴∠FDG=180°﹣∠ADB=60°,设AE=x,∵AE+CF=4,∴CF=4﹣x;∴DE=AD﹣AE=4﹣x,DF=CD﹣CF=4﹣(4﹣x)=x,在Rt△DFG中,FG=DF•sin∠GDF=x,=DE•FG=×(4﹣x)×x=﹣x2+x=﹣(x2﹣4x)=﹣(x﹣2)2+,∴S△DEF∴当x=2时,△DEF面积的最大,最大值为.故答案为:.【点评】此题考查了菱形的性质、三角函数的性质以及二次函数的最值问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与函数思想的应用.6.(2022•杭州模拟)将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.(1)如图1,当α=60°时,△DEB′的形状为等腰直角三角形,连接BD,BB′与CE的数量关系是BB'=CE.(2)当0°<α<360°且a≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点E,C,D,B′为顶点的四边形是平行四边形时,请直接写出BE与B′E的数量关系.。
题型十一 综合探究题 类型四 与旋转有关的探究题(专题训练)(解析版)

题型十一综合探究题类型四与旋转有关的探究题(专题训练)D为BC的中点,E,F分1.(2022·重庆市B卷)在△ABC中,∠BAC=90°,AB=AC=别为AC,AD上任意一点,连接EF,将线段EF绕点E顺时针旋转90°得到线段EG,连接FG,AG.(1)如图1,点E与点C重合,且GF的延长线过点B,若点P为FG的中点,连接PD,求PD的长;(2)如图2,EF的延长线交AB于点M,点N在AC上,∠AGN=∠AEG且GN=MF,求证:AM+AF=;(3)如图3,F为线段AD上一动点,E为AC的中点,连接BE,H为直线BC上一动点,连接EH,将△BEH沿EH翻折至△ABC所在平面内,得到△B′EH,连接B′G,直接写出线段B′G的长度的最小值.【答案】(1)解:如图1,连接CP,由旋转知,CF=CG,∠FCG=90°,∴△FCG为等腰直角三角形,∵点P是FG的中点,∴CP⊥FG,∵点D是BC的中点,BC,∴DP=12在Rt△ABC中,AB=AC==4,∴BC=∴DP=2;(2)证明:如图2,过点E作EH⊥AE交AD的延长线于H,∴∠AEH=90°,由旋转知,EG=EF,∠FEG=90°,∴∠FEG=∠AEH,∴∠AEG=∠HEF,∵AB=AC,点D是BC的中点,∴∠BAD=∠CAD=1∠BAC=45°,2∴∠H=90°―∠CAD=45°=∠CAD,∴AE=HE,∴△EGA≌△EFH(SAS),∴AG=FH,∠EAG=∠H=45°,∴∠EAG=∠BAD=45°,∵∠AMF=180°―∠BAD―∠AFM=135°―∠AFM,∵∠AFM=∠EFH,∴∠AMF=135°―∠EFH,∵∠HEF=180°―∠EFH―∠H=135°―∠EFH,∴∠AMF=∠HEF,∵△EGA≌△EFH,∴∠AEG=∠HEF,∵∠AGN=∠AEG,∴∠AGN=∠HEF,∴∠AGN=∠AMF,∵GN=MF,∴△AGN≌△AMF(AAS),∴AG=AM,∵AG=FH,∴AM=FH,∴AF +AM =AF +FH =AH;(3)解:∵点E 是AC 的中点,∴AE =12AC 根据勾股定理得,BE ==由折叠直,BE =B′E∴点B′是以点E由旋转知,EF =EG ,∴点G 是以点E 为圆心,EG 为半径的圆上,∴B′G 的最小值为B′E ―EG ,要B′G 最小,则EG 最大,即EF 最大,∵点F 在AD 上,∴点在点A 或点D 时,EF∴线段B′G2.(湖南省郴州市2021年中考数学试卷)如图1,在等腰直角三角形ABC 中,90BAC Ð=°.点E ,F 分别为AB ,AC 的中点,H 为线段EF 上一动点(不与点E ,F 重合),将线段AH 绕点A 逆时针方向旋转90°得到AG ,连接GC ,HB .(1)证明:AHB AGC V V ≌;(2)如图2,连接GF ,HC ,AF 交AF 于点Q .①证明:在点H 的运动过程中,总有90HFG Ð=°;②若4AB AC ==,当EH 的长度为多少时,AQG V 为等腰三角形?【答案】(1)见详解;(2)①见详解;②当EH 的长度为2时,AQG V 为等腰三角形【分析】(1)由旋转的性质得AH=AG ,∠HAG=90°,从而得∠BAH=∠CAG ,进而即可得到结论;(2)①由AHB AGC V V ≌,得AH=AG ,再证明AEH AFG V V ≌,进而即可得到结论;②AQG V 为等腰三角形,分3种情况:(a )当∠QAG=∠QGA=45°时,(b )当∠GAQ=∠GQA=67.5°时,(c )当∠AQG=∠AGQ=45°时,分别画出图形求解,即可.【详解】解:(1)∵线段AH 绕点A 逆时针方向旋转90°得到AG ,∴AH=AG ,∠HAG=90°,∵在等腰直角三角形ABC 中,90BAC Ð=°,AB=AC ,∴∠BAH=90°-∠CAH=∠CAG ,∴AHB AGC V V ≌;(2)①∵在等腰直角三角形ABC 中,AB=AC ,点E ,F 分别为AB ,AC 的中点,∴AE=AF ,AEF V 是等腰直角三角形,∵AH=AG ,∠BAH =∠CAG ,∴AEH AFG V V ≌,∴∠AEH=∠AFG=45°,∴∠HFG=∠AFG+∠AFE=45°+45°=90°,即:90HFG Ð=°;②∵4AB AC ==,点E ,F 分别为AB ,AC 的中点,∴AE=AF=2,∵∠AGH=45°,AQG V 为等腰三角形,分3种情况:(a )当∠QAG=∠QGA=45°时,如图,则∠HAF=90°-45°=45°,∴AH 平分∠EAF ,∴点H 是EF 的中点,∴12==(b)当∠GAQ=∠GQA=(180°-45°)÷2=67.5°时,如图,则∠EAH=∠GAQ=67.5°,∴∠EHA=180°-45°-67.5°=67.5°,∴∠EHA=∠EAH,∴EH=EA=2;(c)当∠AQG=∠AGQ=45°时,点H与点F重合,不符合题意,舍去,V为等腰三角形.综上所述:当EH的长度为2时,AQG【点睛】本题主要考查等腰直角三角形的性质,旋转的性质,全等三角形的判定和性质,勾股定理,熟练掌握全等三角形的判定定理,根据题意画出图形,进行分类讨论,是解题的关键.3.(2021·四川中考真题)在等腰ABC V 中,AB AC =,点D 是BC 边上一点(不与点B 、C 重合),连结AD .(1)如图1,若60C Ð=°,点D 关于直线AB 的对称点为点E ,结AE ,DE ,则BDE Ð=________;(2)若60C Ð=°,将线段AD 绕点A 顺时针旋转60°得到线段AE ,连结BE .①在图2中补全图形;②探究CD 与BE 的数量关系,并证明;(3)如图3,若AB AD k BC DE==,且ADE C Ð=Ð,试探究BE 、BD 、AC 之间满足的数量关系,并证明.【答案】(1)30°;(2)①见解析;②CD BE =;见解析;(3)()AC k BD BE =+,见解析【分析】(1)先根据题意得出△ABC 是等边三角形,再利用三角形的外角计算即可(2)①按要求补全图即可②先根据已知条件证明△ABC 是等边三角形,再证明AEB ADC △≌△,即可得出CD BE=(3)先证明AC BC AD DE=,再证明ACB ADE △∽△,得出BAC EAD Ð=Ð,从而证明AEB ADC △≌△,得出BD BE BC +=,从而证明()AC k BD BE =+【详解】解:(1)∵AB AC =,60C Ð=°∴△ABC 是等边三角形∴∠B=60°∵点D 关于直线AB 的对称点为点E∴AB ⊥DE ,∴BDE Ð=30°故答案为:30°;(2)①补全图如图2所示;②CD 与BE 的数量关系为:CD BE =;证明:∵AB AC =,60BAC Ð=°.∴ABC V 为正三角形,又∵AD 绕点A 顺时针旋转60°,∴AD AE =,60EAD Ð=°,∵60BAD DAC Ð+Ð=°,60BAD BAE Ð+Ð=°,∴BAE DAC Ð=Ð,∴AEB ADC △≌△,∴CD BE =.(3)连接AE .∵AB AD k BC DE ==,AB AC =,∴AC AD BC DE=.∴AC BC AD DE =.又∵ADE C Ð=Ð,∴ACB ADE △∽△,∴BAC EAD Ð=Ð.∵AB AC =,∴AE AD =,∴BAD DAC BAD BAE Ð+Ð=Ð+Ð,∴DAC BAE Ð=Ð,∴AEB ADC △≌△,CD BE =.∵BD DC BC +=,∴BD BE BC +=.又∵AC k BC=,∴()AC k BD BE =+.【点睛】本题考查相似三角形的证明及性质、全等三角形的证明及性质、三角形的外角、轴对称,熟练进行角的转换是解题的关键,相似三角形的证明是重点4.(2021·浙江嘉兴市·中考真题)小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD 绕点A 顺时针旋转()090αα°<≤°,得到矩形'''AB C D [探究1]如图1,当90α=°时,点'C 恰好在DB 延长线上.若1AB =,求BC 的长.[探究2]如图2,连结'AC ,过点'D 作'//'D M AC 交BD 于点M .线段'D M 与DM 相等吗?请说明理由.[探究3]在探究2的条件下,射线DB 分别交'AD ,'AC 于点P ,N (如图3),MN ,PN 存在一定的数量关系,并加以证明.【答案】[探究1]BC =;[探究2]'D M DM =,证明见解析;[探究3]2MN PN DN =×,证明见解析【分析】[探究1] 设BC x =,根据旋转和矩形的性质得出''//D C DA ,从而得出''D C B ADB D D ∽,得出比例式'''D C D B AD AB=,列出方程解方程即可;[探究2] 先利用SAS 得出''AC D DBA D D ≌,得出'DAC ADB Ð=Ð,'ADB AD M Ð=Ð,再结合已知条件得出''MDD MD D Ð=Ð,即可得出'D M DM =;[探究3] 连结AM ,先利用SSS 得出ADM ADM D D ≌,从而证得MN AN =,再利用两角对应相等得出NPA NAD D D ∽,得出PN AN AN DN=即可得出结论.【详解】[探究1]如图1,设BC x =.∵矩形ABCD 绕点A 顺时针旋转90°得到矩形'''AB C D ,∴点A ,B ,'D 在同一直线上.∴'AD AD BC x ===,'1DC AB AB ===,∴''1D B AD AB x =-=-.∵'90BAD D Ð=Ð=°,∴//D C DA ¢¢.又∵点'C 在DB 延长线上,∴''D C B ADB D D ∽,∴''D C AD 1x =解得1x =2x (不合题意,舍去)∴BC =[探究2] 'D M DM =.证明:如图2,连结'DD .∵'//'D M AC ,∴'''AD M D AC Ð=Ð.∵'AD AD =,''90AD C DAB Ð=Ð=°,''D C AB =,∴()''AC D DBA SAS D D ≌.∴'D AC ADB ¢Ð=Ð,'ADB AD M Ð=Ð,∵AD AD =,''ADD AD D Ð=Ð,∴''MDD MD D Ð=Ð,∴'D M DM =.[探究3]关系式为2MN PN DN =×.证明:如图3,连结AM .∵'D M DM =,'AD AD =,AM AM =,∴()ADM AD M SSS ¢D D ≌.∴'MAD MAD Ð=Ð,∵AMN MAD NDA Ð=Ð+Ð,'NAM MAD NAP Ð=Ð+Ð,∴AMN NAM Ð=Ð,∴MN AN =.在NAP D 与NDA D 中,ANP DNA Ð=Ð,NAP NDA Ð=Ð,∴NPA NAD D D ∽,∴PN AN AN DN=,∴2AN PN DN =×.∴2MN PN DN =×.【点睛】本题考查了矩形的性质,旋转的性质,全等三角形的判定和性质,相似三角形的判定和性质,解一元二次方程等,解题的关键是灵活运用这些知识解决问题.5.(2021·浙江中考真题)如图,在菱形ABCD 中,ABC Ð是锐角,E 是BC 边上的动点,将射线AE 绕点A 按逆时针方向旋转,交直线CD 于点F .(1)当AE BC EAF ABC ,^Ð=Ð时,①求证:AE AF =;②连结BD EF ,,若25EF BD =,求ABCDn AEF菱形SS的值;(2)当12EAF BAD Ð=Ð时,延长BC 交射线AF 于点M ,延长DC 交射线AE 于点N ,连结AC MN ,,若42AB AC ==,,则当CE 为何值时,AMN V 是等腰三角形.【答案】(1)①见解析;②825;(2)当43CE =或2或45时,AMN V 是等腰三角形.【分析】(1)根据菱形的性质得到边相等,对角相等,根据已知条件证明出BAE DAF Ð=Ð,得到ABE ADF V V ≌,由=AE AF ,CE CF =,得到AC 是EF 的垂直平分线,得到//EF BD ,CEF CBD ∽△△,再根据已知条件证明出AEF BAC V V ∽,算出面积之比;(2)等腰三角形的存在性问题,分为三种情况:当AM AN =时,ANC MAC V V ≌,得到CE=43;当NA NM =时,CEN BEA V V ≌,得到CE=2;当=MA MN 时,CEN BEA ∽△△,得到CE=45.【详解】(1)①证明:在菱形ABCD 中,//AB AD ABC ADC AD BC ,,=Ð=Ð,AE BC AE AD Q ,^\^,90ABE BAE EAF DAF \Ð+Ð=Ð+Ð=°,,EAF ABC BAE DAF Ð=Ð\Ð=ÐQ ,∴ABE ADF V V ≌(ASA),∴=AE AF .②解:如图1,连结AC .由①知,ABE ADF BE DF CE CF V V ≌,,\=\=,AE AF AC EF Q ,=\^.在菱形ABCD 中,//AC BD EF BD CEF CBD V V ,,∽^\\,∴25EC EF BC BD ==,设=2EC a ,则534AB BC a BE a AE a ,,===\=.AE AF AB BC EAF ABC Q ,,==Ð=Ð,∴AEF BAC V V ∽,∴22625=415AEF BAC S AE a S AB a V V æöæöç÷ç÷==ç÷ç÷èøèø,∴1168222525AEF AEF BAC ABCD S S S S V V V 菱形==´=. (2)解:在菱形ABCD 中,1122BAC BAD EAF BAD Q ,Ð=ÐÐ=Ð,BAC EAF BAE CAM ,\Ð=Ð\Ð=Ð,//C AB CD BAE AN ANC CAM Q ,,\Ð=Ð\Ð=Ð,同理,AMC NAC Ð=Ð,∴AC AM MAC ANC CN NAV V ∽,\=.AMN V 是等腰三角形有三种情况:①如图2,当AM AN =时,ANC MAC V V ≌,2CN AC \==,//AB CN CEN BEA Q V V ,∽\,142CE CN AB BE AB Q ,=\==,14433BC CE BC Q ,=\==.②如图3,当NA NM =时,NMA NAM BAC BCA Ð=Ð=Ð=Ð,12AM AC ANM ABC AN AB V V ∽,\==,24CN AC CEN BEA V V ,≌\==\,∴122CE BE BC ===.③如图4,当=MA MN 时,MNA MAN BAC BCA AMN ABC V V ,∽Ð=Ð=Ð=Ð\,1212AM AB CN AC AN AC ,\==\==,14CE CN CEN BEA BE AB QV V ∽,\==,1455CE BC \==.综上所述,当43CE =或2或45时,AMN V 是等腰三角形.【点睛】本题主要考查了菱形的基本性质、相似三角形的判定与性质、菱形中等腰三角形的存在性问题,解决本题的关键在于画出三种情况的等腰三角形(利用两圆一中垂),通过证明三角形相似,利用相似比求出所需线段的长.6.(2020·山东中考真题)在等腰△ABC 中,AC =BC ,ADE V 是直角三角形,∠DAE =90°,∠ADE =12∠ACB ,连接BD ,BE ,点F 是BD 的中点,连接CF .(1)当∠CAB =45°时.①如图1,当顶点D 在边AC 上时,请直接写出∠EAB 与∠CBA 的数量关系是 .线段BE 与线段CF 的数量关系是 ;②如图2,当顶点D 在边AB 上时,(1)中线段BE 与线段CF 的数量关系是否仍然成立?若成立,请给予证明,若不成立,请说明理由;学生经过讨论,探究出以下解决问题的思路,仅供大家参考:思路一:作等腰△ABC 底边上的高CM ,并取BE 的中点N ,再利用三角形全等或相似有关知识来解决问题;思路二:取DE 的中点G ,连接AG ,CG ,并把CAG V 绕点C 逆时针旋转90°,再利用旋转性质、三角形全等或相似有关知识来解快问题.(2)当∠CAB =30°时,如图3,当顶点D 在边AC 上时,写出线段BE 与线段CF 的数量关系,并说明理由.【答案】(1)①EAB ABC Ð=Ð,12CF BE =;②仍然成立,证明见解析;(2)BE =,理由见解析.【分析】(1)①如图1中,连接BE ,设DE 交AB 于T .首先证明,,AD AE BD BE ==再利用直角三角形斜边中线的性质解决问题即可.②解法一:如图2﹣1中,取AB 的中点M ,BE 的中点N ,连接CM ,MN .证明CMF BMN V V ≌(SAS ),可得结论.解法二:如图2﹣2中,取DE 的中点G ,连接AG ,CG ,并把CAG V 绕点C 逆时针旋转90°得到CBT V ,连接DT ,GT ,BG .证明四边形BEGT 是平行四边形,四边形DGBT 是平行四边形,可得结论.(2)结论:BE =.如图3中,取AB 的中点T ,连接CT ,FT .证明BAE CTF V V ∽,可得结论.【详解】解:(1)①如图1中,连接BE ,设DE 交AB 于T .∵CA=CB,∠CAB=45°,∴∠CAB=∠ABC=45°,∴∠ACB=90°,∵∠ADE=12∠ACB=45°,∠DAE=90°,∴∠ADE=∠AED=45°,∴AD=AE,90,DAEÐ=°Q45, EAB DAT ABC\Ð=Ð=Ð=°∴AT⊥DE,DT=ET,∴AB垂直平分DE,∴BD=BE,∵∠BCD=90°,DF=FB,∴CF=12BD,∴CF=12BE.故答案为:∠EAB=∠ABC,CF=12BE.②结论不变.解法一:如图2﹣1中,取AB的中点M,BE的中点N,连接CM,MN.∵∠ACB =90°,CA =CB ,AM =BM ,∴CM ⊥AB ,CM =BM =AM ,由①得:,AD AE =设AD =AE =y .FM =x ,DM =a ,Q 点F 是BD 的中点,则DF =FB =a+x ,∵AM =BM ,∴y+a =a+2x ,∴y =2x ,即AD =2FM ,∵AM =BM ,EN =BN ,∴AE =2MN ,MN ∥AE ,∴MN =FM ,∠BMN =∠EAB =90°,∴∠CMF =∠BMN =90°,∴CMF BMN V V ≌(SAS ),∴CF =BN ,∵BE =2BN ,∴CF =12BE .解法二:如图2﹣2中,取DE 的中点G ,连接AG ,CG ,并把△CAG 绕点C 逆时针旋转90°得到CBT V ,连接DT ,GT ,BG .∵AD =AE ,∠EAD =90°,EG =DG ,∴AG ⊥DE ,∠EAG =∠DAG =45°,AG =DG =EG ,∵∠CAB =45°,∴∠CAG =90°,∴AC ⊥AG ,∴AC ∥DE ,∵∠ACB =∠CBT =90°,//,AC BT \∴AC ∥BT ∥DE ,∵AG =BT ,∴DG =BT =EG ,∴四边形BEGT 是平行四边形,四边形DGBT 是平行四边形,∴BD 与GT 互相平分,,BE GT =∵点F 是BD 的中点,∴BD 与GT 交于点F ,∴GF =FT ,由旋转可得;,90,CG CT GCT =Ð=°\ GCT V 是等腰直角三角形,∴CF =FG =FT ,∴CF =12BE .(2)结论:BE =.理由:如图3中,取AB 的中点T ,连接CT ,FT .∵CA =CB ,∴∠CAB =∠CBA =30°,∠ACB =120°,∵AT =TB ,∴CT ⊥AB ,tan 30CT AT \°==∴AT ,∴AB =,∵DF =FB ,AT =TB ,∴TF ∥AD ,AD =2FT ,∴∠FTB =∠CAB =30°,∵∠CTB =∠DAE =90°,∴∠CTF =∠BAE =60°,∵∠ADE =12∠ACB =60°,tan 60AE AD\°==∴AE =,∴AB AE CT FT==,∴BAE CTF V V ∽,∴BE BA CF CT ==,∴BE =.【点睛】本题属于相似形综合题,考查了等腰三角形的性质,全等三角形的判定和性质,平行四边形的判定和性质,相似三角形的判定和性质,锐角三角函数的应用,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.7.(2021·江苏中考真题)已知正方形ABCD 与正方形AEFG ,正方形AEFG 绕点A 旋转一周.(1)如图①,连接BG 、CF ,求CF BG的值;(2)当正方形AEFG 旋转至图②位置时,连接CF 、BE ,分别去CF 、BE 的中点M 、N ,连接MN 、试探究:MN 与BE 的关系,并说明理由;(3)连接BE 、BF ,分别取BE 、BF 的中点N 、Q ,连接QN ,AE=6,请直接写出线段QN 扫过的面积.【答案】(12)1;2MN BE MN BE ^=;(3)9p 【分析】(1)由旋转的性质联想到连接AF AC 、,证明CAF BAG D D ∽即可求解;(2)由M 、N 分别是CF 、BE 的中点,联想到中位线,故想到连接BM 并延长使BM=MH ,连接FH 、EH ,则可证BMC HMF D D ≌即可得到HF BC BA ==,再由四边形BEFC 内角和为360°可得BAC HFE Ð=Ð,则可证明BAE HFE D D ≌,即BHE D 是等腰直角三角形,最后利用中位线的性质即可求解;(3)Q 、N 两点因旋转位置发生改变,所以Q 、N 两点的轨迹是圆,又Q 、N 两点分别是BF 、BE 中点,所以想到取AB 的中点O ,结合三角形中位线和圆环面积的求解即可解答.【详解】解:(1)连接AF AC、Q 四边形ABCD 和四边形AEFG 是正方形,,90AB BC AG FG BAD GAE CBA AGF \==Ð=Ð=Ð=Ð=°Q AF AC 、分别平分,EAG BADÐÐ45BAC GAF \Ð=Ð=°BAC CAG GAF CAG \Ð+Ð=Ð+Ð即BAG CAFÐ=Ð且,ABC AGF D D 都是等腰直角三角形AC AF AB AG\==CAF BAG \D D ∽CF AC BG AB \==(2)连接BM 并延长使BM=MH ,连接FH 、EHM Q 是CF 的中点CM MF\=又CMB FMHÐ=ÐCMB FMH\D D ≌,BC HF BCM HFM\=Ð=Ð在四边形BEFC 中360BCM CBE BEF EFC Ð+Ð+Ð+Ð=°又90CBA AEF Ð=Ð=°3609090180BCM ABE AEB EFC \Ð+Ð+Ð+Ð=°-°-°=°即180HFM EFC ABE AEB Ð+Ð+Ð+Ð=°即180HFE ABE AEB Ð+Ð+Ð=°180BAE ABE AEB Ð+Ð+Ð=°Q HFE BAE\Ð=Ð又四边形ABCD 和四边形AEFG 是正方形,BC AB FH EA EF\===BAE HFE\D D ≌.BE HE BEA HEF\=Ð=Ð90HEF HEA AEF Ð+Ð=Ð=°Q 90BEA HEA BEH\Ð+Ð=°=Ð\三角形BEH 是等腰直角三角形Q M 、N 分别是BH 、BE 的中点1//,2MN HE MN HE \=190,2MNB HEB MN BE \Ð=Ð=°=1,2MN BE MN BE \^=(3)取AB 的中点O ,连接OQ 、ON ,连接AF在ABF D 中,O 、Q 分别是AB 、BF 的中点12OQ AF \=同理可得12ON AE =AF ==Q3OQ ON \==所以QN扫过的面积是以O为圆心,3为半径的圆环的面积(2239\=-=.S p p p【点睛】本题考察旋转的性质、三角形相似、三角形全等、正方形的性质、中位线的性质与应用和动点问题,属于几何综合题,难度较大.解题的关键是通过相关图形的性质做出辅助线.8.(2020•内江)如图,正方形ABCD中,P是对角线AC上的一个动点(不与A、C重合),连结BP,将BP绕点B顺时针旋转90°到BQ,连结QP交BC于点E,QP延长线与边AD交于点F.(1)连结CQ,求证:AP=CQ;(2)若AP=1AC,求CE:BC的值;4(3)求证:PF=EQ.【分析】(1)证明△BAP≌△BCQ(SAS)可得结论.AC,可以假设AP=CQ=a,则(2)过点C作CH⊥PQ于H,过点B作BT⊥PQ于T.由AP=14PC=3a,解直角三角形求出CH.BT,利用平行线分线段成比例定理解决问题即可.(3)证明△PGB≌△QEB,推出EQ=PG,再证明△PFG是等腰直角三角形即可.【解答】(1)证明:如图1,∵线段BP绕点B顺时针旋转90°得到线段BQ,∴BP=BQ,∠PBQ=90°.∵四边形ABCD 是正方形,∴BA =BC ,∠ABC =90°.∴∠ABC =∠PBQ .∴∠ABC ﹣∠PBC =∠PBQ ﹣∠PBC ,即∠ABP =∠CBQ .在△BAP 和△BCQ 中,∵BA =BC ∠ABP =∠CBQ BP =BQ,∴△BAP ≌△BCQ (SAS ).∴CQ =AP .(2)解:过点C 作CH ⊥PQ 于H ,过点B 作BT ⊥PQ 于T .∵AP =14AC ,∴可以假设AP =CQ =a ,则PC =3a ,∵四边形ABCD 是正方形,∴∠BAC =∠ACB =45°,∵△ABP ≌△CBQ ,∴∠BCQ =∠BAP =45°,∴∠PCQ =90°,∴PQ ==,∵CH ⊥PQ ,∴CH =PC ⋅CQ PQ =,∵BP =BQ ,BT ⊥PQ ,∴PT =TQ ,∵∠PBQ =90°,∴BT =12PQ =,∵CH ∥BT ,∴CEEB =CH BT ==35,∴CE CB =38.(3)解:结论:PF =EQ ,理由是:如图2,当F 在边AD 上时,过P 作PG ⊥FQ ,交AB 于G ,则∠GPF =90°,∵∠BPQ=45°,∴∠GPB=45°,∴∠GPB=∠PQB=45°,∵PB=BQ,∠ABP=∠CBQ,∴△PGB≌△QEB,∴EQ=PG,∵∠BAD=90°,∴F、A、G、P四点共圆,连接FG,∴∠FGP=∠FAP=45°,∴△FPG是等腰直角三角形,∴PF=PG,∴PF=EQ.9.(2020•郴州)如图1,在等腰直角三角形ADC中,∠ADC=90°,AD=4.点E是AD的中点,以DE为边作正方形DEFG,连接AG,CE.将正方形DEFG绕点D顺时针旋转,旋转角为α(0°<α<90°).(1)如图2,在旋转过程中,①判断△AGD与△CED是否全等,并说明理由;②当CE=CD时,AG与EF交于点H,求GH的长.(2)如图3,延长CE交直线AG于点P.①求证:AG⊥CP;②在旋转过程中,线段PC的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.【分析】(1)①结论:△AGD≌△CED.根据SAS证明即可.②如图2中,过点A作AT⊥GD于T.解直角三角形求出AT,GT,再利用相似三角形的性质求解即可.(2)①如图3中,设AD交PC于O.利用全等三角形的性质,解决问题即可.②因为∠CPA=90°,AC是定值,推出当∠ACP最小时,PC的值最大,推出当DE⊥PC时,∠ACP的值最小,此时PC的值最大,此时点F与P重合(如图4中).【解析】(1)①如图2中,结论:△AGD≌△CED.理由:∵四边形EFGD是正方形,∴DG=DE,∠GDE=90°,∵DA=DC,∠ADC=90°,∴∠GDE=∠ADC,∴∠ADG=∠CDE,∴△AGD≌△CED(SAS).②如图2中,过点A作AT⊥GD于T.∵△AGD≌△CED,CD=CE,∴AD=AG=4,∵AT⊥GD,∴TG=TD=1,∴AT==∵EF∥DG,∴∠GHF=∠AGT,∵∠F=∠ATG=90°,∴△GFH∽△ATG,∴GHAG =FGAT,=∴GH∴GH=(2)①如图3中,设AD交PC于O.∵△AGD≌△CED,∴∠DAG=∠DCE,∵∠DCE+∠COD=90°,∠COD=∠AOP,∴∠AOP+∠DAG=90°,∴∠APO=90°,∴CP⊥AG.②∵∠CPA=90°,AC是定值,∴当∠ACP最小时,PC的值最大,∴当DE⊥PC时,∠ACP的值最小,此时PC的值最大,此时点F与P重合(如图4中),∵∠CED=90°,CD=4,DE=2,∴EC==∵EF=DE=2,∴CP=CE+EF=∴PC的最大值为。
备战中考数学——旋转的综合压轴题专题复习含答案

一、旋转真题与模拟题分类汇编(难题易错题)1.如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;(2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为_____;(3)在(1)的条件下,若CD=6,S△BCE=2S△ACD,求AE的长.【答案】(1)见解析(2)AD=BE+DE (3)8【解析】试题分析:(1)延长DA到F,使DF=DE,根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得证;(2)在AD上截取DF=DE,然后根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得到AD=BE+DE;(3)根据等腰直角三角形的性质求出CD=DF=DE,再根据等高的三角形的面积的比等于底边的比求出AF=2AD,然后求出AD的长,再根据AE=AD+DE代入数据进行计算即可得解.试题解析:(1)证明:如图①,延长DA到F,使DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ACD+∠ACF=∠DCF=45°.又∵∠ACB=90°,∠PCQ=45°,∴∠ACD+∠BCE=90°﹣45°=45°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵CE CFACF BCEAC BC=⎧⎪∠=∠⎨⎪=⎩,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;(2)解:如图②,在AD上截取DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=∠DCE+∠DCF=90°,∴∠BCE+∠BCF=∠ECF=90°.又∵∠ACB=90°,∴∠ACF+∠BCF=90°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵CE CFACF BCEAC BC=⎧⎪∠=∠⎨⎪=⎩,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;故答案为:AD=BE+DE.(3)∵∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=45°+45°=90°,∴△ECF是等腰直角三角形,∴CD=DF=DE=6.∵S△BCE=2S△ACD,∴AF=2AD,∴AD=1×6=2,∴AE=AD+DE=2+6=8.12点睛:本题考查了全等三角形的判定与性质,线段垂直平分线上的点到线段两端点的距离相等的性质,等腰直角三角形的性质,综合性较强,但难度不是很大,作辅助线构造出全等三角形是解题的关键.2.已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM 上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.(1)如图1,猜想:△CDE的形状是三角形.(2)请证明(1)中的猜想(3)设OD=m,①当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.②是否存在m的值,使△DEB是直角三角形,若存在,请直接写出m的值;若不存在,请说明理由.【答案】(1)等边;(2)详见解析;(3)3;②当m=2或14时,以D、E、B 为顶点的三角形是直角三角形.【解析】【分析】(1)由旋转的性质猜想结论;(2)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;(3)①当6<m<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;②存在,分四种情况讨论:a)当点D与点B重合时,D,B,E不能构成三角形;b)当0≤m<6时,由旋转的性质得到∠ABE=60°,∠BDE<60°,求得∠BED=90°,根据等边三角形的性质得到∠DEB=60°,求得∠CEB=30°,求得OD=OA﹣DA=6﹣4=2=m;c)当6<m<10时,此时不存在;d)当m>10时,由旋转的性质得到∠DBE=60°,求得∠BDE>60°,于是得到m=14.【详解】(1)等边;(2)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形.(3)①存在,当6<t<10时,由旋转的性质得:BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=23,∴△BDE的最小周长=CD+4=23+4;②存在,分四种情况讨论:a)∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意;b)当0≤m<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°.∵∠CEB=∠CDA,∴∠CDA=30°.∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴m=2;c)当6<m<10时,由∠DBE=120°>90°,∴此时不存在;d)当m>10时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14,∴m=14.综上所述:当m=2或14时,以D、E、B为顶点的三角形是直角三角形.【点睛】本题考查了旋转的性质,等边三角形的判定和性质,三角形周长的计算,直角三角形的判定,熟练掌握旋转的性质是解题的关键.3.如图①,在ABCD中,AB=10cm,BC=4cm,∠BCD=120°,CE平分∠BCD交AB于点E.点P从A点出发,沿AB方向以1cm/s的速度运动,连接CP,将△PCE绕点C逆时针旋转60°,使CE与CB重合,得到△QCB,连接PQ.(1)求证:△PCQ是等边三角形;(2)如图②,当点P在线段EB上运动时,△PBQ的周长是否存在最小值?若存在,求出△PBQ周长的最小值;若不存在,请说明理由;(3)如图③,当点P在射线AM上运动时,是否存在以点P、B、Q为顶点的直角三角形?若存在,求出此时t的值;若不存在,请说明理由.(1)(2)(3)【答案】(1)证明见解析;(2)存在,理由见解析;(3)t为2s或者14s.【解析】分析:(1)根据旋转的性质,证明△PCE≌△QCB,然后根据全等三角形的性质和等边三角形的判定证明即可;(2)利用平行四边形的性质证得△BCE为等边三角形,然后根据全等三角形的性质得到△PBQ的周长为4+CP,然后垂线段最短可由直角三角形的性质求解即可;(3)根据点的移动的距离,分类讨论求解即可.详解:(1)∵旋转∴△PCE≌△QCB∴CP=CQ,∠PCE =∠QCB,∵∠BCD=120°,CE平分∠BCD,∴∠PCQ=60°,∴∠PCE +∠QCE=∠QCB+∠QCE=60°,∴△PCQ为等边三角形.(2)存在∵CE平分∠BCD,∴∠BCE=60 ,∵在平行四边形ABCD 中,∴AB∥CD∴∠ABC=180°﹣120°=60°∴△BCE为等边三角形∴BE=CB=4∵旋转∴△PCE≌△QCB∴EP=BQ,∴C△PBQ=PB+BQ+PQ=PB+EP+PQ=BE+PQ=4+CP∴CP⊥AB时,△PBQ周长最小当CP⊥AB时,CP=BCsin60°=∴△PBQ周长最小为4+(3)①当点B与点P重合时,P,B,Q不能构成三角形②当0≤t<6时,由旋转可知,∠CPE=∠CQB,∠CPQ=∠CPB+∠BPQ=60°则:∠BPQ+∠CQB=60°,又∵∠QPB+∠PQC+∠CQB+∠PBQ=180°∴∠CBQ=180°—60°—60°=60°∴∠QBP=60°,∠BPQ<60°,所以∠PQB可能为直角由(1)知,△PCQ为等边三角形,∴∠PBQ=60°,∠CQB=30°∵∠CQB=∠CPB∴∠CPB=30°∵∠CEB=60°,∴∠ACP=∠APC=30°∴PA=CA=4,所以AP=AE-EP=6-4=2÷=s所以t=212③当6<t<10时,由∠PBQ=120°>90°,所以不存在④当t>10时,由旋转得:∠PBQ=60°,由(1)得∠CPQ=60°∴∠BPQ=∠CPQ+∠BPC=60°+∠BPC,而∠BPC>0°,∴∠BPQ>60°∴∠BPQ=90°,从而∠BCP=30°,所以AP=14cm所以t=14s综上所述:t为2s或者14s时,符合题意。
专题46 以正方形为基础的图形的旋转变换问题(解析版)
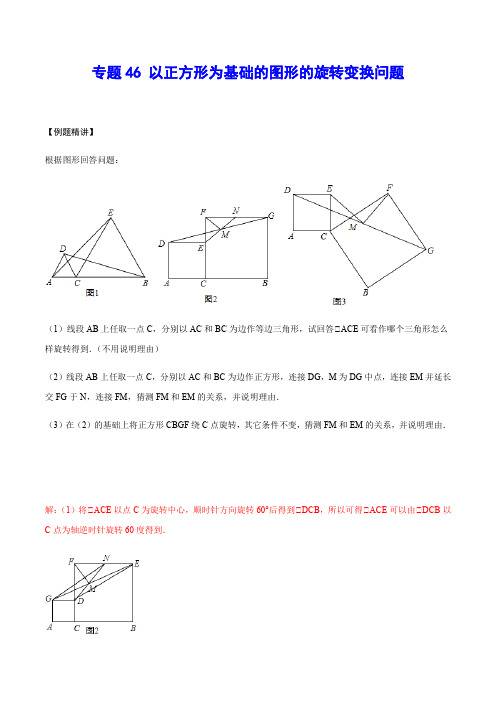
专题46 以正方形为基础的图形的旋转变换问题【例题精讲】根据图形回答问题:(1)线段AB上任取一点C,分别以AC和BC为边作等边三角形,试回答△ACE可看作哪个三角形怎么样旋转得到.(不用说明理由)(2)线段AB上任取一点C,分别以AC和BC为边作正方形,连接DG,M为DG中点,连接EM并延长交FG于N,连接FM,猜测FM和EM的关系,并说明理由.(3)在(2)的基础上将正方形CBGF绕C点旋转,其它条件不变,猜测FM和EM的关系,并说明理由.解:(1)将△ACE以点C为旋转中心,顺时针方向旋转60°后得到△DCB,所以可得△ACE可以由△DCB以C点为轴逆时针旋转60度得到.(2)FM△ME ,FM=ME ,连接GN 和DE , 在△DME 和△GMN 中,MDE MHG DME GMN DM MG ∠∠∠∠⎧⎪⎨⎪⎩===,△△DME△△GMN (AAS ),△DM=MN ,DE=NG ,△FN=FG -NG=FG -DE=FC -EC=FE ,△△NFE 是等腰直角三角形,△FM△ME ,并且FM=ME (等腰三角形中线就是垂线,直角三角形中线等于斜边的一半)(3)延长EM 至N 点,使EM=MN ,连接NG 、EF 、FN .(EC 与DM 的交点标为P ,FC 与DM 交点标为Q )在△DME 和△GMN 中,EM MN DME GMN DM MG ⎪∠⎪⎩∠⎧⎨===,△△DME△△GMN .△DE=NG ,△EDM=△NGM ,△EC=NG ,△△ECF=180°-△CPQ -△CQP=180°-△DPE -△FQG=180°-(90°-△MDE )-(90°-△FGM )=△EDM+△FGM ,△△NGM+△FGM=△NGF ,△△ECF=△NGF ,△EC=DE=NG ,在△ECF 和△NGF 中,FC FG ECF NGF EC NG ⎪∠⎪⎩∠⎧⎨===,△△ECF△△NGF ,△EF=NF ,△EFC=△NFG ,△△EMN=△EFC+△CFN=△NFG+△CFN=△CFG=90°,△△EFN 是等腰直角三角形,△FM△EM ,并且FM=EM 。
2022年九年级数学复习专题---图形的变换(平移、翻折、旋转)综合问题题

2022年中考数学复习专题---图形的变换(平移、翻折、旋转)综合题班级:___________姓名:___________学号:___________1.综合与实践 问题情境:综合与实践课上,同学们以“三角形纸片的折叠与旋转“为主题展开数学活动,探究有关的数学问题. 动手操作:已知:三角形纸片ABC 中,6120AB AC BC BAC ==∠=︒,,.将三角形纸片ABC 按如下步骤进行操作: 第一步:如图1,折叠三角形纸片ABC ,使点C 与点A 重合,然后展开铺平,折痕分别交BC AC ,于点D E ,,连接AD ,易知AD CD =.第二步:在图1的基础上,将三角形纸片ABC 沿AD 剪开,得到ABD ∆和ACD ∆.保持ABD ∆的位置不变,将ACD ∆绕点D 逆时针旋转得到FDG ∆(点F G ,分别是A C ,的对应点),旋转角为()0360αα︒<<︒问题解决:(1)如图2,小彬画出了旋转角0120α︒<<︒时的图形,设线段FG AC ,交于点P ,连接AG DP ,.小彬发现DP 所在直线始终垂直平分线段AG .请证明这一结论;(2)如图3,小颖画出了旋转角90α=︒时的图形,设直线AF 与直线CG 相交于点O ,连接CF 判断此时COF ∆的形状,说明理由;(3)在ACD ∆绕点D 逆时针旋转过程中,当FG BC ⊥时,请直接写出B F ,两点间的距离.2.如图,△ABC 中,已知∠C=90°,∠B=60°,点D 在边BC 上,过D 作DE ⊥AB 于E . (1)连接AD ,取AD 的中点F ,连接CF ,EF ,判断△CEF 的形状,并说明理由(2)若.把△BED 绕着点D 逆时针旋转m (0<m <180)度后,如果点B 恰好落在初始Rt △ABC 的边上,那么m=3.问题背景:如图1,在矩形ABCD 中,30AB ABD =∠=︒,点E 是边AB 的中点,过点E 作EF AB ⊥交BD 于点F . 实验探究:(1)在一次数学活动中,小明在图1中发现AEDF=_________. 将图1中的BEF 绕点B 按逆时针方向旋转90︒,连接,AE DF ,如图2所示,发现AEDF=_________. (2)小亮同学继续将BEF 绕点B 按逆时针方向旋转,连接,AE DF ,旋转至如图3所示位置,请问探究(1)中的结论是否仍然成立?并说明理由. 拓展延伸:(3)在以上探究中,当BEF 旋转至D 、E 、F 三点共线时,AE 的长为____________.4.如图,在Rt ABC 中,90ACB ∠=︒,CD 平分ACB ∠.P 为边BC 上一动点,将DPB 沿着直线DP 翻折到DPE ,点E 恰好落在CDP 的外接圆O 上. (1)求证:D 是AB 的中点.(2)当60BDE ∠=︒,BP =DC 的长.(3)设线段DB 与O 交于点Q ,连结QC ,当QC 垂直于DPE 的一边时,求满足条件的所有QCB ∠的度数.5.如图1,O 为正方形ABCD 的中心,分别延长OA 、OD 到点,F E ,使OF=2OA ,OE 2OD =,连接EF ,将FOE ∆绕点O 按逆时针方向旋转角α得到F OE ''∆,连接,AE BF ''(如图2).(1)探究AE '与BF '的数量关系,并给予证明; (2)当30α=︒时,求证:AOE '为直角三角形.6.如图,在△ABC 中,AB =∠B =45°,∠C =60°. (1)求BC 边上的高线长.(2)点E 为线段AB 的中点,点F 在边AC 上,连结EF ,沿EF 将△AEF 折叠得到△PEF . ①如图2,当点P 落在BC 上时,求∠AEP 的度数. ②如图3,连结AP ,当PF ⊥AC 时,求AP 的长.7.如图1,点C 在线段AB 上,分别以AC 、BC 为边在线段AB 的同侧作正方形ACDE 和正方形BCMN , 连结AM 、BD .(1)AM与BD的关系是:________.(2)如果将正方形BCMN绕点C顺时针旋转锐角α(如图2).(1) 中所得的结论是否仍然成立?请说明理由.(3)在(2)的条件下,连接AB、DM,若AC=4,BC=2,求AB2+DM2的值.8.已知正方形ABCD,一等腰直角三角板的一个锐角顶点与A重合,将此三角板绕A点旋转时,两边分别交直线BC、CD于M、N.(1)当M、N分别在边BC、CD上时(如图1),求证:BM+DN=MN;(2)当M、N分别在边BC、CD所在的直线上时(如图2),线段BM、DN、MN之间又有怎样的数量关系,请直接写出结论;(不用证明)(3)当M、N分别在边BC、CD所在的直线上时(如图3),线段BM、DN、MN之间又有怎样的数量关系,请写出结论并写出证明过程.9.如图,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.(1)如图,当BP=BA时,∠EBF=______°,猜想∠QFC =______°;(2)如图,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.(3)已知线段AB=BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.10.我们知道,直角坐标系是研究“数形结合”的重要工具.请探索研究下列问题:(1)如图1,点A 的坐标为(-5,1),将点A 绕坐标原点(0,0)按顺时针方向旋转90°,得对应点A ',若反比例函数(0)k y x x=>的图像经过点A ',求k 的值.(2)将(1)中的(0)ky x x =>的图像绕坐标原点(0,0)按顺时针方向旋转45°,如图2,旋转后的图像与x 轴相交于点B ,若直线x =C 与点D ,求△BCD 的面积. (3)在(2)的情况下,半径为6的M 的圆心M 在x 轴上,如图3,若要使△BCD 完全在M 的内部,求M 的圆心M 横坐标xm 的范围(直接写出结果,不必写详细的解答过程).11.对于平面直角坐标系xOy 中的点A 和点P ,若将点P 绕点A 逆时针旋转90︒后得到点Q ,则称点Q 为点P 关于点A 的“垂链点”,图1为点P 关于点A 的“垂链点”Q 的示意图.(1)已知点A 的坐标为(0,0),点P 关于点A 的“垂链点”为点Q ;①若点P 的坐标为(2,0),则点Q 的坐标为________; ②若点Q 的坐标为(2,1)-,则点P 的坐标为________; (2)如图2,已知点C 的坐标为(1,0),点D 在直线113y x =+上,若点D 关于点C 的“垂链点”在坐标轴上,试求出点D 的坐标;(3)如图3,已知图形G 是端点为(1,0)和(0,2)-的线段,图形H 是以点O 为中心,各边分别与坐标轴平行的边长为6的正方形,点M 为图形G 上的动点,点N 为图形H 上的动点,若存在点(0,)T t ,使得点M 关于点T 的“垂链点”恰为点N ,请直接写出t 的取值范围.12.如图,正比例函数y =12x 与反比例函数()0k y x x =>的图象交于点A ,将正比例函数y =12x 向上平移6个单位,交y 轴于点C ,交反比例函数图象于点B ,已知AO =2BC . (1)求反比例函数解析式;(2)作直线AB ,将直线AB 向下平移p 个单位,恰与反比例函数图象有唯一交点,求p 的值.13.综合与实践:问题情境:(1)如图,点E 是正方形ABCD 边CD 上的一点,连接BD 、BE ,将DBE ∠绕点B 顺针旋转90︒,旋转后角的两边分别与射线DA 交于点F 和点G .①线段BE 和BF 的数量关系是______.②写出线段DE 、DF 和BD 之间的数量关系.并说明理由;操作探究:(2)在菱形ABCD 中,60ADC ∠=︒,点E 是菱形ABCD 边CD 所在直线上的-点,连接BD 、BE ,将DBE ∠绕点B 顺时针旋转120︒,旋转后角的两边分别与射线DA 交于点F 和点G .①如图,点E 在线段DC 上时,请探究线段DE 、DF 和BD 之间的数量关系,写出结论并给出证明;②如图,点E在线段CD的延长线上时,BE交射线DA于点M,若2==,直接写出线段FM和AGDE DC a的长度.14.两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=4.固定△ABC不动,将△DEF 进行如下操作:(1)操作发现如图①,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC,CF,FB,四边形CDBF的形状在不断的变化,那么它的面积大小是否变化呢?如果不变化,请求出其面积.(2)猜想论证如图②,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.(3)拓展探究如图③,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连接AE,求sinα翻折问题姓名:___________班级:___________学号:___________1.如图将矩形纸片ABCD 沿AE 翻折,使点B 落在线段DC 上,对应的点为F . (1)求证:EFC DAF ∠=∠;(2)若3tan 4AE EFC =∠=,求AB 的长.2.如图,在Rt△ABC 中,∠C=90°,AC=BC=2,AD 是BC 边上的中线,将A 点翻折与点D 重合,得到折痕EF ,求:CE AE 的值.3.如图,点A ,M ,N 在O 上,将MN 沿MN 折叠后,与AM 交于点B .(1)若70MAN ∠=︒,则ANB ∠=________°; (2)如图1,点B 恰好是翻折所得MN 的中点, ①若MA MN =,求AMN ∠的度数;②若tan MAN ∠=tan AMN ∠的值; (3)如图2,若222AB BN MN +=,求MBAB的值.4.已知矩形ABCD 中,AB =2,BC =m ,点E 是边BC 上一点,BE =1,连接AE ,沿AE 翻折△ABE 使点B 落在点F 处.(1)连接CF ,若CF ∥AE ,求m 的值;(2)连接DF ,若65≤DF ,求m 的取值范围.5.如图1,一张矩形纸ABCD ,ABa AD=,点,E F 分别在边,CD AB 上,且AE EF =,把ADE 沿AE 翻折得到AGE .(1)如图1,若1AD =.(Ⅰ)当AD DE =时,AFE ∠=_____度; (Ⅱ)当//AG EF 时,求AF 的长度.(2)若直线EG 与边AB 交于点H ,当2AH FH =时,求a 的最小值.6.如图,在折纸游戏中,正方形ABCD 沿着BE ,BF 将BC ,AB 翻折,使A ,C 两点恰好落在点P . (1)求证:45EBF ∠=︒.(2)如图,过点P 作//MN BC ,交BF 于点Q . ①若5BM =,且10MP PN ⋅=,求正方形折纸的面积. ②若12QP BC =,求AM BM的值.7.如图,在ABC 中,12,120AC BC ACB ==∠=︒,点D 是AB 边上一点,连接CD ,以CD 为边作等边CDE △.(1)如图1,若45CDB ∠=︒,求等边CDE △的边长;(2)如图2,点D 在AB 边上移动过程中,连接BE ,取BE 的中点F ,连接,CF DF ,过点D 作DG AC ⊥于点G . ①求证:CFDF .②如图3,将CFD 沿CF 翻折得CFD ',连接BD ',求出BD '的最小值.8.在矩形ABCD 中,1AB =,BC a =,点E 是边BC 上一动点,连接AE ,将ABE △沿AE 翻折,点B 的对应点为点B '.(1)如图,设BE x =,BC =E 从B 点运动到C 点的过程中. ①AB CB ''+最小值是______,此时x =______; ②点B '的运动路径长为.(2)如图,设35BE a =,当点B 的对应点B '落在矩形ABCD 的边上时,求a 的值.9.如图1,平行四边形ABCD 的对角线AC ,BD 相交于点O ,CD 边的垂直平分线EH 交BD 于点E ,连接AE ,CE .(1)过点A 作//AF EC 交BD 于点F ,求证:AF BF =;(2)如图2,将ABE △沿AB 翻折得到'ABE △.①求证:'//BE CE ;②若'//AE BC ,1OE =,求CE 的长度.10.如图,矩形ABCD 中,已知6AB =.8BC =,点E 是射线BC 上的一个动点,连接AE 并延长,交射线DC 于点F .将ABE △沿直线AE 翻折,点B 的对应点为点B ',延长AB '交直线CD 于点M .(1)如图1,若点B '恰好落在对角线AC 上,求BE CE的值. (2)如图2.当点E 为BC 的中点时,求DM 之长.(3)若32BE CE =,求sin DAB '∠.11.【基础巩固】(1)如图①,ABC ACD CED α∠=∠=∠=,求证:ABC CED ∽△△.【尝试应用】(2)如图②,在菱形ABCD 中,60A ∠=︒,点E ,F 分别为边,AD AB 上两点,将菱形ABCD 沿EF 翻折,点A 恰好落在对角线DB 上的点P 处,若2PD PB =,求AE AF的值. 【拓展提高】(3)如图③,在矩形ABCD 中,点P 是AD 边上一点,连接,PB PC ,若2,4,120PA PD BPC ==∠=︒,求AB 的长.12.如图,在ABC 中,60B ∠=︒,AD BC ⊥于点D ,CE AB ⊥于点E ,AB CE =.(1)如图1,将ABD △沿AD 翻折到AFD ,AF 交CE 于点G ,探索线段AB 、AG 、CG 之间有何等量关系,并加以证明;(2)如图2,H 为直线BC 上任意一点,连接AH ,将AH 绕点A 逆时针旋转60°到AH ',连接CH ',若BD =,求CH '的最小值.13.如图,在矩形ABCD 中,12BC AB =,F 、G 分别为AB 、DC 边上的动点,连接GF ,沿GF 将四边形AFGD 翻折至四边形EFGP ,点E 落在BC 上,EP 交CD 于点H ,连接AE 交GF 于点O(1)GF 与AE 之间的位置关系是:______,GF AE 的值是:______,请证明你的结论;(2)连接CP ,若3tan 4CGP ∠=,GF =CP 的长14.如图,在矩形ABCD 中,8AB =,10BC =,点P 在矩形的边CD 上由点D 向点C 运动.沿直线AP 翻折ADP ∆,形成如下四种情形,设DP x =,ADP ∆和矩形重叠部分(阴影)的面积为y .(1)如图4,当点P 运动到与点C 重合时,求重叠部分的面积y ;(2)如图2,当点P 运动到何处时,翻折ADP ∆后,点D 恰好落在BC 边上?这时重叠部分的面积y 等于多少?15.如图1,ABC 中,AB AC =,点D 在BA 的延长线上,点E 在BC 上,连接DE 、DC ,DE 交AC 于点G ,且DE DC =.(1)找出一个与BDE ∠相等的角;(2)若AB =mAD ,求DG GE的值(用含m 的式子表示); (3)如图2,将ABC 沿BC 翻折,若点A 的对应点A '恰好落在DE 的延长线上,求BE EC的值.16.在等腰直角三角形ABC中,∠BAC=90°,AB=AC,D是斜边BC的中点,连接AD.(1)如图1,E是AC的中点,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′,当时,求AE的值.(2)如图2,在AC上取一点E,使得CE=13AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.。
2024年中考数学-押江苏南京卷第25-26题(二次函数的综合、三角形旋转问题)(解析版)

押江苏南京卷第25-26题押题方向一:二次函数的综合3年江苏南京卷真题考点命题趋势2023年江苏南京卷第26题二次函数的综合从近年江苏南京中考来看,二次函数的综合的考查,难度较大,综合性比较强;预计2024年江苏南京卷还将继续重视对二次函数的综合问题的考查。
2022年江苏南京卷第26题二次函数的综合2021年江苏南京卷第26题二次函数的综合1.(2023·江苏南京·中考真题)已知二次函数223(y ax ax a =-+为常数,0)a ≠.(1)若0a <,求证:该函数的图象与x 轴有两个公共点.(2)若1a =-,求证:当10x -<<时,0y >.(3)若该函数的图象与x 轴有两个公共点1(x ,0),2(x ,0),且1214x x -<<<,则a 的取值范围是3a >或1a <-.【分析】(1)证明240b ac ->即可解决问题.(2)将1a =-代入函数解析式,进行证明即可.(3)对0a >和0a <进行分类讨论即可.【解答】证明:(1)因为22(2)43412a a a a --⨯⨯=-,又因为0a <,所以40a <,30a -<,所以24124(3)0a a a a -=->,所以该函数的图象与x 轴有两个公共点.(2)将1a =-代入函数解析式得,2223(1)4y x x x =-++=--+,所以抛物线的对称轴为直线1x =,开口向下.则当10x -<<时,是AB 上的动点,连接EF ,G 是EF 上一点,且GFk EF=(k 为常数,0k ≠),分别过点F 、G 作AB 、EF 的垂线相交于点P ,设AF 的长为x ,PF 的长为y .(1)若12k =,4x =,则y 的值为________;(2)求y 与x 之间的函数表达式;(3)在点F 从点A 到点B 的整个运动过程中,若线段CD 上存在点P ,则k 的值应满足什么条件?直接写出k 的取值范围.两点.(1)求b 的值.(2)当1c >-时,该函数的图像的顶点的纵坐标的最小值是________.(3)设()0m ,是该函数的图像与x 轴的一个公共点,当13m -<<时,结合函数的图像,直接写出a 的取值范围.即1410 93410 a aa a+-->⎧⎨---<⎩,解得a<0;②如图,当0a>时,当=1x -时,14y a =+-∴当3x =时,93y a =--解得45a >,综上,a 的取值范围为a<【点睛】本题考查了二次函数的图象与性质等知识点,较难的是题(一、二次函数的图象1.二次函数2ax y =(0≠a )的图象是一条抛物线,它关于y 轴对称,顶点是坐标原点.当0>a 时,抛物线开口向上,顶点是抛物线的最低点;当0<a 时,抛物线开口向下,顶点是抛物线的最高点.2.二次函数()2m x a y -=(0≠a )的图象的顶点坐标是(m,0),对称轴是直线m x =.图象的开口方向:当0>a 时,开口向上;当0<a 时,抛物线开口向下.3.二次函数()k m x a y +-=2(0≠a )的图象的顶点坐标是(m,k),对称轴是直线m x =.图象的开口方向:当0>a 时,开口向上;当0<a 时,抛物线开口向下.4.二次函数c bx ax y ++=2(0≠a )的图象是一条抛物线,它de 对称轴是直线2bx a=-,顶点坐标是24,24b ac b aa ⎛⎫-- ⎪⎝⎭,当0>a 时,抛物线开口向上,顶点是抛物线上的最低点;当0<a 时,抛物线开口向下,顶点是抛物线上的最高点.二、二次函数的图象与系数的关系二次函数c bx ax y ++=2(0≠a )的系数与图象的关系(1)a 的符号由抛物线c bx ax y ++=2的开口方向决定:0>⇔a 开口向上,0>⇔a 开口向上;(2)b 的符号由抛物线c bx ax y ++=2的对称轴的位置及a 的符号共同决定:对称轴在y 轴左侧b a ,⇔同号,对称轴在y 轴右侧b a ,⇔异号;(3)c 的符号由抛物线c bx ax y ++=2与y 轴的交点的位置决定:与y 轴正半轴相交0>⇔c ,与y 轴正半轴相交0<⇔c 三、二次函数的图象与几何变换1.二次函数的平移(1)平移步骤:①将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,;②保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位(2)平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”.2.二次函数图象的对称(1)关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;(2)关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;(3)关于原点对称2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-;()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-;4.关于顶点对称2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.1.已知二次函数()244y x a x a =-++(a 为常数且4a ≠).(1)求证:不论a 为何值,该函数的图像与x 轴总有两个公共点(2)设该二次函数的图象与x 轴的两个交点分别记为A 、B ,线段AB (含端点)上有若干个横坐标为整数的点,且这些点的横坐标之和为9.①直接写出a 的取值范围;②若a 为负整数,则函数()244y x a x a =-++的图像与函数y x b =+的图像的交点个数随b 的值变化而变化,直接写出交点个数及对应的b 的取值范围.第二种情况:4b <-时,函数(2y x a =-+第三种情况:直线y x b =+经过(),0a 时,则第四种情况:当4b a -<<-时,有2个交点,如图示:当直线y x b =+与函数()244y x a x =-++联立直线y x b =+与函数()24y x a =-++得()244y x b y x a x a =+⎧⎨=-++-⎩,∴()2340x a x b a -+++=,由()2Δ3a =+∴第五种情况:21094a ab -+=时,直线第七种情况:当21094a ab -+>时,有2个交点,如图示:综上,当4a <时,当4b <-时,函数()244y x a x a =-++的图像与函数当4b =-时,函数()244y x a x a =-++的图像与函数当4b a -<<-或21094a ab -+≥时,函数当=-b a 时,函数()244y x a x a =-++的图像与函数当21094a a ab -+-<<时,函数(2y x =-中曲线AB 为反比例函数图像的一部分,BC 为一次函数图像的一部分.(1)求y 与x 之间的函数表达式;(2)已知每年该产品的研发费用为40万元,该产品成本价为4元/件,设销售产品年利润为w (万元),当销售单价为多少元时,年利润最大?最大年利润是多少?(说明:年利润=年销售利润-研发费用)(1)求证:该函数的图像与x 轴总有两个公共点;(2)若该函数图像与x 轴的两个交点坐标分别为()(),0,0x x ₁,₂,且2x x =-₁₁,求证²0a b +=;(3)若()1,A k y ,()26,B y ,()14,C k y +都在该二次函数的图像上,且212y y <<,结合函数的图像,直接写出k 的取值范围.或此时B 的横坐标小于0,不符合题意,舍去;当20k +>,即2k >-时,∵212y y <<,∴画出草图,如下:∴6262k k k k >⎧⎨+->+-⎩,解得6k >;或∴466242622k k k k k k +<⎧⎪-->+--⎨⎪--<+⎩,解得12k <<,综上,12k <<或6k >.【点睛】本题考查了二次函数与一元二次方程,二次函数的图象与性质,一元二次方程根与系数的关系以及根的判别式等知识,明确题意,合理分类讨论,画出函数图象,数形结合列出不等式组是解答第(3)的关键.4.在二次函数221y x mx m =++-中.(1)求证:不论m 取何值,该函数图像与x 轴总有两个公共点(2)当03x ≤≤时,y 的最小值为3-,则m 的值为________.(3)当0m <时,点()2,A n a -,()4,B b ,(),C n a 都在这个二次函数的图象上,且1a b m <<-.则n 的取值范围是________.5.若一次函数y mx n =+与反比例函数k y x=同时经过点(,)P x y 则称二次函数2y mx nx k =+-为一次函数与反比例函数的“共享函数”,称点P 为共享点.(1)判断21y x =-与3y x=是否存在“共享函数”,如果存在,请求出“共享点”.如果不存在,请说明理由;(2)已知:整数m ,n ,t 满足条件8t n m <<,并且一次函数(1)22y n x m =+++与反比例函数2024y x =存在“共享函数”2()(10)2024y m t x m t x =++--,求m 的值.(3)若一次函数y x m =+和反比例函数213m y x+=在自变量x 的值满足的6m x m ≤≤+的情况下.其“共享函数”的最小值为3,求其“共享函数”的解析式.(m 为常数).(1)求证:不论m 为何值,该函数的图象与x 轴总有公共点.(2)不论m 为何值,该函数的图象经过的定点坐标是.(3)在22x -≤≤的范围中,y 的最大值是2,直接写出m 的值.为常数).(1)若4m =,3n =,求该函数图像与x 轴的两个交点之间的距离;(2)若函数2y x mx n =++的图象与x 轴有两个交点,将该函数的图像向右平移()0k k >个单位长度得到新函数y '的图象,且这两个函数图象与x 轴的四个交点中任意相邻两点之间的距离都相等.①若函数2y x mx n =++的图象如图所示,直接写出新函数y '的表达式;②若函数2y x mx n =++的图象经过点()1,3,当1k =时,求m n ,的值.押题方向二:三角形的旋转3年江苏南京卷真题考点命题趋势2023年江苏南京卷第27题三角形的旋转从近年江苏南京中考来看,三角形的旋转的考查,难度较大,常常与全等和相似三角形结合一起考查,综合性比较强;预计2024年江苏南京卷还将继续重视对三角形的旋转的综合问题的考查。
2023年中考数数学高频考点提升练习 三角形动点问题综合(含解析)

2023年中考九年级数数学高频考点提升练习--三角形动点问题综合1.如图,在△ABC中,∠C=90°,CA=3厘米,CB=2厘米.动点P从点C出发,沿CB方向以1厘米/秒的速度向B运动,动点Q从点B同时出发,沿BC方向以1厘米/秒的速度向C运动.当点P到达点B时,P、Q两点同时停止运动,以CP为一边向上作正方形CPDE,过点Q作QF∥AB,交AC于点F.设点P的运动时间为t秒,正方形CPDE和梯形AFQB重合部分的面积为S平方厘米.(1)当t=秒时,点P于点Q重合;(2)当t=秒时,点D在QF上;(3)当点P在Q、B两点之间(不包括Q、B两点)时,求S与t之间的函数关系式.2.如图,在△ABC中,已知AB=AC=10cm,BC=16cm,AD△BC于D,点E、F分别从B、C两点同时出发,其中点E沿BC向终点C运动,速度为4cm/s;点F沿CA、AB向终点B运动,速度为5cm/s,设它们运动的时间为x(s).(1)求x为何值时,△EFC和△ACD相似;(2)是否存在某一时刻,使得△EFD被AD分得的两部分面积之比为3:5,若存在,求出x的值,若不存在,请说明理由;(3)若以EF为直径的圆与线段AC只有一个公共点,求出相应x的取值范围.3.如图,直线y=kx+b(k≠0)与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.(1)则A点的坐标为,B两点的坐标为;(2)当点P在OA上,且BP平分△OBA时,则此时点P的坐标为;(3)设点P的运动时间为t秒(0≤t≤4),△BPA的面积为S,求S与t之间的函数关系式:并直接写出当S=8时点P的坐标.4.如图,在Rt△ABC中,∠B=90°,AC=40cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤10).过点D作DF⊥BC于点F,连接DE,EF.(1)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(2)当t为何值时,ΔDEF为直角三角形?请说明理由.5.如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,(1)求C点的坐标;(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE△x轴于E点,求OP−DE的值;(3)如图3,已知点F坐标为(−2,−2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持△GFH=90△,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①m−n为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值. 6.如图(1)如图1,点E在四边形ABCD的边BC上,EA=ED,且△AED=△B=△C.判断AB、BC、CD三边的数量关系,并说明理由;(2)如图2,在Rt△ABC中,△C=90°,AC=6,BC=8,点D在线段BC上,CD =3,点E是AC边上一动点,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,当AE的值为多少时,线段BF有最小值?并求出线段BF的最小值.7.如图,在Rt△ABC中,△ACB=90°,AC=6cm,BC=8cm,点P从点A出发沿线段AB以每秒1cm的速度运动,同时点Q从点B出发沿折线B﹣C﹣A以每秒2cm的速度运动.其中一点停止则另一点也随之停止,设运动时间为t秒.(1)①直接写出t的取值范围:;②当点P运动到AB中点时,连结PQ,PC,BQ,求证:△CPQ△△ABQ;(2)当△BPQ是直角三角形时,求t的值.8.已知△ABC中,∠BAC=90∘,AB=AC,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作△ADE,使∠DAE=90∘,AD=AE,连接CE.发现问题:如图1,当点D在边BC上时,(1)请写出BD和CE之间的位置关系为,并猜想BC和CE、CD之间的数量关系:.(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;(3)如图3,当点D在边CB的延长线上且其他条件不变时,若BC=6,CE= 2,求线段ED的长.9.如图,P、Q分别是边长4cm为的等边ΔABC的边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,分别沿AB,BC边运动,点P到点B停止,点Q到点C停止.社运动时间为t秒,他们的速度都为1cm/s.(1)连接AQ,CP相交于M,在点P,Q的运动过程中∠CMQ的大小是否变化?若变化,说明理由;若不变,求出它的度数;(2)当t取何值时,ΔPBQ是直角三角形.10.如图所示,点B坐标为(6,0),点A坐标为(6,12),动点P从点O开始沿OB以每秒1个单位长度的速度向点B移动,动点Q从点B开始沿BA以每秒2个单位长度的速度向点A移动,如果P,Q分别从O,B同时出发,用t(秒)表示移动的时间(0<t≤6).(1)用含t的式子来表示BP=.AQ=.(2)当t为何值时,以点P、B、Q为顶点的三角形与△AOB相似?(3)若四边形OPQA的面积为y,试写出y与t的函数关系式,并求出t取何值时,四边形OPQA的面积最小?(4)在y轴上是否存在点E,使点P、Q在移动过程中,以B、E、Q、P为顶点的四边形的面积是一个常数?若存在请求出点E的坐标;若不存在,请说明理由.11.如图,在平面直角坐标系中,等边△ABC的顶点A,B的坐标分别为(0,0),(6,0),点D是x轴上的一个动点,连接CD,将△ACD绕点C逆时针旋转60°得到△BCE,连接DE.(1)点C的坐标为,△CDE为三角形;(2)当点D在线段AB上运动时,四边形CDBE的周长是否存在最小值?若存在,求出四边形CDBE的周长最小值及此时点D的坐标;若不存在,请说明理由;(3)当△BDE是直角三角形时,请直接写出点D的坐标.12.如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA 上由点C向点A运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过秒后,点P与点Q第一次在△ABC的AC边上相遇?(在横线上直接写出答案,不必书写解题过程)13.如图,点A坐标是(0,0),点C坐标是(2,2),现有E、F两点分别从点D(0,2)和点B(2,0)向下和向右以每秒一个单位速度移动,Q为EF中点.设运动时间为t.(1)在运动过程中始终与线段EC相等的线段是;四边形CEAF面积=.(2)当t=1秒时,求线段CQ的长.(3)过点B作BP平行于CF交EC于点P.当t=▲ 时,线段AP最短,此时作直线EP与x轴交于点K,试证明,点K是线段AB的黄金分割点.14.如图1,已知△ABC是边长为3cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点都停止运动,设点P的运动时间为t(s).(1)当运动时间为t秒时,则BQ的长为cm,BP的长为cm.(用含t的式子表示)(2)当t为何值时,△PBQ是直角三角形;(3)如图2,连接AQ,CP相交于点M,则点P,Q在运动的过程中,∠CMQ的大小会变化吗?若变化,请说明理由.若不变,请直接写出它的度数.15.旋转是一种重要的图形变换,当图形中有一组邻边相等时往往可以通过旋转解决问题.(1)尝试解决:如图①,在等腰Rt△ABC中,∠BAC=90°,AB=AC,点M 是BC上的一点,BM=1cm,CM=2cm,将△ABM绕点A旋转后得到△ACN,连接MN,则AM=cm.(2)类比探究:如图②,在“筝形”四边形ABCD中,AB=AD=a,CB= CD,AB⊥BC于点B,AD⊥CD于点D,点P、Q分别是AB、AD上的点,且∠PCB+∠QCD=∠PCQ,求△APQ的周长.(结果用a表示)(3)拓展应用:如图③,已知四边形ABCD,AD=CD,∠ADC=60°,∠ABC=75°,AB=2√2,BC=2,求四边形ABCD的面积.16.如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,ΔCQP的面积为Scm2.(1)在P、Q两点移动的过程中,ΔCQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由;(2)当运动时间为多少秒时,ΔCPQ与ΔCAB相似.答案解析部分1.【答案】(1)1(2)34(3)解:点P 与点Q 重合时,由(1)知t =1;当点D 在AB 上时,如下图所示:此时DP =CP =BQ =t ,∵∠DPB =∠ACB =90°,∠DBP =∠ABC ,∴△DBP ∽△ABC ,∴DP PB =CA CB =32,∴PB =23DP =23t ,∵CP +PB =CB ,∴t +23t =2, 解得t =65, ∴CE =65.∵QF ∥AB ,∴∠FQC =∠ABC ,又∠FCQ =∠ACB =90°,∴△FQC ∽△ABC ,∴CQ CB =CF CA ,即2−652=CF 3, ∴CF =65,∴t =65时,点E 与点F 重合;当点P 到达B 点时,此时t =2.当点P 在Q 、B 两点之间(不包括Q 、B 两点)时,其运动过程可分析如下:①当1<t≤65时,如下图所示,此时重合部分为梯形GDPQ.则PQ=CP+BQ−CB=2t−2,PD=t,由△FQC∽△ABC得:CF=32CQ=32×(2−t)=3−32t,∴EF=CF−CE=3−32t−t=3−52t,∵QF∥AB,∴∠A=∠EFG,又∠ACB=∠FEG=90°,∴△ABC∽△FGE,∴FE CA=EG CB,∴EG=23EF=23×(3−52t)=2−53t,∴DG=ED−EG=t−(2−53t)=83t−2,∴S梯形GDPQ=12(PQ+DG)⋅DP=12(2t−2+83t−2)⋅t=73t2−2t,∴S=73t2−2t;②当65<t<2时,如下图所示,此时重合部分为一个多边形.则CP=BQ=t,CQ=BP=2−t,易知△ABC∽△FQC∽△MBP∽△MND,可得CF=32CQ=32(2−t)=3−32t,MP=32BP=32(2−t)=3−32t,∴DM=DP−MP=t−(3−32t)=52t−3,∴DN=23DM=23×(52t−3)=53t−2,∴S=S正方形EDPC−S△CFQ−S△MDN=CP2−12CF⋅CQ−12DM⋅DN=t2−12(3−32t)⋅(2−t)−12(52t−3)⋅(53t−2)=−116t2+8t−6;综上,当点P在Q、B两点之间(不包括Q、B两点)时,S与t之间的函数关系式为:S={73t2−2t(1<t≤65)−116t2+8t−6(65<t<2).2.【答案】(1)解:如图1中,点F在AC上,点E在BD上时,①当CFCE=CDAC时,△CFE△△CDA,∴5t16−4t=810,∴t= 64 41,②当CFCE=ACCD时,即5t16−4t= 108,∴t=2,当点F在AB上,点E在CD上时,不存在△EFC和△ACD相似,综上所述,t= 6441s或2s时,△EFC和△ACD相似.(2)解:不存在.理由:如图2中,当点F在AC上,点E在BD上时,作FH△BC 于H,EF交AD于N.∵CF=5t.BE=4t,∴CH=CF•cosC=4t,∴BE=CH,∵AB=AC,AD△BC,∴BD=DC,∴DE=DH,∵DN△FH,∴EDDH=ENNF=1,∴EN=FN,∴S△END=S△FND,∴△EFD被AD分得的两部分面积相等,同法可证当点F在AB上,点E在CD上时,△EFD被AD分得的两部分面积相等,∴不存在某一时刻,使得△EFD被AD分得的两部分面积之比为3:5.(3)解:①如图3中,当以EF为直径的△O经过点A时,△O与线段AC有两个交点,连接AE,则△EAF=90°.由ACEC=cosC= 45,可得1016−4t=45,∴t=78,∴0≤t<78时,△O与线段AC只有一个交点.②如图4中,当△O与AC相切时,满足条件,此时t= 6441.③如图5中,当△O与AB相切时,cosB= BFBE,即45=20−5t4t,解得t= 10041.④如图6中,△O 经过点A 时,连接AE ,则△EAF=90°.由cosB= AB AE = 45 ,即 104t = 45 ,t= 258, ∴258<t≤4时,△O 与线段AC 只有一个交点. 综上所述,当△O 与线段AC 只有一个交点时,0≤t < 78 或 6441 或 10041 或 258<t≤4 3.【答案】(1)(8,0);(0,6)(2)(3,0)(3)解:∵OA=8,v=2,∴t=8÷2=4,∴P 从O 运动到A 的时间为4秒,∴当0≤t≤4时,P 在线段OA 上运动.OP=2t ,PA=8-OP=8-2t ,S=S △BAP = 12 •PA•OB= 12•(8-2t )•6=24-6t. 当S=8时,8=24-6t ,解得:t= 83 ,∴OP=2t =2× 83 = 163 ,∴P ( 163,0).答:S= 24-6t (0≤t≤4),当S=8时,P ( 163,0).4.【答案】(1)解:能.理由如下:在ΔDFC中,∠DFC=90°,∠C=30°,DC=4t,∴DF=2t,又∵AE=2t,∴AE=DF,∵AB⊥BC,DF⊥BC,∴AE//DF,又∵AE=DF,∴四边形AEFD为平行四边形,当AE=AD时,四边形AEFD为菱形,即40−4t=2t,解得t=20 3.∴当t=203秒时,四边形AEFD为菱形.(2)解:①当∠DEF=90°时,由(1)知四边形AEFD为平行四边形,∴EF//AD,∴∠ADE=∠DEF=90°,∵∠A=60°,∴∠AED=30°,∴AD=12AE=t,又AD=40−4t,即40−4t=t,解得t=8;②当∠EDF=90°时,四边形EBFD为矩形,在RtΔAED中∠A=60°,∴∠ADE=90°−∠A=30°,∴AD=2AE,即40−4t=4t,解得t=5.③若∠DFE =90°,则E 与B 重合,D 与A 重合,此种情况不存在.综上所述,当t =8或5秒时,ΔDEF 为直角三角形.5.【答案】(1)解:过C 作CM△x 轴于M 点,如图1,∵CM△OA ,AC△AB ,∴△MAC+△OAB= 90° ,△OAB+△OBA= 90°则△MAC=△OBA在△MAC 和△OBA 中 {∠CMA =∠AOB =90∠MAC =∠OBA AC =BA∘则△MAC△△OBA(AAS)则CM=OA=2,MA=OB=4,则点C 的坐标为(−6,−2);(2)解:过D 作DQ△OP 于Q 点,如图2,则OP−DE=PQ,△APO+△QPD= 90° ,△APO+△OAP= 90° ,则△QPD=△OAP ,在△AOP 和△PDQ 中 {∠AOP =∠PQD =90∘∠QPD =∠OAP AP =PD则△AOP△△PDQ(AAS)∴OP−DE=PQ=OA=2;(3)解:结论②是正确的,m+n=−4,如图3,过点F 分别作FS△x 轴于S 点,FT△y 轴于T 点,则FS=FT=2,△FHS=△HFT=△FGT ,在△FSH 和△FTG 中 {∠FSH =∠FTG =90∘∠FHS =∠FGT FS =FT则△FSH△△FTG(AAS)则GT=HS ,又∵G(0,m),H(n,0),点F 坐标为(−2,−2),∴OT═OS=2,OG=|m|=−m ,OH=n ,∴GT=OG−OT=−m−2,HS=OH+OS=n+2,则−2−m=n+2,则m+n=−4.6.【答案】(1)解:AB ,BC ,CD 三边的数量关系是:AB+CD =BC , 理由如下:∵△AEB+△AED =△BED ,△EDC+△C =△BED ,且△AED =△C ,∴△AEB =△EDC ,在△ABE 和△ECD 中,{∠B =∠C ∠AEB =∠EDC AE =ED,∴△ABE△△ECD (AAS ),∴AB =EC ,BE =DC ,∴AB+CD =BE+EC =BC ;(2)解:如图,过D 作BD 垂线B'D 且使得B'D =BD ,连接B'E ,∵△EDF =△B'DB =90°,∴△BDF+△B'DF =△B'DF+△B'DE ,∴△BDF =△B'DE ,在△B'DE 与△BDF 中,{B ′D =BD ∠BDF =∠B ′DE DE =DF,∴△B'DE△△BDF (SAS ),∴BF =B'E ,∵点到直线垂线段最短,∴B'E△AC 时,B'E 取最小值,过点B'作B'G△AC 交AC 于G ,∵△C =△CDB'=△CGB'=90°,∴四边形CDB'G 为矩形,∴B'G =CD =3,CG =B'D =BD =8﹣3=5,∴BF 取最小值时AE =AG =AC ﹣CG =1,BF 最小值为B'G =3.7.【答案】(1)0≤t≤7;解:②证明:如图1中,由题意点P 运动到AB 的中点时,t =5, ∴CQ =5×2﹣8=2, ∵△ACB =90°,PA =PB ,∴PC =PA =PB =5, ∴△PCQ =△A , ∵QC AQ =24=12 , CP AB =12, ∴QC AQ =CP AB , ∴△QCP△△CAB ,(2)解:①如图2中,当PQ△AC 时,△PQB =△C =90°,∵PQ△AC ,∴BQ BC =BP AB,∴2t 8=10−t 10, 解得: t =207; ②如图3中,当△QPB =90°时,∵△QPB =△ACB =90°,△B =△B ,∴△BPQ△△BCA ,∴PB BC =BP BA, ∴10−t 8=2t 10, 解得: t =5013; 综上所述,满足条件的t 的值为: 207 或 5013. 8.【答案】(1)BD△CE ;BC=CD+CW 尝试探究:(2)解: BD ⊥CE 成立,数量关系不成立,关系为 BC =CE −CD . 理由:如图2中,由 (1) 同理可得,∵∠BAC =∠DAE =90∘ ,∴∠BAC +∠CAD =∠DAE +∠CAD即 ∠BAD =∠CA E ,∴ 在 △ABD 和 △ACE 中,{AB =AC ∠BAD =∠CAE AD =AE,∵△ABD △ △ACE(SAS) ,∴BD =CE , ∠ACE =∠ABC ,∵AB =AC ,∴∠ABC =∠ACB =45∘ ,∴BD =BC +CD ,即 CE =BC +CD , ∠ACE +∠ACB =90∘ , ∴BC =CE −CD ; BD ⊥CE ;拓展延伸:(3)解:如图3中,由 (1) 同理可得,∵∠BAC=∠DAE=90∘,∴∠BAC−∠BAE=∠DAE−∠BAE,即∠BAD=∠EAC,易证△ABD△ △ACE(SAS),∴BD=CE=2,∠ACE=∠ABD=135∘,∴CD=BC+BD=BC+CE=8,∵∠ACB=45∘∴∠DCE=90∘,在Rt△DCE中,由勾股定理得DE2=DC2+CE2=82+22=68,∴DE=2√17.9.【答案】(1)∵△ABC为等边三角形,∴AB=AC,△B=△PAC=60°,∵点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,∴AP=BQ,在△APC和△BQA中{AP=BQ∠PAC=∠B AC=AB,∴△APC△△BQA(SAS),∴△BAQ=△ACP,∴△CMQ=△CAQ+△ACP=△BAQ+△CAQ=△BAC=60°,∴在P、Q运动的过程中,△CMQ不变,△CMQ=60°;(2)∵运动时间为ts,则AP=BQ=t,∴PB=4-t,①当△PQB=90°时,∵△B=60°,∴PB=2BQ,∴4-t=2t,解得t=4 3,②当△BPQ=90°时,∵△B=60°,∴BQ=2PB ,∴t=2(4-t ),解得 t =83, ∴当t 为 43 s 或 83s 时,△PBQ 为直角三角形 10.【答案】(1)6-t ;12-2t(2)解:当 ∠BPQ =∠BOA 时,即 PQ//OA ,则 △BPQ ∼△BOA , ∴BP BO =BQ BA ,即 6−t 6=2t 12, 解得: t =3 ;当 ∠BPQ =∠A 时,则 △BPQ ∼△BAO ,∴BP BA =BQ BO ,即 6−t 12=2t 6, 解得: t =65; ∴当 t =65秒或3秒时,以点P 、B 、Q 为顶点的三角形与 △AOB 相似 (3)解: y =S △OAB −S △BPQ =12×6×12−12×2t ×(6−t)=t 2−6t +36=(t −3)2+27 ,∵a =1 ,∴t =3 时,y 有最小值是27;(4)解:存在,理由如下:当E 在y 轴负半轴上时,以B 、Q 、E 、P 为顶点不能形成四边形; 当E 在y 轴正半轴上时,设 E(0,m) ,∴以B 、Q 、E 、P 为顶点的四边形的面积=梯形 BQEO 的面积- △OPE 的面积, 即 12×6×(m +2t)−12×m ×t =(6−12m)t +3m , 当以B 、Q 、E 、P 为顶点的四边形的面积是一个常数,则 6−12m =0 ,解得: m =12 ,∴点E 的坐标为 (0,12) ;11.【答案】(1)(3,3 √3 );等边(2)解:存在,理由如下:∵△ABC 为等边三角形,∴△ACD+△DCB=60°,∵△DCE为等边三角形,∴△BCE+△DCB=60°,∴△ACD=△BCE,在△ACD和△BCE中,{CA=CB∠ACD=∠BCECD=CE,∴△ACD△△BCE(SAS)∴AD=BE,∴四边形CDBE的周长=CD+DB+BE+CE=CD+DB+AD+CE=6+2CD,当CD最小时,四边形CDBE的周长存在最小值,由垂线段最短可知,CD△AB时,CD最小,CD的最小值为3 √3,∴四边形CDBE的周长最小值为6+6 √3,此时点D的坐标为(3,0)(3)解:由(2)可知,△ACD△△BCE,∴BE=AD,∴△DBE=120°或60°,不能为90°,如图②,△DEB=90°时,△DBE=60°,∴△BDE=30°,∴DB=2BE,∵BE=AD,∴AD=AB=6,此时,点D的坐标为(-6,0),如图③,当△BDE=90°时,△ADC=90°-60°=30°,∵△CAD=60°,∴△ACD=90°,又△ADC=30°,∴AD=2AC=12,此时,点D的坐标为(12,0),综上所述,当△BDE是直角三角形时,点D的坐标为(-6,0)或(12,0).12.【答案】(1)解:①全等,理由如下:∵t=1秒,∴BP=CQ=1×1=1厘米,∵AB=6cm,点D为AB的中点,∴BD=3cm.又∵PC=BC−BP,BC=4cm,∴PC=4−1=3cm,∴PC=BD.∴△BPD≅△CQP;②假设△BPD≅△CQP,∵v P≠v Q,∴BP≠CQ,又∵△BPD≅△CQP,∠B=∠C,则BP=CP=2,BD=CQ=3,∴点P,点Q运动的时间t=BP1=2秒,∴v Q=CQ t=32=1.5cm/s;(2)2413.【答案】(1)FC;4(2)解:∵△CDE△△CBF,∴EC=FC,△DCE=△BCF,∵△DCE+△ECB=90°,∴△BCF+△ECB=90°,即△ECF=90°,∴△ECF是等腰直角三角形,当t=1时,DE=1,在Rt△CDE中,由勾股定理得:CE=√DE2+CD2=√12+22=√5,∴EF=√2CE=√2× √5=√10,∵Q为EF中点,∴CQ=12EF=12×√10=√102;(3)解:t=(√5+1)s∵BP△CF,△ECF=90°,∴△BPC=90°,∴点P的轨迹在以BC为直径的圆弧上,设BC的中点为G,连接AG,如图2所示:当点P在AG上时,AP最短,此时,PG=BG=1,在Rt△ABG中,由勾股定理得AG=√AB2+BG2=√22+12=√5,∴AP=AG﹣PG=√5﹣1,∵BC△DE,∴△AEP=△GCP,∵GC=GP,∴△GCP=△GPC,∵△GPC=△APE,∴△AEP=△APE,∴AP=AE=√5﹣1,∴E (0,1﹣ √5 ),∴DE =2﹣(1﹣ √5 )= √5 +1,∴t =( √5 +1)s ,故答案为:( √5 +1)s ;设CE 的解析式为:y =kx+b (k≠0),将C (2,2)、E (0,1﹣ √5 )代入解析式得: {2k +b =2b =1−√5, 解得: {k =√5+12b =1−√5,∴CE 的解析式为:y = √5+12x+1﹣ √5 , 令y =0,x =3﹣ √5 ,∴K (3﹣ √5 ,0),∴BK =2﹣(3﹣ √5 )= √5 ﹣1,∴BK AB = √5−12, ∴点K 是线段AB 的黄金分割点.14.【答案】(1)t ;(3-t )(2)解:由(1)得:AP =BQ =tcm ,BP =(3−t)cm ,①如图1,当∠PQB =90°时,∵△ABC 是等边三角形,∴∠B =60°,∴∠BPQ =30°,∴PB =2BQ ,即3−t =2t ,解得:t =1,②如图2,当∠BPQ =90°时,∵∠B=60°,∴∠BQP=30°,∴BQ=2BP,即t=2(3−t),解得:t=2,∴当t=1或t=2时,△PBQ为直角三角形;(3)解:不变,∠CMQ=60°.15.【答案】(1)√102(2)解:∵AD⊥CD,CB=CD,AB⊥BC,∴将△BCP绕点C旋转后得到△DCM,此时BC与DC重合,∴△BCP△△DCM,∴△DCM=△PCB,BP=DM,PC=CM,∵∠PCB+∠QCD=∠PCQ,∴∠DCM+∠QCD=∠PCQ,∴∠QCM=∠PCQ,∵PC=CM,QC=QC,∴△QCP△△QCM,∴PQ=QM,∴△APQ的周长=AQ+AP+PQ= AQ+AP+QM= AQ+AP+DQ+DM= AQ+AP+DQ+BP=AD+AB,∵AB=AD=a,∴△APQ的周长=2a;(3)解:如图3,连接BD,由于AD=CD,所以可将△BCD绕点D顺时针方向旋转60°,得到△DAB′,连接BB′,延长BA,作B′E△BE;{AD=CD∠CDB=∠ADB′BD=B′D∴△BCD△△B′AD∴S四边形ABCD=S四边形BDB′A,∵△ABC=75°,△ADC=60°,∴△BAB′=135°∴△B′AE=45°,∵B′A=BC=2∴B′E=AE= √2,∴BE=AB+AE=2 √2+ √2= 3√2,∴BB′=√(√2)2+(3√2)2=2√5∵等边△DBB′,∴BB′上的高= =2√5×√32=√15,∴.SΔABB′=12⋅AB⋅B′E=12×2√2×√2=2∴SΔBDB′=12×2√5×√15=5√3,∴S四边形ABCD=S四边形BDB′A=S△BDB′-S△ABB′= =5√3−2;16.【答案】(1)解:在矩形ABCD中,∵AB=6cm,BC=8cm,∴AC=10cm,AP=2tcm,PC=(10−2t)cm,CQ=tcm,过点P作PH⊥BC于点H,则PH=35(10−2t)cm根据题意,得12t•35(10−2t)=3.6,解得:t1=2,t2=3,∴ΔCQP的面积等于3.6cm2时,t的值为2或3.(2)解:如图1,当∠PQC=90∘时,PQ⊥BC,∵AB⊥BC,AB=6,BC=8,QC=t,PC=10−2t,∴ΔPQC△ ΔABC,∴PCAC=CQBC,即10−2t10=t8,解得t=4013(秒)如图2,当∠CPQ=90∘时,PQ⊥AC,∵∠ACB=∠QCP,∠B=∠QPC,∴ΔCPQ△ ΔCBA,∴CPBC=CQAC,即10−2t8=t10,解得t=257(秒)综上所述,t为4013秒与257时,ΔCPQ与ΔCBA相似.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴AB=2OB=2 ,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
∴ ,
整理得:x2﹣x﹣6=0,
∴(x﹣3)(x+2)=0,
∴x1=3,x2=﹣2,
∴AC=3 ;
②点C与点M重合时,如图2,同理得:∠AMB=90°, ,
设BD=x,则AC= x,
在△AMB中,∠AMB=180°﹣(∠MAB+∠ABM)=180°﹣(∠OAB+∠ABM+∠DBO)=90°;
(3)拓展延伸
①点C与点M重合时,如图1,同(2)得:△AOC∽△BOD,
∴∠AMB=90°, ,
设BD=x,则AC= x,
Rt△COD中,∠OCD=30°,OD=1,
∴CD=2,BC=x﹣2,
(2)将线段BC向右平移至AD(点B对应点A,点C对应点D).
①当点M为x轴上任意点(不与原点重合),ME、CF分别平分∠CMO与∠DCM,若∠AME=α,∠DCF=β,试用含α的代数式表示β;
②点P为线段CD上一点(不与点C、D重合),P的横坐标为t,连接BP、AC,BP交y轴于点E,交AC于点Q,若△CQE与△PQA的面积分别为S1,S2,试用含t的代数式表示S2﹣S1.
∴∠FCM=∠EMC=β,
∴∠AMC=180°﹣2β,
∵∠AME=∠AMC+∠EMC,
填空:① 的值为;
②∠AMB的度数为.
(2)类比探究:如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,CD=2OD,AB=2OB,连接AC交BD的延长线于点M.请求出 的值及∠AMB的度数,并说明理由;
(3)拓展延伸:在(2)的条件下,将△OCD绕点O在平面内旋转,AC、BD所在直线交于点M,若OD=1,OB= ,请直接写出当点C与点M重合时AC的长.
(1)证明:如图①中,连接OP.
∵PA⊥OM,PB⊥ON,
∴∠OAP=∠OBP=90°,
∵OA=OB,OP=OP,
∴Rt△OPA≌Rt△OPB(HL),
∴PA=PB.
(2)如图②中,
∵∠PAO=∠PBO=90°,
∴∠AOB+∠APB=180°,
∵∠CPD+∠AOB=180°,
∴∠CPD=∠APB,
∴∠APC=∠BPD,
解:(1)问题发现
①如图1,∵∠AOB=∠COD=50°,
∴∠COA=∠DOB,
∵OC=OD,OA=OB,
∴△COA≌△DOB(SAS),
∴AC=BD,
∴ =1,
②∵△COA≌△DOB,
∴∠CAO=∠DBO,
∵∠AOB=50°,
∴∠OAB+∠ABO=130°,
在△AMB中,∠AMB=180°﹣(∠CAO+∠OAB+∠ABD)=180°﹣(∠DBO+∠OAB+∠ABD)=180°﹣130°=50°,
故答案为:①1;②50°;
(2)类比探究
如图2, = ,∠AMB=90°,理由是:
Rt△COD中,∠DOC=90°,CD=2DO,
∴∠DCO=30°,
∴ =tan30°= ,
同理得: =tan30°= ,
∴ ,
∵∠AOB=∠COD=90°,
∴∠AOC=∠CAO=∠DBO,
t=25.
④当30≤t<39时,如图3﹣3中,∠APG=(10t﹣300)°,∠BPH=2t,
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时10t﹣300=2t,
t=37.5,
综上所述,满足条件的t的值为15s或25s或37.5s.
2、(1)问题发现:
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=50°,连接AC,BD交于点M.
∵PA=PB,∠PAC=∠PBD=90°,
∴△PAC≌△PBD(ASA),
∴AC=BD,
∴OC+OD=OA+AC+OB﹣BD=2OA=13,
∴OA=6.5.
(3)设点P的旋转时间为t秒.
①当0<t<12时,不存在.
②当12≤t<21时,如图3﹣1中,∠APG=(10t﹣120)°,∠BPH=2t°,
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时10t﹣120=2t,
t=15.
③当21≤t<30时,如图3﹣2中,∠APG=180°﹣∠APA′=180°﹣(10t﹣120)°=(300﹣10t)°,∠BPH=2t,
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时300﹣10t=2t,
解:(1)如图1中,
∵ =0,
又∵ ≥0,|b+2|≥0,(c﹣4)2≥0,
∴a=5,b=﹣2,c=4,
∴A(5,0),B(﹣2,0),C(0,4),
∴OA=5,OB=2,OC=4,
∴AB=OB+OA=2+5=7,
∴S△ABC= •AB•OC= ×7×4=14.
(2)①如图2﹣1中,当点E在射线OB上时,α+β=90°
专题47 三角形中的旋转综合问题
1、如图,点P是∠MON内的一点,过点P作PA⊥OM于点A,PB⊥ON于点B,且OA=OB.
(1)求证:PA=PB;
(2)如图②,点C是射线AM上一点,点D是线段OB上一点,且∠CPD+∠MON=180°,若OC=8,OD=5.求线段OA的长.
(3)如图③,若∠MON=60°,将PB绕点P以每秒2°的速度顺时针旋转,12秒后,PA开始绕点P以每秒10°的速度顺时针旋转,PA旋转270°后停止,此时PB也随之停止旋转.旋转过程中,PA所在直线与OM所在直线的交点记为G,PB所在直线与ON所在直线的交点记为H.问PB旋转几秒时,PG=PH?
理由:∵CD∥AM,
∴∠DCM+∠AMC=180°,
∵∠DCF= ∠DCM=β,∠AME= ∠AMC=α,
∴α+β=90°.
当点M在线段AB上时,如图2﹣2中,α+β=180°.
理由:∵CD∥AM,
∴∠DCM+∠AMC=180°,∠DCM=∠CMB,
∵∠DCM=2∠DCF=2β,∠FCM= ∠DCM,∠EMC= ∠CMB,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
∴ +(x+2)2= ,
整理得x2+x﹣6=0,
∴(x+3)(x﹣2)=0,
∴x1=﹣3,x2=2,
∴AC=2 ;
综上所述,AC的长为3 或2 .
3、已知在平面直角坐标系中,A(a,0),B(b,0)、C(0,c),其中a、b、c满足 =0.
(1)求△ABC的面积;
