飞机动力学仿真模型误差分析及调整
利用Matlab进行动力学建模和仿真分析的基本原理

利用Matlab进行动力学建模和仿真分析的基本原理引言:动力学建模和仿真分析是工程领域中重要的研究方法之一。
利用动力学建模和仿真分析,可以通过数学模型模拟和分析物体的运动、力学响应和控制系统的性能。
而Matlab作为一种功能强大的科学计算软件,为动力学建模和仿真提供了广泛的工具和函数库。
本文将介绍利用Matlab进行动力学建模和仿真分析的基本原理和方法。
一、动力学建模动力学建模是动力学仿真的第一步,它是将实际工程问题转化为数学模型的过程。
在动力学建模中,首先需要确定系统的运动学和动力学特性,然后利用合适的数学模型来描述这些特性。
1. 运动学特性的确定运动学是研究物体运动的几何性质和规律的学科。
在动力学建模中,我们需要确定系统的位置、速度和加速度等运动学变量。
这些变量可以通过对实际系统的观测和测量得到,也可以通过数学关系和几何推导来求解。
2. 动力学特性的确定动力学是研究物体运动的力学性质和规律的学科。
在动力学建模中,我们需要确定系统的力学特性,包括质量、惯性系数、弹性系数和阻尼系数等。
这些特性可以通过实验测量和物理原理推导得到。
3. 数学模型的选择在确定了系统的运动学和动力学特性后,我们需要选择合适的数学模型来描述系统的动力学行为。
常用的数学模型包括常微分方程、偏微分方程和差分方程等。
根据系统的特点和求解的需求,选择适当的数学模型非常重要。
二、动力学仿真分析动力学仿真分析是利用数学模型来模拟和分析系统的运动和响应。
通过仿真分析,我们可以预测系统在不同工况下的运动状态、力学响应和控制性能。
1. 数值解方法数值解方法是求解动力学数学模型的常用方法。
常见的数值解方法包括欧拉方法、改进欧拉方法和四阶龙格-库塔方法等。
通过数值解方法,我们可以将动力学方程离散化,并利用计算机进行求解。
2. 仿真参数的选择在进行动力学仿真分析时,我们需要选择合适的仿真参数。
仿真参数包括系统的初始条件、外部输入信号和仿真时间等。
航空飞行控制系统中的飞行动力学建模与仿真

航空飞行控制系统中的飞行动力学建模与仿真航空飞行控制系统的设计和开发是航空运输领域不可或缺的一部分。
在这个系统中,飞行动力学建模与仿真是重要的组成部分,用于评估飞机的性能和飞行特性,以提升飞行安全和效率。
飞行动力学建模是指将飞机的运动、力学和控制系统建立数学模型,以描述和预测飞机在不同飞行条件下的行为。
这个过程是根据飞机的气动特性、机械特性和控制特性进行建模。
通常,飞行动力学建模分为长期动力学和短期动力学。
长期动力学模型主要关注飞机在稳定飞行状态下的运动。
这包括飞机的纵向稳定性、横向稳定性和方向稳定性等方面。
纵向稳定性模型涉及飞机的俯仰运动,包括速度、攻角、俯仰角和俯仰率等参数的关系。
横向稳定性模型研究航向和滚转运动,包括滚转角、滚转速度和侧滑角等参数的关系。
方向稳定性模型考虑飞机的偏航和转弯运动,包括偏航角、偏航速度和转弯半径等参数的关系。
短期动力学模型主要关注飞机在非稳定飞行状态下的运动,如起飞、爬升、下降、盘旋和着陆等飞行阶段。
短期动力学模型包括非线性运动方程和运动修正方程。
非线性运动方程描述飞机在不同飞行阶段的非线性运动,如加速度、姿态角和控制输入等参数的关系。
运动修正方程用于校正非线性运动方程中的误差,以提高模型的准确性和可靠性。
飞行动力学建模的目的是为飞行控制系统提供准确的输入,以实现对飞机运动的精确控制。
飞行仿真是利用飞行动力学模型进行虚拟飞行试验,并评估飞机在不同操作和环境条件下的性能和飞行特性。
飞行仿真可以模拟飞机在各种飞行阶段的动力学响应,如加速度、姿态角和控制输入等参数的变化。
通过飞行仿真,可以评估飞机在不同飞行条件下的稳定性、敏感性、品质和安全性。
飞行动力学建模与仿真在航空飞行控制系统中的应用非常广泛。
它被广泛用于飞机设计和参数优化,飞行虚拟训练和飞行状态监测等领域。
在飞机设计和参数优化中,飞行动力学建模与仿真可以帮助工程师评估不同设计方案的性能和操控特性。
在飞行虚拟训练中,飞行动力学仿真可以提供逼真的飞行环境,提高飞行员的飞行技能和应急响应能力。
飞行器动力系统仿真设计方法综述和改进方案介绍

飞行器动力系统仿真设计方法综述和改进方案介绍动力系统是飞行器的关键组成部分之一,对飞行器的性能和安全性具有重要影响。
如何有效地进行动力系统的设计和优化是当前飞行器研发领域的热点问题之一。
本文将介绍飞行器动力系统的仿真设计方法的现状,以及一些改进方案。
一、飞行器动力系统仿真设计方法综述1. 机理模型法机理模型法是飞行器动力系统仿真设计的一种基本方法。
它以数学模型来描述飞行器动力系统的工作原理和特性。
通过建立数学关系,可以预测动力系统的性能、燃烧过程以及其它相关参数。
这种方法具有较高的精确度,可以提供详尽的仿真结果,为飞行器动力系统的设计和优化提供了可靠的依据。
2. 传统优化算法传统优化算法如遗传算法、粒子群算法等被广泛应用于飞行器动力系统的仿真设计中。
这些算法通过对动力系统的不同参数进行变异和组合,搜索最优的设计方案。
传统优化算法相对简单易实现,但在面对复杂的多参数优化问题时效率较低。
3. 基于人工智能的优化算法近年来,随着人工智能技术的快速发展,一些基于深度学习和强化学习的优化算法在飞行器动力系统的仿真设计中获得了广泛关注。
这些算法通过自主学习和适应性调整,可以更高效地搜索最优设计方案。
然而,这些算法需要大量的数据支持和计算资源,实际应用面临一定的挑战。
二、改进方案介绍1. 建立动力系统模型的精确度提升针对机理模型法中数学模型的不足,可以通过提高模型的精确度来提升仿真结果的准确性。
可以采用更复杂的物理模型和实验数据来验证模型的可靠性,同时结合实际测试数据进行校正,以获得更准确的仿真结果。
2. 算法改进和混合优化方法传统优化算法在面对复杂多参数的优化问题时效率较低。
可以通过改进算法,如引入自适应权重、动态调整变异因子等,提高算法的搜索效率。
另外,可以将不同的优化算法进行混合使用,充分发挥各自的优点,从而更好地解决动力系统的多参数优化问题。
3. 结合人工智能技术的创新结合人工智能技术如深度学习、强化学习等,可以为飞行器动力系统的仿真设计提供创新的思路。
动力模型拟静力修正方法及误差分析

udt p ai ng,a d ise g n—nay i s a ode n t ie a l ss wa v i d. S ln n e p ltn t o s a o td t th t a u e s a e p i e i tr o ai g me h d wa d p e o mac he me s r d me s g s
e a p e e i e ha h v l p d me h d i f c e ta e ib e frm o e d tn x m lsv rf d t tt e de eo e t o se i i in nd r la l d lup a ig. Asa c s t y,t e mo e ft e o a e sud h d lo h
Ru n iCha Ya z a l t y d b ig o rwa d td wih t e ps u o sa i de p a ig meho n Ya g Be — ng ic b e sa e rd e twe sup ae t h e d t tcmo lu d t t d.W ih t e n t h u ae a a t r pd td p r me es,t o he c mpu e e u t ft e b i g o r c i i e l wi he me s r d o s td r s ls o h rd e twe oncd d wel t t a u e ne . h
mo e p tn p o e s W ih h r c eitc o c c n e t a y a c d lu dai g r c s . t c a a t rsi fr e o c p , d n mi mo e s r n fr d n o sai mo e f r d lwa ta so me i t a ttc d l o
飞机动稳定性分析中的问题及解决方法
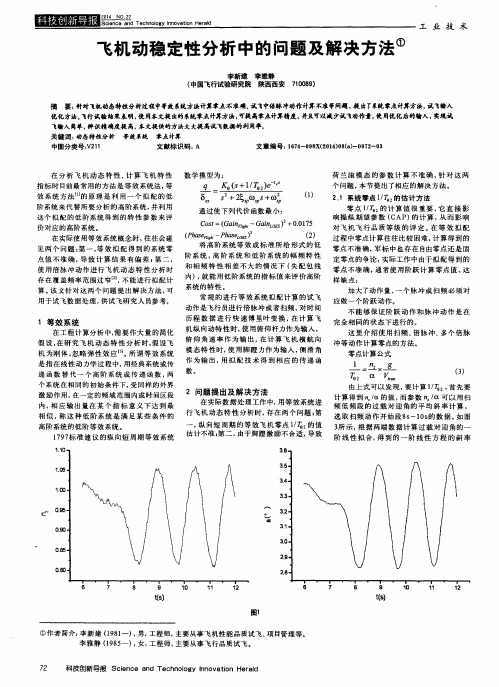
过 程 中零点计 算 往 往 比较 困 难 , 计 算 得 到 的 零点 不准 确 , 军标 中也 存 在 自由零 点 还 是 固
定 零点 的 争论 , 实 际 工作 中 由于拟 配得 到 的
零 点不 准 确 , 通 常 使 用 阶跃 计算 零点 值 , 这 样缺点: 加 大 了动 作 量 , 一个 脉 冲 或 扫 频 必须 对
要: 针对飞机动态特性分析过程中等效秉 统 方法计算零点不准确 , 试 飞中 倍脉 冲动作 计算不准等同 题, 提 出了 系 统 零点计算方法, 试飞输入
优化方法。 飞 行 试验结果表明, 使 用本文提 出的系统零点计算方法, 可 提 高零点计算精度 , 并且可以减少试飞动作量, 使 用优化后的输入 , 实现试 飞输入 简 单, 辨识精确度提 高, 本文提供的方法大大提 高试飞数据 的利用卒。
使 用 俯 仰 杆力作 为输 入 , 在 工 程计 算 分析 中, 需 要 作 大 量 的简 化 机 纵 向动 特 性 时 , 模态特性时, 使 用 脚 蹬 力作 为输 入 , 侧滑 角
作为输 出, 用 拟 配 技 术 得 到相 应 的 传 递 函
数。
这 里 介 绍使 用扫 频 、 倍脉冲、 多个 倍脉
效 系 统 方 法 …的原 理 是 利 用 一 个 拟 配 的 低
9
荷 兰 滚 模 态 的 参 数 计 算 不准 确 , 针 对 这 两 个 问题 , 本节 提 出了相应 的 解 决方 法 。
K o ( +1 / T e 2 ) P
6 甜 一
阶系统 来 代 替 所要 分 析 的高 阶系 统 , 并 利 用
使用 倍 脉 冲 动 作 进行 飞 机 动 态 特 性 分 析 时
仿真实验中的误差分析

仿真实验中的误差分析引言:仿真实验在现代科学研究中扮演着越来越重要的角色。
通过实验室环境中的数值仿真,科学家能够控制变量、模拟复杂的现象,并且可以反复进行实验以验证假设。
然而,仿真实验也存在着一定的误差。
本文将探讨仿真实验中的误差来源和分析方法。
一、建模误差:仿真实验的第一步是建模,即将实际问题转化为数学模型。
然而,在建模过程中,科学家常常需要作一些假设。
这些假设可能不完全准确,导致建模误差。
例如,在飞行器运动模拟中,科学家可能忽略了空气的摩擦阻力,或者简化了其它力的作用。
建模误差对仿真实验的结果产生直接影响,因此需要仔细评估和修正模型。
二、参数误差:在数值仿真中,科学家需要给定参数的数值。
然而,参数的数值通常是基于观察、实验或文献资料得出的,并且往往存在一定的不确定性。
当参数的数值不准确时,仿真实验结果可能与实际情况有所偏差。
因此,在仿真实验中对参数误差进行分析和校正非常重要。
三、数值误差:仿真实验是通过数值计算来获得结果的,而数值计算中存在着各种各样的误差。
例如,舍入误差是由于计算机对实数进行有限的表示而引起的,而截断误差则是由于计算过程中对无限级数、积分等进行近似计算而产生的。
科学家需要了解这些数值误差的性质和大小,以判断仿真实验结果对实际情况的准确程度。
四、算法误差:在仿真实验中,科学家需要选择合适的数值算法来求解模型。
不同的数值算法对结果的准确性和稳定性产生不同的影响。
科学家需要评估不同算法之间的误差,并选择合适的算法来进行仿真实验。
五、边界误差:仿真实验通常需要将问题的边界进行处理。
例如,计算流体力学中,科学家常常设定壁面条件和边界条件来模拟实际流动。
然而,这些边界条件往往包含一定的误差,从而影响仿真实验的结果。
科学家需要仔细评估边界条件的误差,并考虑如何在仿真实验中消除或减小这些误差。
六、灵敏度分析:灵敏度分析是评估仿真实验对参数变化的敏感程度。
通过灵敏度分析,科学家可以确定哪些参数对结果的影响最为重要,从而重点关注这些参数的误差。
飞机起飞着陆性能计算模型及其应用分析

飞机起飞着陆性能计算模型及其应用分析1. 引言1.1 背景介绍飞机起飞性能计算模型及其应用分析是飞行器设计和运行的重要研究领域。
随着航空业的迅速发展,飞机起飞性能的准确计算和分析对于确保飞行安全和提高飞行效率至关重要。
背景介绍部分将从飞机起飞着陆性能计算模型的发展历程、研究热点和应用领域等方面进行介绍。
随着航空技术的不断进步,飞机起飞性能计算模型逐渐变得复杂和精细化。
历史上,人们主要依靠经验公式和实验数据来计算飞机的起飞性能,然而这种方法往往存在一定的误差和局限性。
随着计算机技术和数值模拟方法的发展,飞机起飞性能计算模型得以更精确地建立和应用。
在当今航空产业中,飞机起飞性能计算模型已经成为飞行器设计、测试和运营的重要工具。
准确计算飞机的起飞性能可以帮助设计师优化飞机结构和性能,提高飞行效率和节约燃料。
飞机的起1.2 研究意义飞机起飞着陆性能计算模型及其应用分析在航空领域具有重要的研究意义。
在飞机设计和运行过程中,准确计算飞机的起飞和着陆性能参数是保障飞行安全的基础。
起飞和着陆是飞机飞行过程中最危险的阶段,而性能计算模型可以帮助飞行员提前预判飞机在不同条件下的性能表现,从而有效降低飞行风险。
飞机起飞和着陆的性能计算模型也对飞机制造商和航空公司具有重要意义。
通过对飞机性能的准确计算和分析,可以帮助制造商设计出更安全、更高效的飞机,提高飞机的性能和竞争力。
对于航空公司来说,准确的性能计算可以帮助他们优化飞机运行计划,提高飞行效率,节省燃料成本,增加经济效益。
飞机起飞着陆性能计算模型及其应用分析对于提高飞行安全、优化飞机设计、改善航空运营具有重要意义。
通过深入研究该领域,可以不断完善性能计算模型,提高飞机性能和安全性,推动航空领域的发展和进步。
1.3 研究目的研究目的是为了深入探讨飞机起飞着陆性能计算模型及其应用在实际飞行中的重要性和价值。
通过研究飞机的起降性能,可以帮助航空公司和飞行员更准确地评估飞机在不同环境和条件下的起飞着陆性能,从而提高飞行安全性和效率。
模态综合法在航天器动力学仿真中的精度分析

Precision Analysis of Modal Synthesis Method in Spacecraft Dynamics Simulation
子结构 2
360
1086
1
4
1
17
17
52
总主模态阶数
1446 5 18 69
最高精确结构 频率( Hz) 304290 95 328 491
8
1
6
2
3
4
2
0 100 200 300 400 500 600
(Hz)
图 2 频率截断的加速度响应
Fig. 2 Acceleration response for truncation at
主模态截断的准则是,如何既最大程度上的缩
减结构系统的自由度,又能满足精度要求。 在以往 研究中应用的方法有:频率截断法[4,5,6] 、有效模态 质量截断法[7,8] 、 势能判据截断 法[9] 等。 下 面 结 合 matlab 编程和有限元仿真的方式对于这三种方法进 行对比,建立了某卫星的有限元模型,下部分为平台 子结构 1,上部分为载荷子结构 2,如图 1 所示。
空间电子技术
2020 年第 6 期
SPACE ELECTRONIC TECHNOLOGY
77
模态综合法在航天器动力学仿真中的精度分析①
蔡一波,杜 冬∗,周爱明
( 上海卫星工程研究所,上海 201109)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Analysis and Correction of Errors in Dynamic Simulation Model of Aircraft
LIU Chun, WEI Hui
( Department of Aerospace Engineering,Shenyang Aerospace University,Shenyang Liaoning 110136 ,China) ABSTRACT: The accuracy of dynamic model has a decisive influence on fidelity of dynamic characteristics of aircraft in flight simulation. As the approximation and simplification in modeling and compute,there are certain inconformity between dynamic model and performance of aircraft in real flight. The sources of errors wre analysed and a method of revising these errors was given. Aimed at the main performance indexes of aircraft, the errors were reduced obviously by adjusting these parameters which have effect on the indexes appropriately. Therefore,the consistency between dynamic model and real flight performance is improved. KEYWORDS: Flight simulation; Dynamic model; Parameter adjustment; Performance index of aircraft
— 102 —
其中可能存在误差的参数可以在仿真模型中对其进行一定 幅度的调整, 使得用该参数所得到的性能指标与飞机实际指 标更为接近。 比如下面给出盘旋半径的计算公式: R = g V
2
ΔR = g C 槡
2 ( m + Δ m ) V2
2 2 y
ρ V S - 4 ( m + Δm)
4
2
2
- g C 槡
2 2 4 2 2
n2 f - 1 槡
= g
2 mV
2
2 4 2 2 C2 y ρ V S - 4m 槡
m 表示飞机重量, V 表示飞机飞行 式中 R 表示盘旋半径, g 为重力加速度, C y 表示飞机升力系数, 速度, ρ 表示空气密 S 为机翼面积。 度, 从( 1 ) 式可以看出所有影响 R 的参数, 由 上文分析及工程实践可知, 建模过程中可能存在误差的参数 有飞机重量 m, 升力系数 C y , 空气密度 ρ。 其中空气密度 ρ 本 对最终结果影响不明显, 因此确 身值及可调整幅度都较小, 定针对盘旋半径 R 的可调整参数为飞机重量 m 和升力系数 Cy 。 3. 2 参数调整 在对某个飞机性能指标进行参数调整时, 需要验证调整 前后动力学模型与飞机实际性能指标的吻合程度 。 飞机的实 际性能指标可以通过查阅飞机说明书上相关数据得到, 而对 动力学模型的验证理论上应该在相应的模拟器上进行模拟 飞行获取相关数据来进行验证 。 然而在模拟器上进行模拟飞 受人为因素影响非常大, 而且飞 行跟人的操作有很大关系, 机性能指标往往是在一种极限飞行状态下的数据, 在模拟器 考虑到飞行仿真动力学模 上采集这些数据准确性难以保证 。 型是通过一些输入数据根据飞行力学相关公式进行计算得 到结果, 然后反馈给模拟器进行直观输出, 因此这里省略掉 而是直接采用飞行力学相关理论对动力 模拟器的输出过程, 学模型进行飞行性能指标评价 。
3
模型中飞机主要性能参数的调整
由 2 中论述可知, 最终建立的飞机动力学仿真模型和飞
机实际飞行性能之间存在一定的偏差, 这直接影响了飞行仿 由于飞机的飞行性能主要表现为一系列性能指 真的逼真度。 标, 因此这里提出一种飞机动力学仿真模型参数调整方法, 使得在模型中所得到的飞机性能指标和飞机实际性能指标 之间的差距得到有效弥补 。 3. 1 主要性能指标及可调整参数 飞机的飞行性能主要包括以下几个方面: 基本飞行性 能、 续航性能、 机动飞行性能和起飞着陆性能等 。 衡量这些飞 定常上升率、 静升 行性能的指标主要有: 最大最小平飞速度、 限、 最大航程、 最大航时、 平飞加减速、 盘旋半径、 爬升率、 起 飞离地速度及滑跑距离和降落接地速度及滑行距离等 。 根据 飞行力学知识, 能够找出影响每一个性能指标的参数 。 对于
第 30 卷
第3 期
计
算
机
仿
真
2013 年 3 月
文章编号: 1006 - 9348 ( 2013 ) 03 - 0101 - 04
飞机动力学仿真模型误差分析及调整
刘 春, 魏 辉
( 沈阳航空航天大学 航空航天工程学部, 辽宁 沈阳 110136 ) 摘要: 飞机动力学模型精确度的高低直接决定了飞行性能的可信性, 飞机动力学模型的逼真程度很关键 。 由于在模型建立 及解算过程中采取的种种近似和简化, 导致最终建立的动力学模型和飞机实际动力学特性存在一定误差。 具体分析了建模 过程中的主要误差来源。为解决上述问题, 给出了一种弥补上述误差的方法。 针对飞机的主要性能指标, 通过对影响性能 指标的可调整参数进行适当的调整, 有效缩小了动力学模型和实际之间的误差, 提高了动力学模型和实际飞机动力学特性 之间的吻合程度。 关键词: 飞行仿真; 动力学模型; 参数调整; 飞机性能指标 中图分类号: TP391. 9 文献标识码: B
2 4 ρ0 = 0 . 12492kg·s / m 4 . 25588
2 ) 11000 米 < H ≤ 20000 米:
— 101 —
H - 11000 ρ = e - 6341. 62 ρ11 2 4 ρ11 = 0 . 037109kg·s / m
在建立好数学模型之后, 还要转化为计算机模型, 在转 化过程中及计算机模型计算时都可能产生误差 。 下面以发动 机系统建模为例说明。 在发动机研制过程中, 多数是通过解析法获得其性能 特性参数 。 通过已知的结构 、 性能参数及基本规律, 加上数 然而在飞行仿真中, 由 学推导得到数学模型并计算其结果 。 于实时性要求较高, 一般不采用解析法去获取发动机工作 参数, 而是把发动机的一些数据制作成数据表, 应用时通过 比如需要发动机的推力 查表进行插值计算得到所需数据 。 数据时, 一般研制单位会提供发动机推力曲线图, 如图 2 所 示。 在使用中, 通常是根据该图获取飞机在不同高度和马赫 数情况下的发动机可用推力的一些离散数据点, 仿真程序中 用到某一状态的推力时, 根据高度和速度情况选取合适的已 知点数据, 采用插值算法进行求解, 得到目标状态下发动机 的推力数据。 由于插值算法本身存在误差, 再加上查表过程 中一些偏差在后续计算过程中会放大, 因此最终得到的发动 机推力与实际飞行中的数据也存在误差 。
2 mV2
2 2 y 4 2 2 ρ V S - 4m
( 2) ( 1) 其中 Δm 表示飞机重量 m 的调整幅度, ΔR 表示对应 Δm 的 R 的变化幅度。 为更形象观察 Δm 和 ΔR 之间对应关系, 将 ( 2 ) 式表示为图形形式如图 3 。 由图 3 可以看出, Δm 和 ΔR 之间大致呈线性关系, 当 Δm 在 - 200 到 200 之间变化时, ΔR 在 - 30 到 30 之间变化。 同样在 ΔCy 和 ΔR 之间可以建立如下关系式及关系图 ( 图 4) 。 ΔR = g 2 mV2 ( ΔC y 槡 + Cy ) ρ V S - 4m
3 ) 20000 米 < H ≤ 32000 米: ρ =[ 1 + 4 . 615740 × 10 -6 ( H - 20000) ]-35. 1632 ρ20
2 4 ρ20 = 0 . 0089770kg·s / m
当需要某一个高度的大气密度时只需按照上述公式进 行求解。 然而在实际的大气环境中, 当受到地理位置、 季节和 昼夜等因素的影响时, 大气密度会发生变化, 该模型忽略了 考虑的只是最理想的情况 。 实际的大气中 这些因素的影响, 还存在大气紊流、 风切变和离散突风等现象, 然而这些现象 的建模十分困难, 而且计算量大, 目前还没有有效的手段能 真实的模拟这些大气特征 。 实际应用中只能采取一些简化的 这也造成了所建立的动力学模型与 数学模型或算法去近似, 飞机实际飞行状态有一定偏差 。 2. 2 飞机系统建模中的误差 飞机系统建模对整个飞机的各个系统进行模拟, 包括 飞机控制系统 、 动 力 系 统、 起 落 装 置 等 等。 飞机实际的组 没有办法用一个精确的数学模型对其进行 成非常复杂, 模拟, 只能 对 其 进 行 简化, 找出其中最基本的规律, 建立一 个近似模型。
图1
起落架系统模型 图2 某型飞机发动机可用推力曲线
以飞机起落装置为例, 起落架仿真建模的主要内容包括 缓冲装置、 轮胎、 滑动控制、 刹车等。 通常把起落架简化为一 如图 1 所示。 比如考虑轮胎的建 个质量 - 弹簧 - 阻尼系统, 模, 在轮胎内的气体是等温压缩理想条件下, 可以用图 1 中 的弹簧 - 阻尼系统来描述。 由于气体压缩的特性, 所以模型 中弹簧刚度和阻尼系数均为非线性, 刚度和阻尼系数均要由 试验来确定。 轮胎受的力可按下式计算: Ft = Kt et + Ct st Kt 、 C t 分别表示等效阻尼系数和等 其中 F t 为轮胎受力, et 、 s t 分别表示轮胎压缩量和变化率 。 效刚度系数, 该模型中考虑的是等温压缩的理想条件, 一些数据的获 取要靠试验, 而且气体压缩和弹簧 - 阻尼系统的压缩也存在 一定差别, 这些近似与简化都使得最后模拟结果与真实起落 架之间有一定误差。 2. 3 模型解算中的误差
