部编人教八数上12章专题:全等三角形中的常见解题模型
人教版八年级上册第十二章全等三角形经典题型辅助线作法

全等三角形常见辅助线作法【例1】.已知:如图6,△BCE 、△ACD 分别是以BE 、AD 为斜边的直角三角形,且BE AD =,△CDE 是等边三角形.求证:△ABC 是等边三角形.【例2】、如图,已知BC > AB ,AD=DC 。
BD 平分∠ABC 。
求证:∠A+∠C=180°.一、线段的数量关系: 通过添加辅助线构造全等三角形转移线段到一个三角形中证明线段相等。
1、倍长中线法【例. 3】如图,已知在△ABC 中,90C ︒∠=,30B ︒∠=,AD 平分BAC ∠,交BC 于点D . 求证:2BD CD =证明:延长DC 到E ,使得CE=CD,联结AE ∵∠ADE=60°∵∠C=90° ∴△ADE 为等边三角形 ∴AC ⊥CD ∴AD=DE ∵CD=CE ∵DB=DA∴AD=AE ∴BD=DE ∵∠B=30°∠C=90° ∴BD=2DC ∴∠BAC=60° ∵AD 平分∠BAC ∴∠BAD=30°∴DB=DA ∠ADE=60°DCBADCB EA【例4.】 如图,D 是ABC ∆的边BC 上的点,且CD AB =,ADB BAD ∠=∠,AE 是ABD ∆的中线。
求证:2AC AE =。
证明:延长AE 到点F,使得EF=AE 联结DF在△ABE 和△FDE 中 ∴∠ADC=∠ABD+∠BDABE =DE∵∠ABE=∠FDE∠AEB=∠FED ∴∠ADC=∠ADB+∠FDE AE=FE 即 ∠ADC = ∠ADF ∴△ABE ≌ △FDE (SAS ) 在△ADF 和△ADC 中 ∴AB=FD ∠ABE=∠FDE AD=AD ∵AB=DC ∠ADF = ∠ADC ∴ FD = DC DF =DC∵∠ADC=∠ABD+∠BAD ∴△ ADF ≌ ADC(SAS) ∵ADB BAD ∠=∠ ∴AF=AC ∴AC=2AE【变式练习】、 如图,△ABC 中,BD=DC=AC ,E 是DC 的中点,求证:AD 平分∠BAE.【小结】熟悉法一、法三“倍长中线”的辅助线包含的基本图形“八字型”和“倍长中线”两种基本操作方法,倍长中线,或者倍长过中点的一条线段以后的对于解决含有过中点线段有很好的效果。
初二年级数学八上第十二章全等三角形知识点总结复习及常考题型练习

第十二章全等三角形一、知识框架:二、知识概念:1.基本定义:⑴全等形:能够完全重合的两个图形叫做全等形.⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.理解:①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转可以得到它的全等形;③三角形全等不因位置发生变化而改变。
⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边.⑸对应角:全等三角形中互相重合的角叫做对应角.2.基本性质:⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.理解:①长边对长边,短边对短边;最大角对最大角,最小角对最小角;②对应角的对边为对应边,对应边对的角为对应角。
(3)全等三角形的周长相等、面积相等。
(4)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
3.全等三角形的判定定理:⑴边边边(SSS):三边对应相等的两个三角形全等.⑵边角边(SAS):两边和它们的夹角对应相等的两个三角形全等.⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等.⑸斜边、直角边(HL):斜边和一条直角边对应相等的两个直角三角形全等.4.证明两个三角形全等的基本思路:5.角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上.(4)三角形的三条角平分线交于三角形内部一点,并且这点到三边的距离相等6.证明的基本方法:⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证.⑶经过分析,找出由已知推出求证的途径,写出证明过程.7.学习全等三角形应注意以下几个问题:(1)要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;(2)表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;(3)“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;(4)中线倍长法、截长补短法证三角形全等。
初二物理:全等三角形经典模型及例题详解

初二物理:全等三角形经典模型及例题详解全等三角形是初中物理中重要的概念之一,它涉及到三角形的形状和属性。
全等三角形意味着两个三角形在形状和大小上完全相同。
在本文档中,我们将详细讨论全等三角形的经典模型以及解决例题的方法。
1. 全等三角形的定义全等三角形的定义是指两个三角形的对应边长和对应角度完全相等。
当两个三角形的全部对应边长和对应角度分别相等时,我们可以说它们是全等三角形。
2. 全等三角形的经典模型在初二物理中,有一些经典的全等三角形模型,它们是我们解决问题时的基础。
- SSS模型:当两个三角形的三边对应相等时,它们是全等三角形。
我们可以根据给定的三边长,推导出全等三角形的其他属性。
- SAS模型:当两个三角形的一边和两个对应角相等时,它们是全等三角形。
我们可以根据给定的一个边和两个对应角,推导出全等三角形的其他属性。
- ASA模型:当两个三角形的两个对应角和一边相等时,它们是全等三角形。
我们可以根据给定的两个角和一边,推导出全等三角形的其他属性。
3. 全等三角形的例题详解通过解决一些例题,我们可以更好地理解全等三角形的概念和应用。
例题1:已知三角形ABC和三角形DEF,它们满足AB = DE,BC = EF,∠ABC = ∠DEF。
问:是否可以得出三角形ABC和三角形DEF是全等三角形?解析:根据SSS模型,当两个三角形的三边对应相等时,它们是全等三角形。
根据题目条件,AB = DE,BC = EF,∠ABC =∠DEF,我们可以得出三角形ABC和三角形DEF是全等三角形。
例题2:已知三角形ABC和三角形DEF,它们满足AB = DE,∠ABC = ∠DEF,∠ACB = ∠DFE。
问:是否可以得出三角形ABC和三角形DEF是全等三角形?解析:根据ASA模型,当两个三角形的两个对应角和一边相等时,它们是全等三角形。
根据题目条件,AB = DE,∠ABC =∠DEF,∠ACB = ∠DFE,我们可以得出三角形ABC和三角形DEF是全等三角形。
2020年八年级数学上册第十二章模型构建专题:全等三角形中常见的解题模型

∴在△AFC 和△DEB 中, AF DE, ∠A ∠D, AC DB ∴△AFC≌△DEB(SAS).
在图③中,∵AB=CD,
∴AB-BC=CD-BC,即 AC=BD.
AF DE, 在△AFC 和△DEB 中,∠A ∠D,
AC DB
∴△AFC≌△DEB(SAS).
模型展示:(∠D=∠E=∠BAC)
2.如图,在△ABC 中,AB=AC,∠B=∠C=40°, 点 D 在线段 BC 上运动(D 不与 B、C 重合),连接 AD,作∠ADE=40°,DE 交线段 AC 于点 E. (1)若∠BDA=115°,则∠BAD= 25 °,∠DEC = 115 °;
(2)若 DC=AB,求证:△ABD≌△DCE. 证明:∵∠EDC+∠EDA+∠ADB=180°, ∠DAB+∠B+∠ADB=180°,∠B=∠EDA=40°, ∴∠EDC=∠DAB. ∵∠B=∠C,DC=AB, ∴△ABD≌△DCE(ASA).
∴∠MAC=∠NCB. 在△AMC 和△CNB 中, ∠AMC ∠CNB, ∠MAC ∠NCB, AC CB, ∴△AMC≌△CNB(AAS). ∴AM=CN,MC=NB. ∵MN=CM-CN,∴MN=BN-AM.
AF DE, ∠A ∠D, AC DB
∴△AFC≌△DEB(SAS).
(2)如果将△BDE 沿着 AD 边的方向平行移动,如图 ②,图③时,其余条件不变,结论是否成立?如果 成立,请予以证明;如果不成立,请说明理由. (2)解:在图②,图③中结 论依然成立.证明如下: 同(1)可得∠A=∠D. 在图②中, ∵点 B,C 重合,AB=CD,∴AC=BD.
模型展示:
3.如图,BE、CF 是△ABC 的高,且交于点 O,在 射线 BE 上截取 BP=AC,在射线 CF 上截取 CQ= AB.求证: (1)AP=AQ; 证明:(1)∵CF⊥AB,BE⊥AC, ∴∠AEB=∠AFC=90°. ∴∠ABE=∠ACQ=90°-∠BAC. 在△APB 和△QAC 中,
人教版八年级数学上册 第十二章 全等三角形知识归纳与题型突破(12类题型清单)
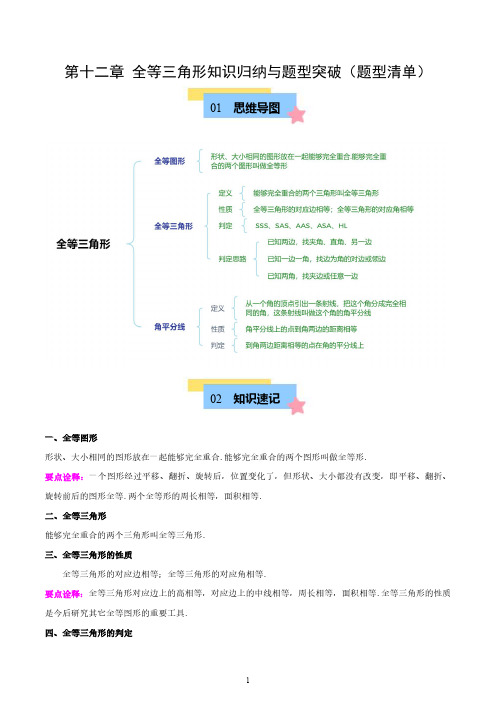
第十二章全等三角形知识归纳与题型突破(题型清单)01思维导图02知识速记一、全等图形形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.要点诠释:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.二、全等三角形能够完全重合的两个三角形叫全等三角形.三、全等三角形的性质全等三角形的对应边相等;全等三角形的对应角相等.要点诠释:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.四、全等三角形的判定五、全等三角形的证明思路SAS HL SSS AAS SAS ASA AAS ASA AAS⎧→⎧⎪⎪→⎨⎪⎪⎪→⎩⎪⎪→→⎧⎪⎪→⎧⎪⎪⎨⎨⎪→⎨⎪⎪⎪⎪⎪→⎩⎩⎪⎪→⎧⎪⎨→⎪⎩⎪⎩找夹角已知两边找直角找另一边边为角的对边找任一角找夹角的另一边已知一边一角边为角的邻边找夹边的另一角找边的对角找夹边已知两角找任一边六、全等三角形证明方法全等三角形是平面几何内容的基础,这是因为全等三角形是研究特殊三角形、四边形、相似图形、圆等图形性质的有力工具,是解决与线段、角相关问题的一个出发点.运用全等三角形,可以证明线段相等、线段的和差倍分关系、角相等、两直线位置关系等常见的几何问题.可以适当总结证明方法.1.证明线段相等的方法:(1)证明两条线段所在的两个三角形全等.(2)利用角平分线的性质证明角平分线上的点到角两边的距离相等.(3)等式性质.2.证明角相等的方法:(1)利用平行线的性质进行证明.(2)证明两个角所在的两个三角形全等.(3)利用角平分线的判定进行证明.(4)同角(等角)的余角(补角)相等.(5)对顶角相等.3.证明两条线段的位置关系(平行、垂直)的方法;可通过证明两个三角形全等,得到对应角相等,再利用平行线的判定或垂直定义证明.4.辅助线的添加:(1)作公共边可构造全等三角形;(2)倍长中线法;(3)作以角平分线为对称轴的翻折变换全等三角形;(4)利用截长(或补短)法作旋转变换的全等三角形.5.证明三角形全等的思维方法:(1)直接利用全等三角形判定和证明两条线段或两个角相等,需要我们敏捷、快速地发现两条线段和两个角所在的两个三角形及它们全等的条件.(2)如果要证明相等的两条线段或两个角所在的三角形全等的条件不充分时,则应根据图形的其它性质或先证明其他的两个三角形全等以补足条件.(3)如果现有图形中的任何两个三角形之间不存在全等关系,此时应添置辅助线,使之出现全等三角形,通过构造出全等三角形来研究平面图形的性质.七、角平分线概念:从一个角的顶点引出一条射线,把这个角分成完全相同的角,这条射线叫做这个角的角平分线。
人教版八年级数学上册课外辅导专题讲义 第12章 全等中的基本模型 (1)

模块一 平移型全等把一个图形经过平移、翻折、旋转后,它们的位置虽然变化了,但是形状、大小都没有改变,即平移、翻折、旋转前后的图形全等. 我们把平移、翻折(轴对称)、旋转称为几何变换. 这一讲我们就来学习基本变换下的全等三角形. 常见平移模型【引例】如图,A E F B 、、、四点在一条直线上,AC CE ⊥,BD DF ⊥,AE BF =,AC BD =.求证:CF DE =能力提升【例1】 如图1,A 、B 、C 、D 在同一直线上,AB CD =,DE AF ∥,且.DE AF =求证:AFC DEB △≌△如果将BD 沿着AC 边的方向平行移动,图2,B 点与C 点重合时;图3,B 点在C 点右侧时,其余条件不变,结论是否成立,如果成立,请选择一种情况请予证明;如果不成立,请说明理由.图1F EDC BA图2FE D(C )B A图3FEDCB A全等中的基本模型FE DCB A模块二 对称型全等知识导航常见轴对称模型夯实基础【例2】 ⑴如图,△ABC 中,AB =AC ,BD ⊥AC 于D ,CE ⊥AB 于E ,BD和CE 交于点O ,AO 的延长线交BC 于F ,则图中全等直角三角形的对数为( )A.3对B.4对C.5对D.6对⑵如图,ABE △和ADC △是ABC △分别沿着AB ,AC 翻折到同一平面内形成的.若1:2:315:2:1∠∠∠=,则4∠=________.能力提升【例3】 如图,AB AC =,D 、E 分别是AB 、AC 的中点,AM CD ⊥于M ,AN BE ⊥于N .求证:AM AN =.E D N M C B A 4321EDCBAD O FE CBA【教师备选】在正ABC △内取一点D ,使DA DB =,在ABC △外取一点E ,使DBE DBC ∠=∠,且BE BA =,求BED ∠.模块三 旋转型全等知识导航常见旋转模型:夯实基础【引例】如图,在ABC △中,::3:5:10A B ACB ∠∠∠=,若将ACB△绕点C 逆时针旋转,使旋转后的A B C ''△中的顶点B '在原三角形的边AC 的延长线上时,求BCA '∠的度数.D E CB AD E C B A A'B'CBA能力提升【教师铺垫】如图,点C 为线段AB 上一点,ACM △、CBN △是等边三角形.请你证明:⑴AN BM =; ⑵60MFA ∠=; ⑶DEC △为等边三角形; ⑷DE AB ∥.【例4】 如图1,若△ABC 和△ADE 为等边三角形,M 、N 分别EB ,CD 的中点,易证:CD=BE ,△AMN 是等边三角形.⑴当把△ADE 绕A 点旋转到图2的位置时,CD=BE 是否仍然成立?若成立请证明,若不成立请说明理由;⑵当把△ADE 绕A 点旋转到图3的位置时,△AMN 是否还是等边三角形?若是,请给出证明;若不是,请说明理由.图2图3图1MNMN N MA BCDE ABC D E ABC EDM D NEC BFA【例5】 如图1,若四边形ABCD 、GFED 都是正方形,显然图中有AG =CE ,AG ⊥CE .⑴当正方形GFED 绕D 旋转到如图2的位置时,AG =CE 是否成立?若成立,请给出证明,若不成立,请说明理由;⑵当正方形GFED 绕D 旋转到B ,D ,G 在一条直线 (如图3)上时,连结CE ,设CE 分别交AG 、AD 于P 、H ,求证:AG ⊥CE .PHG GG图1图3图2FABCEF ABC DEABC DEF D模块四 辅助线添加初步知识导航辅助线:在几何学中用来帮助解答疑难几何图形问题,在原图基础之上另外所作的具有极大价值的直线或者线段. 添辅助线的作用:凸显和集散1. 揭示图形中隐含的性质:当条件与结论间的逻辑关系不明朗时,通过添加适当的辅助线,将条件中隐含的有关图形的性质充分揭示出来,以便取得过渡性的推论,达到推导出结论的目的.2. 聚拢集中原则:通过添置适当的辅助线,将图形中分散、远离的元素,通过变换和转化,使他们相对集中,聚拢到有关图形上来,使题设条件与结论建立逻辑关系,从而推导出要求的结论.3. 化繁为简原则:对一类几何命题,其题设条件与结论之间在已知条件所给的图形中,其逻辑关系不明朗,通过添置适当辅助线,把复杂图形分解成简单图形,从而达到化繁为简、化难为易的目的.4. 发挥特殊点、线的作用:在题设条件所给的图形中,对尚未直接显现出来的各元素,通过添置适当辅助线,将那些特殊点、特殊线、特殊图形性质恰当揭示出来,并充分发挥这些特殊点、线的作用,达到化难为易、导出结论的目的.5. 构造图形的作用:对一类几何证明题,常须用到某种图形,这种图形在题设条件所给的图形中却没有发现,必须添置这些图形,才能导出结论,常用方法有构造出线段和角的和差倍分、新的三角形、直角三角形、等腰三角形等.【例6】 如图△ABC 中,AD 平分∠BAC ,DG ⊥BC 且平分BC ,DE ⊥AB 于E ,DF ⊥AC 于F .⑴说明BE =CF 的理由;⑵如果AB =a ,AC =b ,求AE 、BE 的长.【例7】 如图1,已知ABC △中,1AB BC ==,90ABC =︒∠,把一块含30︒角的直角三角板DEF 的直角顶点D 放在AC 的中点上(直角三角板的短直角边为DE ,长直角边为DF ),将直角三角板DEF 绕D 点按逆时针方向旋转.直线DE 交直线AB 于M ,直线DF 交直线BC 于N . ⑴ 在图1中, ①证明DM DN =;②在这一旋转过程中,直角三角板DEF 与ABC △的重叠部分为四边形DMBN ,请说明四边形DMBN 的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;G D ABC EF⑵ 继续旋转至如图2的位置,DM DN =是否仍然成立?若成立,请给出证明;若不成立,请说明理由;⑶ 继续旋转至如图3的位置,DM DN =是否仍然成立?请写出结论,不用证明.图3图2图1FFFEEEDDC CBB AA【点评】本题的辅助线是根据实际描述所产生的连线,这属于辅助线里最基本的添加方式.【探究对象】常见的全等三角形题目证明思路及辅助线作法【探究目的】除基本模型外,教师可以在常见辅助线版块进行拓展【探究一】证明两条线段相等的步骤:⑴观察要证线段在哪两个可能全等的三角形中,然后证这两个三角形全等;⑵若图中没有全等三角形,可以把求证线段用和它相等的线段代换,再证它们所在的三角形全等;⑶如果没有相等的线段代换,可设法作辅助线构造全等三角形.【变式一】如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM 且与ABC ∠外角的平分线交于点N ,MD 与MN 有怎样的数量关系?GA NB CD EM M E D C B NA【探究二】在一个图形中有多个垂直关系时,常用同角(等角)的余角相等来证明两个角相等,进而创造证明全等的条件.【变式二】如图,在Rt △ABC 中,AB =AC ,∠BAC =90°,过A 作任一条直线AN ,作BD ⊥AN于D ,CE ⊥AN 于E ,求证:DE =BD -CE321N E DC BA【探究三】有和角平分线垂直的线段时,通常把这条线段延长,可归结为“角分垂等腰归”.【变式三】如图,在Rt△ABC中,AB = AC,∠BAC =90°,∠1 = ∠2 ,CE⊥BD的延长线于E,求证:BD=2CE【探究四】有二倍角时常用的辅助线⑴构造等腰三角形使二倍角是等腰三角形的顶角的外角【变式四】如图,在△ABC中,∠1=∠2,∠ABC=2∠C,求证:AB+BD =AC.EDC BA21D C BA【变式五】已知,在△ABC中,BD⊥AC于D,∠BAC = 2∠DBC,求证:∠ABC = ∠ACB ⑵平分二倍角法一:【解析】作∠BAC的平分线AE交BC于E,则∠BAE = ∠CAE = ∠DBC⑶加倍小角法二:【解析】作∠FBD =∠DBC,BF交AC于FEDC BAFAB CD探索创新【例8】 如图所示:AF CD =,BC EF =,AB DE =,A D ∠=∠.求证:BC EF ∥.【教师备选】已知AB=CD=AE=BC +DE =2,∠ABC =∠AED =90°,求五边形ABCDE 的面积.A BCD EFE D CBA实战演练题型一 平移型全等 巩固练习【练习1】 ⑴ 如图⑴,若AB CD =,A E F C 、、、在一条直线上,AE CF =,过E F 、分别作DE AC ⊥,BF AC ⊥.求证:BD 平分EF .⑵ 若将DEC △的边EC 沿AC 方向移动到图⑵的位置时,其他条件不变,上述结论是否成立?请说明理由.(2)(1)ABCDE F GGFEDC BA【点评】 此题难度不大,老师们可以给学生说明图形平移变换的形式和它的简单性质,以及综合题的命题形式和思路.题型二 对称型全等 巩固练习【练习2】 如图,已知Rt △ABC ≌Rt △ADE ,90ABC ADE ∠=∠=︒,BC 与DE 相交于点F ,连接CD 、EB . ⑴图中还有几对全等三角形,请你一一列举; ⑵求证:CF=EF .FED CB A题型三 旋转型全等 巩固练习【练习3】 如图,在Rt ABC △中,AB AC AD BC =⊥,,垂足为D .E F 、分别是CD AD 、上的点,且CE AF =.如果62AED ∠=︒,那 么DBF ∠=__________.【练习4】 如图,已知ABD △和AEC △都是等边三角形,AF CD ⊥于F ,AH BE ⊥于H ,请问:AF 和AH 有何 关系?请说明理由.题型四 辅助线添加初步 巩固练习【练习5】 如图①,一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.⑴ 如图②,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 满足的数量关系,并证明你的猜想;⑵ 若三角尺GEF 旋转到如图③所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与G 的延长线相交于点N ,此时,⑴中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.③②①OOCB DAFGENMEGFADBCCA(G)F BA O HF ED A课后测测1.已知,如图:ABC DEF ∠=∠,AB DE =,要说明ABC △≌DEF △ (1)若以“SAS ”为依据,还要添加的条件为 ; (2)若以“ASA ”为依据,还要添加的条件为 ;测2.已知:如图,点E 是正方形ABCD 的边AB 上任意一点,过点D 作DF DE ⊥交BC 的延长线于点F .求证:DE DF =.测3.已知:如图,OP 是AOC ∠和BOD ∠的平分线,OA OC =, OB OD =.求证:AB CD =.FEDCBA OPDCB AEDB A参考答案模块一 平移型全等【引例】 【解析】 ∵AC CE ⊥,BD DF ⊥∴90ACE BDF ∠=∠=︒ 在Rt ACE △和Rt BDF △中 AC BDAE BF =⎧⎨=⎩∴()Rt Rt HL ACE BDF △≌△ ∴CE DF =,AEC BFD ∠=∠ ∴CEF DFE ∠=∠ 在CEF △和DFE △中 CE DF CEF DFE EF FE =⎧⎪∠=∠⎨⎪=⎩∴CEF DFE △≌△ ∴CF DE =能力提升【例9】 如图1,A 、B 、C 、D 在同一直线上,AB CD =,DE AF ∥,且.DE AF =求证:AFC DEB △≌△【解析】 ∵DE AF ∥,∴A D ∠=∠.∵AB CD =,∴AB BC CD BC +=+,即AC DB =.在AFC △和DEB △中,AC DB A D AF DE =⎧⎪∠=∠⎨⎪=⎩,∴AFC △≌DEB △(SAS ). 另两结论均成立,证明同上.模块二 对称型全等知识导航常见轴对称模型夯实基础【例10】⑴如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于点O,AO的延长线交BC于F,则图中全等直角三角形的对数为()A.3对B.4对C.5对D.6对⑵如图,ABE△和ADC△是ABC△分别沿着AB,AC翻折到同一平面内形成的.若1:2:315:2:1∠∠∠=,则4∠=________.【解析】⑴D;⑵60︒;由外角得()422360∠=∠+∠=°.能力提升【例11】如图,AB AC=,D、E分别是AB、AC的中点,AM CD⊥于M,AN BE⊥于N.求证:AM AN=.【解析】证法一:∵AB AC=,∴ABC ACB∠=∠.∵D、E是AB、AC的中点,∴DB EC=,AD AE=.在DBC△与ECB△中,BC CB=,DBC ECB∠=∠,DB EC=,∴DBC ECB△≌△.∴BDC CEB∠=∠∵ADM BDC∠=∠,AEN CEB∠=∠,∴ADM AEN∠=∠.在AMD△与ANE△中,90M N∠=∠=︒,AD AE=,ADM AEN∠=∠,∴AMD ANE△≌△,∴AM AN=.EDNMCBA4321EDC BADOFECBA证法二:∵AB AC =,D 、E 是AB 、AC 的中点,∴AD AE =.在DAC △与EAB △中, AB AC =,AE AD =,DAC EAB ∠=∠, ∴DAC EAB △≌△, ∴ACD ABE ∠=∠. 又∵AM CD ⊥于M ,AN BE ⊥于N . ∴90M N ∠=∠=︒, 在AMC △与ANB △中,AC AB =,ACM ABN ∠=∠,M N ∠=∠, ∴AMC ANB △≌△, ∴AM AN =.证法三:∵AB AC =,D 、E 是AB 、AC 的中点, ∴12ADC ABC S S =△△,12AEB ABC S S =△△,AD AE =,∴ADC AEB S S =△△,在ADC △与AEB △中,AD AE =,AC AB =,DAC EAB ∠=∠,∴ADC AEB △≌△,∴CD BE =. ∴1122CD AM BE AN ⋅=⋅, ∴AM AN =.【教师备选】在正ABC △内取一点D ,使DA DB =,在ABC △外取一点E ,使DBE DBC ∠=∠,且BE BA =,求BED ∠.【解析】 如图所示,连接DC .因为AD BD =,AC BC =,CD CD =,则ADC BDC △≌△, 故30BCD ∠=︒.而DBE DBC ∠=∠,BE AB BC ==,BD BD =, 因此BDE BDC △≌△,故30BED BCD ∠=∠=︒.E D N M C B A ED N M C B AD E CB AD E C B A模块三 旋转型全等【引例】如图,在ABC △中,::3:5:10A B ACB ∠∠∠=,若将ACB△绕点C 逆时针旋转,使旋转后的A B C ''△中的顶点B '在原三角形的边AC 的延长线上时,求BCA '∠的度数.【解析】 ∵::3:5:10A B ACB ∠∠∠=∴1018010018ACB ∠=︒⨯=︒∵由ACB △绕点C 旋转得到A'B'C △ ∴100A'CB'∠=︒∵180ACB A'CB'BCA'∠+∠-∠=︒ ∴100218020BCA'∠=︒⨯-︒=︒能力提升【教师铺垫】如图,点C 为线段AB 上一点,ACM △、CBN △是等边三角形.请你证明:⑴AN BM =; ⑵60MFA ∠=; ⑶DEC △为等边三角形; ⑷DE AB ∥.【解析】 此图是旋转中的基本图形.其中蕴含了许多等量关系.60MCN ∠=︒,AN BM =,CD CE =,AD ME =,ND BE =;AM CN ∥,CM BN ∥;DE AB ∥;ACN MCB △≌△,ADC MCE △≌△,NDC BEC △≌△;DEC △为等边三角形. ⑴∵ACM △、CBN △是等边三角形,∴MC AC =,CN CB =,ACN MCB ∠=∠ ∴ACN MCB △≌△,∴AN BM =. (找出图中所有的全等三角形,及相等的线段)⑵ 60MFA NAB MBA BMC MBA MCA ∠=∠+∠=∠+∠=∠=︒. (找出图中所有的60︒角) ⑶由ACN MCB △≌△易推得NDC BEC △≌△,所以CD CE =,又60MCN ∠=,进而可得DEC △为等边三角形. ⑷由⑶易得DE AB ∥.AFC BFC ∠=∠以后学习证明.【例12】 如图1,若△ABC 和△ADE 为等边三角形,M 、N 分别EB ,CD 的中点,易证:CD=BE ,△AMN 是等边三角形.⑴当把△ADE 绕A 点旋转到图2的位置时,CD=BE 是否仍然成立?若成立请证明,若不成立请说明理由;⑵当把△ADE 绕A 点旋转到图3的位置时,△AMN 是否还是等边三角形?若是,请给出证明;若不是,请说明理由.A'B'CBAMD NE C BFA图2图3图1MNMN N MA BCDE ABC D E ABC ED【解析】⑴CD =BE .理由如下:∵△ABC 和△ADE 为等边三角形∴AB=AC ,AE=AD ,∠BAC=∠EAD =60o ∵∠BAE =∠BAC -∠EAC =60o -∠EAC , ∠DAC =∠DAE -∠EAC =60o -∠EAC , ∴∠BAE=∠DAC , ∴△ABE ≌ △ACD (SAS ) ∴CD=BE⑵△AMN 是等边三角形.理由如下:∵△ABE ≌ △ACD (SAS ), ∴∠ABE =∠ACD . ∵M 、N 分别是BE 、CD 的中点,∴BM =1122BE CD CN ==又∵AB=AC ,∴△ABM ≌ △ACN (SAS ) ∴AM=AN ,∠MAB=∠NAC .∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC =60o ∴△AMN 是等边三角形.【例13】 如图1,若四边形ABCD 、GFED 都是正方形,显然图中有AG =CE ,AG ⊥CE .⑴当正方形GFED 绕D 旋转到如图2的位置时,AG =CE 是否成立?若成立,请给出证明,若不成立,请说明理由;⑵当正方形GFED 绕D 旋转到B ,D ,G 在一条直线 (如图3)上时,连结CE ,设CE 分别交AG 、AD 于P 、H ,求证:AG ⊥CE .PHG GG图1图3图2FABCEF ABC DEABC DEF D【解析】⑴AG CE =成立.∵四边形ABCD 、四边形DEFG 是正方形,∴,,GD DE AD DC == ∠GDE =∠90ADC =︒. ∴ ∠GDA =90°-∠ADE =∠EDC . ∴ △AGD ≌△CED (SAS) ∴ AG CE =⑵由⑴可知△AGD ≌△CED , ∴∠GAD =∠ECD .∵∠EHA =∠DHC ,∠DHC +∠ECD =90°, ∴∠EHA +∠GAD =90° ∴∠APH =90︒. ∴AG CE ⊥.模块四 辅助线添加初步【例14】 如图△ABC 中,AD 平分∠BAC ,DG ⊥BC 且平分BC ,DE ⊥AB 于E ,DF ⊥AC 于F .⑴说明BE =CF 的理由;⑵如果AB =a ,AC =b ,求AE 、BE 的长.【解析】⑴连接BD 、DCDG 垂直平分BC ,故△BDG ≌△CDG (SAS ) ∴BD =DC又∵AD 平分∠BAC , DE ⊥AB 于E ,DF ⊥AC 于F ,故△AED ≌△AFD (AAS ) ∴ED =DF故Rt △DBE ≌Rt △DFC (HL ) ∴BE =CFGDAB C EFGDABC E F⑵AB +AC =2AE2a bAE += 2a bBE -=【例15】 如图1,已知ABC △中,1AB BC ==,90ABC =︒∠,把一块含30︒角的直角三角板DEF 的直角顶点D 放在AC 的中点上(直角三角板的短直角边为DE ,长直角边为DF ),将直角三角板DEF 绕D 点按逆时针方向旋转.直线DE 交直线AB 于M ,直线DF 交直线BC 于N . ⑴ 在图1中, ①证明DM DN =;②在这一旋转过程中,直角三角板DEF 与ABC △的重叠部分为四边形DMBN ,请说明四边形DMBN 的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;⑵ 继续旋转至如图2的位置,DM DN =是否仍然成立?若成立,请给出证明;若不成立,请说明理由;⑶ 继续旋转至如图3的位置,DM DN =是否仍然成立?请写出结论,不用证明.图3图2图1FFFEEEDDC CBB AA【解析】 ⑴ ①方法一:连接BD ,在Rt ABC △中, ∵AB BC =,AD DC =.∴DB DC AD ==,90BDC =︒∠.∴45ABD C ==︒∠∠.∵90MDB BDN CDN BDN +=+=︒∠∠∠∠, ∴MDB NDC =∠∠. ∴BMD CND △≌△. ∴DM DN =. 方法二:∵45A DBN ==︒∠∠.90ADM MDB BDN MDB +=+=︒∠∠∠∠. ∴ADM BDN =∠∠.NMEFDCBA∴ADM BDN △≌△. ∴DM DN =.②四边形DMBN 的面积不发生变化; 由①知:BMD CND △≌△, ∴BMD CND S S =△△.∴1124DBN DMB DBN DNC DBC ABC DMBN S S S S S S S =+=+===△△△△△△四边形.⑵ DM DN =仍然成立,证明:连接DB . 在Rt ABC △中,∵AB BC =,AD DC =, ∴DB DC =,90BDC =︒∠. ∴45DCB DBC ==︒∠∠. ∴135DBM DCN ==︒∠∠.∵90CDN CDM BDM CDM +=+=︒∠∠∠∠, ∴CDN BDM =∠∠.∴CDN BDM △≌△.∴DM DN =.⑶ DM DN =.【探究一】证明两条线段相等的步骤:【变式一】如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM ⊥且与ABC ∠外角的平分线交于点N ,MD 与MN 有怎样的数量关系?GA NB CD EM M E D C B NA【解析】 DM MN =.在AD 上截取AG AM =,∴DG MB =,∴45AGM =︒∠∴135DGM MBN ==︒∠∠,∴ADM NMB =∠∠, ∴DGM MBN ∆∆≌(ASA ),∴DM MN =.NME FD CB A N M E F DC BA【变式二】如图,在Rt△ABC中,AB=AC,∠BAC=90°,过A作任一条直线AN,作BD⊥AN 于D,CE⊥AN于E,求证:DE=BD-CE【解析】∵∠BAC=90°,BD⊥AN∴∠1+∠2 =90°∠1+∠3=90°∴∠2 =∠3∵BD⊥AN,CE⊥AN∴∠BDA =∠AEC = 90°在△ABD和△CAE中,∠BDA =∠AEC∠2 = ∠3AB = AC∴△ABD ≌△CAE(AAS)∴BD = AE且AD = CE∴AE-AD = BD-CE∴DE = BD-CE【变式三】如图,在Rt△ABC中,AB = AC,∠BAC =90°,∠1 = ∠2 ,CE⊥BD的延长线于E,求证:BD=2CE【解析】分别延长BA、CE交于F∵BE⊥CF∴∠BEF =∠BEC =90°在△BEF和△BEC中∠1 = ∠2BE=BE∠BEF =∠BEC∴△BEF ≌△BEC (ASA)∴CE = FE =12 CF∵∠BAC = 90°, BE⊥CF ∴∠BAC = ∠CAF = 90°∠1+∠BDA = 90°∠1+∠BFC = 90°∠BDA = ∠BFC在△ABD和△ACF中∠BAC = ∠CAF∠BDA = ∠BFCAB = AC∴△ABD ≌△ACF(AAS) ∴BD = CF∴BD = 2CE321NEDCBAEDCBA21FEDCBA【变式四】如图,在△ABC 中,∠1=∠2,∠ABC =2∠C ,求证:AB +BD =AC . 【解析】延长AB 到E ,使BE = BD ,连结DE则∠BED = ∠BDE∵∠ABD =∠E +∠BDE ∴∠ABC =2∠E ∵∠ABC =2∠C∴∠E = ∠C在△AED 和△ACD 中∠E = ∠C ∠1 = ∠2AD = AD∴△AED ≌△ACD (AAS)∴AC = AE∵AE = AB +BE ∴AC = AB +BE 即AB +BD = AC【变式五】已知,在△ABC 中,BD ⊥AC 于D ,∠BAC = 2∠DBC ,求证:∠ABC = ∠ACB ⑵平分二倍角 法一:【解析】作∠BAC 的平分线AE 交BC 于E ,则∠BAE = ∠CAE = ∠DBC∵BD ⊥AC∴∠CBD +∠C =90°∴∠CAE +∠C = 90°∵∠AEC =180°-∠CAE -∠C =90°∴AE ⊥BC∴△ABE ≌△ACE (ASA)∴∠ABC = ∠ACB⑶加倍小角 法二:【解析】作∠FBD =∠DBC ,BF 交AC 于F∴△FBD ≌△CBD (ASA) ∴∠BFC =∠C∵∠BFC =∠A +∠ABF ∠ABC =∠FBC +∠ABF ∵∠A = 2∠DBC=∠FBC ∴∠BFC =∠ABC =∠C E 21D CBA ED CBAF ABCD即∠ABC = ∠ACB探索创新【例16】如图所示:AF CD=,BC EF=,AB DE=,A D∠=∠.求证:BC EF∥.【解析】分别连接BF、CE、BE,利用SAS证得ABF△≌DEC△,∴BF CE=,利用SSS证得BFE△≌ECB△,∴BEF EBC∠=∠,∴BC EF∥.【点评】充分考虑已给条件,添加辅助线凸显条件.【教师备选】已知AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°,求五边形ABCDE的面积.【解析】延长CB至F,使BF=DE,连结AF∵∠ABC=∠AED=90°,AB=AE∴△ABF ≌△AED (SAS)∴AF=AD再证△ACF ≌△ACD (SSS)∴S△ACF=S△ACD=12CD AB=2∴S五边形ABCDE =4ABC DEFEDCBAFBACDEABC DEF实战演练题型一 平移型全等 巩固练习【练习6】 ⑴ 如图⑴,若AB CD =,A E F C 、、、在一条直线上,AE CF =,过E F 、分别作DE AC ⊥,BF AC ⊥.求证:BD 平分EF .⑵ 若将DEC △的边EC 沿AC 方向移动到图⑵的位置时,其他条件不变,上述结论是否成立?请说明理由.(2)(1)ABCDE F GGFEDC BA【解析】 ⑴ ∵AE CF =,∴AE EF CF EF +=+,即AF CE =,∵DE AC ⊥,BF AC ⊥,∴90AFB CED ∠=∠=︒ ∴Rt Rt ABF CDE △≌△, ∴BF DE =,又BGF DGE ∠=∠, ∴BGF DGE △≌△,∴EG FG =,即BD 平分EF⑵ 仍然成立.证明方法同上,不再赘述. 【点评】 此题难度不大,老师们可以给学生说明图形平移变换的形式和它的简单性质,以及综合题的命题形式和思路.题型二 对称型全等 巩固练习【练习7】 如图,已知Rt △ABC ≌Rt △ADE ,90ABC ADE ∠=∠=︒,BC 与DE 相交于点F ,连接CD 、EB . ⑴图中还有几对全等三角形,请你一一列举; ⑵求证:CF=EF .【解析】⑴△ADC ≌△ABE ,△CDF ≌△EBF ⑵证法一:连接CE ∵Rt △ABC ≌Rt △ADE∴AC=AE ,ACB AED ∠=∠ ∴ACE AEC ∠=∠ ∴ACE ACB AEC AED ∠-∠=∠-∠即BCE DEC ∠=∠ FE D CB A FE D C B A∴CF=EF证法二:∵Rt △ABC ≌Rt △ADE∴AC=AE ,AD=AB ,CAB EAD ∠=∠ ∴CAB DAB EAD DAB ∠-∠=∠-∠即CAD EAB ∠=∠∴△ADC ≌△ABE (SAS) ∴CD=EB ,ADC ABE ∠=∠ 又∵ADE ABC ∠=∠ ∴CDF EBF ∠=∠ 又∵DFC BFE ∠=∠∴△CDF ≌△EBF (AAS) ∴CF=EF证法三:连接AF∵Rt △ABC ≌Rt △ADE∴,,90AB AD BC DE ABC ADE ==∠=∠=︒又∵AF AF =∴Rt ABF △≌Rt (HL)ADF ∆ ∴BF DF = 又∵BC=DE∴BC BF DE DF -=- 即CF=EF题型三 旋转型全等 巩固练习【练习8】 如图,在Rt ABC △中,AB AC AD BC =⊥,,垂足为D .E F 、分别是CD AD 、上的点,且CE AF =.如果62AED ∠=︒,那 么DBF ∠=__________.【解析】28︒.【练习9】 如图,已知ABD △和AEC △都是等边三角形,AF CD ⊥于F ,AH BE ⊥于H ,请问:AF 和AH 有何 关系?请说明理由.【解析】 ∵ABD △和AEC △都是等边三角形,∴AD AB =,AC AE =,60DAB CAE ∠=∠=︒, ∴DAC BAE ∠=∠, ∴ADC ABE △≌△, ∴ADF ABH ∠=∠,∵AF CD ⊥,AH BE ⊥,F EDBA O HF ED CA FEDCBAFEDCBA∴90AFD AHB ∠=∠=︒, ∴ADF ABH △≌△, ∴AF AH =.题型四 辅助线添加初步 巩固练习【练习10】 如图①,一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.⑶ 如图②,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 满足的数量关系,并证明你的猜想;⑷ 若三角尺GEF 旋转到如图③所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与G 的延长线相交于点N ,此时,⑴中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.③②①OOCB DAFGENMEGFADBCCA(G)【解析】 ⑴BM FN =.∵GEF △是等腰直角三角形,四边形ABCD 是正方形,∴45ABD F ∠=∠=︒,OB OF =.又∵BOM FON ∠=∠,∴OBM OFN △≌△.即BM FN =. ⑵BM FN =仍然成立.理由是:∵GEF △是等腰直角三角形,四边形ABCD 是正方形, ∴45DBA GFE ∠=∠=︒,OB OF =. ∴135MBO NFO ∠=∠=︒. 又∵BOM FON ∠=∠, ∴OBM OFN △≌△. ∴BM FN =.③②①OOCBDAFGE MN NMEGF ADBCCA(G)课后测测4.已知,如图:ABC DEF ∠=∠,AB DE =,要说明ABC △≌DEF △ (1)若以“SAS ”为依据,还要添加的条件为 ; (2)若以“ASA ”为依据,还要添加的条件为 ;【解析】 ⑴BE=CF 或BC=EF⑵∠A =∠D测5. 已知:如图,点E 是正方形ABCD 的边AB 上任意一点,过点D 作DF DE ⊥交BC 的延长线于点F .求证:DE DF =.【解析】 ∵ADC EDF ∠=∠∴ADE CDF ∠=∠ 在ADE △和CDF △中 DAE DCF AD CD ADE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ADE CDF △≌△ ∴DE DF =测6.已知:如图,OP 是AOC ∠和BOD ∠的平分线,OA OC =, OB OD =.求证:AB CD =.【解析】 证明:∵OP 是AOC ∠和BOD ∠的平分线,∴,AOP COP BOP DOP ∠=∠∠=∠ ∴AOB COD ∠=∠在AOB △和COD △中, ,,,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩∴AOB COD △≌△ ∴AB CD =FED C B A OPDCB AF ED C B A。
人教版初二数学 上册第十二章三角形全等重点题型精选(复习)
人教版初二数学上册第十二章重点题型讲解(复习)本章主要内容是三角形全等的判定,它是培养学生逻辑思维、推理的主要途径,为今后的学习奠定基础。
如何运用三角形的全等的判定来判定两个三角形全等,本文通过对一些常见题型进行整理,经过这些问题的分析、解决,对这一问题给予作答,进而达到复习巩固深化本章所学的知识,进一步形成解题能力。
1.如图,N,C,A三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又△MNC≌△ABC,则∠BCM:∠BCN等于()A.1:2B. 1:3C. 2:3D. 1:4解析:设其中一份为x,∠A:∠ABC:∠ACB=3:5:10,知∠A=3x,∠ABC=5x,∠ACB=10x.由∠A+∠ABC+∠ACB=180得3x+5x+10x=1800,解得x=100,∴∠A=300,∠ABC=500,∠ACB=1000∵∠BCA+∠BCN=1800,∴∠BCN=1800-1000=800.又△MNC≌△ABC,∴∠MCN=∠ACB=1000,∴∠BCM=∠MCN-∠BCN=1000-800=200.∴∠BCM:∠BCN=20:80=1:4,答案选D2.如图,△ABE和△ACD是△ABC分别沿着AB,AC边翻折1800形成的,若∠BAC=1500,求∠α的度数。
解析:因为△ABE和△ACD是△ABC分别沿着AB,AC边翻折1800形成的,∴△△ABC≌△ADC≌△ADE, ∴∠EDA=∠CDA=∠CBA,∠ACD=∠ACB,即∠EDC=2∠CBA,∠BCD=2∠BCA∵∠CBA+∠BCA+∠BAC=1800,∠BAC=1500∴∠CBA+∠BCA=300,∵∠α=∠EDC+∠BCD∴∠α=2(∠CBA+∠BCA)=6003.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,求点D的坐标。
解析:平移,旋转,轴对称变换都能得到全等的图形,所以此题通过翻折,轴对称就可以得出D点坐标为(-1,3)、(-1,-1)(4,-1)4.如图,在△ABC中,∠B=90,ED⊥AB于点D,AD是∠CAB的平分线,且AB=BC,若AB=6,则CD+DE等于()A.4B. 5C. 6D. 7解析:∵∠B=90,∴DB⊥AB,又∵AD是∠CAB的平分线,ED⊥AB∴BD=DE∴CD+DE=CD+BD=BC,∵AB=BC,AB=6, ∴CD+DE=65.如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS.下列结论:①AS=AR;②QP∥AR;③△BRP≌△CSP。
2023八年级数学上册第十二章全等三角形专项1全等三角形的常见模型作业课件新版新人教版
∠ = ∠,
在△ABD和△ACE中,ቐ = ,
∠ = ∠,
∴△ABD≌△ACE(ASA),∴BD=CE.
类型3
手拉手模型
6. 如图,∠BAE=∠CAF=90°,EC,BF相交于点M,AE=AB,AC=AF.
(1)求证:EC=BF.
(2)求证:EC⊥BF.
在△ABC与△DEF中,ቐ∠ = ∠,
= ,
所以△ABC≌△DEF(SAS),所以BC=EF.
类型1
平移模型
2. [2022盐城期中]如图,点B,C,E,F在同一条直线上,BC=EF,AC⊥BC于点C,DF⊥EF于
点F,AC=DF.
求证:(1)△ABC≌△DEF;
(2)AB∥DE.
∵BD=CE,∴AD=AE,AB=AC.
= ,
在△ABE和△ACD中,ቐ∠ = ∠,
= ,
∴△ABE≌△ACD(SAS).
类型2
对称模型
4. [2021邯郸永年区期中]如图,在四边形ACBD中,点P在对角线AB上,连接
PC,PD,∠1=∠2,∠3=∠4.
求证:(1)△BDP≌△BCP;
O,∠B=∠C,BD=CE.
求证:(1)OD=OE;
(2)△ABE≌△ACD.
答案
∠ = ∠,
3.证明:(1)在△BOD和△COE中,ቐ ∠ = ∠,
= ,
∴△BOD≌△COE(AAS),∴OD=OE.
(2)∵点D,E分别是AB,AC的中点,
1
1
∴AD=BD=2AB,AE=CE=2AC.
(3)若∠BAE=∠CAF=m°(m≠90),则(1)(2)中的结论还成立吗?请说明理由.
第12章全等三角形模型一:一线三等角讲义2022—2023学年人教版数学八年级上册
一线三等角模型构造全等三角形【模型说明】在初中数学《全等三角形》中有许多的模型,这些模型是数学重要知识点的总结与运用,很多几何题中都有数学模型的影子,掌握好这些模型,孩子们学习几何就会比较简单,成绩不会差。
今天我要与大家分享是“一线三等角”模型,那么什么是“一线三等角”?顾名思义,一线三等角是指三个相等的角的顶点在同一条直线上。
这个模型贯穿初中几何的始终。
下面我们具体分析一下这个模型。
【同侧型一线三等角(常见)】 在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
锐角一线三等角 直角一线三等角(“K 型图”) 钝角一线三等角直角一线三等角 钝角一线三等角∠FAC=∠ABD=∠CED 添加任一边相等【基础训练】1.如图,在等腰直角三角形ABC 中,,90AB BC ABC =∠=︒,点B 在直线l 上,过A 作AD l ⊥于D ,过C 作CE l ⊥于E .下列给出四个结论:①BD CE =;②BAD ∠与BCE∠互余;③AD CE DE +=.其中正确结论的序号是( )A.①②B.①③C.②③D.①②③2.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,BE=1cm,求DE的长.3.如图1,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE ⊥直线m,垂足分别为D,E.(1)求证:△ABD≌△CAE;(2)若BD=2cm,CE=4cm,DE=cm.4.如图,在△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.若BC=BD,求证:CD=DE.5.在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.6.如图,点P,M,N分别在等边△ABC的各边上,MP⊥AB于点P,MN⊥BC于点M,PN⊥AC于点N.(1)求证:△PMN是等边三角形;(2)若BP=2cm,求等边△ABC的边长.7.如图①,点B 、C 在∠MAN 的边AM 、AN 上,点E ,F 在∠MAN 内部的射线AD 上,∠1、∠2分别是△ABE 、△CAF 的外角.已知AB =AC ,∠1=∠2=∠BAC .求证:△ABE ≌△CAF .8.如图,已知∠DCE =90°,∠DAC =90°,BE ⊥AC 于B ,且DC =EC ,能否在△BCE 中找到与AB+AD 相等的线段,并说明理由.9、如图,在等腰△ABC 中,AB =AC ,点D 、E 、F 分别在AB 、BC 、AC 边上,且BE =CF ,BD =CE .(1)求证:△DEF 是等腰三角形; (2)当∠A =36°时,求∠DEF 的度数.10.如图,在ABC ∆中,2==AC AB ,︒=∠36B ,点D 在线段BC 上运动(点D 不与点B 、C 重合),连接AD ,作︒=∠36ADE ,DE 交线段AC 于点E.线段DC 的长度为何值时,DCEABD∆≅∆请说明理由;【提升训练】1.在△ABO中,∠AOB=90°,AO=BO,直线MN经过点O,且AC⊥MN于C,BD ⊥MN于D(1)当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;(2)当直线MN绕点O旋转到图②的位置时,求证:CD=AC﹣BD;(3)当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明.2.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD ⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.ADEB C3.如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.①如图1,若∠BCA=90°,α=90°,则BE CF;②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立,并说明理由;(2)如图3,若线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.4.(1)如图1,直线m经过等腰直角△ABC的顶点A,过点B、C分别作BD⊥m,CE⊥m,垂足分别为D、E,求证:BD+CE=DE;(2)如图2,直线m经过△ABC的顶点A,AB=AC,在直线m上取两点D,E,使∠ADB=∠AEC=α,补充∠BAC=(用α表示),线段BD,CE与DE之间满足BD+CE=DE,补充条件后并证明;(3)在(2)的条件中,将直线m绕着点A逆时针方向旋转一个角度到如图3的位置,并改变条件∠ADB=∠AEC=(用α表示).通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.5.如图1,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图1:(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;(2)迁移:如图2:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F 处,则CE=.(不要求写过程)6.通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC 于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D.又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE.进而得到AC=,BC=.我们把这个数学模型称为“K字”模型或“一线三等角”模型;【模型应用】(2)如图2,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AH 于点H,DE与直线AH交于点G.求证:点G是DE的中点;7.如图所示,在△ABC中,AB=AC=24cm,BC=18cm,∠B=∠C,D为AB的中点,点P在线段BC上由点B出发向点C运动,同时点Q在线段CA上由点C出发向点A 运动,设运动时间为t(s).(1)若点P与点Q的速度都是3cm/s,则经过多长时间△BPD与△CQP全等?请说明理由.(2)若点P的速度比点Q的速度慢3cm/s,则经过多长时间△BPD与△CQP全等?请求出此时两点的速度.(3)若点P、点Q分别以(2)中的速度同时从点B,C出发,都按逆时针方向沿△ABC 三边运动,则经过多长时间点P与点Q第一次相遇?相遇点在△ABC的哪条边上?请求出相遇点到点B的距离.。
全国人教版数学八年级上册课课练:12章专题训练1 全等三角形的基本模型(word、含答案)
专题训练全等三角形的基本模型▶模型一从教材数学活动(P53)中的筝形,探究全等基本轴对称模型1.定义:两组邻边分别相等的四边形叫做筝形.如图①,若AD=CD,AB=CB,则四边形ABCD是筝形.(1)在同一平面内,△ABC与△ADE按图②所示的方式放置,其中∠B=∠D=90°,AB=AD,BC与DE相交于点F,请你判断四边形ABFD是不是筝形,并说明理由;(2)请你结合图①,写出筝形的一个判定方法(定义除外):在四边形ABCD中,若,则四边形ABCD是筝形.2.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是筝形,其中AB=AD,CB=CD,P是对角线AC上除A,C外的任意一点.求证:∠ABP=∠ADP.常见的轴对称模型还有(如图):▶模型二全等基本旋转模型之一——中点加倍型基本模型:如图①,D是BC的中点,DE=AD.模型变形1:如图②,D是BC的中点,CF⊥AD,BE⊥AD.模型变形2:如图③,D是BC的中点,MD=DN.3.如图,在△ABC中,AB=8,AC=5,AD是△ABC的中线,则AD的取值范围是.4.如图,在△ABC中,AD是中线,CE⊥AD于点E,BF⊥AD交AD的延长线于点F.求证:BF=CE.5.如图所示,∠BAC=∠BCA,AD为△ABC中BC边上的中线,延长BC至点E,使CE=AB,连接AE.求证:∠CAD=∠CAE.6.如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.求证:MN=2AD.常见的旋转模型还有(如图):▶模型三一线三等角模型常见的一线三等角模型:7.探究:如图①,点B,C分别在∠MAN的边AM,AN上,点E,F在∠MAN内部的射线AD 上,∠1,∠2分别是△ABE,△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.拓展:如图②,在△ABC中,AB=AC,AB>BC,点D在边BC上,且CD=2BD,点E,F在线段AD 上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ABE与△CDF的面积之和.8.(1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE.(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,则结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由.答案1.解:(1)四边形ABFD 是筝形. 理由:连接AF .在Rt △AFB 和Rt △AFD 中,{AF =AF ,AB =AD ,∴Rt △AFB ≌Rt △AFD (HL).∴BF=DF . 又∵AB=AD ,∴四边形ABFD 是筝形.(2)答案不唯一,如图AD=CD ,∠ADB=∠CDB 2.证明:在△ABC 和△ADC 中,{AB =AD ,AC =AC ,CB =CD ,∴△ABC ≌△ADC (SSS). ∴∠BAC=∠DAC.在△BAP 和△DAP 中,{AB =AD ,∠BAP =∠DAP ,AP =AP ,∴△BAP ≌△DAP (SAS). ∴∠ABP=∠ADP .3.1.5<AD<6.5 如图,延长AD 到点E ,使DE=AD ,连接BE.∵AD 是△ABC 的中线, ∴BD=CD.在△ADC 和△EDB 中,{CD =BD ,∠ADC =∠EDB ,AD =ED ,∴△ADC ≌△EDB (SAS).∴AC=EB. ∵AB-EB<AE<AB+EB , ∴AB-AC<2AD<AB+AC. ∵AB=8,AC=5,∴1.5<AD<6.5.4.证明:∵CE⊥AD,BF⊥AD,∴∠CED=∠BFD=90°.∵AD是△ABC的中线,∴BD=CD.在△BFD和△CED中,{∠BFD=∠CED,∠BDF=∠CDE, BD=CD,∴△BFD≌△CED(AAS).∴BF=CE.5.证明:如图,延长AD到点F,使得DF=AD,连接CF.∵AD为△ABC中BC边上的中线,∴BD=CD.在△ADB和△FDC中,{AD=FD,∠ADB=∠FDC, BD=CD,∴△ADB≌△FDC(SAS).∴AB=CF,∠B=∠DCF.∵CE=AB,∴CE=CF.∵∠ACE=∠B+∠BAC,∠ACF=∠DCF+∠BCA,∠BAC=∠BCA,∴∠ACE=∠ACF.在△ACF和△ACE中,{AC=AC,∠ACF=∠ACE, CF=CE,∴△ACF≌△ACE(SAS).∴∠CAD=∠CAE.6.证明:如图,延长AD至点E,使DE=AD,连接BE.∵AD是△ABC的中线,∴BD=CD.在△BDE 和△CDA 中,{BD =CD ,∠BDE =∠CDA ,DE =DA ,∴△BDE ≌△CDA (SAS). ∴BE=AC=AN ,∠DBE=∠DCA. ∴AC ∥BE.∴∠ABE+∠BAC=180°. ∵∠BAM=∠CAN=90°, ∴∠MAN+∠BAC=180°. ∴∠ABE=∠MAN.在△ABE 和△MAN 中,{AB =MA ,∠ABE =∠MAN ,BE =AN ,∴△ABE ≌△MAN (SAS).∴AE=MN. ∵AE=2AD ,∴MN=2AD. 7.解:探究:证明:∵∠1=∠2=∠BAC ,且∠1=∠BAE+∠ABE ,∠2=∠CAF+∠ACF ,∠BAC=∠BAE+∠CAF ,∴∠BAE=∠ACF ,∠ABE=∠CAF . 在△ABE 和△CAF 中,{∠BAE =∠ACF ,AB =CA ,∠ABE =∠CAF ,∴△ABE ≌△CAF (ASA). 拓展:∵∠1=∠2=∠BAC ,且∠1=∠BAE+∠ABE ,∠2=∠CAF+∠ACF ,∠BAC=∠BAE+∠CAF , ∴∠BAE=∠ACF ,∠ABE=∠CAF . 在△ABE 和△CAF 中,{∠BAE =∠ACF ,AB =CA ,∠ABE =∠CAF ,∴△ABE ≌△CAF (ASA).∴S △ABE =S △CAF . ∴S △ABE +S △CDF =S △CAF +S △CDF =S △ACD . ∵CD=2BD ,△ABC 的面积为15, ∴S △ACD =10. ∴S △ABE +S △CDF =10.8.解:(1)证明:∵BD ⊥直线m ,CE ⊥直线m ,∴∠BDA=∠AEC=90°.∴∠BAD+∠ABD=90°.∵∠BAC=90°,∴∠BAD+∠CAE=90°.∴∠CAE=∠ABD.在△ADB和△CEA中,{∠ABD=∠CAE,∠BDA=∠AEC, AB=CA,∴△ADB≌△CEA(AAS).∴BD=AE,AD=CE.∴DE=AE+AD=BD+CE.(2)成立.证明:∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠EAC=180°-α.∴∠DBA=∠EAC.在△ADB和△CEA中,{∠DBA=∠EAC,∠BDA=∠AEC, AB=CA,∴△ADB≌△CEA(AAS).∴BD=AE,AD=CE.∴DE=AE+AD=BD+CE.。
