上海市各区县历年中考数学模拟压轴题汇总及答案
2019-2020年上海各区数学中考一模压轴题分类汇编-18题含详解
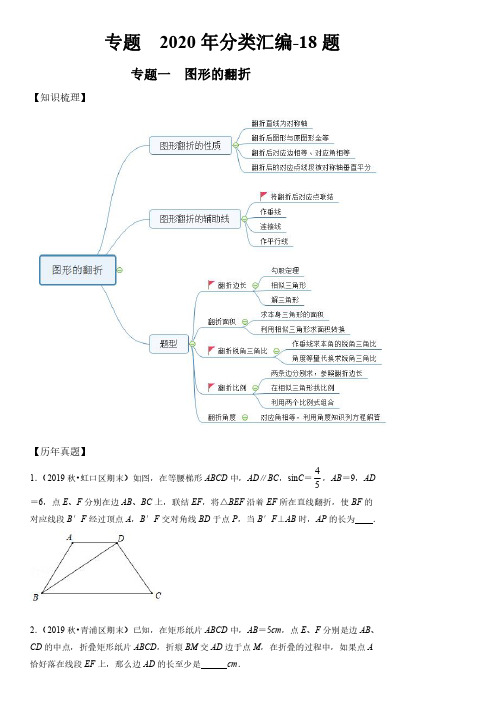
专题2020年分类汇编-18题专题一图形的翻折【知识梳理】【历年真题】1.(2019秋•虹口区期末)如图,在等腰梯形ABCD中,AD∥BC,sin C=45,AB=9,AD=6,点E、F分别在边AB、BC上,联结EF,将△BEF沿着EF所在直线翻折,使BF的对应线段B′F经过顶点A,B′F交对角线BD于点P,当B′F⊥AB时,AP的长为.2.(2019秋•青浦区期末)已知,在矩形纸片ABCD中,AB=5cm,点E、F分别是边AB、CD的中点,折叠矩形纸片ABCD,折痕BM交AD边于点M,在折叠的过程中,如果点A 恰好落在线段EF上,那么边AD的长至少是cm.3.(2019秋•闵行区期末)如图,在等腰△ABC中,AB=AC=4,BC=6,点D在底边BC 上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为.4.(2019秋•杨浦区期末)在Rt△ABC中,∠A=90°,AC=4,AB=a,将△ABC沿着斜边BC翻折,点A落在点A1处,点D、E分别为边AC、BC的中点,联结DE并延长交A1B 所在直线于点F,联结A1E,如果△A1EF为直角三角形时,那么a=.5.(2019秋•崇明区期末)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,D是AC的中点,点E在边AB上,将△ADE沿DE翻折,使得点A落在点A′处,当A′E⊥AB时,则A′A=.6.(2019秋•静安区期末)如图,有一菱形纸片ABCD,∠A=60°,将该菱形纸片折叠,使点A恰好与CD的中点E重合,折痕为FG,点F、G分别在边AB、AD上,联结EF,那么cos∠EFB的值为.专题二图形的旋转【知识梳理】【历年真题】1.(2019秋•奉贤区期末)如图,已知矩形ABCD(AB>BC),将矩形ABCD绕点B顺时针旋转90°,点A、D分别落在点E、F处,连接DF,如果点G是DF的中点,那么∠BEG 的正切值是.2.(2019秋•浦东新区期末)在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别是边BC、AB的中点,将△BDE绕着点B旋转,点D、E旋转后的对应点分别为点D'、E',当直线D'E'经过点A时,线段CD'的长为.3.(2019秋•长宁、金山区期末)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=4点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B 的对应点是点B′,则BB′的长等于.4.(2019秋•松江区期末)如图,矩形ABCD中,AD=1,AB=k,将矩形ABCD绕着点B 顺时针旋转90°得到矩形A′BC′D′,联结AD′,分别交边CD,A′B于E、F,如果AE D′F,那么k=.5.(2019秋•嘉定区期末)在△ABC中,∠ACB=90°,AB=10,cos A=35(如图),把△ABC绕着点C按照顺时针的方向旋转,将A、B的对应点分别记为点A'、B'.如果A'B'恰好经过点A,那么点A与点A'的距离为.6.(2019秋•徐汇区期末)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是.7.(2019秋•普陀区期末)如图,在RtΔABC中,∠C=90°,AC=5,sinB=513,点P为边BC上一点,PC=3,将△ABC绕点P旋转得到△A'B'C'(点A,B、C分别与点A'、B'、C'对应).使B'C'∥AB,边A'C'与边AB交于点G,那么A'G 的长等于.专题三其他题型【知识梳理】根据题目中给的知识点,结合所学函数及图形知识解答【历年真题】1.(2019秋•黄浦区期末)如图,在△ABC中,AB=AC,点D、E在边BC上,∠DAE=∠B=30°,且AD3=AE2,那么DEBC的值是.2.(2019秋•宝山区期末)如图,点A在直线34y x上,如果把抛物线y=x²沿OA方向平移5个单位,那么平移后的抛物线的表达式为__.专题2020年分类汇编-18题专题一图形的翻折【历年真题】1.(2019秋•虹口区期末)如图,在等腰梯形ABCD中,AD∥BC,sin C=45,AB=9,AD=6,点E、F分别在边AB、BC上,联结EF,将△BEF沿着EF所在直线翻折,使BF的对应线段B′F经过顶点A,B′F交对角线BD于点P,当B′F⊥AB时,AP的长为24 7.【考点】相似三角形的判定与性质;解直角三角形;等腰梯形的性质;翻折变换(折叠问题).【专题】图形的相似;解直角三角形及其应用;应用意识.【分析】解直角三角形求出BF,AF,再利用相似三角形的性质求解即可.【解答】解:如图,∵FB′⊥AB,∴∠BAF=90°,∵四边形ABCD是等腰梯形,∴∠ABC=∠C,∴sin∠ABC=sin∠C=AFBF=45,设AF=4k,BF=5k,则AB=9=3k,∴k=3,∴AF=12,BF=15,∵AD∥BF,∴△APD∽△FPB,∴PA AD62=== PF BF155,∴PA=27AF=247,故答案为24 7.【点评】本题考查相似三角形的判定和性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.2.(2019秋•青浦区期末)已知,在矩形纸片ABCD 中,AB =5cm ,点E 、F 分别是边AB 、CD 的中点,折叠矩形纸片ABCD ,折痕BM 交AD 边于点M ,在折叠的过程中,如果点A恰好落在线段EF 上,那么边AD .【考点】翻折变换(折叠问题).【专题】平移、旋转与对称;推理能力.【分析】根据已知条件得到AE =DF =BE =CF ,求得四边形AEFD 是矩形,得到EF =AD ,∠AEN =∠BEN =90°,根据折叠的性质得到BN =AB ,根据直角三角形的性质得到∠BNE =30°,于是得到EN =32BN 到结论.【解答】解:如图,∵在矩形纸片ABCD 中,点E 、F 分别是边AB 、CD 的中点,∴AE =DF =BE =CF ,∴四边形AEFD 是矩形,∴EF =AD ,∠AEN =∠BEN =90°,∵折叠矩形纸片ABCD ,折痕BM 交AD 边于点M ,∴BN =AB ,∵BE =12AB ,∴BE =12BN ,∴∠BNE =30°,∵AB =5cm ,∴EN =32BN∴EF ≥EN 时,点A 恰好落在线段EF 上,即AD∴边AD 的长至少是【点评】本题考查了翻折变换(折叠问题),矩形的性质,直角三角形的性质,正确的识别图形是解题的关键.3.(2019秋•闵行区期末)如图,在等腰△ABC 中,AB =AC =4,BC =6,点D 在底边BC上,且∠DAC =∠ACD ,将△ACD 沿着AD 所在直线翻折,使得点C 落到点E 处,联结BE ,那么BE 的长为1.【考点】翻折变换(折叠问题);等腰三角形的性质;勾股定理.【专题】平移、旋转与对称;推理能力.【分析】只要证明△ABD∽△MBE,得AB BDBM BE=,只要求出BM、BD即可解决问题.【解答】解:∵AB=AC,∴∠ABC=∠C,∵∠DAC=∠ACD,∴∠DAC=∠ABC,∵∠C=∠C,∴△CAD∽△CBA,∴CA CDCB AC=,∴464CD=,∴CD=83,BD=BC﹣CD=103,∵∠DAM=∠DAC=∠DBA,∠ADM=∠ADB,∴△ADM∽△BDA,∴AD DMBD DA=,即8310833DM=,∴DM=3215,MB=BD﹣DM=65,∵∠ABM=∠C=∠MED,∴A、B、E、D四点共圆,∴∠ADB=∠BEM,∠EBM=∠EAD=∠ABD,∴△ABD∽△MBE,(不用四点共圆,可以先证明△BMA∽△EMD,推出△BME∽AMD,推出∠ADB=∠BEM也可以!)∴AB BD BM BE=,∴BE=BD BMAB=1.故答案为:1.【点评】本题考查翻折变换、等腰三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是充分利用相似三角形的性质解决问题,本题需要三次相似解决问题,题目比较难.4.(2019秋•杨浦区期末)在Rt△ABC中,∠A=90°,AC=4,AB=a,将△ABC沿着斜边BC翻折,点A落在点A1处,点D、E分别为边AC、BC的中点,联结DE并延长交A1B所在直线于点F,联结A1E,如果△A1EF为直角三角形时,那么a=4或【考点】翻折变换(折叠问题);勾股定理;三角形中位线定理.【专题】平移、旋转与对称;推理能力.【分析】当△A1EF为直角三角形时,存在两种情况:①当∠A1EF=90°时,如图1,根据对称的性质和平行线可得:A1C=A1E=4,根据直角三角形斜边中线的性质得:BC=2A1B=8,最后利用勾股定理可得AB的长;②当∠A1FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.【解答】解:当△A1EF为直角三角形时,存在两种情况:①当∠A1EF=90°时,如图1,∵△A1BC与△ABC关于BC所在直线对称,∴A1C=AC=4,∠ACB=∠A1CB,∵点D,E分别为AC,BC的中点,∴D、E是△ABC的中位线,∴DE∥AB,∴∠CDE=∠MAN=90°,∴∠CDE=∠A1EF,∴AC∥A1E,∴∠ACB=∠A1EC,∴∠A1CB=∠A1EC,∴A1C=A1E=4,Rt△A1CB中,∵E是斜边BC的中点,∴BC=2A1E=8,由勾股定理得:AB2=BC2﹣AC2,∴AB=;②当∠A1FE=90°时,如图2,∵∠ADF=∠A=∠DFB=90°,∴∠ABF=90°,∵△A1BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA1=45°,∴△ABC是等腰直角三角形,∴AB=AC=4;综上所述,AB的长为或4;故答案为:4;【点评】本题考查了翻折变换(折叠问题),三角形的中位线定理、勾股定理、轴对称的性质、等腰直角三角形的判定、直角三角形斜边中线的性质,并利用分类讨论的思想解决问题.5.(2019秋•崇明区期末)如图,在Rt △ABC 中,∠C =90°,AB =10,AC =8,D 是AC的中点,点E 在边AB 上,将△ADE 沿DE 翻折,使得点A 落在点A ′处,当A ′E ⊥AB 时,则A ′A =2825或425.【考点】翻折变换(折叠问题).【专题】平移、旋转与对称;解直角三角形及其应用.【分析】分两种情形分别求解,作DF ⊥AB 于F ,连接AA ′.想办法求出AE ,利用等腰直角三角形的性质求出AA ′即可.【解答】解:如图,作DF ⊥AB 于F ,连接AA ′.在Rt △ACB 中,BC 22AB AC -=6,∵∠DAF =∠BAC ,∠AFD =∠C =90°,∴△AFD ∽△ACB ,∴DF AD AF BC AB AC ==,∴46108DF AF ==,∴DF =125,AF =165,∵A′E⊥AB,∴∠AEA′=90°,由翻折不变性可知:∠AED=45°,∴EF=DF=125,∴AE=A′E=125+165=285,∴AA′=2825,如图,作DF⊥AB于F,当EA′⊥AB时,同法可得AE=165﹣125=45,AA AE=425.故答案为2825或425.【点评】本题考查翻折变换,相似三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考填空题中的压轴题.6.(2019秋•静安区期末)如图,有一菱形纸片ABCD,∠A=60°,将该菱形纸片折叠,使点A恰好与CD的中点E重合,折痕为FG,点F、G分别在边AB、AD上,联结EF,那么cos∠EFB的值为1 7.【考点】翻折变换(折叠问题);解直角三角形;等边三角形的判定与性质;菱形的性质.【专题】矩形菱形正方形;解直角三角形及其应用.【分析】如图,连接BD.设BC=2a.在Rt△BEF中,求出EF,BF即可解决问题.【解答】解:如图,连接BD.设BC=2a.∵四边形ABC都是菱形,∴AB=BC=CD=AD=2a,∠A=∠C=60°,∴△BDC是等边三角形,∵DE=EC=a,∴BE⊥CD,∴BE=a,∵AB∥CD,BE⊥CD,∴BE⊥AB,∴∠EBF=90°,设AF=EF=x,在Rt△EFB中,则有x2=(2a﹣x)2+a)2,∴x=74a,∴AF=EF=74a,BF=AB﹣AF=4a,∴cos∠EFB=14774aBFaEF==,故答案为1 7.【点评】本题考查菱形的性质,解翻折变换,直角三角形等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.专题二图形的旋转【历年真题】1.(2019秋•奉贤区期末)如图,已知矩形ABCD(AB>BC),将矩形ABCD绕点B顺时针旋转90°,点A、D分别落在点E、F处,连接DF,如果点G是DF的中点,那么∠BEG的正切值是1.【考点】旋转的性质;矩形的性质.【专题】平移、旋转与对称;应用意识.【分析】连接BD,BF,EG.利用四点共圆证明∠BEG=∠BFD=45°即可.【解答】解:连接BD,BF,EG.由题意:BD=BF,∠DBF=90°,∵DG=GF,∴BG⊥DF,∴∠BGF=∠BEF=90°,∴B,G,E,F四点共圆,∠BEG=∠BFD=45°,∴∠BEG的正切值是1.故答案为1.【点评】本题考查旋转变换,等腰直角三角形的判定和性质,四点共圆,锐角三角函数等知识,解题的关键是学会添加常用辅助线解决问题,属于中考常考题型.2.(2019秋•浦东新区期末)在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别是边BC、AB的中点,将△BDE绕着点B旋转,点D、E旋转后的对应点分别为点D'、E',当直线D'E'经过点A时,线段CD'的长为【考点】三角形综合题.【专题】图形的全等;等腰三角形与直角三角形;矩形菱形正方形;图形的相似;推理能力.【分析】分两种情况:①点A在E'D'的延长线上时;②点A在线段D'E'的延长线上时;然后分类讨论,求出线段BD的长各是多少即可.【解答】解:如图1,当点A在E'D'的延长线上时,∵∠C=90°,AC=2,BC=4,∴AB==2,∵点D、E分别是边BC、AB的中点,∴DE∥AC,DE=12AC=1,BD=12BC=2,∴∠EDB=∠ACB=90°,∵将△BDE绕着点B旋转,∴∠BD'E'=∠BDE=90°,D'E'=DE=1,BD=BD'=2,∵在Rt△ABC和Rt△BAD'中,D'B=AC=2,AB=BA,∴Rt△ABC≌Rt△BAD'(HL),∴AD'=BC,且AC=D'B,∴四边形ACBD'是平行四边形,且∠ACB=90°,∴四边形ACBD'是矩形,∴CD'=AB=如图2,当点A在线段D'E'的延长线上时,∵∠AD 'B =90°,∴AD '==4,∴AE '=AD '﹣D 'E '=3,∵将△BDE 绕着点B 旋转,∴∠ABC =∠E 'BD ',∵'12BE AB ==BD BC ,∴△ABE '∽△CBD ',∴''AE AB CD BC=,∴'3254CD =,∴CD '故答案为:.【点评】本题属于三角形综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,矩形的判定和性质,勾股定理等知识,解题的关键是理解题意,正确寻找相似三角形解决问题,属于中考常考题型.3.(2019秋•长宁、金山区期末)如图,在Rt △ABC 中,∠ABC =90°,AB =2,BC =4点P 在边BC 上,联结AP ,将△ABP 绕着点A 旋转,使得点P 与边AC 的中点M 重合,点B的对应点是点B ′,则BB ′的长等于5.【考点】旋转的性质;相似三角形的判定与性质.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.【分析】如图,延长AB '交BC 于E ,过点B '作B 'D ⊥AB 于点D ,由勾股定理可求AC 的长,由旋转的性质可求AP=AM ,∠PAB =∠CAE ,AB =AB '=2,通过证明△ABP ∽△CBA ,可得∠PAB =∠C ,可得CE =AE ,由勾股定理可求CE ,BE 的长,由相似三角形的性质可求B 'D ,BD 的长,即可求解.【解答】解:如图,延长AB '交BC 于E ,过点B '作B 'D ⊥AB 于点D ,∵∠ABC =90°,AB =2,BC =4,∴AC ==∵点M 是AC 中点,∴AM ∵将△ABP 绕着点A 旋转,使得点P 与边AC 的中点M 重合,∴AP =AM ,∠PAB =∠CAE ,AB =AB '=2,∵AP 2=AB 2+PB 2,∴PB =1,∵BA PB =2=BC AB,且∠ABP =∠ABC =90°,∴△ABP ∽△CBA ,∴∠PAB =∠C ,∴∠C =∠CAE ,∴CE =AE ,∵AE 2=AB 2+BE 2,∴CE 2=4+(4﹣CE )2,∴CE =AE =52,∴BE =32,∵B 'D ∥BC ,∴△AB 'D ∽△AEB ,∴''AB AD B D AE AB BE ==,∴'253222AD B D ==,∴AD =85,B 'D =65,∴BD =25,∴BB '=2105,故答案为:5.【点评】本题考查了旋转的性质,相似三角形的判定和性质,等腰三角形的性质,勾股定理等知识,求出CE 的长是本题的关键.4.(2019秋•松江区期末)如图,矩形ABCD 中,AD =1,AB =k ,将矩形ABCD 绕着点B顺时针旋转90°得到矩形A ′BC ′D ′,联结AD ′,分别交边CD ,A ′B 于E 、F ,如果AED ′F ,那么k【考点】旋转的性质;相似三角形的判定与性质;矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;图形的相似;推理能力.【分析】由矩形的性质和旋转的性质可求AD =A 'D '=1,AB =A 'B =k ,∠A '=∠DAB =90°=∠DCB =∠ABC ,通过证明△ADE ∽△FA 'D ',可得''''AD DE AE A F A D D F==,可求DE ,A 'F 的长,通过证明△A 'D 'F ∽△CEF ,由相似三角形的性质可求解.【解答】解:∵将矩形ABCD 绕着点B 顺时针旋转90°得到矩形A ′BC ′D ′,∴AD =A 'D '=1,AB =A 'B =k ,∠A '=∠DAB =90°=∠DCB =∠ABC ,∴A 'D '∥BA ∥CD∴∠A 'D 'F =∠FEC =∠DEA ,且∠D =∠A '=90°,∴△ADE ∽△FA 'D ',∴''''AD DE AE A F A D D F==,且AED ′F ,∴DEA 'D ',A 'FAD =22,∵∠A '=∠DCF =90°,∠A 'FD '=∠EFC ,∴△A 'D 'F ∽△CEF ,∴'''EC FC A D A F =,∴''212222k k A D ---=∴k+1,+1.【点评】本题考查了旋转的性质,矩形的性质,相似三角形的判定和性质,利用相似三角形的性质求DE ,A 'F 的长是本题的关键.5.(2019秋•嘉定区期末)在△ABC 中,∠ACB =90°,AB =10,cos A =35(如图),把△ABC 绕着点C 按照顺时针的方向旋转,将A 、B 的对应点分别记为点A '、B '.如果A 'B '恰好经过点A ,那么点A 与点A '的距离为365.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;推理能力.【分析】如图,过点C 作CE ⊥A 'B ',由锐角三角函数可求AC =6,由旋转的性质可得AC =A 'C =6,∠A '=∠BAC ,即可求A 'E 的长,由等腰三角形的性质可求AA '的长.【解答】解:如图,过点C 作CE ⊥A 'B ',∵在△ABC 中,∠ACB =90°,AB =10,cos ∠BAC =35,∴AC =6,∵把△ABC 绕着点C 按照顺时针的方向旋转,∴AC =A 'C =6,∠A '=∠BAC ,∵cos ∠A '=cos ∠BAC ==35,∴A 'E =185,∵AC =A 'C ,CE ⊥A 'B ',∴AA '=2A 'E =365,故答案我:365.【点评】本题考查了旋转的性质,等腰三角形的性质,锐角三角函数的应用,求出A 'E 的长是本题的关键.6.(2019秋•徐汇区期末)如图,在矩形ABCD 中,AB =3,AD =4,将矩形ABCD 绕着点B 顺时针旋转后得到矩形A 'BC 'D ',点A 的对应点A '在对角线AC 上,点C 、D 分别与点C '、D '对应,A ′D '与边BC 交于点E ,那么BE 的长是258.【考点】旋转的性质;相似三角形的性质;矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;图形的相似;推理能力.【分析】如图,过点B 作BF ⊥AC ,过点E 作EH ⊥AC ,由勾股定理可求AC =5,由面积法可求BF =125,由勾股定理可求AF =95,由旋转的性质可得AB =BA ',∠BAD =∠BA 'D '=90°,可求CA '=75,由等腰三角形的性质可求HC 的长,通过证明△EHC ∽△ABC ,可得EC BC HC AC ,可求EC 的长,即可求解.【解答】解:如图,过点B 作BF ⊥AC ,过点E 作EH ⊥AC ,∵AB =3,AD =4,∠ABC =90°,∴AC ===5,∵S △ABC =12AB ×BC =12AC ×BF ,∴3×4=5BF ,∴BF =125∴AF 22144925AB BF -=-95,∵将矩形ABCD 绕着点B 顺时针旋转后得到矩形A 'BC 'D ',∴AB =BA ',∠BAD =∠BA 'D '=90°,且BF ⊥AC ,∴∠BAC =∠BA 'A ,AF =A 'F =95,∠BA 'A +∠EA 'C =90°,∴A 'C =AC ﹣AA '=75,∵∠BA 'A +∠EA 'C =90°,∠BAA '+∠ACB =90°,∴∠ACB =∠EA 'C ,∴A 'E =EC ,且EH ⊥AC ,∴A 'H =HC =12A 'C =710,∵∠ACB =∠ECH ,∠ABC =∠EHC =90°,∴△EHC ∽△ABC ,∴BC HC AC EC =∴74105EC =∴EC =78,∴BE =BC ﹣EC =4﹣78=258,故答案为:258.【点评】本题考查了旋转的性质,矩形的性质,勾股定理,等腰三角形的性质,相似三角形的判定和性质,求出HC 的长是本题的关键.7.(2019秋•普陀区期末)如图,在RtΔABC 中,∠C=90°,AC=5,sinB=513,点P 为边BC 上一点,PC=3,将△ABC 绕点P 旋转得到△A'B'C'(点A ,B 、C 分别与点A'、B'、C'对应).使B'C'∥AB ,边A'C'与边AB 交于点G ,那么A'G 的长等于2013.【考点】旋转的性质;解直角三角形;平行线的判定,图形的旋转【专题】矩形菱形正方形;平移,旋转与对称;解直角一角形及其应用;应用意识。
上海市历年中考数学试题、模拟题汇编及答案

上海中考试题、模拟题汇编及答案20PP 年上海市初中毕业统一学业考试数学卷 20PP 年上海市初中毕业统一学业考试 20PP 年上海市初中毕业生统一学业考试20PP 年上海市初中毕业生统一学业考试数学试题及答案评分要点20PP 年上海市中考数学试题及答案上海市黄浦区20PP 年九年级数学学业 考试模拟考试 上海市青浦区20PP 学年度九年级数学学业 模拟考试 20PP 上海金山中考 数学模拟试卷--数学 20PP 上海浦东新中考数学预测卷--数学20PP 年上海市初中毕业统一学业考试数学卷(满分150分,考试时间100分钟)、选择题(本大题共 6题,每题4分,满分24分)1. 下列实数中,是无理数的为(C )A. 3.14B. 1C. . 3【解析】无理数即为无限不循环小数,则选 C 。
k2. 在平面直角坐标系中,反比例函数 P = - ( k v 0 )图像的两支分别在(XA.第一、三象限B.第二、四象限C.第一、二象限【解析】设K=-1,则P=2时,P= _丄,点在第四象限;当 P=-2时,P=丄,在第二象限,所以图像过2 2第二、四象限,即使选 B 3.已知一元二次方程 P 2+ P —1 = 0 ,下列判断正确的是( B )A .该方程有两个相等的实数根 B.该方程有两个不相等的实数根 C.该方程无实数根D.该方程根的情况不确定【解析】根据二次方程的根的判别式: A=b 2—4ac=(1 j —4心江(―1 )=5>0,所以方程有两个不相等的实数根,所以选 B4. 某市五月份连续五天的日最高气温分别为 23、20、20、21、26 (单位:°C),这组数据的中位数和众数分别是(D ) A. 22 C, 26°CB. 22 C, 20°CC. 21 C, 26°CD. 21 C, 20°C【解析】中位数定义:将所有数学按从小到大顺序排列后,当数字个数为奇数时即中间那个数为中位 数,当数字的个数为偶数时即中间那两个数的平均数为中位数。
2023上海各区中考一模数学压轴题

中考模拟数学试卷一、单项选择题(共12分)1.如图,四边形ABCD是矩形,E是边BC延长线上的一点,AE与CD相交于点F,则图中的相似三角形共有()A.4对 B.3对C.2对D.1对2.一元二次方程x2﹣3x=0的根是()A.x=3 B.x1=0,x2=﹣3C.x1=0,x2=√3 D.x1=0,x2=33.一元二次方程x2﹣3x=0的根是()A.x=3 B.x1=0,x2=﹣3C.x1=0,x2=√3D.x1=0,x2=34.如图,以A、B、C为顶点的三角形与以D、E、F为顶点的三角形相似,则这两个三角形的相似比为()A.2:1 B.3:1 C.4:3 D.3:25.如图,一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了()A.4圈B.3圈C.5圈D.3.5圈二、填空题(共24分)1.如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30∘方向,同时测得岛礁P正东方向上的避风港M在北偏东60∘方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行小时即可到达()。
(结果保留根号)|与(tanB−√3)2互为相反数,则∠C的度数2.已知△ABC,若有|sinA−12是。
三、解答题3.如图,在四边形A BCD中,A D∥BC,A B⊥BC,点E在A B上,∠DEC=90°。
求证:△ADE∽△BEC。
1.如图,同心圆O,大圆的面积被小圆所平分,若大圆的弦AB,CD分别切小圆于E、F点,当大圆半径为R时,且AB∥CD,求阴影部分面积。
2.如图,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C,在x轴的正半轴上(C在B的右侧),BC=2,AB=2根号3,△ADC与△ABC关于AC所在的直线对称。
上海初三数学各区一模压轴题汇总套全

上海初三数学各区一模压轴题汇总套全TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-2016~2017学年度上海市各区初三一模数学压轴题汇总(18+24+25)共15套整理 廖老师宝山区一模压轴题18(宝山)如图,D 为直角ABC 的斜边AB 上一点,DE AB 交AC 于E ,如果AED 沿着DE 翻折,A 恰好与B 重合,联结CD 交BE 于F ,如果8AC ,1tan 2A ,那么:___________.CF DF24(宝山)如图,二次函数232(0)2y ax x a 的图像与x 轴交于A B 、两点,与y 轴交于点,C 已知点(4,0)A .(1)求抛物线与直线AC 的函数解析式;(2)若点(,)D m n 是抛物线在第二象限的部分上的一动点,四边形OCDA 的面积为S ,求S 关于m 的函数关系;(3)若点E 为抛物线上任意一点,点F 为x 轴上任意一点,当以A C E F 、、、为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E 的坐标.25(宝山)如图(1)所示,E 为矩形ABCD 的边AD 上一点,动点P Q 、同时从点B 出发,点P 以1/cm s 的速度沿着折线BE ED DC 运动到点C 时停止,点Q 以2/cm s 的速度沿着BC 运动到点C 时停止。
设P Q 、同时出发t 秒时,BPQ 的面积为2ycm ,已知y 与t 的函数关系图像如图(2)(其中曲线OG 为抛物线的一部分,其余各部分均为线段).(1)试根据图(2)求05t 时,BPQ 的面积y 关于t 的函数解析式;(2)求出线段BC BE ED 、、的长度;(3)当t 为多少秒时,以B P Q 、、为顶点的三角形和ABE 相似;(4)如图(3)过点E 作EF BC 于F ,BEF 绕点B 按顺时针方向旋转一定角度,如果BEF 中E F 、的对应点H I 、恰好和射线BE CD 、的交点G 在一条直线,求此时C I 、两点之间的距离.崇明县一模压轴题18(崇明)如图,已知 ABC ∆中,45ABC ∠=,AH BC ⊥于点H ,点D 在AH 上,且DH CH =,联结BD ,将BHD 绕点H 旋转,得到EHF ∆(点B 、D 分别与点E 、F 对应),联结AE ,当点F 落在AC 上时,(F 不与C 重合)如果4BC =,tan 3C =,那么AE 的长为 ;24(崇明)在平面直角坐标系中,抛物线235y x bx c =-++与y 轴交于点(0,3)A ,与x轴的正半轴交于点(5,0)B ,点D 在线段OB 上,且1OD = ,联结AD 、将线段AD 绕着点D 顺时针旋转90︒,得到线段DE ,过点E 作直线l x ⊥轴,垂足为H ,交抛物线于点F .(1)求这条抛物线的解析式;(2)联结DF ,求cot EDF ∠的值;(3)点G 在直线l 上,且45EDG ︒∠=,求点G 的坐标.25(崇明)在ABC ∆中,90ACB ︒∠=,3cot 2A =,AC =,以BC 为斜边向右侧作等腰直角EBC ∆,P 是BE 延长线上一点,联结PC ,以PC 为直角边向下方作等腰直角PCD ∆,CD 交线段BE 于点F ,联结BD .(1)求证:PC CE CD BC =; (2)若PE x =,BDP ∆的面积为y ,求y 关于x 的函数解析式,并写出定义域;(3)当BDF ∆为等腰三角形时,求PE 的长.奉贤区一模压轴题18(奉贤)如图3,在矩形ABCD 中,AB =6,AD =3,点P 是边AD 上的一点,联结BP ,将△ABP 沿着BP 所在直线翻折得到△EBP ,点A 落在点E 处,边BE 与边CD 相交于点G ,如果CG=2DG ,那么DP 的长是__ ____.24(奉贤)如图,在平面直角坐标系中xOy 中,抛物线2y x bx c =-++与x 轴相交于点A (-1,0)和点B ,与y 轴相交于点C (0,3),抛物线的顶点为点D ,联结AC 、BC 、DB 、DC .(1)求这条抛物线的表达式及顶点D 的坐标;(2)求证:△ACO ∽△DBC ;(3)如果点E 在x 轴上,且在点B 的右侧,∠BCE=∠ACO ,求点E 的坐标。
2020-2021年上海各区数学中考一模压轴题分类汇编-24题含详解
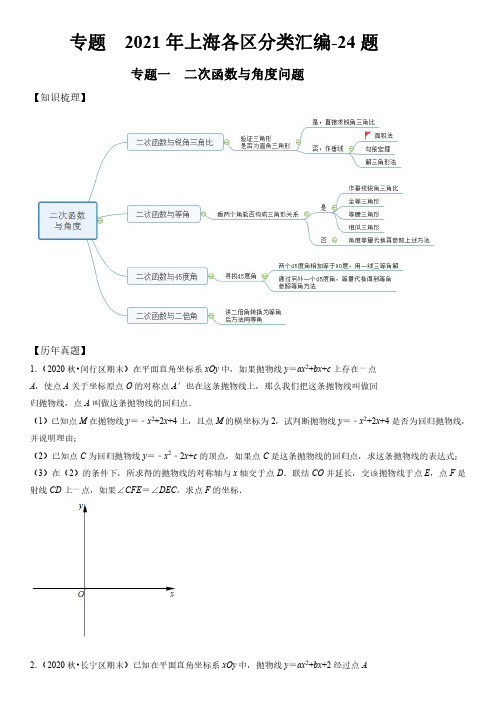
专题2021年上海各区分类汇编-24题专题一二次函数与角度问题【知识梳理】【历年真题】1.(2020秋•闵行区期末)在平面直角坐标系xOy中,如果抛物线y=ax2+bx+c上存在一点A,使点A关于坐标原点O的对称点A′也在这条抛物线上,那么我们把这条抛物线叫做回归抛物线,点A叫做这条抛物线的回归点.(1)已知点M在抛物线y=﹣x2+2x+4上,且点M的横坐标为2,试判断抛物线y=﹣x2+2x+4是否为回归抛物线,并说明理由;(2)已知点C为回归抛物线y=﹣x2﹣2x+c的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;(3)在(2)的条件下,所求得的抛物线的对称轴与x轴交于点D.联结CO并延长,交该抛物线于点E,点F是射线CD上一点,如果∠CFE=∠DEC,求点F的坐标.2.(2020秋•长宁区期末)已知在平面直角坐标系xOy中,抛物线y=ax2+bx+2经过点A(﹣3,﹣6)、B(6,0),与y轴交于点C.(1)求抛物线的表达式;(2)点D是抛物线上的点,且位于线段BC上方,联结CD.①如果点D的横坐标为2.求cot∠DCB的值;②如果∠DCB=2∠CBO,求点D的坐标.3.(2020秋•青浦区期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣4,0)和点B(2,0),与y轴交于点C.(1)求该抛物线的表达式及点C的坐标;(2)如果点D的坐标为(﹣8,0),联结AC、DC,求∠ACD的正切值;(3)在(2)的条件下,点P为抛物线上一点,当∠OCD=∠CAP时,求点P的坐标.4.(2020秋•虹口区期末)如图,在平面直角坐标系xOy中,已知点A(﹣1,0)、B(3,0)、C(0,3),抛物线y=ax2+bx+c经过A、B两点.(1)当该抛物线经过点C时,求该抛物线的表达式;(2)在(1)题的条件下,点P为该抛物线上一点,且位于第三象限,当∠PBC=∠ACB时,求点P的坐标;(3)如果抛物线y=ax2+bx+c的顶点D位于△BOC内,求a的取值范围.5.(2020秋•松江区期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣2经过点A(2,0)和B(﹣1,﹣1),与y轴交于点C.(1)求这个抛物线的表达式;(2)如果点P是抛物线位于第二象限上一点,PC交x轴于点D,23 PDDC .①求P点坐标;②点Q在x轴上,如果∠QCA=∠PCB,求点Q的坐标.6.(2020秋•奉贤区期末)如图,在平面直角坐标系xOy中,抛物线y=﹣12x2+bx+c与x轴正半轴交于点A(4,0),与y轴交于点B(0,2),点C在该抛物线上且在第一象限.(1)求该抛物线的表达式;(2)将该抛物线向下平移m个单位,使得点C落在线段AB上的点D处,当AD=3BD时,求m的值;(3)连接BC,当∠CBA=2∠BAO时,求点C的坐标.专题二二次函数与相似三角形【知识梳理】【历年真题】1.(2020秋•崇明区期末)如图,已知对称轴为直线x=﹣1的抛物线y=ax2+bx+3与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(1,0).(1)求点B的坐标及抛物线的表达式;(2)记抛物线的顶点为P,对称轴与线段BC的交点为Q,将线段PQ绕点Q,按顺时针方向旋转120°,请判断旋转后点P的对应点P′是否还在抛物线上,并说明理由;(3)在x轴上是否存在点M,使△MOC与△BCP相似?若不存在,请说明理由;若存在,请直接写出点M的坐标【不必书写求解过程】.2.(2020秋•黄浦区期末)如图,平面直角坐标系内直线y=x+4与x轴、y轴分别交于点A、B,点C是线段OB的中点.(1)求直线AC的表达式;(2)若抛物线y=ax2+bx+c经过点C,且其顶点位于线段OA上(不含端点O、A).①用含b的代数式表示a,并写出1b c的取值范围;②设该抛物线与直线y=x+4在第一象限内的交点为点D,试问:△DBC与△DAC能否相似?如果能,请求此时抛物线的表达式;如果不能,请说明理由.3.(2020秋•浦东新区期末)二次函数y=ax2+bx+c(a≠0)的图象经过点A(2,4)、B(5,0)和O(0,0).(1)求二次函数的解析式;(2)联结AO,过点B作BC⊥AO于点C,与该二次函数图象的对称轴交于点P,联结AP,求∠BAP的余切值;(3)在(2)的条件下,点M在经过点A且与x轴垂直的直线上,当△AMO与△ABP相似时,求点M的坐标.4.(2020秋•普陀区期末)在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+1与y轴交于点A,顶点B的坐标为(2,﹣1).(1)直接写出点A的坐标,并求抛物线的表达式;(2)设点C在x轴上,且∠CAB=90°,直线AC与抛物线的另一个交点为点D.①求点C、D的坐标;②将抛物线y=ax2+bx+1沿着射线BD的方向平移;平移后的抛物线顶点仍在线段BD上;点A的对应点为点P.设线段AB与x轴的交点为点Q,如果△ADP与△CBQ相似,求点P的坐标.专题三二次函数与其他【知识梳理】【历年真题】1.(2020秋•嘉定区期末)在平面直角坐标系xOy中,已知点A(﹣1,2),点B(1,6),点C(1,4),如果抛物线y=ax2+bx+3(a≠0)恰好经过这三个点之中的两个点.(1)试推断抛物线y=ax2+bx+3经过点A、B、C之中的哪两个点?简述理由;(2)求常数a与b的值;(3)将抛物线y=ax2+bx+3先沿与y轴平行的方向向下平移2个单位长度,再与沿x轴平行的方向向右平移t(t >0)个单位长度,如果所得到的新抛物线经过点C(1,4),设这个新抛物线的顶点是D,试探究△ABD的形状.2.(2020秋•金山区期末)在平面直角坐标系xOy中,直线y=﹣34x+2与直线y=12x﹣3相交于点A,抛物线y=ax2+bx﹣1(a≠0)经过点A.(1)求点A的坐标;(2)若抛物线y=ax2+bx﹣1向上平移两个单位后,经过点(1,﹣2),求抛物线y=ax2+bx﹣1的表达式;(3)若抛物线y=a'x2+b'x+c(a'<0)与y=ax2+bx﹣1关于x轴对称,且这两条抛物线的顶点分别是点P'与点P,当S△OPP′=3时,求抛物线y=ax2+bx﹣1的表达式.3.(2020秋•徐汇区期末)已知二次函数y=ax2﹣2ax+a+4(a<0)的大致图象如图所示,这个函数图象的顶点为点D.(1)求该函数图象的开口方向、对称轴及点D的坐标;(2)设该函数图象与y轴正半轴交于点C,与x轴正半轴交于点B,图象的对称轴与x轴交于点A,如果DC⊥BC,1tan 3DBC ∠=,求该二次函数的解析式;(3)在(2)的条件下,设点M 在第一象限该函数的图象上,且点M 的横坐标为t (t >1),如果△ACM 的面积是258,求点M 的坐标.4.(2020秋•静安区期末)如图,在平面直角坐标系xOy 中,直线y =﹣x +m (m >0)与x 轴、y 轴分别交于点A ,B ,抛物线y =ax 2+bx +4(a ≠0)经过点A ,且与y 轴相交于点C ,∠OCA =∠OAB .(1)求直线AB 的表达式;(2)如果点D 在线段AB 的延长线上,且AD =AC ,求经过点D 的抛物线y =ax 2+bx +4的表达式;(3)如果抛物线y =ax 2+bx +4的对称轴与线段AB 、AC 分别相交于点E ,F ,且EF =1,求此抛物线的顶点坐标.5.(2020秋•杨浦区期末)已知在平面直角坐标系xOy 中,抛物线y =﹣(x ﹣m )2+4与y轴交于点B ,与x 轴交于点C 、D (点C 在点D 左侧),顶点A 在第一象限,异于顶点A 的点P (1,n )在该抛物线上.(1)如果点P 与点C 重合,求线段AP 的长;(2)如果抛物线经过原点,点Q是抛物线上一点,tan∠OPQ=3,求点Q的坐标;(3)如果直线PB与x轴的负半轴相交,求m的取值范围.专题四二次函数与平行四边形【知识梳理】【历年真题】1.(2020秋•宝山区期末)已知抛物线y=ax2+bx(a≠0)经过A(4,0),B(﹣1,3)两点,抛物线的对称轴与x轴交于点C,点D与点B关于抛物线的对称轴对称,联结BC、BD.(1)求该抛物线的表达式以及对称轴;(2)点E在线段BC上,当∠CED=∠OBD时,求点E的坐标;(3)点M在对称轴上,点N在抛物线上,当以点O、A、M、N为顶点的四边形是平行四边形时,求这个平行四边形的面积.专题2021年上海各区分类汇编-24题专题一二次函数与角度问题【历年真题】1.(2020秋•闵行区期末)在平面直角坐标系xOy中,如果抛物线y=ax2+bx+c上存在一点A,使点A关于坐标原点O的对称点A′也在这条抛物线上,那么我们把这条抛物线叫做回归抛物线,点A叫做这条抛物线的回归点.(1)已知点M在抛物线y=﹣x2+2x+4上,且点M的横坐标为2,试判断抛物线y=﹣x2+2x+4是否为回归抛物线,并说明理由;(2)已知点C为回归抛物线y=﹣x2﹣2x+c的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;(3)在(2)的条件下,所求得的抛物线的对称轴与x轴交于点D.联结CO并延长,交该抛物线于点E,点F是射线CD上一点,如果∠CFE=∠DEC,求点F的坐标.【考点】二次函数综合题.【专题】二次函数图象及其性质;图形的相似;推理能力;应用意识.【分析】(1)先求出点M坐标,M'的坐标,代入解析式可求解;(2)先求出点C坐标,C'的坐标,利用回归点的定义可求解;(3)通过证明△CEF∽△CDE,可得CF CECE CD,可求CF=10,即可求解.【解答】解:(1)抛物线y=﹣x2+2x+4是回归抛物线,理由如下:∵点M在抛物线y=﹣x2+2x+4上,∴y=﹣4+4+4=4,∴点M(2,4),∴点M关于坐标原点O的对称点M'(﹣2,﹣4),当x=﹣2时,y=﹣4﹣4+4=﹣4,∴点M'在抛物线上,∴抛物线y=﹣x2+2x+4是回归抛物线;(2)∵点C为回归抛物线y=﹣x2﹣2x+c的顶点,∴点C(﹣1,c+1),∴点C关于原点O的对称点C'(1,﹣c﹣1),∵点C是这条抛物线的回归点,∴﹣c﹣1=﹣1﹣2+c,∴c=1,∴抛物线解析式为:y=﹣x2﹣2x+1;(3)∵抛物线y=﹣x2﹣2x+1,∴对称点为x=﹣1,∴点D(﹣1,0),点C(﹣1,2),∴直线CO解析式为y=﹣2x,联立方程组2212y x xy x⎧=--+⎨=-⎩,∴1212xy=⎧⎨=-⎩,2212xy=-⎧⎨=⎩,点E(1,﹣2),在△CEF和△CDE中,∠CFE=∠CED,∠FCE=∠ECD,∴△CEF∽△CDE,∴CF CECE CD=,∴CE2=CD•CF,∴(﹣1﹣1)2+(2+2)2=2CF,∴CF=10,∴F(﹣1,﹣8).【点评】本题是二次函数综合题,考查了二次函数的性质,相似三角形的判定和性质,理解新定义并运用是解题的关键.2.(2020秋•长宁区期末)已知在平面直角坐标系xOy中,抛物线y=ax2+bx+2经过点A(﹣3,﹣6)、B(6,0),与y轴交于点C.(1)求抛物线的表达式;(2)点D是抛物线上的点,且位于线段BC上方,联结CD.①如果点D的横坐标为2.求cot∠DCB的值;②如果∠DCB=2∠CBO,求点D的坐标.【考点】二次函数综合题.【专题】综合题;推理能力.【分析】(1)将点A,B坐标代入抛物线解析式中,解方程组,即可得出结论;(2)①先求出点D坐标,进而求出BC,CD,DB,判断出△BDC是直角三角形,即可得出结论;②构造出等腰三角形,利用对称性求出点F的坐标,进而求出直线CF的解析式,进而联立抛物线解析式,解方程组,即可得出结论.【解答】解:(1)∵抛物线y=ax2+bx+2经过点A(﹣3,﹣6)、B(6,0),∴932636620a ba b-+=-⎧⎨++=⎩,∴1353ab⎧=-⎪⎪⎨⎪=⎪⎩,∴抛物线的表达式为y=﹣13x2+53x+2;(2)①如图1,由(1)知,抛物线的解析式为y=﹣13x2+53x+2,当x=0时,y=2,∴C(0,2),当x=2时,y=﹣13×4+53×2+2=4,∴D(2,4),∵B(6,0),∴CD2=(2﹣0)2+(4﹣2)2=8,BC2=(6﹣0)2+(0﹣2)2=40,DB2=(6﹣2)2+(0﹣4)2=32,∴CD2+BC2=DB2,∴△BCD是直角三角形,∠BDC=90°,在Rt△BDC中,CD=,BD=,∴cot∠DCB=12 CDBD==;②如图2,过点C作CE∥x轴,则∠BCE=∠CBO,∵∠DCB=2∠CBO,∴∠DCE=∠BCE,过点B作BE⊥CE,并延长交CD的延长线于F,∵C(0,2),B(6,0),∴F(6,4),设直线CF的解析式为y=kx+2,∴6k+2=4,∴k=1 3,∴直线CF的解析式为y=13x+2①,∵抛物线的解析式为y=﹣13x2+53x+2②,联立①②,解得2xy=⎧⎨=⎩或4103xy=⎧⎪⎨=⎪⎩,∴D(4,10 3).【点评】此题是二次函数综合题,主要考查了待定系数法,勾股定理的逆定理,等腰三角形的性质,构造出等腰三角形是解本题的关键.3.(2020秋•青浦区期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣4,0)和点B(2,0),与y轴交于点C.(1)求该抛物线的表达式及点C的坐标;(2)如果点D的坐标为(﹣8,0),联结AC、DC,求∠ACD的正切值;(3)在(2)的条件下,点P为抛物线上一点,当∠OCD=∠CAP时,求点P的坐标.【考点】二次函数综合题.【专题】二次函数的应用;图形的相似;解直角三角形及其应用;应用意识.【分析】(1)利用待定系数法可求解析式;(2)过D作DE⊥AC交CA延长线于E,通过证明∴△EAD∽△OAC,由相似三角形的性质可求ED=2,EC=,即可求解;(3)由角的数量关系可求∠ACP =∠BAP ,由锐角三角函数可求解.【解答】解:(1)将点A (﹣4,0)和点B (2,0)代入抛物线y =ax 2+bx ﹣4,可得164404240a ab --=⎧⎨+-=⎩,解得:12a =,1b =∴抛物线的解析式为2142y x x =+-,当x =0时,y =﹣4,∴C (0,﹣4);(2)如图1,过D 作DE ⊥AC 交CA 延长线于E ,∵C (0,﹣4),点A (﹣4,0),∴OA =OC =4,∴AC =,∵∠EAD =∠OAC ,∠DEA =∠COA ,∴△EAD ∽△OAC ,∴DE EA DA CO OA CA ===,∴44DE EA ==∴DE =EA =,∴EC =,∴DE 1tan ACD==EC 3∠;(3)如图2,过点P 作PF ⊥x 轴于F ,设21(,4)2P t t t +-,∵∠OCD =∠CAP ,∴∠OCA +∠ACD =∠CAB +∠BAP ,∴45°+∠ACD=45°+∠BAP,∴∠ACD=∠BAP,∴1 tan BAP=tan ACD=3∠∠,∴tan∠BAP=21t+t-4PF12==AF t+43,∴83t 或t=﹣4(舍去),∴820 (,) 39 P.【点评】本题是二次函数综合题,考查了二次函数的性质,相似三角形的判定和性质,锐角三角函数等知识,灵活运用这些性质解决问题是本题的关键.4.(2020秋•虹口区期末)如图,在平面直角坐标系xOy中,已知点A(﹣1,0)、B(3,0)、C(0,3),抛物线y=ax2+bx+c经过A、B两点.(1)当该抛物线经过点C时,求该抛物线的表达式;(2)在(1)题的条件下,点P为该抛物线上一点,且位于第三象限,当∠PBC=∠ACB时,求点P的坐标;(3)如果抛物线y=ax2+bx+c的顶点D位于△BOC内,求a的取值范围.【考点】二次函数综合题.【专题】压轴题;应用意识.【分析】(1)设抛物线的解析式为y=a(x﹣3)(x+1),将点C的坐标代入求得a的值,可得抛物线的解析式;(2)先根据点B和C的坐标证明△OCB是等腰直角三角形,得∠OBC=∠OCB=45°,根据等式的性质得:∠OAC =∠PBO,利用三角函数列式可得OE的长,利用待定系数法求PB的解析式,联立抛物线和直线PB的解析式组成方程组可得点P的坐标即可;(3)先确定抛物线的对称轴,计算边界点D的坐标和对应a的值,根据图形可知:符合条件的a一定是负数,从而得解.【解答】解:(1)设抛物线的解析式为y=a(x﹣3)(x+1).将点C的坐标(0,3)代入得:﹣3a=3,解得:a=﹣1,∴抛物线的解析式为y=﹣x2+2x+3;(2)如图1,设PB交y轴于点E,∵C(0,3),B(3,0),∴OB=OC=3,∵∠COB=90°,∴∠OCB=∠OBC=45°,又∵∠ACB=∠PCB,∴∠ACB﹣∠OCB=∠PBC﹣∠OBC,即∠OCA=∠PBO,∴tan∠OCA=tan∠PBO,即OA OE OC OB=,∴133OE=,∴OE=1,∵点P在第三象限,∴E(0,﹣1),设PB的解析式为:y=kx+b(k≠0),把E(0,﹣1)和B(3,0)代入得:130bk b=-⎧⎨+=⎩,解得:131kb⎧=⎪⎨⎪=-⎩,∴PB的解析式为:y=13x﹣1,则223113y x xb x⎧=-++⎪⎨=-⎪⎩,解得:113xy=⎧⎨=⎩或2243139xy⎧=-⎪⎪⎨⎪=-⎪⎩,∴P(﹣43,﹣139);(3)∵抛物线y=ax2+bx+c经过A、B两点,∴对称轴是:直线x=312-=1,∵B(3,0)、C(0,3),同理得BC的解析式为:y=﹣x+3,当x=1时,y=2,当顶点D(1,2)时,设抛物线的解析式为y=a(x﹣3)(x+1),把顶点D(1,2)代入得:a=﹣1 2,∴抛物线y=ax2+bx+c的顶点D位于△BOC内,a的取值范围是﹣12<a<0.【点评】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式,三角函数,对称的性质,二次函数的性质等知识,熟知利用方程组的解确定两函数的交点坐标是本题的关键.5.(2020秋•松江区期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣2经过点A(2,0)和B(﹣1,﹣1),与y轴交于点C.(1)求这个抛物线的表达式;(2)如果点P是抛物线位于第二象限上一点,PC交x轴于点D,23 PDDC=.①求P点坐标;②点Q在x轴上,如果∠QCA=∠PCB,求点Q的坐标.【考点】二次函数综合题.【专题】二次函数的应用;图形的全等;图形的相似;应用意识.【分析】(1)由待定系数法可求解析式;(2)①过点P作PE⊥x轴于E,由平行线分线段成比例可求PE的长,代入解析式可求解;②分两种情况讨论,利用全等三角形的性质和相似三角形的性质可求解.【解答】解:(1)∵抛物线y=ax2+bx﹣2经过点A(2,0)和B(﹣1,﹣1),∴120422a ba b-=--⎧⎨=+-⎩,解得:2313ab⎧=⎪⎪⎨⎪=-⎪⎩,∴抛物线解析式为:y=23x2﹣13x﹣2;(2)①如图1,过点P作PE⊥x轴于E,∵抛物线y=ax2+bx﹣2与y轴交于点C,∴点C(0,﹣2),∴OC=2,∵PE∥OC,∴23PE PDOC DC===EDDO,∴PE=43,∴43=23x2﹣13x﹣2,∴x=﹣2或x=52(不合题意舍去),∴点P(﹣2,4 3);②如图2,过点B作BH⊥CO于H,由①可知DO==,∵B(﹣1,﹣1),点C(0,﹣2),A(2,0)∴OA=OC=2,BH=CH=1,∴∠BCH=45°=∠OCA,∴∠BCA=90°,当点Q在线段AO上时,∵∠QCA=∠PCB,∴∠DCO=∠QCO,又∵CO=CO,∠DOC=∠QOC=90°,∴△DOC≌△QOC(ASA),∴DO=QO=6 5,∴点Q坐标为(65,0),当点Q'在射线OA上时,∵∠Q'CA=∠PCB,∴∠DCQ'=90°,∴∠CDO +∠DQ 'C =90°,∠DCO +∠CDO =90°,∴∠DQ 'C =∠DCO ,又∵∠DOC =∠Q 'OC =90°,∴△DOC ∽△COQ ',∴'DO CO OC Q O=,∴4=65×Q 'O ,∴Q 'O =103,∴点Q '(103,0),综上所述:点Q 坐标为(65,0)或(103,0).【点评】本题二次函数综合题,考查了待定系数法求解析式,二次函数的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,灵活运用这些知识解决问题是解题的关键.6.(2020秋•奉贤区期末)如图,在平面直角坐标系xOy 中,抛物线y =﹣12x 2+bx +c 与x 轴正半轴交于点A (4,0),与y 轴交于点B (0,2),点C 在该抛物线上且在第一象限.(1)求该抛物线的表达式;(2)将该抛物线向下平移m 个单位,使得点C 落在线段AB 上的点D 处,当AD =3BD 时,求m 的值;(3)连接BC ,当∠CBA =2∠BAO 时,求点C的坐标.【考点】二次函数综合题.【专题】压轴题;应用意识.【分析】(1)利用待定系数法求抛物线的解析式即可;(2)如图1,过点D 作DG ⊥x 轴于G ,利用平行证明△ADG ∽△ABO ,列比例式可以计算OG 和DG 的长,从而得D (1,32),最后由平移的性质可得m 的值;(3)如图2,作辅助线,构建等腰△ABF ,确定点F 的坐标,计算BF 的解析式,联立抛物线和BF 的解析式,方程组的一个解就是点C 的坐标.【解答】解:(1)把点A (4,0)和点B (0,2)代入抛物线y =﹣12x 2+bx +c 中得:1-16+4b+c=02c=2⎧⨯⎪⎨⎪⎩,解得:3b=-2c=2⎧⎪⎨⎪⎩,∴抛物线的解析式为:y=﹣12x2+32x+2;(2)如图1,过点D作DG⊥x轴于G,∴DG∥OB,∴△ADG∽△ABO,∴AD DG AG AB OB OA==,∵AD=3BD,∴AG=3OG,∵A(4,0),B(0,2),∴OA=4,OB=2,∴OG=1,DG=3 2,∵D(1,3 2),由平移得:点C的横坐标为1,当x=1时,y=﹣12×1+32×1+2=3,∴m=3﹣32=32;(3)∵∠CBA=2∠BAO,点C在该抛物线上且在第一象限,∴点C在AB的上方,如图2,过A作AF⊥x轴于A,交BC的延长线于点F,过B作BE⊥AF于点E,∴BE∥OA,∴∠BAO=∠ABE,∵∠CBA=2∠BAO=∠ABE+∠EBF,∴∠FBE=∠ABE,∵∠BEF=∠AEB=90°,∴∠F=∠BAF,∴AB=BF,∴AE=EF=OB=2,∴F(4,4),设BF的解析式为:y=kx+n,则402k nn+=⎧⎨=⎩,解得:122kn⎧=⎪⎨⎪=⎩,∴BF的解析式为:y=12x+2,∴212213222y xy x x⎧=+⎪⎪⎨⎪=++⎪⎩,解得2xy=⎧⎨=⎩或23xy=⎧⎨=⎩,∴C(2,3).【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等腰三角形的性质和相似三角形的判定与性质;会利用待定系数法求抛物线和一次函数的解析式;灵活应用相似比表示线段之间的关系;理解坐标与图形的性质;会利用数形结合的思想解决数学问题.专题二二次函数与相似三角形【历年真题】1.(2020秋•崇明区期末)如图,已知对称轴为直线x=﹣1的抛物线y=ax2+bx+3与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(1,0).(1)求点B的坐标及抛物线的表达式;(2)记抛物线的顶点为P,对称轴与线段BC的交点为Q,将线段PQ绕点Q,按顺时针方向旋转120°,请判断旋转后点P的对应点P′是否还在抛物线上,并说明理由;(3)在x轴上是否存在点M,使△MOC与△BCP相似?若不存在,请说明理由;若存在,请直接写出点M的坐标【不必书写求解过程】.【考点】二次函数综合题.【专题】代数几何综合题;推理能力.【分析】(1)构建方程组求解即可.(2)如图1中,过点P′作P′H⊥PQ于H.求出点P′的坐标,即可判断.(3)首先证明∠PCB=90°,由PC:BC=1:3,推出OM:OC=1:3或OC:OM=1:3,推出OM=1或9,由此即可解决问题.【解答】解:(1)由题意,3012a bba++=⎧⎪⎨-=-⎪⎩,解得12ab=-⎧⎨=-⎩,∴抛物线的解析式y=﹣x2﹣2x+3,令y=0,则﹣x2﹣2x+3=0,解得x=1或﹣3,∴B(﹣3,0).(2)点P′在抛物线上,理由:如图1中,过点P′作P′H⊥PQ于H.∵y=﹣x2﹣2x+3=﹣(x+1)2+4,∴顶点P(﹣1,4),∵B(﹣3,0),C(0,3),∴直线BC的解析式为y=x+3,∵PQ∥y轴,∴Q(﹣1,2),∴PQ=2,在Rt△P′QH中,∠P′HQ=90°,∠P′QH=180°﹣120°=60°,P′Q=PQ=2,∴PH=P′Q•sin60PH=P′Q•cos60°=1,∴P1,1),当x﹣1时,y1)2﹣2﹣1)+3=1,∴点P′在抛物线上.(3)存在.如图2中,连接PB,PC.∵B(﹣3,0),P(﹣1,4),C(0,3),∴BC=,PC,PB=∴PB2=PC2+CB2,∴∠PCB=90°,PC:BC=:=1:3,当MO:OC=1:3或OC:MO=1:3时,△COM与△BCP相似,∴OM=1或9,∴满足条件的点M的坐标为(1,0)或(﹣1,0)或(9,0)或(﹣9,0).【点评】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,相似三角形的判定和性质,解直角三角形等知识,解题的关键是学会利用参数构建方程组解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.2.(2020秋•黄浦区期末)如图,平面直角坐标系内直线y=x+4与x轴、y轴分别交于点A、B,点C是线段OB的中点.(1)求直线AC的表达式;(2)若抛物线y=ax2+bx+c经过点C,且其顶点位于线段OA上(不含端点O、A).①用含b的代数式表示a,并写出1b c的取值范围;②设该抛物线与直线y=x+4在第一象限内的交点为点D,试问:△DBC与△DAC能否相似?如果能,请求此时抛物线的表达式;如果不能,请说明理由.【考点】二次函数综合题.【专题】代数几何综合题;推理能力.【分析】(1)求出A,C两点坐标,利用待定系数法解决问题即可.(2)①根据顶点的纵坐标为0,对称轴在线段OA上,构建方程与不等式即可解决问题.②能相似.利用相似三角形的性质构建方程,求出点D的坐标,再利用待定系数法解决问题即可.【解答】解:(1)∵直线y=x+4与x轴、y轴分别交于点A、B,∴A(﹣4,0),B(0,4),∴OA=OB=4,∵BC=OC=2,∴C(0,2),设直线AC的解析式为y=mx+n,则有240n m n =⎧⎨-+=⎩,解得122m n ⎧=-⎪⎨⎪=⎩,∴直线AC 的解析式为y =12x +2.(2)①由题意,2240402c b ac b a ⎧⎪=⎪-=⎨⎪⎪-<-<⎩,∴a =18b 2,1>1b>0.②能相似.如图,在Rt △AOC 中,∠AOC =90°,OA =4,OC =2,∴AC=2,∵△△DBC 与△DAC 相似,∠CDB =∠ADC ,∴当∠BCD =∠DAC 时,△DCB ∽△DAC ,∴55DC CB DA AC ===,∵点D 在直线y =x +4上,∴可以假设D (t ,t +4),5=,解得t =1或﹣32(舍弃),经检验,t =1是方程的根,∴D (1,5),∵抛物线y =ax 2+bx +2经过D (1,5),∴a +b +2=5,∴a +b =3,∵a =18b 2,∴3﹣b =18b 2,∴b 2+8b ﹣24=0,∴b =﹣4﹣,∴a =7﹣∴抛物线的解析式为y =(7﹣x 2+(﹣x +2.【点评】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,相似三角形的判定和性质等知识,解题的关键是学会利用参数构建方程或不等式解决问题,属于中考压轴题.3.(2020秋•浦东新区期末)二次函数y=ax2+bx+c(a≠0)的图象经过点A(2,4)、B(5,0)和O(0,0).(1)求二次函数的解析式;(2)联结AO,过点B作BC⊥AO于点C,与该二次函数图象的对称轴交于点P,联结AP,求∠BAP的余切值;(3)在(2)的条件下,点M在经过点A且与x轴垂直的直线上,当△AMO与△ABP相似时,求点M的坐标.【考点】二次函数综合题.【专题】综合题;推理能力.【分析】(1)利用待定系数法,即可得出结论;(2)先判断出OB=AB,进而判断出△OBP≌△ABP,得出∠BOP=∠BAP,再求出直线BC的解析式,求出点P 的坐标,构造直角三角形,即可得出结论;(3)先判断出∠OAE=∠OBC,进而得出OM=AM或OA=OM,即可得出结论.【解答】解:(1)二次函数y=ax2+bx+c(a≠0)的图象经过点B(5,0)和O(0,0),∴设二次函数的解析式为y=ax(x﹣5),将点A(2,4)代入y=ax(x﹣5)中,得4=a×2(2﹣5),∴a=﹣2 3,∴二次函数的解析式为y=﹣23x(x﹣5)=﹣23x2+103x;(2)如图1,连接OP,∵A(2,4)、B(5,0)和O(0,0),∴OB=5,AB5,∴OB=AB,∵BC⊥OA,∴BC是OA的垂直平分线,∴AP=OP,∵BP=BP∴△OBP≌△ABP(SSS),∴∠BOP=∠BAP,∵AC=OC,A(2,4),∴点C(1,2),∴直线BC的解析式为y=﹣12x+52,由(1)知,二次函数的解析式为y=﹣23x2+103x,∴对称轴为直线x=52,∴P(52,54),∴OD=52,PD=54,∴cot∠BAP=cot∠BOP=ODPD=2;(3)∵BC⊥OA,AE⊥OB,∴∠ACB=∠AEB=90°,∵∠AMC=∠BME,∴∠OAE=∠OBC,∵点P在抛物线的对称轴上,∴OP=PB,∴△BOP是等腰三角形,∵△AMO与△ABP相似,∴△AMO与△OBP相似,∴OM=AM或OA=OM,设M(2,m),当OM=AM时,OM=AM=4﹣m,在Rt△OEM中,EM=m,根据勾股定理得,OM2﹣EM2=OE2,∴(4﹣m)2﹣m2=4,∴m=3 2,当OA=OM时,AE=M'E,∴M'(2,﹣4)即满足条件的点M的坐标为(2,32)或(2,﹣4).4.(2020秋•普陀区期末)在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+1与y轴交于点A,顶点B的坐标为(2,﹣1).(1)直接写出点A的坐标,并求抛物线的表达式;(2)设点C在x轴上,且∠CAB=90°,直线AC与抛物线的另一个交点为点D.①求点C、D的坐标;②将抛物线y=ax2+bx+1沿着射线BD的方向平移;平移后的抛物线顶点仍在线段BD上;点A的对应点为点P.设线段AB与x轴的交点为点Q,如果△ADP与△CBQ相似,求点P的坐标.【考点】二次函数综合题.【专题】压轴题;应用意识.【分析】(1)先令x=0可得y=1,得点A的坐标,根据抛物线的顶点B(2,﹣1),利用待定系数法可得抛物线的表达式;(2)①根据点A和B的坐标得∠BAO=45°,所以∠CAO=45°,可知△ACO是等腰直角三角形,可得C的坐标,从而得AC的解析式,联立方程组可得直线AC与抛物线的交点D的坐标;②先证明∠PAD=∠ADB=∠BCQ,设P(m,2m+1),根据平移后B的对称点B'在线段BD上可知0≤m≤4,如果△ADP与△CBQ相似,存在两种情况:AP ADCQ BC=或AP ADBC CQ=,列方程可得结论.【解答】解:(1)当x =0时,y =1,∴A (0,1),设抛物线的解析式为:y =a (x ﹣2)2﹣1,把A (0,1)代入得:1=a (0﹣2)2﹣1,∴a=,∴抛物线的表达式为:y =(x ﹣2)2﹣1;(2)①如图1,∵A (0,1),B (2,﹣1),∴∠BAO =45°,∵∠CAB =90°,∴∠CAO =45°,∴OC =OA =1,∴C (﹣1,0),设AC 的解析式为:y =kx +m ,则01k m m -+=⎧⎨=⎩,解得:11k m =⎧⎨=⎩,∴AC 的解析式为:y =x +1,则211(2)12y x y x =+⎧⎪⎨=--⎪⎩,解得:1101x y =⎧⎨=⎩或2267x y =⎧⎨=⎩,∴D (6,7);②∵A (0,1),B (2,﹣1),同理得直线AB 的解析式为:y =﹣x +1,∴Q (1,0),∴CQ =2,BC=∵D (6,7),A (0,1),∴AD=AB=如图2,同理得:直线BD 的解析式为:y =2x ﹣5,由平移得:AP ∥BD ,则直线AP 的解析式为:y =2x +1,∴∠PAD =∠ADB ,∵tan ∠BCQ =13AB AD==tan ∠ADB ,∴∠PAD =∠BCQ ,设抛物线平移后的顶点为B ',P (m ,2m +1),则AP 5m ,B '(m +2,2m ﹣1),∵抛物线y =ax 2+bx +1沿着射线BD 的方向平移;平移后的抛物线顶点仍在线段BD 上,∴0≤m ≤4,如果△ADP 与△CBQ 相似,有以下两种情况:i )当AP AD CQ BC =时,即562210m =,解得:m =2.4,∴P (2.4,5.8);ii )当AP AD BC CQ =562210m=,解得:m =6(不符合题意,舍去),综上,P (2.4,5.8).【点评】本题是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数和一次函数的解析式,两点的距离公式,相似三角形的性质和判定,平移的性质等知识,解题时,注意数形结合,使抽象的问题变得具体化,降低了解题的难度.专题三二次函数与其他【历年真题】1.(2020秋•嘉定区期末)在平面直角坐标系xOy 中,已知点A (﹣1,2),点B (1,6),点C (1,4),如果抛物线y =ax 2+bx +3(a ≠0)恰好经过这三个点之中的两个点.(1)试推断抛物线y =ax 2+bx +3经过点A 、B 、C 之中的哪两个点?简述理由;(2)求常数a与b的值;(3)将抛物线y=ax2+bx+3先沿与y轴平行的方向向下平移2个单位长度,再与沿x轴平行的方向向右平移t(t >0)个单位长度,如果所得到的新抛物线经过点C(1,4),设这个新抛物线的顶点是D,试探究△ABD的形状.【考点】二次函数综合题.【专题】综合题;推理能力.【分析】(1)先求出抛物线必经过点E(0,3),再判断出BC∥y轴,再判断出点A、E、C在同一条直线上,即可得出结论;(2)将点A,B坐标代入抛物线解析式中,即可得而出结论;(3)先用t表示出新抛物线的解析式,再将点C坐标代入,即可得出新抛物线的解析式,最后求出AB,AD,BD 即可得出结论.【解答】解:(1)抛物线与y轴的交点记作点E,针对于抛物线y=ax2+bx+3,当x=0时,y=3,∴抛物线与y轴的交点E的坐标为(0,3),∵点B(1,6),点C(1,4),∴BC∥y轴,∴抛物线y=ax2+bx+3经过点B、C两点中其中的一点,而点A(﹣1,2),E(0,3),C(1,4),∴点A,E,C从左到右,横坐标依次增加1,纵坐标也依次增加1,∴点A,E,C再同一条直线上,∴点C不在物线y=ax2+bx+3上,即抛物线y=ax2+bx+3经过点A、B、C之中的A、B两个点;(2)将点A(﹣1,2)、B(1,6)代入抛物线y=ax2+bx+3中,得3236 a ba b-+=⎧⎨++=⎩,∴12ab=⎧⎨=⎩,即a,b的值分别为1,2;(3)由(2)知,a=1,b=2,∴抛物线的解析式为y=x2+2x+3=(x+1)2+2,由平移得,平移后新抛物线的解析式为y=(x+1﹣t)2+2﹣2,即新抛物线的解析式为y=(x+1﹣t)2,∵抛物线经过点C(1,4),∴4=(1+1﹣t)2,∴t=0(舍)或t=4,∴新抛物线的解析式为y=(x﹣3)2,∴顶点D(3,0),∵点A(﹣1,2)、B(1,6),∴AB=AD=BD=∴AB=AD,AB2+AD2=20+20=40=BD2,∴△ABD是等腰直角三角形.【点评】此题是二次函数综合题,主要考查了待定系数法,平移的规律,两点间的距离公式,等腰直角三角形的判定,判断出抛物线必经过点E是解本题的关键.2.(2020秋•金山区期末)在平面直角坐标系xOy中,直线y=﹣34x+2与直线y=12x﹣3相交于点A,抛物线y=ax2+bx﹣1(a≠0)经过点A.(1)求点A的坐标;(2)若抛物线y=ax2+bx﹣1向上平移两个单位后,经过点(1,﹣2),求抛物线y=ax2+bx﹣1的表达式;(3)若抛物线y=a'x2+b'x+c(a'<0)与y=ax2+bx﹣1关于x轴对称,且这两条抛物线的顶点分别是点P'与点P,当S△OPP′=3时,求抛物线y=ax2+bx﹣1的表达式.【考点】二次函数综合题.【专题】代数几何综合题;二次函数图象及其性质;平移、旋转与对称;运算能力;推理能力.【分析】(1)联立两直线解析式,解二元一次方程组即可得出答案;(2)由抛物线经过点A可得出b=﹣4a,由平移的性质可得出答案;(3)求出顶点P的坐标为(2,﹣4a﹣1),由轴对称的性质可得出P'的坐标,求出PP'的长,根据三角形的面积公式可得出方程,解方程可得出答案.【解答】解:(1)∵直线y=﹣34x+2与直线y=12x﹣3相交于点A,∴324132y xy x⎧=-+⎪⎪⎨⎪=-⎪⎩,解得:41xy=⎧⎨=-⎩;∴点A的坐标为(4,﹣1).(2)∵抛物线y=ax2+bx﹣1(a≠0)经过点A(4,﹣1),∴16a+4b﹣1=﹣1,即b=﹣4a,∴y=ax2﹣4ax﹣1,∴平移后的抛物线的表达式是y =ax 2﹣4ax +1,∴﹣2=a ﹣4a +1,解得:a =1,∴抛物线y =ax 2+bx ﹣1的表达式是:y =x 2﹣4x ﹣1.(3)如图,∵y =ax 2﹣4ax ﹣1=a (x ﹣2)2﹣4a ﹣1,∴P (2,﹣4a ﹣1),∵抛物线y =a 'x 2+b 'x +c (a '<0)与y =ax 2﹣4ax ﹣1关于x 轴对称,∴P '(2,4a +1),∵a '<0,∴a >0,∴P 'P =8a +2,又∵OD =2,S △OPP '=12×OD ×PP ',∴12(82)32a ⨯⨯+=,解得:a =18,∴抛物线y =ax 2+bx ﹣1的表达式是y =21182x x -x ﹣1.【点评】本题是二次函数综合题,考查了求两直线的交点坐标,二次函数的性质,待定系数法,平移的性质,轴对称的性质,三角形的面积公式,利用参数列出方程是本题的关键.3.(2020秋•徐汇区期末)已知二次函数y =ax 2﹣2ax +a +4(a <0)的大致图象如图所示,这个函数图象的顶点为点D .(1)求该函数图象的开口方向、对称轴及点D 的坐标;(2)设该函数图象与y 轴正半轴交于点C ,与x 轴正半轴交于点B ,图象的对称轴与x 轴交于点A ,如果DC ⊥BC ,1tan 3DBC ∠=,求该二次函数的解析式;(3)在(2)的条件下,设点M 在第一象限该函数的图象上,且点M 的横坐标为t (t >1),如果△ACM 的面积是258,求点M 的坐标.。
2019-2020年上海各区数学中考一模压轴题分类汇编-25题含详解

专题2020年上海各区分类汇编-25题专题一动点函数下的相似三角形【知识梳理】【历年真题】1.(2019秋•奉贤区期末)如图,已知平行四边形ABCD中,AD AB=5,tan A=2,点E在射线AD上,过点E作EF⊥AD,垂足为点E,交射线AB于点F,交射线CB于点G,联结CE、CF,设AE=m.(1)当点E在边AD上时,①求△CEF的面积;(用含m的代数式表示)②当S△DCE=4S△BFG时,求AE:ED的值;(2)当点E在边AD的延长线上时,如果△AEF与△CFG相似,求m的值.2.(2019秋•杨浦区期末)已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;(3)联结PQ,直线PQ与直线BC交于点E,如果△QCE与△BCP相似,求线段BP的长.专题二动点函数背景下的面积问题【知识梳理】【历年真题】1.(2019秋•黄浦区期末)如图,△ABC 是边长为2的等边三角形,点D 与点B 分别位于直线AC 的两侧,且AD =AC ,联结BD 、CD ,BD 交直线AC 于点E .(1)当∠CAD =90°时,求线段AE 的长.(2)过点A 作AH ⊥CD ,垂足为点H ,直线AH 交BD 于点F ,①当∠CAD <120°时,设AE =x ,y =BCE AEFS S ∆∆(其中S △BCE 表示△BCE 的面积,S △AEF 表示△AEF 的面积),求y 关于x 的函数关系式,并写出x 的取值范围;②当BCE AEFS S ∆∆=7时,请直接写出线段AE 的长.2.(2019秋•松江区期末)已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.(1)如图(1),作AE⊥ON,垂足为点E,当m=2时,求线段EF的长度.(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;(3)如图(3),当△AFD与△CDF相似时,求m的值.专题三动点函数背景下的等腰三角形【知识梳理】【历年真题】1.(2019秋•浦东新区期末)在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.(1)如图,当ED=EB时,求AD的长;(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.2.(2019秋•青浦区期末)如图,在梯形ABCD中,AD∥BC,BC=BD=10,CD=4,AD=6.点P是线段BD上的动点,点E、Q分别是线段DA、BD上的点,且DE=DQ=BP,联结EP、EQ.(1)求证:EQ∥DC;(2)当BP>BQ时,如果△EPQ是以EQ为腰的等腰三角形,求线段BP的长;(3)当BP=m(0<m<5)时,求∠PEQ的正切值.(用含m的式子表示)3.(2019秋•闵行区期末)已知:如图,在Rt△ABC和Rt△ACD中,AC=BC,∠ACB=90°,∠ADC=90°,CD=2,(点A、B分别在直线CD的左右两侧),射线CD交边AB于点E,点G是Rt△ABC的重心,射线CG交边AB于点F,AD=x,CE=y.(1)求证:∠DAB=∠DCF;(2)当点E在边CD上时,求y关于x的函数关系式,并写出x的取值范围;(3)如果△CDG是以CG为腰的等腰三角形,试求AD的长.4.(2019秋•崇明区期末)如图,在△ABC中,AB=AC=10,BC=16,点D为BC边上的一个动点(点D不与点B、点C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F.(1)求证:AB•CE=BD•CD;(2)当DF平分∠ADC时,求AE的长;(3)当△AEF是等腰三角形时,求BD的长.5.(2019秋•宝山区期末)如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=k⋅OC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;(3)写出当△ONB为等腰三角形时,旋转角α的度数.专题四动点函数背景下的线段问题【知识梳理】【历年真题】1.(2019秋•虹口区期末)如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=3 5,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;=y,求y关于x的函数关系式(不需要写函数的定义域);(2)当点D在BC的延长线上时,设AG=x,S△DAF(3)如果AG=8,求DE的长.2.(2019秋•静安区期末)已知:如图1,在△ABC中,AB=AC,点D、E分别在边BC、DC上,AB2=BE•DC,DE:EC=3:1,F是边AC上的一点,DF与AE交于点G.(1)找出图中与△ACD相似的三角形,并说明理由;(2)当DF平分∠ADC时,求DG:DF的值;(3)如图2,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.专题四动点函数背景下四边形【知识梳理】【历年真题】1.(2019秋•长宁、金山区期末)如图,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,点P、Q分别在边AC、射线CB上,且AP=CQ,过点P作PM⊥AB,垂足为点M,联结PQ,以PM、PQ为邻边作平行四边形PQNM,设AP=x,平行四边形PQNM的面积为y.(1)当平行四边形PQNM为矩形时,求∠PQM的正切值;(2)当点N在△ABC内,求y关于x的函数解析式,并写出它的定义域;(3)当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时,直接写出x的值.2.(2019秋•嘉定区期末)已知:点P在△ABC内,且满足∠APB=∠APC(如图),∠APB+∠BAC=180°.(1)求证:△PAB∽△PCA;(2)如果∠APB=120°,∠ABC=90°,求PCPB的值;(3)如果∠BAC=45°,且△ABC是等腰三角形,试求tan∠PBC的值.3.(2019秋•徐汇区期末)如图,在△ABC中,AB=AC=5,BC=6,点D是边AB上的动点(点D不与点AB重合),点G在边AB的延长线上,∠CDE=∠A,∠GBE=∠ABC,DE与边BC交于点F.(1)求cos A的值;(2)当∠A=2∠ACD时,求AD的长;(3)点D在边AB上运动的过程中,AD:BE的值是否会发生变化?如果不变化,请求AD:BE的值;如果变化,请说明理由.4.(2019秋•普陀区期末)如图,在梯形ABCD中,AD//BC,∠C=90°,AD=2,BC=5,DC=3,点E在边BC上,tan∠AEC=3,点M是射线DC上一个动点(不与点D、C重合),联结BM交射线AE于点N,设DM=x,AN=y.(1)求BE的长;(2)当动点M在线段DC上时,试求y与x之间的函数解析式,并写出函数的定义域;(3)当动点M运动时,直线BM与直线AE的夹角等于45°,请直接写出这时线段DM的长.专题2020年上海各区分类汇编-25题专题一动点函数下的相似三角形【历年真题】1.(2019秋•奉贤区期末)如图,已知平行四边形ABCD 中,AD AB =5,tan A =2,点E 在射线AD 上,过点E 作EF ⊥AD ,垂足为点E ,交射线AB 于点F ,交射线CB 于点G ,联结CE 、CF ,设AE =m .(1)当点E 在边AD 上时,①求△CEF 的面积;(用含m 的代数式表示)②当S △DCE =4S △BFG 时,求AE :ED 的值;(2)当点E 在边AD 的延长线上时,如果△AEF 与△CFG 相似,求m 的值.【考点】相似形综合题.【专题】综合题;运算能力;推理能力.【分析】(1)①先根据三角函数表示出EF ,再用勾股定理表示出AF ,再判断出△AEF ∽△BGF ,得出比例式表示出CG ,即可得出结论;②先表示出FG ,再用S △DCE =4S △BFG 建立方程求出m ,即可得出结论;(2)分两种情况:①当△AEF ∽△CGF 时,得出∠AFE =∠CFG ,进而得出BG =12BC =52,FG =BG tan ∠CBFBF =52,进而得出AF =AB +BF =5+52=152,最后判断出△BGF ∽△AEF ,得出比例式建立方程求解即可得出结论;②当△AEF ∽△CGF 时,先判断出∠AFC =90°,进而得出CF =2BF ,再根据勾股定理得,求出BF =1,得出AF =AB +BF =6,同理:BG =,再判断出△BGF ∽△AEF ,得出比例式建立方程求解即可得出结论.【解答】解:(1)①∵EF ⊥AD ,∴∠AEF =90°,在Rt △AEF 中,tan A =2,AE =m ,∴EF =AE tan A =2m ,根据勾股定理得,AF ,∵AB =5,∴BF =5,∵四边形ABCD 是平行四边形,∴BC =AD AD ∥BC ,∴∠G =∠AEF =90°,∴△AEF ∽△BGF ,∴AE AFBG BF =,∴m BG =,∴BG m ,∴CG =BC +BG =m =m ,∴S △CEF =12EF •CG =12•2m •(m )=m ﹣m 2;②由①知,△AEF ∽△BGF ,∴BF FG AF EF =,∴FG =BFAF •EF •2m =2m ),∴EG =EF +FG =2m +2﹣m )=∴S △CDE =12DE •EG =12(m )•5,S △BFG =12BG •FG =12m )•2m ﹣m )2,S △DCE =4S △BFG 时,∴5=4m )2,∴m m =354,∴DE =AD ﹣AE ﹣4=4,∴AE :ED =354:54=3,即:AE :ED 的值为3;(2)∵四边形ABCD 是平行四边形,∴BC =AD ,AD ∥BC ,∵EF ⊥AD ,∴EF ⊥BC ,∴∠AEF =∠CGF =90°,∵△AEF 与△CFG 相似,∴①当△AEF ∽△CGF 时,如图1,∴∠AFE =∠CFG ,∵EF ⊥BC ,∴BG =12BC =52,∵AD ∥BC ,∴∠CBF =∠A ,∵tan A =2,∴tan ∠CBF =2,在Rt △BGF 中,FG =BG tan ∠CBF根据勾股定理得,BF 52,∴AF =AB +BF =5+52=152,∵BC∥AD,∴△BGF∽△AEF,∴BG BFAE AF=,∴,∴m =35 2;②当△AEF∽△CGF时,如图2,∴∠EAF=∠GFC,∵∠EAF+∠AFE=90°,∴∠GFC+∠AFE=90°,∴∠AFC=90°,∵AD∥BC,∴∠CBF=∠A,∴tan∠CBF=tan A=2,在Rt△BFC中,CF=BF•∠CBF=2BF,根据勾股定理得,BF2+CF2=BC2,∴BF2+4BF2)2,∴BF=1,∴AF=AB+BF=6,在Rt△BGF中,同理:BG =5 5,∵AD∥BC,∴△BGF∽△AEF,∴AE AFBG BF=6155=,∴m =655.即:如果△AEF与△CFG相似,m 的值为35 2或.【点评】此题是相似形综合题,主要考查了平行四边形的性质,锐角三角函数,三角形的面积公式,相似三角形的判定和性质,用方程的思想解决问题是解本题的关键.2.(2019秋•杨浦区期末)已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;(3)联结PQ ,直线PQ 与直线BC 交于点E ,如果△QCE 与△BCP 相似,求线段BP 的长.【考点】相似形综合题.【专题】几何综合题;应用意识.【分析】(1)如图1中,作PH ⊥BC 于H .解直角三角形求出BH ,PH ,在Rt △PCH 中,理由勾股定理即可解决问题.(2)如图1中,作PH ⊥BC 于H ,连接PQ ,设PC 交BD 于O .证明△POQ ∽△BOC ,推出∠OPQ =∠OBC =30°=∠PCQ ,推出PQ =CQ =y ,推出PC ,在Rt △PHB 中,BH =12x ,PH =2x ,根据PC 2=PH 2+CH 2,可得结论.(3)分两种情形:①如图2中,若直线QP 交直线BC 于B 点左侧于E .②如图3中,若直线QP 交直线BC 于C 点右侧于E .分别求解即可.【解答】解:(1)如图1中,作PH ⊥BC 于H .∵四边形ABCD 是菱形,∴AB =BC =4,AD ∥BC ,∴∠A +∠ABC =180°,∵∠A =120°,∴∠PBH =60°,∵PB =3,∠PHB =90°,∴BH =PB •cos60°=32,PH =PB •sin60°=332,∴CH =BC ﹣BH =4﹣32=52,∴PC =.(2)如图1中,作PH ⊥BC 于H ,连接PQ ,设PC 交BD 于O .∵四边形ABCD 是菱形,∴∠ABD =∠CBD =30°,∵∠PCQ =30°,∴∠PBO =∠QCO ,∵∠POB=∠QOC,∴△POB∽△QOC,∴PO BOQO CO=,∴PO QOBO CO=,∵∠POQ=∠BOC,∴△POQ∽△BOC,∴∠OPQ=∠OBC=30°=∠PCQ,∴PQ=CQ=y,∴PC y,在Rt△PHB中,BH=12x,PH=32x,∵PC2=PH2+CH2,∴3y2=(2x)2+(4﹣12x)2,∴y=3(0≤x<8).(3)①如图2中,若直线QP交直线BC于B点左侧于E.此时∠CQE=120°,∵∠PBC=60°,∴△PBC中,不存在角与∠CQE相等,此时△QCE与△BCP不可能相似.②如图3中,若直线QP交直线BC于C点右侧于E.则∠CQE=∠B=QBC+∠QCP=60°=∠CBP,∵∠PCB>∠E,∴只可能∠BCP=∠QCE=75°,作CF⊥AB于F,则BF=2,CF=PCF=45°,∴PF=CF=,此时PB=2+2,③如图4中,当点P在AB的延长线上时,∵△QCE 与△BCP 相似,∴∠CQE =∠CBP =120°,∴∠QCE =∠PCB =15°,作CF ⊥AB 于F .∵∠FCB =30°,∴∠FCP =45°,∴BF =12BC =2,CF =PF =23∴PB =3﹣2.综上所述,满足条件的PB 的值为3或232.【点评】本题考查相似形综合题,考查了菱形的性质,解直角三角形,相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.专题二动点函数背景下的面积问题【历年真题】1.(2019秋•黄浦区期末)如图,△ABC 是边长为2的等边三角形,点D 与点B 分别位于直线AC 的两侧,且AD =AC ,联结BD 、CD ,BD 交直线AC 于点E .(1)当∠CAD =90°时,求线段AE 的长.(2)过点A 作AH ⊥CD ,垂足为点H ,直线AH 交BD 于点F ,①当∠CAD <120°时,设AE =x ,y =BCE AEFS S ∆∆(其中S △BCE 表示△BCE 的面积,S △AEF 表示△AEF 的面积),求y 关于x 的函数关系式,并写出x 的取值范围;②当BCE AEFS S ∆∆=7时,请直接写出线段AE的长.【考点】三角形综合题.【专题】等腰三角形与直角三角形;应用意识.【分析】(1)过点E 作EG ⊥BC ,垂足为点G .AE =x ,则EC =2﹣x .根据BG =EG 构建方程求出x 即可解决问题.(2)①证明△AEF ∽△BEC ,可得22BCE AEF S BE S AE∆∆=,由此构建关系式即可解决问题.②分两种情形:当∠CAD <120°时,当120°<∠CAD <180°时,分别求解即可解决问题.【解答】解:(1)∵△ABC 是等边三角形,∴AB =BC =AC =2,∠BAC =∠ABC =∠ACB =60°.∵AD =AC ,∴AD =AB ,∴∠ABD =∠ADB ,∵∠ABD +∠ADB +∠BAC +∠CAD =180°,∠CAD =90°,∠ABD =15°,∴∠EBC =45°.过点E 作EG ⊥BC ,垂足为点G.设AE =x ,则EC =2﹣x .在Rt △CGE 中,∠ACB =60°,∴3sin ACB=)2EG EC x =- ∠,1cos ACB=12CG EC x =- ∠,∴BG =2﹣CG =1+12x ,在Rt △BGE 中,∠EBC =45°,∴131)22x x +=-,解得4x =-.所以线段AE的长是4-.(2)①设∠ABD =α,则∠BDA =α,∠DAC =∠BAD ﹣∠BAC =120°﹣2α.∵AD =AC ,AH ⊥CD ,∴1CAF=DAC=60-2α ∠∠,又∵∠AEF =60°+α,∴∠AFE =60°,∴∠AFE =∠ACB ,又∵∠AEF =∠BEC ,∴△AEF ∽△BEC ,∴22BCE AEF S BE S AE∆∆=,由(1)得在Rt △CGE 中,BG =1+12x,EG )2x =-,∴BE 2=BG 2+EG 2=x 2﹣2x +4,∴2224x x y x-+=(0<x <2).②当∠CAD <120°时,y =7,则有7=2224x x x-+,整理得3x 2+x ﹣2=0,解得x =23或﹣1(舍弃),2AE=3.当120°<∠CAD <180°时,同法可得22+24x x y x +=当y=7时,7=22+24x xx,整理得3x2﹣x﹣2=0,解得x=﹣23(舍弃)或1,∴AE=1.【点评】本题属于三角形综合题,考查了等边三角形的性质,解直角三角形,相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考常考题型.2.(2019秋•松江区期末)已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.(1)如图(1),作AE⊥ON,垂足为点E,当m=2时,求线段EF的长度.(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;(3)如图(3),当△AFD与△CDF相似时,求m的值.【考点】相似形综合题.【专题】分类讨论;图形的相似;推理能力.【分析】(1)如图1,延长FC交OM于点G,证∠BCG=∠MON,在Rt△AOE中,设OE=a,可求得OA,OG,OF的长,则EF=OF﹣OE=65 5;(2)如图2,延长FC交OM于点G,由(1)得CG=5,推出CO=CG=5,在Rt△COB中,由勾股定理求出a的值,得出OF的长,可求出cos∠COF的值,进一步推出sin∠COF的值;(3)需分情况讨论:当D在∠MON内部时,△FDA∽△FDC时,此时CD=AD=2,m=2;当△FDA∽△CDF 时,延长CD交ON于点Q,过F作FP⊥CQ于P,可利用三角函数求出m的值;当D在∠MON外部时,可利用相似的性质等求出m的值.【解答】解:(1)如图1,延长FC交OM于点G,∵∠BCG+∠CGB=90°,∠MON+∠CGB=90°,∴∠BCG=∠MON,则tan∠BCG=tan∠MON=2,∴BG=2BC=4,CG=,在Rt△AOE中,设OE=a,由tan∠MON=2,可得OA a,则OG+6,OF=OG=a+,∴EF=OF﹣OE=65 5;(2)如图2,延长FC交OM于点G,由(1)得CG=∵CD平分∠FCO,∴∠FCD=∠DCO,∵CD∥OM,∴∠FCD=∠CGO,∠DCO=∠COG,∴∠CGO=∠COG,∴CO=CG=在Rt△COB中,由BC2+BO2=OC2,得22++2)2=(2,解得a1=﹣655(舍去),a2=255,∴OF=a+5=5,cos∠COF=45 OFOC=,∴sin∠COF=3 5;(3)当D在∠MON内部时,①如图3﹣1,△FDA∽△FDC时,此时CD=AD=2,∴m=2;②当△FDA∽△CDF时,如图3﹣2,延长CD交ON于点Q,过F作FP⊥CQ于P,则∠FDC=∠FDA=135°,∴∠FDP=45°,∵PC=FP•tan∠PFC=FP•tan∠MON=2FP=2DP=CD+DP,∴FP=PD=CD=m,∴FD m,∵△FDA∽△CDF,∴FD CD DA FD=,∴FD==,∴m=1;当D在∠MON外部时,∠ADF>90°,∠DFC>90°,∴∠ADF =∠DFC ,∴∠DFI =∠FDI ,ID =IF ,①如图3﹣3,△FDA ∽△DFC 时,此时△FDA ≌△DFC ,∴CF =AD =2,∵∠DAF =∠FCD =∠FHD ,∴A 、O 重合,延长BC 交ON 于R ,∴FR =2CF =4,CR =BR =,∴m =CD =AB =12BR =;②如图3﹣4,△FDA ∽△CFD 时,设CF =(t >0),延长BC 交ON 于R ,过F 作FS ⊥CD 于S ,∵△DFC ≌△FDH ,∴DH =FC ,∴ID =IF =12CF ,∴IS =t ,FS =2t ,CS =4t ,DS )t ,DH =FC =,∵△FDA ∽△CFD ,∴AD DF DF FC=,∴DF 2=AD •FC =2DH =t ,∵DF 2=DS 2+FS 2,∴=4t 2+)2t 2,解得t 1=512-,t 2=0(舍去),∴DH =t =52=AD ,矛盾,综上所述:m =1或m =2,或m =【点评】本题考查了解直角三角形,等腰三角形的性质,相似三角形的判定与性质等,解题关键是注意分类讨论思想的运用.专题三动点函数背景下的等腰三角形【历年真题】1.(2019秋•浦东新区期末)在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.(1)如图,当ED=EB时,求AD的长;(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.【考点】几何变换综合题.【专题】几何综合题;应用意识.【分析】(1)证明∠ACD=∠EDB=∠B,推出tan∠ACD=tan∠B,可得AD ACAC AB=,由此构建方程即可解决问题.(2)如图1中,作EH⊥BD于H.证明△ACD∽△HDE,推出AC ADDH EH=,由此构建关系式即可解决问题.(3)分两种情形:①如图3﹣1中,设CB′交AB于K,作AE⊥CK于E,DM⊥CB′于M,DN⊥BC于N.利用角平分线的性质定理求出BD即可.②如图3﹣2中,当CB′交BA的延长线于K时,同法可得BD.【解答】解:(1)∵ED=EB,∴∠EDB=∠B,∵CD⊥DE,∴∠CDE=∠A=90°,∵∠ACD+∠ADC=90°,∠ADC+∠EDH=90°,∴∠ACD=∠EDB=∠B,∴tan∠ACD=tan∠B,∴AD ACAC AB=,∴334AD=,∴94AD=.(2)如图1中,作EH⊥BD于H.在Rt△ACB中,∵∠A=90°,AC=3,AB=4,∴BC=5,∵BE=y,∴EH=35y,BH=45y,DH=AB﹣AD﹣BH=4﹣x﹣45y,∵∠A=∠DHE=90°,∠ACD=∠EDH,∴△ACD∽△HDE,∴AC AD=DH EH,∴3x=434-x-55y y,∴220594x xyx-=+(0<x<4).(3)①如图3﹣1中,设CB′交AB于K,作AE⊥CK于E,DM⊥CB′于M,DN⊥BC于N∵AC =AB ′=3,AE ⊥CB ′,∴CE ='EB ='12CB =52,∴AE 22225113()22AC CE -=-,由△ACE ∽△KCA ,可得AK =3115,CK =185,∴BK =AB ﹣AK =4﹣3115,∵∠DCK =∠DCB ,DM ⊥CM ,DN ⊥CB ,∴DM =DN ,∴181185215252CDK CDB CK DM S DK CK S DB CB BC DN ∆∆===== ,∴BD =2543BK =10043151143,∴AD =AB ﹣BD =4﹣(10043151143)=7242151143.②如图3﹣2中,当CB ′交BA 的延长线于K 时,同法可得BD =2543BK =10043151143,∴AD =AB ﹣BD =7242﹣151143.【点评】本题属于几何变换综合题,考查了解直角三角形,相似三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.2.(2019秋•青浦区期末)如图,在梯形ABCD 中,AD ∥BC ,BC =BD =10,CD =4,AD=6.点P 是线段BD 上的动点,点E 、Q 分别是线段DA 、BD 上的点,且DE =DQ =BP ,联结EP 、EQ .(1)求证:EQ ∥DC ;(2)当BP >BQ 时,如果△EPQ 是以EQ 为腰的等腰三角形,求线段BP 的长;(3)当BP =m (0<m <5)时,求∠PEQ 的正切值.(用含m 的式子表示)【考点】相似形综合题.【专题】综合题;运算能力;推理能力.【分析】(1)先利用两边对应成比例,夹角相等,判断出△DEQ ∽△BCD ,得出∠DQE =∠BDC ,即可得出结论;(2)先用△DEQ ∽△BCD ,得出比例式表示出EQ ,再分两种情况,建立方程求解,即可得出结论;(3)先判得出△PHQ ∽△BGD ,得出PH PQ HQ BG BD GD ==,进而表示出HQ =1025m -,PH =26(102)5m -,即可得出结论.【解答】解:(1)∵AD ∥BC ,∴∠EDQ =∠DBC ,∵DE =DQ ,BD =BC ,∴1DE DQ =,BD BC =1,∴DE BD DQ BC=,∴△DEQ ∽△BCD ,∴∠DQE =∠BDC ,∴EQ ∥CD ;(2)设BP =x ,则DQ =x ,QP =2x ﹣10,∵△DEQ∽△BCD,∴EQ QDDC BC=,∴410EQ x=,∴EQ=25x,∵△EPQ是以EQ为腰的等腰三角形,∴Ⅰ、当EQ=EP时,∴∠EQP=∠EPQ,∵DE=DQ,∴∠EQP=∠QED,∴∠EPQ=∠QED,∴△EQP∽△DEQ,∴,∴EQ2=DE•QP,∴(25x)2=(2x﹣10)•x,解得,x=0(舍)或x=12523<6,即:BP=12523,Ⅱ、当QE=QP时,25x=2x﹣10,解得,x=254>6,此种情况不存在,即:BP=125 23;(3)如图,过点P作PH⊥EQ,交EQ的延长线于点H,过点B作BG⊥DC,垂足为点G,∵BD=BC,BG⊥DC,∴DG=2,BG=,∵BP=DQ=m,∴PQ=10﹣2m,∵EQ∥DC,∴∠PQH=∠BDG,∵∠PHQ=∠BGD=90°,∴△PHQ∽△BGD,∴PH PQ HQBG BD GD==102102m HQ-==,∴HQ=1025m-,PH=2)5m-,∴EH=102255m m-+=2,∴tan∠PEQ=PHEH=2)5m-12⨯=﹣5m.【点评】此题是相似形综合题,主要考查了相似三角形的判定和性质,平行线的性质,锐角三角函数,用方程的思想解决问题是解本题的关键.3.(2019秋•闵行区期末)已知:如图,在Rt△ABC和Rt△ACD中,AC=BC,∠ACB=90°,∠ADC=90°,CD=2,(点A、B分别在直线CD的左右两侧),射线CD交边AB于点E,点G是Rt△ABC的重心,射线CG交边AB于点F,AD=x,CE=y.(1)求证:∠DAB=∠DCF;(2)当点E在边CD上时,求y关于x的函数关系式,并写出x的取值范围;(3)如果△CDG是以CG为腰的等腰三角形,试求AD的长.【考点】相似形综合题.【专题】图形的相似;推理能力.【分析】(1)由点G是Rt△ABC的重心,证明CF⊥AB,即∠AFC=90°,利用外角的性质即可证明结论;(2)过点B作BH⊥CD于点H,先证△CAD≌△BCH,得出BH=CD=2,CH=AD=x,DH=2﹣x,再证△ADE ∽△BHE,利用合比性质即可求出结论;(3)分两种情况讨论,当GC=GD时,如图2﹣1,取AC的中点M,联结MD,可证AD=CH=12CD=1;当CG=CD时,如图2﹣2,可由重心分别求出CF,AC,CD的长,可由勾股定理求出AD的长.【解答】(1)证明:∵点G是Rt△ABC的重心,∴CF是Rt△ABC的中线,又∵在Rt△ABC中,AC=BC,∠ACB=90°,∴CF⊥AB,即∠AFC=90°,∵∠DEF=∠ADE+∠DAE=∠EFC+∠ECF,且∠ADE=∠EFC=90°,∴∠DAB=∠DCF;(2)解:如图1,过点B作BH⊥CD于点H,则∠CBH+∠BCH=90°,又∵∠BCH+∠ACD=90°,∴∠ACD=∠CBH,又∵∠ADC=∠CHB=90°,AC=CB,∴△CAD≌△BCH,∴BH=CD=2,CH=AD=x,DH=2﹣x,∵∠ADC=∠CHB=∠BHD=90°,∴AD∥BH,∴△ADE∽△BHE,∴AD DEBH EH=,∴2x DEEH=,∴22x DE EH DHEH EH++==,∴4-2xEH=x+2,∴2424(02)22x xy CE CH HE x xx x-+==+=+=<≤++;(3)解:当GC=GD时,如图2﹣1,取AC的中点M,联结MD,那么MD=MC,联结MG,MG⊥CD,且直线MG经过点B,那么BH与MG共线,又CH =AD ,那么AD =CH =12CD =1;当CG =CD 时,如图2﹣2,即CG =2,点G 为△ABC 的重心,∴332CF CG ==,∴AB =2CF =6,∴22AC AB ==,∴AD ==;综上所述,AD =1【点评】本题考查了函数,相似三角形的判定与性质,重心的性质等,解题关键是熟练掌握重心的性质.4.(2019秋•崇明区期末)如图,在△ABC 中,AB =AC =10,BC =16,点D 为BC 边上的一个动点(点D 不与点B 、点C 重合).以D 为顶点作∠ADE =∠B ,射线DE 交AC 边于点E ,过点A 作AF ⊥AD 交射线DE 于点F .(1)求证:AB •CE =BD •CD ;(2)当DF 平分∠ADC 时,求AE 的长;(3)当△AEF 是等腰三角形时,求BD 的长.【考点】相似形综合题.【专题】几何综合题;图形的相似;推理能力.【分析】(1)根据等腰三角形的性质得到∠B =∠C ,根据三角形的外角性质得到∠BAD =∠CDE ,得到△BAD ∽△CDE ,根据相似三角形的性质证明结论;(2)证明DF ∥AB ,根据平行线的性质得到AE BD AC BC =,证明△BDA ∽△BAC ,根据相似三角形的性质列式计算,得到答案;(3)分点F 在DE 的延长线上、点F 在线段DE 上两种情况,根据等腰三角形的性质计算即可.【解答】(1)证明:∵AB =AC ,∴∠B =∠C ,∠ADC =∠BAD +∠B ,∠ADE =∠B ,∴∠BAD =∠CDE ,又∠B =∠C ,∴△BAD ∽△CDE ,∴AB BD CD CE=,即AB •CE =BD •CD ;(2)解:∵DF 平分∠ADC ,∴∠ADE =∠CDE ,∵∠CDE =∠BAD ,∴∠ADE =∠BAD ,∴DF ∥AB ,∴AE BD AC BC=,∵∠BAD =∠ADE =∠B ,∴∠BAD =∠C ,又∠B =∠B ,∴△BDA ∽△BAC ,∴BD BA BA BC =,即101016BD =解得,254BD =,∴2541016AE =,解得,AE =12532;(3)解:作AH ⊥BC 于H ,∵AB =AC ,AH ⊥BC ,∴BH =HC =12BC =8,由勾股定理得,AH 22221086AB BH -=-=,∴tan B =AH BH =34,∴tan ∠ADF =AF AD =34,设AF =3x ,则AD =4x ,由勾股定理得,DF 22AD AF +=5x ,∵△BAD ∽△CDE ,∴AD AB DE CD =,当点F在DE的延长线上,FA=FE时,DE=5x﹣3x=2x,∴1042xCD x=,解得,CD=5,∴BD=BC﹣CD=11,当EA=EF时,DE=EF=2.5x,∴1042.5xCD x=,解得,CD=254,∴BD=BC﹣CD=39 4;当AE=AF=3x时,DE=75x,∴10475xCD x=,解得,CD=72,∴BD=BC﹣CD=252;当点F在线段DE上时,∠AFE为钝角,∴只有FA=FE=3x,则DE=8x,∴1048x CD x=,解得,CD=20>16,不合题意,∴△AEF是等腰三角形时,BD的长为11或394或252.【点评】本题考查的是相似三角形的判定和性质、等腰三角形的性质,掌握相似三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.5.(2019秋•宝山区期末)如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=k⋅OC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;(3)写出当△ONB为等腰三角形时,旋转角α的度数.【考点】几何变换综合题.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.【分析】(1)通过证明△ODE ∽△OCA ,可得2()DEO OAC S OD S OC∆∆=,即可求解;(2)通过证明△OEM ∽△BAC ,可得∠EOM =∠ABC =36°,分两种情况讨论可求解;(3)分四种情况讨论,由等腰三角形的性质可求解.【解答】解:(1)∵OC 是△ABC 中AB 边的中线,△ABC 的面积为26,∴S △OAC =13,∵DE ∥AC ,∴△ODE ∽△OCA ,∠OEM =∠OAC ,∴2()DEO OAC S OD S OC∆∆=,且OD =k ⋅OC ,∴S △ODE =13k 2,(2)∵△ODE ∽△OCA ,∴OE OD DE k OA OC AC ===,∵OC 是△ABC 中AB 边的中线,点M 是DE 的中点,∴AB =2AO ,EM =12DE ,∴2OE k EM AB AC==,且∠OEM =∠OAC ,∴△OEM ∽△BAC ,∴∠EOM =∠ABC =36°,如图2,当0<α<144°时,∵∠AON =∠B +∠ONB ,∴∠AOE +∠EOM =∠B +∠ONB ∴y =α如图3,当144°<α<180°时,∵∠BON =∠EOM ﹣∠BOE =36°﹣(180°﹣α)∴∠NOB =α﹣144°,∵∠BNO =∠ABC ﹣∠NOB =36°﹣(α﹣144°)=180°﹣α;(3)当0<α<144°时,若OB=ON,则∠ABC=∠BNO=36°=α,若OB=BN,则∠ONB=180362-=72°=α,若ON=BN,则∠ABC=∠BON=36°,∴∠ONB=180°﹣2×36°=108°=α,当144°<α<180°时,若OB=BN,则∠N=∠NOB=18°=180°﹣α,∴α=162°.【点评】本题是几何变换综合题,考查了相似三角形的判定和性质,旋转的性质,等腰三角形的性质等知识,证明△OEM∽△BAC是本题的关键.专题四动点函数背景下的线段问题【历年真题】1.(2019秋•虹口区期末)如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=3 5,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;(2)当点D在BC的延长线上时,设AG=x,S△DAF=y,求y关于x的函数关系式(不需要写函数的定义域);(3)如果AG=8,求DE的长.【考点】三角形综合题.【专题】几何综合题;等腰三角形与直角三角形;解直角三角形及其应用;运算能力;推理能力;应用意识.【分析】(1)求出AC=3,可得∠DAC=∠FBC,则tan∠FBC=tan∠DAC=23 DCAC=;(2)由条件可得∠AGF=∠CBF,可得AF CFAG BC=,可用x表示CF和AF的长,求出CD,则S△DAF=12AF CD,可用x表示结果;(3)分两种情况,①当点D 在BC 的延长线上时,②当点D 在BC 的边上时,可求出AE 长AD 的长,则DE =AD ﹣AE 可求出.【解答】解:(1)∵∠ACB =90°,BC =4,sin ∠ABC =35,∴设AC =3x ,AB =5x ,∴(3x )2+16=(5x )2,∴x =1,即AC =3,∵BE ⊥AD ,∴∠AEF =90°,∵∠AFE =∠CFB ,∴∠DAC =∠FBC ,∴tan ∠FBC =tan ∠DAC =23DC AC =;(2)∵AG ∥BD ,∴∠AGF =∠CBF ,∴tan ∠AGF =tan ∠CBF ,∴AF CF AG BC =,AG AF BC CF =,∴34x CF CF-=,∴124CF x =+.∴12334AF CF x =-=-+=34x x+.∵∠EAF =∠CBF ,∴CD CF AC BC =,∴94CD x =+,∴S △DAF =12AF CD =2193272442(4)x x x x x ⨯⨯=+++;(3)①当点D 在BC 的延长线上时,如图1,∵AG =8,BC =4,AG ∥BD ,∴21AG AF BC CF ==,∴AF =2CF ,∵AC =3,∴AF =2,CF =1,∴CF 1tan AGE=tan CBF==BC 4∠∠,∴AE 1=GE 4,设AE =x ,GE =4x ,∴x 2+16x 2=82,解得x =,即AE .同理tan ∠DAC =tan ∠CBF ,∴DC 1=AC 4,∴DC =34,∴AD∴DE AD AE=-=②当点D在BC的边上时,如图2,∵AG∥BD,AG=8,BC=4,∴8241AG AFBC CF===.∴AF=6,∵∠EAF=∠CBF=∠ABC,∴cos∠EAF=cos∠ABC,∴654AE=,∴245AE=,同理AC BCAD AB=,∴345AD=,∴154AD=.∴DE=AE﹣AD=241521 5420-=.综合以上可得DE的长为191768或2120.【点评】本题是三角形综合题,考查了勾股定理,平行线的性质,三角形的面积,锐角三角函数等知识,熟练掌握锐角三角函数的定义是解题的关键.2.(2019秋•静安区期末)已知:如图1,在△ABC中,AB=AC,点D、E分别在边BC、DC上,AB2=BE•DC,DE:EC=3:1,F是边AC上的一点,DF与AE交于点G.(1)找出图中与△ACD相似的三角形,并说明理由;(2)当DF平分∠ADC时,求DG:DF的值;(3)如图2,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.【考点】相似三角形的判定与性质;等腰三角形的判定与性质.【专题】等腰三角形与直角三角形;图形的相似;推理能力.【分析】(1)根据相似三角形的判定定理进行判定即可;(2)由相似三角形的性质即可得出答案;(3)由等腰直角三角形的性质、相似三角形的判定与性质即可得出答案.【解答】解:(1)与△ACD 相似的三角形有:△ABE 、△ADE ,理由如下:∵AB 2=BE •DC ,∴BE AB AB DC=,∵AB =AC ,∴∠B =∠C ,BE AC AB DC =,∴△ABE ∽△DCA .∵△ABE ∽△DCA ,∴∠AED =∠DAC .∵∠AED =∠C +∠EAC ,∠DAC =∠DAE +∠EAC ,∴∠DAE =∠C .∴△ADE ∽△CDA ;(2)∵△ADE ∽△CDA ,又∵DF 平分∠ADC ,∴DG DE AD DF AD CD==,设CE =a ,则DE =3CE =3a ,CD =4a ,∴34a AD AD a=,解得:AD =23a ,∴23342DG AD a DF CD a ===;(3)∵∠BAC =90°,AB =AC ,∴∠B =∠C =45°,∴∠DAE =∠C =45°∵DG ⊥AE ,∴∠DAG =∠ADF =45°,∴AG =DG =22AD =22×236a ,∴EG 2222(3)(6)3DE DG a a -=-a ,∴AE =AG +EG =(63)a ,∵∠AED =∠DAC ,∴△ADE ∽△DFA ,∴AD AE DF AD=,∴22AD AE ==a ,∴24DG DF +==.【点评】本题考查了相似三角形的判定与性质、等腰直角三角形的性质、勾股定理等知识;熟记相似三角形的判定定理是解题的关键.专题四动点函数背景下四边形【历年真题】1.(2019秋•长宁、金山区期末)如图,已知在Rt △ABC 中,∠C =90°,AC =8,BC =6,点P 、Q 分别在边AC 、射线CB 上,且AP =CQ ,过点P 作PM ⊥AB ,垂足为点M ,联结PQ ,以PM 、PQ 为邻边作平行四边形PQNM ,设AP =x ,平行四边形PQNM 的面积为y .(1)当平行四边形PQNM 为矩形时,求∠PQM 的正切值;(2)当点N 在△ABC 内,求y 关于x 的函数解析式,并写出它的定义域;(3)当过点P 且平行于BC 的直线经过平行四边形PQNM 一边的中点时,直接写出x 的值.【考点】四边形综合题.【专题】几何综合题;应用意识.【分析】(1)当四边形PQMN 是矩形时,PQ ∥AB .根据tan ∠PQM =PM PQ求解即可.(2)如图1中,延长QN 交AB 于K .求出MK ,PM ,根据y =PM •MK 求解即可.(3)分两种情形:①如图3﹣1中,当平分MN 时,D 为MN 的中点,作NE ∥BC 交PQ 于E ,作NH ⊥CB 交CB 的延长线于H ,EG ⊥BC 于G .根据EG =12PC 构建方程求解.②如图3﹣2中,当平分NQ 时,D 是NQ 的中点,作DH ⊥CB 交CB 的延长线于H .根据PC =GH 构建方程求解即可.【解答】解:(1)在Rt △ACB 中,∵∠C =90°,AC =8,BC =6,∴AB ==10,当四边形PQMN是矩形时,PQ∥AB.∴tan∠PQM=PMPQ=3955253PACQ=.(2)如图1中,延长QN交AB于K.由题意BQ=6﹣x,QN=PM=35x,AM=45x,KQ=45BQ=2445x-,BK=35BQ=1835x-,∴MK=AB﹣AM﹣BK=325x-,∵QN<QK,∴35x<2445x-,∴x<247,∴y=PM•MK=296325x x-(0<x<247).(3)①如图3﹣1中,当平分MN时,D为MN的中点,作NE∥BC交PQ于E,作NH⊥CB交CB的延长线于H,EG⊥BC于G.∵PD∥BC,EN∥BC,∴PD∥NE,∵PE∥DN,∴四边形PDNE是平行四边形,∴PE=DN,∵DN=DM,PQ=MN,∴PE=EQ,∵EG∥PC,∴CG=GQ,∴EG=12PC,∵四边形EGHN是矩形,∴NH=EG=35NQ=35PM=925x,PC=8﹣x,∴925x=12•(8﹣x),解得x=20043.②如图3﹣2中,当平分NQ时,D是NQ的中点,作DH⊥CB交CB的延长线于H.∵DH=PC,∴8﹣x=12•925x,解得x=40059,综上所述,满足条件x的值为20043或40059.【点评】本题属于四边形综合题,考查了平行四边形的性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.2.(2019秋•嘉定区期末)已知:点P在△ABC内,且满足∠APB=∠APC(如图),∠APB+∠BAC=180°.(1)求证:△PAB∽△PCA;(2)如果∠APB=120°,∠ABC=90°,求PCPB的值;(3)如果∠BAC=45°,且△ABC是等腰三角形,试求tan∠PBC的值.【考点】相似三角形的判定与性质;解直角三角形;等腰三角形的性质.【专题】图形的相似;应用意识.【分析】(1)根据两角对应相等的两个三角形相似证明即可.(2)证明△PAB∽△PCA,利用相似三角形的性质解决问题即可.(3)分三种情形:AB=AC,AB=BC,AC=BC分别求解即可解决问题.【解答】证明:(1)∵∠ABP +∠BAP +∠APB =180°,∠APB +∠BAC =180°,∴∠ABP +∠BAP +∠APB =∠APB +∠BAC ,即∠ABP +∠BAP +∠APB =∠APB +∠BAP +∠CAP ,∴∠ABP =∠CAP ,又∵∠APB =∠APC ,∴△PAB ∽△PCA .(2)如图1中,∵∠APB +∠BAC =180°,∠APB =120°,∴∠BAC =60°,在△ABC 中,∵∠ABC =90°,∠BAC =60°,∴,又∵△PAB ∽△PCA ,∴12PB PA AB PA PC AC ===,∴14PB PB PA PC PA PC == ,即4PC PB =.(3)∵∠BAC =45°,∠APB +∠BAC =180°,∠APB =∠APC ,∴∠APB =∠APC =135°.∴∠BPC =360°﹣∠APB ﹣∠APC =360°﹣135°﹣135°=90°,∵△PCA ∽△PAB ,∴PA PC AC PB PA AB==,∴163.①如图2中,当△ABC 是等腰三角形,且AB =AC 时,2tan PBC=()=1PC AC PB AB =∠.②如图3中,当△ABC 是等腰三角形,且AB =BC 时,∠ACB =∠BAC =45°,∠ABC =90°,易得2AC AB ,∴2tan PBC=()=2PC AC PB AB=∠.③如图10﹣4,当△ABC 是等腰三角形,且AC =BC 时,∠ABC =∠BAC =45°,∠ACB =90°,易得2=2AC AB ,∴21tan PBC=()=2PC AC PB AB =∠.【点评】本题考查相似三角形的判定和性质,解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.3.(2019秋•徐汇区期末)如图,在△ABC 中,AB =AC =5,BC =6,点D 是边AB 上的动点(点D 不与点AB 重合),点G 在边AB 的延长线上,∠CDE =∠A ,∠GBE =∠ABC ,DE 与边BC 交于点F .(1)求cos A 的值;(2)当∠A =2∠ACD 时,求AD 的长;(3)点D 在边AB 上运动的过程中,AD :BE 的值是否会发生变化?如果不变化,请求AD :BE 的值;如果变化,请说明理由.【考点】三角形综合题.。
马井堂上海市各区县历年中考数学模拟压轴题汇总

上海市各区县历年中考数学二模试卷压轴题汇总1. 已知,如图,△ABC 是等边三角形,过AC 边上的点D 作 DG //BC ,交AB 于点G ,在GD 的延长线上取点E ,使DE=DC ,连接AE 、BD .(1)求证:△AGE ≌△DAB ;(2)过点E 作EF //DB ,交BC 于点F ,连AF ,求∠AEF 的度数.D A C GE F2、 如图,菱形OABC 放在平面直角坐标系内,点A 在x 轴的正半轴上,点B 在第一象限,其坐标为(8,4).抛物线2bx c y ax ++=过点O 、A 、C .(1)求抛物线的解析式?(2)将菱形向左平移,设抛物线与线段AB 的交点为D,连接CD .① 当点C 又在抛物线上时求点D的坐标?② 当△BCD 是直角三角形时,3、如图,在平面直角坐标系中,等腰梯形OABC,CB//OA,且点A在x轴正半轴上.已知C(2,4),BC= 4.(1)求过O、C、B三点的抛物线解析式,并写出顶点坐标和对称轴;(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合),使得P点到两坐标轴的距离相等.如果存在,求出P点坐标;如果不存在,请说明理由.4、 如图,AD//BC ,点E 、F 在BC 上,∠1=∠2,AF ⊥DE ,垂足为点O. (1)求证:四边形AEFD 是菱形;(2)若BE=EF=FC ,求∠BAD+∠ADC 的度数;(3)若BE=EF=FC ,设AB = m ,CD = n ,求四边形ABCD 的面积.21OFEDCBA5、如图,在平面直角坐标系中,抛物线6422++-=x x y 与x 轴交于A 、B 两点(A 点在B 点左侧),与y 轴交于C 点,顶点为D.过点C 、D 的直线与x 轴交于E 点,以OE 为直径画⊙O 1,交直线CD 于P 、E 两点. (1)求E 点的坐标;(2)联结PO 1、PA.求证:BCD ∆~A PO 1∆;(3) ①以点O 2 (0,m)为圆心画⊙O 2,使得⊙O 2与⊙O 1相切,当⊙O 2经过点C 时,求实数m 的值;②在①的情形下,试在坐标轴上找一点O 3,以O 3为圆心画⊙O 3,使得⊙O 3与⊙O 1、⊙O 2同时相切.直接写出满足条件的点O 3的坐标(不需写出计算过程).6.如图,EF是平行四边形ABCD的对角线BD的垂直平分线,EF与边AD、BC分别交于点E、F.(1)求证:四边形BFDE是菱形;(2)若E为线段AD的中点,求证:AB⊥BD.EA DOB F C7. 在平面直角坐标系中,抛物线2y x bx c =++经过点(0,2)和点(3,5).(1)求该抛物线的表达式并写出顶点坐标;(2)点P 为抛物线上一动点,如果直径为4的⊙P 与y 轴相切,求点P 的坐标.bx c ++8. 如图,在Rt △ABC 中,∠BAC = 90°,AB =3,AC =4,AD 是BC 边上的高,点E 、F 分别是AB 边和AC 边上的动点,且∠EDF = 90°.(1)求DE ︰DF 的值;(2)联结EF ,设点B 与点E 间的距离为x ,△DEF 的面积为y ,求y 关于x 的函数解析式,并写出x 的取值范围; (3)设直线DF 与直线AB 相交于点G ,△EFG 能否成为等腰三角形?若能,请直接写出线段BE 的长;若不能,请说明理由.CE FA备用图1BCD 备用图2BCA A9. 如图,已知抛物线c bx x y ++-=2与x 轴负半轴交于点A ,与y 轴正半轴交于点B ,且OB OA =.(1) 求c b +的值;(2) 若点C 在抛物线上,且四边形OABC 是平行四边形,试求抛物线的解析式; (3) 在(2)的条件下,作∠OBC 的角平分线,10.如图1,已知⊙O的半径长为1,PQ是⊙O的直径,点M是PQ延长线上一点,以点M为圆心作圆,与⊙O交于A、B两点,联结PA并延长,交⊙M于另外一点C.(1) 若AB恰好是⊙O的直径,设OM=x,AC=y,试在图2中画出符合要求的大致图形,并求y关于x的函数解析式;(2) 联结OA、MA、MC,若OA⊥MA,且△OMA与△PMC相似,求OM的长度和⊙M的半径长;(3) 是否存在⊙M,使得AB、AC恰好是一个正五边形的两条边?若存在,试求OM的长度和⊙M的半径长;若不存在,试说明理由.图2上海市各区县历年中考数学二模试卷压轴题答案1.(1)∵△ABC 是等边三角形,DG //BC ,∴△AGD 是等边三角形.AG =GD =AD ,∠AGD =60°.∵DE =DC ,∴GE =GD +DE =AD +DC =AC =AB .∵∠AGD =∠BAD ,AG =AD ,∴△AGE ≌△DAB . …………………………(5分) (2)由(1)知AE =BD ,∠ABD =∠AEG …………………………………………(6分) ∵EF ∥DB ,DG ∥BC ,∴四边形BFED 是平行四边形 ………………………… (7分) ∴∠DBC =∠DEF ,∴∠AEF=∠AEG +∠DEF =∠ABD +∠DBC=∠ABC =60°(8分)2、(本题12分)(1)A (0,3),C(3,0) ∵3m=3 ∴m=1∴抛物线的解析式为322++-=x x y ………2分(2)∵m=1 ∴322++-=x x y ∴AO=3 点32,(2++-x x x D ),连结OD当y=0时,即0322=++-x x ,解得x 1=-1 x 2=3 ∴OC=3∴S= S △AOD + S △DOC =292923)32(32132122++-=++-⨯⨯+⨯x x x x x ∴S 与x 的函数关系式S=2929232++-x x (0<x <3) …………………………4分当232=-=a b x 符合(0<x <3) S 最大值=863)23(4)29(29)23(44422=-⨯-⨯-⨯=-a b ac ……6分(3)…………………………………………7分假设存在点P ,使AC 把△PCD 分成面积之比为2:1的两部分,分两种情况讨论: (ⅰ)当△CDE 与△CEP 的面积之比为2:1时,DE=2EP ∴DP=3EP即)3(3322+-=++-x x x 整理得:0652=+-x x解得;21=x 32=x (不合题意,舍去), 此时点P 的坐标是(2,0)… 9分 (ⅱ)当△CEP 与△CDE 的面积之比为2:1时, EP DE 21=, ∴EP DP 23= 即)3(23322+-=++-x x x 整理得:03722=+-x x BED PO xy3453OA OC AOC Rt ECP EP PC x==∴∴∠=︒∴==-为等腰54321OFEDCB A 解得:213=x 34=x (不合题意,舍去),此时点P 的坐标是(21,0) …………………………………………11分综上所述,使直线AC 把△PCD 分成面积之比为2:1两部分的点P 存在,点P 的坐标是(2,0)或(21,0)……………………… 12分3、(12分)解:(1) ( 6分)∵C(2,4), BC=4 且 BC//OA ∴ B(6,4) 1分设抛物线为c bx ax y ++=2()0≠a将O(0,0),C(2,4),B(6,4)代入得⎪⎩⎪⎨⎧=+=++=)3(4636)2(424)1(0b a c b a c 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=03831c b a 3分∴x x y 38312+-= 1分∴顶点)316,4( 对称轴:直线4=x 2分(2) (6分)据题意,设),(a a P 或),(a a P -()0≠a 1分将),(a a P 代入抛物线得a a a =+-38312 解得0,521==a a (舍) 2分将),(a a P -代入抛物线得a a a -=+-38312 解得0,1121==a a (舍) 2分∴符合条件的点)5,5(p 和)11,11(-p 1分4、(12分)(1)( 4分)证明:(方法一)∵AF ⊥DE∴∠1+∠3=90° 即:∠3=90°-∠1∴∠2+∠4=90° 即:∠4=90°-∠2又∵∠1=∠2 ∴∠3=∠4 ∴AE = EF∵AD//BC ∴∠2=∠5 ∵∠1=∠2 ∴∠1=∠5∴AE = AD ∴EF = AD 2分 ∵AD//EF ∴四边形AEFD 是平行四边形 1分 又∵AE = AD∴四边形AEFD 是菱形 1分(方法二)∵AD//BC ∴∠2=∠5 ∵∠1=∠2 ∴∠1=∠5∵AF ⊥DE ∴∠AOE=∠AOD =90°在△AEO 和△ADO 中⎪⎩⎪⎨⎧=∠=∠∠=∠AO AO AOD AOE 51 ∴△AEO ≅△ADO ∴EO=OD在△AEO 和△FEO 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠FOE AOE EO EO 21∴△AEO ≅△FEO ∴AO=FO 2分 ∴AF 与ED 互相平分 1分 ∴四边形AEFD 是平行四边形 又∵AF ⊥DE ∴四边形AEFD 是菱形 1分 (2)( 5分)∵菱形AEFD ∴AD=EF ∵BE=EF ∴AD=BE又∵AD//BC ∴四边形ABED 是平行四边形 1分 ∴AB//DE ∴∠BAF=∠EOF同理可知 四边形AFCD 是平行四边形 ∴AF//DC ∴∠EDC=∠EOF又∵AF ⊥ED ∴∠EOF=∠AOD=90° ∴∠BAF=∠EDC=∠EOF=90° 2分 ∴∠5 +∠6=90° 1分∴∠BAD+∠ADC=∠BAF+∠6 +∠5+∠EDC =270° 1分(3)( 3分)由(2)知∠BAF =90°平行四边形AFCD ∴AF=CD=n又∵AB=m mn 21AF AB 21S ABF =⋅=∆ 1分 由(2)知 平行四边形ABED ∴DE=AB=m 由(1)知OD=m DE 21= mn 21OD AF S AFCD =⋅=四边形 1分 mn S AFCD ABCD =+=∆四边形四边形S S ABF 1分5、(14分)解:(1) ( 3分)()81264222+--=++-=x x x y ∴)8,1(),6,0(D C 1分设直线CD:()0≠+=k b kx y 将C 、D 代入得⎩⎨⎧+==686k b 解得⎩⎨⎧==62b k∴CD 直线解析式:62+=x y 1分 )0,3(-E 1分 (2) ( 4分)令y=0 得06422=++-x x 解得3,121=-=x x ∴)0,3()0,1(B A - 1分又∵)0,0(O 、)0,3(-E ∴以OE 为直径的圆心)0,(231-O 、半径231=r .设)62,(+t t P 由231=PO 得232223)62()(=+++t t 解得3,25121-=-=t t (舍) ∴),(56512-P 2分∴585=PA 211=AO54321OFEDCB A6又 5=DC 53=CB 172=DB∴5211===PADBPO CB AO DC 1分 ∴BC D ∆~A PO 1∆ (3) ( 7分)① )0,(231-O 231=r),0(2m O 据题意,显然点2O 在点C 下方 m C O r -==622当⊙O 2与⊙O 1外切时 2121r r O O +=代入得()()m m -+=+6232223 解得 2,51821==m m (舍)2分 当⊙O 2与⊙O 1内切时 2121r r O O -=代入得()()m m --=+6232223 解得 518,221==m m (舍) 2分 ∴2,51821==m m ② ⎪⎭⎫ ⎝⎛518,03O ⎪⎭⎫ ⎝⎛-710,03O ⎪⎭⎫ ⎝⎛0,233O ⎪⎭⎫ ⎝⎛-0,14453O ⎪⎭⎫ ⎝⎛1514,03O ()2,03O ⎪⎭⎫⎝⎛0,2213O 3分6、.证明:(1)∵四边形ABCD 是平行四边形∴ED ∥BF ,得∠EDB =∠FBD ……………………………………………………(2分)∵EF 垂直平分BD∴BO=DO ,∠DOE =∠BOF =90°∴△DOE ≌△BOF ……………………………………………………………………(2分) ∴ EO=FO∴四边形BFDE 是平行四边形 ……………………………………………………(1分) 又∵EF ⊥BD∴四边形BFDE 是菱形 ……………………………………………………………(1分) (2)∵四边形BFDE 是菱形∴ED=BF ∵AE=ED∴AE=BF ………………………………………………………………………………(2分) 又∵AE ∥BF∴四边形ABFE 是平行四边形………………………………………………………(1分) ∴AB ∥EF ……………………………………………………………………………(1分) ∴∠ABD =∠DOE ……………………………………………………………………(1分) ∵∠DOE =90° ∴∠ABD =90°即AB ⊥BD ……………………………………………………………………………(1分)7.解:(1)把(0,2)、(3,5)分别代入2y x bx c =++得 2593cb c =⎧⎨=++⎩解得22b c =-⎧⎨=⎩……………………………………………(3分) ∴抛物线的解析式为222y x x =-+ ………………………………………………(1分) ∴抛物线的顶点为(1,1)………………………………………………………………(2分) (2)设点P 到y 轴的距离为d ,⊙P 的半径为r∵⊙P 与y 轴相切 ∴1422d r ==⨯= ∴点P 的横坐标为2±…………………………………………………………………(2分)当2x =时, 2y = ∴点P 的坐标为(2,2) …………………………………(2分)当2x =-时,10y = ∴点P 的坐标为(2,10)- ………………………………(2分)∴点P 的坐标为(2,2)或(2,10)-.8.解:(1)∵∠BAC = 90° ∴∠B +∠C =90°,∵AD 是BC 边上的高 ∴∠DAC +∠C =90°∴∠B =∠DAC ………………………………………………………………………(1分) 又∵∠EDF = 90°∴∠BDE +∠EDA =∠ADF +∠EDA = 90° ∴∠BDE =∠ADF∴△BED ∽△AFD ……………………………………………………………………(1分)∴DE BDDF AD =…………………………………………………………………………(1分) ∵3cot 4BD AB B AD AC === ∴DE ︰DF =34…………………………………………………………………………(1分)(2)由△BED ∽△AFD 得34BE BD AF AD ==∴4433AF BE x == …………………………………………………………………(1分)∵BE x = ∴3AE x =-∵∠BAC = 90°∴2222425(3)()6939EF x x x x =-+=-+………………………………………(1分) ∵DE ︰D F =3︰4,∠EDF =90°∴ED =35EF ,FD =45EF …………………………………………………………………(1分) ∴216225y ED FD EF =⋅=∴22365432525y x x =-+ (03)x ≤≤ ………………………………………………(2分) (3)能. BE 的长为543255或.……………………………………………………………(5分)(说明:BE 的长一个正确得3分,全对得5分)9、解:(1)由题意得:点B 的坐标为),0(c ,其中0>c ,c OB = (1分) ∵OB OA =,点A 在x 轴的负半轴上,∴点A 的坐标为)0,(c - (1分)∵点A 在抛物线c bx x y ++-=2上,∴c bc c +--=20 (1分)∴ 1=+c b (因为0>c ) (1分)(2)∵四边形OABC 是平行四边形∴c AO BC ==,又BC ∥x 轴,点B 的坐标为),0(c∴点C 的坐标为),(c c (1分) 又点C 在抛物线上,∴c bc c c ++-=2∴0=-c b 或0=c (舍去) (1分) 又 由(1)知:1=+c b ∴21=b ,21=c . 抛物线的解析式为21212++-=x x y . (2分) (3)过点P 作⊥PM y 轴,⊥PN BC ,垂足分别为M 、N ∵ BP 平分CBO ∠ ∴ PN PM = (1分) 设点P 的坐标为)2121(2++-x x x , ∴x x x =++--)2121(212 (1分) 解得:23=x 或0=x (舍去) (1分) 所以,点P 的坐标为)21,23(- (1分)10、(1)图画正确 (1分)过点M 作AC MN ⊥,垂足为N∴y NC AN 21== 由题意得:AB PM ⊥, 又AB 是圆O 的直径∴1==OP OA ∴︒=∠45APO , 2=PA∴y PN 212+=(1分) 在Rt △PNM 中,PMPNNPM =∠cos 又x PM +=1,︒=∠45NPM∴ 22121245cos =++=︒x y∴ y 关于x 的函数解析式为22-=x y (1>x ) (2分)(2)设圆M 的半径为r因为 OA ⊥MA ,∴∠OAM=90°,12+=r OM又△OMA 与△PMC 相似,所以△PMC 是直角三角形。
2020-2021年上海各区数学中考一模压轴题分类汇编-18题含详解
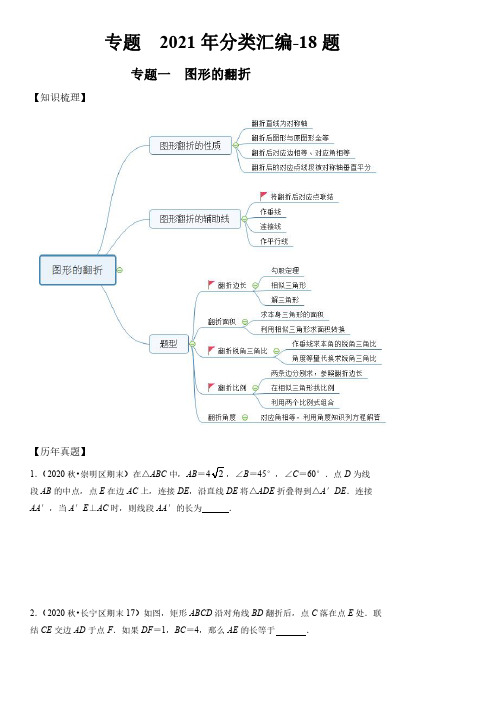
专题2021年分类汇编-18题专题一图形的翻折【知识梳理】【历年真题】1.(2020秋•崇明区期末)在△ABC中,AB=,∠B=45°,∠C=60°.点D为线段AB的中点,点E在边AC上,连接DE,沿直线DE将△ADE折叠得到△A′DE.连接AA′,当A′E⊥AC时,则线段AA′的长为.2.(2020秋•长宁区期末17)如图,矩形ABCD沿对角线BD翻折后,点C落在点E处.联结CE交边AD于点F.如果DF=1,BC=4,那么AE的长等于.3.(2020秋•虹口区期末)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.D是BC的中点,点E在边AB上,将△BDE沿直线DE翻折,使得点B落在同一平面内的点B'处,线段B'D交边AB于点F,联结AB'.当△AB'F是直角三角形时,BE的长为.5.(2020秋•松江区期末)如图,已知矩形纸片ABCD,点E在边AB上,且BE=1,将△CBE沿直线CE翻折,使点B落在对角线AC上的点F处,联结DF,如果点D、F、E在同一直线上,则线段AE的长为.6.(2020秋•普陀区期末)如图,在▱ABCD中,点E在边BC上,将△ABE沿着直线AE翻折得到△AFE,点B的对应点F恰好落在线段DE上,线段AF的延长线交边CD于点G,如果BE:EC=3:2,那么AF:FG的值等于.专题二图形的旋转【知识梳理】【历年真题】1.(2020秋•嘉定区期末)已知在△ABC中,∠ACB=90°,AB=10,sin A=55(如图),把△ABC绕着点C按顺时针方向旋转α°(0<α<360),将点A、B的对应点分别记为点A′,B′,如果△AA′C为直角三角形,那么点A与点B'的距离为.2.(2020秋•闵行区期末)如图,在Rt△ABC中,∠ACB=90°,AB=3,tan B=.将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF=.3.(2020秋•静安区期末)在Rt △ABC 中,∠C =90°,AB =13,tan B =23(如图),将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',A 'B '与边BC 相交于点D ,那么'CD A D 的值为.4.(2020秋•杨浦区期末)如图,已知在△ABC 中,∠B =45°,∠C =60°,将△ABC 绕点A 旋转,点B 、C 分别落在点B 1、C 1处,如果BB 1∥AC ,联结C 1B 1交边AB 于点D ,那么1BD B D 的值为.5.(2020秋•宝山区期末)在Rt △ABC 中,∠ACB =90°,AC =BC ,点E 、F 分别是边CA 、CB 的中点,已知点P 在线段EF 上,联结AP ,将线段AP 绕点P 逆时针旋转90°得到线段DP ,如果点P 、D 、C 在同一直线上,那么tan ∠CAP =.6.(2020秋•奉贤区期末)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,CD 是△ABC 的角平分线,将Rt △ABC 绕点A 旋转,如果点C 落在射线CD 上,点B 落在点E 处,联结DE ,那么∠AED 的正切值为.专题三定义新图形【知识梳理】根据题目中给的知识点,结合所学函数及图形知识解答【历年真题】1.(2020秋•长宁区期末)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC3AD=CD=32,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于.2.(2020秋•青浦区期末)如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ=.3.(2020秋•浦东新区期末)如图,△ABC中,AB=10,BC=12,AC=8,点D是边BC上一点,且BD:CD=2:1,联结AD,过AD中点M的直线将△ABC分成周长相等的两部分,这条直线分别与边BC、AC相交于点E、F,那么线段BE的长为.4.(2020秋•徐汇区期末)如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE=45,ED=5,如果△ECD的面积是6,那么BC的长是.5.(2020秋•金山区期末)已知在Rt△ABC中,∠C=90°,BC=1,AC=2,以点C为直角顶点的Rt△DCE的顶点D在BA的延长线上,DE交CA的延长线于点G,若tan∠CED=12,CE=GE,那么BD的长等于.6.(2020秋•黄浦区期末)已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为.专题2021年分类汇编-18题专题一图形的翻折【历年真题】1.(2020秋•崇明区期末)在△ABC中,AB=,∠B=45°,∠C=60°.点D为线段AB的中点,点E在边AC上,连接DE,沿直线DE将△ADE折叠得到△A′DE.连接AA′,当A′E⊥AC时,则线段AA′的长为2.【考点】翻折变换(折叠问题).【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;解直角三角形及其应用;运算能力;推理能力.【分析】画出相应的图形,结合图形通过作高构造直角三角形,求出AM=BM=4,进而求出AC,再利用相似三角形的性质和判定求出AE,根据对称在Rt△AEF中求出AF即可.【解答】解:如图,过点A作AM⊥BC,垂足为M,在Rt△ABM中,∠B=45°,AB=,∴AM=BM=AB•sin∠B=4,在Rt△ACM中,AM=4,∠C=60°,∴AC=AM4=sin C sin60∠,又∵A′E⊥AC,∴∠A′EC=90°,由折叠得∠AED=∠A′ED=12(180°﹣90°)=45°,AA′⊥DE,∵∠AED=45°=∠B,∠DAE=∠CAB,∴△DAE∽△CAB,∴AE AD=AB DC,∵点D为线段AB的中点,∴AD=BD=12AB=,833AE=,在Rt△AEF中,AF=EF=AE•sin∠AED=×2,∴AA′=2AF=,故答案为:.【点评】本题考查轴对称的性质,相似三角形的判定和性质,解直角三角形,掌握轴对称、相似三角形的性质以及解直角三角形是解决问题的关键.2.(2020秋•长宁区期末17)如图,矩形ABCD 沿对角线BD 翻折后,点C 落在点E 处.联结CE 交边AD 于点F .如果DF =1,BC =4,那么AE 的长等于655.【考点】翻折变换(折叠问题);矩形的性质.【专题】矩形菱形正方形;推理能力.【分析】首先根据题意得到EG =CG ,CE ⊥BD ,证明△CDF ∽△BCD 和△CDG ∽△BDC ,可计算CD 和CG 的长,再证明△EFD ∽△AED ,可得AE 的长.【解答】解:由折叠得:CE ⊥BD ,CG =EG ,∴∠DGF =90°,∴∠DFG +∠FDG =90°,∵四边形ABCD 是矩形,∴∠ADC =∠BCD =90°,∴∠ADG +∠CDG =90°,∴∠CDG =∠DFG ,∵∠CDF =∠BCD =90°,∴△CDF ∽△BCD ,∴CD DF =BC CD,∵AB =4,DF =1,∴CD 1=4CD,∴CD =2,由勾股定理得:CF =221+2=5,BD 222+45,同理得:△CDG∽△BDC,∴CD CG=BD BCCG4,∴CG =455,∴CE=2CG =85 5,∴EF=CE﹣CF =855=355,∵DF1=ED2,ED21==AD42,且∠EDF=∠AED,∴△EFD∽△AED,∴EF DF=AE DE ,即15=AE2,∴AE【点评】本题主要考查了几何变换中的翻折变换、相似三角形的性质和判定、矩形的性质、勾股定理;熟练掌握翻折变换和矩形的性质,利用相似三角形列比例式是本题的关键.3.(2020秋•虹口区期末)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.D是BC的中点,点E在边AB上,将△BDE沿直线DE翻折,使得点B落在同一平面内的点B'处,线段B'D交边AB于点F,联结AB'.当△AB'F是直角三角形时,BE的长为2或40 17.【考点】翻折变换(折叠问题);相似三角形的判定与性质;勾股定理.【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力;推理能力.【分析】分两种情况画出图形,①方法一:如图1,当∠AFB′=90°时,由相似三角形的性质及直角三角形的性质可求出答案;方法二:过点E作EH⊥BC于点H,设EH=3a,BE=5a,则BH=4a,由BF的长列出方程,解方程求出a即可;②方法一如图2,当∠AB′F=90°时,由相似三角形的性质及直角三角形的性质可求出答案.方法二:过点E作EG⊥BD于点G,设EG=3a,BG=4a,BE=5a,得出9442a a+=,求出a的值则可得出答案.【解答】解:①方法一:如图1,当∠AFB′=90°时.在Rt △ABC 中,∵AC =6,BC =8,∴AB 22226810AC BC +=+=,∵D 是BC 的中点,∴BD =CD =12BC =4,∵∠AFB '=∠BFD =90°,∠ACB =90°,∴∠DFB =∠ACB ,又∵∠DBF =∠ABC ,∴△BDF ∽△BAC ,∴BF BD BC AB =,即4810BF =,解得:BF =165,设BE =B 'E =x ,则EF =165﹣x ,∵∠B =∠FB 'E ,∴sin ∠B =sin ∠FB 'E ,∴'AC EF AB B E =,∴166510x x-=,解得x =2.∴BE =2.方法二:过点E 作EH ⊥BC 于点H ,设EH =3a ,BE =5a ,则BH =4a ,∵将△BDE 沿直线DE 翻折,∴EF =3a ,∴BF =8a =BD •cos ∠B =4×45,∴a =25,∴BE =5a =2;②如图2中,当∠AB ′F =90°时,连接AD ,作EH ⊥AB ′交AB ′的延长线于H.∵AD =AD ,CD =DB ′,∴Rt △ADC ≌Rt △ADB ′(HL ),∴AC =AB ′=6,∵将△BDE 沿直线DE 翻折,∴∠B =∠DB 'E ,∵AB '⊥DB ',EH ⊥AH ,∴DB '∥EH ,∴∠DB 'E =∠B 'EH ,∴∠B =∠B 'EH ,∴sin ∠B =sin ∠B 'EH ,设BE =x ,则B 'H =35x ,EH =45x ,在Rt △AEH 中,AH 2+EH 2=AE 2,∴22234(6)()(10)55x x x ++=-,解得x =4017,∴BE =4017.则BE 的长为2或4017.方法二:过点E 作EG ⊥BD 于点G ,设EG =3a ,BG =4a ,BE =5a ,∴DG =EG ×32=92a ,∵DG +GB =DB ,∴9442a a +=,∴a =817,∴BE =4017.故答案为:2或4017.【点评】本题考查了翻折变换、勾股定理、解直角三角形、相似三角形的判定与性质、全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想解决问题.5.(2020秋•松江区期末)如图,已知矩形纸片ABCD ,点E 在边AB 上,且BE =1,将△CBE 沿直线CE 翻折,使点B 落在对角线AC 上的点F 处,联结DF ,如果点D 、F 、E 在同一直线上,则线段AE 的长为152+.【考点】翻折变换(折叠问题);矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;运算能力;推理能力.【分析】根据矩形的性质得到AD =BC ,∠ADC =∠B =∠DAE =90°,根据折叠的性质得到CF =BC ,∠CFE =∠B =90°,EF =BE =1,DC =DE ,证明△AEF ∽△DEA ,根据相似三角形的性质即可得到结论.【解答】解:∵四边形ABCD 是矩形,∴AD =BC ,AB =CD ,∠ADC =∠B =∠DAE =90°,∵把△BCE 沿直线CE 对折,使点B 落在对角线AC 上的点F 处,∴CF =BC ,∠CFE =∠B =90°,EF =BE =1,∠CEB =∠CEF ,∵矩形ABCD 中,DC ∥AB ,∴∠DCE =∠CEB ,∴∠CEF =∠DCE ,∴DC =DE ,设AE=x,则AB=CD=DE=x+1,∵∠AFE=∠CFD=90°,∴∠AFE=∠DAE=90°,∵∠AEF=∠DEA,∴△AEF∽△DEA,∴AF DEEF AE=,∴11x xx+=,解得x=152+或x=152(舍去),∴AE=12.故答案为:15 2.【点评】本题考查了翻折变换(折叠问题),平行线的性质,相似三角形的判定和性质,矩形的性质,正确的识别图形是解题的关键.6.(2020秋•普陀区期末)如图,在▱ABCD中,点E在边BC上,将△ABE沿着直线AE翻折得到△AFE,点B的对应点F恰好落在线段DE上,线段AF的延长线交边CD于点G,如果BE:EC=3:2,那么AF:FG的值等于214.【考点】相似三角形的判定与性质;平行四边形的性质;翻折变换(折叠问题).【专题】多边形与平行四边形;平移、旋转与对称;图形的相似;推理能力.【分析】延长BC,AG交于点H,设BE=3x,EC=2x,由平行四边形的性质可得AD=BC=5x,AD∥BC,由折叠的性质可得∠AEB=∠AEF,BE=EF=3x,通过证明△ADF∽△HEF,△ADG∽△HCG,可求AF=425y,FG=AG﹣AF=85y,即可求解.【解答】解:如图,延长BC,AG交于点H,∵BE:EC=3:2,∴设BE=3x,EC=2x,∵四边形ABCD是平行四边形,∴AD=BC=5x,AD∥BC,∴∠DAE=∠AEB,∵将△ABE沿着直线AE翻折得到△AFE,∴∠AEB=∠AEF,BE=EF=3x,∴∠DAE=∠AED,∴AD=DE=5x,∴DF=2x,∵AD∥BC,∴△ADF∽△HEF,∴AD DF AFEH EF FH==,∴523x AFEH FH==,∴EH=152x,AF=23FH,∴CH=EH﹣EC =x,∵AD∥BC,∴△ADG∽△HCG,∴AD AGCH GH=,∴51011112x AGGHx==,∴设AG=10y,GH=11y,∴AH=21y,∴AF=215y×2=425y,∴FG=AG﹣AF=85y,∴AF:FG=21:4=21 4,故答案为21 4.【点评】本题考查了相似三角形的判定和性质,折叠的性质,平行四边形的性质,灵活运用这些性质进行推理是解题的关键.专题二图形的旋转【历年真题】1.(2020秋•嘉定区期末)已知在△ABC中,∠ACB=90°,AB=10,sin A=5(如图),把△ABC绕着点C按顺时针方向旋转α°(0<α<360),将点A、B的对应点分别记为点A′,B′,如果△AA′C为直角三角形,那么点A与点B'的距离为【考点】旋转的性质;解直角三角形.【专题】分类讨论;平移、旋转与对称;几何直观.【分析】根据△AA′C为直角三角形,分两种情况:①当点B'在线段AC上时,△AA′C为直角三角形;②当点B'在线段AC的延长线上时,△AA′C为直角三角形,依据线段的和差关系进行计算即可得到点A与点B'的距离.【解答】解:分两种情况:①当点B '在线段AC 上时,△AA ′C 为直角三角形,∵∠ACB =90°,AB =10,sin A =5,∴BC =AB ×55=10×55=∴B 'C =AC =,∴AB '=AC ﹣B 'C =②当点B '在线段AC 的延长线上时,△AA ′C 为直角三角形,同理可得,B 'C =AC =,∴AB '=AC +B 'C =综上所述,点A 与点B '的距离为故答案为:【点评】本题考查了旋转的性质,勾股定理,锐角三角函数的应用,运用分类思想是本题的关键.2.(2020秋•闵行区期末)如图,在Rt △ABC 中,∠ACB =90°,AB =3,tan B =.将△ABC 绕着点A 顺时针旋转后,点B 恰好落在射线CA 上的点D 处,点C 落在点E 处,射线DE 与边AB 相交于点F ,那么BF =3【考点】旋转的性质;解直角三角形.【专题】平移、旋转与对称;解直角三角形及其应用;运算能力;推理能力.【分析】过点F 作FG ⊥AC 于点G ,由旋转的性质得出∠B =∠D ,得出tan ∠B =tan ∠D =12FG GD =,由平行线的性质得出∠B =∠AFG ,设AG =x ,则FG =2x ,则2132x x =+,求出AG =1,则可得出答案.【解答】解:如图,过点F 作FG ⊥AC 于点G ,∵将△ABC 绕着点A 顺时针旋转后,点B 恰好落在射线CA 上的点D 处,∴∠B =∠D ,∴tan ∠B =tan ∠D =12FG GD =,∵∠ACB =∠FGA =90°,∴BC ∥FG ,∴∠B =∠AFG ,∴tan ∠B =tan ∠AFG =12AG FG =,设AG =x ,则FG =2x ,∴2132x x =+,解得x =1,∴AG =1,FG =2,∴AF 225FG AG +=∴BF =AB ﹣AF =35.故答案为:35【点评】本题考查了旋转的性质,直角三角形的性质,锐角三角函数的定义,勾股定理,熟练掌握旋转的性质是解题的关键.3.(2020秋•静安区期末)在Rt △ABC 中,∠C =90°,AB =13,tan B =23(如图),将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',A 'B '与边BC 相交于点D ,那么'CD A D【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;几何直观.【分析】过C 作CE ⊥AB 于E ,根据勾股定理和正切的定义得到AC =,BC =,根据三角形面积得到CE =6,再根据旋转的性质和相似三角形的判定与性质即可求解.【解答】解:过C 作CE ⊥AB 于E ,∵tan B =23,∴23AC BC =,设AC =2x ,则BC =3x ,在Rt △ABC 中,AB =13,解得x =AC =,BC =,S △ABC =12AC •BC =12AB •CE ,即12××312×13×CE ,解得CE =6,∵tan B =CE EB =23,∴EB =9,∵将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',∴∠B =∠B ′,AC =AC ′,∵CE ⊥AB ,∴AE ′=AE =AB ﹣BE =13﹣9=4,∴A ′B =AB ﹣A ′E =9﹣4=5,∵∠A ′DB =∠CDB ′,∴△A ′DB ∽△B ′DC ,∴'CD A D =''CB A B ='CB A B ..【点评】本题考查了勾股定理,解直角三角形,旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.4.(2020秋•杨浦区期末)如图,已知在△ABC 中,∠B =45°,∠C =60°,将△ABC 绕点A 旋转,点B 、C 分别落在点B 1、C 1处,如果BB 1∥AC ,联结C 1B 1交边AB 于点D ,那么1BD B D 的值为622.【考点】旋转的性质;平行线的性质.【专题】平移、旋转与对称;推理能力.【分析】由旋转的性质和等腰三角形的性质可求∠B 1AB =30°,由直角三角形的性质可求DB 1=2DE ,DB =3﹣DE ,即可求解.【解答】解:如图,过点D 作DE ⊥AB 1于E,∵∠B =45°,∠C =60°,∴∠CAB =75°,∵BB 1∥AC ,∴∠CAB =∠ABB 1=75°,∵将△ABC 绕点A 旋转,∴AB =AB 1,∠AB 1C 1=∠ABC =45°,∴∠AB 1B =∠ABB 1=75°,∴∠B 1AB =30°,又∵DE ⊥AB 1,∠AB 1C 1=45°,∴AD =2DE ,AE=DE ,DE =B 1E ,∴AB 1DE +DE =AB ,DB 1DE ,∴DB =AB ﹣ADDE ﹣DE ,∴1BD B D622=,故答案为:2.【点评】本题考查了旋转的性质,等腰三角形的性质,直角三角形的性质,灵活运用这些性质进行推理是本题的关键.5.(2020秋•宝山区期末)在Rt △ABC 中,∠ACB =90°,AC =BC ,点E 、F 分别是边CA 、CB 的中点,已知点P 在线段EF 上,联结AP ,将线段AP 绕点P 逆时针旋转90°得到线段DP ,如果点P 、D 、C 在同一直线上,那么tan ∠CAP﹣1.【考点】旋转的性质;解直角三角形;等腰直角三角形;三角形中位线定理.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;解直角三角形及其应用;推理能力.【分析】分两种情形:①当点D 在线段PC 上时,延长AD 交BC 的延长线于H .证明AD =DC 即可解决问题.②当点P 在线段CD 上时,同法可证:DA =DC 解决问题.【解答】解:如图1,当点D 在线段PC 上时,延长AD 交BC 的延长线于H.∵CE =EA ,CF =FB ,∴EF ∥AB ,∴∠EFC =∠ABC =45°,∵∠PAO =45°,∴∠PAO =∠OFH ,∵∠POA =∠FOH ,∴∠H =∠APO ,∵∠APC =90°,EA =EC ,∴PE =EA =EC ,∴∠EPA =∠EAP =∠BAH ,∴∠H =∠BAH ,∴BH =BA ,∵∠ADP =∠BDC =45°,∴∠ADB =90°,∴BD ⊥AH ,∴∠DBA =∠DBC =22.5°,∵∠ADB =∠ACB =90°,∴A ,D ,C ,B 四点共圆,∠DAC=∠DBC=22.5°,∠DCA=∠ABD=22.5°,∴∠DAC=∠DCA=22.5°,∴DA=DC,设AD=a,则DC=AD=a,AP=PD=2a,∴PC=a+2a,∴tan∠CAP=22122a aCPAP+==;如图2中,当点P在线段CD上时,同法可证:DA=DC,设AD=a,则CD=AD=a,PD =2 2 a,∴PC=a ﹣22 a,∴tan∠CAP=22122a aCPAP+==,∵点P在线段EF上,∴情形1,不满足条件,情形2满足条件,﹣1.【点评】本题考查了旋转变换,等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.6.(2020秋•奉贤区期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD是△ABC的角平分线,将Rt△ABC绕点A旋转,如果点C落在射线CD上,点B落在点E处,联结DE,那么∠AED的正切值为3 7.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;推理能力.【分析】设点C落在射线CD上的点C'处,由勾股定理可求AB=5,由旋转的性质可得∠ACD=∠AC'C=45°=∠DCB,∠EAB=∠CAC',由平行线分线段成比例可求AD的长,即可求解.【解答】解:如图,设点C落在射线CD上的点C'处,∵∠ACB=90°,AC=3,BC=4,∴AB=5,∵CD是△ABC的角平分线,∴∠ACD=∠DCB=45°,∵将Rt△ABC绕点A旋转,∴∠ACD=∠AC'C=45°=∠DCB,∠EAB=∠CAC',∴∠CAC'=90°=∠EAB,∴AC'∥BC,∴'34AD ACDB BC==,∴AD=157,∴tan∠AED=37 ADAE=,故答案为:3 7.【点评】本题考查了旋转的性质,勾股定理,锐角三角函数,平行线的性质等知识,灵活运用这些性质解决问题是本题的关键.专题三定义新图形【历年真题】1.(2020秋•长宁区期末)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC AD=CD=32,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于414.【考点】相似图形;三角形中位线定理.【专题】图形的相似;推理能力.【分析】利用相似三角形的性质求出BC长,再利用等腰三角形的性质和勾股定理计算出EF的长即可.【解答】解:如图所示:∵AB=AC,AD=CD,△ABC∽△DAC,∴AC2=BC•AD,∵AC AD=32,∴CB=2,∵△ABC∽△DAC,∴∠ACB=∠CAD,∴CB∥AD,∵AB=AC,F为BC中点,∴AF⊥CB,BF=CF=1,∴∠AFC=90°,∵CB∥AD,∴∠FAE=∠AFC=90°,∵AC Rt△AFC中AF==,∵AD=32,E为AD中点,∴AE=34,∴EF414 =.故答案为:41 4.【点评】此题主要考查了相似三角形的性质,以及等腰三角形的性质和勾股定理,关键是掌握相似三角形对应边成比例、对应角相等.2.(2020秋•青浦区期末)如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ=或.【考点】相似图形.【专题】图形的相似;推理能力.【分析】如图,当∠1=∠2=∠3时,△BAQ∽△QDC∽△CQB,设AQ=x.利用相似三角形的性质,构建方程求解即可.【解答】解:如图,当∠1=∠2=∠3时,△BAQ∽△QDC∽△CQB,设AQ=x.过点A作AE⊥BC于E,过点D作DF⊥BC于F,则四边形AEFD是矩形,∴AD=EF,∵AB=CD=2,AD∥BC,∴四边形ABCD是等腰梯形,∴∠ABE=∠DCF=60°,BE=AB•cos60°=1,CF=CD•cos60°=1,∴EF=BC﹣BE﹣CF=6,∴AD=EF=6,DQ=6﹣x,∵△BAQ∽△QDC,∴AB AQ=QD CD,∴x(6﹣x)=4,解得x=3±5,∴AQ=3±5故答案为:5或3-5【点评】本题考查相似三角形的判定和性质,等腰梯形的性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.3.(2020秋•浦东新区期末)如图,△ABC中,AB=10,BC=12,AC=8,点D是边BC上一点,且BD:CD=2:1,联结AD,过AD中点M的直线将△ABC分成周长相等的两部分,这条直线分别与边BC、AC相交于点E、F,那么线段BE的长为2.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】先求出BD =8,CD =4,再求出MH =4,DH =2,设BE =x ,得出CE =12﹣x ,CF =3+x ,EH =10﹣x ,再判断出△EHM ∽△ECF ,得出比例式,建立方程求解,即可得出结论.【解答】解:如图,∵点D 是BC 上一点,BC =12,∴BD :CD =2:1,∴BD =8,CD =4,过点M 作MH ∥AC 交CD 于H ,∴△DHM ∽△DCA ,∴MH DH =AC DM CD AD=,∴点M 是AD 的中点,∴AD =2DM ,∵AC =8,∴MH DH 1=842=,∴MH =4,DH =2,过点M 作MG ∥AB 交BD 于G ,同理得,BG =DG =4,∵AB =10,BC =12,AC =8,∴△ABC 的周长为10+12+8=30,∵过AD 中点M 的直线将△ABC 分成周长相等的两部分,∴CE +CF =15,设BE =x ,则CE =12﹣x ,∴CF =15﹣(12﹣x )=3+x ,EH =CE ﹣CH =CE ﹣(CD ﹣DH )=12﹣x ﹣2=10﹣x ,∵MH ∥AC ,∴△EHM ∽△ECF ,∴MH EH =CF CE ,∴410-=3+12x x x-,∴x =2或x =9,当x =9时,CF =12>AC ,点F 不在边AC 上,此种情况不符合题意,即BE =x =2,故答案为:2.【点评】此题主要考查了相似三角形的判定和性质,构造出相似三角形是解本题的关键.4.(2020秋•徐汇区期末)如图,在△ABC 中,∠ABC =120°,AB =12,点D 在边AC 上,点E 在边BC 上,sin ∠ADE =45,ED =5,如果△ECD 的面积是6,那么BC 的长是﹣6.【考点】解直角三角形;三角形的面积.【专题】解直角三角形及其应用;推理能力.【分析】如图,过点E 作EF ⊥BC 于F ,过点A 作AH ⊥CB 交CB 的延长线于H .解直角三角形求出BH ,CH 即可解决问题.【解答】解:如图,过点E 作EF ⊥BC 于F ,过点A 作AH ⊥CB 交CB 的延长线于H .∵∠ABC =120°,∴∠ABH =180°﹣∠ABC =60°,∵AB =12,∠H =90°,∴BH =AB •cos60°=6,AH =AB •sin60°=,∵EF ⊥DF ,DE =5,∴sin ∠ADE =EF DE =45,∴EF =4,∴DF 3==,∵S △CDE =6,∴12•CD •EF =6,∴CD =3,∴CF =CD +DF =6,∵tan C =EF AH CF CH =,∴4636CH=,∴CH =,∴BC =CH ﹣BH =6.故答案为:﹣6.【点评】本题考查解直角三角形,三角形的面积等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.5.(2020秋•金山区期末)已知在Rt △ABC 中,∠C =90°,BC =1,AC =2,以点C 为直角顶点的Rt △DCE 的顶点D 在BA 的延长线上,DE 交CA 的延长线于点G ,若tan ∠CED=12,CE =GE ,那么BD 的长等于2+【考点】解直角三角形;勾股定理.【专题】解直角三角形及其应用;推理能力.【分析】如图,过点A 作AH ⊥CE 于H .想办法证明AK =AC ,推出HK =CH ,推出AK =AD =2,即可解决问题.【解答】解:如图,过点A 作AH ⊥CE 于H .∵tan ∠CED =12=tan ∠BAC ,∴∠E =∠BAC ,∵CE =EG ,∴∠CGE =∠ECG ,∵∠BAC+∠GAK=180°,∴∠E+∠GAK=180°,∴∠AGE+∠AKE=180°,∵∠AKE+∠AKC=180°,∴∠AKC=∠CGE,∴∠AKC=∠ACK,∴AC=AK=2,∵AH⊥CK,∴KH=CH,∵∠AHE=∠DCK=90°,∴AH∥CD,∴KA=AD,∴DK=2AK=4,AD=AK=2,∵∠ACB=90°,BC=1,AC=2,∴AB=∴BD=AB+AD=,故答案为:【点评】本题考查解直角三角形,勾股定理,三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题.6.(2020秋·黄浦区期末)已知一个矩形的两邻边长之比为1:2.5.一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为2:1或1:2或1:1.【考点】相似多边形的性质;矩形的性质,四手拉手模型【专题】图形的相似;推理能力.【分析】如图,设AB=a,AD=2.5a,AE=x,则DE=2.5a-x,利用相似多边形的性质,构建方程求解,另外两个矩形全等也符合题意.【解答】解:如图,设AB=a,AD=2.5a,,AE=x,则DE=2.5a-x.∵矩形ABFE∽矩形EDCF∴AE EF=EF DE∴=2.5x aa a x-整理得,x2-2.5xa+a2=0,解得x=2a或0.5a,∴矩形ABFE与矩形EDCF相似,相似比为2:1或1:2.当E,F分别是AD,BC的中点时,两个矩形全等,也符合题意,相似比为:1:1故答案为:2:1或1:2或1:1.【点评】本题考查相似多边形的性质,解题的关键是学会利用参数构建方程求解,属干电考常考题型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(本小题满分10分)已知,如图,△ABC 是等边三角形,过AC 边上的点作 DG x 2bx c y ax ++=知C(2,4),BC= 4.(1)求过O 、C 、B 三点的抛物线解析式,并写出顶点坐标和对称轴;(2)经过O 、C 、B 三点的抛物线上是否存在P 点(坐标轴的距离相等.如果存在,求出P 点坐标;如果不存在,请说明理由. 4、 (本题12分)如图,AD(1)求证:四边形AEFD 是菱形; (2)若BE=EF=FC ,求∠BAD+∠ADC 的度数;(3)若BE=EF=FC ,设AB = m ,CD = n ,求四边形ABCD 的面积. 5、 (本题14分)如图,在平面直角坐标系中,抛物线6422++-=x x y 与 x 轴交于A 、B 两点(A 点在B 点左侧),与y 轴交于C 点,顶点为D.过点 C 、D 的直线与x 轴交于E 点,以OE 为直径画⊙O 1,交直线CD 于P 、E 两点.(1)求E 点的坐标;(2)联结PO 1、PA.求证:BCD ∆~A PO 1∆;(3) ①以点O 2 (0,m)为圆心画⊙O 2,使得⊙O 2与⊙O 1相切,当⊙O 2经过点C 时,求实数m 的值;②在①的情形下,试在坐标轴上找一点O 3,以O 3为圆心画⊙O 3,使得⊙O 3与⊙O 1、⊙O 2同时相切.直接写出满足条件的点O 3的坐标(不需写出计算过程).6.(本题满分12分,第(1)小题6分,第(2)小题6分)(第24题图)如图,EF 是平行四边形ABCD 的对角线BD 的垂直平分线,EF 与边AD 、BC 分别交于点E 、F .(1)求证:四边形BFDE 是菱形;(2)若E 为线段AD 的中点,求证:AB ⊥BD .7.(本题满分12分,第(1)小题6分,第(2)小题6分)在平面直角坐标系中,抛物线2y x bx c =++经过点(0,2)和点(3,5). (1)求该抛物线的表达式并写出顶点坐标; (2)点P 为抛物线上一动点,如果直径为4⊙P 与y 轴相切,求点P 的坐标.8.(本题满分14分,第(1)小题4分,第(25分)如图,在Rt △ABC 中,∠BAC = 90°,AB =3,E 、F 分别是AB 边和AC 边上的动点,且∠EDF = 90°.(1)求DE ︰DF 的值;(2)联结EF ,设点B 与点E 间的距离为x ,△DEF 的面积为y ,求y 关于x 的函数解析式,并写出x 的取值范围;(3)设直线DF 与直线AB 相交于点G ,△EFG 能否成为等腰三角形?若能,请直接写出线段BE 的长;若不能,请说明理由.9.(本题满分12分,每小题各如图10,已知抛物线交于点B ,且OB OA =. (1) 求c b +的值; (2) 若点C 第24题图A DE CO第25题B C D EFA(3) 在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标.10.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图11,已知⊙O的半径长为1,PQ是⊙O的直径,点M是PQ延长线上一点,以点M为圆心作圆,与⊙O交于A、B两点,联结PA并延长,交⊙M于另外一点C.(1) 若AB恰好是⊙O的直径,设OM=x,AC=y,试在图12中画出符合要求的大致图形,并求y关于x的函数解析式;(2) 联结OA、MA、MC,若OA⊥MA,且△OMA与△PMC相似,求OM的长度和⊙M 的半径长;(3) 是否存在⊙M,使得AB、AC恰好是一个正五边形的两条边?若存在,试求OM的长度和⊙M的半径长;若不存在,试说明理由.图1254321OFEDCBA 1.(1)∵△ABC 是等边三DG 322++-=x x y 322++-=x x y 32,(2++-x x x D 0322=++-x x 292923)32(32132122++-=++-⨯⨯+⨯x x x x x 2929232++-x x 232=-=a b x 863)23(4)29(29)23(44422=-⨯-⨯-⨯=-a b ac )3(3322+-=++-x x x 0652=+-x x 21=x 32=x EP DE 21=EP DP 23=)3(23322+-=++-x x x 03722=+-x x 213=x 34=x 2121c bx ax y ++=2()0≠a ⎪⎩⎪⎨⎧=+=++=)3(4636)2(424)1(0b a c b a c ⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=03831c b a x x y 38312+-=)316,4(4=x ),(a a P ),(a a P -()0≠a ),(a a P a a a =+-383120,521==a a ),(a a P -aa a -=+-383120,1121==a a )5,5(p )11,11(-p ⎪⎩⎪⎨⎧=∠=∠∠=∠AO AO AODAOE 51≅⎪⎩⎪⎨⎧∠=∠=∠=∠FOE AOE EO EO 21≅mn 21AF AB 21S ABF =⋅=∆m DE 21=mn 21OD AF S AFCD =⋅=四边形mnS AFCD ABCD =+=∆四边形四边形S S ABF ()81264222+--=++-=x x x y )8,1(),6,0(D C ()0≠+=k b kx y ⎩⎨⎧+==686k b ⎩⎨⎧==62b k 62+=x y 3453OA OC AOC Rt ECP EP PC x==∴∴∠=︒∴==-Q V V 为等腰)0,3(-E 06422=++-x x 3,121=-=x x )0,3()0,1(B A -)0,0(O )0,3(-E )0,(231-O 231=r 设)62,(+t t P由231=PO 得 232223)62()(=+++t t 解得3,25121-=-=t t (舍) ∴),(56512-P 2分∴585=PA 211=AO又 5=DC 53=CB 172=DB ∴5211===PADB PO CB AO DC 1分 ∴BCD ∆~A PO 1∆ (3) ( 7分)① )0,(231-O 231=r),0(2m O 据题意,显然点2O 在点C 下方 m C O r -==622当⊙O 2与⊙O 1外切时 2121r r O O +=代入得()()m m -+=+6232223 解得 2,51821==m m (舍)2分 当⊙O 2与⊙O 1内切时 2121r r O O -=代入得()()m m --=+6232223 解得 518,221==m m (舍) 2分 ∴2,51821==m m ② ⎪⎭⎫ ⎝⎛518,03O ⎪⎭⎫ ⎝⎛-710,03O ⎪⎭⎫ ⎝⎛0,233O ⎪⎭⎫ ⎝⎛-0,14453O ⎪⎭⎫⎝⎛1514,03O ()2,03O ⎪⎭⎫ ⎝⎛0,2213O 3分6、.证明:(1)∵四边形ABCD 是平行四边形∴ED ∥BF ,得∠EDB =∠FBD ……………………………………………………(2分)∵EF 垂直平分BD∴BO=DO ,∠DOE =∠BOF =90° ∴△DOE ≌△BOF……………………………………………………………………(2分)∴ EO=FO∴四边形BFDE是平行四边形……………………………………………………(1分)又∵EF⊥BD∴四边形BFDE是菱形……………………………………………………………(1分)(2)∵四边形BFDE是菱形∴ED=BF∵AE=ED∴AE=BF………………………………………………………………………………(2分)又∵AE∥BF∴四边形ABFE是平行四边形………………………………………………………(1分)∴AB∥EF ……………………………………………………………………………(1分)∴∠ABD=∠DOE ……………………………………………………………………(1分)∵∠DOE=90°∴∠ABD=90°即AB⊥BD……………………………………………………………………………(1分)7.解:(1)把(0,2)、(3,5)分别代入2y x bx c=++得2593cb c=⎧⎨=++⎩解得22bc=-⎧⎨=⎩……………………………………………(3分)∴抛物线的解析式为222y x x=-+………………………………………………(1分)∴抛物线的顶点为(1,1)………………………………………………………………(2分)(2)设点P到y轴的距离为d,⊙P的半径为r∵⊙P与y轴相切∴1422d r==⨯=∴点P的横坐标为2±…………………………………………………………………(2分)当2x=时,2y=∴点P的坐标为(2,2)…………………………………(2分)当2x=-时,10y=∴点P的坐标为(2,10)-………………………………(2分)∴点P的坐标为(2,2)或(2,10)-.8.解:(1)∵∠BAC= 90°∴∠B +∠C=90°,∵AD是BC边上的高∴∠DAC+∠C=90°∴∠ B =∠DAC………………………………………………………………………(1分)又∵∠EDF= 90°∴∠BDE+∠EDA=∠ADF +∠EDA = 90°∴∠BDE =∠ADF ∴△BED ∽△AFD ……………………………………………………………………(1分)∴DE BDDF AD=…………………………………………………………………………(1分)∵3cot 4BD AB B AD AC === ∴DE ︰DF=34…………………………………………………………………………(1分)(2)由△BED ∽△AFD 得34BE BD AF AD == ∴4433AF BE x == …………………………………………………………………(1分)∵BE x = ∴3AE x =- ∵∠BAC = 90° ∴2222425(3)()6939EF x x x x =-+=-+………………………………………(1分) ∵DE ︰D F =3︰4,∠EDF =90°∴ED =35EF ,FD =45EF …………………………………………………………………(1分)∴216225y ED FD EF =⋅=∴22365432525y x x =-+ (03)x ≤≤ ………………………………………………(2分)(3)能. BE 的长为543255或.……………………………………………………………(5分)(说明:BE 的长一个正确得3分,全对得5分)9、解:(1)由题意得:点B 的坐标为),0(c ,其中0>c ,c OB = (1分) ∵OB OA =,点A 在x 轴的负半轴上,∴点A 的坐标为)0,(c - (1分) ∵点A 在抛物线c bx x y ++-=2上,∴c bc c +--=20 (1分) ∴ 1=+c b (因为0>c ) (1分)(2)∵四边形OABC 是平行四边形∴c AO BC ==,又BC ∥x 轴,点B 的坐标为),0(c∴点C 的坐标为),(c c (1分) 又点C 在抛物线上,∴c bc c c ++-=2 ∴0=-c b 或0=c (舍去) (1分) 又 由(1)知:1=+c b ∴21=b ,21=c . 抛物线的解析式为21212++-=x x y . (2分) (3)过点P 作⊥PM y 轴,⊥PN BC ,垂足分别为M 、N ∵ BP 平分CBO ∠ ∴ PN PM = (1分) 设点P 的坐标为)2121(2++-x x x , ∴ x x x =++--)2121(212 (1分) 解得:23=x 或0=x (舍去) (1分) 所以,点P 的坐标为)21,23(- (1分) 10、(1)图画正确 (1分)过点M 作AC MN ⊥,垂足为N ∴y NC AN 21== 由题意得:AB PM ⊥, 又AB 是圆O 的直径 ∴1==OP OA ∴︒=∠45APO , 2=PA ∴y PN 212+= (1分)在Rt △PNM 中,PMPN NPM =∠cos又x PM +=1,︒=∠45NPM∴ 22121245cos =++=︒x y∴ y 关于x 的函数解析式为22-=x y (1>x ) (2分) (2)设圆M 的半径为r因为 OA ⊥MA ,∴∠OAM=90°,12+=r OM 又△OMA 与△PMC 相似,所以△PMC 是直角三角形。
