2010年四川大学模拟竞赛论文
2010年全国大学生数学建模竞赛B题优秀论文

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期: 2010年 9 月 13 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):上海世博会影响力的定量评估模型及讨论摘要:本文围绕上海世博会的影响力进行了定量评估,对国际旅游入境人数、外国游客人数、港澳台游客人数、国际旅游外汇收入、上海市的财政收入五个方面分别建立了本底趋势线模型,并对求解结果作了分析。
第一步,我们对2000年至2009年的国际旅游入境人数、外国游客人数、港澳台游客人数、国际旅游外汇收入、上海市的财政收入这五个方面分别进行数据内插处理,对各个指标在起伏过大的某一年份对其前后各1年的数据采用SPSS 的EM(期望最大化)方法进行内插处理(内插后的值称为内插值),使得本底趋势线最符合实际情况。
第二步,用Excel 的指数模型、乘幂模型和SPSS 的指数-三角函数复合模型()()ϕω++=t q rt y y t sin ex p 0、直线-逻辑线增长复合模型()/1exp t y a bt K c rt =+++-⎡⎤⎣⎦、直线-三角函数复合模型()ϕω+++=t q bt a y t sin 对各个指标进行拟合,确定有关参数,获得各个指标的趋势线模型和方程,并计算各年的本底值;第三步,用第二步所得各个指标的趋势线方程,计算各个指标本底值与各年各个指标内插值的相关系数,根据该相关系数确定最终的趋势线模型和方程。
四川大学关于学位(毕业)论文抄袭、剽窃等学术不端行为的处理办法(试行)(川大校〔2010)2号

关于印发《四川大学关于学位(毕业)论文抄袭、剽窃等学术不端行为的处理办法(试行)》的通知川大校〔2010〕2号校内各单位:为维护学术尊严,规范学术行为,加强校风学风建设,促进我校学术研究健康发展,根据国家有关法律法规、教育部有关文件精神和学校相关文件规定,在已经实施的《四川大学学术道德规范》和《四川大学关于违反学术道德规范的处理规定》的基础上,学校制定了《四川大学关于学位(毕业)论文抄袭、剽窃等学术不端行为的处理办法(试行)》,现印发给你们,请认真学习,并遵照执行。
附件:四川大学关于学位(毕业)论文抄袭、剽窃等学术不端行为的处理办法(试行)四川大学二○一○年一月二十一日主题词:学术行为规范办法通知四川大学校长办公室二○一○年一月二十九日印发打字:贾盛庆校对:秦远清印数:500份附件2四川大学关于学位(毕业)论文抄袭、剽窃等学术不端行为的处理办法(试行)第一条指导思想为维护学术尊严,规范学术行为,保障学术自由,加强我校校风学风建设,促进我校学术研究健康发展,依据《中华人民共和国著作权法》、《中华人民共和国著作权法实施细则》、教育部《关于树立社会主义荣辱观进一步加强学术道德建设的意见》、《关于严肃处理高等学校学术不端行为的通知》等法律法规、文件,并在我校已经出台实施的《四川大学学术道德规范》、《四川大学关于违反学术道德规范的处理规定》的基础上,学校决定进一步加强对学位(毕业)论文的规范管理,防范和惩治学位(毕业)论文抄袭、剽窃等学术不端行为,特制定本办法。
第二条适用范围本办法适用于攻读我校学位(指博士、硕士、学士学位)的研究生、本科生等撰写的以我校为著作权人单位的学位(毕业)论文。
我校教职工和学生都应严格遵守学术规范,恪守学术道德,弘扬优良学风,杜绝学术不端。
本办法专门针对学位(毕业)论文中的抄袭、剽窃等学术不端行为进行认定和处理,其它学术不端行为按《四川大学学术道德规范》和《四川大学关于违反学术道德规范的处理规定》处理。
2010“高教社杯”全国大学生数学建模大赛A题论文

基于微元法的变位储油罐罐容表标定问题摘要加油站当地下储油罐发生一定程度变位时,需要重新标定其罐容表,优化“油位计量管理系统”,目的是得到地下储油罐内油量的真实值,所以研究该问题对加油站具有重要意义。
本文主要利用微元法建立积分模型,解决了储油罐的变位识别与罐容表标定的问题,得到了实验储油罐变位后罐容表新的标定值,实际储油罐变位后储油量与油位高度及变位参数之间的关系,以及实际储油罐变位后罐容表新的标定值。
问题一中,首先对纵向倾斜的小椭圆油罐进行分析,将油罐从罐中无油到加满油的过程分为7个部分来分析,分别是:(1)从罐中无油到将油加到刚好不接触油浮子;(2)从油开始接触油浮子到油灌满倾斜角但刚好不接触罐右侧壁;(3)从罐中油开始接触右侧壁到油灌到左侧壁中点水平线;(4)油从左侧壁中点灌到左侧壁终点水平线;(5)油从左侧壁终点灌到右侧壁中点水平线;(6)油从右侧壁中点灌到油浮子刚好显示油满;(7)从油浮子刚好显示油满到将油罐灌满。
分别分析这7个加油的过程,建立模型,用微元法求解每个部分罐中油体积的变化,根据体积的变化得到油面高度的变化,将变位后的油面高度与无变位时的油面高度作比较,分析得出变位对罐容表的影响。
最后由变位后油面的高度,用Matlab编程序得到变位后罐容表新的标定值。
问题二中,经过对实际储油罐的形状与倾斜及偏转角度情况的分析,我们利用割补法建立罐体变位后的数学模型,先分别分析储油罐只纵向倾斜和只横向偏转的情况,用h的函数关系式,再分析储油罐同时纵向倾微元法得到罐中油体积与变位后罐容表刻度斜和横向偏转的情况,我们将模型转变为先将储油罐横向偏转,然后在横向偏转的基础上再纵向倾斜,由所给的实际储油罐的数据,分别结合只进行纵向倾斜和只进行横向偏转的情况,用拟合的方法,利用Simpson公式,近似得到了倾斜角α=4.5230,偏转角β=1.220。
在α和β确定之后,罐内储油量与油位高度及倾斜角α、偏转角β的关系式即转化为油体积与油位高度的关系式,进而计算得到变位后油位间隔为10cm的罐容表新标定值。
2010年“高教社杯”全国大学生数学建模竞赛四川赛区四川省获奖名单
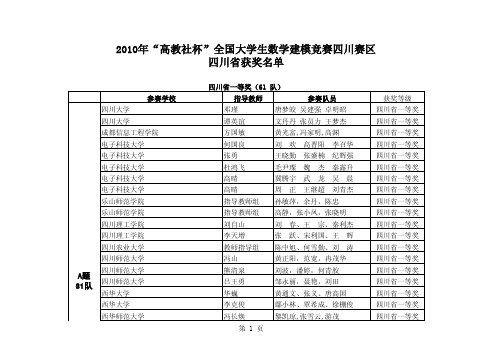
A题 38队
西华师范大学 西华师范大学 西南财经大学 西南财经大学 西南财经大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学
西南交通大学 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南科技大学 西南科技大学 西南民族大学 西南石油大学 中国民航飞行学院 四川大学 四川大学 成都信息工程学院 电子科技大学 乐山师范学院 成都理工大学工程技术学院 四川师范大学 四川师范大学 B题 19队 四川师范大学 四川师范大学文理学院 西南财经大学 西南交通大学 西南交通大学
四川省二等奖(75队) 四川大学 四川大学 韩会磊 韩会磊 第 3 页 范洋宇 张莞鹭 胡静泓 贾宗霖 冯翠英 刘赛 四川省二等奖 四川省二等奖
四川大学 四川大学 四川大学 成都大学 成都大学 成都理工大学工程技术学院 成都信息工程学院 电子科技大学 电子科技大学 四川理工学院 四川理工学院 四川师范大学 四川师范大学 四川师范大学 西华大学 西华大学
李绍文 李绍文 骆川义 丁川 韩本三 吴萌 孙云龙 韩本三 丁川 梁 林军 周 游 涛 张兴元
张曦、马骏、何云娟 张君、邓小华、赵敏智 景龙、王颖、段成林 周宏宇、肖佳文、郑晓琪 潘丽莉、郭晶旭、雷 梁瑧、王超、梁艳 陈文军、屈婷婷、陈志 王梦阳、蒋思慧、王 鞠蕾 陈海军 王昕 周大海,何永刚,黄立群 周航成,雷崇超,李宗霖 郭 邓 状,崔圣华,王 李文俊 肖 淞 章宇 巨 敏 忠 奎 亮 娟 赵媛媛、张子婷、李若诗
王继超
孙敏萍,余丹,陈忠 高静,张小凤,张晓明 刘 张 春、王 宗、秦利杰 跃、宋利国、王
陈中旭、何雪勤、刘 黄正阳,范宽,冉茂华 刘波,潘婷,何青胶 邹永丽,聂艳,刘田 黄通文、张义、唐高国
2010年全国大学生数学建模大赛川区成绩

西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学峨眉校区 西南石油大学 阿坝师范高等专科学校 成都电子机械高等专科学校 成都纺织高等专科学校 成都纺织高等专科学校 成都理工大学工程技术学院 泸州职业技术学院 四川职业技术学院 宜宾学院 宜宾学院 宜宾学院 宜宾学院 成都纺织高等专科学校 D题 5队 四川水利职业技术学院 四川信息职业技术学院 四川职业技术学院 宜宾学院
数模指导教练组 廖琪 曾丹丹 李文祥 第 6 页
四川省三等奖(85队 四川省三等奖(85队) 四川大学 西华大学 西华大学 西南科技大学 攀枝花学院 西南交通大学 成都理工大学 电子科技大学 成都信息工程学院 西华大学 西南交通大学 四川师范大学 西南财经大学 西南科技大学 成都理工大学 四川大学 西华大学 西南交通大学峨眉校区 四川大学 A题 41队 41队 西南交通大学 西南交通大学 西南财经大学 四川理工学院 陈琼 张雪征 刘志伟 林军 李思霖等 何 平 黄光鑫 杜鸿飞 吴泽忠 郑鹏社 薛长虹 吕王勇 丁川 林军 黄光鑫 韩会磊 裴峥 符伟 谭英谊 叶建军 徐跃良 孙云龙 张新华 第 7 页 宋晶 赵阳 冉启航 彭怡、胡军、张宽慎 刘问军、柳霜、李亚辉 肖华强,秦玲,刘鹏飞 屈江山,李国伟,阳彬 苏建家 刘总真 陈晔 周武林,魏科峰,刘少东 陈子玉 潘明争 张林炼 刘晨雨,陈裕兴,叶帮苹 钟全能、余武、李星君 孙宇 陈辉 卢毓江 阮靖云,张平,周立会 张梦柯、李江源、何岱泉 苗瑷琳,王恒,刘菁伟 陈丽娟,陈 建,王阳林 范丞君 刘雅婷 冯畅 陈小英、吴阳、徐明波 杨天翔,陈景琪,艾毅 郝颖坤 李双龙 行亚楠 孙小飞 王飞 张雪 杨云 吴卓智 姚祥骁 潘婕、康攀、吴亚东 赵天荣、张洪波、张 懿 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖 四川省三等奖
【全国大学生数学建模竞赛获奖优秀论文作品学习借鉴】2010数学建模C题,输油管的布置、获奖论文

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):1328303所属学校(请填写完整的全名):武汉职业技术学院参赛队员(打印并签名):1. XXX2. XXX3. X X指导教师或指导教师组负责人(打印并签名):数模指导组日期:2010年9月12日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):输油管的布置摘要本文对输油管线的布置主要从建设费用最省的角度进行研究。
首先,对问题一,我们按照共用管线与非共用管线铺设费用相同或不相同,进行分类讨论。
为了更好的说明,我们根据共用管线与非共用管线铺设费用相同或不同及两炼油厂连线与铁路线垂直或不垂直分成四类讨论。
其次,对问题二,由于需要考虑在城区中铺设管线,涉及到拆迁补偿费等。
通过对三个公司的估算费用加权,求得期望值021.5P (万元)。
并利用建立的规划模型②求得管道建设的最省费用为282.70万元。
其中共用管线长度为1.85千米,炼油厂B在城区铺设的管道线对城郊分界线的射影为0.63千米。
最后,对问题三,由于炼油厂A和B的输油管线铺设费用不同,所以最短管道长度和未必能保证铺设总费用最省,因而我们又建立了规划模型③,通过LINGO软件求得管道建设的最省费用为251.97万元,三种管道的结合点O到炼油厂A与铁路垂线的距离为6.13千米,结合点O到铁路的距离为0.14千米,炼油厂B在城区铺设的管道线对城郊分界线的射影为0.72千米。
2010年全国研究生数学建模竞赛优秀论文A5
2010年建模优秀论文解析
储油罐的变位识别与罐容表标定目录摘要本文对储油罐的变为识别和罐容表的标定问题进行了深入的探讨,针对这一问题,我们建立了数学模型,并利用matlab等软件对其进行求解。
针对问题一,我们利用了积分的方法推导出小椭圆储油罐在无变位和发生纵向倾斜变位时的储油量与油位高度之间的一般公式,然后把附表一中的变位前后油位高度分别代入两个模型求得体积,所求得的体积与附表一中相对应的累加进油量和罐内容量初始值之和基本相符,说明我们建立的模型是可以接受的。
用这两个模型变位前后的曲线,计算测量值与实际值之间的误差。
并利用变位后的模型给出间隔1cm的罐容表的标定值。
针对问题二,我们先考虑纵向倾斜,将实际模型分为三部分,分别求出左右球冠体,中间部分,的体积。
用Matlab求出高度H和体积V的一般关系。
再考虑横向倾斜,得到综合横向倾斜和纵向倾斜后H和V的关系。
根据附表2,用Matlab进行最小二乘,求解最小误差下纵向倾斜角α和横向倾斜角β。
得到油位高度间隔为10cm的罐容表标定值。
并通过附件2中实际数据,检验此模型可行性。
关键词:微元法;最小二乘法;Matlab;一问题重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
问题一:为了掌握罐体变位后对罐容表的影响,利用题中所给的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,并给出附件一。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
2010数学建模优秀论文(1).doc
数学建模比赛预选赛温室中的绿色生态臭氧病虫害防治2009年12月,哥本哈根国际气候大会在丹麦举行之后,温室效应再次成为国际社会的热点。
如何有效地利用温室效应来造福人类,减少其对人类的负面影响成为全社会的聚焦点。
臭氧对植物生长具有保护与破坏双重影响,其中臭氧浓度与作用时间是关键因素,臭氧在温室中的利用属于摸索探究阶段。
假设农药锐劲特的价格为10万元/吨,锐劲特使用量10mg/kg-1水稻;肥料100元/亩;水稻种子的购买价格为5.60元/公斤,每亩土地需要水稻种子为2公斤;水稻自然产量为800公斤/亩,水稻生长自然周期为5个月;水稻出售价格为2.28元/公斤。
根据背景材料和数据,回答以下问题:(1)在自然条件下,建立病虫害与生长作物之间相互影响的数学模型;以中华稻蝗和稻纵卷叶螟两种病虫为例,分析其对水稻影响的综合作用并进行模型求解和分析。
(2)在杀虫剂作用下,建立生长作物、病虫害和杀虫剂之间作用的数学模型;以水稻为例,给出分别以水稻的产量和水稻利润为目标的模型和农药锐劲特使用方案。
(3)受绿色食品与生态种植理念的影响,在温室中引入O3型杀虫剂。
建立O3对温室植物与病虫害作用的数学模型,并建立效用评价函数。
需要考虑O3浓度、合适的使用时间与频率。
(4)通过分析臭氧在温室里扩散速度与扩散规律,设计O3在温室中的扩散方案。
可以考虑利用压力风扇、管道等辅助设备。
假设温室长50 m、宽11 m、高3.5 m,通过数值模拟给出臭氧的动态分布图,建立评价模型说明扩散方案的优劣。
(5)请分别给出在农业生产特别是水稻中杀虫剂使用策略、在温室中臭氧应用于病虫害防治的可行性分析报告,字数800-1000字。
论文题目:温室中的绿色生态臭氧病虫害防治姓名1:学号:专业:姓名1:学号:专业:姓名1:学号:专业:2010 年5月3日目录一.摘要 (4)二.问题的提出 (5)三.问题的分析 (5)四.建模过程 (6)1)问题一 (6)1.模型假设 (6)2.定义符号说明 (6)3.模型建立 (6)4.模型求解 (7)2)问题二 (9)1.基本假设 (9)2.定义符号说明 (10)3.模型建立 (10)4.模型求解 (11)3)问题三 (12)1.基本假设 (12)2.定义符号说明 (12)3.模型建立 (13)4.模型求解 (13)5.模型检验与分析 (14)6.效用评价函数 (15)7.方案 (16)4).问题四 (17)1.基本假设 (17)2.定义符号说明 (17)3.模型建立 (18)4.动态分布图 (19)5.评价方案 (19)五.模型的评价与改进 (20)六.参考文献 (21)一.摘要:“温室中的绿色生态臭氧病虫害防治”数学模型是通过臭氧来探讨如何有效地利用温室效应造福人类,减少其对人类的负面影响。
2010全国数学建模大赛B题论文
世博效应:对上海会展业的影响摘要:会展业是会议业和展览业的总称,隶属于服务业,即通过举办各种形式的会议和展览,吸引大量商务客和游客,促进产品市场的开拓、技术和信息交流、对外贸易和旅游观光,并以此带动交通、住宿、等多项相关产业的发展,并被称为“无烟工业”.2010年世博会对上海会展业影响深远,世博会带来的机遇表现在:首先,场馆建设和基础设施为会展提供良好的硬件环境.根据规划,整个世博园区提供了将近二百个展览场馆,世博会举办前、举办中以及举办后都将为上海的会展业带来巨大的发展空间.其次,世博会加快人才的大量培养,为上海会展行业储备和积聚人才.最后,世博会推进会展项目的国际化、专业化、品牌化发展.上海会展业已成为上海服务业的重要组成部分,是提升城市形象、增强城市服务功能和促进社会建设的新兴产业,因此我国各大城市都在大力发展会展业,使其成为地区新的经济引擎,会展业的竞争力是城市综合竞争力的重要反映.我们将建立两种模型,来综合的评估世博会对上海会展业的影响:1. 模糊归一化法评估上海会展业竞争力的综合评价指标;我们可以具体从经济发展水平,商贸发展水平,会展业发展水平,社会事业发展水平,区域交通条件,地理区位条件和旅游业发展水平的评价指标来对会展业的竞争力进行定量的评估.2. 预测会展业未来的发展趋势.“后事件效应”,即在重大事件活动举办之后呈现下降的典型特点,世博会谢幕后,由于国际入境旅游人数的减少,展馆被拆迁或改建等因素,会展业的利润收入会受到波动,因此我们用微分方程构造的数学模型对会展业未来的发展趋势作出一定的预测.通过采集数据,建立模型,用Excel程序包 ,MATLAB 等软件对采集到的数据进行统计分析等处理,来对2010年世博会对上海会展业的影响效应进行定量的评估.关键字:世博会会展业模糊归一假设法一、问题重述以“城市,让生活更美好”为主题,首次在中国举办的中国2010年上海世博会,是一次中国加强与世界交流,近距离对话世界多元文化,向世界学习的重要契机,更是实现科学发展、促进社会和谐的重要机遇.世界博览会不仅仅是为了商业性的目的,更为世界各国展示社会、经济、文化、科技各方面的成就以及发展的前景,提供了绝佳的机遇.中国申办2010年世博会获得成功,上海将获得可观的经济效益.世博会使上海的知名度再次提升,并且通过与同世界的更多接触,能使上海人民的精神面貌、素质得到提高.上海对世博会场址规划的深化和调整,世博园区面积从原来的240公顷增加到310公顷,加上60公顷的停车场和30公顷的世博村,总面积达400公顷.请你们选择感兴趣的某个侧面,建立数学模型,利用互联网数据,定量评估2010年上海世博会的影响力.二、问题的分析2010申博成功已经成为上海会展业发展的“助推器”,为整个会展业及相关行业注入了新的活力,使上海面临着建成世界级会展城市的历史机遇.会展业已经初显格局,区域化发展也进一步增强,会展的数量和收入都大幅上涨,其对于上海的发展发挥的作用也越来越大.会展业的竞争力成为城市综合竞争力的重要反映,Baker等(1993)和陈志平等(2005)提出的城市展业竞争力评价因素,可分为经济、贸易发展水平,社会、科技事业发展水平,地域、交通条件和会展业四个方面.我们可以具体从经济发展水平,商贸发展水平,会展业发展水平,社会事业发展水平,区域交通条件,地理区位条件和旅游业发展水平的评价指标来对会展业的竞争力进行定量的评估.我们根据会展业在世博会开幕前的利润收入,根据假设的增长函数,用MATLAB拟合曲线,得到近几年的增长曲线图,并且对未来的发展趋势作出预测.三、模型假设1. 世博会期间上海的其他行业平稳发展, 没有突发事件发生;2. 上海在预测年内没有举办其他的大型活动;3. 所有附件上提供的相关数据来源网可靠,真实;4. 会展业的利润收入每年的增长率为K(t).四、符号定义及说明iS-第i个城市的会展业竞争力综合评价值,竞争力随值的增大而增大;jV-第j个二级指标的权重;ijW-第i个城市第j个二级指标的标准值;m - 指标数;n - 年份;X-各评价指标原始值maxX-对应评价指标最大值minX-对应评价指标最小值t:初始年份2000t :第 2000 + t 年N 0:t年份的会展利润收入,即2000年是利润N(t):初始年份的会展利润收入K(t):第t年的增长率五、模型建立与求解模糊归一化综合分析方法模型的原理:模糊评价即在评价过程中引入模糊性概念,运用模糊数学来处理世博会影响的一些问题,以反映世博会对各行业影响的不确定性;归一化是一种简化计算的方式即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量,从而定量计算出世博会对上海会展业竞争力的纵向的影响.(一)会展城市竞争力模糊关系评价指标体系的建立本文从动态关系出发,从时间维度分析了上海会展业竞争力的变化情况,从而表现出上海举办世博会对上海会展业竞争力的影响.1、城市会展业竞争力评价因素的确定本文采用城市会展业竞争力评级体系中的影响因素,包括经济、贸易发展水平,社会、科技事业发展水平,地域、交通条件和会展业现实水平四个方面.而具体的评价指标可被继续分解为经济发展水平、商贸发展水平、会展业发展水平、社会事业发展水平、区域交通条件、地理区位条件和旅游业发展水平七个方面,所以对会展业竞争力的评估也应从以上七个方面着手:l).经济发展水平指标衡量区域经济发展水平的最好的指标莫过于区域国内生产总值(GDP),所谓区域的国内生产总值,指的是一个区域国民经济各部门在一定时间(通常为一年)内,扣除来自国外的劳动报酬和财产收入后的全部社会最终产品和劳务价值的总和.而会展业的发展所依赖的支柱性产业的实力,从实际的情况来看多来自于工业,故可以用该地区的工业总产值来表示该地区工业发展水平,也就是会展业发展的产业基础.最后,鉴于我国会展业发展的现实情况,不仅交通条件的改善要依赖于城市政府的财政收入,展览场馆的建设也离不开政府的巨额投入,至于现在普遍存在的政府办展的问题,没有一定的财政收入,城市会展业的发展举步维艰. 2).商贸发展水平指标商贸发展水平体现的是一个地区现有商品流通、交易的状况.作为物质、文化交流的途径,会展业的发展必须有一定区域商贸发展水平为基础.我们选取批发零售贸易业商品销售总额作为城市商贸发展水平的指标,以反映批发零售贸易企业在国风市场上销售商品以及出口商品的总量.3).会展业发展水平指标我们选取国际展览会平均展览面积体现会展业发展的基础和现实水平.上海的展览会数量有所减少,但其平均规模都在不断提升.选取国际展览会平均展览面积更能体现上海会展业会展质量的提高.4).社会事业发展水平指标我们选取上海市国民经济结构中的第三产业的比重,来体现上海市第三产业发展水平;选择上海市当年的技术合同成交额来体现城市的科技水平.5).地理区位条件指标可根据城市行政级别和周边城市经济实力来体现地理区位条件指标,上海的此指标可假设不变.6).区域交通条件指标城市的交通便利的状况主要体现在城市物资、人员流动的情况之中,因此可用城市货运总量和客运总量来量化区域交通条件指标.7).旅游业发展水平指标旅游业与会展业关系最为密切,城市旅游业的发展水平直接影响着会展期间参展人员的接待能力,城市的旅游资源对参展商也有着相当的影响力.因此我们选择上海市的国内旅游人数和国内旅游者消费总收入来体现城市旅游业的接待能力和质量.2、求出上海市会展业竞争力综合评价指标权重参考网上相关专家资料,并结合实际,征询经济学院教授得到相关指标打分,然后构造两两比较的判断矩阵;求得特征根和特征向量,并进行一致性检验,得到各级指标的权重如下表一:根据各级指标的权重用Excel作出其柱状图(如图1、2):图1:第一层次指标的权重图2:第二层次指标的权重(二)模型建立通过上海统计局网站公布资料和其他统计资料整理出上地区会展行业竞争力综合评价指标的各项数据(表二):表二:上海地区会展行业竞争力综合评价指标注:其实本模型只针对上海市,地理区位指数不变.归一化处理后得(表三):注:指标的标准值,实际上是对原始数据归一化处理后得到的与原始值相对应而数值在[0,1]区间内的优化值,标准值和权值的使用能使不同的指标在总指标中占有相对应的重要程度.本文使用如下的归一化处理方法:⎩⎨⎧≥=时当--时=当min min max min min X X ,)X )/(X X (X ,0X X W ij (2)上海会展业竞争力综合评价指标体系相应的数学模型如下:),...,3,2,1(1001n i W V S mj ij j i =⨯=∑= (1)根据城市会展业竞争力综合评价指标体系相应的数学模型用matlab 计算得到上海市竞争力综合评价值(表四)和对应曲线图(图2):上海地区会展行业竞争力综合评价标准化指标图2假设法预测未来的趋势设t 年的上海的会展的利润为N(t),2000年为t=0,此时利润收入为N 0, t 年的利润增长率为K (t )(单位时间内N (t )的增量与N (t )的比例系数),根据假设可得,N (t )满足的微分方程为:()()()00dNK t N t dtN N ⎧=⎪⎨⎪=⎩(2) 若增长率K (t )为常数,设K (t )≡K 0,则(2)变为()000dNK N dtN N ⎧=⎪⎨⎪=⎩(3) 解之得:()00K t N t N e = (4)表明利润收入将按指数规律无限增长(K>0).将t 为单位离散化,(4)式表明利润收入以0k e 为公比的等比例增长.因为此时K 表示天增长率,通常K 0<=1,故可用近似关系0k e ≈1+K 0,将(4)式写为()()001tN t N K ≈+ (5)通过比较(1)和(5)可知,模型(1)不过是指数增长率模型离散形式的近似表示.因此,模型(2)式比模型(1)式更广泛.假设K (t )为常数,在世博会前是合理的,但随着世博会的谢幕,国际旅游人数的减少,展馆关闭或拆迁的影响,K (t )一般不是一个常数;为此假设K(t)是一个连续函数,可构造K (t )如下:()()()01122,00,,K t T T t T K t r t s t T t T≤≤⎧⎪<<=⎨⎪-≤≤⎩(6) 其中从0到T 1为世博会开馆的初期,在这个时期利润收入按指数增长;从T 1到T 2为开馆时期,此时由于客流量被控制在一定的范围内,利润收入尚且认为变化不明显,或就没有发生变化,这一时期是很短暂的,随之而来的是世博后效应后展馆的支出函数s(t)大于世博后会展业总的经济收入函数r(t),此一时期利润开始下降.若r(t),s(t)皆为常数,则r(t)-s(t)亦为常数.则由(4)式知当r(t)-s(t)<0时,利润收入按指数律下降.将(6)式代入(2),通过MATLAB 软件求解微分方程可得从2000—2023年的会展业利的变化曲线大致为:对应的用 MATLAB 软解得到增长率K(t)的变化曲线如下:图中显示了K(t)的变化越来越慢,当达到一定程度的时候几乎不在发生变化!但由于外界的影响,K(t)会减小.注:世博会前的展馆平均面积的变化如下表:得到近几年的平均展馆的面积的变化如下图所示: 图3:世博会前的总的展馆面积的变化如下表:假设预测法模型的推广为了准确地预测会展利润收入,利用微分方程构造的数学模型虽然能够预测会展业利润收入的增长规律,但通过与实际数据拟合发现,其精度并不高.为了提高精度,构造如下模型:()1i mt i i N t c e α==∑ (7)其中m 为某个正整数,121,,...,,,...,m m C C C αα为待定常数.为了确定待定常数,利用非先行最小二乘法确定这些常数.首先,根据统计数据(上海地区)得到每年会展业的利润收入,比如01,,(1,2,...,...)i t t i i n ===相对应的利润收入为N 0,N 1,N 2,…,N n ,…,构造函数: ()21111,...,,,...,i j nm t m m i j j i f c c c e N ααα==⎛⎫=- ⎪⎝⎭∑∑ (8)通过求解下列无约束优化问题而得到实验数据11,...,,,...,m mC C αα****()11min ,...,,,...,m m f C C αα (9) 利用()1i mt i i N t C e α**==∑ (10)预测n 年之后的利润收入,例如n+1年的利润收入为()()111i mn ii N n C eα*+*=+=∑.求解无约束优化问题(9),首先求()111,...,,,...,m m f C C C αα对,…,m C 和1,...,m αα的偏导数并令其为0得:1120,1,2,...,k ji jnm t t i j j i eC e N k m αα==⎛⎫-== ⎪⎝⎭∑∑ (11) 1120,1,2,...,k ji jnm t t k j i j j i C t eC e N k m αα==⎛⎫-== ⎪⎝⎭∑∑ (12) 这是一个具有2m 个方程2m 未知量的非线性方程组.由于上述模型(9)不易求解,故将试验函数(7)简化为:()2N t at bt c =++ (13)由()00N N =知0C N *=,下面需确定出试验参数,a b ,根据已测每年的利润收入,(1,2,...)i t i i n ==,相应的利润收入分别为(1,2,...,)iN i n =利用最小二乘法确定,ab ,即构造函数(),f a b 为()()2201,ni i f a b ai bi N N ==++-∑ (14)极小化(),f a b 可得a 和b .求(),f a b 分别对a 和b 的偏导数并令其为0得()()220120100n i i ni i i ai bi N N i ai bi N N ==⎧++-=⎪⎪⎨⎪++-=⎪⎩∑∑ 即()()4320111320111n n ni i i i n n ni i i i a i b i i N N a i b i i N N ======⎧+=-⎪⎪⎨⎪+=-⎪⎩∑∑∑∑∑∑ (15) 故()()()()4320111124231112230011114232111()n nn ni i i i i i nnn i i i n nn nii i i i i n nni i i i i NN i i N N b i i i i i NN i i N N a i ii *=======*=======⋅--⋅-=⎛⎫⋅- ⎪⎝⎭⋅--⋅-=⋅-∑∑∑∑∑∑∑∑∑∑∑∑∑∑从而.()2N t a t b t c ***=++ (16)可作为t 年会展业的利润收入,因此函数可预测第n 年以后的利润收入.六、模型比较与评价数学模型一:在市场经济条件下,会展业可以以其相对优势和绝对优势,向国内或国际市场提供有效服务从而获得比其他行业更高的市场份额的能力.竞争力评价是对竞争优势的定量化描述.通过上面的数据说明了不同年份的会展业具有不同的竞争力,这种竞争力的研究不仅说明了世博会对上海会展业的影响,也对提升其竞争力、促进与推动会展城市会展经济的可持续发展有很大地启发和帮助.模型一是对上海会展业竞争力的评价.通过实例分析证明了模型的有效性.从而进一步研究方向是建立对会展企业竞争力评价模型.数学模型二:此模型不但可以用来预测每年的利润收入,而且还可以预测会展业的未来的发展趋势.通过分析数学模型可得出世博会对会展业现状,未来的影响,从而提放政府采取相应的措施来弥补会展业对上海经济产生的影响!但是该模型不能进行长期的预测,对每年的利润收入在整个过程缺乏必要确切的信息支持,特别是假设利润收入的增长率K 已不能尽用一个常数来表示,因此模型具有明显的缺点.对于本文建立的微分方程模型,其可以对利润收入进行长期预测,该模型是一个能够预测及对政府采取措施来弥补经济的发展提供可靠和足够信息的模型,但建立该模型的困难是需要具体确定增长率函数()k t 则需要大量的数据和实验来分析.而这些具体的相关的数据及其资料却很难在网上搜索到.总体来说:在上海世博会的推动下,2010年上海会展业在国民经济中的地位得到了提高,会展业增加值占GDP 和第三产业增加值的比重都在2010年得到了提高,但是“后事件效应”即在重大事件活动举办之后呈现下降的典型特点,我们预测在2011年会呈现下降趋势.但是不能否定上海世博会在上海的会展业在国民经济中的地位超常规地获得了提高的作用.由于许多重大事件活动的内部的财务、金融等数据资料很难获得,对其影响和效应进行评估变得非常困难、甚至几乎不可能进行量化计算,我们用多个分析法从多个角度进行比较、互证,得出可以自圆其说的结论.七、参考文献[1]万中,曾金平,《数学实验》,科学出版社,2001年.[2]李继玲,沈跃月,韩鑫《数学实验基础》,清华大学出版社,2004年.[3]M.Braun,微分方程及其应用,(张鸿林译)人民教育出版社,1980年.[4]孙明贵,《会展经济学》,机械工业出版社,2006[5]韩中庚,《数学建模竞赛》,科学出版社,2007[6]/中国统计局[7]/2004shtj/tjnj/tjnj2010.htm上海统计局全国的统计数据:年份国内生产总值(亿元)工业生产总值(亿元)货运总量(亿吨公里)客运总量(亿人公里)国内旅游者消费总收入(亿元)国内旅游人数(亿人次)第三产业比重(%)2000 99214.6 40033.6 1358682 1478573 3175.54 7.44 34.8 2001 109655.2 43580.6 1401786 153**** ****.37 7.84 48.2 2002 120332.7 47431.3 1483447 1608150 3878.36 8.78 45.7 2003 135822.8 54945.5 1564492 158**** ****.27 8.7 38.1 2004 159878.3 65210 1706412 176**** ****.71 11.02 40.0 2005 183217.4 77230.8 1862066 184**** ****.86 12.12 40.3 2006 211923.5 91310.9 2037060 2024158 6229.7 13.94 41.7 2007 257305.6 110534.9 2275822 2227761 7770.6 16.1 42.4 2008 300670 129112 2587413 2867892 1.1 17.12 42.9 2009 15046.45 5408.75 76967 11136 1.24 1913.5 59.4年份技术合同成交额(亿元)财政总收入(亿元)批发零售贸易业商销售总额(亿元)国际会展次数(次)2000 \ 13395.23 154.32 \ 2001 73.90 16386.04 165.68 20002002 106.16 18903.64 179.34 30002003 120.22 21715.25 174.93 \2004 142.78 26396.47 181.252005 171.70 31649.29 195.92 38002006 231.73 38760.2 203.51 \2007 344.43 51321.78 204.46 \2008 432.64 61330.35 202.84 \2009 485.75 7760.97 205.49 \上海省统计数据:年份国内生产总值(亿元)工业生产总值(亿元)货运总量(亿吨公里)客运总量(亿人公里)国内旅游者消费总收入(亿元)国内旅游人数(亿人次)第三产业比重(%)2000 4551.15 1956.66 47954 6893 802.8 0.78 50.6 2001 4950.84 2121.19 49545 6324 1009.6 0.83 50.7 2002 5408.76 2312.77 54196 7326 993.5 0.88 51.0 2003 6250.81 2865.85 58669 7212 1113.8 0.76 48.4 2004 7450.27 3492.89 63180 8968 1216.2 0.85 47.9 2005 9164.1 4129.52 68741 9487 1308.5 0.90 50.4 2006 10366.37 4670.11 72617 9619 1419.7 0.97 50.6 2007 12188.85 5298.08 78108 10371 1611.1 1.02 52.6 2008 14069.87 5576.79 84347 10927 1612.4 1.10 53.7 2009 15046.45 5408.75 76967 11136 1913.5 1.24 59.4年份技术合同成交额(亿元) 财政总收入(亿元)批发零售贸易业商销售总额(亿元)国际会展次数(次)平均参展面积(平方米)展览总面积(万平米)第三产业产值(亿元)星级酒店总收入(亿元)2000 0.15085 1752.69 0.750985 89.12 2001 0.216715 1995.62 0.806268 278 0.58 162 2 728.94 94.23 2002 0.245417 2202.25 0.872743 314 1 316 3 038.90 97.95 2003 0.291471 2828.87 0.851282 306 1.36 417 3 404.19 96.91 2004 0.350508 3591.73 0.882038 202 1.51 306 4 097.26 139.69 2005 0.473054 4095.81 0.953428 276 1.36 376 4 620.92 152.54 2006 0.703119 4798.93 0.990364 295 1.47 434 5 244.20 154.11 2007 0.883191 7310.26 0.994988 309 1.54 475 6 408.50 159.7 2008 0.99161 7532.91 0.987104 294 2.03 597 7 350.43 154.59 2009 0 7760.97 1 243 2.33 566 8930.9 131.53。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年四川大学数学建模暑期模拟竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):36所属学校(请填写完整的全名):四川大学参赛队员(打印并签名) :1. 朱名发2. 杨博3. 刘娜日期: 2010 年 8 月 30 日林区汽车修理网的优化布局模型摘要本文以图论[1]、运筹学[2]理论为基础,针对不同情况下大修厂布局规划问题分别建立优化模型,提供了合理的大修方案,使得林区整体经济效益最优。
因为在模型建立与求解过程中,多处用到各厂点间最小运送费用,所以在优化模型建立之前,我们模仿最短路径问题,建立图论模型,利用弗洛伊德算法,通过matlab编程求得了各厂点间最小运费流。
然后,根据题目要求分别建立5个优化模型,得到5种优化方案。
对问题(1),我们采用分治策略,先对各协作区分别建立整数规划子模型,并分别求得最优解,然后综合各子模型求得整个林区的最优解。
最后,我们通过最小元素法和位势法对结果进行了验证,得到总费用为6188300元。
对问题(2),将林区看成一整体,建立整数规划模型。
为了验证模型的有效性,我们引入一个虚拟点0,该点的汽车数设为林区生产规模总数与林区汽车总数的差值,此处为1400-1170=230,设该点到各厂点的单位修理成本均为9900元(保证是所有单位成本(含运费)中最高的)。
用最小元素法和位势法同样可以求出最优方案,得到的方案中只有林业局(12)的大修厂是闲置的,因此我们建议关闭该大修厂,此方案总费用为6141350元。
对问题(3),把拟定扩建厂点的生产规模作相应的扩大处理,虚拟点的汽车数增加到230+805=630,其余解法与问题2情况相同,进而求得最优解。
结果表明,此条件下应该关闭编号为(1)(5)(6)(11)(12)(15)的林业局大修厂,此方案的总费用为5896800元。
对问题(4),在模型(2)的基础上增加0—1变量,建立0—1规划模型,得到第1小问题的最优解,即最小总费用为5770950。
然后,模仿自由分配模型,假设所有厂点的生产规模都不受限制,得到林区大修厂点布局规划的最优方案,并对其灵敏度进行了详细分析。
在此方案中,整个林区车辆的大修工作,全部集中在编号为(3)(8)(14)(18)的四个厂点完成,其它厂点全部关闭。
其中(3)(8)(14)三个厂点的生产规模分别从原来的40、200、180增加到270、500、345,而(18)厂点应当保持原有生产规模不变,总费用为5639450元。
最后,通过数形结合的方法,我们对这五种大修方案进行了对比分析,并给出了合理评价,同时结合实际情况对模型进行了优化推广。
关键字:Floyd算法、整数规划模型、最小元素法、位势法、最小运费流目录1 问题的重述 (4)2 问题的分析 (4)3 模型的假设 (5)4 符号的说明 (5)5 模型的准备 (6)5.1 最小运费流 (6)5.2 题中表1数据处理 (7)6 模型的建立与求解 (9)6.1 问题(1)的模型建立与求解 (9)6.2 问题(2)的模型建立与求解 (13)6.3 问题(3)的模型建立与求解 (15)6.4 问题(4)的模型建立与求解 (16)7 模型的结果分析 (21)8 模型的推广与评价 (22)9 参考文献 (23)10 附件 (23)10.1 附件Ⅰ (23)10.2 附件Ⅱ (24)10.3 附件Ⅲ (26)10.4 附件Ⅳ (26)10.5 附件Ⅴ (28)1 问题的重述在林业生产中,汽车是主要的运输工具。
为了确保汽车在使用中有良好的技术状态和较长的使用寿命,需定期对汽车保养与维修,大修是重要的一个环节。
但目前各林业局都设有大修厂,由于厂点多、规模小、技术落后等原因,导致了大修成本高、质量低等问题。
现需对林区的大修厂作出合理布局,使林区整体经济效益最优。
题目中,给出了某林区某年各大修厂的产量及成本,也给出了某林区各大修厂的现有生产规模和车辆数。
题目还给出了此林区18个林业局的分布图,图中各线段上的数字是两林业局间的距离(单位:公里)。
当把一个林业局的汽车送到另一个林业局大修时,每辆车的运送费(双程)为:公路每公里8元,铁路每公里5元。
假设每辆汽车一年大修一次,不考虑关闭、扩建大修厂的费用。
题目要求分别对以下几种情况求出大修方案,作出大修厂的布局规划。
分协作区大修不分协作区大修(整个林区)拟定对林业局(2)、(5)、(8)、(14)、(16)大修厂进行扩建,使生产规模分别增加80辆。
集中到问题3中拟定的两个厂点大修是否更好?给出此厂点和生产规模。
并问是否有更好的建议。
2 问题的分析由题意可知,为了使林区整体经济效益最优,一方面应当使每辆车的修理费用最少;另一方面还要调整厂点布局,使得厂点数量适当减少,生产规模适当扩大。
在分协作区大修的情况下,各区的汽车都在该区内部的厂点维修。
规划的时候,可以先求出此区内总生产规模与总汽车数的差值,若差值小于该区内任意一厂点的生产规模,那么此区内所有厂点都不能关闭;若差值不是比所有厂点的生产规模都小,则此区生产规模不大于该差值的大修厂有可能被关闭,此时需要求出该区汽车大修的最优方案以确定是否要关闭某些大修厂,可以利用最小元素法求出该区车辆大修方案的基可行解,再用位势法求出最优解,若最优解中有未参与修车的大修厂则将其关闭,当然我们也可通过建立整数规划模型,利用LINGO 编程求解。
在不分协作区大修的情况下,可以直接用最小元素法和位势法求出最优解,最优解中闲置的大修厂应当关闭。
对部分大修厂进行扩建的最优解法也是如此,只需在求解时将扩建的大修厂的生产规模相应增大。
对于集中到林业局(2)、(5)、(8)、(14)、(16)中两个点的情况,可以设置五个0-1变量利用LINGO求出最优解,再与之前的方案比较谁更好。
探讨更好的布局规划时,由于各大修厂可以无限制扩建,因此可对每一个林业局选择单位成本(含运费)最低的大修厂,将所有的汽车全部送到该厂大修,这样得到的方案就是最优方案。
3 模型的假设1)根据题目假设,我们认为每辆汽车一年大修一次,并且不考虑关闭、扩建大修厂的费用;2)假设公路运输与铁路运输的转换过程不会影响运输成本,两种运输方式均能正常进行,不会存在运输故障,交通路线保持不变;3)假设各林业局厂点大修的单位成本每年都保持一样,并且认为与题中表1给出的对应单位成本始终一致;4)考虑小规模、厂点多而分散的布局方式,对林区整体经济效益带来的负面影响。
我们认为适当扩大产生规模的集中化布局方式,更有利于林区整体经济效益的提高。
4 符号的说明1):第i个大修厂的现有汽车数量(i=1,2,...18);2):第i个大修厂的现有生产规模(i=1,2,...18);3):第i个大修厂的单位成本(i=1,2,...18);4):i厂单位汽车到j大修厂修理最少路费(i=1,2,..18;j=1,2,..18);5):i厂单位汽车到j大修厂修理的总花费,包括路费及对应的大修成本(i=1,2,..18;j=1,2,..18)6):i厂汽车到j大修厂修理的汽车数量(i=1,2,..18;j=1,2,..18)7):i大修厂修理汽车的总数量(i=1,2,..18);8)X j:变量,在求解第四问时用到,为1表示该厂不关闭,为0表示该厂关闭;9)Max: 表示生产规模无穷大,在第四问求两个集中点不限制生产规模时用到,实际用时可以取为现有汽车总数1170;10)S:表示在给定的条件下,林区整体最少费用;11)S i: 表示分区协作条件下,第i区的最少费用。
5 模型的准备5.1 最小运费流在汽车的大修处理过程中,每个林业局的汽车都有两种可能的处理方式:方式一,在本林业局内部分进行,这种情况下只需要大修成本即可;方式二,到其它林业局修理,这时候不仅需要大修成本,也需要运送费用,而且到不同的林业局运送费用不同,大修成本也各不相同。
这样一来,就可能得到多种处理方法,这些方法需要的费用却各不相同。
决策者应当从中选择一种最优的处理方法,使得费用最低,因此,我们首先应该求得的就是各个林业局之间的最小运送费用。
为了更好的用图论[1]方法解决问题,我们将各林业局的位置及它们之间的交通关系通过一个无向赋权图来表示,如图5.1所示。
在此无向赋权图中,连通的相邻林业局之间通过直线连接,直线上的权值表示这两个林业局之间每辆车的运送费(双程)。
建立这个关系网后,我们可以利用弗洛伊德Floyd算法,建立关于汽车运送费用的最短路径模型。
这里的最短路径,我们定义为:路径L(i,j)表示的是林业局i的每一辆车送到林业局j进行大修处理所需要的最小总运送费用。
求最短路径的算法描述如下:根据图5.1建立关于各个林业区之间运送费用的赋权邻接矩阵D;用D(i,j)表示林业区i到林业区j的运送费用;通过状态转移方程进行循环求解,当k,i,j 都从1遍历到18以后,得到的矩阵D,即为我们所要的最短路径矩阵。
具体程序实现见【附件Ⅰ】,程序运行结果见【附件Ⅲ】的表10-3-1。
图5.15.2 题中表1数据处理为了便于建模时的对比分析及判断,我们画出题目中表一给出的各厂点大修单位成本及产量图普分析如图5-2-1和5-2-2。
图5-2-1图5-2-26 模型的建立与求解6.1 问题(1)的模型建立与求解6.1.1 模型Ⅰ的建立在分协作区的条件下,各林业局厂点只能在给定的区域内相互协作修理本区车辆。
要使林区整体经济效益最优,可以采用分治策略,首先分别对各区进行最优化处理,然后得到此约束条件下的一个整体最优解。
首先,针对每个区,建立一个整数规划子模型。
在每个子模型中,我们都将该区总花费作为目标函数,求出此目标函数的最小值。
将这些子模型综合起来,得到关于林区整体优化问题的一个整数规划模型,我们将它记为【模型Ⅰ】。
s等于该区所有汽车的修理费之和。
而在第i(i=1,2,3,4,5)个区中,总花费i每一辆汽车可以到该区的任一大修厂修理,这就相当于一个最优分配问题,其目标是:如何合理的分配该区内各厂点修车情况,使此区总花费最少。
其中,每一辆汽车的修理费C ij = 最少路费L ij + 所去修理厂的单位成本C j,而最小路费在模型准备阶段最小运费流中已经求得。
