2021国考笔试刷题预测 模拟预测-数资(全部讲义+笔记) (4)
2021行测笔试刷题预测 真题组卷-数资(讲义+笔记) (3)

启智职教的店资料分析第一篇2016 年,S 省建筑业增加值共完成 895.6 亿元,同比增长 5.7%,占 GDP 的比重上升,达到 6.9%,比上年提高了 0.3 个百分点。
2016 年,全省有工作量的总承包和专业承包建筑业企业 2532 家,完成建筑业总产值 3318.5 亿元。
其中,省内产值完成 2064.7 亿元,同比增长 9.4%,增速比上年提高 21.3 个百分点;省外完成产值 1253.8 亿元,同比增长 20.1%,增速比上年提高 11.4 个百分点。
2016 年,全省建筑业直接从事生产经营活动的平均人数达到 112.3 万人,比上年增加 12.8 万人,同比增长 12.8%。
其中工程技术人员达到 12.5 万人,比上年增加 0.5 万人,同比增长 4.5%;一级建造师 0.8 万人,比上年增加 0.1 万人,同比增长 11.4%。
【注意】第一篇是综合类材料,文字+图表,建议先花 10~20 秒的时间浏览一下材料,从每一段中找出 1~2 个标志词,第一段:2016 年,关于建筑增加值;第二段:2016 年,关于建筑业企业数量和总产值;第三段:时间不变,和人数相关。
图表:看标题,包含总产值、增加值,GDP 比重等。
116.2016 年,S 省平均每家有工作量的总承包和专业承包建筑业企业完成产值约:A.1.1 亿元B.1.3 亿元C.1.5 亿元D.1.7 亿元【解析】116.现期时间+平均,现期平均数问题,平均数=产值/家数,对应材料第二段,直接代入数据:3318.5/2532,简单的一步除法,观察选项,选项首位相同,次位差 3-1=2>首位 1,首位商 1,次位商 3,对应 B 项。
【选 B 】117.2016 年,S 省有工作量的总承包和专业承包建筑业企业完成省外产值比 2014 年高约:A.153 亿元B.210 亿元C.293 亿元D.407 亿元【解析】117.方法一:省外产值对应产值,对应文字部分第二段,已知 201 6 年完成省外产值,问 2016 年比 2014 年高多少,做差即可。
2021国考笔试特训预测 方法精讲-资料分析 (全部讲义+笔记) (4)

方法精讲-资料 4(笔记)第九节特殊增长率【注意】一般增长率是指相邻的两个年份的增长率,如 2016 年比 2015 年的增长率,或是 2013 年比上年的增长率。
一、间隔增长率【例 1】(2019 广东)2018 年,我国全社会用电量 68449 亿千瓦时,同比增长 8.5%,增幅同比提高 1.9 个百分点。
具体来看,第一产业用电量 728 亿千瓦时,同比增长 9.8%;第二产业用电量 47235 亿千瓦时,同比增长 7.2%;第三产业用电量 10801 亿千瓦时,同比增长 12.7%;城乡居民生活用电量 9685 亿千瓦时,同比增长 10.4%。
2018 年,我国全社会用电量较 2016 年增加了约:A.13.7%B.15.7%C.17.9%D.19.9%【解析】例 1.“增加+%”,增长率计算,问 2018 年比 2016 年增长了多少, 中间隔了一个 2017 年,属于间隔年份求增长率,是间隔增长率问题。
公式:r= r 1+r 2+r 1*r 2,r 1 和 r 2 分别对应 2018 年和 2017 年的增速。
“2018 年,我国全社会用电量 68449 亿千瓦时,同比增长 8.5%,增幅同比提高 1.9 个百分点”,r 1 比 r 2多了 1.9 个百分点,所以 r 2=r 1-1.9%=8.5%-1.9%==6.6%,代入公式:8.5%+6.6%+ 8.5%*6.6%=15+%。
【选 B 】【注意】刚开始做题一定要按部就班,只有把基础打好了,学会了走路,才能跑起来。
题目做的越多,速度提起来不是问题。
(2)结合选项或百化分。
如28%*26%,将百分数转化为分数,26%≈25%=1/4,原式≈28%*1/4=7%,乘积只需要保留一位有效数字即可。
5.练习:(1)8%+5%+8%*5%≈13%。
(2)18%+5%+18%*5%=23%+18%*1/20=23+1%-=24%-。
(3)28%+25%+28%*25%=28%+25%+28%*1/4=28%+25%+7%。
2021国考笔试特训预测方法精讲-数量关系与资料分析 (全部讲义+笔记) (4)

方法精讲-数量 4(笔记)启智职教的店第八节容斥原理【知识点】1.两集合容斥原理。
(1)识别:多主体(两主体)、有交叉。
(2)公式:A+B-A∩B=总数-A、B都不满足个数。
(3)公式推导:如图所示,圈A和圈B,中学学的几何问题,就是求两个圈覆盖的面积,A+B,多加了中间相交的部分,所以减去A∩B,则等式可写为:A+B-A∩B=总-空白。
公务员考试中会把面积变成一些条件,例如满足条件1 的、满足条件2的、两个条件均满足的等。
(4)例如:我们班在线听课的有150人,有钱的有90人,任性的有70人,没钱不任性的有3人,求有钱任性的人数?答:该题为容斥原理问题,有钱的为90人,任性的有70人,“有钱的”为条件A,“任性的”为条件B,设有钱任性的为x人,根据公式B=总数-A、B都不满足个数,代入数据得90+70-x=150-3。
2.三集合容斥原理(一会讲)。
【例 1】(2019 江苏)市电视台向 150 位观众调查前一天晚上甲、乙两个频道的收视情况,其中 108 人看过甲频道,36 人看过乙频道,23 人既看过甲频道又看过乙频道,则受调查观众中在前一天晚上两个频道均未看过的人数是:A.17B.22C.29D.38【解析】例 1.“108 人看过甲频道,36 人看过乙频道”,出现两个主体,且两主体有交叉,属于两集合容斥原理问题,公式:A+B-A∩B=总数-都不满足的,代入数据,108+36-23=150-x,计算时结合选项,选项尾数不同,考虑尾数法, 8+6 尾数为 4,4-3 尾数为 1,则左边尾数为 1,右边 10-9 尾数才为 1,对应 C 项。
【选C】【注意】考试中一旦考查容斥原理问题,必须要拿分。
【例 2】(2018 广州)篮子里有苹果和梨两种水果若干个,将这些水果分发给 13 个人,每人最少拿一个,最多拿两个不同的水果。
已知有 9 个人拿到了苹果,有 8 个人拿到了梨,最后全部分完。
那么,有多少人只拿到了苹果?A.4B.5C.6D.7【解析】例 2.问“只拿到苹果”“已知有 9 个人拿到了苹果,有 8 个人拿到了梨”出现两个条件,总共有 13 人,肯定重复交叉,属于容斥原理问题。
2021国考笔试预测强化冲刺-数资(讲义 笔记) (2)

强化冲刺-数资 2(笔记)考点二:平均考点题量比较多,相对比较重要,需要认真复习。
【知识点】平均:考点题量比较多,相对比较重要,需要认真复习。
现期平均数:1. 题型识别:实践材料与材料时间一致+平均(均/每/单位),例如:单位面积产量=产量/面积。
比重的问题一般会出现“占”,谁占谁或谁是谁的占比,或者 A/B 的形式或者答案出现%。
2. 题型 1:平均数=总数/个数,已知几个数求平均数=几个数之和/数的个数。
3. 题型 2:后/前。
4. 举例:(1)单位面积产量=产量/面积,后除前; (2) 人均收入=收入/人数。
(3) 平均每人次旅客运输距离=旅客周转量/客运量。
2015 年我国钟表全行业实现工业总产值约 675 亿元,同比增长 3.2%,增速 比上年同期提高 1.7 个百分点。
全行业全年生产手表 10.7 亿只,同比增长 3.9%,完成产值约 417 亿元,同比增长 4.3%,增速提高 1.9 个百分点;生产时钟(含钟心)5.2 亿只,同比下降3.7%,完成产值 162 亿元,同比下降 4.7%,降幅扩大 1.3 个百分点;钟表零配件、定时器及其它计时仪器产值 96 亿元,同比增长 14.3%,增速基本保持上年水平。
【例 1】(2017 国考)2015 年钟表全行业平均每制造一只手表,能实现约多少元的产值?A.36B.39C.42D.63启智职教的店【解析】例 1.出现“平均每”、手表、产值,用产值/手表个数=417 亿/10.7 亿。
注意“675 亿元”是钟表全行业实现工业产值,不是手表产值,注意对应关系。
417/10.7 首位商不到 4,排除 C、D 项,A、B 项首位相同,次位差=首位,保留三位相除。
或者大概相除 410+/100+接近 4,但是商不到 4,对应 B 项。
【选B】【例 2】(2019 上海)2016 年我国城市天然气用气人口中,平均每人每月使用天然气约()立方米。
A.32B.65C.167D.380【解析】例 2.方法一:出现“平均每”,问“平均每人每月”平均了两次,需要(天然气总量/ 人数)/ 月数= 天然气总量/(人数* 月数)=1171.73/(30855.57*12),选项差距大,采用估算,原式≈1171 万/36 万+,首位只能商 3,比3 略多一点,对应 A 项,由于A、D 项的第二位相差很远,无需代入单位细算。
公考行测笔试- 模拟预测-数资 (行测讲义+笔记) (1)

模拟预测-数资(讲义)行测预测卷(地市级一)数量关系61.某人数不到一百人的合唱团参加比赛,要求每排站的人数必须相同。
如果排成 7 排,则缺少 1 人。
如果排成 9 排,则多出 6 人无法排到队伍中。
问如果排成正方形实心方阵,则可能有几人不能参加比赛?A.5B.6C.7D.862.完成一项工程,甲队需要 15 天,乙队需要 25 天,丙队需要 30 天。
如果甲、乙两队合作,则效率都降低 1/4;如果甲、丙两队合作,则效率都降低 1/15;乙、丙两队合作,则效率都提高 2/11。
现在计划 13 天完成该工程,问至少有多少天是两队合作施工?(不存在三队一起合作的情况)A.5B.623C.73D.10463.10 名同学参加某竞赛,考场有从前到后编号依次为 1-10 的十个座位。
若甲、乙、丙、丁 4 名同学的座位号必须构成公差为 2 的等差数列,则参加竞赛的10 名同学共有多少种安排座位的方式?A.不到40000B.40000~60000C.60001~80000D.超过 8000064.现有一盆康乃馨,两盆百合,三盆月季,6 盆花卉的颜色大小均各不相同。
现将 6 盆花卉随机摆放成一横排,则同一种类的花卉都不相邻的概率是:A.9/10B.1/9C.1/10D.1/665.小张今年(2019 年)二十多岁,小李今年不到十岁,两人今年的年龄都恰好等于自己出生年份的数字之和。
问今年小张的年龄是小李的几倍?A.5B.4C.3D.266.若商店按定价出售 A、B 商品各一件,分别可以获得 35 元、25 元的利润。
现在 A 商品按比定价少 20%的价格出售,B 商品降价 17 元出售,则出售 A 商品 6 件所获得的利润与出售 B 商品 9 件所获得的利润相同。
A 商品的进价为每件多少元?A.60B.70C.80D.9067.如图所示,在五边形 ABCDE 中,∠A=90°,∠ABE=∠C=60°,BE=DE=6 厘米。
2021国考行测模考解析课-判断 (讲义+笔记) (4)
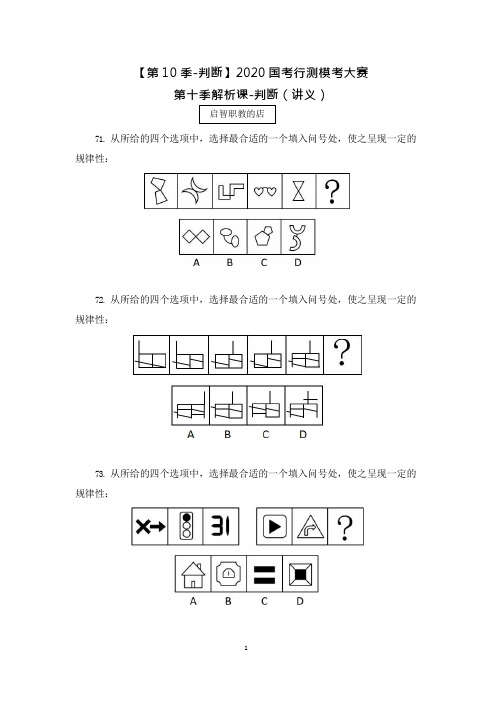
【第 10 季-判断】2020 国考行测模考大赛第十季解析课-判断(讲义)71.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:72.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:73.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:启智职教的店74.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:75.左边给定的是正方体的外表面展开图,下面哪一项能由它折叠而成?76.左边为同样大小的正方体堆叠而成的多面体,该多面体可拆分为①、②、③和④共 4 个多面体的组合,请问不能将下列哪一项填入问号处?77.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:78.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:79.把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:A.①③④,②⑤⑥B.①③⑥,②④⑤C.①④⑤,②③⑥D.①④⑥,②③⑤80.把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:A.①④⑤,②③⑥B.①③⑥,②④⑤C.①④⑥,②③⑤D.①⑤⑥,②③④81.流动餐桌是指由食品采购、加工、服务人员组成的团队,在宴席举办者提供的场所为家庭聚餐提供餐饮服务的具有营利性质的行业,是餐饮服务业的新生事物。
流动餐桌改变了传统自办聚餐模式,尤其是农村家庭聚餐方式的改革。
根据以上定义,下列选项属于流动餐桌的是:A.小明上市重点高中期间,他的父母在学校旁开了一家“小餐桌”,有 20 名学生在那里解决一日三餐的问题B.从传媒行业退休的老李回到农村老家,自己组建了一个礼仪团队,专门主持农村家庭婚丧嫁娶等宴席活动C.小赵在市里开了一家餐饮公司,他发现农村的年味更加浓厚,他便从公司抽调人力,上门给农村家庭制作年夜饭D.村委会组成了“空巢群体”公益关爱机构,每日餐时,都会有志愿者团队前往空巢老人、重病老人家中为其做饭82.补偿教育是指针对在经济上和社会地位上处于不利地位的、没有机会享受正规教育的、丧失了良好教育权利的少数民族儿童进行的教育。
2021国考笔试刷题预测 模拟预测-判断(全部讲义+笔记) (1)

模拟预测-判断(全部讲义)启智职教的店2020 年中央机关及其直属机构录用公务员考试行测预测套卷(地市级一)一、图形推理。
请按每道题的答题要求作答。
请开始答题:71.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
72.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
73.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
74.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
75.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
76.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
77.左边给定的是正方体的外表面展开图,右边哪一项能由它折叠而成?78.把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:A.①②④,③⑤⑥B.①③⑥,②④⑤C.①③⑤,②④⑥ D.①⑤⑥,②③④79.把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:A.①②③,④⑤⑥B.①②⑥,③④⑤C.①③④,②⑤⑥ D.①④⑥,②③⑤80.把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:A.①②③,④⑤⑥B.①②④,③⑤⑥C.①④⑥,②③⑤ D.①③⑤,②④⑥二、定义判断。
每道题给出一个或者多个概念的定义,然后分别列出四种情况,要求严格依据定义选出最符合或最不符合该定义的答案。
请开始答题:81.相关谬误是论证者利用语言表达情感的功能,以言词来激起人们心理上的恐惧、敌意、怜悯或热情,引诱人们接受其论题。
其中诉诸权力是指论证者借助强力或威胁,迫使人接受其论题;诉诸权威是在论证中以本人或他人的权威为根据来论证某一论题;诉诸无知是以人们对某一个命题的无知为根据,从而断言该命题是真的。
根据上述定义,下列属于诉诸无知的是:A.鬼是存在的,因为很多人都说见到过鬼B.“地心说”是不能怀疑的,因为亚里士多德就是这么认为的C.学生李某数学没考好,他找到老师说:“如果您给我不及格,我的奖学金就没了”D.鬼是存在的,因为还没有人能够证明鬼是不存在的82.代理是指在授权范围内进行对被代理人直接发生法律效力的法律行为。
2021年省考行测笔试专项点拨-数资-资料分析(讲义+笔记) (4)

【名师专项点拨-数资】资料分析 4(讲义)一、平均数问题1.现期平均数【例 1】(2021 国考)2020 年1-2 月,我国境内投资者共对全球 147 个国家和地区的 1733 家境外企业进行了非金融类直接投资,累计实现投资 1078.6 亿元人民币,同比增长 1.8%。
2020 年 1-2 月,我国境内投资者对每个当期内产生非金融类直接投资的境外企业的非金融类直接投资额均值约为多少亿元人民币?A.1.6B.1.3C.0.8D.0.6【例 2】(2020 北京)2016 年末,A 自治区城镇人口为 1542.1 万人,城镇化率(城镇人口占总人口比重)为 61.2%。
2016 年末A 自治区城镇人均居住面积达 32.20 平方米,比 1978 年末增长了5.5 倍;农村牧区人均居住面积达 27.40 平方米,比 1985 年末增长 103%。
2016 年末A 自治区城镇人口总居住面积约为多少亿平方米?A.3B.5C.7D.9【例 3】(2021 北京)2016—2018 年我国茶叶月均出口量约比 2013—2015 年间高多少万吨?A.3.2B.1.5C.0.8D.0.3【例4】(2021 上海)2019 年7—9 月,日均湿垃圾分出量约为多少吨?A.8803B.8702C.9200D.8800【例 5】(2021 国考)表中所列 2019 年地铁客运量超过 10 亿人次的城市中,2019 年平均每条地铁运营线路长度超过 40 公里的城市有几个?A.1B.2C.3D.4【例 6】(2017 联考)2015 年一般公共预算收入高于表中七个省(市)平均值的有:A.上海、安徽、福建、江西B.江苏、浙江、安徽、山东C.上海、江苏、浙江、山东D.安徽、福建、江西、山东【例7】(2019 广东)2014-2017 年,A 省平均每年新增申报无公害农产品产地认定()个。
A.184B.202C.221D.230【例 8】(2020 联考)平均通勤距离超过了四个城市平均值的有:A.一个城市B.两个城市C.三个城市D.四个城市【例 9】(2019 四川)2018 年4 月手机产量前 12 位的省市中,4 月手机产量高于 1~3 月平均水平的有几个?A.5B.6C.7D.8【例 10】(2019 江苏)2018 年国家统计局组织开展了第二次全国时间利用的随机抽样调查,共调查 48580 人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模拟预测-数资 4(笔记)行测预测套卷(副省级二)数量关系【知识点】不定方程:ax+by=c。
方法:1.奇偶特性。
(1)ax+by=M,当a、b 恰好一奇一偶时,考虑奇偶特性。
(2)【例】3x+4y=25,x=?(x、y 均为正整数)A.2B.3C.4D.5答:25 是奇数,4y 是偶数,奇数+偶数=奇数,所以 3x 一定是奇数。
要想3x 为奇数,3 是奇数,则 x 一定是奇数,排除 A、C 项;剩二代一,满足就选,不满足选另一个。
选择 B 项。
2.倍数特性(等式左右两边有共同的因子)。
(1)问某个量的最值:ax+by=M,当 a 或b 与M 有公因子时,考虑倍数特性。
【引例1】7x+3y=60,y 最大为多少?(x、y 均为正整数且不为0)A.12B.13C.16D.18答:60、3y 都可以被 3 整除,则 7x 也是 3 的倍数,7 不是 3 的倍数,则 x 是 3 的倍数。
不定方程的最值中心思想就是此消彼长,问 y 的最大值,y 越大,则 x 越小,即 x 越小越好,x=3、6、9……,最小选 3,x=3 时,解得 y=13,有公因子的方程,用约分。
选择 B 项。
(2)问整体量的最值:如问“x+y”最大是多少,方法是凑,求什么凑什么。
【引例 2】7x+3y=60,x+y 最大为多少?(x、y 均为正整数且不为 0)A.12B.13C.16D.18答:7x+3y=60→4x+3x+3y=60→4x+3(x+y)=60,要让 x+y 最大,则让 x 最小。
求什么凑什么,谁少就凑谁,就像一个木桶能盛多少水,取决于最短的木板,还像行测考试能考多少分,往往取决于你最不擅长的部分(数量)能考多少分。
60、3y 是3 的倍数,则 7x 是3 的倍数,7不是3 的倍数,则 x 是3 的倍数,x=3、6、9……,x 最小是 3,当 x=3 时,约分得,7+y=20,解得 y=13,x+y=3+13=16。
选择 C 项。
(3)问差的最值:如问“y-x”最大是多少,如我的体重-你的体重,最大是多少斤(我比你多多少斤),则我要使劲吃、你要减肥,即前面尽量大、后面尽量小,你的分数-对手的分数如何最大,则你考得尽量多、他考得尽量少。
【引例3】7x+3y=60,y-x 最大为多少?(x、y 均为正整数且不为 0)A.10B.11C.12D.13答:60、3y 是3 的倍数,则 7x 是3 的倍数,7 不是3 的倍数,则 x 是3 的倍数,x=3、6、9……,x 最小是 3,当 x=3 时,解得 y=13,y-x=13-3=10。
选择A 项。
(4)梳理:①问某个量的最值,不定方程的核心思想是此消彼长。
②问整体量的最值,关键是凑。
③问差的最值,让前面的尽量大、后面的尽量小。
3.尾数法(x、y 的系数的尾数为 0)。
(1)ax+by=M,当 a 或 b 尾数是 0 时,考虑尾数。
(2)【例】37x+20y=271,x=?(x、y 均为正整数)A.1B.3C.2D.4答:可以用奇偶性,奇数+偶数=奇数,要让 37x 奇数,则x 是奇数,排除 C、D 项,代入排除就可以。
尾数法:当系数的尾数是 0 时,用尾数法,y 是整数,则20y 尾数是 0,37x+尾数 0=尾数 1,3*7=尾数 1,只有 B 项与37 相乘尾数是 1。
选择 B 项。
4.代入排除。
5.大小特性。
61.老张每天能加工 3 个 A 零件或 9 个 B 零件,小李每天能加工 2 个 A 零件或 7 个B 零件。
两人 20 天共加工 A 零件和 B 零件 150 个,并且每人都有加工 A、B 零件。
则两人加工的 B 零件一共有多少个?A.70B.73C.77D.80【解析】61.问 B 零件,设老张加工 B 零件用 x 小时,总共是 20 天,则老张加工 A 零件用(20-x)天;设小李加工 B 零件用 y 天,则小李加工 A 零件用(20-y)天。
根据题意列式子,3*(20-x)+9x+2*(20-y)+7y=150,化简可得 6x+5y=50,属于不定方程,方法有 5 种:奇偶、倍数、尾数、代入排除、大小等。
50、5y 能被 5 整除,则 6x 也是 5 的倍数,6 不是 5 的倍数,则 x 是5 的倍数,x 最小是5,当 x=5 时,约分约掉 5,变为 6+y=10,解得 y=4,9*5+4*7=45+28=尾数 5+尾数8=尾数 3,对应 B 项。
【选B】【注意】本题重点看问法,问 B 零件,求出时间就可以。
根据题意列方程,计算时该约分约分。
【知识点】牛吃草:1.基本公式 y=(N-x)*T,N 是消耗,x 是指生长。
假设有一片草地,有一群牛吃草,每天消耗 10,每天生长 8,则额外消耗的量=10-8,y 是原有草量的消耗量,则 y=(10-8)*T。
2.各字母代表:(1)y:代表原有存量的消耗量(比如:原有草量吃完啦)。
(2)N:促使原有存量消耗的变量(比如:牛数)。
(3)x:存量的自然生长速度(比如:草长速度)。
(4)T:时间。
3.【引例 1】一片草地每天都以平均速度生长,已知这片草地可以供 25 头牛吃 12 天,或者供 40 头牛吃 6 天。
(1)草生长速度是多少?答:y=(N-x)*T=(N-x)T 的模式,这种模式主要是为了约分,代入数据y=(25-x)*12=(40-x)*6,约分得,50-2x=40-x,解得 x=10,草的生长速度是 10。
(2)这片草地有多少草?答:把 x=10 代入原式,y=(40-10)*6=180。
(3)问这片草地可以供 50 头牛吃多少天?答:代入公式,180=(50-10)*T,解得 T=180/40=18/4=9/2=4.5,不要计算,而是进行约分。
(4)要想 6 天,原有草,地还剩 50%,需要多少头牛?答:等式左边是原有草量的消耗量,剩余 50%,则吃了 50%,则 50%*y=(N-x)*T,90=(N-10)*6,15=N-10,解得 N=25。
(5)要想 T 天,原有草地还剩 40%,需要多少头牛?答:剩余 40%,则吃了 60%,60%*y=(N-x)*T,108=(N-10)*6,解得 N=28。
4.牛吃草归根到底就是工程问题。
多台机器、多头牛,可以赋值单个效率是1,假设吃的是 1 份,则设 x 也是份。
5.作业:(1)作业一:把不定方程最值分析三种问法整理一下。
(2)作业二:牛吃草问题整理一下。
整理完后在粉笔 APP 上有一个“数学运算”,在里面找到“牛吃草问题”,要求做完,并达到 80%(及以上)正确率。
【例 1】(2019 安徽)某河道由于淤泥堆积影响到船只航行安全,现由工程队使用挖沙机进行清淤工作,清淤时上游河水又会带来新的泥沙。
若使用 1 台挖沙机 300 天可完成清淤工作,使用 2 台挖沙机 100 天可完成清淤工作。
为了尽快让河道恢复使用,上级部门要求工程队 25 天内完成河道的全部清淤工作,那么工程队至少要有多少台挖沙机同时工作?A.4B.5C.6D.7【解析】例 1.牛吃草往往在工程问题中出现:(1)出现消耗+生长;(2)有明显排比句(不断生长)。
y=(N-x)*T,出现多台机器,每台效率为 1,则 y=(1-x)*300=(2-x)*100,解得 x=0.5,代入解得 y=150。
要想 25 天完成,则150=(N-0.5)*25,约分得,6=N-0.5,解得 N=6.5,机器是整数,至少需要 6.5 台,6 台不行,所以是 7 台。
【选D】62.某饲料加工厂开工前已囤积了一批原材料,开工后每天运进相同的原材料。
如果开动 18 台机器加工,12 天可以把原材料用完;如果开动 20 台机器加工,10 天可以把原材料用完。
现开动若干台机器,加工了 8 天后,有 5 台机器需要维护,其余机器又加工了 2 天,才把原材料用完。
则一开始开动了多少台机器加工原材料?A.21B.16C.25D.20【解析】62.有生长+消耗,y=(N-x)*T,x 是生长的意思。
则 y=(18-x)*12=(20-x)*10,约分,约去 2,则18*6-6x=100-5x,解得 x=8,代入解得 y=120。
牛吃草问题,两个问题,代入原式,设 N 台,时间是8,则120=(N-8)*8+(105-8)*2,约分得,60=4N-32+N-13,105=5N,解得 N=21,对应 A 项。
【选 A】63.一项工程由甲、乙两队承包,15 天可以完成,需支付 22500 元;由乙、丙两队承包,20 天可以完成,需支付 22000 元;由甲、丙两队承包,30 天可以完成,需支付 18000 元。
因工期需要在 50 天内结束,选择一个队单独承包的最少费用为多少?A.12000 元B.18000 元C.20000 元D.24000 元【解析】63.属于工程问题给定时间类型,要求费用,首先要知道时间,总量=效率*时间,赋值总量是 60,甲、乙时间是 15 天、则效率是 4,乙、丙时间是 20 天、则效率是 3,甲、丙时间是 30 天、则效率是 2,甲+乙=4,乙+丙=3,甲+丙=2,所以甲+乙+丙=(4+3+2)/2=4.5,解得,甲=1.5、乙=2.5、丙=0.5,不要硬算,找技巧。
15 天需要 22500 元,则甲+乙每天的费用是 22500/2=1500,乙+丙每天的费用是 22000/2=1100,甲+丙每天的费用是 600 元,则甲+乙+丙每天的费用是(1500+1100+600)/2=1600,解得,甲每天需要 500 元,乙每天需要1000 元,丙不好确认(丙每天需要 100 元,但是丙的工期是 60/0.5=120 天,超过 50 天,排除),甲单独需要的天数=60/1.5=40 天,则甲单独承包总费用=500*40=20000 ;乙单独需要的天数=60/2.5=24 天,则乙单独承包总费用=1000*24=24000,甲更便宜,最少费用是 20000 元,对应 C 项。
【选 C】【注意】本题是工程问题+经济利润的综合体,单独经济利润可以做、单独工程问题可以做,混合在一起就往后放。
64.某商品主机的成本是定价的 70%,配件的定价是 200 元,成本是 150 元。
现在把 1 个主机和 2 个配件配套卖出,以原来定价的九折售出,这样每套可获利360 元。
问主机的成本是多少元?A.1650B.1500C.1155D.1050【解析】64.单独的经济利润分析。
方法一:分为主件和配件,列表,主件:设定价是 x,则成本是 0.7x,售价为 0.9x,则利润=0.9x-0.7x=0.2x。
配件:成本是 150,定价是 200,售价是 180,则利润=180-150=30,则0.2x+2*30=360,解得 x=300/0.2=3000/2=1500,问成本,则 0.7x=0.7*1500=1050,对应 D 项。
