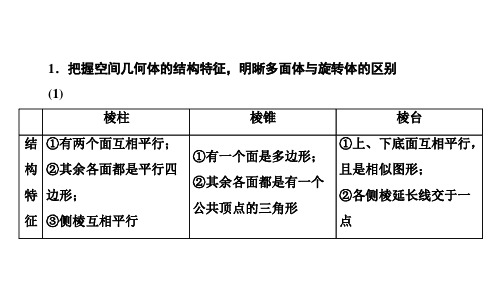
空间几何体 复习课件

2
即此正四棱台 ABCD-A1B1C1D1 的侧面积是 112。
错因分析：正四棱台的正视图与侧视图的高是正四棱台的 高，但不是其侧面梯形的高。上面的解法由于对三视图认 识不到位而导致错误。 正解：正四棱台的直观图如图所示。
由三视图可知，A1B1=B1C1=6，AB=BC=8， 取上底中心 O1，下底中心 O，连接 O1O，则 O1O=4，取 B1C1 的中
规律方法 由几何体的三视图求几何体的体积、表面积问题，一般
情况下先确定几何体的结构特征，再由三视图中的数据确定 几何体中的相关数据，代入公式求解即可。
四、球与其他几何体的组合问题
【典例4】 （2018·湖南郴州二模）底面为正方形，顶点在底面的投
影为底面中心的棱锥P-ABCD的五个顶点在同一球面上，若该棱锥的底
3
3
3
0＜h＜6，从而 V′= 26 (36-3h2)=26(12-h2)。
3
令 V′=0，得 h=2 3 或 h=-2 3 （舍）。 当 0＜h＜2 3 时，V′＞0，V 是单调增函数； 当 2 3 ＜h＜6 时，V′＜0，V 是单调减函数。 故 h=2 3 时，V 取得极大值，也是最大值。 因此,当 PO1=2 3 m 时，仓库的容积最大。
所以
S梯形BCC1B1
=
1 2
(6+8)×
17 =7
17 。
从而此正四棱台的侧面积是 28 17 。
【典例6】 一个几何体的三视图如图所示（单位：m），则该
几何体的表面积为
m3。
错解：由三视图可以得到原几何体是一个圆柱与圆锥的组合体，其表面积是 S=2π×1×4+π×12+π×2×2 2 +π×22 =8π+π+4 2 π+4π =(13π+4 2 π)(m3)。
+2S 下底面积=(1+1+2+ 2 )×2+2× 1 ×(1+2)×1=11+2 2 ，故选 B。
2
（5）有一几何体的三视图如图,则该几何体体积为( )
(A)4+ 5π (B)4+ 3π
2
2
(C)4+ π (D)4+π 2
解析：（2）由三视图可知该几何体是如图所示的几何体， 所以 V=π×12×2+ 1 ×π×12×1+2×2×1
解析：如图为该几何体的直观图，易知该几何体中有两个全等的 梯形，其中一个梯形的面积为 S= 1 ×(2+4)×2=6，故这些梯形面
2
积之和为 6×2=12。故选 B。
3.（2017·全国Ⅱ卷，文6）如图，网格纸上小正方形的边长为1，粗实线 画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后 所得，则该几何体的体积为（ B ）
3
S= 7 ·4πR2+ 3 πR2=17π。故选 A。
8
4
2.（2017·全国Ⅰ卷，理7）某多面体的三视图如图所示，其中正视图 和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视 图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯 形的面积之和为（ B ）
（A）10 （B）12 （C）14 （D）16
2
=4+ 5π ,
2
故选 A。
（3）已知圆柱的高为 2，它的两个底面的圆周在直径为 4 的同 一个球的球面上,则该圆柱的体积是( )
(A)π (B) 3π (C) π (D)6π
4
2
解析：（3）如图所示，圆柱的高为 2，它的两个底面的圆周在直 径为 4 的同一个球的球面上，所以该圆柱底面圆周半径为 r= 22 12 = 3 ，所以该圆柱的体积为 V=Sh=π·( 3 )2·2=6π。 故选 D。
点 M，BC 的中点 N，连接 MN，O1M，ON，则由于梯形 BCC1B1 是等腰 梯形，MN 即为其高。由于 M，N 分别是 B1C1,BC 的中点，可知 O1M ∥ON,且 O1M=3，ON=4，四边形 O1ONM 是一个直角梯形，过 M 作 MH ⊥ON，则 MH=O1O=4。从而 MN= MH 2 HN 2 = 16 1 = 17 ，
错因分析：解答本题失误的主要原因是未减去圆锥与圆柱重叠部分的面 积造成了重复计算。 正解：由三视图可知原几何体上部是一个圆锥、下部是一个圆柱，其表面积 是 S=2π×1×4+π×12+π×2×2 2 +π×22-π×12 =8π+π+4 2 π+4π-π =(12π+4 2 π)(m3)
答案：12π +4 2 π
第一章 空间几何体 复习课件
网络建构
知识辨析
判断下列说法是否正确（请在括号中填“√”或“×”） 1.有两个面互相平行，其余各面都是平行四边形的几何体叫做棱柱。（× ） 2.有一个面是多边形，其余各面都是梯形的几何体叫做棱台。（ × ） 3.圆锥是由一个直角三角形绕其一边旋转得来的。（ × ） 4.到定点的距离等于定长的点的集合是球。（ × ） 5.若一个几何体的三视图都是一样的图形，则这个几何体一定是球。（× ） 6.正方形利用斜二测画法画出的直观图是菱形。（ × ） 7.圆台的侧面积公式是π（r+R）l，其中r和R分别是圆台的上、下底面半径， l是其母线长。（ √ ）
条。
解析：（2）由斜二测画法可知，原图形为直角三角形，且∠B=90°， 又D为AC的中点，由直角三角形的性质可知，BD=AD=DC，即与BD的长度 相等的线段有2条。
答案：（2）2
规律方法 （1）由三视图还原几何体时，要根据几何体的正视图、侧 视图、俯视图的几何特征，想象整个几何体的特征，从而判 断三视图所描述的几何体。 （2）有关直观图的计算问题，关键是把握直观图与原图形 的联系。
8.（2016·江苏卷，17）现需要设计一个仓库，它由上下两部分组成， 上部分的形状是正四棱锥P-A1B1C1D1，下部分的形状是正四棱柱ABCDA1B1C1D1（如图所示），并要求正四棱柱的高O1O是正四棱锥的高PO1的4 倍。
（1）若AB=6m，PO1=2m，则仓库的容积是多少；
解：（1）由 PO1=2 知 O1O=4PO1=8。 因为 A1B1=AB=6， 所以正四棱锥 P-A1B1C1D1 的体积
解析：（1）由正视图、俯视图可知该几何体由半圆锥与 三棱锥构成，且有共同的顶点，中间的线是可以看得到的 为实线，所以侧视图为D项.
答案：（1）D
（2）如图所示为水平放置的△ABC在坐标系中的直观图，其中D′
是A′C′的中点，且∠ACB≠30°，∠BAC≠30°，则原图形中与线
段BD的长相等的线段有
谢谢
面边长为4，侧棱长为2，则这个球的表面积为
。
解析：正四棱锥P-ABCD外接球的球心在它的高PO1上，记为O， OP=OA=R，PO1=4，OO1=4-R， 或OO1=R-4（此时O在PO1的延长线上）。 在Rt△AO1O中，R2=8+（R-4）2得R=3， 所以球的表面积S=36π。
答案：36π
规律方法 （1）与球有关的组合体，一种是内切，一种是外接，解题时要认真分析 图形，充分发挥空间想象能力，做到以下几点： ①明确切点和接点的位置； ②确定有关元素间的数量关系； ③作出合适的截面图。 （2）一般地，作出的截面图中应包括每个几何体的主要元素，能反映出 几何体与球体之间的主要位置关系和数量关系，将立体问题转化为平面 问题解决。
解：（2）两底边中点的连线与两底垂直，因此旋转得到的几何体 是圆台。 （3）绕较长的底边所在直线旋转一周形成的几何体是一圆柱与一 圆锥组成的组合体。
规律方法 有关空间几何体的概念辨析问题，要紧紧围绕基本概
念、结构特征逐条验证，且勿想当然做出判断。
二、空间几何体的三视图与直观图 【典例2】 （1）在一个几何体的三视图中，正视图与俯视图如图所示， 则侧视图为（ ）
五、易错题辨析 【典例5】 如图所示是正四棱台（上、下底面都是正方形，且上、下底 面的中心的连线垂直于上、下底面）ABCD-A1B1C1D1的三视图。
根据图中所给数据，求这个正四棱台的侧面积。
错解：正四棱台的侧面是四个一样大小的等腰梯形。且每个梯 形的高是 4，上底是 6，下底是 8，从而 S 侧=4[ 1 (6+8)×4]=112。
真题体验
真题引领·感悟提升
1.（2016·全国Ⅰ卷，理6）如图，某几何体的三视图是三个半径相等
的圆及每个圆中两条相互垂直的半径。若该几何体的体积是 28π ，则
3
它的表面积是（ A ）
（A）17π （C）20π
（B）18π （D）28π
解析:由三视图知 7 · 4 πR3= 28π ，R=2，
83
（A）90π （C）42π
（B）63π （D）36π
解析:该几何体为下面是高为 4，底面为半径为 3 的圆的圆柱， 上面是同底且高为 6 的圆柱的一半，故 V=π×9×4+ 1 ×π
2
×9×6=63π，故选 B。
4.在封闭的直三棱柱 ABC-A1B1C1 内有一个体积为 V 的球，若 AB⊥BC，AB=6，BC=8，AA1=3，则 V 的最大值是（ B ）
三、空间几何体的体积与表面积 【典例 3】（1）某几何体的三视图如图所示,则该几何体的表面积等于( )
(A)8+2 2 (C)14+2 2
(B)11+2 2 (D)15
解析：（1）由题中三视图可知，该几何体是底面为直角梯形、高 为 2 并且侧棱垂直于底面的四棱柱，所以其表面积为 S 表面积=S 侧面积
答案：2
7.（2016·浙江卷，理11）某几何体的三视图如图所示（单位：cm），
则该几何体的表面积是
cm2，体积是
cm3。
解析：几何体为两个相同长方体组合，长方体的长宽高分别为4，2，2， 所以体积为2×（2×2×4）=32，由于两个长方体重叠部分为一个边长 为2的正方形，所以表面积为2（2×2×2+2×4×4）-2（2×2）=72。 答案：72 32