学而思勾股定理
第三节 勾股定理及逆定理的综合-学而思培优
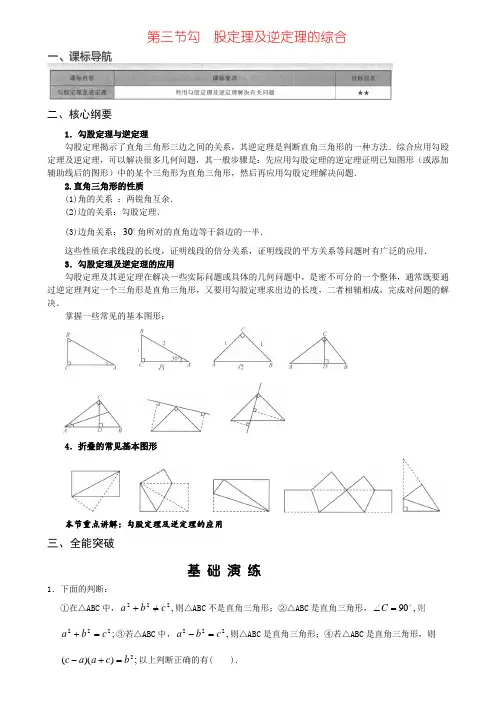
第三节勾 股定理及逆定理的综合二、核心纲要1.勾股定理与逆定理勾股定理揭示了直角三角形三边之间的关系,其逆定理是判断直角三角形的一种方法.综合应用勾殴定理及逆定理,可以解决很多几何问题,其一般步骤是:先应用勾股定理的逆定理证明已知图形(或添加辅助线后的图形)中的某个三角形为直角三角形,然后再应用勾股定理解决问题.2.直角三角形的性质(1)角的关系 :两锐角互余.(2)边的关系:勾股定理.(3)边角关系:30角所对的直角边等于斜边的一半.这些性质在求线段的长度,证明线段的倍分关系,证明线段的平方关系等问题时有广泛的应用.3.勾股定理及逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体,通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决.掌握一些常见的基本图形:4.折叠的常见基本图形本节重点讲解:勾股定理及逆定理的应用三、全能突破基 础 演 练1.下面的判断:①在△ABC 中,,222c b a =/+则△ABC 不是直角三角形;②△ABC 是直角三角形,,90 =∠C 则 ;222c b a =+③若△ABC 中,,222c b a =-则△ABC 是直角三角形;④若△ABC 是直角三角形,则 ;))((2b c a a c =+-以上判断正确的有( ).A .4个B .3个C .2个D .1个2.图17 -3—1所示是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m 和8m .按照输油中心0到三条支路的距离相等来连接管道,则0到三条支路的管道总长(计算时视管道为线,中心O 为点)是( ).m A 2. m B 3. m c 6. m D 9.3.如图17-3-2所示,在△ABC 中,,30,90=∠=∠B C AB 的垂直平分线交BC 于点D ,垂足为E ,BD= 4cm .则CD 的长为4.如图17-3-3所示,在一棵树的10米高B 处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A 处;另一只爬到树顶D 后直接跃到A 处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高 米.5..一张直角三角形的纸片,按图17-3-4所示折叠,使两个锐角的顶点A 、B 重合,若,3,30==∠AC B则DC 的长为6.如图17-3-5所示,折叠长方形的一边AD ,使点D 落在BC 边的点F 处,已知,10,8cm BC cm AB == 求△EFC 的面积.7.如图17-3-6所示,在△ABC 中,,2,30,45==∠=∠AB C B 求ABC s ∆的面积.能 力 提 升8.某市在“旧城改造”中计划在市内一块如图17-3-7所示的三角形空地上种植某种草皮以美化环境,其中20,150==∠AB A米,=AC 30米,已知这种草皮每平方米售价a 元,则购买这种草皮至少需要 元.9.如图17-3-8所示,长方形ABCD 中,,4,8==BC AB 将长方形沿AC 折叠,点D 落在/D 处,则重叠部 分△AFC 的面积是10.如图17-3-9所示,把长方形ABCD 纸片折叠,使点B 落在点D 处,点C 落在/C 处,折痕EF 与BD 交于点0,已知AB=16,AD=12,则折痕EF 的长为11.如图17 -3 -10所示,在△ABC 中,P BC AC ACB ,,90==∠ 是△ABC 内的一点,且,2,1==PC PB ,3=PA 将△PBC 绕点C 旋转后,与C AP /∆重合,连接,/PP 则=/PP BPC ∠,的度数为12.等腰三角形的一边长是12,另一边长是10,则其面积为13.如图17 -3 -11所示,公路MN 和公路PQ 在点P 处交汇,且,30=∠QPN 点A 处有一所中学,AP= 160m.假设拖拉机行驶时,周围100m 以内会受到噪音的影响,那么拖拉机在公路MN 上沿PN 方向行驶时,学校是否会受到噪声影响?请说明理由,如果受影响,已知拖拉机的速度为18km/h ,那么学校受影响的时间为多少秒?14.如图17 -3 -12所示,在一笔直的公路MN 的同一旁有两个新开发区A 、B ,已知AB=10千米,直线 AB 与公路MN 的夹角,30=∠AOM 新开发区B 到公路MN 的距离BC=3千米.(1)求新开发区A 到公路MN 的距离;(2)现要在MN 上某点P 处向新开发区A 、B 修两条公路PA 、PB ,使点P 到新开发区A 、B 的距离和最短.请你用尺规作图在图中找出点P 的位置(不用证明,不写作法,保留作图痕迹),并求出时PA+PB 的值.15.(1)如图17 -3 -13所示,已知,在等腰,90,4,=∠==Φ∆ACB BC AC ABC Rt 点P 在线段BC 上,且,2=PC①若点D 在线段AB 上运动,求PD 的最小值;②若点P 从初始位置先运动到AC 边上,再运动到AB 边上,求点P 运动的最短路径.(2)如图17 -3 -14所示,已知,在△ABC 中,,90,6,8=∠==ACB BC AC 点P 在线段BC 上,且PC=2,若点P 从初始位置先运动到AC 边上,再运动到AB 边上,求点P 运动的最短路径.16.在△ABC 中,AB 、BC 、AC 三边的长’分别为,13105、、求这个三角形的面积.小宝同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC 三个顶点都在小正方形的顶点处),如图17-3-15(a)所示.这样不需求△ABC 的高,而借用网格就能计算出它的面积.(1)请你将△ABC 的面积直接填写在横线上思维拓展(2)我们把上述求△ABC 面积的方法叫做构图法,若△ABC 三边的长分别为a a a 17132、、(a>0),请利用图17-3-15(b)的正方形网格(每个小正方形的边长为a )画出相应的△ABC,并求出它的面积填写在横线上探索创新(3)若△ABC 中有两边的长分别为),0(102>a a a 、且△ABC 的面积为,22a 试运用构图法在图17-3-15(c)的正方形网格(每个小正方形的边长为a )中画出所有符合题意的△ABC (全等的三角形视为同一种情况),并求出它的第三条边长填写在横线上(4)利用上述解题方法完成下题:如图17-3-15(d)所示,一个六边形绿化区ABCDEF 被分割成7个部分,其中正方形ABQP 、CDRQ 、EFPR 的面积分别为13、20、29,且△PQR、△BCQ、△DER、△APF 的面积相等, 求六边形绿化区ABCDEF 的面积.17.如图17 -3 -16所示,在等腰直角△ABC 中,AB=AC ,点D 是斜边BC 的中点,点F 、E 分别为AB 、AC 边上的点,且DE ⊥DF .(1)证明:.222EF CE BF =+(2)若BF=12,CE=5,求△DEF 的面积.18.如图17 -3 -17所示,在△ABC 中,AM 是BC 边的中线,AE 为BC 边上的高.试判断2222BM AM AC AB ++与的关系.并说明理由.19.如图17 -3 -18所示,已知:AB MP CM AM C ⋅⊥==∠,,90于点P.求证:.222BC AP BP +=20.如图17 -3 -19所示,在Rt△ABC 中,AB CD ACB ⊥=∠,90于点D ,BE 平分∠CBA 交CD 于点F ,交CA 于点E ,且FG//AB 交CA 于点G ,若,5,13==BD BC(1)判断△CEF 的形状.(2)求AG 的长.21.【背景材料】小颖和小强在做课后习题时,遇到这样一道题:“已知Rt△ABC 中,==∠CA ACB ,90,45, =∠MCN CB 如图17-3-20(a)所示,当点M 、N 在AB 上时,则,.,222BN AM MN +=小颖的解题思路:如图17-3-20(b)所示,将△ACM 沿直线CM 对折,得,/CM A ∆连,/N A 进而证明,/BCN CN A ∆≅∆结论得证.【解决问题】当M 在BA 的延长线上,点N 在线段AB 上,其他条件不变,如图17-3-20 (c)所示,关系式222BN AM MN +=是否仍然成立?根据上述材料请你帮助小颖判断结论,并给出证明. 中 考 连 接22.(2011.山东烟台)如图17 -3 - 21所示,在四边形ABCD 中,,90 =∠ABC =+⊥22,CD AD AD CD 22AB(1)求证:AB=BC .(2)当AD BE ⊥于点E 时,试证明:.CD AE BE +=23.(2012.山东荷泽)如图17-3-22所示,OABC 是一张放在平面直角坐标系中的长方形纸片,0为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA =10,OC=8,在OC 边上取一点D ,将纸片沿AD 翻折,使点0落在BC 边上的点E 处,求D 、E 两点的坐标,巅 峰 突 破24.如图17-3-23所示,ABCD 是一张长方形纸片,将AD 、BC 折起,使A 、B 两点重合于CD 边上的点P ,然后压平得折痕EF 与GH.若.10,6,8cm EG cm PG cm PF ===则长方形纸片ABCD 的面积为6.105.A 4.110.B 2.115.C 8.124.D25.探究:如图17-3-24所示,C 为线段BD 上一动点,分别过点B 、D 作,,BD ED BD AB ⊥⊥连接AC 、 EC.已知.,8,1,5x CD BD DE AB ====设(1)用含x 的代数式表示AC+CE 的值.(2)请问点C 满足什么条件时,AC+CE 的值最小?(3)根据(2)中的规律和结论,请构图求出代数式9)12(422+-++x x 的最小值.拓展:仿照上面的方法,请用构图法求出代数式49)4(22+-+-x x (x 是任意实数)的最大值.。
勾股定理与旋图
奥数专题 (几何) 勾股定理与旋图
1、6年级几何:勾股定理与旋图
难度:高难度
在一个正方形中放入一个四个顶点与大正方形相接的一个小正方形(如图(1)),如果两个正方形的周长相差厘米,面积相差平方厘米,求小正方形的面积是多少平方厘米?
2、6年级几何:勾股定理与旋图
难度:高难度
7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?
3、6年级几何:勾股定理与旋图
难度:高难度
如图,边长是整数的四边形的面积是48平方厘米,FB为8厘米.那么,正方形
的面积是平方厘米.
4、6年级几何:勾股定理与旋图
难度:高难度
一个大长方形若能分割成若干个大小不同的小正方形,则称为完美长方形.下面一个长方形是由9个小正方形组成的完美长方形.图中正方形和的边长分别是7厘米和4厘米,那么这个完美长方形的面积分别是多少平方厘米?
5、6年级几何:勾股定理与旋图
难度:高难度
如图所示,甲、乙、丙、丁四个长方形拼成一个正方形,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是,四边形的面积是.⑴求正方形的边长?
⑵求甲、乙、丙、丁四个长方形周长的总和?
学而思奥数网奥数专题(几何)勾股定理与旋图答案1、6年级勾股定理与旋图习题答案:
解析:
2、6年级勾股定理与旋图习题答案:
解析:
3、6年级勾股定理与旋图习题答案:
解析:
4、6年级勾股定理与旋图习题答案:
解析:
5、6年级勾股定理与旋图习题答案:解析:。
学而思中考数学第2讲.第二轮复习之图形变换与动手操作.提高班.教师版
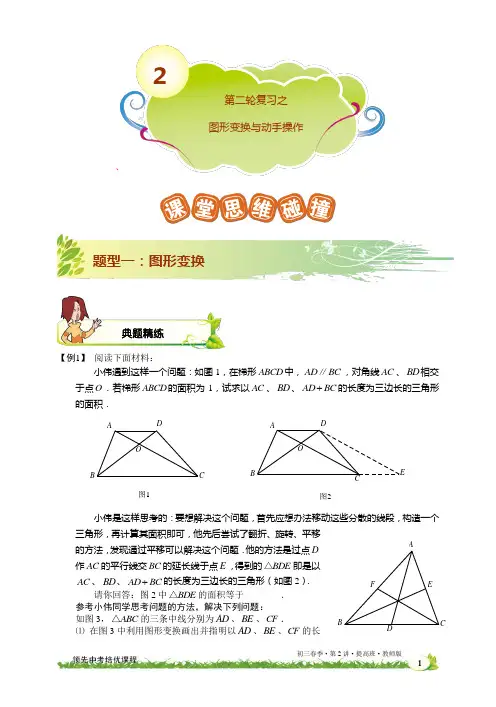
`【例1】 阅读下面材料:小伟遇到这样一个问题:如图1,在梯形ABCD 中,AD BC ∥,对角线AC 、BD 相交于点O .若梯形ABCD 的面积为1,试求以AC 、BD 、AD BC +的长度为三边长的三角形的面积.图1图2ADBCOADBCOE小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可,他先后尝试了翻折、旋转、平移的方法,发现通过平移可以解决这个问题.他的方法是过点D 作AC 的平行线交BC 的延长线于点E ,得到的BDE △即是以AC 、BD 、AD BC +的长度为三边长的三角形(如图2). 请你回答:图2中BDE △的面积等于________. 参考小伟同学思考问题的方法,解决下列问题:如图3,ABC △的三条中线分别为AD 、BE 、CF .⑴ 在图3中利用图形变换画出并指明以AD 、BE 、CF 的长典题精练2第二轮复习之 图形变换与动手操作题型一:图形变换图3AFE CD B度为三边长的一个三角形(保留画图痕迹);⑵ 若ABC △的面积为1,则以AD 、BE 、CF 的长度为三边长的三角形的面积等于________.(2011北京)【解析】BDE △的面积等于 1 .⑴ 如图.以AD 、BE 、CF 的长度为三边长的一个三角形是CFP △. ⑵ 以AD 、BE 、CF 的长度为三边长的三角形的面积等于34. 【例2】 阅读下面材料:小明遇到这样一个问题:我们定义: 如果一个图形绕着某定点旋转一定的角度α (0︒ <α <360︒) 后所得的图形与原图形重合,则称此图形是旋转对称图形. 如等边三角形就是一个旋转角为120︒的旋转对称图形. 如图1,点O 是等边三角形△ABC 的中心, D 、E 、F 分别为AB 、BC 、 CA 的中点, 请你将△ABC 分割并拼补成一个与△ABC 面积相等的新的旋转对称图形.FDEF DBACOABCO图1 图2小明利用旋转解决了这个问题,图2中阴影部分所示的图形即是与△ABC 面积相等的新的旋转对称图形.请你参考小明同学解决问题的方法,利用图形变换解决下列问题: 如图3,在等边△ABC 中, E 1、E 2、E 3分别为AB 、 BC 、CA 的中点,P 1、P 2, M 1、M 2, N 1、N 2分别为 AB 、BC 、CA 的三等分点.(1)在图3中画出一个和△ABC 面积相等的新的旋转 对称图形,并用阴影表示(保留画图痕迹); (2)若△ABC 的面积为a ,则图3中△FGH 的面积为 . (2012海淀二模) 【解析】(1)画图如下:(2)图3中△FGH 的面积为7a.图3H G F CBN 2N 1M 1M 2E 1E 2E 3P 2P 1AAPEFC DBH F GA BCE 1E 2E 3P 1P 2M 1M 2N 1N 2动手操作分为:1、立体图形及展开图;2、骰子问题;3、折纸问题;4、图形的分割;5、图形的剪拼.【例3】 ⑴如图,已知MN 是圆柱底面直径,NP 是圆柱的高.在圆柱的侧面上,过点M 、P 嵌有一圈路径最短的金属丝.现将圆柱侧面沿NP 剪开, 所得的侧面展开图是( )A. B. C. D. ⑵在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退.开始时骰子如图 ①那样摆放,朝上的点数是2;最后翻动到如图②所示的位置,此时骰子朝上的点 数不可能...是下列数中( )A .5B .4C .3D .1⑶ 如图,矩形纸片ABCD 中,8AB =,将纸片折叠,使顶点B 落在边AD 上的点为E ,折痕的一端G 点在边BC 上()BG GC <,另一端F 落在矩形的边上,10BG =.①请你在备用图中画出满足条件的图形;典题精练题型二:动手操作PNM P /N /PNMP /N /PNMP /N /PNMM /P /N /PNM②求出折痕GF 的长为 .备用图(3)G 备用图(2)G DADG 备用图(1)【解析】 ⑴321n -2n ≥). ⑵ ①正确画出图⑴、图⑵ ②545情况一:如图⑴,当点F 在AB 上时,过点G 作GH AD ⊥,则四边形ABGH 为矩形,∴8GH AB ==,10AH BG ==,设BF x =, 由图形的折叠可知BFG EFG △≌△, ∴10EG BG ==,BF EF x ==,在Rt GEH △中,由勾股定理,得6EH =,∴4AE =. ∵90A ∠=︒,8AF x =-,EF x =,222EF AF AE =+ ∴()22284x x =-+解方程,得 5x .=∴5BF =,∵10BG =,∴2255FG BG BF .=+=情况二:如图⑵,当点F 在AD 边上时,因为四边形HFGE 由四边形ABGF 折叠得到, 由折叠可知,BG EG =,AB EH =,BGF EGF ∠=∠, ∵EF BG ∥,∴BGF EFG ∠=∠,∴EGF EFG ∠=∠, ∴EF EG =,∴BG EF =,∴四边形BGEF 为平行四边形 又∵EF EG =,∴平行四边形BGEF 为菱形 连结BE ,BE 与 FG 互相垂直平分,在Rt EFH △中,10EF BG ==,8EH AB ==, 由勾股定理可得6FH AF ==,∴16AE =, ∴2285BE AE AB =+∴45BO =∴222245FG OG BG BO ==-=.【例4】 ⑴在ABC △中,沿着中位线EF 一刀剪切后,用得到的AEF △和四边形EBCF 可以拼成平行四边形EBCP ,剪切线与拼图如图所示,仿上述的方法,按要求完成下列操作设计,并画出图示.①在ABC △中,增加条件 ,沿着 H E F 图(1)G DCBA O E(B)H(A)F图(2)GDCB AA一刀剪切后可以拼成矩形;②在ABC △中,增加条件 ,沿着 一刀剪切后可以拼成菱形;③在ABC △中,增加条件 ,沿着 一刀剪切后可以拼成正方形;④在ABC △()AB AC ≠中,一刀剪切后也可以拼成等腰梯形,首先要确定剪切线,其操作过程(剪切线的作法)是: .⑵在ABC △中,BC a =,BC 边上的高2h a =,沿图中线段DE 、CF 将ABC △剪开,分成的三块图形恰能拼成正方形CFHG ,如图⑴所示.请你解决如下问题: 在A B C '''△中,B C a ''=,B C ''边上的高12h a =.请你设计两种不同的分割方法,将A B C '''△ 沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图⑵、图⑶中,画出分割线及拼接后的图形.【解析】 ⑴ ①方法一:90B ∠=︒,中位线EF ,如图⑴.方法二:AB AC =,中线(或高)AD ,如图⑵.②2AB BC =(或者90C ∠=︒,30A ∠=︒),中位线EF ,如图⑶. ③方法一:90B ∠=︒且2AB BC =,中位线EF ,如图⑷.方法二:AB AC =且90BAC ∠=︒,中线(或高)AD ,如图⑸.④方法一:不妨设B C ∠>∠,在BC 边上取一点D ,作GDB B ∠=∠交AB 于G ,过AC 的中点E 作EF GD ∥交BC 于F ,则EF 为剪切线.如图⑹方法二:不妨设B C ∠>∠,分别取AB 、AC 的中点D 、E ,过D 、E 作BC 的垂线,G 、H 为垂足,在HC 上截取HF GB =,连结EF ,则EF 为剪切线.如图⑺图(1)①②③H F E D B图(4)图(3)图(2)图(1)P(E)C(A)FEBAP(E)FEC(A)BAP(D)D C(A)BAP(E)FEC(A)BA图(3)图(2)A'B 'C'C'B 'A'方法三:不妨设B C ∠>∠,作高AD ,在DC 上截取DG DB =,连结AG ,过AC 的中点E 作EF AG ∥交BC 于F ,则EF 为剪切线.如图⑻图(8)图(7)图(6)图(5)P(F)A(C)ECFG D BP(F)A(C)ECFH GBD EC FGD BP(F)A(C)P(D)D C(A)BA⑵ 答案如下图:【例5】 阅读下列材料:小明遇到一个问题:如图1,正方形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 和DA 边上靠近A 、B 、C 、D 的n 等分点,连结AF 、BG 、CH 、DE ,形成四边形MNPQ .求四边形MNPQ 与正方形ABCD 的面积比(用含n 的代数式表示).小明的做法是:先取2n =,如图2,将ABN △绕点B 顺时针旋转90︒至CBN '△,再将ADM △绕点D 逆时针旋转90︒至CDM '△,得到5个小正方形,所以四边形MNPQ 与正方形ABCD 的面积比是15;然后取3n =,如图3,将ABN △绕点B 顺时针旋转90︒至CBN '△,再将ADM △绕点D 逆时针旋转90︒至CDM '△,得到10个小正方形,所以四边形MNPQ 与正方形ABCD 的面积比是410,即25;……请你参考小明的做法,解决下列问题:⑴在图4中探究4n =时四边形MNPQ 与正方形ABCD 的面积比(在图4上画图并直接写出结果);⑵图5是矩形纸片剪去一个小矩形后的示意图,请你将它剪成三块后再拼成正方形(在图5中画出并指明拼接后的正方形).(3)(2)(1)M'N'GH GH G BCEFPQM N A BCD EF PQ M NN'M'N MQ PF ED CB A ①③②图(5)A'B 'C'C'B'A'①②②①【解析】 ⑴四边形MNPQ 与正方形ABCD 的面积比是917.⑵ 如图所示:【例6】 操作探究:一动点沿着数轴向右平移5个单位,再向左平移2个单位,相当于向右平移3个单位.用实数加法表示为 5+(2-)=3.若平面直角坐标系xOy 中的点作如下平移:沿x 轴方向平移的数量为a (向右为正,向左为负,平移a 个单位),沿y 轴方向平移的数量为b (向上为正,向下为负,平移b 个单位),则把有序数对{a ,b }叫做这一平移的“平移量”.规定“平移量”{a ,b }与“平移量”{c ,d }的加法运算法则为}{}{}{d b c a d c b a ++=+,,,. (1)计算:{3,1}+{1,2};(2)若一动点从点A (1,1)出发,先按照“平移量”{2,1}平移到点B ,再按照“平移量”{-1,2}平移到点C ;最后按照“平移量”{-2,-1}平移到点D ,在图中画出四边形ABCD ,并直接写出点D 的坐标;(3)将(2)中的四边形ABCD 以点A 为中心,顺时针旋转90°,点B 旋转到点E ,连结典题精练H G M'N'A BC DEF PQMN DCB(5)(4)H GAB C D EF P Q MN题型三:新定义AE、BE若动点P从点A出发,沿△AEB的三边AE、EB、BA平移一周.请用“平移量”加法算式表示动点P的平移过程.(2013丰台二模)【解析】(1){4,3}.(2)①画图②D(0,3).(3){1,-2}+{1,3}+{-2,-1}.yxO 11yxBACDO 11【例7】 如图1,四边形ABCD 中,AC 、BD 为它的对角线,E 为AB 边上一动点(点E 不与点A 、B 重合),EF ∥AC 交BC 于点F ,FG ∥BD 交DC 于点G ,GH ∥AC 交AD 于点H ,连接HE .记四边形EFGH 的周长为p ,如果在点E 的运动过程中,p 的值不变,则我们称四边形ABCD 为“Ω四边形”, 此时p 的值称为它的“Ω值”.经过探究,可得矩形是“Ω四边形”.如图2,矩形ABCD 中,若AB =4,BC =3,则它的“Ω值”为 .图1B FCGD HE A图2D CBA图3ODBA(1)等腰梯形 (填“是”或 “不是”)“Ω四边形”;(2)如图3,BD 是⊙O 的直径,A 是⊙O 上一点,=34AD AB =,,点C 为»AB 上的一动点,将△DAB 沿CD 的中垂线翻折,得到△CEF .当点C 运动到某一位置时,以A 、B 、C 、D 、E 、F 中的任意四个点为顶点的“Ω四边形”最多,最多有 个.(2013海淀二模)【解析】 “Ω值”为10.(1)是;(2)最多有5个.训练1. ⑴将如右图所示的圆心角为90︒的扇形纸片AOB 围成圆锥形纸帽,使扇形的两条半径OA 与OB 重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是( )⑵如图是一个等腰直角三角形纸片,按图中裁剪线将这个纸片裁剪成三部分.请你将这三部分小纸片重新分别拼接成:(1)一个非矩形的平行四边形; (2)一个等腰梯形;(3)一个正方形.请画出拼接后的三个图形.【解析】 ⑴B. ⑵训练2. 图⑴、图⑵均为76⨯的正方形网格,点A 、B 、C 在格点上.⑴在图⑴中确定格点D ,并画出以A 、B 、C 、D 为顶点的四边形,使其为轴对称图形.(画一个即可)⑵在图⑵中确定格点E ,并画出以A 、B 、C 、E 为顶点的四边形,使其为中心对称图形.(画一个即可)(吉林长春)【解析】 ⑴ 有以下答案供参考:思维拓展训练(选讲)图(2)图(1)ABCCBADD A BCCBA⑵ 有以下答案供参考:EEABCCBA训练3. ⑴图⑴是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图⑵将纸板沿虚线进行切割,无缝隙无重叠的拼成图⑶所示的大正方形,其面积为842+则图⑶中线段AB 的长为 .(海淀二模)图(3)图(2)图(1)BA⑵如图⑶,在55⨯的网格中有一个正方形,把正方形的各边三等分,分别以居中那条线段为斜边向外作等腰直角三角形,去掉居中的那条线段,得到图⑷,请把图⑷中的图形剪拼成正方形,并在图⑷中画出剪裁线,在图⑸中画出剪拼后的正方形.(石景山一模)图(5)图(4)图(3)【解析】215.⑵如图所示:【练习1】 已知ABC △,63ABC ACB ∠=∠=°.如图1所示,取三边中点,可以把ABC △分割成四个等腰三角形.请你在图2中,用另外四种不同的方法把ABC △分割成四个等腰三角形,并标明分割后的四个等腰三角形的底角..的度数(如果经过变换后两个图形重合,则视为同一种方法).(海淀二模)【解析】 分割为等腰三角形常用方法:①角分线+平行线.如图⑴和图⑵ ②直角三角形+斜边中线.如图⑶(和图⑴)③顶角为特殊角度108︒的等腰三角形可以无限分割成36︒和72︒为底角的等腰三角形.如图⑷④知一等腰三角形,做此三角形的对称轴,然后再去分割.如图⑸复习巩固图1CBACB AAB C C B AAB C 图254°54°72°54°36°36°36°31.5°31.5°31.5°27°27°27°27°27°27°27°27°27°63°63°63°63°63°63°63°63°63°63°63°63°63°63°63°36°72°54°27°31.5°63°(5)(4)(3)(2)(1)【练习2】 现场学习题问题背景:在ABC △中,AB 、BC 、AC 21317三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点ABC △(即ABC △三个顶点都在小正方形的顶点处),如图⑴所示.这样不需求ABC △的高,而借用网格就能计算出它的面积. ⑴请你将ABC △的面积直接填写在横线上.________ 思维拓展:⑵我们把上述求ABC △面积的方法叫做构图法.若ABC △2a 、25a 26a (0)a >,请利用图⑵的正方形网格(每个小正方形的边长为a )画出相应的ABC △,并求出它的面积是: . 探索创新:⑶若ABC △三边的长分别为224m n +、2216m n +、222m n +(0,0,)m n m n >>≠ ,请运用构图法在图⑶指定区域内画出示意图,并求出ABC △的面积为: .【解析】 ⑴25. ⑵ 面积:23a .⑶ 面积:3mn .图(2)A B C 4m 2m 2m n n 2n C B A 图(3)图(3)图(2)图(1)A B C【练习3】 在如图1中,正方形ABCD 的边长为a ,等腰直角三角形FAE的斜边2AE b =,且边AD 和AE 在同一直线上. 操作示例:当2b a <时,如图1,在BA 上选取点G ,使BG b =,连结FG 和CG ,裁掉FAG △和CGB △并分别拼接到FEH △和CHD △的位置构成四边形FGCH .思考发现:小明在操作后发现:该剪拼方法就是先将FAG △绕点F 逆时针旋转90︒到FEH △的位置,易知EH 与AD 在同一直线上.连结CH ,由剪拼方法可得DH BG =,故CHD CBG △≌△,从而又可将CGB △绕点C 顺时针旋转90︒到CHD △的位置.这样,对于剪拼得到的四边形FGCH (如图1),过点F 作FM AE ⊥于点M (图略),利用SAS 公理可判断HFM CHD △≌△,易得FH HC GC FG ===,90FHC ∠=︒.进而根据正方形的判定方法,可以判断出四边形FGCH 是正方形.实践探究:⑴ 正方形FGCH 的面积是__________;(用含a ,b 的式子表示)⑵ 类比图1的剪拼方法,请你就如图2至如图4的三种情形分别画出剪拼成一个新正方形的示意图.联想拓展:小明通过探究后发现:当b a ≤时,此类图形都能剪拼成正方形,且所选取的点G 的位置在BA 方向上随着b 的增大不断上移.⑶ 当b a >时,如图5的图形能否剪拼成一个正方形?若能,请你在图中画出剪拼的示意图;若不能,简要说明理由.【分析】 抓22a b +,结合四边形ABCD 为正方形及给出的图1中的作法,只需满足BG DH =,由全等三角形即可得出CG 和CH 互相垂直平分且相等.再按照提示方法可以证明四边形GCHF 为正方形.【解析】 ⑴ 22a b +; ⑵ 剪拼方法如图2至图4.⑶ 能;剪拼方法如图5(图中BG DH b ==).先沿FH 剪一刀,将FEH △拼接到图1(2b <a )H G FE DCB A 图2FA B C(E ) DH G F 图4ABC DF图3A BCEHD G C F图5ABDG H a<2b=a FEDC B A图3FD(E )C BA 图2a<2b<2a FEDCBA图3b>b=a 图4ABC DEF图5FEDCB A b>a 图5FE D C BA△即可.FAG△拼接到HDC△;再沿GC剪一刀,将GBC第十八种品格:坚持坚持即是成功有一个少年,拜在一位师傅门下,想学功夫。
第一节 勾股定理(含答案)...八年级数学 学而思

第一节 勾股定理1.勾股定理如果直角三角形的两直角边分别是a ,b ,斜边为c ,那么.222c b a =+即直角三角形中两直角边的平方和等于斜边的平方,如图7-1-1所示,注:勾——最短的边, 股——较长的直角边, 弦——斜边.勾股定理反映了直角三角形中三边间的关系,因此利用它可以解决有关边长的计算问题,也可以解决与直角三角形有关的一些平方关系的证明问题. 2.勾股定理的证明如图7-1-1所示,图①是一个直角三角形,方法一:将四个全等的直角三角形拼成如图②所示的正方形:.,214)(S 22222c b a ab c b a ABCD =+∴⨯+=+=正方形Θ方法二:将四个全等的直角三角形拼成如图③所示的正方形:.,214)(S 22222EF c b a ab b a c GH =+∴⨯+-==正方形Θ方法三:“总统”法,如图④所示将两个直角三角形拼成直角梯形:.,212122))((S 2222ABCD c b a c ab b a b a =+∴+⨯=++=梯形117--3.直角三角形的性质(1)两锐角互余.(2)三边满足勾股定理.(3)斜边上的中线等于斜边的一半. (4)ο30角所对的直角边等于斜边的一半,另外,直角三角形中还有一个重要的结论:两直角边的乘积等于斜边与斜边上高的乘积,即.ch ab =4. 直角三角形的判定 (1)有一个角是直角. (2)两锐角互余.(3)勾股定理的逆定理.(4)一条边上的中线等于这条边的一半(用时需证).1.勾股定理应用常见注意事项(1)勾股定理只适用于直角三角形.(2)运用勾股定理时,要分清直角边和斜边,如果题目没有指明,则需分类讨论. (3)勾股定理将“数”与“形”有机结合,是数形结合思想方法的典范, 2.勾股定理证明方法的注意事项(1)目前已知的勾股定理证明方法有几百种,大多本质是应用面积方法算两次,即利用同一个图形公式法算出的面积和割补法算出的面积相等这一等量关系列出方程进行证明; (2)如图7-1-1所示,图②,③这两个弦图是正方形或者等腰直角三角形证明过程中的常用模型,必须掌握熟练. 3. 构造直角三角形的常用方法(1)作高,如图7-1- 201,②所示.(2)补全,如图7-1 - 2③,④所示. 图7- I-2(3)分割,如图7—1—2⑤所示. 4.直角三角形边的关系(1)斜边上的高×斜边=直角边乘积. (2)斜边上的中线等于斜边的一半.(3) 30。
第三节 勾股定理及逆定理的综合运用(含答案)...八年级数学 学而思
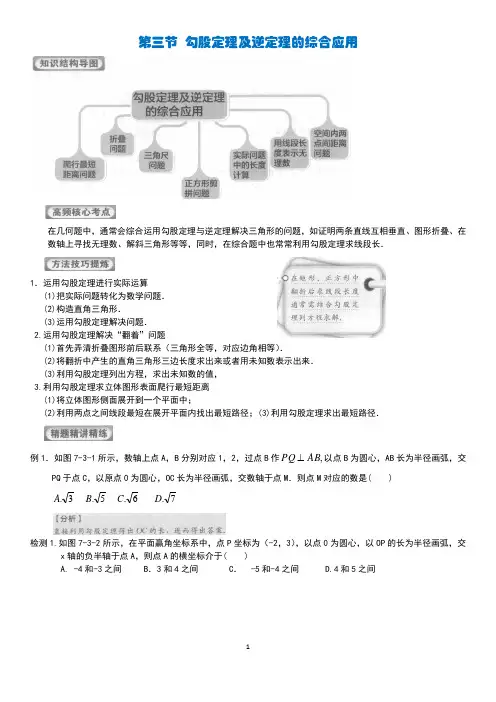
第三节 勾股定理及逆定理的综合应用在几何题中,通常会综合运用勾股定理与逆定理解决三角形的问题,如证明两条直线互相垂直、图形折叠、在数轴上寻找无理数、解斜三角形等等,同时,在综合题中也常常利用勾股定理求线段长.1.运用勾股定理进行实际运算(1)把实际问题转化为数学问题.(2)构造直角三角形.(3)运用勾股定理解决问题.2.运用勾股定理解决“翻着”问题(1)首先弄清折叠图形前后联系(三角形全等,对应边角相等).(2)将翻折中产生的直角三角形三边长度求出来或者用未知数表示出来.(3)利用勾股定理列出方程,求出未知数的值,3.利用勾股定理求立体图形表面爬行最短距离(1)将立体图形侧面展开到一个平面中;(2)利用两点之间线段最短在展开平面内找出最短路径;(3)利用勾股定理求出最短路径.例1.如图7-3-1所示,数轴上点A ,B 分别对应1,2,过点B 作,AB PQ 以点B 为圆心,AB 长为半径画弧,交PQ 于点C ,以原点0为圆心,OC 长为半径画弧,交数轴于点M .则点M 对应的数是( ) 3.A 5.B 6.C 7.D检测1.如图7-3-2所示,在平面赢角坐标系中,点P 坐标为(-2,3),以点0为圆心,以OP 的长为半径画弧,交x 轴的负半轴于点A ,则点A 的横坐标介于( )A. -4和-3之间 B .3和4之间 C . -5和-4之间 D.4和5之间137-- 237-- 337--例2.(广东深圳校级期末)如图7-3-3所示,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是( )295.A 35.B 5510.+C 25.D检测2.如图7-3-5所示,A 是高为10 cm 的圆柱底面圆上一点,一只蜗牛从A 点出发,沿30。
角绕圆柱侧面爬行,当他爬到顶上时,他沿圆柱侧面爬行的最短距离是( )cm A 10. cm B 20. cm C 30. cm D 40.例3.(江西宁都县期末)如图7-3-6所示,将一根25 cm 长的细木棒放入长、宽、高分别为cm cm 6,8和cm 310的长方体无盖盒子中,求细木棒露在盒外面的最短长度是多少.537-- 637-- 737--检测3.如图7-3-7所示,是一个直圆柱状的饮料瓶,由内部测得其底面半径为3厘米,高为8厘米,今有一支13厘米的吸管任意斜放干杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度最小为 厘米.例4.小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5 m 远的水底,竹竿高出水面0.5 m ,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为 m.检测4.如图7-3-9所示,一个梯子AB 长2.5米,顶端A 靠在墙AC 上,这时梯子下端B 与墙角C 距离为1.5米,梯子滑动后停在DE 的位置上,测得BD 长为0.5米,则梯子顶端A 下落了( )米5.0.A 1.B 5.1.C 2.D937-- 1037-- 1237--例5.(山东省威海市)如图7 -3- 10所示,在矩形ABCD 中,,4=AB ,6=BC 点E 为BC 的中点,将△ABE 沿AE 折叠,使点B 落在矩形内点F 处,连接CF ,则CF 的长为( )59.A 512.B 516.C518.D检测5.如图7 -3 -12所示,已知矩形ABCD 沿着直线BD 折叠,使点C 落在C 处,BC 交AD 于,8,16,==AB AD E则DE 的长为第三节 勾股定理及逆定理的综合应用(建议用时35分钟)实战演练1.如图7-3-1所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,折断的一端恰好落到地面的B 处,经测量AB =2米,则树高为( )3.A 米 3.B 米 5.C 米 )15.(+D 米2.一只蚂蚁沿如图7-3-2所示折线从A 点爬到D 点,共爬行了( )(图中方格边长为1 cm)cm A 12. cm B 10. cm C 14. D .以上答案都不对3.如图7-3-3所示,四边形ACED为平行四边形,DF垂直平分BE,甲乙两虫同时从A点开始爬行到点F,甲虫沿着A-D-E-F的路线爬行,乙虫沿着A-C-B-F的路线爬行,若它们的爬行速度相同,则( )A.甲虫先到 B.乙虫先到 C.两虫同时到 D.无法确定137--237--337--4.如图7-3-4所示,一圆柱高4 cm,底面半径1 cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(丌取3)是( )cmA6.cmB5.cmC7. D.无法确定5.如图7-3-5所示,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直,且,300,400mADmAB==.400mCE=如果小明站在南京路与八一街的交叉口,准备去书店(E点处),按图中的街道行走,最近的路程约为( )mA600.mB500.mC400.mD300.437--537--637--6.如图7-3-6所示,有一张直角三角形纸片,两直角边,8,6cmBCcmAC==将△ABC折叠,使B点与A点重合,折痕为DE.则CD等于( )cmA425.cmB322.cmC47.cmD35.7.将边长分别为cmcmcm2,3,3的等腰三角形从一个圆钢圈中穿过,那么这个圆钢圈的最小直径是( )cm2.A22.B3.C234.D8.如图7-3-7所示,梯子AB斜靠在墙上,,,BCACBCAC=⊥当梯子的顶端A沿AC方向下滑x米时,梯足B 沿CB方向滑动y米,则x与y的大小关系是( )yxA=.yxB>.yxC<. D.不确定9.放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为米.10.某楼梯的侧面视图如图7-3-8所示,其中,90,30,4ο=∠=∠=CBACAB o米因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的长度应为737--837--937--11.(山东省临沂中考)如图7-3-9所示,将一矩形纸片ABCD 折叠,使两个顶点A ,C 重合,折痕为FG .若,8,4==BC AB 则△ABF 的面积为12.如图7 -3 - 10所示,一架长2.5 m 的梯子,斜靠在一面竖直的墙上,这时梯子底端离墙0.7 m ,为了安装壁灯,梯子顶端需离地面2m ,请你计算一下,此时梯子底端应再远离墙 m13.已知,如图7-3 -11所示,折叠长方形的一边AD ,使点D 落在BC 边的点F 处,如果,10,8cm BC cm AB ==则EC 的长为 .cm14.(江苏徐州二模)一副三角板如图7-3 - 12所示放置,点C 在FD 的延长线上,,//CF AB ,90ο=∠=∠ACB F ,45ο=∠E ,60ο=∠A 若,8==DE AB 则=BE (结果保留根号).1237-- 1337--15.如图7-3- 13所示是一个三级台阶,它的每一级的长、宽和高分别等于5 cm ,3 cm 和1cm ,A 和B 是这个台阶的两个相对的端点,A 点上有一只蚂蚁,想到B 点去吃可口的食物.请你想一想,这只蚂蚁从A 点出发,沿着台阶面爬到B 点,最短线路的长是16.细心观察图7-3 - 14,认真分析各式,然后解答问题:;21S 21)1(12==+;;22S 31)2(22==+;⋅==+23S 41)3(32; ①用含有n n (是正整数)的等式表示上述变化规律:②推算出10OA 的长:③求出210232221S ++++ΛS s S 的值.1437--17.假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图7-3 - 15所示),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏点B 的直线距离是多少千米.1537--18.两个正方形如下图并列排列,要求剪两刀(剪切线为直线哦),使之拼成一个新的正方形.(1)如图7 -3 - 16所示,若正方形边长分别为1,2,请在图中画出剪切线;(2)如图7-3 -17所示,若正方形边长分别为),(,b a b a >请画出剪切线并标出各边的长度;(3)若要求剪三刀拼成一个正方形,请在图7-3 - 18中画出剪切线.1637-- 1737-- 1837--19.如图7-3 - 19所示,在Rt△Poo 中,M OQ OP ,4==是PQ 中点,把一三角尺的直角顶角顶点放在点M 处,以M 为旋转中心,旋转三角尺,三角尺的两直角边与△P OQ 的两直角边分别交于点.,B A(1)求证:;MB MA =(2)连接AB ,探究:在旋转三角尺的过程中,△AOB 的周长是否存在最小值?若存在,求出最小值;若不存在,请说明理由,1937--拓展创新20.如图7-3 - 20所示,圆柱形玻璃杯,高为6 cm ,底面周长为16 cm ,在杯内离杯底2 cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,在离杯上沿2 cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为 cm.拓展1.为了庆祝国庆,学校准备在教学楼大厅的圆柱体柱子上贴彩带,如图7 -3 - 21所示,已知柱子的底面周长为1 m ,高为3 m.如果要求彩带从柱子底端的A 处绕柱子4圈后到达柱子顶端的B 处,那么至少应购买彩带 m.2037-- 2137-- 2237--拓展2.如图7 -3 - 22所示,长方体的底面边长分别为1 cm 和3 cm ,高为6 cm.如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B ,那么所用细线最短需要 cm ;如果从点A 开始经过4个侧面缠绕n 圈到达点B ,那么所用细线最短需要 cm.极限挑战21.将两块斜边长相等的等腰直角三角尺按如图7-3 - 23摆放.(1)点M ,N 在AB 上(不与A ,B 重合)时,若,15,12cm MN cm AM ==求BN 的长;(2)当点M 在AB 上,点N 在AB 的延长线上(如图7-3 - 24)时,若==BM cm AM ,20,16cm 求BN 的长.2337-- 2437--答案。
学而思讲义

小学阶段的几何知识主要包括直线型面积、曲线型面积、立体图形的表面积和体积等.初中阶段的几何知识以全等三角形、相似三角形及其性质定理和判定定理的应用为重点.分班考试的命题重在考查学生对这两部分知识关联性和数学思想转换的理解和应用.作为各类竞赛和考试的重点,几何问题一直是学生的一个难点,所以在本次分班考试课中,我们安排了两讲几何内容,通过对解决几何问题常用数学方法的分类学习,梳理小学和初中的几何知识,以期融会贯通之效.上一讲我们以“割补法”为主线,将小学阶段的直线型面积和初中阶段的平面几何融合在一起,初步探知全等三角形和相似三角形,涉及“平移”、“旋转”、“勾股定理”等知识.这一讲以立体几何为主,在探究趣味新题目的同时,学习折叠、全等三角形和相似三角形的基础知识 以及简单的物理常识,培养空间思维能力.真题演练1.折叠后,原平行四边形面积是折叠后图形面积的1.5 倍.已知阴影部分面积之和为1 ,则重叠部分(即空白部分)的面积是多少?【分析】折叠后图形的面积为原来图形面积的 2 ,所以由于重叠而消失的面积等于原来面积的1 - 2 = 1,3 即右图中空白三角形的面积为原来图形面积的 1313 3,所以未重叠的阴影部分面积之和也等于原来图形面积的 3,即与重叠部分面积相等,所以重叠部分(即空白部分)的面积是1 .2.将一正方形的纸对折 2 次后,还是正方形,用同样的方法,可把某种形状的纸对折 3 次后,成为三角形.已知可把 4 种形状的纸对折 3 次后,折成如图的三角形,请画出这 4 种形状.【分析】此题虽然不难,但需要用逆向思维解决.从小三角形开始,向外展开,分别讨论不同展开方向下变成的形状,可得如下 4 种:第 8 讲人大附分班考试真题与模拟专题之几何(二)HIFGHIFG3.已知∆ABC 中,AB =AC =12cm ,∆ABC 的面积是42cm2 ,P 是BC 上任意一点,P 到AB ,AC的距离分别是x 厘米、y 厘米,那么x +y = .AP C【分析】如图所示,连接AP .三角形ABC 的面积等于三角形APB 与三角形APC 的面积之和,而这两个三角形的底AB 、AC 相等,高分别为x 和y ,所以12 ⨯(x +y )⨯1 = 42 ,可得x +y = 7 .2本题也可运用特殊值法,设P 在B 点,则此时x = 0 ,那么S x +y = 7 .∆ABC=1AC ⨯y = 42 ,得到y = 7 ,24.右图中,正方形ABCD 的边长为8 厘米,E 为AD 的中点,F 为CE 的中点,G 为BF 的中点,H为AG 的中点.四边形FGHI 的面积比三角形DIE 的面积大平方厘米.A E D A E DB C B C【分析】如图,连接EG 、EH 、EB .根据差不变原理,要求四边形FGHI 与三角形DIE 的面积差,相当于求四边形EFGA 与三角形DAH 的面积差.而三角形DAH 的面积等于三角形EAH 的面积的2 倍,三角形EAG 的面积也等于三角形EAH 的面积的2 倍,所以四边形EFGA 与三角形DAH 的面积差就等于∆EFG 的面积.根据题意,∆EFG 的面积等于∆EFB 的面积的一半,∆EFB 的面积等于∆ECB 的面积的一半,∆ECB的面积等于正方形ABCD 面积的一半,所以∆EFG 的面积等于正方形ABCD 面积的1⨯1⨯1=1,2 2 2 8为82 ⨯1= 8 平方厘米,所以四边形FGHI 的面积比三角形DIE 的面积大8 平方厘米.85.如图所示,铁板A 中有个半径为3.2cm 的圆形孔,孔内有96 个齿.还有一个半径为1.2cm ,且外侧有36 个齿的齿轮B .其中在距齿轮B 的中心为0.6cm 的地方打了一个圆孔C ,圆孔C 内插有一枝圆珠笔.现转动笔让齿轮B 与A 相啮合并沿A 齿轮的齿作旋转.问此时圆珠笔所画出的图形是下图哪一个?ABCDEF【分析】 先要确定齿轮 B 沿铁板 A 的内孔旋转多少周,圆珠笔才能回到初始位置.由于 A 齿轮有96 个齿,B 齿轮有36 个齿,由于(96,36) = 12 ,而96 = 12 ⨯ 8 , 36 = 12 ⨯ 3 ,因此,考虑到在12 ⨯ 8 ⨯ 3 = 288 个齿咬合之后,则绕 A 孔旋转了 288 ÷ 96 = 3 圈,而齿轮 B 则旋转 288 ÷ 36 = 8 圈.这就是说,当齿轮 B 绕着 A 孔转了8 圈后便返回到原来所在的位置.由此可知,圆珠笔应该有8 次离 A 孔的距离最近.此后,圆珠笔则重复原来已画出的曲线,不会显出新图形.所以圆珠笔画出的图形应该有 8 个顶点, A 、 B 、 E 、 F 均不合题意.另外,而在绕 A 孔旋转一圈的过程里,齿轮 B 自身所转的圈数为 3 圈,而 D 图中的图形只转了 1 圈,不合题意,所以正确的图形应该是C 图.[拓展]如果齿轮 B 的半径是1.6cm , B 圆周上的点C 画出来的轨迹是什么图形?[分析]此时齿轮 B 的半径等于 A 的圆形孔的半径的一半,点C 画出来的轨迹是圆形孔的一条直径.真题精讲1.如图⑴,线段 MN 将长方形纸分成面积相等的两部分.沿 MN 将这张长方形纸对折后得到图⑵,将图⑵沿对称轴对折,得到图⑶,已知图⑶所覆盖的面积占长方形纸面积的 310,阴影部分面积为 6 平方厘米.则长方形的面积是多少平方厘米?⑴ ⑵ ⑶【分析】根据折叠的过程可知,图⑶中阴影部分是 2 层,空白部分是 4 层,如果将阴影部分缩小一半,即变为 3 平方厘米,那么阴影部分也变成 4 层,此时覆盖的面积占长方形纸片面积的 1,即缩小的43 平方厘米相当于长方形纸片面积的( 3 - 1 ) ,所以长方形纸片面积为3 ÷ ( 3 - 1) = 60 平方厘米.10 4 10 4OOD EDBDE2.在长方形纸片 ABCD 中, AD = 4 , AB = 3 ,现在将它折叠,使得 C 与 A 重合,则折痕的长度是 . AFD ABCH F DEC【分析】如右图所示,连接 FC ,过 E 作 AD 的垂线 EH .由于折痕 EF 过 AC 的中点,且与 AC 垂直,设 AF = CF = x ,则 FD = 4 - x ,在直角三角形 FDC中,根据勾股定理,有: (4 - x )2+ 32 = x 2 ,则 x = 25 , FD = 4 - 25 = 7 ,那么 HE = 3 , FH = 4 - BE - FD = 4 - 2FD = 9 ,8 8 8 4再由勾股定理,得 EF = 15 .即折痕的长度为15.4 4[巩固]如右图,长方形的长为8 ,宽为 4 ,将长方形沿一条对角线折起压平,求重叠部分(阴影部分)的面积.8D[分析]如右上图,因为∠EDB = ∠EBD ,所以 BE = DE ,AE = CE .设 BE = DE = x ,则 AE = CE = 8 - x .由勾股定理得(8 - x )2+ 42 = x 2 ,解得 x = 5 .所以 S = 1 ⋅ BE ⋅ CD = 1⨯ 5 ⨯ 4 = 10 ,所以重叠部分(灰2 2色三角形)的面积为10 .3.如图,直角梯形 ABCD 中, AD ∥ BC , AB ⊥ BC , AD = 2 , BC = 3 ,将腰CD 以 D 为中心逆时针旋转90︒ 至 ED ,连接 AE 、CE ,则∆ADE 的面积是 .FEAABCBHC【分析】如图所示,将∆ADE 以 D 为中心顺时针旋转90︒ ,到∆FDC 的位置.延长 FD 与 BC 交于H . 由于 ABCD 是直角梯形, AD 与 FD 垂直,则四边形 ADHB 是长方形,则 BH = AD .由于∆ADE 与 ∆FDC 面积相等,而∆FDC 的底边 FD = AD = 2 ,高CH = BC - BH = 3 - 2 = 1 ,所以∆FDC 的面积为2 ⨯1 ÷ 2 = 1 ,那么∆ADE 的面积也为 1.4. 如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点 P 为中心转动一个正方形.当BAB = 5 厘米, BC = 13 厘米, CA = 12 厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).【分析】右图由左图旋转而得,则右图中的 8 个空白小三角形都是完全相同的,右图中重叠部分的面积等于正方形面积减去 4 个小三角形的面积,从右图中可以看出正方形的边长为5 + 13 + 12 = 30 厘米, 所以重叠部分的面积为: 302 - 4 ⨯ (5 ⨯12 ÷ 2) = 780 (平方厘米).5.有 2 个大小不同的正方形 A 和 B .如下左图所示的那样,在将 B 正方形的对角线的交点与 A 正方形的一个顶点相重叠时,相重叠部分的面积为 A 正方形面积的 1.求 9A 与B 的边长之比.如果当按下右图那样,将 A 和 B 反向重叠的话,所重叠部分的面积是 B 的几分之几?左图 右图【分析】以 B 正方形为中心,将整体图形放大后,如右上图所示.图中,由于 A 和 B 均为正方形,所以可认为画阴影的两个三角形是以 B 的对角线的交点为中心转过90︒ 所形成的.因此,所求的 A 与 B 所重合部分的面积,只要让 B 的对角线的交点与 A 的一个顶点相重合,则不管什么情况下,该面积均为 B 正方形面积的 1 .这样, A 4 的面积的 1 9 与 B 的面积的 1相等,故 A 与 B 的面积之比为49 : 4 .因为二者均为正方形,所以其边长之比为3 : 2 .如果 A 的对角线的交点与 B 的一个顶点相重合的话,所重合部分的面积仍为 A 的面积的 1.但是4由于 B 的面积是 A 的面积的 4 ,所以重合部分的面积应为 B 的面积的 1 ÷ 4 = 9.9 4 9 166.往容器里倒啤酒时,啤酒会分成液体部分和泡沫部分.过一会儿后泡沫会变成液体的啤酒,这时,1体积会缩小到 3(也就是说泡沫的体积是相应液体的3 倍).另外,因倒入方法的不同而使液体与泡沫的比例不同.即使是往相同的容器里倒入的啤酒量,也会因倒入的方法不同而不同.如图, 往深度为30 厘米的圆柱形的容器里倒入500 毫升的啤酒,从容器的底部到以上15 厘米高处的部 分是液体,再往上一直到容器的顶端,全都是泡沫(第一次).然后,往相同的容器里倒入700 毫升的啤酒,从容器的底部到以上 x 高处的部分是液体,再往上一直到容器的顶端,全都是泡沫(第二次).求 x 的值.P第二次【分析】第一次泡沫全部变成液体时,高度是15 + 15 ÷ 3 = 20 (厘米),因此高度1 厘米的液体是25 毫升;第二次泡沫全部变成液体时,高度是700 ÷ 25 = 28 (厘米),高度是1 厘米的液体成为泡沫时变为 高3 厘米,高度增加2 厘米,有(30 - 28) ÷ 2 = 1 厘米,即由泡沫变成的液体有 1 厘米,那么原有的 液体为 x = 28 -1 = 27 (厘米). 7.右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2 倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的 倍.【分析】本题中的两个图都是立体图形的平面展开图,将它们还原成立体图形,可得到如下两图:其中左图是以⑴⑵⑶⑷为平面展开图的立体图形,是一个四个面都是正三角形的正四面体,右图以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形,是一个不规则图形,底面是⑾,四个侧面是⑺⑻⑼ ⑽,两个斜面是⑸⑹.对于这两个立体图形的体积,可以采用套模法来求,也就是对于这种我们不熟悉的立体图形,用一些我们熟悉的基本立体图形来套,看看它们与基本立体图形相比,缺少了哪些部分.由于左图四个面都是正三角形,右图底面是正方形,侧面是等腰直角三角形,想到都用正方体来套. 对于左图来说,相当于由一个正方体切去 4 个角后得到(如下左图,切去 ABDA 1 、 CBDC 1 、D 1 A 1C 1D 、 B 1 A 1C 1B );而对于右图来说,相当于由一个正方体切去 2 个角后得到(如下右图,切去 BACB 1 、 DACD 1 ).⑵ ⑶⑴ ⑷⑸ ⑺⑻ ⑹⑾⑼ ⑽B1DB1DB HB C AB CA C1C1A1 D1 A1 D1假设左图中的立方体的棱长为 a ,右图中的立方体的棱长为b ,则以⑴⑵⑶⑷为平面展开图的立体图形的体积为:a3 -1a2 ⨯a ⨯1⨯ 4 =1a3 ,2 3 3以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积为b3 -1b2 ⨯b ⨯1⨯ 2 =2b3 .2 3 3由于右图中的立方体的棱长即是题中正方形⑾的边长,而左图中的立方体的每一个面的对角线恰好是正三角形⑴的边长,通过将等腰直角三角形⑺分成4 个相同的小等腰直角三角形可以得到右图中的立方体的棱长是左图中的立方体的棱长的2 倍,即b = 2a .那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积的比为:1a3 :2b3 =1a3 :2⨯(2a)3 =1:16,也就是说以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立3 3 3 3体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16 倍.8.如图所示的立体ABCD -EFGH 是长1 米、宽1 米、高2 米的长方体的箱子,在这个箱子里有一根直棒,棒的一端在顶点G 处,另一端在棱AE 的中点I 处.在不考虑棒的粗细的情况下,请问:⑴在点 F 处有一亮着的灯泡,请画出棒IG 在面AEHD 和面DHGC 上形成的阴影;⑵在EF 边的中点J 处有一亮着的灯泡,请画出棒IG 在面AEHD 和面DHGC 上形成的阴影.D C CAIG GE F【分析】⑴棒IG 在面AEHD 和面DHGC 上形成的阴影是两条直线段,而且它们与∆IFG 在同一个平面上.连结IF ,过点I 作IK ∥FG 交DH 于K (实际上K 就是DH 的中点),连结KG 即可.KBHABIHEJFDCADDCAIIKKGEF EHHGDCA D D CGIMEHHG⑵连结GJ 延长与 HE 的延长线交于点 M ,连结 MI 并延长与 DH 交于点 D ,连结 DG 即可. 点评:本题涉及两个重要的知识点: ①光线的传播路径是直线;②公理:直线和不在这条直线上的一点共面.在本题的应用就是光源、棒 IG 、光线的传播路径、在面上形成的阴影共面.[拓展]如图,一个边长为5 厘米的正方体,这个正方体由边长为1 厘米的小正方体组成.A 、B 、C 、D 、E 、F 、G 、H 分别是大正方体的各个顶点, P 是 ABCD 面上 AC 与 BD 的交点,请问:A G⑴如右上图所示,用一个 E 、P 、F 三点所在的平面将大正方体切开,这时切开的面是什么形状? ⑵经过⑴切开后剩下部分(包括 E 、 F 、G 、 H 面)的体积是多少?⑶再分别用 F 、P 、G 三点所在的平面, G 、P 、H 三点所在的平面, H 、P 、E 三点所在的平面进一步切割剩余部分,最后剩余的是一个包括 E 、 F 、G 、 H 面的立体图形,请写出这个立体图形的名称(即是哪种形状的立体图形).⑷在最后剩下的立体图形中,包括几个完整的边长为1 厘米的小正方体?[分析]⑴切开的面是四边形,两组对边分别平行且相等,但相邻两边长度均不相等, 4 个角都是直角,所以是长方形.HGHG⑵切下部分的体积正好是原体积的 1 ,所以剩下部分的体积是5 ⨯ 5 ⨯ 5 ⨯ 3= 93.75 立方厘米.4 4D CPPPABHGEF E F EF⑶如上图,在 ABCD 面中最后剩下 P 点,底面 EFGH 完好,连结 PE 、PF 、PG 、PH ,所以剩下的立体图形是底面为正方形的正四棱锥,如右上图.⑷切完后,从正面、侧面看均如下图所示,从下往上数,第一层是 3 ⨯ 3 = 9 (个),第二层是 3 ⨯ 3 = 9 (个),第三层是1 个,第四层是1 个,共9 + 9 + 1 + 1 = 20 个边长为 1 厘米的小正方体.真题模拟1.右图为一个正八边形,它的每条边长都是10 厘米,每个内角都相等,求图中阴影部分与非阴影部分的面积之差.【分析】如右上图,延长正八边形的两组对边,并连接竖直方向的两条对角线.图中标有 1,2,3,4 的4 个等腰直角三角形合起来为一个边长为 10 厘米的正方形,所以它们的面积之和为10 ⨯10 = 100 平方厘米.而中间标有 5 的空白小正方形的面积也为10 ⨯10 = 100 平方厘米,所以这个空白小正方形的面积等于四个角上的小三角形的面积之和.至于剩下的部分,容易看出标有 6,7 的两个空白长方形与标有 8,9 的两个阴影长方形的面积相等,所以图中阴影部分与非阴影部分的面积相等,它们的面积差为零.2.将边长分别为 4、8、12、16、20 的正方形并排在一起(如图),一条与正方形的边平行的直线CD 将该图形分为面积相等的两个部分,那么 AB 的长是多少?182657 394BBA BA 16 4CD81220A164CD81220【分析】如图所示,作出边长为 12 的正方形的上面的边所在的直线,这条直线也将整个图形分成两部分.整个图形的面积为42 + 82 + 122 + 162 + 202 = 42 ⨯ (12 + 22 + 32 + 42 + 52 ) = 16 ⨯ 1⨯ 5 ⨯ 6 ⨯11 = 880 ,所6以直线CD 所分成的两部分的面积都为880 ÷ 2 = 440 .图中虚线所分成的两部分,上面的部分的面积为: 42 + (20 + 16)⨯ (20 - 12) = 304 ,所以这条直线与 直 线 CD 之 间 的 图 形 的 面 积 为 440 - 304 = 136 . 这 个 图 形 是 一 个 长 方 形 , 它 的 长 为12 + 20 + 16 = 48 ,所以它的宽为:136 ÷ 48 = 2 5.6那么 AB 的长为: 20 - 12 + 2 5 = 10 5.6 63.如图,在相距9cm 的平行线 a 和b 之间有一个直角三角形 A 和长方形 B .直角三角形沿直线a 以1cm/s 、长方形 B 沿直线b 以3cm/s 的速度同时朝箭头所指方向开始运动.问 A 和 B 开始运动后从多少秒到多少秒 A 与 B 所重合部分的面积是一个定值(即保持不变).a6cm b 12cm A 12cm B 20cma 6cmb图⑴aabb图⑵ 图⑶【分析】先考虑在长方形 B 的左上角顶点与直角三角形 A 接触时,位于直角三角形斜边的哪个位置.由于长方形 B 的高为6cm ,即上边离b 直线之距离为6cm ,所以上边到直线a 的距离是3cm .另外, 由于直角三角形 A 下边的顶点到直线a 的距离为6cm ,所以当直角三角形与长方形相交时,则长方形的上侧边通过直角三角形斜边的中点.这样,在重合之前的状态(图⑴),各横向长度如图所示.在图⑴中,由于三角形上侧的边长为12cm ,而过斜边的中点的虚线长度6cm ,即是该直角三角形的切口长度,这个长度正好等于上侧边长的一半.A 与B 两图形重合时的面积保持定值是指从图⑵的重合状态到图⑶的重合状态,将该状态与图⑴ 时的状态相比较,可知,直角三角形与长方形所移动的长度之和分别是:到图⑵状态为20cm , 到图⑶状态则为26cm .由于直角三角形的速度是1cm/s 、长方形的速度是3cm/s ,相加便知二者A BAB以每秒4cm 相互接近.所以到达图⑵状态时,需要20 ÷ 4 = 5(s) ;到达图⑶状态需要26 ÷ 4 = 6.5(s) , 也就是说,从5s ∼ 6.5s 之间重合的面积是定值.4.如图所示,圆紧贴着全长为30 厘米、有直角拐弯的折线从一端滚动到另一端(没有离开也没有滑动),在圆周上设一个定点 P ,点 P 从圆开始滚动时是接触折线的,当圆停止滚动时也接触到折线,然而在圆滚动的全部过程中 P 点是不接触折线的.请问:圆的半径是多少厘米?( π = 3.14 , 保留两位小数).⑴caba⑵⑶【分析】设半径为a 厘米,首先考虑一下圆在直线上滚动过的角度是90︒ 时转了 1 圈,如图⑴所示.图中 14 4圆的弧长和圆滚动过的距离相等,即 PQ = 2a ⨯ 3.14 ÷ 4 = 1.57a 厘米.由于本题中在圆滚动的全部 过程中 P 点是不接触折线的,于是圆滚动到拐角时滚动过的角度有以下两种情况:①滚动到拐角时不满270︒ :此时圆恰好转了270︒ ,即 3圈,而图⑵中的b + c 是圆滚动过的距离,4因此b + c = 1.57a ⨯ 3 , b + a + a + c = 1.57a ⨯ 3 + a + a = 16 + 14 ,得到a ≈ 4.47 厘米;②滚动到拐角时滚动过的角度不小于270︒ 也不大于360︒ :此时圆共转动了270︒ + 360︒ = 630︒ ,即圆恰好转 7圈,而图⑶中的d + e 是圆滚动过的距离,因此d + a + a + e = 1.57a ⨯ 7 + a + a = 16 + 14 ,4得到a ≈ 2.31 厘米.检验是否满足条件: d = 16 - 2.31 = 13.69 厘米;圆周 = 2.31⨯ 2 ⨯ 3.14 ≈ 14.51 > d > e .所以在开始滚动和结束滚动以外,点 P 没有接触到折线,所以a = 2.31 厘米也满足条件.P14P16 O a P1.57 Qead aEF真题巩固1.以长方形 ABCD 的边 AB 和CD 为斜边向长方形内作等腰直角三角形 ABE 和CDF ,已知三角形 ABE 的面积为16 ,长方形的周长为 44 ,则三角形 BED 的面积是 . A DB C【分析】由于三角形 ABE 是等腰直角三角形,所以四个这样的三角形可以拼成一个边长为 AB 的正方形,故16 = 1⨯ AB 2 ,得到 AB = 8 .由周长为 44 可知 BC = 44 ÷ 2 - 8 = 14 ,4则 S ∆BED = S ∆ABD - S ∆ABE - S ∆AED = 14 ⨯ 8 ÷ 2 - 16 -14 ⨯ 4 ÷ 2 = 12 . 2.如图,将边长为 1 的正三角形Ⅰ放在一条直线上,让三角形绕顶点C 顺时针转动到达Ⅱ,再继续这样转动到达Ⅲ,则 A 点走过的路程的长为 .AC【分析】图中圆弧即为 A 点走过的路程,分为两段,均为圆心角为120︒ 、半径为 1 的扇形的圆弧.所以,两个扇形圆弧长之和= 2 ⨯ π ⨯1⨯ 120 ⨯ 2 = 4π ,即 A 点走过的路程的长是 4π.360 3 33.如右图,面积为 l 的 ∆ABC 中,BD : DE : EC = 1: 2 :1 ,CF : FG : GA = 1: 2 :1 ,AH : HI : IB = 1: 2 :1 ,求阴影部分面积.A ABCC【分析】设 IG 交 HF 于 M , IG 交 HD 于 N ,如果能求出 IM 和 IG 以及 IN 和 IG 的长度之比,根据面积比例模型就可以求出∆HMN 的面积,进而求出阴影部分的面积.而要求 IM 和 IG 以及 IN 和 IG 的长度之比,只需要求 IM 和 MG 以及 IN 和 NG 的长度之比,为此连接 DI 、 DG 、 IF 、GH .由于 S= 2 S= 2 ⨯ 1 ⨯ 3 S= 1 , S = ⎛1 - 1 ⨯ 1 - 3 ⨯ 3 - 1 ⨯ 3 ⎫S = 3 ,∆HID 3 ∆HBD 3 4 4 ∆ABC 8∆HGD 4 4 4 4 4 4 ⎪∆ABC 16 ⎝ ⎭(如果对线段的平行关系较为熟悉,可以看出 HG ∥ BC ,GD ∥ AB ,所以 BDGH 是平行四边形,那么 S ∆HGD = S ∆BDH = 1 ⨯ 3 S 4 4 ∆ABC = 3 ) 16HGMIF NHGI FB Ⅰ ⅡⅢ根据蝴蝶定理, IN : NG = S∆HID : S ∆HGD = 1 : 3 8 16 = 2 : 3 ,所以 IN = 2IG ;5由于 S ∆HIF = 2 S 3 ∆AIF = 2 ⨯ 3 ⨯ 3 S 3 4 4 ∆ABC = 3 , S 8 ∆HGF = 2 S 3 ∆HAF = 2 ⨯ 1 ⨯ 3 S 3 4 4 ∆ABC = 1,根据蝴蝶定理, 8IM : MG = S : S= 3 : 1 = 3 :1 ,所以 IM = 3IG ; ∆HIF ∆HGF8 8 4(同样地,有 HG ∥ BC , IF ∥ BC ,所以 HG ∥ IF ,且 HG = 1 BC , IF = 3BC ,根据相似三角4 4形性质,有 IM : MG = IF : HG = 3 :1 )所 以 MN = IM - IN = 3 IG - 2 IG = 7IG ,4 5 20那么 S ∆HMN = 7 S 20 ∆HGI = 7 ⨯ 2 S 20 3 ∆AGI = 7 ⨯ 2 ⨯ 1 ⨯ 3 S 20 3 4 4 ∆ABC = 7 . 160同理可得其他 5 个阴影小三角形的面积均为 7 ,所以阴影部分的面积为 7 ⨯ 6 = 21.160 160 804. 四个面积为1 的正六边形如图摆放,求阴影三角形的面积.【分析】如图,将原图扩展成一个大正三角形 DEF ,则∆AGF 与∆CEH 都是正三角形.假设正六边形的边长为为a ,则∆AGF 与∆CEH 的边长都是4a ,所以大正三角形 DEF 的边长为 4 ⨯ 2 - 1 = 7 ,那么它的面积为单位小正三角形面积的 49 倍.而一个正六边形是由 6 个单位小正三角形组成的,所以一个单位小正三角形的面积为 1 ,三角形 DEF 的面积为 49.6 6由于 FA = 4a , FB = 3a ,所以∆AFB 与三角形 DEF 的面积之比为 4 ⨯ 3 = 12.7 7 49同理可知∆BDC 、∆AEC 与三角形 DEF 的面积之比都为 12,所以∆ABC 的面积占三角形 DEF 面49积的1 - 12 ⨯ 3 = 13 ,所以∆ABC 的面积的面积为 49 ⨯ 13 = 13.49 49 6 49 65.有同样大小的立方体 27 个,把它们竖 3 个,横 3 个,高 3 个,紧密地没有缝隙地搭成一个大的立方体.如果有 1 根很直的细铁丝穿过这个大立方体,最多可以穿透几个小的立方体?【分析】假设铁丝穿过3 ⨯ 3 ⨯ 3 的立方体每穿过一个小立方体就被小立方体的面给切断,那么本题可以先考虑铁丝最多可以被切成几段.由于3 ⨯ 3 ⨯ 3 的立方体内部有 6 个截面(每个方向 2 个),铁丝穿过时 不可能与其中的某个截面有 2 个或 2 个以上的交点,也就是说与每个截面最多有 1 个交点,那么 与 6 个截面最多有 6 个交点,铁丝最多被切成 7 段.由于每一段铁丝对应一个小立方体,所以最 多可以穿过 7 个小立方体.。
学而思初二数学秋季班第12讲.几何综合.尖子班.学生版
47初二秋季·第13讲·尖子班·学生版全等三角形是初中几何学习中的重要内容之一,是今后学习其他知识的基础。
判断三角形全等的公理有SAS 、ASA 、AAS 、SSS 和HL (直角三角形),如果所给条件充足,则可直接根据相应的公理证明,但是如果给出的条件不全,就需要根据已知的条件结合相应的公理进行分析,先推导出所缺的条件,引出相应的辅助线然后再证明。
一、常见辅助线的作法有以下几种:1. 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对称”;2. 若遇到三角形的中线,可倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”;3. 遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对称”,所考知识点常常是角平分线的性质定理或逆定理;思路导航13名校期末试题点拨——几何部分题型一:全等三角形与轴对称484. 过图形上某一点作特定的平行线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”;5. 截长法与补短法,具体作法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明。
这种作法,适合于证明线段的和、差、倍、分等类的题目。
二、常见模型1.最值问题:“将军饮马”模型;2. 全等三角形经典模型:三垂直模型、手拉手模型、半角模型以及双垂模型等。
三、尺规作图部分地区会考察尺规作图,难点在于构造轴对称图形解决几何问题。
【例1】 ⑴如下左图,把△ABC 沿EF 对折,叠合后的图形如图所示.若∠A =60°,∠1=95°,则∠2的度数为( )A .24°B .25°C .30°D .35°⑵长为20,宽为a 的矩形纸片(10<a <20),如上右图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去,若在第n 次操作后,剩下的矩形为正方形,则操作停止.当n =3时,a 的值为 .【例2】 ⑴如图所示,在长方形ABCD 称轴l 上找点P ,使得△P AB 、典题精练21C'B'FE CBA 第二次操作第一次操作l DCBA49初二秋季·第13讲·尖子班·学生版△PBC 均为等腰三角形,则满足条件的点P 有( ). A .1个 B .3个 C .5个 D .6个⑵改为:在长方形ABCD ()2AB BC AB BC >≠且的对称轴上找点P ,使得△P AB 、△PBC 均为等腰三角形,则满足条件的点P 有 个⑵已知,横线和竖线相交的点叫做格点,P 、A 、B 为格点上的点,A 、B 的位置如图所示,若此三点能够构成等腰三角形,P 点有 种不同的位置? 【解析】12种,如下图所示:【例3】 ⑴ 如图1,在等边三角形ABC 中,AB =2,点E 是AB 的中点,AD 是高,在AD 上找一点P ,使BP +PE 的值最小;⑵ 如图2,正方形ABCD 的边长为2,E 为AB 的中点,在AC 上找一点P ,使PB +PE 的值最小;⑶ 如图3,⊙O 的半径为2,点A 、B 、C 在⊙O 上,OA ⊥OB ,∠AOC =60°,P 是OB 上一动点,求P A +PC 的最小值;⑷ 如图4,在四边形ABCD 的对角线AC 上找一点P ,使∠APB =∠APD .保留作图痕迹,不必写出作法.图4图3图2图1P DCAOP C BAP E D CB AP E D CBA50【例4】 如图,AD=BC ,DF=CA ,∠C =∠D ,AD 交BC 于点H ,AE ⊥BC 于点E ,点F 在BC上.⑴ 若AN 是△AEC 的角平分线,求证:::AEN ACN S S AE AC △△;⑵ 当∠B=∠BAD +12°时,求∠B 的度数.NNMN ABCDEFHABCEFH H FED CBA【例5】如图1,在ABC∠=∠,BAC∠的平分线ACB B△中,2AO交BC于点D,点H为AO上一动点,过点H作直线l AO⊥于H,分别交直线AB AC BC、、于点、、.N E M⑴当直线l经过点C时(如图2),证明:BN CD=;⑵当M是BC的中点时,写出CE和CD之间的等量关系,并加以证明;⑶请直接写出BN CE CD、、之间的等量关系.初二秋季·第13讲·尖子班·学生版5152一、直角三角形的性质 1. 直角三角形的两个锐角互余;2. 直角三角形斜边上的中线等于斜边的一半;3. 直角三角形的两直角边的乘积等于斜边与斜边上高的乘积,即ab =c h ;4. 勾股定理:直角三角形两直角边的平方和等于斜边的平方,即222c b a =+;5. 在直角三角形中,30°角所对的直角边等于斜边的一半(或含30°的直角三角形三边之比为1:3:2);6. 含45°角的直角三角形三边之比为1:1:2. 二、直角三角形的判定1. 有一个角为90°的三角形是直角三角形;2. 两个锐角互余的三角形是直角三角形;3. 勾股定理的逆定理:在以a 、b 、c 为边的三角形中,若222c b a =+,则这个三角形是以c 为斜边的直角三角形; 思路导航题型二:直角三角形与勾股定理53初二秋季·第13讲·尖子班·学生版4. 一个三角形,如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形.【例6】 在给定的图形内作一条折线AB 1C 1D 1E ,使AB 1⊥AB ,B 1C 1⊥BC ,C 1D 1⊥CD ,D 1E ⊥DE ,且A ,B ,C ,D ,E ,B 1,C 1,D 1都是格点.EDCBA【例7】 如图,AC =AB ,DC =DB ,∠CAB =60°,∠CDB =120°,E 是AC 上一点,F 是AB 延长线上一点,且CE =BF .图1C AEG BFD图2DABCE 思考验证:⑴求证:DE =DF ;⑵在图1中,若G 在AB 上且∠EDG =60°,试猜想CE 、EG 、BG 之间的数量关系并证明; 探究应用:⑶运用⑴⑵解答中所积累的经验和知识,完成下题:如图2,∠ABC =90°,∠CAB =∠CAD =30°,E 在AB 上,DE ⊥AB ,且∠DCE =60°,若AE =3,求BE 的长.典题精练【例85455初二秋季·第13讲·尖子班·学生版NMDC BA训练1. ⑴如图所示,EFGH 是一个台球桌面,有黑白两球分别置于A B 、两点的位置上,试问怎样撞击黑球A ,经桌面HE EF 、连续反弹后,准确击中白球B ?(写出作法并画图)HGF EAB⑵如图,在锐角△ABC 中,4245AB BAC =∠=,°,BAC ∠的平分线交BC于点D ,M 、N 分别是AD 和AB 上的动点,则BM +MN 的最小值是___________.训练2. 如图,在△ABC 中,AC =BC ,∠ACB =90°. 将△ABC 绕点C 逆时针旋转α角,得到△A 1B 1C ,连结BB 1,设B 1C 交AB 于D ,A 1B 1分别交AB 、AC 于E 、F .⑴ 当090︒<α<︒时,如图1,请在不添加任何线段的情况下,找出一对全等三角形,并加以证明(△ABC ≌△A 1B 1C 除外);⑵ 在⑴的条件下,当△BB 1D 是等腰三角形时,求α;⑶ 当90180︒<α<︒时,如图2,求证:△A 1CF ≌△BCD .图2图1ABCA 1B 1E F DDFEB 1A 1CBA训练3. 已知如图,AB=AC ,PB=PC ,PD ⊥AB ,PE ⊥AC ,垂足分别为D 、E .思维拓展训练(选讲)56PEDC B A AB C DEP⑴ 求证:PD=PE ;⑵ 若BP AB =,o 45=∠DBP ,2=AP ,求四边形ADPE 的面积.训练4. ⑴如图,等腰直角三角形ABC 分别沿着某条直线对称得到图形b 、c 、d .若上述对称关系保持不变.平移ABC ∆,使得四个图形能够拼成一个重叠且无缝隙的正方形,此时点C 的坐标和正方形的边长为( )A .11222⎛⎫- ⎪⎝⎭,, B .(11)2-,,C.(11)-, D.1122⎛⎫- ⎪⎝⎭,⑵如图,△ABC 中,AB =BC ,∠B =120°,AB 的垂直平分线交DC 间的数量关系,并证明.57初二秋季·第13讲·尖子班·学生版【练习1】 ⑴如图,正方形纸片ABCD 的边长为1,M ,N 分别是AD 、BC 边上的点,将纸片的一角沿过点B 的直线折叠,使点A 落在MN 上,落点记为A ',折痕交AD 于点E .若M 、N 分别是AD 、BC 边的中点, 则A N '=_________;若M 、N 分别是AD 、BC 边上距DC 最近的n 等 分点(2n ≥,且n 为整数),则A N '=_________(用含有n 的式子表示) ⑵如图,D 为ABC △内一点,CD 平分ACB ∠, BD CD ⊥,A ABD ∠=∠, 若5AC =,3BC =,则BD 的长为( ) A .1 B .1.5 C .2 D .2.5【练习2】 如图,ABC △是等腰三角形,AB AC =,AD 是角平分线,以AC 为边向外作等边三角形ACE ,BE 分别与AD 、AC 交于点F 、点G ,连接CF .⑴ 求证:FBD FCD ∠=∠;⑵ 若1FD =,求线段BF 的长.复习巩固DCB AG F EDCB A第十五种品格:创新创新的力量20世纪40年代,美国有许多制糖公司向南美洲出口方糖,因方糖在海运中会有受潮现象,这给公司带来巨大损失。
聚焦思维:数学教学的根本要义——以“勾股定理(第1课时)”教学为例
为 探 究 引 航 ,不 断 唤 醒 和 激 活 思 维 ,将 学 生 的 学 习 引
焦数学思维活动.聚力学生思维发展。
向 深 人 ,让 学 生 建 立 “属 于 自 己 ”的 知 识 结 构 、思 维 方
2 . 1 情 境 引 学 ,点燃思维
式和学习经验。
《义 务 教 育 数 学 课 程 标 准 (2 0 1 1 年 版 )》指 出 :创
析 、检 验 ,从 而 建 立 完 整 清 晰 的 知 识 结 构 。本 节 课 从 完 成 题 组 、梳 理 知 识 点 ,到 串 点 连 线 、厘 清 知 识 内 部 关 联 ,再 到 拉 线 成 网 、建 立 知 识 网 络 ,均 由 学 生 自 主 完 成 ,教 师 仅 提 供 学 习 素 材 ,设 计 问 题 帮 助 学 生 思 考 ,在 学 生 建 构 过 程 中 给 予 积 极 的 评 价 ,整 个 教 学 过 程 充 分 体 现 了 有 效 教 学 活 动 中 学 生 的 “学 ”与 教 师 的 “教 ”的 和 谐 统 一 ,学 生 是 学 习 的 主 体 ,教 师 是 教 学 活 动 的 组 织 者 、合 作 者 和 引 导 者 。 3 . 2 注重板书设计
循 序 渐 进 不 断 探 究 。如 图 1 ,若 正 方 形 网 格 中 每 个 小
都 能 有 效 地 启 发 学 生 的 思 考 ,使 学 生 成 为 学 习 的 主
体,逐 步 学 会 学 习 。
正 方 形 边 长 为 1 ,显 然 易 知 两 直 角 边 的 长 分 别 为 3 和 4 ( 可 以 数 出 来 ),关 键 是 斜 边 如 何 知 道 呢 ? 学 生 小 组
摘 要 :数 学 是 关 于 思 维 的 科 学 ,培 养 学 生 的 思 维 是 数 学 学 科 独 特 的 育 人 功 能 。 教 学 实 践 中 ,要 对 教 与 学
学而思初二数学秋季班第10讲.勾股定理与逆定理.提高班.教师版
1初二秋季·第10讲·提高班·教师版OD?满分晋级漫画释义三角形12级 成比例线段三角形11级特殊三角形之直角三角形三角形10级 勾股定理与逆定理 10勾股定理与逆定理2初二秋季·第10讲·提高班·教师版勾股定理是几何中几个最重要的定理之一,它揭示了一个直角三角形三条边之间的数量关系,它可以解决许多直角三角形中的计算问题,是解直角三角形的主要依据之一,在生产生活实际中用途很大。
它不仅在数学中,而且在其它自然科学中也被广泛地应用。
勾股定理:如果直角三角形的两直角边长分别为a b ,,斜边长为c ,那么222a b c +=. 直角三角形中常用数:⑴ 整数边:()345,,;()6810,,;()51213,,;()72425,,;()81517,,;()94041,,; ⑵如果()a b c ,,是一组勾股数,那么()ak bk ck ,,也是一组勾股数(k 为正数);⑶含特殊角:()306090︒︒︒,,和()454590︒︒︒,,的三角形三边之比分别为132∶∶和112∶∶.【引例】 一旗杆离地面6m 处折断,旗杆顶部落在离旗杆底部8m 处,旗杆折断之前有多高? 【解析】 如图,设原旗杆底端点为A ,顶端点B ,从C 点处折断,则由题意可知图中6m AC =,8m AB =,90A ∠=︒, 在Rt ABC △中,90A ∠=︒, ∴222AC AB BC +=, ∴2210BC AC AB =+=, ∴61016h =+=例题精讲思路导航知识互联网题型一:勾股定理CBA3初二秋季·第10讲·提高班·教师版∴旗杆折断之前高16m .【例1】 1. 图1和图2中的三角形都是直角三角形,四边形都是正方形,利用图1或图2两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为 ,该定理的结论其数学表达式是 .其中图1是中国数学史上有名的(数学家的名字)弦图.简单写出证明过程.(浙江湖州、新疆中考)【解析】 勾股定理,222a b c +=(直角三角形两直角边的平方和等于斜边的平方.)赵爽(中国数学家,主要贡献是深入研究了《周髀算经》,涉及了勾股定理的理论和证明.)证明:大正方形面积=四个全等直角三角形面积+中间小正方形面积.图1:22224()2abc b a a b =⨯+-=+图2:22()42aba b c +=⨯+,即222a b c +=.【点评】 勾股定理的证明方法很多,比如可用方格来验证勾股定理等等.2. ⑴ 如图1是一个重要公式的几何解释.请你写出这个公式;⑵ 如图2,Rt Rt ABC CDE △≌△,90B D ∠=∠=︒,且B C D ,,三点共线.试证明90ACE ∠=︒;⑶ 伽菲尔德(Garfield ,1881年任美国第20届总统)利用1中的公式和图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.(丰台期末)【解析】 ⑴ 这个公式为222()2a b a ab b +=++.⑵ ∵ABC CDE △≌△,∴BAC DCE ∠=∠.典题精练图2图1a bca bc a b ca b c a b c a b c a bc c b a CBAa bb a图1ab ccA E DC Bb 图24初二秋季·第10讲·提高班·教师版90ACB DCE ACB BAC ∠+∠=∠+∠=∴°. 由于B C D ,,共线, 所以()180ACE ACB DCE ∠=︒-∠+∠1809090=︒-︒=︒.⑶ 梯形ABDE 的面积为()()()()2111222AB ED BD a b a b a b +⋅=++=+;另一方面,梯形ABDE 可分成三个直角三角形,其面积又可以表示成2111222ab ab c ++ ∴()2211112222a b ab ab c +=++,即222a b c +=3. 勾股证明的方法成百上千种,其中《几何原本》中的证法非常经典,是在一个我们非常熟悉的几何图形中实现的(如图所示),同学们,如果直角三角形ABC 的三边长为a b c ,,(c 为斜边),试利用此图证明222a b c +=. cbaNMHFE DCBA ABCE FHMNP【解析】 如右图可知:22ADB ACF ACED AFGP ACF ADB S S S S ==正方形矩形,,△△△≌△∴2AFGP b S =矩形,同理2GHBP a S =矩形,∴222a b c +=【探究对象】勾股定理的分类证明【探究目的】勾股定理是几何学中的明珠,千百年来,人们对它的证明趋之若骛,有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法,这是任何定理无法比拟的。
第一节 勾股定理-学而思培优
第一节 勾股定理二、核心纲要1.勾股定理如果直角三角形两直角边长分别为a 、b,斜边长为c ,那么.222C b a =+即直角三角形两直角边的平方和等于斜边的平方.注:(1)如右图所示,直角三角形中较短的直角边是勾,较长的直角边是股,斜边是弦.(2)勾股定理只对直角三角形适用,而不适用于锐角三角形和钝角三角形.(3)为方便应用勾股定理进行计算,常将222c b a =+进行如下变形: ;222b c a -=①;222a c b -=②;22b c a -=③;22a c b -=④.2b a c +=⑤(4)勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用: ①已知直角三角形的两边求第三边;②已知直角三角形的一边与另两边的关系,求直角三角形的边;③证明三角形中的某些线段的平方关系;④作长为n 的线段.2.勾股定理的证明勾股定理的证明实际采用的是图形面积与代数恒等式的关系相互转化进行证明的,体现了数形结合 的思想.(1)证法一:赵爽的“勾股圆方图”(又称“赵爽弦图”)右图是由4个全等的直角三角形拼成的大正方形,直角三角形的两条直角边分别为a 、b(b>a),斜边为c ,中间是正方形,且边长为b-a .∵ 以c 为边的大正方形的面积为,2c 而4个直角三角形的面积和为,214ab ⨯中间的小正方形的面积为,)(2a b - .)(21422a b ab c -+⨯=∴即.222c b a =+ (2)证法二:邹元治的证明右图是由4个全等的直角三角形拼成的大正方形,直角三角形的两条直角边分别为a 、b ,斜边为c ,中间是正方形,且边长为c .∵ 四个直角三角形的面积与小正方形面积的和为,221422C ab c ab s +=+⨯=大正方形面积 ,)(2b a s +=且四个直角三角形的面积与小正方形面积的和等于大正方形的面积,.2)(22C ab b a +=+∴.222C b a =+∴(3)证法三:1876年美国总统伽菲尔德(Garfield)的证明右图是由2个以a 、b 为直角边,以c 为斜边作两个全等的直角三角形和一个以c 为直角边的等腰直角三角形拼成的直角梯形.,21212122,)(21)()(21222c ab c ab S S s b a b a b a s DEC ADE +=+⋅=+=+=+⋅+=∆∆梯形梯形.21)(2122c ab b a +=+∴ .222C b a =+∴ (4)证法四:陈杰的证明如右图所示,直角边长分别为a 、b 的四个三角形全等,斜边长为c ,图中有3个正方形边长分别为a 、b 、c ,设整个图形面积为S .,212,212222222ab C ab c S ab b a ab b a s +=⨯+=++=⨯++= .222ab c ab b a +=++∴.222c b a =+∴(5)证法五:火柴盒拼图右图火柴盒的一个侧面ABCD 倒下到///D C AB 的位置,连接,/C C 可得到直角梯形//D BCC 和等腰直角三角形./AC C 设AB=a ,BC=b ,AC=c ,利用梯形//D BCC 的面积即可证明勾股定理. ,2)()(212/////b a BD D C BC S D BCC +=⋅+=梯形 ,2221212122D C D BCC /////ab c ab C ab s s s S AC AC ABC +=++=++=∆∆∆梯形 ⋅+=+∴222)(22ab c b a .222c b a =+∴说明:上面的“火柴盒拼图法”曾以证明题的形式出现在中考卷中,其验证过程的实质就是伽菲尔德 总统证法.勾股定理的证明方法有很多种,我们选取了其中比较容易理解的五种,仅供读者参考.3.直角三角形斜边上的高的求法 如右图所示,⋅=⇒=c ab h ch ab4.数学思想 本节涉及到的常用数学思想有:(1)方程思想:勾股定理表达式中有三个量,如果条件中只有一个量,通常需要巧设未知数,灵活地寻找题目中的等量关系,然后利用勾股定理建立方程(组)解题;进而将几何问题代数化.(2)分类讨论思想:有的题目没有明确指出是怎样的三角形,那么就需要对三角形的形状进行讨论,有时指明了是直角三角形,但没有指明哪条边是斜边,也需要对边的情况进行讨论.(3)数形结合思想:勾股定理揭示了直角三角形三边之间的关系,本身体现了数形结合的思想.(4)转化思想:有些问题如果直接解决难以人手,如果换个方向、角度或观点来考虑,使得问题更清晰,更简单.(5)类比思想:类比思想涉及知识的迁移,它把两个(或两类)不同的数学对象进行比较,如果发现它们在某些方面有相同或类似之处,那么就推断它们在其他方面也有可能有相同或类似之处. 本节重点讲解:一个定理,五个证明,五个思想.三、全能突破基 础 演 练1.如图17 -1-1所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.2.A3.B4.C5.D2.一艘轮船以16海里/时的速度离开A 港向东南方向航行,另一艘轮船同时以12海里/时的速度离开A 港向西南方向航行,经过1.5小时后它们相距( ).A.25海里 B .30海里 C .40海里 D .32海里3.若直角三角形两条直角边长分别是3cm 和4cm ,则斜边上的高是( ).cm A 5. cm B 4. cm C 3. cm D 512.4.三个正方形的面积如图17 -1-2所示,则正方形A 的面积为5.在△ABC 中,C B A C ∠∠∠=∠、、,90所对的边分别是a 、b 、c ,若,32=+c a ,5:3:=c a 则△ABC的面积为6.图17 -1-3所示是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A 和B 的距离为 mm.7.某楼梯的侧面视图如图17 -1-4所示,其中AB=4米,,90,30=∠=∠C BAC 因某种活动要求铺设红色地毯,则在AB 段楼梯所铺地毯的长度应为 米.8.如图17 -1-5所示,铁路上A 、B 两地相距25km ,C 、D 为两村庄,DA ⊥AB 于点A .CB ⊥AB 于点B ,已知,10,15km CB km DA ==现在要在铁路AB 上建一个土特产收购站E ,使得C 、D 两村到E 站距离相等,则E 站应建在距A 地多少千米处?能 力 提 升9.如图17 -1-6所示,一个长为10m 的梯子,斜靠在墙上,梯子的顶端距地面的垂直距离为8m ,如果梯子的顶端下滑Im ,那么,梯子与地面和墙围成的三角形的面积( ).A .不变B .大于224mC .小于224mD .不确定10.在△ABC 中,,12,13,20===AD AC AB 高则△ABC 的周长为( ).54.A 44.B 4454.或C 3242.或D11.如图17 -1-7所示,在直线L 上依次摆放着七个正方形,正放置的四个正方形的面积为从左到右依次是1.21,1,1.44,1.69,则=++321s s s ( )21.2.A 65.3.B 34.5.C 78.7.D12.如图17 -1-8所示,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则边AC 上的高为( ).223.A 5103.B 553.C 554.D13.以某直角三角形三边分别作三个正方形,其中两个正方形面积分别为225cm 和,122cm 则第三个正方形的面积是 14.在Rt△ABC 中,,8,6,90cm CA cm BC C ===∠ 动点P 从C 点出发,以每秒2cm 的速度沿CA →AB运动到点B ,则从点C 出发 秒时,可使⋅=∆∆ABC BCP S s 3115.(1)已知Rt△ABC 的周长为,62+其中斜边AB=2,则这个三角形的面积为(2)已知,如图17 -1-9所示,AB CD c ⊥=∠,90 于点,6,13,==CD AB D 则=+BC AC16.图17 -1-10中的螺旋形由一系列等腰直角三角形组成,其序号依次为①、②、③、④、⑤……,则第 n 个等腰直角三角形的斜边长为17.如图17 -1-11所示,,6,10,60,90===∠=∠=∠CD AB A D B求四边形ABCD 的面积.18.如果把勾股定理的边的平方理解为正方形的面积,那么从面积的角度来说,勾股定理可以推广.(1)如图17-1-12(a)所示,以Rt△ABC 的三边长为边作三个等边三角形,则这三个等边三角形的面 积321S S S 、、之间有何关系?并说明理由.(2)如图17-1-12(b)所示,以Rt△ABC 的三边长为直径作三个半圆,则这三个半圆的面积321s s s 、、 之间有何关系?(3)如果将上图中斜边上的半圆沿斜边翻折,180如图17-1-12(c)所示,请探讨两个阴影部分的面积 之和与直角三角形的面积之间的关系,并说明理由.(此阴影部分在数学史上称为“希波克拉底月牙”)19.图17 -1-13所示是一块长、宽、高分别为3cm 、4cm 、6cm 的长方体纸箱(箱纸厚度忽略不计),(1)求长方体底面的对角线长;(2)若揭开盖子EFGH 后,插入一根长为10cm 的细木棒,则细木棒露在外面的最短长度是多少?(3)在A 处有一只蚂蚁,在G 处有一滴蜂蜜,蚂蚁从A 沿表面爬行到G ,求蚂蚁爬行的最短路径长.(4)若蜂蜜在点M 处,且距离F 为lcm ,蚂蚁从A 沿表面爬行到M ,求蚂蚁爬行的最短路径长.(直接写出结果)20.如图17 -1-14所示,在平面直角坐标系中,△ABC 满足:,1,2,90===∠BC AC C点A 、C 分别在x 轴、y 轴上,当A 点从原点开始沿x 轴的正半轴运动,点C 沿y 轴的正半轴运动.(1)当A 在原点时,求原点0到点B 的距离OB ;(2)当OA =OC 时,求原点0到点B 的距离OB .21.在△ABC 中,.,,c AB b AC a BC ===如图17-1-15 (a)所示,,90 =∠C 根据勾股定理,则.222c b a =+若△ABC 不是直角三角形,如图17-1-15(b)和图17-1-15 (c)所示,请你类比勾股定理,试猜想22b a +2c 与的关系,并证明你的结论.中 考 连 接22.(2012.山东青岛)如图17 -1-16所示,圆柱形玻璃杯,高为12cm ,底面周长为18cm ,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为 cm.23 .(2012.陕西)如图17 -1-17所示,从点A(O ,2)发出的一束光,经x 轴反射,过点B(4,3),则这束光从点A 到点B 所经过路径的长为24.(2012.山东泰安)如图17 -1-18所示,在△ABC 中,,,,45AC BE AB CD ABC ⊥⊥=∠垂足分别为D 、E ,F 为BC 中点,BE 与DF 、DC 分别交于点G 、H ,.CBE ABE ∠=∠(1)线段BH 与AC 相等吗?若相等,给予证明;若不相等,请说明理由;(2)求证:.222EA GE BG =-巅 峰 突 破25.在Rt△ABC 中,D BC AC ACB o,12,5,90===∠是BC 上一点,当AD 是么A 的平分线时,则CD26.在等腰△ABC 中,AB=AC ,D 为直线BC 上任意一点,(1)试探究:22AD AB -与BD .DC 之间的关系. (2)应用上述结论解决问题:在△ABC 中,若AB=AC=1,BC 边上有2012个不同的点、、、 21P P ,2012p 记 ),2012321(2、、、、 =⋅+=i C P BP AP m i i i i 则=+++201221m m m (直接写出结果)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
第9级下·超常-超常123·答案版
第一讲 勾股定理
【练习1】 (1)
S 3S 2
S 1
C
B
A
【分析】 3214812S S S =+=+=
(2)
A
B
C
D
【分析】 连结AC ,根据勾股定理222222201525AC AB BC =+=+=,所以25AC =。
而
22
2
72425+=
,所以90D ∠= ,因为四边形内角和为360 ,所以180A C ∠+∠=
【练习2】
【分析】 根据题意可知,图中的2
2
2
2
2
2
503040BC AB AC =-=-=,所以40AB m =,这个车的速度
为40220/m s ÷=,20/72/70/m s km h km h =>,所以这辆车超速了。
【练习3】
【分析】 设旗杆为x 米,则绳子就有1x +米,由勾股定理可知:()2
2251x x +=+,解得12x =米。
【练习4】
【分析】 设这个直角三角形的一条直角边为a ,那么就有22144a a +=,272a =则斜边上的高
272126a c =÷=÷=。
观测点
2
第一讲
第9级下·超常-超常123·答案版
学理科到学而思
【练习5】
【分析】 根据勾股定理,22213512-=,即楼梯的长度为12m ,那么铺在楼梯上的地毯的长度为
51217m +=(平移)
,地毯宽即为楼梯宽是2m ,那么地毯的面积是217234m ⨯=,需要1834612⨯=元。
5m
13m
【练习6】
图1
2
10
【分析】 矩形的面积为10220⨯=,所以拼成的正方形的边长不是整数。
204422=⨯+⨯,422-=,
1
2442
⨯⨯=。
尝试分成四个三角形和一个正方形。
图2
图32
22
10。
