五年级奥数.几何.勾股定理与弦图(C级).学生版
五年级奥数[1].几何.勾股定理与弦图(B级)学生版
![五年级奥数[1].几何.勾股定理与弦图(B级)学生版](https://img.taocdn.com/s3/m/b30f9bca3169a4517623a337.png)
勾股定理与弦图课前预习华盛顿的傍晚友爱的小伴侣们：“在那山的那边海那边的美国首都华盛顿，有一位中年人，他聪慧又勤奋，他潜心探讨，他反复思考与演算……”那是1876年一个周末的傍晚，在美国首都华盛顿的郊外，有一位中年人正在闲逛，观赏黄昏的美景，他就是当时美国俄亥俄州共和党议员加菲尔德。
他走着走着，突然发觉四周的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争辩，时而小声探讨。
由于奇异心驱使，加菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么。
只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。
于是加菲尔德便问他们在干什么？那个小男孩头也不抬地说：“请问先生，假如直角三角形的两条直角边分别为3和4，那么斜边长为多少呢？”加菲尔德答道：“是5呀。
”小男孩又问道：“假如两条直角边分别为5和7，那么这个直角三角形的斜边长又是多少？”加菲尔德不加思考地回答到：“那斜边的平方确定等于5的平方加上7的平方．”小男孩说：“先生，你能说出其中的道理吗？”加菲尔德一时语塞，无法说明白，心里很不是味道。
加菲尔德不再闲逛，马上回家，潜心探讨小男孩给他出的难题。
他经过反复思考与演算，最终弄清了其中的道理，并给出了简洁的证明方法。
具体方法如下：两个全等的Rt△ABC和Rt△BDE可以拼成直角梯形ACDE，则梯形面积等于三个直角三角形面积之和。
即（AC＋DE）×CD÷2＝AC×BC÷2＋BD×DE÷2＋AB×BE÷2（a＋b）2÷2＝a×b÷2＋a×b÷2＋c×c÷2化简整理得a2＋b2＝c2点评：此种解法主要利用了三角形的面积公式：底×高÷2，和梯形的面积公式：（上底+下底）×高÷2． 而在我国对于勾股定理的证明又做出了那些贡献哪？ 在我国古代，把直角三角形叫做勾股形。
通用版五年级奥数《勾股定理与弦图》讲义
华盛顿的傍晚亲爱的小朋友们：“在那山的那边海那边的的美国首都华盛顿，有一位中年人，他聪明又勤奋，他潜心探讨，他反复思考与演算……，那是1876年一个周末的傍晚，在美国首都华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员加菲尔德。
他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨。
由于好奇心驱使，加菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么。
只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。
于是加菲尔德便问他在干什么？那个小男孩头也不抬地说：“请问先生，如果直角三角形的两条直角边分别为3和4，那么斜边长为多少呢？”加菲尔德答道：“是5呀。
”小男孩又问道：“如果两条直角边分别为5和7，那么这个直角三角形的斜边长又是多少？”加菲尔德不加思索地回答到：“那斜边的平方一定等于5的平方加上7的平方．”小男孩说：“先生，你能说出其中的道理吗？”加菲尔德一时语塞，无法解释了，心里很不是滋味。
加菲尔德不再散步，立即回家，潜心探讨小男孩给他出的难题。
他经过反复思考与演算，终于弄清了其中的道理，并给出了简洁的证明方法。
具体方法如下： 两个全等的Rt△ABC和Rt △BDE 可以拼成直角梯形ACDE ， 则梯形面积等于三个直角三角形面积之和。
即（AC ＋DE ）×CD÷2＝AC×BC÷2＋BD×DE÷2＋AB×BE÷2 （a ＋b ）2÷2＝a×b÷2＋a×b÷2＋c×c÷2 化简整理得a 2＋b 2＝c 2课前预习勾股定理与弦图点评：此种解法主要利用了三角形的面积公式：底×高÷2，和梯形的面积公式：（上底+下底）×高÷2．而在我国对于勾股定理的证明又做出了那些贡献哪？ 在我国古代，把直角三角形叫做勾股形。
小学奥数题库《几何》-直线型-勾股定理和弦图-5星题(含解析)
几何-直线型几何-勾股定理和弦图-5星题课程目标知识提要勾股定理和弦图• 勾股定理在直角三角形中，两条直角边的平方和等于斜边的平方。
即：AB 2 + AC 2 = BC 2 • 勾股图与弦图(a +b)2−4ab 2=a 2+2ab +b 2−2ab =c 2，所以c 2=a 2+b 2 (a −b)2+4ab2=a 2−2ab +b 2+2ab =c 2，所以c 2=a 2+b 2精选例题勾股定理和弦图1. 如下列图所示，长方形ABCD 中被嵌入了6个相同的正方形．AB =22厘米．BC =20厘米，那么每一个正方形的面积为平方厘米．【答案】40【分析】如下列图所示，对每个正方形作弦图，设小直角三角形的长直角边为x 厘米，短直角边为y 厘米，那么{3x +y =203x +2y =22，所以{x =6y =2，小正方形面积为62+22=40(平方厘米)． 2. 在下列图中，将一个每边长均为12厘米的正八边形的8个顶点间隔地连线，可以连出两个正方形．图中阴影局部的面积是平方厘米．【答案】288【分析】如下左图，记AD =a ，由对称性知，DB =a ，BC =a ．取E 为DC 中点，连接BE ，将△ABC 分成直角三角形ABE 和等腰直角三角形BEC ． 四个△BEC 可以拼成一个边长a 的正方形．记BE=b，那么CE=b，DE=b．由AE=a+b，BE=b知：由4个△ABE和一个以a为边长的正方形可拼成一个以AB为边长的正方形〔如下右弦图〕．题中阴影可看做8个△ABE再加上8个△BEC的面积和，4个△ABE与4个△BEC拼成边长为12的正方形，因此此题答案为122×2=288平方厘米．3. 如下列图所示，一块边长为180厘米的正方形铁片，四角各被截去了一个边长为40厘米的小正方形．现在要从剩下的铁片中剪出一块完整的正方形铁片来．剪出的正方形面积最大为平方厘米．【答案】18000【分析】如右图所示，铁片分为中间的正方形和四个长方形两局部，中间局部的面积为1002= 10000平方厘米，四个长方形每个的面积为40×100=4000平方厘米，剪出的最大正方形为中间的正方形加上四个长方形的一半，面积为10000+4000÷2×4=18000平方厘米．4. 平面上的五个点A，B，C，D，E满足：AB=16厘米，BC=8厘米，AD=10厘米，DE= 2厘米，AC=24厘米，AE=12厘米．如果三角形EAB的面积为96平方厘米，那么点A到CD的距离等于厘米．【答案】12013【分析】得三角形CAD是直角三角形，CD=26厘米，点A到CD的距离为10×2426=12013厘米．5. 如图，在正方形ABCD中，E、F分别在BC与CD上，且CE=2BE，CF=2DF，连接BF、DE，相交于点G，过G作MN、PQ得到两个正方形MGQA和PCNG，设正方形MGQA的面积为S1，正方形PCNG的面积为S2，那么S1:S2=．【答案】9:4【分析】连接BD、EF．设正方形ABCD边长为3，那么CE=CF=2,BE=DF=1,所以，EF2=22+22=8,BD2=32+32=18.因为EF2⋅BD2=8×18=144=122,所以EF⋅BD=12.由梯形蝴蝶定理，得S△GEF:S△GBD:S△DGF:S nBGE=EF2:BD2:EF⋅BD:EF⋅BD=8:18:12:12=4:9:6:6,所以，S△BGE=64+9+6+6S梯形BDFE=625S梯形BDFE.因为S△BCD=3×3÷2=92,S△CEF=2×2÷2=2,所以S 梯形BDFE =S △BCD −S △CEF =52, 所以， S △BGE =625×52=35. 由于△BGE 底边BE 上的高即为正方形PCNG 的边长，所以 CN =35×2÷1=65, ND =3−65=95, 所以AM:CN =DN:CN =3:2,那么S 1:S 2=AM 2:CN 2=9:4.6. 将矩形ABCD 分成四个全等的矩形，如下列图所示．假设AE =29厘米AF =41厘米，请问AC 的长度是多少厘米？【答案】71厘米【分析】设AD =a ，DE =EF =b ，所以a 2+b 2=292，a 2+(2b)2=412，由此得b 2=280．于是AC 2=a 2+(4b)2=(a 2+b 2)+15b 2=292+15×280=5041=712．所以AC =71厘米．7. 如下列图所示，长方形ABCD ，AB =24，BC =18，把AB 边对折到AC 上与AC 重合，把AD 边也对折到AC 上与AC 重合，请问得到的新图形的面积是多少？【答案】255【分析】如上图所示，把AB 对折到AC 上与AC 重合，把AD 对折到AC 上与AC 重合，得到四边形AECF ，由勾股定理，AC =30，设BE =EG =x ，S △ABC =S △BAE +S △AEC ，所以24×18÷2=24x ÷2+30x ÷2，那么x =8，设FH =DF =y ，S △ADC =S △ADF +S △AFC ，所以24×18÷2=18y ÷2+30y ÷2，那么y =9，S 四边形AECF =S △AEC +S △AFC =30×(8+9)÷2=255．8. 三角形ABC 中，线段AR ．BQ 分别是BC 、AC 边上的中线，且BQ 与AR 互相垂直．如下图，AC =8、BC =6．请问AB 2+BC 2+CA 2等于多少？【答案】120【分析】如右图所示，连接RQ ，AR 与BQ 交于O 点，设AO =c ，BO =a ，OR =d ，OQ =b ，因为c 2+b 2=AQ 2=14AC 2=16，a 2+d 2=BR 2=14BC 2=9， 又因为a 2+c 2=AB 2，b 2+d 2=QR 2=14AB 2，所以54AB 2=a 2+b 2+c 2+d 2=16+9=25．所以AB 2=20．所以AB 2+AC 2+BC 2=20+64+36=120．9. 如下列图所示，点E 是正方形ABCD 的CD 边上的一点，以BE 为一条直角边作等腰直角三角形BEF ，斜边BF 交AD 于G ，AG =5厘米，GD =15厘米．求三角形BEF 的面积．【答案】272平方厘米【分析】如下列图作辅助线，由于AG =5，而AB =20，令SF =a ，而SB =4a ．而MN =20+20−a =4a ．解之得a=8，那么FN=12，MN=32，NE=20，那么阴影局部面积为：(122+202)÷2= 272(平方厘米)．10. 下列图是由边长为3厘米和4厘米的两个正方形组成．请按尺寸在发给你的彩纸上画上这一图形，再将它剪成3块，拼成一个大的正方形，并求这个大正方形的边长是多少？【答案】5厘米【分析】此题考査考生对弦图的认识．面积和=32+42=52，所以拼成大正方形边长为5．边长5厘米．拼法如下列图所示．11. 如下列图所示，对角线BD将矩形ABCD分割为两个三角形，AE和CF分別是两个三角形上的高，长度都等于6厘米，EF的长度为5厘米，求矩形ABCD的面积．【答案】78【分析】如下列图所示，将AE平移到AʹF，因为AE是三角形ABD的高，所以AE⊥BD，AʹF⊥BD，AAʹFE是矩形，并且Aʹ、F、C在同一条直线上面，再根据AAʹ⊥AʹF，运用勾股定理可以得到AC2=AAʹ2+AʹC2，其中AAʹ=EF=5厘米，AʹC=AE+FC=12厘米，由此根据勾股定理可求得矩形ABCD的对角线AC的长度为13厘米，由于BD也是矩形ABCD的对角线，所以BD 的长度也为13厘米，那么矩形ABCD的面积为三角形ABD和三角形BCD的面积之和，为13×6÷2×2=78(平方厘米)．12. 如下列图两个正方形的边长分别是a和b〔a>b〕，将边长为a的正方形切成四块大小、形状都相同的图形，与另一个正方形拼在一起组成一个正方形．【答案】见解析．【分析】拼成大正方形的面积应是a×a+b×b，设边长c，那么有等式c×c=a×a+b×b，又因为将边长为a的正方形切成四个全等形，那么分割线一定经过正方形中心，假设切割线MN为大正方形边长，如图〔1〕，一定有MN×MN=a×a+b×b，而MH=a，那么：NH=b，所以AN=CM=BH=(a−b)÷2，由此可以确定MN，然后将MN绕中心O旋转90∘到EF位置，即可把正方形切成符合要求的4块．如图〔2〕与图〔3〕．这种分法同时确保图〔3〕的中间局部就是边长为b的小正方形．这是因为：中心四边形的角即边长为a的正方形的四个角，∠A，∠B，∠C，∠D，又因为各边长度相等．因此中心四边形是正方形．中心正方形的边长=[a−(a−b)÷2]−(a−b)÷2=a−(a−b)=b．因此，中间局部是边长为b的正方形．13. 如图，以AD为直径的半圆O内接一个等腰梯形ABCD，梯形的上底是60，下底是100，以梯形上底和腰为直径向外作半圆，形成的阴影局部的面积是多少？〔π取3.14〕【答案】2258【分析】由可得，阴影局部的面积为梯形面积加以AB、BC、CD为直径的半圆面积减去以AD 为直径的半圆面积，作OE垂直于BC，根据勾股定理可得梯形的高OE为40，那么AB2=BF2+ AF2=402+202=2000，阴影局部的面积为：1 2(AD+BC)⋅OE+12π(AB2)2+12π(CD2)2+12π(BC2)2−12π(AO2)2=2258.14. 从一块正方形的玻璃板上锯下宽为0.5米的一个长方形玻璃条后，剩下的长方形的面积为5平方米，请问锯下的长方形玻璃条的面积等于多少？【答案】1.25平方米【分析】我们先按题目中的条件画出示意图〔如图a〕，我们先看图中剩下的长方形，它的面积为5平方米，它的长和宽相差0.5米，我们可以将这样形状的四个长方形拼成一个弦图〔如图b〕．图b 是一个大正方形，它的边长等于长方形的长和宽之和，中间的那个小正方形的边长，等于长方形的长和宽之差，即0.5米．所以中间的小正方形的面积为0.5×0.5=0.25平方米那么大正方形的面积为5×4+0.25=20.25平方米因为4.5×4.5=20.25所以大正方形的边长等于4.5米．所以原题中剩下的长方形的长与宽的和为4.5米，而长与宽的差为0.5米，所以剩下的长方形的长为：(4.5+0.5)÷2=2.5米即原正方形的边长为2.5米．又知锯下的长方形玻璃条的宽为0.5米，于是可得锯下的长方形玻璃条的面积为2.5×0.5=1.25平方米15. 如下列图所示，这是一张十字形纸片，它是由五个全等正方形组成，试沿一直线将它剪成两片，然后再沿另一直线将其中一片剪成两片，使得最后得到的三片拼成两个并列的正方形．【答案】见解析．【分析】实际拼成两个并列的正方形就是一个长方形，其长是宽的2倍，设十字形面积是5个平方单位，长方形的长为x 长度单位，宽为x 2长度单位，那么有x x 2=5,x 2=10，即x 2=32+12，由勾股定理可知：所求长方形的长可视为一直角三角形直角边分别是3和1的斜边．它恰是两个对角顶点的连线．剪拼方法如下列图所示，甲拼在甲′位置，乙拼在乙′位置，就可得符合题意的图形．【总结】假假设沿第二条线把另一片也剪成两片，那么共剪成的4片是4个全等多边形，这时两条直线都经过十字形的中心，并且互相垂直．剪开的这4个图形其中一个绕中心旋转90∘也和另一个重合．由此我们便得到一个重要结论：对于一个正方形来讲，如果从中心沿360∘÷4=90∘角的两边切开，得到整个图形的14，这个14的图形假设绕中心旋转90∘一定和另外的14的图形重合．对于一个正三角形来讲，如果从中心沿360∘÷3=120∘角的两边切开，得到整个图形的13，这个13的图形假设绕中心旋转120∘一定也和另外的13的图形重合．一般情况：对于一个正n 边形，如果从它的中心沿360∘n 的角的两边剪开，得到整个图形的1n ，这个1n 的图形假设绕中心旋转360∘n 角，一定也和另一个1n 图形重合． 16. 从一个正方形的木板上锯下宽1m 的一个长方形木条后，剩下的长方形面积为6m 2，问锯下的长方形木条面积是多少？【答案】6m 2【分析】我们用构造“弦图〞的方法，取同样大小的4个剩下的长方形木板拼成一个大正方形〔如右下列图〕，同时中间形成了一个小正方形〔图中阴影局部〕．仔细观察这幅图就会发现，中间阴影小正方形的边长正好是长方形木板的长与宽之差〔1m 〕．那么，阴影小正方形的面积1×1=1(m 2)所以，整个大正方形的面积是1+4×6=25=5×5(m 2)求得大正方形的边长为5m ．那么，剩下的长方形木条的长−宽=1，长+宽=5，可得剩下的长方形木条的长为(5+1)÷2=3(m)宽为(5−1)÷2=2(m)所以，锯下的长方形木条面积是3×2=6(m2)。
勾股定理与弦图
E A
3
B
4CD【今日讲来自】 例2，例3，例5，【讲题心得】 ______________________________________________________________.
【家长评价】 ______________________________________________________________ ______________________________________________________________.
本讲主线
1. 勾股定理、勾股数 2. 弦图模型的应用
勾股定理与弦图
1. 勾股定理：在直角三角形中,两条直角边的平方和等于斜边的平方. 2. 公式：a2 b2 c2
c a
？
？
3
5
b
4
12
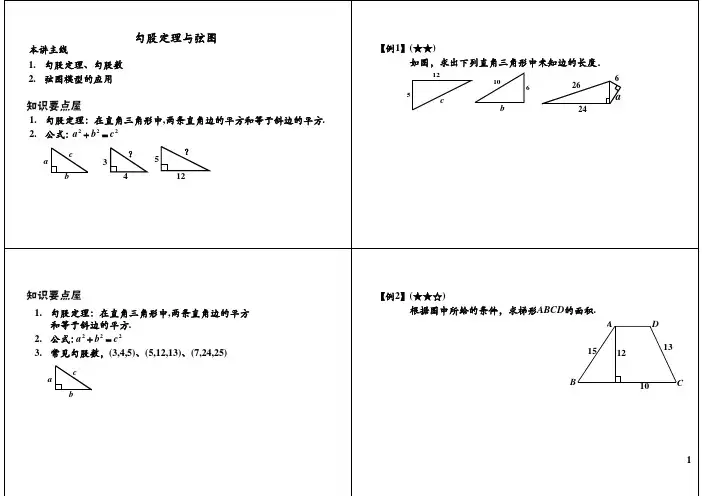
【例1】(★★) 如图，求出下列直角三角形中未知边的长度．
12
5
c
10 6
b
6 26
a
24
1. 勾股定理：在直角三角形中,两条直角边的平方 和等于斜边的平方.
3
A
C
D
2
【例5】(★★★☆) 试用图形证明勾股定理.
两种弦图模型：
“屁股向内”
“屁股向外”
知识大总结 1. 勾股定理公式：a2 b2 c2 2. 常见勾股数(3,4,5)、(5,12,13)、(7,24,25) 3. 两个弦图模型
c ab
“屁股向内” “屁股向外” “大裤衩”
【例6】(★★★★☆) (第7届日本算术奥林匹克决赛试题) 在直角边为3与4的直角三角形各边上向外分别作正方形，三个正 方形顶点顺次连接成如左下图所示的六边形ABCDEF. 求这个六边 形的面积是多少？ F
五年级春季第1讲——勾股定理
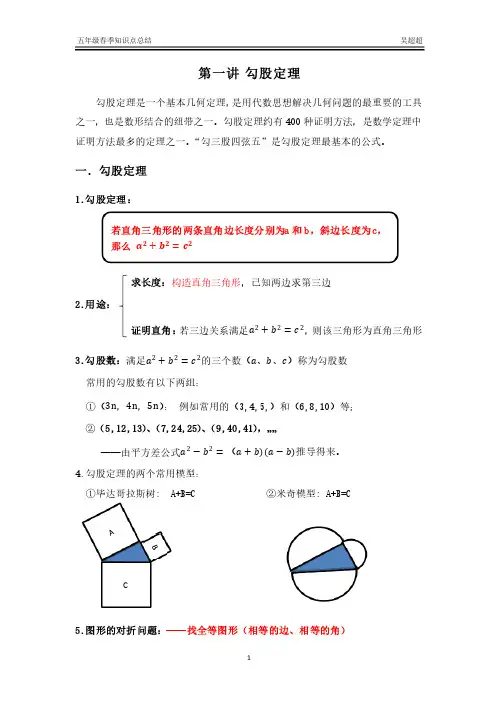
第一讲勾股定理勾股定理是一个基本几何定理，是用代数思想解决几何问题的最重要的工具之一，之一，也是数形结合的纽带之一。
勾股定理约有也是数形结合的纽带之一。
勾股定理约有400种证明方法，是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
“勾三股四弦五”是勾股定理最基本的公式。
一．勾股定理1.勾股定理：求长度：构造直角三角形，已知两边求第三边2.用途：证明直角：若三边关系满足a2+b2=c2，则该三角形为直角三角形则该三角形为直角三角形 3.勾股数：满足a2+b2=c2的三个数（a、b、c）称为勾股数常用的勾股数有以下两组：常用的勾股数有以下两组：常用的勾股数有以下两组：①（①（3n，4n，5n）：例如常用的（例如常用的（3,4,5,3,4,5,3,4,5,）和（）和（）和（6,8,106,8,106,8,10）等；）等；）等；②（5,12,13）、（7,24,25）、（9,40,41），……——由平方差公式——由平方差公式a2−b2=（a+b)(a−b)推导得来。
推导得来。
4.4.勾股定理的两个常用模型：勾股定理的两个常用模型：勾股定理的两个常用模型：①毕达哥拉斯树①毕达哥拉斯树①毕达哥拉斯树: A+B=C: A+B=C: A+B=C ②米奇模型②米奇模型②米奇模型: A+B=C: A+B=C5.图形的对折问题：——找全等图形（相等的边、相等的角）若直角三角形的两条直角边长度分别为a和b，斜边长度为c，那么a2+b2=c2C 二．常用公式复习1.平方差公式：a 2−b 2=（a +b)(a −b)推导过程： 如图：大正方形边长为a ，小正方形边长为b ；那么：S 阴影=a 2−b 2；将阴影部分重新剪拼将阴影部分重新剪拼又可得：S 阴影=（a +b)(a −b)2.完全平方公式：(a ±b)2=a 2±2ab +b 2 以以(a +b)2=a 2+2ab +b 2为例，推导过程如下：为例，推导过程如下：如图：小、中正方形边长分别为如图：小、中正方形边长分别为a ，b整体：整体：S 大正方形=(a +b)2 分解：分解：S 大正方形=a 2+2ab +b 2三．练习题【练习1】根据下图所给数据，求出AB 长度。
勾股定理与弦图
勾股定理与弦图公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]
课前热身
神奇的无字证明
求下面各三角形中未知边的长度。
有一个直角边为1和1的直角三角形，以它的斜边和1为直角边，向外作另一个直角三角形。
重复以上操作，如下图。
求第1023个直角三角形的斜边长度是_____。
第_____个直角三角形的斜边长度是17。
勾股定理与弦图
(★★)
(★★★
(★★★
根据图中所给的条件，求梯形ABCD的面积。
(★★★
如图，请根据所给的条件，计算出大梯形的面积（单位：厘米）。
(★★★
如图，在四边形ABCD中，AB＝30 ，AD＝48，BC＝14 ，CD＝40，∠ADB＋∠DBC＝90°。
请问：四边形ABCD的面积是多少
弦图
⑴大正方形边长为：a＋b
⑵小正方形边长为：a－b
⑶中正方形边长为：c
(★★★
一个直角三角形的斜边长8厘米，两个直角边的长度差为2厘米，求这个三角形的面积
(★★★★
从一块正方形玻璃上裁下宽为16分米的一长方形条后，剩下的那块长方形的面积为336平方分米，原来正方形的面积是多少平方分米
本讲总结
重点例题：例1，例2，例6，例7。
小学奥数-勾股与弦图
勾股与弦图定 义：勾股定理：如果直角三角形的两直角边长分别为，斜边长为，那么a b ，c ．222a b c +=中， ,则Rt ABC △90C ∠=︒222a b c +=直角三角形中常用数：⑴ 整数边：；；；；；()345，，()6810，，()51213，，()72425，，()81517，，等；()94041，，⑵ 如果是一组勾股数，那么也是一组勾股数（k 为正数） ()a b c ，，()ak bk ck ，，勾股定理的使用常常会联系弦图，如下图分别为外弦图和内弦图：外弦图内弦图cba C B A【例1】如图，要将楼梯铺上地毯，则需要 米的地毯．【例2】如图，以三角形ABC的三边为边长向外作三个正方形，正方形内的数代表正方形的面积，求未知正方形的面积.【例3】如图，是由一个直角边都是1的直角三角形向外作直角三角形得到，形成一个美丽的螺旋图案，第8个直角三角形的斜边是多少？【例4】如图所示，三角形都是直角三角形，四边形都是正方形，最大正方形的边长是7，问：除最大正方形外的所有正方形的面积之和是多少？【例5】如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为 ．【例6】下图是学校一个正方形花圃的设计图，图中阴影部分是花圃，空白部分是草坪。
求花圃的面积是多少平方米？【例7】 如图，是由四个完全相同的长方形拼成，大正方形的面积是100平方分米，小正方形的面积是16平方分米，则每个长方形的面积是多少平方分米，长方形的短边是多少分米？【例8】如图，CDEF 是正方形，ABCD 是等腰梯形，它的上底AD=23厘米，下底BC=35厘米，求三角形ADE 的面积.【例9】如下图所示，两个正方形ABCD 和DEFG 的边长都是整数厘米，点E 在线段CD 上，且CE<DE,线段CF=5厘米，则五边形ABCFG 的面积等于多少平方厘米？FGDECB A【例10】如下图所示，一个边长为10厘米的正方形木板斜靠在墙角上（木板厚度不计），AO距离为8厘米，那么点C距离地面的高度是多少厘米？。
勾股定理与弦图
直角三角形的斜边长度是_____。第_____个直角三角形的斜边长
度是17。
11
1
1
1
1
1 1
…………… 1
【例3】（★★★） 根据图中所给的条件，求梯形ABCD的面积。
AD
15 12 13
BE
C
10
【例4】（★★☆） 如图，请根据所给的条件，计算出大梯形的面积（单位：厘米）。
A
D
8
6
B
C
15
1
【例5】（★★★） 如图，在四边形ABCD中，AB＝30 ， AD＝48，BC＝14 ，CD＝ 40，∠ADB＋∠DBC＝90°。请问：四边形ABCD的面积是多少？
课前热身
B c
a
C
b
勾股定理与弦图
勾股定理 △ABC为直角三角形
A
a2 b2 c2
神奇的无字证明
【例1】（★） 求下面各三角形中未知边的长度。
B
5
c
B
a
5
C
12 A C
A 4
6 26
b 24
【例2】（★★☆）
有一个直角边为1和1的直角三角形，以它的斜边和1为直角边，
向外作另一个直角三角形。重复以上操作，如下图。求第1023个
【例7】（★★★★） 从一块正方形玻璃上裁下宽为16分米的一长方形条后，剩下的 那块长方形的面积为336平方分米，原来正方形的面积是多少平 方分米？
2
A
D
B
C
弦图
⑴大正方形边长为：a＋b ⑵中正方形边长为：c ⑶小正方形边长为：b－a
【例6】（★★★） 图中有三个大小不同的正方形，其中大正方形的周长比小正方形 的周长大8，大正方形的面积比中正方形的面积大12，大正方形 的面积是多少？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
勾股定理与弦图课前预习华盛顿的傍晚亲爱的小朋友们：“在那山的那边海的那边的美国首都华盛顿，有一位中年人，他聪明又勤奋，他潜心探讨，他反复思考与演算……”，那是1876年一个周末的傍晚，在美国首都华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员加菲尔德。
他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨。
由于好奇心驱使，加菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么。
只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。
于是加菲尔德便问他们在干什么？那个小男孩头也不抬地说：“请问先生，如果直角三角形的两条直角边分别为3和4，那么斜边长为多少呢？”加菲尔德答道：“是5呀。
”小男孩又问道：“如果两条直角边分别为5和7，那么这个直角三角形的斜边长又是多少？”加菲尔德不加思索地回答到：“那斜边的平方一定等于5的平方加上7的平方．”小男孩说：“先生，你能说出其中的道理吗？”加菲尔德一时语塞，无法解释了，心里很不是滋味。
加菲尔德不再散步，立即回家，潜心探讨小男孩给他出的难题。
他经过反复思考与演算，终于弄清了其中的道理，并给出了简洁的证明方法。
具体方法如下：两个全等的Rt△ABC和Rt△BDE可以拼成直角梯形ACDE，则梯形面积等于三个直角三角形面积之和。
即（AC＋DE）×CD÷2＝AC×BC÷2＋BD×DE÷2＋AB×BE÷2（a＋b）2÷2＝a×b÷2＋a×b÷2＋c×c÷2化简整理得a2＋b2＝c2点评：此种解法主要利用了三角形的面积公式：底×高÷2，和梯形的面积公式：（上底+下底）×高÷2． 而在我国对于勾股定理的证明又做出了那些贡献哪？在我国古代，把直角三角形叫做勾股形。
把直角三角形的较短直角边称为“勾”，较长直角边为“股”，斜边称为“弦”，所以把这个定理称为“勾股定理”。
勾股定理揭示了直角三角形边之间的关系。
即：在直角三角形中俩条直角边的平方和等于斜边的平方。
公元前11世纪的《周髀算经》中提到:故折矩,以为句广三,股修四、径修五．既方之.外半卿一矩,环而共盘.得成三、四、五．三国时期的赵爽注解道:句股各自乘,并之为弦实,开方除之,即弦.案:弦图又可以句股相乘为朱实二,倍之为朱实四,以句股之差自相乘为中黄实,加差之,亦成弦实．汉朝张苍、狄昌寿整理的《九章算术》第九卷为《句股》.其中解释到:短面曰句，长面曰股，相与结角曰弦.句短其股，股短其弦．句股各自乘，并，而开方除之，即弦。
勾股定理的证明：（1）方法一：将四个全等的直角三角形拼成如图所示的正方形：()22222142.ABCD S a b c aba b c =+=+⨯∴+=正方形DCB A（2）方法二:将四个全等的直角三角形拼成如图所示的正方形：()22222142.S c a b aba b c =-+⨯∴+=正方形EFGHGFEH（3）方法三：“总统”法.如图所示将两个直角三角形拼成直角梯形：2()()112222ABCD a b a b S ab c ++==⨯+梯形 222.a b c ∴+=勾股定理:直角三角形中的两直角边平方后的和等于斜边的平方．注：勾——最短的边、股——较长的直角边、 弦——斜边。
勾股定理实际上包含两方面的内容：① 如果一个三角形是直角三角形，那么两条直角边的平方之和等于斜边的平方； ② 如果一个三角形有两边的平方和等于第三边的平方，那么它一定是直角三角形． 勾股数：满足a 2 +b 2=c 2的三个正整数，称为勾股数．勾股数扩大相同倍数后，仍为勾股数．常用勾股数：3、4、5； 5、12、13；7、24、25；8、15、17。
弦图：知识框架GFEHCABcba1.会用勾股定理解决简单问题。
2.会用勾股定理的逆定理判定三角形是否为直角三角形3.勾股定理与弦图的联系与应用【例1】如图，以一个直角三角形的三边为边长分别向外作三个正方形，如果两个较大正方形的面积分别是576和676，那么最小的正方形的面积为【巩固】如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm,则正方形A ，B ，C ，D 的面积之和为___________cm 2。
【例2】已知，如图，四边形ABCD 中，AB=3cm ，AD=4cm ，BC=13cm ，CD=12cm ，且 ∠A=90°，求四边形ABCD 的面积。
例题精讲重难点ABCD7cm A D【例3】在B 港有甲、乙两艘渔船，若甲船沿北偏东６0°方向以每小时8海里的速度前进，乙船沿南偏东某个角度以每小时15海里的速度前进，2小时后，甲船到M 岛，乙船到P 岛，两岛相距34海里，你知道乙船是沿哪个方向航行的吗？【巩固】如图，某沿海开放城市A 接到台风警报，在该市正南方向100km 的B 处有一台风中心，沿BC 方向以20km/h 的速度向D 移动，已知城市A 到BC 的距离AD=60km ，那么台风中心经过多长时间从B 点移到D 点？如果在距台风中心30km 的圆形区域内都将有受到台风的破坏的危险，正在D 点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险？【例4】 从一个正方形的木板上锯下宽0.5米的一个长方形木条以后，剩下的长方形的面积为5平方米，问锯下的长方形木条的面积等于多少？A BC D【巩固】从一块正方形玻璃上裁下宽为16分米的一长方形条后，剩下的那块长方形的面积为336平方分米，原来正方形的面积是多少平方分米？【例5】如图,P是正方形ABCD外面一点,船为12厘米.△APB的面积是90平方厘米，ACPB的面积是48平方厘米．请你回答:正方形ABCD的面积是多少平方厘米?【巩固】有一个长方形，它的长是宽的4倍，对角线长34cm。
求这个长方形的面积。
【例6】.如图，EFGH是正方形ABCD的内接四边形，四边形EFGH的面积是94.5.已知EG=15,FH=13,求正方形ABCD的面积．【巩固】如图所示，在四边形ABCD中，E，F，G，H分别是ABCD各边的中点，求阴影部分与四边形PQRS 的面积之比。
【例7】.如图,一张长14厘米,宽11厘米的长方形纸片最多能裁出多少个长4厘米、宽1厘米的纸片?怎样裁?请画图说明．【巩固】三个面积都是12的正方形放在一个长方形的盒子里面，如图7-15，盒中空白部分的面积已经标出，求图中大长方形的面积？【例8】.有5个长方形,它们的长和宽都是整数,且5个长和5个宽恰好是1～10这10个整数；现在用这5个长方形拼成1个大正方形,那么,大正方形面积的最小值为多少? 【巩固】已知两数的和为3，两数的积为1.25，求两数？【例9】.如图,A在线段BG上,ABCD和DEFG都是正方形,面积分别为7和11.求三角形CDE的面积的平方值?【巩固】(第8届华罗庚金杯赛小学组第一试决赛试题第4题)如图32-6(b),平面上CDEF是正方形,ABCD 是等腰梯形,它的上底肋为23厘米,下底口C为35厘米.求三角形ADE的面积．【例10】园林小路,曲径通幽.如图32-7所示,小路由白色正方形石板和青、红两色的三角形石板铺成.问：内圈三角形石板的总面积大,还是外圈三角形的总面积大?请说明理由．【巩固】一个长方形若能分割成大小不一样的小正方形，则称它为完美长方形。
下图完美长方形可以分割成9个小正方形，其中小正方形A和B的边长分别为5厘米和9厘米，那么大长方形的面积是多少平方厘米？1、四个完全一样的直角三角形和一个小正方形拼成一个大正方形（如图）如果小正方形的面积是1平方米，大正方形的面积是5平方米，那么直角三角形中，最短的直角边长度是 米。
2、请问下图正方形的面积是 平方厘米。
3、如图7-4，一个边长为1米的正方形被分成4个小长方形，他们的面积分别是103平方米、52平方米、51平方米和101平方米。
已知图中的阴影部分是正方形，那么它的面积是多少平方米？课堂检测复习总结根据直角三角形计算出三角形中第三边的长度，在计算时可以借助分解质因数，或者根据三遍关系判断是直角三角形；有直角的通过加辅助线构造直角三角形；通过对弦图进行观察分析得出构成弦图的直角三角形两直角边的关系，始终要有方程意识家庭作业1、左下图中有三个直角三角形。
请问x= 厘米。
2、用同样的长方形条砖，在一丛花的周围镶成一个正方形边框，如右图.边框的周长为264厘米.里边小正方形的面积为900平方厘米，问每块长方形条砖的长和宽各是多少厘米？3．如下图所示，红、黄、绿三块大小一样的正它们方形纸片，放在一个正方形盒内，它们之间相互叠合，已知露在外面的部分中，红色的面积是20，黄色的面积是14，绿色的面积是10，那么，正方形盒子的底面积是__________．(2003年一零一培训学校期末考试题(2003年12月)4．如图:长方形的面积是小于100的整数，他的内部由三个边长是整数的正方形，正方形①的边长是长方形长的125，正方形②的边长是长方形宽的81，那么图中阴影部分的面积是多少？①②5．在直角边为3与4的直角三角形各边上向外作正方形，三个正方形顶点连接如图所示的六边形ABCDE F ，则这个六边形的面积是_______________．ABCD E F34学生对本次课的评价○特别满意○满意○一般家长意见及建议教学反馈家长签字：。