2008年西南交通大学管理运筹学考研真题
西南交通大学 管理运筹学试题(B)

管理运筹学试题(B)一.单项选择(将唯一正确答案前面的字母填入题后的括号里。
正确得1分,选错、多选或不选得0分。
共15分)1.线性规划标准型中bi(i=1,2,……m)必须是()A.正数B.非负数C.无约束D.非零的正确答案:A: B: C: D:2.线性规划问题的基本可行解X对应于可行域D的()A.外点B.所有点C.内点D.极点正确答案:A: B: C: D:3.基本可行解中的非零变量的个数小于约束条件数时,该问题可求得 ( )A.基本解B.退化解C.多重解D.无解正确答案:A: B: C: D:4.原问题的第i个约束方程是“=”型,则对偶问题的变量qi是()A.多余变量B.自由变量C.松弛变量D.非负变量正确答案:A: B: C: D:5.若原问题是求目标最小,则对偶问题的最优解值就等于原问题最优表中多余变量的()A.机会费用B.个数C.值D.机会费用的相反数正确答案:A: B: C: D:6.求解指派问题的匈牙利方法要求系数矩阵中每个元素都是()A.非负的B.大于零C.无约束D.非零常数正确答案:A: B: C: D:7.设V是一个有n个顶点的非空集合,V={v1,v2,……,vn},E是一个有m条边的集合,E={e1,e2,……em},E中任意一条边e是V的一个有序元素对[u,v],(u≠v),则称V和E这两个集合组成了一个()A.无向图B.有向图C.完备图D.树正确答案:A: B: C: D:8.若一个闭链C除了第一个顶点和最后一个顶点相同外,没有相同的顶点和相同的边,则该闭链C称为()A.初等链B.圈C.回路D.饱和链正确答案:A: B: C: D:9.若有向图G有根u,且基本图是一棵树,则称G 为以u为根的()A.有向树B.完备图C.简单图D.分离图正确答案:A: B: C: D:10.若Q为f增流链,则Q中所有前向边都为f ()A.对边B.饱和边C.邻边D.不饱和边正确答案:A: B: C: D:11.若G中不存在流f增流链,则f为G的()A.最小流B.最大流C.最小费用流D.无法确定正确答案:A: B: C: D:12.若f 是G的一个流,K为G的一个割,且Valf=CapK,则K一定是()A.最小割B.最大割C.最小流D.最大流正确答案:A: B: C: D:13.若树T有n个顶点,那么它的边数一定是()A.n2 B.n C.n+1 D.n-1正确答案:A: B: C: D:14.对偶单纯型法与标准单纯型法的主要区别是每次迭代的基变量都满足最优检验但不完全满足()A.等式约束B.“≤”型约束C.“≥”约束D.非负约束正确答案:A: B: C: D:15.用割平面法求解整数规划时,构造的割平面只能切去()A.整数可行解B.整数解最优解C.非整数解D.无法确定正确答案:A: B: C: D:二.多项选择题(每题至少有一个答案是正确的。
全国各院校考研专业课[管理运筹学],近年考试真题答案解析
![全国各院校考研专业课[管理运筹学],近年考试真题答案解析](https://img.taocdn.com/s3/m/6230afa388eb172ded630b1c59eef8c75fbf952e.png)
全国各院校考研专业课[管理运筹学],近年考试真题答案解析管理运筹学是考研专业课中的一项重要内容,近年来,各院校对此科目的考试真题难度逐年提高,考查范围广泛,要求考生具备扎实的理论基础和较强的实际应用能力。
以下是对近年考试真题的答案解析,以供考生参考。
一、选择题1. 下列关于线性规划问题的说法,正确的是()。
A. 线性规划问题的目标函数可以是线性的,也可以是非线性的B. 线性规划问题的约束条件必须是线性的C. 线性规划问题的决策变量可以是整数D. 线性规划问题可以没有约束条件答案:B解析:线性规划问题的目标函数和约束条件都必须是线性的。
决策变量可以是实数,但不一定是整数。
2. 在非线性规划中,下列哪个条件是凸规划问题必须满足的()。
A. 目标函数是凸函数B. 约束条件是凸集C. 目标函数和约束条件都是凸函数D. 目标函数和约束条件都是凹函数答案:A解析:凸规划问题要求目标函数是凸函数,而约束条件可以是凸集或非凸集。
二、填空题1. 在目标规划中,如果决策变量有上下界限制,则该问题可以转化为线性规划问题。
答案:对解析:在目标规划中,如果决策变量有上下界限制,可以通过引入松弛变量和人工变量,将问题转化为线性规划问题。
2. 在对偶规划中,原问题的最优解与对偶问题的最优解是相互关联的。
答案:对解析:对偶规划的原问题和对偶问题存在一定的关联性,原问题的最优解与对偶问题的最优解是相互关联的。
三、计算题1. 某企业生产甲、乙两种产品,甲产品的单位利润为100元,乙产品的单位利润为150元。
生产甲产品需要消耗2小时机器时间,1小时人工时间;生产乙产品需要消耗3小时机器时间,2小时人工时间。
企业每周最多可利用机器时间100小时,人工时间80小时。
求企业每周生产甲、乙两种产品的最大利润。
答案:设甲产品生产x件,乙产品生产y件,目标函数为Z=100x+150y。
约束条件为:2x + 3y ≤ 100(机器时间)x + 2y ≤ 80(人工时间)x, y ≥ 0求解得:x=20,y=20,最大利润为5000元。
2008年西南交通大学交通运输规划与管理研究生专业课入学考试—运筹学—真题

一. 简答题(每道题5分,共5道题25分。
用文字、公式或图表均可。
判断性题答错理由不得分)1. 定理说,线性规划只要有可行解一定有基本可行解。
那么,能否确定一定存在最优解?2. 已知原问题有最优解,那么对偶问题呢?它们的什么是相等的? 3. 就指定的教材,简述求0-1规划的算法。
4. 运输网络中最小费流在网络弧(有向边)上的分布是否唯一? 5. 压缩关键路线上的关键工序时间一定能缩短总工期吗? 二. 证明题(每题10分,共20分)1. 已知线性规划问题⎪⎩⎪⎨⎧≥≤-+-≤++--=0,,122..max 32132132121x x x x x x x x x t s x x Z 试用对偶理论证明该规划问题无最优解。
2. 证明:运输问题一定有最优解。
三. 计算与建模题(每道题15分,共105分)1. 已知线性规划标准模型==nj jj x c z 1max,约束条件为b AX =,其中1)(,)(⨯⨯==m i n m ij b b a A ,X为决策变量组成的向量。
若该规划有可行解,求出单纯形法迭代时相邻两次目标函数值之间的数量关系式。
2. 下表是求某极大化线性规划问题计算得到的单纯形表,表中无人工变量,21321,,,,,c c d a a a 为待定常数,试说明这些常数分别取何值时,以下结论成立。
(1)表中的解为唯一最优解;(3分)(2)表中解为最优解,但存在无穷多最优解;(4分)(3)该线性规划问题具有无界解;(4分)(4)表中解非最优,为对解进行改进,换入变量为x,换出变量为6x.1(4分)3.已知某工厂计划生产甲乙丙三种产品,各产品需要在设备A、B上加工,有关数据见下表:建立线性规划模型,求每月最优生产计划并回答(计算分析)下列问题。
(1)最优生产计划中各设备是否得到了充分利用,为什么?(2)若为了增加产量,计划租用别的工厂设备A、B,每月都可租用60台时。
每月租金在什么范围就可以租用设备A和B?(3)若经过技术改造,生产单位甲产品对设备A、B的消耗分别为1.5和2.5,单位盈利为,改进技术必要吗?4.某物资从产地A1、A2、A3运往销售地B1、B2、B3。
交大运筹学2套往年试卷及答案(包含各题型_期末考试绝对有用)

北京交通大学考试试题答案(A卷)——运筹学A一、单选题5分,每题1分。
二1.设甲、乙产品的产量分别为x1,x2件,线性规划模型为:max z=3x1+2x2s.t. 2x1+4x2≤1603x1+2x2≤180x1 , x2≥0标准型及单纯形计算如下:max z=3x1+2x2s.t. 2x1+4x2+x3=1603x1+2x2+x4=180x1 , x2, x3, x4≥60最优方案为甲生产50件,乙生产15件,或甲生产60件,乙生产0件,或上述两种方式的凸组合。
最大利润为180。
15分,模型5分,标准型与初始表5分,计算3分,结论2分。
2.影子价格分别为0和14分,各2分,计算错误扣1分。
3.产品丙的检验数为-1,不值得生产。
5分,公式2分,计算2分,结论1分。
4.原料B 的灵敏度范围0-240,最多应购买60千克。
6分,公式2分,计算3分,结论1分。
三、(15分)①正确列出运价表如右:7分 ②最小元素法方案3分 ③位势法求检验数4分 ④给出正确的调运方案1分四、(10分)分配甲、乙、丙三个人去完成A 、B 、C 、D 四项任务,每个人完成各项任务的时间如表所示。
其中任务D 必须完成,且每个人只能完成一项任务,每项任务只能由一个人完成。
试确定最优分配方案,使完成任务的总时间最少。
①正确列出效益表如右:5分 ②匈牙利法计算结果3分 ③给出正确的分配方案2分第五题定义状态:s1=x1+s2 s2=x2+s3 s3=x3 故 s1<=8(3分) k=3时f3(s3)=Max {4*x3} ,此时 0<=x3<=s3即x3=s3时f3(s3)=4*s3(3分)k=2时f2(s2)=Max {3*x2+f3(s3)}= Max {3*x2+4*(s2-x2)} 0<=x2<=s2即x2=0时f2(s2)=4*s2(3分)k=3时f1(s1)=Max {x1*x1+ f2(s2)}=Max{x1*x1-4*x1+4*s1} ,此时0<=x1<=s1 由于s1<=8,故x1=s1=8时f1(s1)=64(3分)因此,x1=8, x2=0, x3=0时z取得最大值,最大值为64。
运筹学考研真题及答案

运筹学考研真题及答案运筹学考研真题及答案一、选择题1. 在线性规划中,若最优化问题的对偶问题有最优解,则原始问题也有最优解。
(正确)解析:线性规划理论中对偶定理:“若原始问题的对偶问题有可行解,且存在最优解,则原始问题也有最优解。
”2. 若在线性规划的单纯形法中,某一回路上的所有非基变量(非基变量为0)均为0,则这一问题无有限最优解。
(错误)解析:所有非基变量为0时,相应的基变量可以任意非负,问题有无穷多最优解。
3. 在线性规划中,若某元组在原始问题和对偶问题下都是可行解,则该元组是原始问题和对偶问题的最优解。
(错误)解析:若某元组在原始问题和对偶问题下都是可行解,则该元组满足原始问题的可行性和对偶问题的可行性,但并不一定是最优解。
4. 线性规划的最优性条件是原始问题的可行解和对偶问题的可行解所对应的目标函数值相等。
(正确)解析:线性规划理论中最优性条件:“若原始问题的可行解与对偶问题的可行解所对应的目标函数值相等,则解是原始问题和对偶问题的最优解。
”5. 线性规划的可行性要求约束条件为不等式约束。
(错误)解析:线性规划的可行性要求是所有约束条件都满足,包括等式约束和不等式约束。
二、填空题1. 与线性规划的相对论证法相对应的是(单纯形法)。
解析:线性规划的相对论证法和单纯形法是互为相对的两种求解方法。
2. 在线性规划中,若最优差异为0,则最优解是(非唯一)。
解析:最优差异为0意味着最优解是非唯一的,有多个最优解。
3. 线性规划的最优性条件是(对偶定理)与最优条件相对应。
解析:线性规划的最优性条件是对偶定理,而最优条件是原始问题的可行解和对偶问题可行解所对应的目标函数值相等。
4. 在线性规划中,若一个可行解在原始问题和对偶问题下都是最优解,则称为(互补性)条件。
解析:若一个可行解在原始问题和对偶问题下都是最优解,则满足互补性条件。
三、应用题1.某公司生产两种产品A和B,每个产品的制造工序及所需时间如下表,在一天内,公司有8小时的工时可用,每个工序只能由一名员工负责完成。
西南交通大学-2008年硕士研究生招生入学考试公共经济学试卷

西南交通大学2008年硕士研究生招生入学考试试题名称:公共经济学考试时间:2008年1 月考生请注意:1. 本试题共六题,共四页,满分150分,请认真检查;2. 答题时,直接将答题内容写在考场提供的答题纸上,答在试卷上的内容无效;3. 请在答题纸上按要求填写试题代码和试题名称;4. 试卷不得拆开,否则遗失后果自负。
一、单选题(每小题1 分,共20分)1. 公共部门的核心层次是指()。
A. 中央政府的各部、委、办、厅、局及其附属物B. 中央政府+地方政府C. 中央政府+地方政府+非金融性公共企业D·中央政府+地方政府+非金融性公共企业÷政策畦官方金融机构2、以下不属于完全竞争市场的基本特征的是()。
A.人数众多的小规模卖者和卖者B. 信息与知识完全的对称C. 产品是异质的,D. 经济利益的可分性和所有权的确定性3、沿街居民在阳台上放几盆花让过路入赏心悦目,这种现象为()。
A. 生产的外部收益B. 消费的外部收益C. 生产的外部成本D. 消费的外部成本4. 下列属于典型的社会市场型混合经济体制的是()。
A. 美国B. 德国C. 英国D. 法国5. 在西方国家中;针对立法机关的立法过程的特点,利益集团往往充当()的角色。
A.民意代表B. 监督者C,顾问 D. 说客6. 政治家对公共产品的需求遵循( )的规律。
A. 边际收益递减B. 边际收益递增C. 边际成本递减D. 边际成本递增7. 在唐斯的政治竞争模塑中,政党在竞选时追求的是( )A. 社会福利最大化B、经济利益最大化C. 选票最大化D. 预算最大化8、功能预算论的核心是( )。
A. 自发调节机制B. 市场竞争原则C.政府干预 D.相机抉择9.下列政府支出不属于消耗性支出的有( )。
A.社会保障支出 B.公共教育支出C.公共投资支出 D.国防支出10.财政补贴中数额最大的一项内容是( )。
A.企业亏损补贴 B.财政贴息c.职工和居民生活补贴 D.价格补贴11.一般认为,税收转嫁的最典型和最普遍的形式是( )。
(完整版)2008西南交大电路分析考研真题
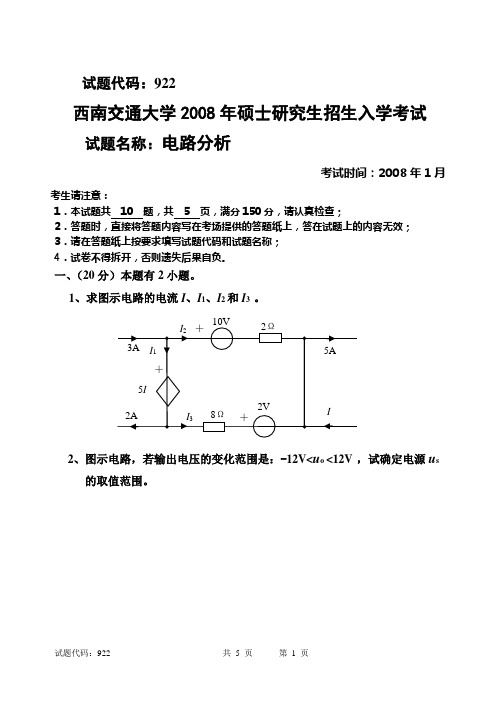
试题代码:922西南交通大学2008年硕士研究生招生入学考试试题名称:电路分析考试时间:2008年1月考生请注意:1.本试题共10 题,共 5 页,满分150分,请认真检查;2.答题时,直接将答题内容写在考场提供的答题纸上,答在试题上的内容无效;3.请在答题纸上按要求填写试题代码和试题名称;4.试卷不得拆开,否则遗失后果自负。
一、(20分)本题有2小题。
1、求图示电路的电流I、I1、I2和I3 。
2、图示电路,若输出电压的变化范围是:-12V<u o<12V,试确定电源u s的取值范围。
二、(15分)电路如图所示,用结点电压法求结点电压U a 、U b 。
三、(20分)本题有2小题。
1、电路如图,已知A I ︒∠=6010 ,功率因数21cos =ϕ(感性),电路吸收的有功功率W P 500=,电感吸收的无功功率var 1000=L Q 。
求电流R I 、L I 、C I 。
CIu s o+-2、图示正弦交流电路中,)( 400cos 51A t i =,)( 400cos 22A t i =,求)(t i 和)(t u 。
四、(15分)图示三相交流电源对称,且︒∠=30220AU V ,负载Ω-=3040j Z 。
分别求出开关K 闭合、打开情况下的电流A I 、B I 、C I 以及三相电源发出的总的有功功率。
五、(15分)已知电路中A i s 101=,A t i s )30200cos(52︒+=。
求R u 及其有效值、瓦特表的读数。
i 1i 2Z1s i 2s i六、(10分)电路如图,N 为无源(互易)双口网络。
已知︒∠=048sU V ,当∞=L Z 时,︒∠=0322U V ;当0=LZ 时,︒∠=061I A ,︒∠=18032I A 。
求双口网络N 的Z 参数矩阵。
七、(15分) 0<t 时电路处于稳态, 0=t 时开关K 闭合。
用时域法求0≥t时的)(t i 和)(t u 。
西南交通大学管理运筹学929-2018年试题和解析

西南交通大学管理运筹学929-2018年试题和解析(总10页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--机密★启用前西南交通大学2018年硕士研究生招生入学考试试卷试题代码:929试题名称:管理运筹学一考试时间:2017年12月考生注意:1.本试题共三大题,共3页,满分150分,请认真检查;2.答题时,请直接将答题内容写在考场提供的答题纸上,答在试卷上的内容无效;3.请在答题纸上按要求填写试题代码和试题名称;4.试卷不得拆开,否则遗失后果自负。
一、 问答题(60分,共10小题,每小题6分)(答在试卷上的内容无效) 1、 线性规划模型中,何谓自由变量自由变量和决策变量是什么关系解答:用设定的未知数来表示线性规划问题问题中的未知量,这个设定的未知量就叫做决策变量,决策变量没有非负约束即为自由变量;自由变量一定是决策变量,但决策变量不一定是自由变量。
2、 请分别解释无可行解、无界解、最优解的概念。
解答:无可行解:约束方程组没有公共解,造成线性规划模型无解的解。
无界解:没有任何一个可行解能使得目标函数达到最优,即目标函数没有上界或下界。
最优解:在线性规划模型的所有可行解中,使得目标函数达到最优的解。
3、 说明下面的数学模型不符合线性规划模型的什么特点123312232131264323018..3()249,0z x x x x x x x x s t x x x x =+++≠⎧⎪+≥⎨+≤⎪≥⎩ 解答:(1) 此模型不符合线性规划模型目标函数应该是线性函数的特点; (2) 此模型不符合线性规划模型目标函数求最大值最小值的特点; (3) 此模型不符合线性规划模型约束条件方程组由线性的等式或线性的不等式的特点。
4、以目标函数Min 型为例,从基本可行解、求检验数以及基本可行解改进三个方面说明单纯形法和表上作业法的区别。
解答:(1) 基本可行解:单纯形法是通过构造单位矩阵来确定初始基本可行解,而表上作业法是通过另外的西北角法、最小元素法或差值法来确定初始基本可行解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
出。已知 B1、B2 、B3 需求量分别为 9,8,5。要求 A1 处至少发出 7 个单 位,最多发出 11 个单位;A2 处必须发出 6 个单位;A3 处至少发出 3 个单 位。现在拟用表上作业法求最优方案,请建立模型。
考试代码:929
2008 年研究生运筹学考试
运价 产地 A1 A2 A3
销地
B1 4 3 5
B2 6)到(6)的最小费用最大流,弧上的数字代表 单位费用和容量。 (2) (3,3) (4) (1,4) (2,5) (1) (1,1) (2,1) (1,3) (6) (3,5) (4,2) (3) (4,2) (5) 6. 在某单人理发店顾客到达为泊松流,平均到达间隔时间为 20 分钟;理 发时间服从负指数分布,平均时间为 15 分钟。求解下列问题: (1) 顾客到达不必等待的概率; (2) 理发店内顾客平均数; (3) 若顾客在店内平均停留时间超过 1.25 小时, 店主将考虑增加设备 及服务员。问平均到达率达到多少时,店主才做这样的考虑? 7. 某商店销售某产品,购进单价为 K,单位存贮费为 C1,订购费 C2(商务 费等,不包括产品单价) 。已知单位时间产品需求量 R 为常数,要求不能 缺货,库存为零时可以瞬间补货,相关单位费用不变化,求最经济的订 购批量 Q、订货间隔时间及最低费用。 (直接套公式不得分) 。
z c j x j ,约束条件为 AX b ,其中
j 1
n
A (aij )mn , b (bi )m1 ,X 为决策变量组成的向量。 若该规划有可行解,
求出单纯形法迭代时相邻两次目标函数值之间的数量关系式。 2. 下表是求某极大化线性规划问题计算得到的单纯形表,表中无人工变 量, a1, a2 , a3 , d , c1, c2 为待定常数,试说明这些常数分别取何值时,以下 结论成立。
2008 年研究生运筹学考试
一. 简答题(每道题 5 分,共 5 道题 25 分。用文字、公式或图表均可。判断 性题答错理由不得分) 1. 定理说,线性规划只要有可行解一定有基本可行解。那么,能否确定 一定存在最优解? 2. 已知原问题有最优解,那么对偶问题呢?它们的什么是相等的? 3. 就指定的教材,简述求 0-1 规划的算法。 4. 运输网络中最小费流在网络弧(有向边)上的分布是否唯一? 5. 压缩关键路线上的关键工序时间一定能缩短总工期吗? 二. 证明题(每题 10 分,共 20 分) 1. 已知线性规划问题
考试代码:929
2008 年研究生运筹学考试
(1) 表中的解为唯一最优解; (3 分) (2) 表中解为最优解,但存在无穷多最优解; (4 分) (3) 该线性规划问题具有无界解; (4 分) (4) 表中解非最优, 为对解进行改进,换入变量为 x1 ,换出变量为 x6 . (4 分) 基 x3 x4 x6 b(资源) d 2 3 检验数→ x1 4 -1 a3 c1 x2 a1 -3 -5 c2 x3 1 0 0 0 x4 0 1 0 0 x5 a2 -1 -4 -3 x6 0 0 1 0
3. 已知某工厂计划生产甲乙丙三种产品, 各产品需要在设备 A、 B 上加工, 有关数据见下表:
单位产品台时消耗 设备 产品
甲
乙
丙
设备有效台时(每月)
设备 A 设备 B 单位产品利润 (千元)
2 3 40
3 3 45
1 2 24
100 120
建立线性规划模型,求每月最优生产计划并回答(计算分析)下列问题。 (1) 最优生产计划中各设备是否得到了充分利用,为什么? (2) 若为了增加产量,计划租用别的工厂设备 A、B,每月都可租用 60 台时。每月租金在什么范围就可以租用设备 A 和 B? (3) 若经过技术改造,生产单位甲产品对设备 A、B 的消耗分别为 1.5 和 2.5,单位盈利为,改进技术必要吗?
考试代码:929
max Z x1 x2 x1 x2 x3 2 s.t. 2 x1 x2 x3 1 x , x , x 0 1 2 3
试用对偶理论证明该规划问题无最优解。 2. 证明:运输问题一定有最优解。 三. 计算与建模题(每道题 15 分,共 105 分) 1. 已知线性规划标准模型 max
