2020六年级数学下册考点过关卷(二)式与方程、比与比例的对比新人教版
人教版六年级下册数学2式与方程 比和比例课件(共32张PPT)
4＋3×1
4＋3×2
n
4＋3×（n－1）
（1）你能发现什么规律？如果摆n个正方形，需要3__n_＋___根小棒。
（2）摆150个正方形，需要_4_5___根小棒。3×150 1
1
＋1
人教版数学 六年级下册 第六单元 总复习 （第2课时）
方法总结 用方程解决实际问题有哪些步骤？
课堂练习
8.一台电视机打八8%五5 折后售价为2975元，这台电视机原价是多少钱？
出发，相向而行，经过2.5小时相遇。甲车每小时行65千米，乙车每
小时行多少千米？（列方程解答） 同时相向而行：
解：设乙车每小时行x千米，可得方程： （65＋x）×2.5＝350
相遇路程＝速度和×相遇时间
（65＋x）×2.5÷2.5＝350÷2.5
相遇时间＝相遇路程÷速度和
65＋x＝140 65＋x－65＝140－65
速度和＝相遇路程÷相遇时间
x＝140－65
x＝75
答：乙车每小时行75千米。
讲义练习
【变式3】甲、乙两艘轮船同时沿一条海上航道从青岛开往广州，甲 船每小时行29千米，乙船每小时行32千米。几小时后两船相距10.5 千米？（列方程解答）
讲义练习
【例4】清明节，实验小学组织五、六年级共390名学生去参加“烈 士陵园祭扫”活动。其中六年级参加的人数是五年级的1.6倍。五、 六年级各参加了多少人？（列方程解答） 单位
方程
方程和等式有何联系与区别？
所有的方程一定是等式，但等式不一定是方程。
你能将韦恩图 补充完整吗？
等式
方程
课堂活动
解方程
解：
解：
等式性质1：等式两边同时加上（减去） 同一个数，结果仍然相等。
考点过关卷2式与方程比与比例的对比
考点过关卷2式与方程比与比例的对比式与方程是数学中的基本概念，也是数学思维的基础。
比与比例则是应用数学的重要知识点。
本文将通过对比式与方程以及比与比例的概念、性质和应用进行详细阐述，帮助读者更好地理解和应用这些数学知识点。
一、式与方程1.概念式是由数、字母及其组合所构成的数学语言表达方式，它是一个没有等号的数学表达式。
例如：3x+2、4x²-5y等都是数学式。
方程则是包含有等号的数学式，它是两个数学表达式相等的关系。
例如：3x+2=8、4x²-5y=10等都是数学方程。
2.性质式的性质主要包括可计算性和可变性。
可计算性指的是式能够用具体数值代替其中的变量进行计算。
可变性指的是式中的变量可以取不同的值，从而得到不同的结果。
方程的性质主要包括等式的可解性和解的唯一性。
等式的可解性指的是方程是否存在解，解的唯一性指的是方程的解是否唯一、对于一元一次方程来说，它一定有解且解唯一；而对于高次方程或者含有多个变量的方程，通常需要具体条件下才能确定是否有解，以及解的个数。
3.应用方程在数学中有广泛的应用。
例如在几何学中，可以通过方程来描述和求解直线、曲线等几何图形；在物理学中，方程可以用来描述物体的运动状态；在经济学中，方程可以用来描述供求关系或者市场竞争等问题。
二、比与比例1.概念比是表示两个量之间的相对关系的数学表达式。
比通常用冒号“：”表示。
例如：3:5表示3和5的比，即3比5，表示3是5的三分之一比例则是指两个或多个比之间存在着相等关系。
比例通常用等号“=”表示。
例如：3:5=6:10表示3:5的比等于6:10的比，即3比5和6比10的比是相等的。
2.性质比的性质主要包括比的三个基本要素：比的大小、比的相等和比的简化。
比的大小是指比较两个比的大小，通常可以通过比的分子和分母的大小进行比较。
比的相等是指两个比相等，则表示两者的比例是相等的。
比的简化是指将一个比写成最简形式，即分子和分母没有公共的因子。
2021年名校小升初六年级真题试卷考点过关卷2 式与方程、比与比例的对比
小升初总复习考点过关卷2式与方程、比与比例的对比一、我会填。
(每空2分，共22分)1．一个士兵练习射击，命中率是97%，共发射子弹200发，没命中()发。
2．5.4∶63%的比值是()，化成最简整数比是()。
3．春天容易感冒，这天，某班的出勤率是95%，出勤人数和缺勤人数的比是()。
4．笑笑的爸爸的身高是1.80 m，他在天安门照了一张照片，照片上的身高是9 cm，这张照片使用的拍摄比例是()。
5．把()g盐放入100 g水中，盐与盐水的比是1∶51。
6．三个连续的偶数，第一个数是a，那么第三个数是()，它们的和是()。
7．当x＝0.5时，x2＝()，2x＝()；当y＝()时，y2＝2y。
二、我会辨。
(每题2分，共6分)1．当b＜1时，b2＜2b。
() 2．当n是自然数时，2n＋1一定是偶数。
() 3．当a3＝729时，a＝363。
()三、我会选。
(每题3分，共12分)1．把一些树苗按2∶3∶5分配给一、二、三班学生去种植，一班比三班的树苗少( )。
A ．60% B ．40% C ．20%D ．80%2．等腰三角形的一个底角是a °，它的顶角是( )。
A ．a °B ．90°－a °C ．180°－2a °3．如果3x ＋6＝30，那么( )x ＋12＝60。
A ．6B ．4C ．无法确定4．某水果店运进苹果m 千克，比梨的4倍少n 千克。
求运进梨多少千克。
正确的算式是( )。
A ．m ÷4－n B ．(m －n )÷4 C ．(m ＋n )÷4D ．4m －n四、计算挑战。
(共31分)1．先化简各比，再求比值。
(每题4分，共16分)0.51∶0.68 2.5小时∶25分钟0.125∶783813∶19392．求未知数。
(每题3分，共15分)5(x －1.2)＝14062%x ＋3.5＝3.8127∶x＝0.8∶2.1 x8＝4.53.6(1.42＋x)×4＝21.68五、走进生活，解决问题。
人教版六年级数学下册小升初专项试卷 计算能力过关(数的运算与解方程、比例)附答案
人教版六年级数学下册5.计算能力过关（数的运算与解方程、比例）一、仔细审题，填一填。
(每空1分，共22分) 1.12（ ）＝0.75＝21÷( )＝( )24＝( )%2.在 里填上“＞”“＜”或“＝”。
6.9×2.5 6.98.96÷1.2 8.965.6－87 4.645×1 45÷1 105÷32 105×320÷314 314＋0 3.甲、乙、丙三个数的比是2: 3：5，如果丙数是4.5，这三个数的平均数是( )。
4.一个零件长3 mm ，画在图纸上长6 cm ，这张图纸的比例尺是( )。
5.在有余数的除法算式□÷9＝16……☆中，被除数最小是( )，余数最大是( )。
6.甲数比乙数多25%，则乙数比甲数少( )%。
7.一个三位小数保留两位小数后是7.25，这个三位小数最大是( )，最小是( )。
8.一个数扩大到它的100倍后是6.08，这个数是( )，把0.4缩小到它的1100后是( )。
9.小明15小时走了34 km ，平均每小时走( )km ，平均每千米用( )小时。
10.美国国家航空航天局宣布开普勒空间望远镜发现了外行星开普勒 452b ，这颗行星的直径比地球的直径大35。
地球的直径约为12756千米，开普勒 452b 的直径约为( )千米。
二、火眼金睛，判对错。
(对的在括号里画“√”，错的画“×”)(每小题1分，共5分)1.4900÷400＝49÷4＝12……1。
( )2.A ，B 都是大于0的自然数，若A ＝6B ，则A 与B 的最大公因数是B ，最小公倍数是A 。
( )3.把34和15通分后，分数的大小不变，分数单位变了。
( )4.含有未知数的比例是方程。
( )5.一杯牛奶含水60%，喝掉12后含水30%。
( )三、仔细推敲，选一选。
最新六年级数学下册---第二单元--比例知识点和习题
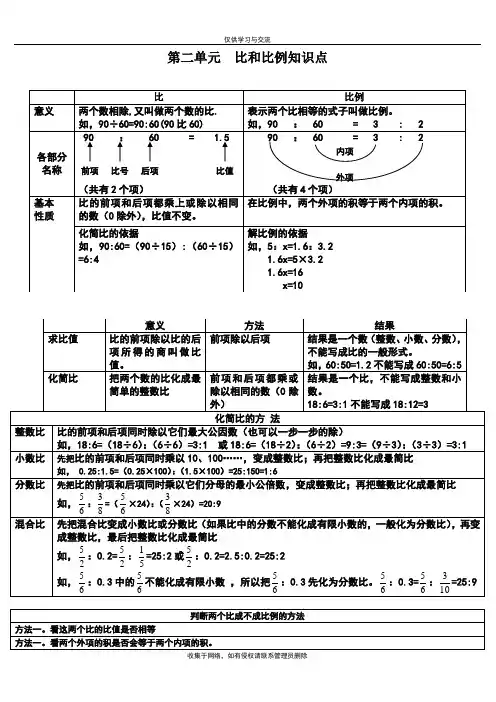
第二单元比和比例知识点知识点一：比例尺的意义例1：一张地图上2厘米的距离表示实际距离1000米。
求图上距离和实际距离的比。
过关精炼：1）用图上距离5厘米，表示实际距离200米，这幅图的比例尺是（ ）一、图上距离：实际距离=1cm ：50km=1cm :( )cm=1:( )3）在一幅地图上，用3厘米的线段表示18千米的实际距离，这幅地图的比例尺是（ ）。
4）一幢教学大楼平面图的比例尺是1/200，表示实际距离是图上距离的（ ）倍。
知识总结：前项是“1”的比例尺，称为缩小比例尺 例2：一个cpu 零件的长为3厘米,画在纸上的长为18厘米,求这幅图的比例尺。
过关精炼：长4毫米的零件，画在图纸上是4厘米，这幅图的比例尺是（ ）知识总结：像4:1、6:1这样后项为“1”的比例尺称为放大比例尺。
点击突破1：在图幅相等的情况下，比例尺越大，表示的范围越 ，表示的内容越 ；反之，比例尺越小，表示的范围越 ，表示的内容越 。
比和比例练习题一、 填空：1. 甲乙两数的比是11:9,甲数占甲、乙两数和的)()(，乙数占甲、乙两数和的)()(。
甲、乙两数的比是3:2，甲数是乙数的（ ）倍，乙数是甲数的)()(。
2. 某班男生人数与女生人数的比是43，女生人数与男生人数的比是（ ），男生人数和女生人数的比是（ ）。
女生人数是总人数的比是（ ）。
3. 如果7x=8y ，那么x ：y=（ ）：（ ）。
4. 一根绳长2米，把它平均剪成5段，每段长是)()(米，每段是这根绳子的)()(。
5. 王老师用180张纸订5本本子，用纸的张数和所订的本子数的比是（ ），这个比的比值的意义是（ ）。
6. 一个正方形的周长是58米，它的面积是（ ）平方米。
7. 89吨大豆可榨油31吨，1吨大豆可榨油（ ）吨，要榨1吨油需大豆（ ）吨。
8. 甲数的32等于乙数的52，甲数与乙数的比是（ ）。
9. 把甲数的71给乙，甲、乙两数相等，甲数是乙数的)()(，甲数比乙数多)()(。
人教版六年级下册正比例和反比例的对比
判断下面的两个量成正比例、 判断下面的两个量成正比例、反比例还是不成比例 ①圆的周长和半径。（ 圆的周长和半径。（
正比例
）
②圆的面积和半径。（ 不成比例 ） 圆的面积和半径。（ ③正方形的周长和边长。（ 正方形的周长和边长。（个自然数和它的倒数。（
江西省于都实验中学附属小学 华攸盛制作
正比例
相同点
1.一种量在增加，另一种量也 一种量在增加， 一种量在增加 在增加，一种量在减少， 在增加，一种量在减少，另一 不同点 种量也在减少。 种量也在减少。 比值或者商一 2.相对应的两个量比值或者商一 相对应的两个量比值或者商
定 3.
反比例
1.一种量在增加，另一种量 一种量在增加， 一种量在增加 反而在减少，一种量在减少， 反而在减少，一种量在减少， 另一种量反而在增加。 另一种量反而在增加。
反比例
⑤全班人数一定，出勤人数和出勤率（正比例 比例。 全班人数一定，出勤人数和出勤率（ ）比例。
江西省于都实验中学附属小学 华攸盛制作
判断并且说明理由 1.一个因数不变，积与另一个因数成正比例．（ 一个因数不变，积与另一个因数成正比例．（ 一个因数不变 2.圆的半径和周长成正比例．（ 圆的半径和周长成正比例．（ 圆的半径和周长成正比例 ） ） ） ） ）
2.相对应的两个量积一定 相对应的两个量积 相对应的两个量 3.
都是两种相关联的量，一种量在变化，另一种量也在变化。 都是两种相关联的量，一种量在变化，另一种量也在变化。
y = k ( 一定） x
xy = k (一定）
江西省于都实验中学附属小学 华攸盛制作
聪聪在同一时刻测量了直立在太阳下的四根 竹竿的影长，结果如下： 竹竿的影长，结果如下：
人教版六下比和比例知识点与易错习题
人教版六下比和比例知识点与易错习题知识点三：求比值和化简比 知识点四：正比例和反比例的意义和判断方法1、 正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。
正比例的关系式：k xy=（一定） 2、 反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。
反比例的关系式：k xy=（一定） 3、 判断正、反比例的方法：一找二看三判断（1） 找变量：分析数量关系，确定哪两种量是相关联的量。
（2） 看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。
（3） 判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例 4、 正比例、反比例的区别与联系知识点五：用比例知识解决问题 1、 按比例分配问题 （1） 按比例分配应用题：把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。
（2） 解题方法一般方法：把比转化成为分数，用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数，先求出各部分的总分数，然后再用“总量÷总份数=平均每份的量（归一）”，再用“一份的量⨯各部分量所对应的份数”，求出各部分的量。
用比例知识解答：首先设未知量为。
再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x 的比例式，再解比例求出x 。
2、 用正、反比例知识解答应用题的步骤（1）分析数量关系。
判断成什么比例。
（２）找等量关系。
如果成正比例，则按等比找等量关系式；如果成反比例，则按等积找等量关系式。
（３）解比例式。
设未知数为x ，并代入等量关系式，得正比例式或反比例式。
六年级数学下册---第二单元--比例知识点和习题 复习试卷试题
第二单元比和比例知识点知识点一：比例尺的意义例1：一张地图上2厘米的距离表示实际距离1000米。
求图上距离和实际距离的比。
过关精炼：1）用图上距离5厘米, 表示实际距离200米, 这幅图的比例尺是（ ） 一、图上距离：实际距离=1cm ：50km=1cm :( )cm=1:( )3）在一幅地图上, 用3厘米的线段表示18千米的实际距离, 这幅地图的比例尺是（ ）。
4）一幢教学大楼平面图的比例尺是1/200, 表示实际距离是图上距离的（ ）倍。
知识总结：前项是“1”的比例尺, 称为缩小比例尺例2：一个cpu 零件的长为3厘米, 画在纸上的长为18厘米, 求这幅图的比例尺。
过关精炼：长4毫米的零件, 画在图纸上是4厘米, 这幅图的比例尺是（ ） 知识总结：像4:1、6:1这样后项为“1”的比例尺称为放大比例尺。
点击突破1：在图幅相等的情况下, 比例尺越大, 表示的范围越 , 表示的内容越 ；反之, 比例尺越小, 表示的范围越 , 表示的内容越 。
比和比例练习题一、 填空：1. 甲乙两数的比是11:9, 甲数占甲、乙两数和的)()(, 乙数占甲、乙两数和的)()(。
甲、乙两数的比是3:2, 甲数是乙数的（ ）倍, 乙数是甲数的)()(。
2. 某班男生人数与女生人数的比是43, 女生人数与男生人数的比是（ ）, 男生人数和女生人数的比是（ ）。
女生人数是总人数的比是（ ）。
3. 如果7x=8y, 那么x ：y=（ ）：（ ）。
4. 一根绳长2米, 把它平均剪成5段, 每段长是)()(米, 每段是这根绳子的)()(。
5. 王老师用180张纸订5本本子, 用纸的张数和所订的本子数的比是（ ）, 这个比的比值的意义是（ ）。
6. 一个正方形的周长是58米, 它的面积是（ ）平方米。
7.89吨大豆可榨油31吨, 1吨大豆可榨油（ ）吨, 要榨1吨油需大豆（ ）吨。
8. 甲数的32等于乙数的52, 甲数与乙数的比是（ ）。
最新人教版六年级下册比例的各章节知识点以及练习题
最新六年级下册比例的各章节知识点以及练习题表示两个比相等的式子叫做比例。
1、思考一下，下面哪一组中的两个比可以组成比例，并写出相应的比例。
7∶14和6∶12 13∶14和16∶183．5∶7和1∶14 0.4∶1.6和3∶122、把下面左、右两边相等的比用线连起来。
0．8∶3.2 10∶4 2．5∶4 4.5∶18 1∶25 2.7∶1.50．9∶0.5 2∶3.23、写出比值是58的两个比，再组成一个比例： 。
4、（ ）叫做比例。
5、火车4小时行240千米，火车行驶的路程和时间的比是( )∶( )，化成最简整数比是( )∶( )，比值是( )。
6、把159106：改写成比的形式是（ ）：（ ）=（ ）：（ ） 7、写出比值是43的两个比：（ ）：（ ）、（ ）：（ ），再把他们组成比例是： 。
8、能与41:51：组成比例的是（ ）。
A. 51:41B. 4：5C. 5：4D. 4151：9、下列每组中的四个数，可以组成比例的是（ ）。
A. 0.3、4.5、0.5和217B. 0.3、4.5、6143和C. 1.2、1.6、6143和10、在线段AF 中，AB=BC=CD=DE=EF ，下面的四个式子中，哪一个是比例，填可以或者不可以？（1）AB ：BC=AC ：DE （ ）（2）AE ：CD=BF ：BE （ ） （3）AC ：BC=EF ：DF （ ） （4）AD ：BC=CF ：EF ． （ ） 组成比例的四个数，叫做比例的项。
两端的两项叫做外项，中间的两项叫做内项。
比例的基本性质：在比例里，两个外项的积等于两个内向的积。
这叫做比例的基本性质。
1、在比例324.243.0 中，（ ）和（ ）是外项，（ ）和（ ）是内项。
2、组成比例的四个数叫做比例的（ ），中间的两个数叫做比例的（ ），两端的两个数叫做比例的（ ）。
3、在比例里两个（ ）积等于两个（ ）积这叫做比例的基本性质。
4、合唱组人数比绘画组人数多20%，合唱组人数与绘画组人数的比是（ ）。
人教版2020年六年级数学下学期过关检测试题 附解析
乡镇（街道） 学校 班级 姓名 学号………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…绝密★启用前人教版2020年六年级数学下学期过关检测试题 附解析题 号 填空题 选择题 判断题 计算题 综合题 应用题 总分得 分考试须知：1、考试时间：100分钟，本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
3、请在试卷指定位置作答，在试卷密封线外作答无效，不予评分。
一、填空题（共10小题，每题2分，共计20分）1、把一个棱长是4厘米的正方体削成一个最大的圆柱体，这个圆柱的表面积是（ ）平方厘米，削去的体积是（ ）立方厘米。
2、A 、B 两个数是互质数，它们的最大公因数是（ ），最小公倍数是（ ）。
3、分数单位是7 1 的最大真分数是（ ），它至少再添上（ ）个这样的分 数单位就成了假分数。
4、已知一个比例中两个外项的积是最小的合数，一个内项是5/6，另一个内项是（ ）。
5、若5ａ＝3ｂ（ａ、ｂ均不为0）那么ｂ：ａ＝（ ）：（ ）。
6、小红把2000元存入银行，存期一年，年利率为2.68%，利息税是5%，那么到期时可得利息（ ）元。
7、七亿五千零七万八千写作（ ），把它改写成用万作单位的数是（ ），省略亿后面的尾数是（ ）。
8、（ ）÷36=20：（ ）= 1/4 =( )(填小数) =（ ）% =（ ）折 9、甲乙两地相距26km ，在地图上的距离是5.2cm ，这幅地图的比例尺是（ ）。
10、一根铁丝长25.12米，把它焊接成一个圆，圆的半径是（ ），面积是（ ）平方米。
二、选择题（共10小题，每题1.5分，共计15分）1、在2、3、4、5这四个数中，一共可以找出（ ）对互质数。
A 、4 B 、5 C 、62、甲数的5/6等于乙数，甲数不为“0”，则（ ）。
A 、甲数>乙数 B 、甲数=乙数 C 、甲数<乙数 D 、不确定3、要考查一个学生一年级到六年级的学习成绩进步情况，采用（ ）比较合适。
人教版数学六年级下册比和比例整理复习及典型易错题解析
比和比例的整理复习与典型易错题解析教学目标：1、情感目标：在复习活动中让学生体验数学与生活实际的密切联系，培养学生的数学应用意识，激发学生成功学习数学和自信心和创新意识，渗透事物间是相互联系的辩证唯物主义观点。
2、能力目标：通过小组合作整理知识框架，提高学习的系统性，培养学生归纳、总结等自我复习能力及团队合作精神，加强生与生之间的合作学习能力和综合运用数学知识解决实际生活问题的能力。
3、知识目标：使学生进一步掌握比和比例的意义、性质，能正确迅速地解比例、化简比、求比值和解决比与比例的实际应用问题。
教学重点：理解比和比例的意义、性质，掌握关于比和比例的一些实际运用和计算。
教学难点：能理清知识间的联系，建构起知识网络，以及对易错题型的理解。
教学过程：一、谈话引入，激发兴趣师：比和比例是小学数学教学中的重点内容，也是初中数学学习的必备知识，所以牢固理解、掌握比和比例的有关内容至关重要。
那么今天我们就一起来梳理一下他们之间的知识联系并对一些典型易错题型进行解析。
二、梳理知识，探寻联系（一）小组合作要求：课前我已经请同学们自己整理的这部分知识点，现在请你们以小组为单位进行交流讨论，丰富补充，形成本组的最优成果。
（二）小组汇报展示1、小组展示本组成果，其他组补充，教师进行评价。
2、课件展示知识网络，强化理解记忆。
三、典型易错题解析师：经过大家的共同努力，我们对比和比例有了更深的了解和认识。
课下，老师搜集了一些有关的典型易错题型，接下来就是大家一显身手的时候了，同学们，你们准备好了吗？！（一）出示解题要求1、单独审题作答2、组内相互订正改错3、总结错误原因和解决方法4、形成本组结论以备汇报交流（二）小组分享交流本组在做题时出现的问题和解决方法。
（三）根据学生的汇报，教师补充强调。
1、10克盐溶解在100克水中，这时盐和盐水的比是（）。
解析：比是有顺序的2、1吨∶250千克的最简整数比是（），比值是（）。
解析：先统一单位再化简求比值3、在4∶8中，如果前项加上8，要使比值不变，后项应扩大（）倍或加上（）。
人教版六年级数学解比例练习题及答案
4
:3
8:x=
0．6∶4＝2.4∶x
8
9
=x
4.56x
=
2.2
111
10
:x=8
:4
2.8:4.2=x:9.6
4
3
5
:4
6∶x＝11532.4
x
3
4
:x=3:12
3654x
=
3
5118
:6
=x:
12
0.61.5
12x
45:x=18:26
3141142511∶＝x∶∶＝x x∶42512536142
4
3
11122.4
=
3x
12
:=
5
114
:x
0.8:4=x:83:x=3:121.25:0.25=x:1.6
2=
8
36x
=
543
x:
2.8:4.2=x:9.:x=4
35:
4
0.6＝1.512x
10∶50＝x∶40
4.680.2＝x
4
23
=6:
2425
11110
:x=8
:
4
2.8:4.2=x:9.6x:24=
2
1
3
3
3
2
8
0.36×5-3x =
x- 0.8x = 16+0 x
X＋25%X=90X2X +535
25% + 10X =
5
X - 15%X = X7
23–.5= 1.538X= X+0%X =. X1
2x-
x -4=1
－273
4
×31
新人教版6年级下册数学同步复习与测试讲义第4讲 比例热点难点一网打尽(学生版)
第4讲比例热点难点一网打尽1、比例的意义：比例的意义表示两个比相等的式子叫做比例。
组成比例的四个数，叫做比例的项。
两端的两项叫做外项，中间的两项叫做内项。
2、比例的基本性质：在比例里，两个外项的积等于两个两个内项的积。
这叫做比例的基本性质。
3、比和比例的区别（1）比表示两个量相除的关系，它有两项（即前、后项）；比例表示两个比相等的式子，它有四项（即两个内项和两个外项）。
（2）比有基本性质，它是化简比的依据；比例出有基本性质，它是解比例的依据。
4、解比例：根据比例的基本性质，把比例转化成以前学过的方程，求比例中的未知项，叫做解比例。
5、成正比例的量：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，他们的关系叫做正比例关系。
用字母表示y/x=k（一定）6、成反比例的量：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，他们的关系叫做反比例关系。
用字母表示x×y=k（一定）7、判断两种量成正比例还是成反比例的方法：关键是看这两个相关联的量中相对就的两个数的商一定还是积一定，如果商一定，就成正比例；如果积一定，就成反比例。
8、比例尺：一幅图的图上距离和实际距离的比，叫做这幅图的比例尺。
9、比例尺的分数（1）数值比例尺和线段比例尺（2）缩小比例尺和放大比例尺10、图上距离：实际距离=比例尺实际距离×比例尺=图上距离图上距离÷比例尺=实际距离11、应用比例尺画图（1）写出图的名称、（2）确定比例尺；（3）根据比例尺求出图上距离；（4）画图（画出单位长度）（5）标出实际距离，写清地点名称（6）标出比例尺12、图形的放大与缩小：形状相同，大小不同。
（相似图形）13、用比例解决问题：根据问题中的不变量找出两种相关联的量，并正确判断这两种相关联的量成什么比例关系，并根据正、反比例关系式列出相应的方程并求解。
人教版六年级下册数学2式与方程 比和比例(课件)
58b表示___b_个__篮__球__的__总__价_____________； 58-a表示篮__球___单__价__比__足___球__单__价__贵__的___价__钱；
独立完成，时间 限定2分钟。
9a+58b表示买_9__个__足__球__和__b_个__篮___球__共__用__的__钱_；
“1” 五年级参加的人数＋六年级参加的人数＝390
解：设五年级参加x人，则六年级参加1.6x人。 x＋1.6x＝390
人教版数学 六年级下册 第六单元 总复习
比和比例
整体复习
知识梳理
比的后项不能是零。
知识梳理
复习巩固
课本P84.1
1.在下表中写出比例的一些知识，再举例说明。
比
比例
意义
两个数的比表示两个数 表示两个比相等
出发，相向而行，经过2.5小时相遇。甲车每小时行65千米，乙车每
小时行多少千米？（列方程解答） 同时相向而行：
解：设乙车每小时行x千米，可得方程： （65＋x）×2.5＝350
相遇路程＝速度和×相遇时间
（65＋x）×2.5÷2.5＝350÷2.5
相遇时间＝相遇路程÷速度和
65＋x＝140 65＋x－65＝140－65
如果a=45，b=6，பைடு நூலகம்9a+58b=7_5________；
3
讲义练习
【例1】聪聪看一本500页的故事书，已经看了5天，每天看x页， 已经看了（ 5x ）页；当x＝30时，还剩下（350 ）页。
【变式1】每个足球x元，李老师买了4个足球，付了200元，找回 ( )元，如果x＝45，应找回( )元。
六年级下册数学试题比例含答案人教版
正比例和反比例（一）正比例的认识两种相关联的量，一种量变化，另一种量也随着变化；如果这两种量中相对应的两个数的比值也就是商一定，这两种量就叫做成正比例的量，它们的关系就叫做成正比例关系。
把握三个要素：第一：两种相关联的量。
第二：其中一个量增加，另一个量也增加；一个量减少，另一个量也减少。
第三：两个量的比值一定。
用字母表示正比例的关系。
如果用字母x和y表示两种相关联的量，用k表示它们的比值（一定），比例关系可以用这样的式子表示：x/y=k (一定)（二）反比例的认识两种相关联的量，一种量变化，另一种量也随着变化，这两种量中相对应的两个数的积一定。
这两种量叫做成反比例的量。
它们的关系叫做反比例关系。
用k=y*x(一定）x不等于0，k不等于0来表示。
把握三个要素：第一：两种相关联的量第二：其中一个量扩大，另一种量缩小，一种量缩而另一种量则扩大，积不变．第三：两个量的积一定用字母表示反比例的关系。
如果用字母x和y表示两种相关联的量，用k表示它们的积（一定），比例关系可以用这样的式子表示：x*y=k (一定)（三）正比例与反比例的相同与不同相同点：两种量都是相关联的量，一种量变化，另一种量也随着变化．不同点：两种量成正比例，是一种量扩大，另一种量也随着扩大，一种量缩小，另一种量也随着缩小，它们扩大，缩小的规律是，这两种量相对应的两个数的比值不变，即商一定．两种量成反比例是一种量扩大，另一种量反而缩小一种量缩小，另一种量反而扩大，它们变化的规律是这两种量中，相对应的两个数积不变（一定）．知识点一：正比例例一：3a=4b，a和b（）A．成正比例B．成反比例C．不成比例【解答】解：因为a：b=4：3=（一定），是比值一定，所以a和b成正比例关系．故选：A．例二：如果y=8x，则x与y 成比例；如果=y ：1，则x：y=【解答】解：因为y=8x，所以x：y=1：8，所以x：y=，是比值一定，所以x与y成正比例；因为=y：1，所以x：4=y：1，x：y=4：1．故答案为：正，4：1．练习一：根据表格判断数量间的比例关系，时间与路程（）时间（小时）23578…路程（千米）101525354…A．成正比例B．成反比例C．不成比例知识点二：反比例例一：下面各题中，两种量成反比例的是（）A．ab=10B．2×5=10C．a+b=10【解答】解：A、因为ab=10（一定），所以a和b成反比例；B、2×5=10，是等式，都是定制，不成比例；C、因为a+b=10（一定），是和一定，所以a和b不成比例；故选：A．例二：如果x=y，那么与y成（）比例．A．正B．反C．不成D．无法确定【解答】解：因为x=y，则=，×y=4（值一定），所以和y成反比例；故选：B．练习1：圆柱体底面积与高（）圆柱体底面积（平方分米）3215121…圆柱体高（分米）23456…A．成正比例B．成反比例C．不成比例知识点三：正比例反比例综合例一：速度、路程和时间这三种量，一定时，和成正比例．一定时，和成反比例．【解答】解：因为路程÷时间=速度（一定），则路程和时间成正比例；又因速度×时间=路程（一定），所以速度和时间成反比例；故答案为：速度、路程、时间，路程、速度、时间．练习1：一列动车在高速铁路上行驶的时间和路程如图．看图填写如表：时间/小时3路程/千米800（1）这列动车行驶的时间和路程成正比例（2）照这样的速度，行1800千米需要9小时．A基础演练1.当两个变量成反比例关系时，所绘成的图是一条（）A．z直线B．曲线C．折线2.铺地的方砖的面积一定，方砖的边长与所需方砖的块数（）A．成正比例B．成反比例C．不成比例3.下面各题中的两种相关联的量，不成比例关系的是（）A．每分钟写字速度一定，写字总数和写字时间B．圆的面积和半径C．一段路，每天修的米数和所用的天数D．正方形的边长和周长4.下列各式中，a和b成反比例的是（）A．9a=6b B．a×=1C．a×8=5.从儿童节那天开始，小明前4天看了72页书，照这样计算，这个月小明一共可以看多少页书？（用比例知识解）6.解比例或解方程．9：=x：149：4.5=（x+6）：8：x=：B巩固提升1.下列关系式中x、y 都不为0，则x与y不是成反比例关系的是（）A．x=B．y=3÷x C．x=×πD．x=下列式子中（a、b都不为0），a和b成反比例的是（）2.A．9×a=2×b B．a×﹣4÷b=0C．a=D．a×7=3.花生的出油率一定，花生的重量和油的重量（）A．成正比例B．成反比例C．不成比例4.表示x和y成反比例关系的式子是（）A．x+y=12B．y=x C．=y D．6x=y5.甲乙两地相距440千米，一辆汽车从甲地开往乙地，3小时行了240千米，照这样计算，几小时可以到达乙地？（用比例解）6.解方程．①x：=16：3②x+x=42．7.先完成下面汽车行驶的路程表，再按要求回答问题．时间/时12356路程/km80160320在如图中描出表示路程和相应时间的点，然后把它们按顺序连起来．并估计一下行驶120km大约要用多长时间．因为=速度（一定）所以时间与路程成正比例．1、正方形的周长和它的边长（）A．成正比例B．成反比例C．不成比例2.下列各式中（a、b均不为0），a和b成反比例的是（）A．a×8=B．9a=6b C．a×﹣1÷b=0D．=b3.表示x和y成正比例关系的式子是（）A．x+y=12B．y=0.8x C．x﹣y=20D．xy=104.已知X和Y是两个相关联的量，并且5：X=Y：6，那么X与Y（）A．成正比例B．成反比例C．不成比例5.解方程．x：=2：x÷15=6.白寨距郑州有20km，一辆公交车从白寨开往郑州，2小时可以行60km，照这样计算．这辆公交车几小时可到达目的地？（用比例解答）_________________________________________________________________________________1.下面构成正比例的是（）A．总页数一定，每天看的页数与天数B．长方形周长一定，长和宽C．x=y，x与y2.圆的周长公式中，当C 一定时，π 与d（）A．成正比例B．成反比例C．不成比例3.如果a与b成正比例，那么x是；如果a与b成反比例，那么x是．a200160b4x4.求未知数xx+3.5=4x：0.5=7：．5.一辆货车从甲地去相距315km的乙地送货．已知前3小时行了135km，如果用同样的速度行完剩下的路程，还要行几小时？（用比例解）6.右面的图象表示小军骑车的路程和时间的关系．（1）看图填表．时间/分30路程/千米24（2）小军骑车行驶的路程和时间成比例，这是因为：．（3）利用图象估计，小军20分钟大约行千米；行20千米大约需要分钟．7.实践活动：旗杆有多高？操场上，同学们正在阳光下测量竹竿、木棒的高度以及它们影子的长度，测量数据如下表：实际高度（m）影长（m）实际高度与影长的比值竹竿120.5竹竿2 1.60.4木棒110.25（1）计算并填写表格；（2）仔细观察表格中竹竿、木棒的实际高度与影长的比值，你有什么发现？（3）根据你的发现想一想，如果这时同学们测出旗杆的影长是 3.2 米，那么旗杆的实际高度应是米．课程顾问签字： 教学主管签字：参考答案知识点一：1.【解答】解：因为a：b=4：3=（一定），是比值一定，所以a和b成正比例关系．故选：A．2.例二：（2016秋•德江县期末）如果y=8x，则x与y成正比例；如果=y：1，则x：y=4：13.练习1【解答】解：当2小时路程是100千米，路程：时间=100：2=50；150：3=50；250：5=50；350：7=50；400：8=50，路程和时间的比一定，那么它们成正比例；路程随着时间的增加而增加，而且单位时间里增加的路程是一定的，那么路程和时间就成正比例；故选A．知识点二：1【解答】解：A、因为ab=10（一定），所以a和b成反比例；B、2×5=10，是等式，都是定制，不成比例；C、因为a+b=10（一定），是和一定，所以a和b不成比例；故选：A．2.【解答】解：因为x=y，则=，×y=4（值一定），所以和y成反比例；故选：B．练习【解答】解：300×2=600；200×3=600；150×4=600；120×5=600；100×6=600；…可以看出，圆柱的底面积和高是两种相关联的量，高随底面积变化而变化．圆柱的底面积和高相对应数的乘积一定，符合反比例的意义．故圆柱的底面积和高成反比例关系．故选：B．知识点三：1【解答】解：因为路程÷时间=速度（一定），则路程和时间成正比例；又因速度×时间=路程（一定），所以速度和时间成反比例；故答案为：速度、路程、时间，路程、速度、时间．2【解答】解：（1）因为图中是一条直线，所以这列动车行驶的时间和路程成正比例．（2）设这列动车行驶了1800千米所用的时间是x小时，由题意得：1800：x=200：1200x=1800×1200x=1800x=9答：这列动车行驶了1800千米所用的时间是9小时．时间/小时34路程/千米600800A1.B2.【解答】解：方砖面积×方砖块数=铺地的总面积（一定），可以看出，每块方砖的面积与方砖块数成反比例关系，而每块方砖的面积等于边长的平方，也就是说，铺地的方砖的面积一定时方砖的块数只是与方砖边长的平方成比例关系，与边长不成比例关系．故选：C．3.【解答】解：A、根据：写字总数÷写字时间=每分钟写字速度（一定），写字总数和写字时间成正比例；B、圆的面积公式s=πr2，从这个公式可以看出：s：r2=π（一定），也就是圆的面积只是与半径的平方成正比例关系，和半径不成比例关系．C、这段路的长度一定，也就是每天修的米数和所用的天数的乘积一定，所以每天修的米数和所用的天数成反比例；D、因为正方形的周长=边长×4，所以正方形的周长÷边长=4（一定），即正方形的周长和它的边长的比值一定，符合正比例的意义，所以正方形的边长和周长成正比例；故选：B．4.【解答】解：选项A，因为9a=6b，则=，无法确定a和b的乘积是否一定，则不成反比例；选项B，因为a×=1，则ab=3（值一定），所以a和b成反比例；选项C，因为a×8=，则=40，无法确定a和b的乘积是否一定，则不成反比例；故答案为：B．5.【解答】解：设小明一个月（30天）可以x页书，4x=72×30x=540．答：这个月小明一共可以看540页书．6.【解答】解：（1）9：=x：14，x=9×14，x×2=126×2，x=252；（2）9：4.5=（x+6）：84.5×（x+6）=9×8，4.5×（x+6）÷4.5=72÷4.5，x+6﹣6=16﹣6，x=10；（3）：x=：，x=，x×10=×10，x=B1.【解答】解：A、因为x=，则有xy=4（一定），所以x和y成反比例；B、因为y=3÷x，则有xy=3（一定），所以x和y成反比例；C、因为x=×π，则有xy=π（一定），所以x和y成反比例；D、因为x=，则有=4（一定），所以x和y成正比例；故选：D．2.【解答】解：A、因为9×a=2×b，所以a：b=（一定），是比值一定，不符合反比例的意义，所以a和b不成反比例；B、因为a×﹣4÷b=0，所以a=，即ab=6，是乘积一定，符合反比例的意义，所以a和b成反比例；C、因为a=，所以5a=3b﹣1，不符合反比例的意义，所以a和b不成反比例；D、因为a×7=，所以a：b=（一定）是比值一定，不符合反比例的意义，所以a 和b不成反比例；故选：B．3.【解答】解：花生的重量和油的重量是两种相关联的量，它们与花生的出油率有下面的关系：=花生的出油率（一定）；已知花生的出油率一定，就是油的重量和花生的重量的比值是一定的，所以花生的重量和油的重量成正比例．故选A．4.【解答】解：A、x+y=12（一定），是和一定，所以x和y不成比例；B、y=x，则y：x=（一定），所以x和y正比例；C、，则xy=6（一定），所以y和x成反比例；D、6x=y，则=6（一定），所以x和y正比例．故选：C．5.【解答】解：设x小时可以到达乙地，440：x=240：3，240x=440×3，x=，x=5.5；答：5.5小时可以到达乙地．6.【解答】解：①x：=16：33x=×163x÷3=12÷3x=4；②x+x=42x=42x÷=42÷x=36．7.【解答】解：（1）时间/时123456路程/km80160240320400480根据路程和时间的比值一定，答案依次为：4，240，400，480．（2）作图如下，从图中看出行驶120km大约要用 1.5小时的时间．1.【解答】解：正方形的周长÷边长=4（一定），是比值一定，所以正方形的周长和它的边长成正比例；故选：A．2.【解答】解：A选项：a×8=，所以b：a=40（一定），a与b成正比例；B选项：因为9a=6b，所以a：b=（一定），a与b成正比例；C选项：因为a×﹣1÷b=0，所以a×b=3（一定），a与b成反比例；D选项不成正比例也不成反比例．故选：C3.【解答】解：A、x+y=12，x与y的和一定，不符合题意；B、y=0.8x，所以=0.8（一定），所以x、y比值一定，x与y成正比例，符合题意；C、x﹣y=20，x与y的差一定，不符合题意；D、xy=10（一定），积一定，x、y成反比例，不符合题意；故选：B．4.【解答】解：A、x+y=12，x与y的和一定，不符合题意；B、y=0.8x，所以=0.8（一定），所以x、y比值一定，x与y成正比例，符合题意；C、x﹣y=20，x与y的差一定，不符合题意；D、xy=10（一定），积一定，x、y成反比例，不符合题意；故选：B．5.【解答】解：6.（1）x：=2：x=2×x÷=÷x=；（2）0.75x=0.5×60.75x÷0.75=3÷0.75x=4；（3）5x=2×205x÷5=40÷5x=8；（4）x÷15=x=x÷=÷x=．6.【解答】解：设这辆公交车x小时可到达目的地；60：2=20：x，60x=20×2，x=，x=；答：这辆公交车小时可到达目的地．1.【解答】解：A．每天看的页数×天数=总页数（积一定），总页数一定，每天看的页数与天数成反比例；B．长+宽=长方形周长的一半（和一定），不成比例；C.x=y，y÷x=（比值一定），x与y成正比例，故选：C．2.【解答】解：因为在圆的周长公式中，圆周率是一个固定不变的数，是定量，它不能随着直径的变化而变化，所有当C一定时，π和d就都是定量，就没有变量了，所有当C一定时，π 与d不成比例；故选：C．3.【解答】解：200：4=160：x200x=4×160200x=640x=3.2160x=200×4160x=800x=5答：如果a与b成正比例，那么x是3.2；如果a与b成反比例，那么x是5．故答案为：3.2，5．4.【解答】解：①x+3.5=4x+3.5﹣3.5=4﹣3.5x=0.625x×=0.625×x=0.9375②x：0.5=7：0.1x=3.50.1x÷0.1=3.5÷0.1x=355.【解答】解：还要行x小时，135：3=（315﹣135）：x，135：3=180：x，135x=180×3，x=，x=4；答：还要行4小时．6.【解答】解：（1）时间/分3090路程/千米824（2）小军骑车行驶的路程和时间成正比例，因为速度一定，路程与时间成正比；（3）由图象可得小军20分钟大约行5千米，行20千米时大约用了75分钟．故答案为：（1）8；90（2）正，速度一定，路程与时间成正比，（3）5，75．7.【解答】解：（1）2：0.5=2÷0.5=4，1.6：0.4=1.6÷0.4=4，1：0.25=1÷0.25=4，填表如下：实际高度（m）影长（m）实际高度与影长的比值竹竿120.54竹竿2 1.60.44木棒110.254（2）仔细观察表格中竹竿、木棒的实际高度与影长的比值，4=4=4=，发现比值是比值一定，所以实际高度与影长之间成正比例；（3）3.2×4=12.8（米）；答：旗杆的实际高度应是12.8米，故答案为：12.8．。
六年级下册数学人教版考点过关卷2式与方程、比与比例的对比(含答案)
考点过关卷2式与方程、比与比例的对比一、我会填。
(每空2分，共22分)1．一个士兵练习射击，命中率是97%，共发射子弹200发，没命中()发。
2．5.4∶63%的比值是()，化成最简整数比是()。
3．春天容易感冒，这天，某班的出勤率是95%，出勤人数和缺勤人数的比是()。
4．笑笑的爸爸的身高是1.80m，他在天安门照了一张照片，照片上的身高是9cm，这张照片使用的拍摄比例是()。
5．把()g盐放入100g水中，盐与盐水的比是1∶51。
6．三个连续的偶数，第一个数是a，那么第三个数是()，它们的和是()。
7．当x＝0.5时，x2＝()，2x＝()；当y＝()时，y2＝2y。
二、我会辨。
(每题2分，共6分)1．当b＜1时，b2＜2b。
() 2．当n是自然数时，2n＋1一定是偶数。
() 3．当a3＝729时，a＝363。
()三、我会选。
(每题3分，共12分)1．把一些树苗按2∶3∶5分配给一、二、三班学生去种植，一班比三班的树苗少()。
A．60%B．40%C ．20%D ．80%2．等腰三角形的一个底角是a °，它的顶角是()。
A ．a °B ．90°－a °C ．180°－2a °3．如果3x ＋6＝30，那么()x ＋12＝60。
A ．6B ．4C ．无法确定4．某水果店运进苹果m 千克，比梨的4倍少n 千克。
求运进梨多少千克。
正确的算式是()。
A ．m ÷4－nB ．(m －n )÷4C ．(m ＋n )÷4D ．4m －n四、计算挑战。
(共31分)1．先化简各比，再求比值。
(每题4分，共16分)0.51∶0.68 2.5小时∶25分钟0.125∶783813∶19392．求未知数。
(每题3分，共15分)5(x －1.2)＝14062%x ＋3.5＝3.8127∶x ＝0.8∶2.1x 8＝4.53.6(1.42＋x )×4＝21.68五、走进生活，解决问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
考点过关卷（二）——式与方程、比与比例的对比
一、我会填。
(每空2分，共22分)
1．一个士兵练习射击，命中率是97%，共发射子弹200发，没命中( )发。
2．5.4∶ 63%的比值是( )，化成最简整数比是( )。
3．春天容易感冒，这天，某班的出勤率是95%，出勤人数和缺勤人数的比是( )。
4．笑笑的爸爸的身高是1.80 m，他在天安门照了一张照片，照片上的身高是9 cm，这张照片使用的拍摄比例是( )。
5．把( )g盐放入100 g水中，盐与盐水的比是1∶51。
6．三个连续的偶数，第一个数是a，那么第三个数是( )，它们的和是( )。
7．当x＝0.5时，x2＝( )，2x＝( )；当y＝( )时，y2＝2y。
二、我会辨。
(每题2分，共6分)
1．当b＜1时，b2＜2b。
( )
2．当n是自然数时，2n＋1一定是偶数。
( )
3．当a3＝729时，a＝363。
( )
三、我会选。
(每题3分，共12分)
1．把一些树苗按2∶3∶5分配给一、二、三班学生去种植，一班比三班的树苗少( )。
A．60% B．40%
C．20% D．80%
2．等腰三角形的一个底角是a°，它的顶角是( )。
A．a° B．90°－a° C．180°－2a°
3．如果3x＋6＝30，那么( )x＋12＝60。
A．6 B．4 C．无法确定
4．某水果店运进苹果m千克，比梨的4倍少n千克。
求运进梨多少千克。
正确的算式是( )。
A．m÷4－n B．(m－n)÷4
C．(m＋n)÷4 D．4m－n
四、计算挑战。
(共31分)
1．先化简各比，再求比值。
(每题4分，共16分)
0.51∶0.68 2.5小时∶25分钟
0.125∶7
8
3813∶1939
2．求未知数。
(每题3分，共15分) 5(x －1.2)＝140 62%x ＋3.5＝3.81
2
7∶x ＝0.8∶2.1
x 8＝4.53.6
(1.42＋x)×4＝21.68
五、走进生活，解决问题。
(1题5分，其余每题6分，共29分)
1．六(2)班书架上共有350本书，下层书的本数是上层的2.5倍。
上、下层各有多少本书？(列方程解)
2．妈妈调的果汁是由苹果汁和水按3∶4混合而成的。
如果水是60 g ，苹果汁有多少克？如果果汁是70 g ，那么水和苹果汁各多少克？
3．在比例尺是1∶5000000的地图上，量得A.B 两地的距离是6 cm 。
甲、乙两车同时从A.B 两地相向开出，3小时相遇，甲、乙两车的速度比是2∶3，甲、乙两车每小时各行驶多少千米？
4．某洗衣机厂5月份计划生产洗衣机504台，实际上半月完成了59，下半月完成了2
3。
这个
月超额生产洗衣机多少台？
5．一份稿件，甲单独录入需5小时完成，乙单独录入需4小时完成。
这份稿件先由甲录入2小时后，剩下的两人合录，还需多长时间才能录完？
参考答案
一、1.6 2.60
7 60∶7 3.19∶1 4.1∶20
5．2 6.a ＋4 3a ＋6 7．0.25 1 0或2 二、1.× 2.× 3.× 三、1.A 2.C 3.A 4.C 四、1. 0.51∶0.68＝51∶68＝3∶4＝34
2.5小时∶25分钟 ＝150分钟∶25分钟 ＝6∶1 ＝6 0.125∶7
8
＝18∶78 ＝1∶7 ＝17 3813∶1939 ＝3813×3919 ＝6∶1 ＝6
2．5(x －1.2)＝140 解：x －1.2＝28 x ＝29.2 62%x ＋3.5＝3.81 解： 0.62x ＝0.31
x ＝0.5
2
7∶x ＝0.8∶2.1 解： 0.8x ＝2
7×2.1
0.8x ＝0.6 x ＝34 x 8＝4.53.6
解： 3.6x ＝8×4.5 x ＝10
(1.42＋x)×4＝21.68 解： 1.42＋x ＝5.42 x ＝4
五、1.解：设上层有x 本书，那么下层有2.5x 本书。
x ＋2.5x ＝350 x ＝100
下层：100×2.5＝250(本)
答：上层有100本书，下层有250本书。
[点拨]往往设一倍量为x ，那么n 倍量就为nx 。
2．60÷4×3＝45(g) 70÷(3＋4)×3＝30(g) 70÷(3＋4)×4＝40(g)
答：如果水是60 g ，苹果汁有45 g ；如果果汁是70 g ，那么水是40 g ，苹果汁是30 g 。
3．6×5000000＝30000000(cm)＝300(km) 300÷3＝100(km)
甲：100÷(2＋3)×2＝40(km) 乙：100÷(2＋3)×3＝60(km)
答：甲车每小时行驶40 km ，乙车每小时行驶60 km 。
4． 504×⎝ ⎛⎭
⎪⎫59＋23－1
＝504×2
9
＝112(台)
答：这个月超额生产洗衣机112台。
[点拨]单位“1”是计划生产504台。
5.15×2＝25
⎝ ⎛⎭⎪⎫1－25÷⎝ ⎛⎭
⎪⎫14＋15＝43(小时) 答：还需4
3小时才能录完。