椭圆与双曲线知识点集合
高中数学【椭圆与双曲线】知识点总结

高中数学【椭圆与双曲线】知识点总结姓名:(一)椭圆1.椭圆的定义如果平面内一动点到两定点距离之和等于正的常数(大于两定点的距离),则动点的规迹是椭圆即|PF1|+|PF2|=2a其中P是动点,F1,F2是定点且|F1F2|=2C当a>c时表示当a=c时表示当a<c时第二定义:动点M与一个定点的距离和它到一条定直线的距离的比是常数e(0<e<1)时,这个点的规迹是椭圆。
定点是,定直是e是2.椭圆的标准方程参数方程(1)标准方程(2)参数方程3.椭圆的性质(1)焦点在x轴上的椭圆标准方程x,y的范围顶点焦点对称轴对称中心长半轴的长短半轴的长焦距离心率e=范围e越大椭圆越e越小椭圆越准线焦半径公式|PF1|=|PF2|=(F1,F2分别为椭圆的左右两焦点,P为椭圆上的一点)椭圆的通径(过椭圆的一个焦点F且垂直于它过焦点的对称轴的弦)|P1P2|=(2)焦点在y轴上的椭圆标准方程x,y的范围顶点焦点对称轴对称中心长半轴的长短半轴的长焦距离心率e=范围e越大椭圆越e越小椭圆越准线焦半径公式|PF1|=|PF2|=(F1,F2分别为椭圆的下上两焦点,P为椭圆上的一点)4.椭圆系(1)共焦点的椭圆系方程为2221x yk k c+=-(其中k>c2,c为半焦距)(2)具有相同离心率的标准椭圆系的方程2222(0) x ya bλλ+=>(二)双曲线1.双曲线的定义如果平面内一个动点到两定点距离之差的绝对值等于正的常数(小于两定点间的距离),那么动点的轨迹是双曲线若一个动点到两定点距离之差等于一个常数,常数的绝对值小于两定点间的距离,那么动点的轨迹是双曲线的一支F1,F2为两定点,P为一动点,(1)若||PF1|-|PF2||=2a①0<2a<|F1F2|则动点P的轨迹是②2a=|F1F2|则动点P的轨迹是③2a=0则动点P的轨迹是(2)若|P F1|-|PF2|=2a①0<2a<|F1F2|则动点P的轨迹是②2a=|F1F2|则动点P的轨迹是③2a=0则动点P的轨迹是2.双曲线的标准方程3.双曲线的性质(1)焦点在x轴上的双曲线标准方程x,y的范围顶点焦点对称轴对称中心实半轴的长虚半轴的长焦距离心率e=范围e越大双曲线的开口越e越小双曲线的开口越准线渐近线焦半径公式|PF1|=|PF2|= (F1,F2分别为双曲线的左右两焦点,P为椭圆上的一点)(3)焦点在y轴上的双曲线标准方程x,y的范围顶点焦点对称轴对称中心实半轴的长虚半轴的长焦距离心率e=范围e越大双曲线的开口越e越小双曲线的开口越准线渐近线焦半径公式|PF1|=|PF2|= (F1,F2分别为双曲线的下上两焦点,P为椭圆上的一点)4.等轴双曲线22(0)x yλλ=±③离心率为-=≠特点①实轴与虚轴长相等②渐近线互相垂直y x5.共轭双曲线以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫原双曲线的共轭双曲线特点①有共同的渐近线②四焦点共圆双曲线22221x ya b+=的共轭双曲线是6.双曲线系(1)共焦点的双曲线的方程为2221x yk k c+=-(0<k<c2,c为半焦距)(2)共渐近线的双曲线的方程为2222(0) x ya bλλ-=≠。
椭圆双曲线抛物线知识点汇总

椭圆双曲线抛物线知识点汇总椭圆、双曲线、抛物线知识点汇总一、椭圆(Ellipse)1. 定义:椭圆是平面上所有到两个固定点(焦点)距离之和为常数的点的集合。
2. 标准方程:\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)其中,\(a\) 是椭圆的长半轴,\(b\) 是短半轴。
3. 性质:- 焦点:椭圆上任意一点到两个焦点的距离之和是一个大于两焦点间距离的常数,即 \(2a\)。
- 椭圆的长轴和短轴互相垂直。
- 椭圆的面积 \(A = \pi a b\)。
4. 焦点性质:- 椭圆上任意一点 \(P\) 与两个焦点 \(F_1\) 和 \(F_2\) 构成的三角形中,\(PF_1 + PF_2 = 2a\)。
5. 椭圆的离心率 \(e\):\(e = \frac{c}{a}\)其中,\(c = \sqrt{a^2 - b^2}\) 是焦点到中心的距离。
二、双曲线(Hyperbola)1. 定义:双曲线是平面上所有到两个固定点(焦点)距离之差为常数的点的集合。
2. 标准方程:\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\) 为右开口双曲线;\(\frac{y^2}{b^2} - \frac{x^2}{a^2} = 1\) 为上开口双曲线。
3. 性质:- 焦点:双曲线上任意一点到两个焦点的距离之差是一个小于两焦点间距离的常数,即 \(2a\)。
- 双曲线的两个分支分别位于中心点的两侧。
- 双曲线的面积无限大。
4. 焦点性质:- 双曲线上任意一点 \(P\) 与两个焦点 \(F_1\) 和 \(F_2\) 构成的三角形中,\(PF_1 - PF_2 = 2a\)。
5. 双曲线的离心率 \(e\):\(e = \frac{c}{a}\)其中,\(c = \sqrt{a^2 + b^2}\) 是焦点到中心的距离,且 \(e > 1\)。
椭圆双曲线抛物线知识点汇总

椭圆双曲线抛物线知识点汇总一、椭圆椭圆是平面内到定点 F1、F2 的距离之和等于常数(大于|F1F2|)的动点 P 的轨迹,F1、F2 称为椭圆的焦点,两焦点的距离|F1F2|称为椭圆的焦距。
1、椭圆的标准方程焦点在 x 轴上:\(\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\)(\(a > b > 0\)),其中\(a\)为长半轴长,\(b\)为短半轴长,\(c\)为半焦距,满足\(c^2 = a^2 b^2\)。
焦点在 y 轴上:\(\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1\)(\(a > b > 0\))。
2、椭圆的性质范围:对于焦点在 x 轴上的椭圆,\(a \leq x \leq a\),\(b\leq y \leq b\);对于焦点在 y 轴上的椭圆,\(b \leq x \leq b\),\(a \leq y \leq a\)。
对称性:椭圆关于 x 轴、y 轴和原点对称。
顶点:焦点在 x 轴上时,顶点坐标为\((\pm a, 0)\),\((0, \pm b)\);焦点在 y 轴上时,顶点坐标为\((0, \pm a)\),\((\pm b, 0)\)。
离心率:椭圆的离心率\(e =\frac{c}{a}\)(\(0 < e <1\)),它反映了椭圆的扁平程度,\(e\)越接近0,椭圆越接近圆;\(e\)越接近 1,椭圆越扁。
3、椭圆的参数方程焦点在 x 轴上:\(\begin{cases}x = a\cos\theta \\ y =b\sin\theta\end{cases}\)(\(\theta\)为参数)焦点在 y 轴上:\(\begin{cases}x = b\cos\theta \\ y =a\sin\theta\end{cases}\)(\(\theta\)为参数)4、椭圆中的焦点三角形设 P 为椭圆上一点,F1、F2 为焦点,\(\angle F1PF2 =\theta\),则三角形 PF1F2 的面积为\(S = b^2\tan\frac{\theta}{2}\)。
椭圆与双曲线知识点集合
x0 2 a2
y02 b2
1
点P在椭圆 C外
| PF1 | | PF2 | 2a
面积 S b2 cot ( 2
F1PF2 )
已知点(P
x0 , y0)和双曲线
C:x a
2 2
y2 b2
1(a
b
0);
F1, F2是双曲线的两焦点,则
x02 a2
y0 2 b2
1
点 P在双曲线两支间
| PF1 | | PF2 | 2a
2
焦点弦为通径时最短,长为 2b a
左 | AB | |2a e(x 1 x2 )|; 右 | AB | |2a e(x 1 x2 )|
下 | AB | |2a e( y 1 y2 )|; 上 | AB | |2a e( y 1 y2 )|
2
同侧焦点弦为通径时最短,长为 2b a
异侧焦点弦为实轴时最短,长为 2a;
F 是椭圆的一个焦点。 l 叫做焦点 F 对应的准线。
焦点在 x 轴上
焦点在 y 轴上
| x | a, y R
| y | a,x R
左 A1 ( a,0); 右 A2 (a,0)
下 A1( a,0); 上 A2 (a,0)
渐近线 y
b x
a
a
渐近线 y
x
b
实轴 A1 A2; 实轴长 2a;虚轴 B1B2; 虚轴长 2b
1 1 k2
( y1 y2) 2 4 y1y2
2
2
已知点(P x0, y0)在椭圆 C:ax2
y b2
1(a
b
0)上; 则
则过(P x0, y0)的椭圆 C的切线方程为
x0 a2
双曲线和椭圆知识点汇总

椭圆知识点知识要点小结:知识点一:椭圆的定义平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距. 注意:若)(2121F F PF PF =+,则动点P 的轨迹为线段21F F ; 若)(2121F F PF PF <+,则动点P 的轨迹无图形.知识点二:椭圆的标准方程1.当焦点在x 轴上时,椭圆的标准方程:12222=+by a x )0(>>b a ,其中222b a c -=2.当焦点在y 轴上时,椭圆的标准方程:12222=+bx a y )0(>>b a ,其中222b a c -=;注意:1.只有当椭圆的中心为坐标原点,对称轴为坐标轴建立直角坐标系时, 才能得到椭圆的标准方程;2.在椭圆的两种标准方程中,都有)0(>>b a 和222b a c -=; 3.椭圆的焦点总在长轴上.当焦点在x 轴上时,椭圆的焦点坐标为)0,(c ,)0,(c -; 当焦点在y 轴上时,椭圆的焦点坐标为),0(c ,),0(c - 知识点三:椭圆的简单几何性质椭圆:12222=+by a x )0(>>b a 的简单几何性质(1)对称性:对于椭圆标准方程12222=+by a x )0(>>b a :说明:把x 换成x -、或把y 换成y -、或把x 、y 同时换成x -、y -、原方程都不变,所以椭圆12222=+by a x 是以x 轴、y 轴为对称轴的轴对称图形,并且是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心。
(2)范围:椭圆上所有的点都位于直线a x ±=和b y ±=所围成的矩形内,所以椭圆上点的坐标满足a x ≤,b y ≤。
(3)顶点:①椭圆的对称轴与椭圆的交点称为椭圆的顶点。
高中椭圆双曲线抛物线知识点汇总

高中椭圆双曲线抛物线知识点汇总一、椭圆的定义和基本特性1. 椭圆的定义:椭圆是平面上到两定点F1和F2的距离之和为常数2a (a>0)的点P的轨迹。
2. 椭圆的基本特性:椭圆有两条对称轴,长轴和短轴,焦点到中心的距离为c,满足c²=a²-b²,离心率e的定义为e=c/a。
3. 椭圆的标准方程:椭圆的标准方程为x²/a²+y²/b²=1(a>b>0),中心在原点,长轴与x轴平行。
二、双曲线的定义和基本特性1. 双曲线的定义:双曲线是平面上到两定点F1和F2的距离之差为常数2a的点P的轨迹。
2. 双曲线的基本特性:双曲线有两条对称轴,两个顶点,离心率e的定义为e=c/a。
3. 双曲线的标准方程:双曲线的标准方程为x²/a²-y²/b²=1(a>0,b>0),中心在原点,x²项系数为正。
三、抛物线的定义和基本特性1. 抛物线的定义:抛物线是平面上到定点F与直线l的距离相等的点P 的轨迹。
2. 抛物线的基本特性:抛物线有焦点F和直线l两个重要元素,焦点到顶点的距离为p,离心率e的定义为e=1。
3. 抛物线的标准方程:抛物线的标准方程为y²=2px(p>0),焦点在y轴上。
四、椭圆双曲线抛物线的性质比较1. 焦点、离心率和轴与方程的关系:椭圆的焦点在轴上,双曲线的焦点在中心轴的延长线上,抛物线的焦点在轴上。
2. 直线与曲线的关系:椭圆是对称轴与任意直线的交点个数有限,双曲线是对称轴与任意直线的交点有两个,抛物线是对称轴与任意直线的交点有且仅有一个。
3. 其他性质:椭圆和双曲线是封闭曲线,抛物线是开口向上或者向下的曲线。
五、高中数学中的应用1. 物理中的应用:椭圆、双曲线和抛物线在经典力学、电磁学等物理学科中有着重要的应用,比如行星轨道、抛物线运动等。
双曲线和椭圆的知识点

双曲线和椭圆的知识点一、双曲线的定义和基本性质双曲线是平面上的一种曲线,由两个相交的直线割成两个分支。
它的定义式为x^2/a^2-y^2/b^2=1或y^2/b^2-x^2/a^2=1,其中a和b为正实数。
双曲线有以下基本性质:1. 双曲线关于x轴、y轴对称;2. 双曲线有两条渐近线,即与x轴和y轴夹角趋近于0或π/2的直线;3. 双曲线在两条渐近线处无界;4. 双曲线分为左右两个分支,左分支开口向左,右分支开口向右;5. 双曲线在x=a和x=-a处有垂直渐近线。
二、椭圆的定义和基本性质椭圆是平面上一条封闭弧形,其所有点到两个定点之距离之和等于定长(即椭圆长轴),定义式为(x-h)^2/a^2+(y-k)^2/b^2=1或(x-h)^2/b^2+(y-k)^2/a^2=1,其中(h,k)为椭圆中心坐标,a和b为长短半轴长度。
椭圆有以下基本性质:1. 椭圆关于x轴、y轴对称;2. 椭圆有两条主轴,即长轴和短轴,交于椭圆中心;3. 椭圆的离心率为e=c/a,其中c为焦点到中心的距离;4. 椭圆上任意一点P(x,y)到焦点F1和F2的距离之和等于椭圆长轴长度;5. 椭圆在x=h处有垂直渐近线。
三、双曲线和椭圆的参数方程双曲线的参数方程为x=acosht,y=bsinht或x=asect,y=btant,其中t为参数。
这两种参数方程对应左右两个分支。
椭圆的参数方程为x=h+acosθ,y=k+bsinθ或x=h+bsinθ,y=k+acosθ,其中θ为参数。
四、双曲线和椭圆的焦点双曲线有两个焦点F1(ae,0)和F2(-ae,0),其中e为离心率。
椭圆也有两个焦点F1(h+ae,k)和F2(h-ae,k),其中a、b、h、k、e均已定义。
五、双曲线和椭圆的面积双曲线面积公式为S=abπ,其中a和b分别为左右两个分支的半轴长度。
椭圆面积公式为S=abπ,其中a和b分别为长轴和短轴长度。
六、双曲线和椭圆的应用1. 双曲线在物理学中有许多应用,如描述电磁波传播、天体运动等。
椭圆与双曲线知识点集合

椭圆与双曲线知识点集合椭圆和双曲线是平面内的两种点的轨迹。
椭圆是指与两个定点F1和F2的距离的和等于常数(大于|F1,F2|)的点的轨迹,这两个点被称为椭圆的焦点。
双曲线是指与两个定点F1和F2的距离的差的绝对值等于常数(大于且小于|F1,F2|)的点的轨迹,这两个点被称为双曲线的焦点。
椭圆和双曲线的定义中,参数2a的范围限制符号不同。
对于椭圆,焦点在x轴上或y轴上,有P={M||MF1|+|MF2|=2a}(2a>|F1F2|);对于双曲线,焦点在x轴上或y轴上,有P={M||MF1|-|MF2|=2a}(0<2a<|F1F2|)。
标准方程是表示椭圆和双曲线的一种方式。
在求标准方程时,一定要考虑焦点位置,即焦距|F1F2|=2c。
椭圆和双曲线的长轴和短轴的长度关系为a2=b2+c2和c2=a2+b2.几何含义是|x|≤a,|y|≤b,或者|x|≤b,|y|≤a,或者|x|≥a,y∈R。
椭圆有4个顶点,双曲线有2个顶点,椭圆没有渐近线,双曲线有两条渐近线。
椭圆和双曲线的顶点和长轴、短轴的长度可以通过求解标准方程得到。
长轴和短轴分别被称为实轴和虚轴,实轴的长度为2a,虚轴的长度为2b。
离心率是描述椭圆和双曲线形状的一个参数,其取值范围为c∈(0,1)和c∈(1,∞)。
离心率越大,椭圆或双曲线越扁,离心率越小,椭圆或双曲线越圆(椭圆)或开口越小(双曲线)。
在平面内,对于一个点到定点F的距离与到定直线l的距离之比为常数e。
这是第一定义。
第二定义是,对于平面内到定点F的距离与到定直线l的距离之比为(<e<1)的点的轨迹是椭圆,其中F在l外。
F是椭圆的一个焦点,而l是焦点F对应的准线。
同样地,当常数(ee1)时,点的轨迹是双曲线。
F是双曲线的一个焦点,而l是焦点F对应的准线。
焦点可以在x轴上或y轴上。
椭圆的准线在两侧,而双曲线的准线在两支之间。
准线方程如下:左准线x a2/c,右准线x a2/c下准线y c2/b,上准线y c2/b左焦半径|PF1|a ex,右焦半径|PF2|a ex下焦半径|PF1|a ey,上焦半径|PF2|a ey左焦半径|PF1||a ex|,右焦半径|PF2||a ex| 下焦半径|PF1||a ey|,上焦半径|PF2||a ey| 焦准距p b2/c焦半径公式是焦半径取值范围[a-c,a+c]左焦点弦|AB|2a e(x1x2),右焦点弦|AB|2a e(x1x2)下焦点弦|AB|2a e(y1y2),上焦点弦|AB|2a e(y1y2)左|AB||2a e(x1x2)|,右|AB||2a e(x1x2)|下|AB||2a e(y1y2)|,上|AB||2a e(y1y2)|焦点弦为长轴时最长,长为2a;焦点弦为通径时最短,长为2b2/a;同侧焦点弦为通径时最短,长为2b2/a;异侧焦点弦为实轴时最短,长为2a。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
'.
椭圆与双曲线知识点总结
椭 圆
双曲线
备注
第一定义
文字语言
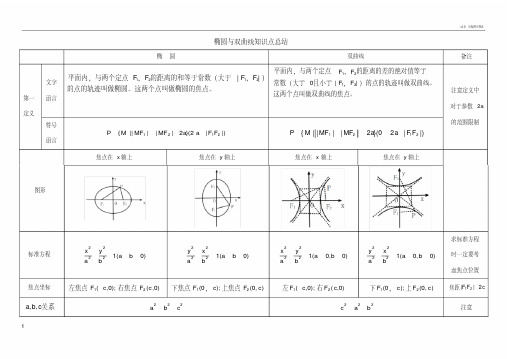
1212F F F F 平面内,与两个定点,的距离的和等于常数(大于|,|)的点的轨迹叫做椭圆。
这两个点叫做椭圆的焦点。
1212F F F F 平面内,与两个定点,的距离的差的绝对值等于常数(大于0且小于|,|)的点的轨迹叫做双曲线。
这两个点叫做双曲线的焦点。
注意定义中对于参数2a 的范围限制
符号语言
1212{|||||2}(2||)P M MF MF a a F F =+=>
1212{|||||2}(02||)P M MF MF a a F F =-=<<
图形 焦点在x 轴上
焦点在y 轴上
焦点在x 轴上
焦点在y 轴上
标准方程
22
22
1(0)x y a b a b +=>> 22
22
1(0)y x a b a b +=>> 22
22
1(0,0)x y a b a b -=>> 22
22
1(0,0)y x a b a b -=>> 求标准方程
时一定要考虑焦点位置
焦点坐标
12(,0);(,0)F c F c -左焦点右焦点
12(0);(0,)F c F c -下焦点,上焦点
12(,0);(,0)F c F c -左右
12(0);(0,)F c F c -下,上
12||2F F c =焦距
,,a b c 关系
2
2
2
a b c =+
2
2
2
c a b =+
注意 几何含义
范围 ||,||x a y b ≤≤
||,||x b y a ≤≤
||,x a y R ≥∈
||,y a x R ≥∈
顶点和 渐近线
12(,0);(,0)(0,);(0,)
A a A a
B b B b --左顶点右顶点下顶点上顶点
12(,0);(,0)(0,);(0,)
B b B b A a A a --左顶点右顶点下顶点上顶点
12(,0);(,0)A a A a -左右
12(,0);(,0)A a A a -下上
椭圆4个;双曲线2个;椭
'.
渐近线b y x a
=±
渐近线a y x b
=±
圆无渐近线
轴
1212;2;;2A A a B B b 长轴长轴长短轴短轴长 1212;2;;2A A a B B b 实轴实轴长虚轴虚轴长
离心率
(0,1)
10c
e a
e e =∈越大,越接近,椭圆越扁;越小,越接近,椭圆越圆 (1,)
c
e a
e e =
∈∞越大,双曲线开口越大;越小,双曲线开口越小 求离心率时应注意取值范围
第二定义
01F l e
<e <F l F l F 平面内,到定点的距离与到定直线的距离之比为常数()的点的轨迹是椭圆。
(在外)是椭圆的一个焦点。
叫做焦点对应的准线。
1F l e e F l F l F >平面内,到定点的距离与到定直线的距离之比为
常数()的点的轨迹是双曲线。
(在外)是双曲线的一个焦点。
叫做焦点对应的准线。
图形
焦点在x 轴上
焦点在y 轴上
焦点在x 轴上
焦点在y 轴上
椭圆的准线
在两侧;双曲线的准线在两支之间
准线方程
22
;a a x x c c =-=左准线右准线
22
;a a y y c c =-=下准线上准线
22
;a a x x c c =-=左右
22
;a a y y c c =-=下上
2
b p c
=焦准距
焦半径公式 1020
||;||PF a ex PF a ex =+=-左焦半径右焦半径
1020
||;||PF a ey PF a ey =+=-下焦半径上焦半径
1020||||;||||
PF a ex PF a ex =+=-左焦半径右焦半径
1020||||;||||
PF a ey PF a ey =+=-下焦半径上焦半径
[]a -c,a+c 焦半径取值范围
[);[+);
c a,c a,-+∞+∞同侧焦半径取值范围异侧焦半径取值范围
'.
'.
2
2
2
12121212
2
1
()4;1()4x x x x y y y y k
+-=++-。
