基于αβ坐标系模型的双馈风力发电机参数辨识
基于Matlab的双馈风力发电机的模型研究与仿真

胡绍猫, 陈秉均 ( 华南理工大学, 广东 广州 510640)
Sim ulation Research on the M odel of Doubly fed Wind T urbine Based on M atlab
HU Shao mao, CHEN Bing jun ( South China U niver sity of T echno lo gy , Guangzhou 510640, China)
[ 1] 刘天羽 , 于书芳 , 等 . 无刷 电机在 风力发 电机变 速恒 频 控制中的研究 [ J] . 内 蒙古 电力 技术 , 2002, 20( 4) : 13. [ 2] [ 3] 贺益康 , 郑 康 , 等 . 交流 励磁变 速恒频 风电系 统运 行 研究[ J] . 电力系统自动化 , 2004, 28( 13) : 55- 59, 68. 聂春燕 . 基于 M at lab/ Simulink 异步电动机动态仿真模 型的研究 [ J] . 电工技术杂志 , 2000, ( 8) : 22- 24. 作者简介 : 胡绍猫 ( 1978- ) , 男 , 江西新余人 , 华南理工大 学
发电效率下降. 为在各种风速下实现最大风能捕获, 需根据风速调节风力机的转速, 即作变速恒频发电 运行. 实现变速恒频发电的方式很多 , 其中交流励磁 方案很具优势. 这种变速恒频方式采用双馈型发电 机 , 其定子并网, 转子由变频器提供三相滑差频率电 流进行励磁 . 在追踪最大风能捕获的变速运行中 , 随 时调节励磁电流的 频率、 相序 , 使发电 机能在同步 上、 下广泛范围内作变速恒频运行. 进行各种运行状 态下风力发电机组的动态仿真, 对其运行和设计具 有重要意义 .
基于粒子群算法的双馈风电场模型参数辨识

A b s t r a c t: D o u b l y f e d i n d u c t i o n g e n e r a t o r ( D F I G ) i S t h e m a i n s t r e a m m o d e l o f f o r e i g n a n d d o m e s t i c w i n d t u r b i n e s g e n e r a t o r ( W T G ) . I n o r d e r t o s t u d y t h e i m p a c t o f l a r g e — s c a l e w i n d p y s t e m n e t w o r k , w e m u s t
删
1 D F I G模 型
行产 生重大影响。 为 了研 究风 电机组接入对 电网的具体影 响及其
解 决措施 , 就必须要 有精确 的风 力发 电机模 型和参数 。 由于 目前 的研 究成 果主要是从理论上做定性分析, 对参数 的精确性要求不 高, 一般 只要取值合 理就行 , 大部分使用 的都是各类 仿真软件 中
f a r m m o d e l p a r me a t e r s b y t h e p a r t i c l e s w a r m a l g o r i t h m( P S O ) , i n o r d e r t o o b t a i n a m o r e a c c u r a t e e l e c t r i c a l
基于改进粒子群算法的双馈感应发电机参数辨识

基于改进粒子群算法的双馈感应发电机参数辨识刘永康;潘学萍;鞠平【摘要】To overcome the inherent deficiencies in the particle swarm optimization ( PSO ) algorithm, such as premature convergence, and to take into account the effects of inertia weight on the identification accuracy, an improved PSO algorithm, which combines the adaptive inertia weight PSO algorithm with the global optimum location mutation PSO algorithm, is proposed in this paper, in order to identify the double-fed induction generator ( DFIG) parameters. First, the identifiability of the DFIG parameters and the difficulties in identification are analyzed. Then, the identification steps based on this improved PSO algorithm are illustrated. Compared with the basic PSO algorithm, the adaptive inertia weight PSO algorithm, and the global optimum location mutation PSO algorithm, the proposed algorithm has faster convergence, smaller errors, and higher identification accuracy, even at a wide search range.%基本粒子群算法( PSO)存在早熟问题,且惯性权重对参数辨识结果的影响较大,为此提出将变权重PSO算法和全局最优位置变异PSO算法相结合的改进PSO算法,并将其应用于双馈感应发电机( DFIG)的参数辨识。
双馈异步风力发电机参数辨识

双馈异步风力发电机参数辨识双馈异步风力发电机参数辨识引言:随着可再生能源的发展和利用的日益增长,风力发电作为清洁能源之一,受到了广泛关注。
双馈异步风力发电机作为一种常见的风力发电机类型,其具有较高的效能和较低的成本,被广泛应用于风电场。
然而,双馈异步风力发电机的参数辨识一直是一个具有挑战性的问题。
本文将介绍双馈异步风力发电机的基本原理和结构,讨论参数辨识的方法,以及未来可能的研究方向。
一、双馈异步风力发电机的原理和结构双馈异步风力发电机由风轮、转子、变压器、逆变器和电网组成。
其基本原理是通过风轮受到的风力驱动转子旋转,产生的机械能通过变压器和逆变器转换成电能,并输入到电网中。
双馈异步风力发电机与传统的固定转子异步发电机相比,具有转矩平稳、输出功率高、噪音低等优点。
二、双馈异步风力发电机参数辨识的方法1. 试验法:通过搭建试验平台,采集双馈异步风力发电机在运行过程中的电流、电压、速度等数据,利用系统辨识方法进行参数的估计。
试验法需要高昂的成本和大量的时间投入,但可以获取具有较高精度的参数估计结果。
2. 基于数学模型的辨识方法:利用数学建模方法建立双馈异步风力发电机的数学模型,然后利用系统辨识方法对模型进行参数辨识。
该方法不需要进行试验,成本较低,但需要对风力发电机的工作原理和电气特性有较深入的理解。
3. 人工智能方法:利用人工智能算法,如神经网络、遗传算法等,对双馈异步风力发电机的参数进行辨识。
这种方法具有较高的自适应性和鲁棒性,但需要大量的数据支持和计算资源。
三、双馈异步风力发电机参数辨识的挑战和应对双馈异步风力发电机参数辨识面临以下挑战:1. 参数难以测量:双馈异步风力发电机的某些参数难以直接测量,需要通过间接手段进行辨识。
2. 参数受环境影响较大:风力发电机的工作环境复杂多变,受到风速、湍流、温度等因素的影响,导致参数辨识的结果不稳定。
3. 系统非线性:双馈异步风力发电机的系统具有非线性特性,使得参数辨识更加困难。
基于αβ坐标系模型的双馈风力发电机参数辨识

基于αβ坐标系模型的双馈风力发电机参数辨识王红;梁俊霞;胡佳琳【摘要】目前双馈式风力发电机(DFIG)为国内外风力发电机的主流机型。
要研究大规模风电并网对电力系统可靠性和稳定性等方面产生的影响,必须要有准确的风力发电机的模型和参数。
研究了双馈风力发电机的模型参数辨识方法。
首先在Matlab/Simulink 环境中搭建了风力发电机并网的仿真模型,得到并网的实测数据。
然后选用发电机的坐标系数学模型,在对模型进行可辨识性分析的基础上得到定子自感、定转子互感的表达式。
最后利用遗传算法,并采用分步辨识策略,进一步辨识出转子初相位0θ角、定子自感、定转子互感、转子互感等风力发电机参数。
为研究大规模风电并网等课题提供了可靠的理论依据。
%Doubly-fed wind power generator (DFIG) type is the mainstream model of the wind turbine at home and abroad at present. To study the impact on reliability and stability of power system with large-scale wind power grid, it must have accurate model and parameters of wind turbine. Therefore, this paper studies the model parameter identification method of doubly-fed wind power generator. First, in the Matlab/Simulink environment, it sets up a simulation model for the wind turbine grid-connected and gets the measured data. Afterwards, by using the generator αβ coordinate system (mathematical) model, it analyzes the identifiability to illustrate the convergence for the proposed model, and then through the analysis of the mathematical model, gets an expression of stator self-induction and the mutual inductance. Finally, the rotor initial phase angleθ , stator self inductance, mutual inductance, and 0 mutual inductance between rotorand stator can be identified by using genetic algorithm with identification strategy step by step. It provides reliable theory for the study of large-scale wind power grid.【期刊名称】《电力系统保护与控制》【年(卷),期】2014(000)020【总页数】5页(P81-85)【关键词】双馈风力发电机;参数辨识;遗传算法【作者】王红;梁俊霞;胡佳琳【作者单位】燕山大学电气工程学院,河北秦皇岛 066004;云南电网北京能源新技术研究发展中心,北京 100084;中国电能成套设备有限公司,北京 100000【正文语种】中文【中图分类】TM614风电并网的技术日臻完善,因此大量的风电场投入了商业运营[1]。
基于贝叶斯神经网络的风电机组参数辨识

基于贝叶斯神经网络的风电机组参数辨识
BN是一种模型不确定性较低的神经网络,其核心思想是将输入和输出之间的关系建模成概率分布,并通过观察样本数据来学习模型参数。
在风电机组参数辨识中,BN模型的输入包括风速、风向、外部负荷和旋转速度等变量,而输出则是风电机组的电功率、机械转矩和转速等参数。
与传统方法相比,BN模型具有以下优点:
1. 可以充分利用先验知识:贝叶斯统计方法可以将先验知识引入到模型中,从而提高模型准确性和鲁棒性。
2. 可以处理不确定性问题:BN模型可以通过概率分布来反映不确定性因素,从而提高模型的可靠性。
3. 可以进行在线学习:BN模型可以在不断观测新数据的过程中进行在线学习,从而逐步改进模型的预测性能。
因此,基于贝叶斯神经网络的风电机组参数辨识方法具有很大的应用前景。
未来,可以进一步研究如何优化该方法的算法和模型结构,以及如何将其应用于更广泛的风电机组系统中,从而促进风力发电技术的发展和推广。
基于αβ坐标系下双馈异步风力发电机串补输电系统次同步谐振的比例谐振控制

基于αβ坐标系下双馈异步风力发电机串补输电系统次同步谐振的比例谐振控制任佳佳;胡应宏;纪延超【摘要】According to the sub-synchronous resonance of DFIG(Doubly-fed Induction Generator) connected to series compensation transmission system,the transfer function is formulated via establishing a mathematical model of DFIG series compensated transmission system.PR control based on static rotor axis is used to suppress the sub-synchronous resonance.By transforming the sub-synchronous frequency component of the system current into αβ component that b ased on static rotor axis,the frequency of the αβ component can coincide with the resonant frequency of PR control.As such,the control strategy can enhance the suppression of the sub-synchronous resonance from the rotor side converter of the wind turbine.The validity and effectiveness of the proposed control strategy are proved by simulative results.%针对双馈异步风力发电机(DFIG)串补输电系统中存在的次同步谐振问题,通过建立DFIG串补输电系统的数学模型,推导出其传递函数;然后采用基于转子静止坐标系下的PR控制来抑制次同步谐振.将系统电流的次同步频率分量转化为转子静止坐标系下的αβ分量,使PR控制的谐振频率点与次同步频率转子静止坐标系下的αβ分量相吻合,用风力发电机实现对次同步谐振的抑制.通过算例仿真分析、硬件在环实验,验证了所提控制策略的有效性和正确性,以及所提方法具有计算简单、便于实现的优点.【期刊名称】《电力自动化设备》【年(卷),期】2017(037)009【总页数】6页(P90-95)【关键词】比例谐振控制;双馈异步风力发电机;串补;输电系统;次同步谐振;风电【作者】任佳佳;胡应宏;纪延超【作者单位】哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001;华北电力科学研究院有限责任公司,北京100045;哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001【正文语种】中文【中图分类】TM3150 引言大容量远距离输电是我国风力发电发展的主要特点,串补输电系统是提升风电输送能力的重要手段,已经在国内得到了广泛的应用[1-3]。
基于Matlab的由双馈风力发电机组成的风电场仿真
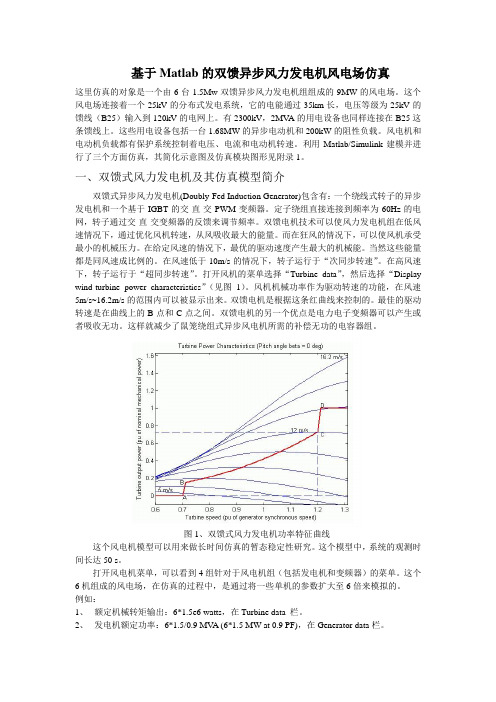
基于Matlab的双馈异步风力发电机风电场仿真这里仿真的对象是一个由6台1.5Mw双馈异步风力发电机组组成的9MW的风电场。
这个风电场连接着一个25kV的分布式发电系统,它的电能通过35km长,电压等级为25kV的馈线(B25)输入到120kV的电网上。
有2300kV,2MV A的用电设备也同样连接在B25这条馈线上。
这些用电设备包括一台1.68MW的异步电动机和200kW的阻性负载。
风电机和电动机负载都有保护系统控制着电压、电流和电动机转速。
利用Matlab/Simulink建模并进行了三个方面仿真,其简化示意图及仿真模块图形见附录1。
一、双馈式风力发电机及其仿真模型简介双馈式异步风力发电机(Doubly-Fed Induction Generator)包含有:一个绕线式转子的异步发电机和一个基于IGBT的交-直-交PWM变频器。
定子绕组直接连接到频率为60Hz的电网,转子通过交-直-交变频器的反馈来调节频率。
双馈电机技术可以使风力发电机组在低风速情况下,通过优化风机转速,从风吸收最大的能量。
而在狂风的情况下,可以使风机承受最小的机械压力。
在给定风速的情况下,最优的驱动速度产生最大的机械能。
当然这些能量都是同风速成比例的。
在风速低于10m/s的情况下,转子运行于“次同步转速”。
在高风速下,转子运行于“超同步转速”。
打开风机的菜单选择“Turbine data”,然后选择“Display wind-turbine power characteristics”(见图1)。
风机机械功率作为驱动转速的功能,在风速5m/s~16.2m/s的范围内可以被显示出来。
双馈电机是根据这条红曲线来控制的。
最佳的驱动转速是在曲线上的B点和C点之间。
双馈电机的另一个优点是电力电子变频器可以产生或者吸收无功。
这样就减少了鼠笼绕组式异步风电机所需的补偿无功的电容器组。
图1、双馈式风力发电机功率特征曲线这个风电机模型可以用来做长时间仿真的暂态稳定性研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ls (设定值为 0.18)
子初始位置,ω 为转换为电角度的转子角速度, 如果 电机匀速运行, 则θ = θ 0 + ∫ ω dt ;rs 为定子电阻,Ls
0 t
为定子自感, Lm 为定转子互感, p 为微分算子。由 于同处一个坐标系下,电感矩阵已经是常数矩阵。 待 辨识的参数为 rs , Ls , Lm ,θ 0 。 1.2 可辨识性分析 可辨识性是指根据所测量到的输入-输出量的动 态数据,能唯一确定模型的参数[9]。除了唯一能确定 模型的参数外,还要求模型是收敛的,若模型是收敛
- 82 -
电力系统保护与控制
辨识时这个角度参数是未知的,因此运用 αβ 坐标系 辨识 模型辨识要比 dq0 坐标系模型少辨识一个参数, 过程简单化。 由于风力发电机的电气参数能够表征其 并网后的电气特性, 磁链的变化与并网后的稳定情况 密不可分, 因此本文只对风力发电机的电气参数进行 了辨识。本文选用 αβ 坐标系数学模型,对该模型参 数进行可辨识性分析。由于定子自感、转子自感及定 转子互感无法同时辨识,因此选用分步辨识策略[8]。 辨识算法选用遗传算法, 将参数估计问题转化为参数 寻优问题,在一定的范围内搜索得到最优解, 得到辨 识的参数。
的且能唯一确定模型参数, 则可认为所选用的模型具 有可辨识性。 假设若干组 rs , Ls , Lm ,θ 0 值,根据式(1)计算每 一组假设值对应的ψ sα 和ψ sβ ,再根据式(2)计算该 组假设值对应的 irαr,βi ,反变换计算求得对应的
ira , irb , irc ,与实测值 i 'ra , i 'rb , i 'rc 进行比较,定义目标函
usαs αsα rs = βsβ 0 usβs ψ 0 −i + p rs −i ψ −isα ψ sα Ls 0 Lm 0 −isβ = ψ sβ 0 Ls α 0 Lm ir irβ
0
引言
风电并网的技术日臻完善,因此大量的风电场 现如今, 风力发电机(WTG)的主 投入了商业运营[1]。 越来越多的风 流机型为双馈式风力发电机(DFIG)[2]。 力发电机组接入电网, 会对电力系统的安全稳定运行 [3] 产生重大影响 。 风电机组参数表征其本质机理和特 性, 形式表现为机组各组成部分的具体参数,如风力 发电机的电抗、电阻、时间常数、转动惯量等。要研 究大规模风电接入对电网产生的影响及解决措施, 就 [4] 必须要有准确的风力发电机组参数 。
(2)
irαr cos θ − sin θ i ' α (3) = i ' irβ sin θ cos θ r β 式中:ψ sα 和ψ sβ 为 αβ 轴磁链,该模型中不含有转子
电压分量,且 usαs,βu ' , i ' 均为测量的瞬时值, sαsβ, i , i , irαr β 其中 irαr,βi 为由 irαr' β , i ' 从转子侧经绕组归算到定子侧 得到;式(3)中 θ = θ 0 + ∫ ω dt 为转子位置,θ 0 为转
数F为
F= 1
∑ (i
i =1
l
rai
− i ) + ∑ (irbi − i ) + ∑ (irci − i )
' 2 rai ' 2 rbi 1 1
l
l
(4)
' 2 rci
1
DFIG 数学模型的可辨识性分析
本文中选用的是 αβ 坐标系数学模型,运用此模 型进行参数辨识时需要进行可辨识性分析, αβ 坐标 系数学模型只有在可辨识的情况下才能用于参数的 辨识。 1.1 αβ 磁链动态模型方程 选用定子侧的模型进行辨识,采用分步辨识策 略, 在定子侧参数已辨识的情况下, 辨识转子侧参数。 αβ 坐标定子磁链动态模型方程为
表1 参数变化引起目标函数收敛性变化值 Table 1 Value of objective function convergence due to parameters change
参数 rs (设定值为 0.023) 变化情况 降低1% 降低5% 降低10% 增加1% 增加5% 增加10% 降低1% 降低5% 降低10% 增加1% 增加5% 增加10% 降低1% 降低5% 降低10% 增加1% 增加5% 增加10% 降低1% 降低5% 降低10% 增加1% 增加5% 增加10% 目标函数值 24.228 1 16.572 0 10.647 2 24.122 8 16.197 0 10.624 3 19.684 21 16.617 9 15.471 2 19.954 3 16.417 9 15.942 6 19.615 5 16.319 8 14.946 8 18.731 6 14.971 6 12.718 2 15.605 5 14.559 5 12.034 6 16.067 5 14.856 7 12.031
Байду номын сангаас
Lm (设定值为 2.9)
θ0
(设定值为 200°)
王 红,等
基于 αβ 坐标系模型的双馈风力发电机参数辨识
- 83 -
Doubly-fed wind power generator parameter identification based on the αβ coordinate model
WANG Hong1, LIANG Jun-xia2, HU Jia-lin3 (1. School of Electrical Engineering, Yanshan University, Qinhuangdao 066004, China; 2. Yunnan Power Grid Beijing New Energy Technology Research and Development Center, Beijing 100084, China; 3. China Power Complete Equipment Co., Ltd., Beijing 100000, China) Abstract: Doubly-fed wind power generator (DFIG) type is the mainstream model of the wind turbine at home and abroad at present. To study the impact on reliability and stability of power system with large-scale wind power grid, it must have accurate model and parameters of wind turbine. Therefore, this paper studies the model parameter identification method of doubly-fed wind power generator. First, in the Matlab/Simulink environment, it sets up a simulation model for the wind turbine grid-connected and gets the measured data. Afterwards, by using the generator αβ coordinate system (mathematical) model, it analyzes the identifiability to illustrate the convergence for the proposed model, and then through the analysis of the mathematical model, gets an expression of stator self-induction and the mutual inductance. Finally, the rotor initial phase angle θ 0 , stator self inductance, mutual inductance, and mutual inductance between rotor and stator can be identified by using genetic algorithm with identification strategy step by step. It provides reliable theory for the study of large-scale wind power grid. Key words: doubly-fed wind power generator; parameter identification; genetic algorithm 中图分类号: TM614 文献标识码:A 文章编号: 1674-3415(2014)20-0081-05
(1)
式中, l 为观测量采样点数。 如此重复上述过程,直至目标函数得到的值最 大,即得到最优解。 总之,进行 αβ 坐标系数学模型可辨识性分析, 其中一个量发生 就是分析在一组 rs , Ls , Lm ,θ 0 数值时, 变化,分析目标函数值的变化情况。 该分析的意义在 于判断目标函数是不是具有收敛性。 假设一组参数, 如表 1 所示, 以此参数结合模型 方程,求式(4)的 20 000 个点的目标函数值。分别 对表中 rs , Ls , Lm ,θ 0 这四个参数值进行单一变化, 无论 偏差大小,观看目标函数的大小,参数单一变化后, 目标函数值如表 1 所示。
基金项目:中国南方电网公司科技项目(K-YN2012-018)
从双馈式风力发电机参数辨识新情况来看, 文献 [5]运用最小二乘法, 研究了 2.2 kW 实验风机的三参 数辨识问题,仿真和实验验证结果具有很好的精度。 文献[6]基于 LabVIEW2009 软件搭建的双馈电机参 数辨识平台,采用图形化编程语言, 实现了双馈电机 的参数辨识。 文献[7]运用 Matlab/Simulink 仿真工具, 给定一些参数, 对 1.5 MW 双馈风电机组故障状态进 行仿真分析。 在选用风力发电机数学模型上也各有不同, 国内 外研究者大多选用风力发电机的三阶、 五阶暂态数学 模型或者选用经坐标变换得到的 dq0 坐标系模型。 αβ 坐标系与 dq0 坐标系之间有一定的角度,当由 αβ 坐标系变换到 dq0 坐标系时附加了一个角度参数, 而
