矿大采矿材料力学B题库精选题8
矿大采矿材料力学B题库精选题6
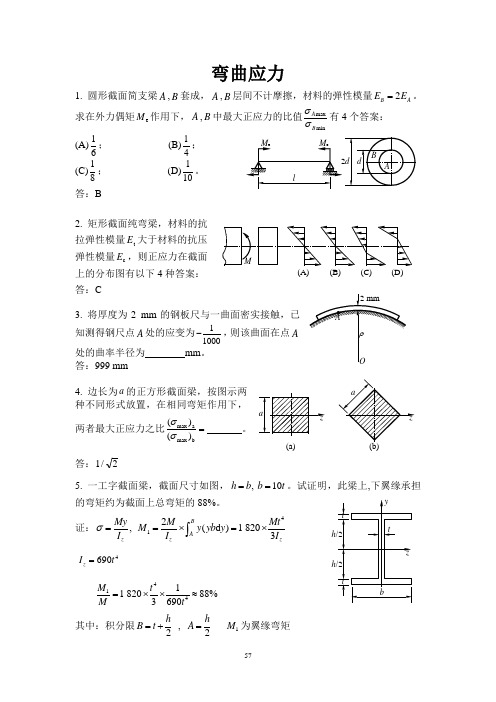
(A)(B)(C)(D)弯曲应力1. 圆形截面简支梁A,B套成,A,B层间不计摩擦,材料的弹性模量2B AE E=。
求在外力偶矩eM作用下,A,B中最大正应力的比值maxminABσσ有4个答案:(A)16;(B)14;(C)18;(D)110。
答:B2. 矩形截面纯弯梁,材料的抗拉弹性模量tE大于材料的抗压弹性模量cE,则正应力在截面上的分布图有以下4种答案:答:C3. 将厚度为2 mm的钢板尺与一曲面密实接触,已知测得钢尺点A处的应变为11000-,则该曲面在点A处的曲率半径为mm。
答:999 mm4. 边长为a的正方形截面梁,按图示两种不同形式放置,在相同弯矩作用下,两者最大正应力之比max amax b()()σσ=。
答:2/15. 一工字截面梁,截面尺寸如图,,10h b b t==。
试证明,此梁上,下翼缘承担的弯矩约为截面上总弯矩的88%。
证:412,(d) 1 8203BAz z zMy M MtM y yb yI I Iσ==⨯=⨯⎰4690zI t=41411 82088%3690M tM t=⨯⨯≈其中:积分限1,22h hB t A M=+=为翼缘弯矩(a)6. 直径20 mm d =的圆截面钢梁受力如图,已知弹性模量200 GPa E =,200 mm a =,欲将其中段AB 弯成 m ρ=12的圆弧,试求所需载荷,并计算最大弯曲正应力。
解:1MEIρ=而M Fa = 4840.78510 m , 0.654 kN 64d EII F aπρ-==⨯==33max80.654100.22010167 MPa 2220.78510M d Fad I I σ--⋅⨯⨯⨯⨯====⨯⨯ 7. 钢筋横截面积为A ,密度为 ρ,放在刚性平面上,一端加力F ,提起钢筋离开地面长度3l 。
试问F 应多大? 解:截面C 曲率为零2(/3)0, 326C Fl gA l gAl M F ρρ=-==8. 矩形截面钢条长l ,总重为F ,放在刚性水平面上,在钢条A 端作用3F向上的拉力时,试求钢条内最大正应力。
材料力学题库及答案

《材料力学》试题库及答案一、判断题(共266小题)材料力学主要研究杆件受力后变形与破坏的规律。
( A )2、内力只能是力。
( B )3、若物体各点均无位移,则该物体必定无变形。
( A )4、截面法是分析应力的基本方法。
( B )5、构件抵抗破坏的能力,称为刚度。
( B )6、构件抵抗变形的能力,称为强度。
( B )7、构件在原有几何形状下保持平衡的能力,称为构件的稳定性。
( A )8、连续性假设,是对变形固体所作的基本假设之一。
( A )9、材料沿不同方向呈现不同的力学性能,这一性质称为各向同性。
( B )10、材料力学只研究处于完全弹性变形的构件。
( A )11、长度远大于横向尺寸的构件,称为杆件。
( A )12、研究构件的内力,通常采用实验法。
( B )13、求内力的方法,可以归纳为“截-取-代-平”四个字。
( A )14、1MPa=109Pa=1KN/mm2。
( B )15、轴向拉压时 45º斜截面上切应力为最大,其值为横截面上正应力的一半( A )16、杆件在拉伸时,纵向缩短,ε<0。
( B )17、杆件在压缩时,纵向缩短,ε<0;横向增大,ε'>0。
( A )18、σb是衡量材料强度的重要指标。
( A)19、δ=7%的材料是塑性材料。
( A )20、塑性材料的极限应力为其屈服点应力。
( A )21、“许用应力”为允许达到的最大工作应力。
( A )22、“静不定系统”中一定存在“多余约束力”。
( A )23、用脆性材料制成的杆件,应考虑“应力集中”的影响。
( A )24、进行挤压计算时,圆柱面挤压面面积取为实际接触面的正投影面面积。
( A )25、冲床冲剪工件,属于利用“剪切破坏”问题。
( A )26、同一件上有两个剪切面的剪切称为单剪切。
( B )27、等直圆轴扭转时,横截面上只存在切应力。
( A )28、圆轴扭转时,最大切应力发生在截面中心处。
( B )29、在截面面积相等的条件下,空心圆轴的抗扭能力比实心圆轴大。
2008考研卷(采矿)

3.图示(a)、(b)两根梁的最大弯矩之比值 等于:
(A) 1;(B) 2;(C) 3;(D) 4。
正确答案是______。
4.图示梁的材料为铸铁,截面形式有4种如图:
最佳形式为。
中国矿业大学2008年硕士研究生入学考试试题
5.圆截面直杆一端铰支于地面,另一端斜靠于光滑的铅直墙上,在自重作用下,该杆的变形有四种答案:
有一钢丝绳,预加初拉力 后固定于A、B两点。在离点B高为h的C处加一向下的载荷 。已知绳长为l,而且绳只能承受拉力。问:当(1) ,(2) 时,AC段和CB段绳中的拉力为多少?
四、计算题(15分)
共页第页
作图示梁的剪力图和弯矩图。
中国矿业大学2008年硕士研究生入学考试试题
五、计算题(15分)
图示矩形截面钢杆。用应变片测得杆件上下表面的轴向正应变分别为 与 ,材料的弹性模量 。试求:
1.一板形试件,在其表面沿纵向和横向粘帖两片电阻应变片,用以测量试件的应变。实验时,载荷F增加到 时测得 , ,该试件的拉压弹性模量 ,剪切弹性模量 ,泊松比 。
2.图示直杆长为l,横截面面积为A,其材料的应力-应变关系为 ,其中C和m为已知的材料常数。当直杆轴向拉伸时,测得杆的伸长为 ,则拉力 。
八、计算题(19分)
图示梁AB和杆CD由 钢制成,弹性模量 , , ,梁AB横截面为矩形,其高 ,宽 。杆CD横截面直径 ,直线经验公式为 ,试求:
(1)杆CD的临界压力 ;
共页第页
(2)按杆CD的稳定问题计算临界分布载荷 。
(C)CD段受拉,轴力为F;A和B两端不受力;
(D)AC和DB段受压,轴力均为-F;CD段不受力。
正确答案是______。
材料力学-考试题集(含答案解析)

《材料力学》考试题集一、单选题1.构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关(B)只与构件的形状尺寸有关(C)与二者都有关(D)与二者都无关2.一直拉杆如图所示,在P力作用下。
(C) 横截面c上的轴力最大(D) 三个截面上的轴力一样大3.在杆件的某一截面上,各点的剪应力。
(A)大小一定相等(B)方向一定平行(C)均作用在同一平面内(D)—定为零4.在下列杆件中,图所示杆是轴向拉伸杆。
P (A) (B)(C) (D)5.图示拉杆承受轴向拉力P的作用,斜截面m-m的面积为A,则σ=P/A为。
(A)横截面上的正应力(B)斜截面上的剪应力(C)斜截面上的正应力(D)斜截面上的应力6.解除外力后,消失的变形和遗留的变形。
(A)分别称为弹性变形、塑性变形(B)通称为塑性变形(C)分别称为塑性变形、弹性变形(D)通称为弹性变形7.一圆截面轴向拉、压杆若其直径增加—倍,则抗拉。
(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍(C)强度和刚度均是原来的2倍(D)强度和刚度均是原来的4倍8.图中接头处的挤压面积等于。
(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示,已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2(B)τ(C)2τ(D)010.下图是矩形截面,则m—m线以上部分和以下部分对形心轴的两个静矩的。
P(A)绝对值相等,正负号相同(B)绝对值相等,正负号不同(C)绝对值不等,正负号相同(D)绝对值不等,正负号不同11.平面弯曲变形的特征是。
(A)弯曲时横截面仍保持为平面(B)弯曲载荷均作用在同—平面内;(C)弯曲变形后的轴线是一条平面曲线(D)弯曲变形后的轴线与载荷作用面同在—个平面内12.图示悬臂梁的AC段上,各个截面上的。
(A)剪力相同,弯矩不同(B)剪力不同,弯矩相同(C)剪力和弯矩均相同(D)剪力和弯矩均不同13.当横向力作用于杆件的纵向对称面内时,关于杆件横截面上的内力与应力有以下四个结论。
大学材料力学习题及答案(题库)

一.是非题:(正确的在括号中打“√”、错误的打“×”) (60小题) 1.材料力学研究的主要问题是微小弹性变形问题,因此在研究构件的平衡与运动时,可不计构件的变形。
( √ )2.构件的强度、刚度、稳定性与其所用材料的力学性质有关,而材料的力学性质又是通过试验测定的。
( √ ) 3.在载荷作用下,构件截面上某点处分布内力的集度,称为该点的应力。
(√ ) 4.在载荷作用下,构件所发生的形状和尺寸改变,均称为变形。
( √ ) 5.截面上某点处的总应力p 可分解为垂直于该截面的正应力σ和与该截面相切的剪应力τ,它们的单位相同。
( √ )6.线应变ε和剪应变γ都是度量构件内一点处变形程度的两个基本量,它们都是无量纲的量。
( √ )7.材料力学性质是指材料在外力作用下在强度方面表现出来的性能。
( ) 8.在强度计算中,塑性材料的极限应力是指比例极限p σ,而脆性材料的极限应力是指强度极限b σ。
( )9.低碳钢在常温静载下拉伸,若应力不超过屈服极限s σ,则正应力σ与线应变ε成正比,称这一关系为拉伸(或压缩)的虎克定律。
( )10.当应力不超过比例极限时,直杆的轴向变形与其轴力、杆的原长成正比,而与横截面面积成反比。
( √ )11.铸铁试件压缩时破坏断面与轴线大致成450,这是由压应力引起的缘故。
( )12.低碳钢拉伸时,当进入屈服阶段时,试件表面上出现与轴线成45o 的滑移线,这是由最大剪应力max τ引起的,但拉断时截面仍为横截面,这是由最大拉应力max σ引起的。
( √ )13.杆件在拉伸或压缩时,任意截面上的剪应力均为零。
( ) 14.EA 称为材料的截面抗拉(或抗压)刚度。
( √ ) 15.解决超静定问题的关键是建立补充方程,而要建立的补充方程就必须研究构件的变形几何关系,称这种关系为变形协调关系。
( √ ) 16.因截面的骤然改变而使最小横截面上的应力有局部陡增的现象,称为应力集中。
材料力学考试试卷B卷及答案修订精修订

材料力学考试试卷B卷及答案修订GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-交通学院期末考试试卷一、填空题(总分20分,每题2分)1、杆件在外力作用下,其内部各部分间产生的,称为内力。
2、杆件在轴向拉压时强度条件的表达式是。
3、低碳钢拉伸时,其应力与应变曲线的四个特征阶段为阶段,阶段,阶段,阶段。
4、线应变指的是的改变,而切应变指的是的改变。
5.梁截面上弯矩正负号规定,当截面上的弯矩使其所在的微段梁凹向下时为。
6.梁必须满足强度和刚度条件。
在建筑中,起控制做用的一般是条件。
7、第一和第二强度理论适用于 材料,第三和第四强度理论适用于 材料。
8、求解组合变形的基本方法是 。
9、力作用于杆端方式的不同,只会使与杆端距离在较小的范围内受到影响,该原理被称为。
10、欧拉公式是用来计算拉(压)杆的 ,它只适用于 杆。
二、 单项选择(总分20分,每题2分)1、用截面法可求出图示轴向拉压杆a-a 截面的内力12N P P =-,下面说法正确的是( )A. N 其实是应力B. N 是拉力C. N 是压力D. N 的作用线与杆件轴线重合2、构件的强度是指( )A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持原有平衡态的能力C. 在外力作用下构件抵抗破坏的能力D. 在外力作用下构件保持原有平稳态的能力3、现有钢、铸铁两种杆材,其直径相同。
从承载能力与经济效益两个方面考虑,图示结构中两种合理选择方案是( )A. 1杆为钢,2杆为铸铁B. 1杆为铸铁,2杆为钢C. 2杆均为钢D. 2杆均为铸铁4、从拉压杆轴向伸长(缩短)量的计算公式EANl l =∆可以看出,E 和A 值越大,l ∆越小,故( )。
A. E 为杆的抗拉(压)刚度。
B. 乘积EA 表示材料抵抗拉伸(压缩)变形的能力。
C. 乘积EA 为杆的抗拉(压)刚度D. 以上说法都不正确。
(冶金行业)中国矿大(徐州)考研材料力学精选题章

(冶金行业)中国矿大(徐州)考研材料力学精选题章精选题1轴向拉压1.等截面直杆CD位于俩块夹板之间,如图示。
杆件和夹板间的摩擦力和杆件自重保持平衡。
设杆CD俩侧的摩擦力沿轴线方向均匀分布,且俩侧摩擦力的集度均为q,杆CD的横截面面积为A,质量密度为,试问下列结论中哪壹个是正确的?(A);(B)杆内最大轴力;(C)杆内各横截面上的轴力;(D)杆内各横截面上的轴力。
2.低碳钢试样拉伸时,横截面上的应力公式适用于以下哪壹种情况?(A)只适用于≤;(B)只适用于≤;(C)只适用于≤;(D)在试样拉断前都适用。
3.在A示。
点A(A);(B);(C);(D)。
4.(A);(B); (C);(D)。
5.设受力在弹性范围内,问空心圆杆受轴向拉伸时,外径和壁厚的下列四种变形关系中哪壹种是正确的?(A)外径和壁厚都增大;(B)外径和壁厚都减小; (C)外径减小,壁厚增大;(D)外径增大,壁厚减小。
6.三杆结构如图所示。
今欲使杆3的轴力减小,问应采取以下哪壹种措施?(A) 加大杆3的横截面面积; (B)减小杆3的横截面面积; (C) 三杆的横截面面积壹起加大; (D)增大角。
7.图示超静定结构中,梁AB 为刚性梁。
设和分别表示杆1的伸长和杆2的缩短,(A); (B); (C); (D)。
8.图示结构,AC 为刚性杆,杆1和杆2俩杆的轴力变化可能有以下四种情况,问哪壹种正确?(A)俩杆轴力均减小; (B)俩杆轴力均增大;(C)杆1轴力减小,杆2轴力增大;(D)杆1轴力增大,杆2轴力减小。
9.结构由于温度变化,则:(A)静定结构中将引起应力,超静定结构中也将引起应力;(B)静定结构中将引起变形,超静定结构中将引起应力和变形;(C)无论静定结构或超静定结构,都将引起应力和变形;(D)静定结构中将引起应力和变形,超静定结构中将引起应力。
10.图示受力结构中,若杆1和杆2的拉压刚度EA相同,则节点A的铅垂位移,水平位移。
11.壹轴向拉杆,横截面为(a﹥b)的矩形,受轴向载荷作用变形后截面长边和短边的比值为。
材料力学试卷及答案(B卷)

3. 作用力和反作用力总是同时存在,两个力大小 ,方向 ,作用线 ,分别作用在两个相互作用的物体上。
4. 根据切应力互等定理,在单元体相互垂直的两个平面上,切应力必然成对存在,且数值 ,两者都 于两个平面的交线,方向则共同指向或共同背离这一交线。
5. 根据梁的支座约束类型可将梁简化为 、外伸梁和 等三种基本形式的静定梁。
三、选择题(每题3分,共30分)1. 下列不属于材料力学三大基本假设之一的是( )A. 均匀性假设B. 连续性假设C. 平面假设D. 各向同性假设 2. 关于静定与静不定结构,下列说法正确的是( )。
A. 静定结构会产生温度应力。
B. 静定结构会产生装配应力。
C. 静不定结构会产生装配应力。
D. 静不定结构的问题无法求解。
3. 内力和应力的关系是( )。
A. 内力大于应力B. 内力等于应力的代数和C. 内力是矢量,应力是标量D. 应力是内力的集度 4. 轴力沿轴向变化的杆件在发生破坏的截面上( )A. 外力一定最大,且面积一定最小;B. 轴力一定最大,且面积一定最小;C. 轴力不一定最大,但面积一定最小;D. 轴力和面积之比一定最大。
5. 低碳钢拉伸时,应力应变是线性变化的,则应力必须低于( )。
A. b σ B. s σ C. e σ D. p σ6. 工程上区分塑性和脆性材料的标准是看其延伸率是否大于( )。
A. 1% B. 3% C. 5% D. 10%7. 如下有关塑性材料许用应力的说法中,正确的是( )。
A. 许用应力等于比例极限除以安全系数 B. 许用应力等于屈服极限除以安全系数 C. 许用应力等于强度极限除以安全系数 D. 许用应力等于比例极限8. 当水平梁某横截面弯矩为负值时,则该横截面上正应力的正确分布图是( )。
9. 载荷在梁的全长或者部分长度上是连续分布的,则该载荷称为( )。
A. 分布载荷 B. 集中力偶 C. 弯矩 D. 集中载荷 10. 外力撤除后不能完全消除的变形被称为( )A. 塑性变形B. 屈服变形C. 弹性变形D. 回复变形四、计算题(共30分)1. (10分)图示悬臂梁截面为矩形,承受载荷110kN F 作用,试计算梁内的最大弯曲正应力及该应力所在截面上K 点处的弯曲正应力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应力状态 强度理论1. 图示单元体,试求 (1) 指定斜截面上的应力;(2) 主应力大小及主平面位置,并将主平面标在单元体上。
解:(1) MPa 6.762sin 2cos 22=--++=ατασσσσσαx yx yxM P a7.322cos 2sin 2-=+-=ατασσταx yx (2)22min max )2(2xy y x y x τσσσσσσ+-±+=98.12198.81-=MPa 98.811=σMPa ,02=σ,98.1213-=σMPa35.3940200arctan 21)2arctan(210==--=y x xy σστα2. 某点应力状态如图示。
试求该点的主应力。
解:取合适坐标轴令25=x σ MPa ,9.129-=x τ MPa 由02cos 2sin 2120=+-=ατασστxy yx 得125-=y σMPa 所以22min max )2(2xy y x y x τσσσσσσ+-±+= 20010015050)9.129(755022-=±-=-+±-= MPa 1001=σ MPa ,02=σ,2003-=σ MPa3. 一点处两个互成 45平面上的应力如图所示,其中σ未知,求该点主应力。
解:150=y σ MPa ,120-=x τ MPa 由 ατασστ2cos 2sin 245xy yx +-=802150-=-=x σ得 10-=x σ MPaMPa所以22min max )2(2xy y x y x τσσσσσσ+-±+= 22.7422.214-=MPa22.2141=σ MPa ,02=σ,22.743-=σ MPa4. 图示封闭薄壁圆筒,内径100=d mm ,壁厚2=t mm ,承受内压4=p MPa ,外力偶矩192.0=e M kN ·m 。
求靠圆筒内壁任一点处的主应力。
解:75.505.032)1.0104.0(π10192.0443=⨯-⨯=x τ MPa504==t pd x σ MPa1002==tpd y σ MPa35.497.100)2(222min max =+-±+=xy y x y x τσσσσσσ MPa 7.1001=σ MPa ,35.492=σ MPa ,43-=σ MPa5. 受力体某点平面上的应力如图示,求其主应力大小。
解:取坐标轴使100=x σMPa ,20=x τMPaατασσσσσα2sin 2cos 22x yx yx --++=40120sin 20120cos 21002100=--++= yyσσ得1.43=y σMPa22min max )2(2xy y x y x τσσσσσσ+-±+=77.3633.106=MPa 33.1061=σMPa ,77.362=σMPa ,03=σ'45-M e6.解:22min max )2(2xy y x y x τσσσσσσ+-±+= 16.4216.5216.47540252203022-=±=+±-=MPa 所以2.521=σMPa ,102=σMPa ,16.423-=σMPa2.47231max =-=σστMPa7. 图示工字形截面梁AB ,截面的惯性矩61056.72-⨯=z I m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
解:17.361056.7207.075.0105063=⨯⨯⨯⨯=-σ MPa (压应力) 8.81056.7203.01085301501050693=⨯⨯⨯⨯⨯⨯⨯=--τ MPa22min max )2(2xy y x y x τσσσσσσ+-±+=2.3803.2-= MPa 03.21=σ MPa ,02=σ,2.383-=σ MPa05.7717.368.82arctan 21)2arctan(210=⨯-=--=y x xy σστα8. 图示矩形截面拉杆受轴向拉力F ,若截面尺寸b 、h 和材料的弹性模量E ,泊松比ν均已知,试求杆表面 45方向线段AB 的改变量=∆AB L ?解:bhFx =σ,0=y σ,0=xy τ bh F2=ασ,bh F 22=+απσ( 45=α)所以)1(2)22(145v EbhF bh F bh F E -=-=νε EbF EbhFh AB L AB 2)1(2)1(2245ννε-=-⨯==∆50kNA B0.75mσ305.77τaσaσ19. 一边长为50 mm 的正方形硬铝板处于纯剪切状态,若切应力80=τ MPa ,并已知材料的弹性模量72=E GPa ,泊松比34.0=ν。
试求对角线AC 的伸长量。
解:8045= σMPa ,80135-= σMPa39451048.1)8034.080(10721-⨯=⨯+⨯=ε 25=AC L00105.01048.1253=⨯⨯=∆-AC L mm10. 一变形体A 四周和底边均与刚性边界光滑接触,上边受均布压力0σ。
已知材料的的弹性模量E ,泊松比ν,求竖向和水平方向上的应变和应力。
解:0σσ-=y ,z x σσ=,0==z x εε0)]([1=+-=z y x x E σσνσε,得到10-==ννσσσz x )121()]12([1)]([12000ννσννσνσσσνσε---=---=+-=E E E z x y y11. 设地层由石灰岩组成,其密度3105.2⨯=ρ kg/m 3,泊松比2.0=ν。
计算离地面200m 深处的地压应力。
解: 9.42008.9105.23-=⨯⨯⨯-=y σ MPaz x σσ=,0==z x εε 0)]9.4(2.0[1=+-⨯-=z x x Eσσε 得到22.1-==z x σσ MPa12. 一体积为101010⨯⨯ mm 3的立方铝块,将其放入宽为10 mm 的刚性槽中。
已知铝的泊松比ν33.0=,求铝块的三个主应力。
解: 6001.001.010633-=⨯⨯-=σMPa, 01=σ 由 0)6033.0(122=⨯+=σεE得 8.192-=σMPa200mσxσzσy13. 直径为D 的实心圆轴,受外力偶e M 作用如图。
测得轴表面点A 与轴线成 45方向的线应变为ε,试导出用e M 、D 、ε表示的切变弹性模量G 的表达式。
解:τσ=- 45, τσ-= 45τνε)1(145+=E,所以ετG 2= 又316D M e πτ=,所以ED M G e38π=14. 直径100=d mm 的圆轴,受轴向拉力F 和力偶矩e M 作用。
材料的弹性模量200=E GPa ,泊松比3.0=ν。
现测得圆轴表面的轴向线应变6010500-⨯=ε,45方向的线应变64510400-⨯= ε,求F 和e M 。
解:7850=⋅=A E F ε kN 设力偶矩引起的切应力为ττσ+=-5045,τσ-=5045)(1454545 νσσε-=-E ]10)50(3.010)50[(102001669⨯-⨯-⨯+⨯=ττ 610400-⨯=6.34=τ MPa ,又3)1.0(π16⨯=M τ 8.6=e M kN ·m15. 直径100=d mm 的实心钢球,受静水压力42=p MPa 作用。
求直径和体积的缩减量。
设钢球的弹性模量210=E GPa ,泊松比3.0=ν。
解:因为42321-=-===q σσσ MPa所以333211024.042310210)3.021()(21-⨯-=⨯⨯⨯⨯--=++-=σσσνθE 533211108102108.16)]([1-⨯-=⨯-=+-=σσνσεE 得 23310257.1100)6(1024.0--⨯-=⨯⨯⨯-==∆πθV V mm 3351108100108--⨯-=⨯⨯-==∆d d εmmττ16. 边长10=a 0 mm 的立方体,已知弹性模量200=E GPa ,泊松比3.0=ν。
如将立方体沉入100 m 深的水中,求其体积变化。
解:因为1321-=-===gh ρσσσMPa)(21321σσσνθ++-=E 63106)3(102006.01-⨯-=-⨯⨯-= 61.01.01.01066-=⨯⨯⨯⨯--==∆-V V θ mm 317. 图示拉杆,F ,b ,h 及材料的弹性常数E 、ν均为已知。
试求线段AB 的正应变和转角。
解:bh F x =σ,bhF213545== σσ所以)1(2)(!13545ννσσε-=-=bhE FE AB 又因为bhEF x =ε,bhEFvy -=ε所以bhEv F bhE vF bhE F AB )1()(45+-=+-== γϕ 18. 图示曲拐ABC 在水平面内,悬臂端C 处作用铅垂集中力F 。
在上表面E 处,沿与母线成 45方向贴一应变片,已测得线应变 45ε,求载荷F 值。
已知长度l 、a 、直径d 及材料的常数E 、v 。
解:应力状态如图示,332d Fl πσ=,316d Faπτ= τσσ+=245,τσσ-=-245所以)(!454545 --=σσεv E 所以)1(16)1(16345v a v l dE F ++-=πε19. 三个弹性常数之间的关系:)]1(2/[ν+=E G 适用于(A)任何材料在任何变形阶段; (B)各向同性材料在任何变形阶段; (C)各向同性材料应力在比例极限范围内; (D)任何材料在弹性变形范围内。
答:C20. 一实心均质钢球,当其外表面处迅速均匀加热,则球心O 点处的应力状态。
(A)单向拉伸应力状态; (B)二向拉伸应力状态; (C)三向等值拉伸应力状态; (D)三向压缩应力状态。
答:C/2στσ/2σ21. 混凝土立方体试样作单向压缩试验时,若在其上、下压板面上涂有润滑剂,则试样破坏时将沿纵向剖面裂开的主要原因。
(A)最大压应力; (B)最大切应力; (C)最大伸长线应变; (D)存在横向拉应力。
答:C22. 已知单元体的主应力为1σ,2σ,推证两相互垂直的截面上的正应力之和为常数 。
证:ασσσσσα2cos 222121-++=)90(2cos 222121︒+-++=ασσσσσβ=+=+21σσσσβα常数 得证。
23. 受内压的薄壁圆筒,已知内压为p ,平均直径为D ,壁厚为t ,弹性常数为E 、ν。
试确定圆筒薄壁上任一点的主应力、主应变及第三、第四强度理论的相当应力。
解:t pD 21=σ,t pD42=σ,03=σ)2(4)42(1)(1211νννσσε-=-=-=tE pD t pD t pD E E)21(4)24(1)(1122νννσσε-=-=-=tE pD t pD t pD E EtEpD t pD E E 43]430[1)](0[1213ννσσνε-=-=+-=tpD231r3=-=σσσ])()()[(21213232221r4σσσσσσσ-+-+-=t pD 43=24. 图示正方形截面棱柱体,弹性常数E 、ν均为已知。
