第七章第4课时 特殊角的三角函数
特殊角的三角函数ppt课件
5、 cos 45
tan2 30
6
计算:
(1)sin600-cos450;(2)cos600+tan600;
3 2 sin 450 sin 600 2 cos 450.
2
4 2 sin 2 300 cos2 600 2 cos2 450.
2
7
例2.已知∠A为锐角,cosA= 3 , 2
15
3
sin 30 1 cos30 3
2
2
tan 30 3 3
sin 45 2 cos 45 2 tan 45 1
2
2
sin 60 3 2
cos60 1 2
tan 60 3
一定要记住哦!4
认真观察一下特殊角三角函数值表 格,你能发现什么规律?
角α
B
D
C
13
(1).2
sin
60°
3
tan
30°
1 3
0
(1)2009
(2). (
3
2)0
1 3
1
பைடு நூலகம்
4
cos
30°
|
12 |
(3).( 2 1)2 8 6 sin 45° (1)2009
14
今天你有什么收获?
请你谈谈对本节学习内容的 体会和感受。
三角函数
sinα
cosα
tanα
30°
1 2
3 2
3
3
45°
2 2
2
2
1
60°
3 2
1 2
特殊角的三角函数值优秀课件

老师期望: 你可以对伴随你九个学年的这副三角尺所具有的功能来 个重新认识和评价.
第六页,共十八页。
做一做
B
2
1
45°
A1C
sin 45 ° = 2
2
cos 45°= 2
2
tan 45°= 1
第七页,共十八页。
做一做
B
2
3
60°
A
C
1
sin 60 ° = 3
30°,45°,60°角的三角函数值
第一页,共十八页。
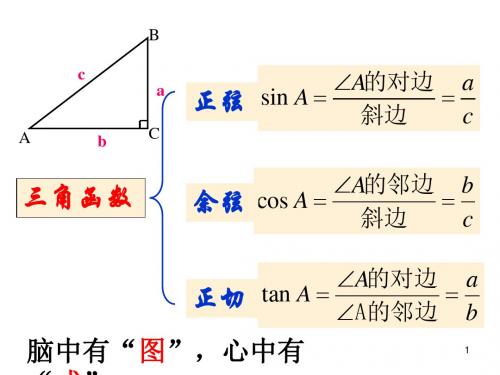
脑中有“图”,心中有“式”
直角三角形中边与角的关系:锐角三角函数. 如图,在直角三角形中,若一个锐角确定,则这个角的 对边,邻边和斜边之间的比值也随之确定.
sin A a , c
sin B b , c
tan A= a b
cos A b , c
w互余两角之间的三角函数关系. w同角之间的三角函数关系.
B
c
a
┌
A
b
C
30°
45°
45° ┌
60° ┌
第十五页,共十八页。
习题
1. 计算: (1)tan 45°-sin 30°; (2)cos 60°+ sin 45°-tan 30°; (3)6tan 30°- si3n 60°- 2cos 45°.
45°
(3)tan 30°等于多少? 45° ┌
请与同伴交流你是怎么想的又是怎么做的.
30°
60° ┌
第四页,共十八页。
做一做
B
2
1
30°
A
C
3
sin 30°=
1 2
特殊角的三角函数30度 45度 60度 课件

tan 45 cos60 2、 tan30 sin 60
例题2、 Rt△ABC中,∠c=90°,a、b、c分别 为∠A、∠B、∠C的对边长
①已知a=6,b=6 3 ,求c及∠A
在Rt △ABC中
∵a2+b2=c2 ∴c2=144 ∴ c=12
B
c
A
a
b
C
变式、
Rt△ABC中,∠c=90°,a、b、c分别
30°、45°、60°
三角函数: 正切: tanA 正弦: sinA
∠A的对边 = ∠A的邻边 ∠A的对边 = 斜边
∠A的邻边 = 斜边
= =
a b a c
b c
B c a
余弦: cosA
=
A
b
C
学习目标
• 1、会计算30°、 45° 、60°角 的三角函数值。 • 2、能够根据30°、 45° 、60° 角的三角函数值,求出其所对应的 锐角的度数。
sinα
30° 45°
1 2 2 2
3 2
cosα
3 2
tanα
3 3
60°
2 2 1 2
1
3
2 1
3
1 1
2
在直角三角形中如图所示 (1)在45°直角三角形中三边 AC:BC:AB之比为 1 : 1 : 2 。 (2)在30°、60°直角三角形中三边 BC : AC :AB之比为 1 : 3 : 2 。
为∠A、∠B、∠C的对边长
③已知a=12, 4 3 ,求∠B ②已知a=12, ∠A=300 ,求b. b
a 3 tan A b 3 12 3 , b 3 3b 36, b 12 3
特殊角的三角函数

特殊角的三角函数特殊角的三角函数在数学中,三角函数是研究角的一种函数关系。
在平面几何中,角是指由两条射线共享一个公共端点而形成的图形。
经典的三角函数包括正弦、余弦和正切函数,它们在各种数学和科学领域中都有广泛的应用。
常见的三角函数可以在单位圆上进行定义。
我们可以将单位圆的圆心放在坐标系的原点上,然后画出和半径相交的射线。
射线与单位圆的交点将定义出特殊角(特殊角通常是指30°、45°、60°等特殊的角度)。
在此基础上,我们可以定义出特殊角的三角函数值。
首先,我们来定义特殊角的正弦函数。
对于单位圆上的特殊角A,正弦函数的值等于射线在单位圆上的交点纵坐标的值。
例如,对于二等分特殊角,即45°角,正弦函数的值为根号二分之一或1/根号二。
同样地,对于1/3等分特殊角,即60°角,正弦函数的值为根号三分之一或1/根号三。
接下来我们来定义特殊角的余弦函数。
对于单位圆上的特殊角A,余弦函数的值等于射线在单位圆上的交点横坐标的值。
例如,对于二等分特殊角,即45°角,余弦函数的值也为根号二分之一或1/根号二。
对于1/3等分特殊角,即60°角,余弦函数的值为半。
另外一个常见的特殊角函数是正切函数。
对于单位圆上的特殊角A,正切函数的值等于射线在单位圆上的交点纵坐标和横坐标的比值。
例如,对于二等分特殊角,即45°角,正切函数的值为1。
对于1/3等分特殊角,即60°角,正切函数的值为根号三。
特殊角的三角函数在数学和物理学中都有广泛的应用。
它们可以帮助我们计算各种角度的三角函数值,从而应用到各种实际问题中。
例如,在三角学和几何学中,我们可以利用正弦、余弦和正切函数计算和解决各种三角形的相关问题。
在物理学中,特殊角的三角函数也经常用于描述和计算物体的运动和力学性质。
特殊角的三角函数在数学教育中也有重要的地位。
它们作为基础概念的一部分,帮助学生建立对三角函数的直观认识和理解。
人教版数学九年级下册 课件28.1《锐角三角函数》第4课时特殊角的三角函数(共35张PPT)

2
2
2
3
1
3
3
归纳:
(1)增减性记忆法:
锐角a 三角 函数
30° 45° 60°
sin a
1
2
3
2
2
2
cos a
3
2
1
2
2
2
tan a
3
1
3
3
1.对于sinA与tanA ,角
度越大,函数值也越大 ;
对于cosA ,角度越大,
函数值越小 .
归纳
(2)图形记忆法:如图所示.
14
知识点二 特殊角的三角函数值的特点
2.已知α,β均为锐角,且满足 则α+β=___7_5°____.
解:∵
∴ sinα- 1 0 , tanβ-1=0
2
∴ sinα= 1 , tanβ=1,
2
∴ ∠α=30°,∠β=45°, ∴ α+β=75°
3 .已知 △ABC 中的 ∠A 与 ∠B 满足 (1-tanA)2 +|sinB- 3 |=0,试 2
2
3 3 3 21 2 3
31 21 2
3
解:原式 3 2 2 2
3 1 3 3 2 3 1 1 3 1 5
3 ( 3) 2 3 1
负指数幂,例如:
23 1 1 23 8
2 3
1
23
1 8
1 8
1
2
3
1 1 2 3
1 1 9
9
借助计算器求锐角三角函数值 以求sin18°为例.
sin 60
解:(1) 2 (2) 2 (3)2 (4) 3 1 4
布置作业
完成《数学创优作业》第52页至53页1---18题
乐乐课堂数学特殊角的三角函数

乐乐课堂数学特殊角的三角函数数学中的特殊角是指具有特殊性质的角度,常见的特殊角有30度、45度、60度以及在此基础上的延申角度。
这些角度在三角函数中具有特殊的数值关系,对于解决各种几何和三角函数问题有很大的帮助。
下面我们将从30度开始逐一介绍。
30度角可以被表示为π/6弧度或0.5圆周角。
它是一个直角三角形中较小角度,其中边长比为1:2的特殊三角形。
在三角函数中,正弦(sin)、余弦(cos)和正切(tan)函数在30度角下的数值如下:sin(30°)=1/2cos(30°)=√3/2tan(30°)=1/√3或√3/3在圆周角视角上,30度角对应于π/6弧度或1/12圆周角。
对于其他三角函数,正割(sec)、余割(csc)和余切(cot)函数在30度角下的数值如下:sec(30°)=2/√3或2√3/3csc(30°)=2cot(30°)=√3或1/√3下一个特殊角是45度角,它可以被表示为π/4弧度或1/8圆周角。
它是等腰直角三角形的角度,其中两条边的长度相等。
在三角函数中,正弦、余弦和正切函数在45度角下的数值如下:sin(45°)=√2/2cos(45°)=√2/2tan(45°)=1在圆周角视角上,45度角对应于π/4弧度或1/8圆周角。
对于其他三角函数,正割、余割和余切函数在45度角下的数值如下:sec(45°)=√2csc(45°)=√2cot(45°)=1再来看60度角,它可以被表示为π/3弧度或1/6圆周角。
它是等边三角形的角度,其中三条边的长度相等。
在三角函数中,正弦、余弦和正切函数在60度角下的数值如下:sin(60°)=√3/2cos(60°)=1/2tan(60°)=√3在圆周角视角上,60度角对应于π/3弧度或1/6圆周角。
三角函数特殊角

三角函数特殊角三角函数是数学中常见的函数类型之一,而在三角函数中,特殊角是指能够通过明确的数值计算得出精确值的角度。
特殊角是三角函数的重要概念之一,在解决各种数学问题中具有重要作用。
本文将重点讨论一些常见的三角函数特殊角及其计算方法。
正弦函数和余弦函数在三角函数中,最常见的两个函数是正弦函数和余弦函数。
在单位圆上,我们定义特殊角为0度、30度、45度、60度和90度时,正弦函数和余弦函数的数值如下:•当角度为0度时,正弦函数的值为0,余弦函数的值为1。
•当角度为30度时,正弦函数的值为1/2,余弦函数的值为√3/2。
•当角度为45度时,正弦函数的值为√2/2,余弦函数的值也为√2/2。
•当角度为60度时,正弦函数的值为√3/2,余弦函数的值为1/2。
•当角度为90度时,正弦函数的值为1,余弦函数的值为0。
正切函数另一个常见的三角函数是正切函数。
在特殊角中,我们定义角度为0度、45度和90度时,正切函数的数值如下:•当角度为0度时,正切函数的值为0。
•当角度为45度时,正切函数的值为1。
•当角度为90度时,正切函数的值为不存在,因为在这个角度上正切函数的值趋近于无穷大。
应用举例特殊角在数学问题中有很多应用,例如在三角形的计算中,我们可以通过特殊角来求解各种未知量。
又如在物理学中,特殊角的概念也被广泛运用,例如在力学问题中,根据特殊角可以方便地计算各种受力方向与大小之间的关系。
总结特殊角是三角函数中的重要概念,通过熟练掌握特殊角的数值和计算方法,可以帮助我们更好地理解和运用三角函数。
特殊角的认识不仅在数学问题中有应用,也可以在其他学科领域中发挥重要作用。
因此,对于特殊角的理解和掌握具有重要意义。
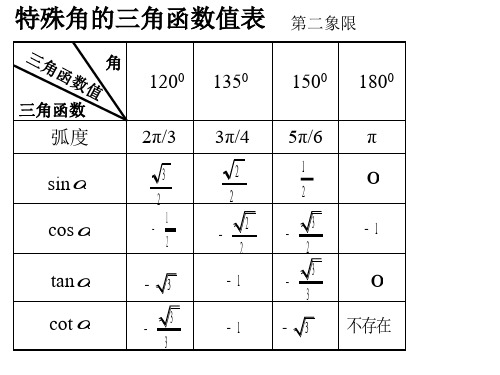
特殊角的三角函数值表ppt课件
1
0 不存在
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
第三象限
角
三角函数
弧度
2100 7π/6
sin
1 2
cos
3
2
tan
3
3
cot
3
2250
5π/4
2 2
2 2 1
1
2400 2700
4π/3 3π/2
3
1
2
1 2
0
3 不存在
3
0
3
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
第四象限
角
三角函数
弧度
3000 5π/3
sin
3
2
cos
1
2
tan
3
cot
3
3
3150
7π/4
2 2 2 2
1
1
3300 3600
11π/6 2π
1
0
2
3
1
2
3
0
3
3 不存在
特殊角的三角函数值总表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4课时 特殊角的三角函数
班级 姓名 学号 [学习目标]
1. 能通过推理得30°、45°、60°角的三角函数值,进一步体会三角函数的意义。
2. 会计算含有30°、45°、60°角的三角函数的值。
3. 能根据30°、45°、60°角的三角函数值,说出相应锐角的大小。
4. 经历探索30°、45°、60°角的三角函数值的过程,发展同学们的推理能力和计算能力。
[学习过程]
问题1、你能分别说出30°,45°,60°角的三角函数值吗?将它们填在下表中,试试看能否立刻记住。
从表中数字你可看出哪些规律?
问题2、求下列各式的值
(1)2sin30°-cos45° (2)sin60°·cos60° (3)sin 230°+cos 230° [练习]
(1)cos45°-sin30° (2)sin 2
60°+cos 2
60° (3)tan45°-sin30°·cos60° (4) 0
202
30
tan 45cos (5)2 sin30°+3 cos60°—4tan45°(6)cos30°sin45°+ sin30°cos45°
问题3、求满足下列条件的锐角α (1) cos α=2
3 (2)2sin α=1 (3)2sin α-2=0 (4)3tan α-1=0
[练习]
求满足下列条件的锐角α: (1)cos α
-23=0 (2)-3tan α
+3=0
(3)2cos α-1=0 (4)tan (α+10°)
=3
问题4、(1)若∠A=520,则cosA 的大致范围是 ( ) A 、10cos 2
A <<
B 、
1cos 2
2
A <<
C 、
cos 2
2
A <<
D 、
cos 12
A <<
(2)α是锐角,且sin α=
4
3,则α的大致范围是 ( )
A 、0°<α<30°
B 、30°<α<45°
C 、45°<α<60°
D 、60°<α<90° 问题5、如图,在Rt △ABC 中,∠C=90°,CD ⊥AB ,垂足为D ,BC=2,。
分别求出△ABC 、△ACD 、△BCD 中各锐角。
[练习]如图,在△ABD 中,AC 是边BD 上的高,BC=15cm ,∠BAC=30°,∠DAC=45°,求AD 。
第七章 锐角三角函数
C
A
B
D
A
B
D
[作业]
1、填空:cos30°= ; sin45°= ; tan °
; 60°=
12。
2、根据30°、45°、60°角的三角函数值填空:当锐角α变大时,sin α的值变_____,cos α的值变_______,tan α的值变_______.
3、已知∠A 为锐角,若cosA=45
,则sinA= ,tanA= ;若tanA=45
,求sinA= ,cosA= .
4、在锐角△ABC 中,若
2,∠B=750
,则cos C= .
5、在△ABC 中,若tanA=1,sinB=
2
2,则△ABC 的形状是 .
6、在Rt △ABC 中,∠C=90°,若sinA=2
1,则BC ∶AC ∶AB 等于 。
7、若∠A=410,则cosA 的大致范围是 ( ) A 、10cos 2
A <<
B
、
1cos 2
2
A <<
C
、
cos 2
2
A <<
D
、
cos 12
A <<
8、α是锐角,且cos α=4
3,则α的大致范围是 ( )
A 、0°<α<30°
B 、30°<α<45°
C 、45°<α<60°
D 、60°<α<90° 9、计算下列各式的值.
(1)3cos30°+2sin45°(2)2sin60°cos45°+ tan30° (3) sin30°+ cos 260°—2cos45°
(4)2cos45°+32-
(5)
45
tan 260
tan 1
60sin -- (6)
060
sin 60
cos 45tan -·tan30°
10、求下列各式中的锐角θ
(1)2cos θ=1 (2)2sin θ
(3)tan2θ
(4)2sin 2θ—5 sin θ+2=0
11、已知α为锐角,当α
tan 12-无意义时,求tan(α+15°)—tan(α-15°)的值.
12、等腰三角形的一腰长为6㎝,底边长为63㎝,请你判断这个三角形是锐角三角形、直角形还是钝角三角形? 它的三个角分别是多少?
13、已知△ABC 中,AD 是BC 边上的高,AD=2,AC=22,AB=4,求∠BAC 的度数.
14、要求tan30°的值,可构造如图所示的直角三角形进行计算:作Rt △ABC , 使∠C=90°,斜边AB=2,直角边AC=1,那么BC=3,∠ABC=30°,tan30°=
BC
AC =
3
33
1=。
在此图的基础上通过添加
适当的辅助线,可求出tan15°的值,请你写出添加辅助线的方法,并求出tan15°的值。
A
C。
