特殊角的三角函数值的巧记
特殊角的三角函数值的巧记

特殊角的三角函数值的巧记特殊角的三角函数值在计算,求值,解直角三角形和今后的学习中,常常会用到,所以一定要熟记.要在理解的基础上,采用巧妙的方法加强记忆.这里关键的问题还是要明白和掌握这些三角函数值是怎样求出的,既便遗忘了,自己也能推算出来,切莫死记硬背.那么怎样才能更好地记熟它们呢?下面介绍几种方法,供同学们借鉴。
1、“三角板”记法根据含有特殊角的直角三角形的知识,利用你手里的一套三角板,就可以帮助你记住30°、45°、60°角的三角函数值.我们不妨称这种方法为“三角板”记法.首先,如图所标明的那样,先把手中一套三角板的构造特点弄明白,记清它们的边角是什么关系.对左边第一块三角板,要抓住在直角三角形中,30°角的对边是斜边的一半的特点,再应用勾股定理.可以知道在这个直角三角形中30°角的对边、邻边、斜边的比是掌握了这个比例关系,就可以依定义求出30°、60°角的任意一个锐角三角函数值,如:001sin 30,cos302== 求60°角的三角函数值,还应抓住60°角是30°角的余角这一特点.在右边那块三角板中,应注意在直角三角形中,若有一锐角为45°,则此三角形是等腰直角三角形,且两直角边与斜边的比是1∶1,那么,就不难记住:00sin 45cos 45==,00tan 45cot 451==。
这种方法形象、直观、简单、易记,同时巩固了三角函数的定义.二、列表法:说明:正弦值随角度变化,即0˚ →30˚→45˚ →60˚ →90˚变化;值从0→21→22→23→1变化,其余类似记忆. 三、口诀记忆法口诀是:“一、二、三,三、二、一,三、九、二十七,弦是二,切是三,分子根号不能删.”前三句中的1,2,3;3,2,1;3,9,27,分别是30°,45°,60°角的正弦、余弦、正切值中分子根号内的值.弦是二、切是三是指正弦、余弦的分母为2,正切的分母为3.最后一句,讲的是各函数值中分子都加上根号,不能丢掉.如tan60°=3=tan45°=13=.这种方法有趣、简单、易记. 四、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:①有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
特殊三角函数的记忆技巧

特殊三角函数的记忆技巧
特殊三角函数包括正弦函数、余弦函数和正切函数。
记忆它们的一种简单方法是使用“东南西北”的方位词来帮助记忆。
1. 正弦函数(sin):
- 正弦函数在第一象限的值为正,可以记忆为“东正西正”。
- 正弦函数在第二象限的值为正,可以记忆为“东正北正”。
- 正弦函数在第三象限的值为负,可以记忆为“南负西负”。
- 正弦函数在第四象限的值为负,可以记忆为“南负北负”。
2. 余弦函数(cos):
- 余弦函数在第一象限的值为正,可以记忆为“东正北正”。
- 余弦函数在第二象限的值为负,可以记忆为“东负北负”。
- 余弦函数在第三象限的值为负,可以记忆为“南负西负”。
- 余弦函数在第四象限的值为正,可以记忆为“南正西正”。
3. 正切函数(tan):
- 正切函数在第一象限的值为正,可以记忆为“东正北正”。
- 正切函数在第二象限的值为负,可以记忆为“东负北负”。
- 正切函数在第三象限的值为正,可以记忆为“南正西正”。
- 正切函数在第四象限的值为负,可以记忆为“南负西负”。
通过以上的方位词记忆方法,可以帮助记忆特殊三角函数的正负性,从而更容易在计算中应用它们。
巧记三角函数值口诀大全

巧记三角函数值口诀大全
三角函数在数学中是一种非常重要的概念,掌握三角函数的值可以帮助我们快速解决各种数学问题。
为了方便记忆三角函数的值,有许多口诀和技巧。
下面将介绍几种巧记三角函数值的口诀大全。
正弦函数值口诀
正弦函数是三角函数中的一种,通常用sin表示,下面是一个常用的口诀来记忆正弦函数值:
正比三高,半分一;永居四配二厕。
根据这个口诀,我们可以记忆正弦函数在0°、30°、45°、60°、90°五个特殊角度下的取值。
例如,当角度为30°时,sin30°=1/2。
余弦函数值口诀
余弦函数是另一种常用的三角函数,通常用cos表示,下面是一个口诀来记忆余弦函数值:
梅大连港,臭鸡蛋。
根据这个口诀,我们可以记忆余弦函数在0°、30°、45°、60°、90°五个特殊角度下的取值。
例如,当角度为45°时,cos45°=1/√2。
正切函数值口诀
正切函数是三角函数中的另一种,通常用tan表示,下面是一个口诀来记忆正切函数值:
狼跑点鼠,动动算算。
根据这个口诀,我们可以记忆正切函数在0°、30°、45°、60°、90°五个特殊角度下的取值。
例如,当角度为60°时,tan60°=√3。
通过以上口诀,我们可以轻松记忆三角函数在常见角度下的取值,为解决数学问题提供了便利。
希望这些口诀可以帮助大家更好地理解三角函数的知识。
【数学知识点】特殊三角函数值顺口溜

【数学知识点】特殊三角函数值顺口溜1、三十,四五,六十度,三角函数记牢固;分母弦二切是三,分子要把根号添;一二三来三二一,切值三九二十七;递增正切和正弦,余弦函数要递减。
2、三角函数是函数,象限符号坐标注。
函数图象单位圆,周期奇偶增减现。
同角关系很重要,化简证明都需要。
正六边形顶点处,从上到下弦切割。
三角函数是基本初等函数之一,是以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
也可以等价地用与单位圆有关的各种线段的长度来定义。
三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究周期性现象的基础数学工具。
在数学分析中,三角函数也被定义为无穷级数或特定微分方程的解,允许它们的取值扩展到任意实数值,甚至是复数值。
常见的三角函数包括正弦函数、余弦函数和正切函数。
在航海学、测绘学、工程学等其他学科中,还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。
不同的三角函数之间的关系可以通过几何直观或者计算得出,称为三角恒等式。
三角函数一般用于计算三角形中未知长度的边和未知的角度,在导航、工程学以及物理学方面都有广泛的用途。
另外,以三角函数为模版,可以定义一类相似的函数,叫做双曲函数。
常见的双曲函数也被称为双曲正弦函数、双曲余弦函数等等。
三角函数(也叫做圆函数)是角的函数;它们在研究三角形和建模周期现象和许多其他应用中是很重要的。
三角函数通常定义为包含这个角的直角三角形的两个边的比率,也可以等价的定义为单位圆上的各种线段的长度。
更现代的定义把它们表达为无穷级数或特定微分方程的解,允许它们扩展到任意正数和负数值,甚至是复数值。
感谢您的阅读,祝您生活愉快。
华东师大版数学九年级上册24.3巧记特殊角的三角函数值
巧记特殊角的三角函数值
特殊角的三角函数值有着广泛的应用,要求大家必须熟记,为了帮助记忆,可采用下面的方法.
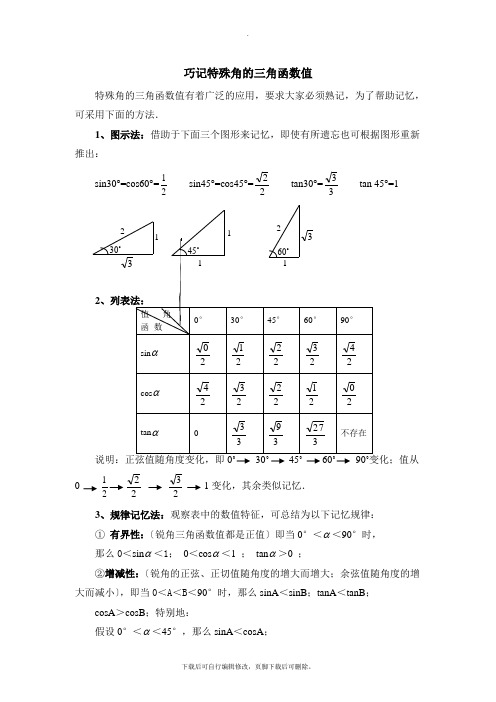
1、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出:
sin30°=cos60°=
21 sin45°=cos45°=2
2
tan30°=33 tan 45°=1
2
2 2
3 1变化,其余类似记忆. 3、规律记忆法:观察表中的数值特征,可总结为以下记忆规律: ① 有界性:〔锐角三角函数值都是正值〕即当0°<α<90°时, 那么0<sin α<1; 0<cos α<1 ; tan α>0 ;
②增减性:〔锐角的正弦、正切值随角度的增大而增大;余弦值随角度的增大而减小〕,即当0<A <B <90°时,那么sinA <sinB ;tanA <tanB ;
cosA >cosB ;特别地:
假设0°<α<45°,那么sinA <cosA ;
假设45°<A <90°,那么sinA >cosA . 4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为
2m 形式,正切值可表示为3
m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.。
巧背特殊角的三角函数值

要记住一些特殊角的三角函数值 ,可以通过下面的方法:1、首先必须记住下面20个字的歌诀:正弦 对比斜 , 余弦 邻比斜 , 正切 对比邻 , 余切 邻比对。
2、再结合下面两个三角形就可以记住这些三角函数值。
请大家一定要注意,图上标的数值并不是指的三角形的边长,而是三边之间的长度的倍数关系,或者是比例关系,这一点一定要记牢!!!对于30°的角来说,它的对(就是指对边)是1 ,它的邻(就是指邻边)就是 3 , 对于60°的角来说,它的对(就是指对边)是3 ,它的邻(就是指邻边)就是 1 , 对于30° 和 60°的角来说, 斜(就是指斜边) 都是 2 ,所以30°的正弦记作 sin30°= 21 30°的余弦记作 cos30°=23 30°的正切记作tan30°=3331= 30°的余切记作cot30°=313= 60°的正弦记作 sin60°= 23 60°的余弦记作 cos60°=21 60°的正切记作tan60°=313= 60°的余切记作cot60°=3331=45°的正弦记作sin45°= 2221= 45°的余弦记作cos45°=2221=45°的正切记作tan45°=111=45°的余切记作cot45°=111= 对于0°和90°角的三角函数值,同学们可以自己开动脑筋来记忆,但是关键是要把锐角三角函数的定义搞清楚!。
(完整版)特殊角的三角函数值的巧记

特殊角的三角函数值的巧记特殊角的三角函数值在计算,求值,解直角三角形和今后的学习中,常常会用到,所以一定要熟记.要在理解的基础上,采用巧妙的方法加强记忆.这里关键的问题还是要明白和掌握这些三角函数值是怎样求出的,既便遗忘了,自己也能推算出来,切莫死记硬背.那么怎样才能更好地记熟它们呢?下面介绍几种方法,供同学们借鉴。
1、“三角板”记法根据含有特殊角的直角三角形的知识,利用你手里的一套三角板,就可以帮助你记住30°、45°、60°角的三角函数值.我们不妨称这种方法为“三角板”记法.首先,如图所标明的那样,先把手中一套三角板的构造特点弄明白,记清它们的边角是什么关系.对左边第一块三角板,要抓住在直角三角形中,30°角的对边是斜边的一半的特点,再应用勾股定理.可以知道在这个直角三角形中30°角的对边、邻边、斜边的比是3掌握了这个比例关系,就可以依定义求出30°、60°角的任意一个锐角三角函数值,如:0013sin 30,cos302== 求60°角的三角函数值,还应抓住60°角是30°角的余角这一特点.在右边那块三角板中,应注意在直角三角形中,若有一锐角为45°,则此三角形是等腰直角三角形,且两直角边与斜边的比是1∶12,那么,就不难记住:002sin 45cos 452==,00tan 45cot 451==。
这种方法形象、直观、简单、易记,同时巩固了三角函数的定义.二、列表法:说明:正弦值随角度变化,即0˚ →30˚→45˚ →60˚ →90˚变化;值从0→21→22→23→1变化,其余类似记忆. 三、口诀记忆法口诀是:“一、二、三,三、二、一,三、九、二十七,弦是二,切是三,分子根号不能删.”前三句中的1,2,3;3,2,1;3,9,27,分别是30°,45°,60°角的正弦、余弦、正切值中分子根号内的值.弦是二、切是三是指正弦、余弦的分母为2,正切的分母为3.最后一句,讲的是各函数值中分子都加上根号,不能丢掉.如tan60°==tan45°=13=.这种方法有趣、简单、易记. 四、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:①有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
巧记特殊角的三角函数值

巧记特殊角的三角函数值
初学三角函数,记忆特殊角三角函数值易错易混。
若在理解掌握的基础上,经过变形,使其呈现某种规律,再配以歌诀,则可浅显易记,触目成诵。
仔细观察表1,你会发现重要的规律。
表1中,三角函数值的前三行,分子被开方数排列特征依次为“1,2,3,3,2,1,3,9,27”。
“一二三,三二一,三九二十七”。
记此歌诀即可。
观察表2也可发现重要的规律。
表2中,弦函数分子被开方数分别为1,2,3,3,2,1,分母都是2;切函数分子的幂指数分别是1,2,3,3,2,1,分母都是3。
据此概括歌诀为:“一二三,三二一,弦内切外莫忘记。
分母弦二切为三,正、余只把顺序翻。
”这两个歌诀记住一个即可,两歌诀一起记应用更方便。
1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊角的三角函数值的巧记
特殊角的三角函数值在计算,求值,解直角三角形和今后的学习中,常常会用到,所以一定要熟记.要在理解的基础上,采用巧妙的方法加强记忆.这里关键的问题还是要明白和掌握这些三角函数值是怎样求出的,既便遗忘了,自己也能推算出来,切莫死记硬背.
那么怎样才能更好地记熟它们呢?下面介绍几种方法,供同学们借鉴。
1、“三角板”记法
根据含有特殊角的直角三角形的知识,利用你手里的一套三角板,就可以帮助你记住30°、45°、60°角的三角函数值.我们不妨称这种方法为“三角板”记法.
首先,如图所标明的那样,先把手中一套三角板的构造特点弄明白,记清它们的边角是什么关系.
对左边第一块三角板,要抓住在直角三角形中,30°角的对边是斜边的一半的特点,再应用勾股定理.可以知道在这个直角三角形中30°角的对边、邻边、斜边的比是3掌握了这个比例关系,就可以依定义求出30°、60°角的任意一个锐角三角函数值,如:0013sin 30,cos302== 求60°角的三角函数值,还应抓住60°角是30°角的余角这一特点.
在右边那块三角板中,应注意在直角三角形中,若有一锐角为45°,则此三角形是等腰直角三角形,且两直角边与斜边的比是1∶12,那么,就不难记住:002sin 45cos 452
==,00tan 45cot 451==。
这种方法形象、直观、简单、易记,同时巩固了三角函数的定义.
二、列表法:
说明:正弦值随角度变化,即0˚ →30˚→45˚ →60˚ →90˚变化;值从
0→2
1→22→23→1变化,其余类似记忆. 三、口诀记忆法
口诀是:“一、二、三,三、二、一,三、九、二十七,弦是二,切是三,分子根号不能删.”前三句中的1,2,3;3,2,1;3,9,27,分别是30°,45°,60°角的正弦、余弦、正切值中分子根号内的值.弦是二、切是三是指正弦、余弦的分母为2,正切的分母为3.最后一句,讲的是各函数值中分子都加上根号,
不能丢掉.如tan60°==tan45°=13=.这种方法有趣、简单、易记. 四、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:
①有界性:(锐角三角函数值都是正值)即当0°<α<90°时,
则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sinA <sinB ;tanA <tanB ;cosA >cosB ;cotA >cotB ;特别地:若0°<α<45°,则sinA <cosA ;tanA <cotA ;若45°<A <90°,则sinA >cosA ;tanA >cotA .
例1.tan30°的值等于( )
A .12
B .2
C .3 D
分析:本题考查特殊锐角三角函数值理解情况.解决本题需要熟练记住特殊锐角的三角函数值.
解:选C .
评注:如果没有记住30°的正切值,可以先画一个含有30°角的直角三角形,根据30°角所对的直角边等于斜边的一半,找到三边关系,根据定义求解.
例2.如果a ∠是等腰直角三角形的一个锐角,则tan α的值是( )
A .12
B
C .1 D
析解:本题主要考查特殊锐角三角函数值理解情况.解决本题需要熟练记住特殊锐角的三角函数值.因为等腰直角三角形的锐角045a ∠=,所以0tan tan 451α==,故选C 。
评注:如果没有记住45°的正切值,可以在等腰直角三角形中借助勾股定理找到三边关系,然后根据三角函数定义求解.
例3.已知1sin 2
A =,且∠A 为锐角,则∠A=( ) A.30° B.45° C.60° D.75° 析解:根据2
130sin 0=可得,A 等于30°,故选A . 评注:特殊锐角三角函数值在解决实际问题中应用非常广泛,所以我们要熟练掌握30°,45°、60°角的三角函数值,
例4.计算tan 602sin 452cos30+-的结果是( )
A .2
B .
C
D .1
分析:本题是一道与锐角三角函数值有关的计算问题,解决问题的关键是先确定函数值,然后再进行实数的运算.
解:tan 602sin 452cos30+-
2222
=⨯-⨯=
故选C.
评注:与特殊锐角三角函数值的有关运算,先写出每个锐角函数值,然后转成具体的实数运算,应注意运算的顺序和计算的方法.。
