Rapid prototyping of a Self-Timed ALU with FPGAs
信息素平滑机制

信息素平滑机制
信息素平滑机制是一种常见的机器学习技术,用于解决分类问题中的过拟合问题。
在计算机视觉、自然语言处理等领域,信息素平滑机制被广泛应用。
信息素平滑机制的基本思想是通过在训练数据中加入噪音来减少模型的过拟合。
具体来说,信息素平滑机制会对训练数据中的特征进行随机扰动,使得模型在训练过程中不会过于依赖某些特征,从而提高模型的泛化能力。
信息素平滑机制的实现有多种方法,其中一种常见的方法是拉普拉斯平滑。
拉普拉斯平滑是通过在特征出现的次数中添加一个小的常数来实现的,这样可以避免某些特征在训练数据中没有出现而导致的概率为零的情况。
除了拉普拉斯平滑,信息素平滑机制还有其他实现方法,例如贝叶斯平滑、加和平滑等。
这些方法都是在原始模型的基础上添加一些噪音或平滑项,从而减少模型的过拟合。
信息素平滑机制的优点在于可以有效地减少模型的过拟合,提高模型的泛化能力。
另外,信息素平滑机制的实现比较简单,不需要对模型进行过多的修改。
然而,信息素平滑机制也存在一些缺点。
首先,信息素平滑机制可
能会降低模型的准确率,因为它会对训练数据进行扰动。
其次,信息素平滑机制需要进行大量的计算,可能会增加训练时间和计算资源的消耗。
总的来说,信息素平滑机制是一种常见的机器学习技术,可以有效地减少模型的过拟合。
但是,在使用信息素平滑机制时,需要权衡准确率和计算资源的消耗,选择合适的平滑方法和参数。
Self-timed CMOS static logic circuit
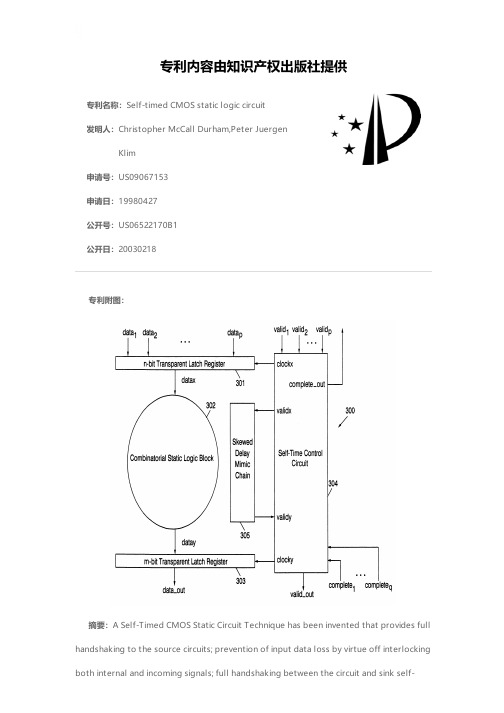
专利名称:Self-timed CMOS static logic circuit发明人:Christopher McCall Durham,Peter JuergenKlim申请号:US09067153申请日:19980427公开号:US06522170B1公开日:20030218专利内容由知识产权出版社提供专利附图:摘要:A Self-Timed CMOS Static Circuit Technique has been invented that provides full handshaking to the source circuits; prevention of input data loss by virtue off interlocking both internal and incoming signals; full handshaking between the circuit and sink self-timed circuitry; prevention of lost access operation information by virtue of an internal lock-out for the output data information; and plug-in compatibility for some classes of dynamic self-timed systems. The net result of the overall system is that static CMOS circuits can now be used to generate a self-timed system. This is in contrast to existing self-timed systems that rely on dynamic circuits. Thus, the qualities of the static circuitry can be preserved and utilized to their fullest advantage.申请人:INTERNATIONAL BUSINESS MACHINES CORPORATION代理机构:Winstead Sechrest & Minick P.C.代理人:Kelly K. Kordzik,Robert M. Carwell更多信息请下载全文后查看。
吴恩达提示词系列解读

吴恩达提示词系列解读摘要:1.吴恩达简介2.提示词系列的背景和意义3.深度学习提示词解读4.强化学习提示词解读5.计算机视觉提示词解读6.自然语言处理提示词解读7.总结正文:吴恩达,全球知名的AI专家,拥有丰富的学术和产业经验,他的一系列提示词为广大AI学习者提供了宝贵的指导。
本文将针对吴恩达提示词系列进行解读,以期帮助大家更好地理解和学习AI技术。
1.吴恩达简介吴恩达,Andrew Ng,曾是斯坦福大学的人工智能教授,后来创立了Google Brain项目,并成为了百度首席科学家。
他一直致力于推动AI技术的发展和应用,尤其是在深度学习和强化学习领域。
2.提示词系列的背景和意义吴恩达提示词系列是他对AI领域的重要观点和思考的总结,涵盖了深度学习、强化学习、计算机视觉、自然语言处理等多个领域。
这些提示词对于AI学习者来说,具有很高的参考价值,可以帮助我们更好地理解AI技术的发展趋势和应用方向。
3.深度学习提示词解读吴恩达的深度学习提示词主要包括“神经网络”、“反向传播”、“卷积神经网络”、“循环神经网络”等。
这些提示词概括了深度学习的核心概念和技术,对于理解深度学习的基本原理和应用至关重要。
4.强化学习提示词解读吴恩达的强化学习提示词主要包括“智能体”、“环境”、“状态”、“动作”、“奖励”等。
这些提示词揭示了强化学习的本质,即智能体如何在环境中通过选择动作来获得奖励,从而实现学习。
5.计算机视觉提示词解读吴恩达的计算机视觉提示词主要包括“图像分类”、“目标检测”、“语义分割”等。
这些提示词代表了计算机视觉的主要任务,对于我们理解和应用计算机视觉技术具有重要意义。
6.自然语言处理提示词解读吴恩达的自然语言处理提示词主要包括“词向量”、“序列到序列模型”、“注意力机制”等。
这些提示词概括了自然语言处理的核心技术,对于我们理解和应用自然语言处理技术具有重要价值。
大语言模型增强因果推断

大语言模型(LLM)是一种强大的自然语言处理技术,它可以理解和生成自然语言文本,并具有广泛的应用场景。
然而,虽然LLM能够生成流畅、自然的文本,但在因果推断方面,它仍存在一些限制。
通过增强LLM的因果推断能力,我们可以更好地理解和解释人工智能系统的行为,从而提高其可信度和可靠性。
首先,我们可以通过将LLM与额外的上下文信息结合,来增强其因果推断能力。
上下文信息包括时间、地点、背景、情感等各个方面,它们可以为LLM提供更全面的信息,使其能够更好地理解事件之间的因果关系。
通过这种方式,LLM可以更好地预测未来的结果,并解释其预测的依据。
其次,我们可以通过引入可解释性建模技术,来增强LLM的因果推断能力。
这些技术包括决策树、规则归纳、贝叶斯网络等,它们可以帮助我们更好地理解LLM的决策过程,从而更准确地预测其结果。
此外,这些技术还可以帮助我们识别因果关系的路径,从而更深入地了解因果关系。
最后,我们可以通过将LLM与其他领域的知识结合,来增强其因果推断能力。
例如,我们可以将经济学、心理学、社会学等领域的知识融入LLM中,以帮助其更好地理解和解释因果关系。
通过这种方式,LLM可以更全面地考虑各种因素,从而更准确地预测和解释因果关系。
在应用方面,增强因果推断能力的LLM可以为许多领域提供更准确、更可靠的决策支持。
例如,在医疗领域,它可以辅助医生制定更有效的治疗方案;在金融领域,它可以辅助投资者做出更明智的投资决策;在政策制定领域,它可以为政策制定者提供更全面、更准确的政策建议。
总之,通过增强大语言模型(LLM)的因果推断能力,我们可以更好地理解和解释人工智能系统的行为,从而提高其可信度和可靠性。
这将有助于推动人工智能技术的广泛应用和发展,为社会带来更多的便利和价值。
同时,我们也需要关注和解决相关伦理和社会问题,以确保人工智能技术的发展符合人类的价值观和利益。
Ellis-Corrective-Feedback

T tries to elicit correct pronunciation and the corrects
S: alib[ai]
S fails again
T: okay, listen, listen, alb[ay] T models correct pronunciation
SS: alib(ay)
Theoretical perspectives
1. The Interaction Hypothesis (Long 1996) 2. The Output Hypothesis (Swain 1985;
1995) 3. The Noticing Hypothesis (Schmidt
1994; 2001) 4. Focus on form (Long 1991)
2. In the course of this, they produce errors. 3. They receive feedback that they recognize as
corrective. 4. The feedback causes them to notice the errors they
first row. (uptake)
The complexity of corrective feedback
Corrective feedback (CF) occurs frequently in instructional settings (but much less frequently in naturalistic settings)
Commentary
Initial focus on meaning Student perceives the feedback as corrective
3D快速建模【英文】

CHAPTER 19
Rapid prototyping
• • • • • Introduction Subtractive processes Additive process Virtual Prototyping Applications
Additive Process
Require elaborate software
1 : Obtain cad file
2 : Computer then constructs slices of a 3-dimensional part 3 : slice analyzed and compiled to provide the rapid prototyping machine 4 : setup of the proper unattended and provide rough part after few hours 5 : Finishing operations and sanding and painting
Advantages
• CAD data files can be manufactured in hours. • Tool for visualization and concept verification. • Prototype used in subsequent manufacturing operations to obtain final part • Tooling for manufacturing operations can be produced
• Manufacturing Software (Planning Machining operations)
T.W. ANDERSON (1971). The Statistical Analysis of Time Series. Series in Probability and Ma

425 BibliographyH.A KAIKE(1974).Markovian representation of stochastic processes and its application to the analysis of autoregressive moving average processes.Annals Institute Statistical Mathematics,vol.26,pp.363-387. B.D.O.A NDERSON and J.B.M OORE(1979).Optimal rmation and System Sciences Series, Prentice Hall,Englewood Cliffs,NJ.T.W.A NDERSON(1971).The Statistical Analysis of Time Series.Series in Probability and Mathematical Statistics,Wiley,New York.R.A NDRE-O BRECHT(1988).A new statistical approach for the automatic segmentation of continuous speech signals.IEEE Trans.Acoustics,Speech,Signal Processing,vol.ASSP-36,no1,pp.29-40.R.A NDRE-O BRECHT(1990).Reconnaissance automatique de parole`a partir de segments acoustiques et de mod`e les de Markov cach´e s.Proc.Journ´e es Etude de la Parole,Montr´e al,May1990(in French).R.A NDRE-O BRECHT and H.Y.S U(1988).Three acoustic labellings for phoneme based continuous speech recognition.Proc.Speech’88,Edinburgh,UK,pp.943-950.U.A PPEL and A.VON B RANDT(1983).Adaptive sequential segmentation of piecewise stationary time rmation Sciences,vol.29,no1,pp.27-56.L.A.A ROIAN and H.L EVENE(1950).The effectiveness of quality control procedures.Jal American Statis-tical Association,vol.45,pp.520-529.K.J.A STR¨OM and B.W ITTENMARK(1984).Computer Controlled Systems:Theory and rma-tion and System Sciences Series,Prentice Hall,Englewood Cliffs,NJ.M.B AGSHAW and R.A.J OHNSON(1975a).The effect of serial correlation on the performance of CUSUM tests-Part II.Technometrics,vol.17,no1,pp.73-80.M.B AGSHAW and R.A.J OHNSON(1975b).The influence of reference values and estimated variance on the ARL of CUSUM tests.Jal Royal Statistical Society,vol.37(B),no3,pp.413-420.M.B AGSHAW and R.A.J OHNSON(1977).Sequential procedures for detecting parameter changes in a time-series model.Jal American Statistical Association,vol.72,no359,pp.593-597.R.K.B ANSAL and P.P APANTONI-K AZAKOS(1986).An algorithm for detecting a change in a stochastic process.IEEE rmation Theory,vol.IT-32,no2,pp.227-235.G.A.B ARNARD(1959).Control charts and stochastic processes.Jal Royal Statistical Society,vol.B.21, pp.239-271.A.E.B ASHARINOV andB.S.F LEISHMAN(1962).Methods of the statistical sequential analysis and their radiotechnical applications.Sovetskoe Radio,Moscow(in Russian).M.B ASSEVILLE(1978).D´e viations par rapport au maximum:formules d’arrˆe t et martingales associ´e es. Compte-rendus du S´e minaire de Probabilit´e s,Universit´e de Rennes I.M.B ASSEVILLE(1981).Edge detection using sequential methods for change in level-Part II:Sequential detection of change in mean.IEEE Trans.Acoustics,Speech,Signal Processing,vol.ASSP-29,no1,pp.32-50.426B IBLIOGRAPHY M.B ASSEVILLE(1982).A survey of statistical failure detection techniques.In Contribution`a la D´e tectionS´e quentielle de Ruptures de Mod`e les Statistiques,Th`e se d’Etat,Universit´e de Rennes I,France(in English). M.B ASSEVILLE(1986).The two-models approach for the on-line detection of changes in AR processes. In Detection of Abrupt Changes in Signals and Dynamical Systems(M.Basseville,A.Benveniste,eds.). Lecture Notes in Control and Information Sciences,LNCIS77,Springer,New York,pp.169-215.M.B ASSEVILLE(1988).Detecting changes in signals and systems-A survey.Automatica,vol.24,pp.309-326.M.B ASSEVILLE(1989).Distance measures for signal processing and pattern recognition.Signal Process-ing,vol.18,pp.349-369.M.B ASSEVILLE and A.B ENVENISTE(1983a).Design and comparative study of some sequential jump detection algorithms for digital signals.IEEE Trans.Acoustics,Speech,Signal Processing,vol.ASSP-31, no3,pp.521-535.M.B ASSEVILLE and A.B ENVENISTE(1983b).Sequential detection of abrupt changes in spectral charac-teristics of digital signals.IEEE rmation Theory,vol.IT-29,no5,pp.709-724.M.B ASSEVILLE and A.B ENVENISTE,eds.(1986).Detection of Abrupt Changes in Signals and Dynamical Systems.Lecture Notes in Control and Information Sciences,LNCIS77,Springer,New York.M.B ASSEVILLE and I.N IKIFOROV(1991).A unified framework for statistical change detection.Proc.30th IEEE Conference on Decision and Control,Brighton,UK.M.B ASSEVILLE,B.E SPIAU and J.G ASNIER(1981).Edge detection using sequential methods for change in level-Part I:A sequential edge detection algorithm.IEEE Trans.Acoustics,Speech,Signal Processing, vol.ASSP-29,no1,pp.24-31.M.B ASSEVILLE, A.B ENVENISTE and G.M OUSTAKIDES(1986).Detection and diagnosis of abrupt changes in modal characteristics of nonstationary digital signals.IEEE rmation Theory,vol.IT-32,no3,pp.412-417.M.B ASSEVILLE,A.B ENVENISTE,G.M OUSTAKIDES and A.R OUG´E E(1987a).Detection and diagnosis of changes in the eigenstructure of nonstationary multivariable systems.Automatica,vol.23,no3,pp.479-489. M.B ASSEVILLE,A.B ENVENISTE,G.M OUSTAKIDES and A.R OUG´E E(1987b).Optimal sensor location for detecting changes in dynamical behavior.IEEE Trans.Automatic Control,vol.AC-32,no12,pp.1067-1075.M.B ASSEVILLE,A.B ENVENISTE,B.G ACH-D EVAUCHELLE,M.G OURSAT,D.B ONNECASE,P.D OREY, M.P REVOSTO and M.O LAGNON(1993).Damage monitoring in vibration mechanics:issues in diagnos-tics and predictive maintenance.Mechanical Systems and Signal Processing,vol.7,no5,pp.401-423.R.V.B EARD(1971).Failure Accommodation in Linear Systems through Self-reorganization.Ph.D.Thesis, Dept.Aeronautics and Astronautics,MIT,Cambridge,MA.A.B ENVENISTE and J.J.F UCHS(1985).Single sample modal identification of a nonstationary stochastic process.IEEE Trans.Automatic Control,vol.AC-30,no1,pp.66-74.A.B ENVENISTE,M.B ASSEVILLE and G.M OUSTAKIDES(1987).The asymptotic local approach to change detection and model validation.IEEE Trans.Automatic Control,vol.AC-32,no7,pp.583-592.A.B ENVENISTE,M.M ETIVIER and P.P RIOURET(1990).Adaptive Algorithms and Stochastic Approxima-tions.Series on Applications of Mathematics,(A.V.Balakrishnan,I.Karatzas,M.Yor,eds.).Springer,New York.A.B ENVENISTE,M.B ASSEVILLE,L.E L G HAOUI,R.N IKOUKHAH and A.S.W ILLSKY(1992).An optimum robust approach to statistical failure detection and identification.IFAC World Conference,Sydney, July1993.B IBLIOGRAPHY427 R.H.B ERK(1973).Some asymptotic aspects of sequential analysis.Annals Statistics,vol.1,no6,pp.1126-1138.R.H.B ERK(1975).Locally most powerful sequential test.Annals Statistics,vol.3,no2,pp.373-381.P.B ILLINGSLEY(1968).Convergence of Probability Measures.Wiley,New York.A.F.B ISSELL(1969).Cusum techniques for quality control.Applied Statistics,vol.18,pp.1-30.M.E.B IVAIKOV(1991).Control of the sample size for recursive estimation of parameters subject to abrupt changes.Automation and Remote Control,no9,pp.96-103.R.E.B LAHUT(1987).Principles and Practice of Information Theory.Addison-Wesley,Reading,MA.I.F.B LAKE and W.C.L INDSEY(1973).Level-crossing problems for random processes.IEEE r-mation Theory,vol.IT-19,no3,pp.295-315.G.B ODENSTEIN and H.M.P RAETORIUS(1977).Feature extraction from the encephalogram by adaptive segmentation.Proc.IEEE,vol.65,pp.642-652.T.B OHLIN(1977).Analysis of EEG signals with changing spectra using a short word Kalman estimator. Mathematical Biosciences,vol.35,pp.221-259.W.B¨OHM and P.H ACKL(1990).Improved bounds for the average run length of control charts based on finite weighted sums.Annals Statistics,vol.18,no4,pp.1895-1899.T.B OJDECKI and J.H OSZA(1984).On a generalized disorder problem.Stochastic Processes and their Applications,vol.18,pp.349-359.L.I.B ORODKIN and V.V.M OTTL’(1976).Algorithm forfinding the jump times of random process equation parameters.Automation and Remote Control,vol.37,no6,Part1,pp.23-32.A.A.B OROVKOV(1984).Theory of Mathematical Statistics-Estimation and Hypotheses Testing,Naouka, Moscow(in Russian).Translated in French under the title Statistique Math´e matique-Estimation et Tests d’Hypoth`e ses,Mir,Paris,1987.G.E.P.B OX and G.M.J ENKINS(1970).Time Series Analysis,Forecasting and Control.Series in Time Series Analysis,Holden-Day,San Francisco.A.VON B RANDT(1983).Detecting and estimating parameters jumps using ladder algorithms and likelihood ratio test.Proc.ICASSP,Boston,MA,pp.1017-1020.A.VON B RANDT(1984).Modellierung von Signalen mit Sprunghaft Ver¨a nderlichem Leistungsspektrum durch Adaptive Segmentierung.Doctor-Engineer Dissertation,M¨u nchen,RFA(in German).S.B RAUN,ed.(1986).Mechanical Signature Analysis-Theory and Applications.Academic Press,London. L.B REIMAN(1968).Probability.Series in Statistics,Addison-Wesley,Reading,MA.G.S.B RITOV and L.A.M IRONOVSKI(1972).Diagnostics of linear systems of automatic regulation.Tekh. Kibernetics,vol.1,pp.76-83.B.E.B RODSKIY and B.S.D ARKHOVSKIY(1992).Nonparametric Methods in Change-point Problems. Kluwer Academic,Boston.L.D.B ROEMELING(1982).Jal Econometrics,vol.19,Special issue on structural change in Econometrics. L.D.B ROEMELING and H.T SURUMI(1987).Econometrics and Structural Change.Dekker,New York. D.B ROOK and D.A.E VANS(1972).An approach to the probability distribution of Cusum run length. Biometrika,vol.59,pp.539-550.J.B RUNET,D.J AUME,M.L ABARR`E RE,A.R AULT and M.V ERG´E(1990).D´e tection et Diagnostic de Pannes.Trait´e des Nouvelles Technologies,S´e rie Diagnostic et Maintenance,Herm`e s,Paris(in French).428B IBLIOGRAPHY S.P.B RUZZONE and M.K AVEH(1984).Information tradeoffs in using the sample autocorrelation function in ARMA parameter estimation.IEEE Trans.Acoustics,Speech,Signal Processing,vol.ASSP-32,no4, pp.701-715.A.K.C AGLAYAN(1980).Necessary and sufficient conditions for detectability of jumps in linear systems. IEEE Trans.Automatic Control,vol.AC-25,no4,pp.833-834.A.K.C AGLAYAN and R.E.L ANCRAFT(1983).Reinitialization issues in fault tolerant systems.Proc.Amer-ican Control Conf.,pp.952-955.A.K.C AGLAYAN,S.M.A LLEN and K.W EHMULLER(1988).Evaluation of a second generation reconfigu-ration strategy for aircraftflight control systems subjected to actuator failure/surface damage.Proc.National Aerospace and Electronic Conference,Dayton,OH.P.E.C AINES(1988).Linear Stochastic Systems.Series in Probability and Mathematical Statistics,Wiley, New York.M.J.C HEN and J.P.N ORTON(1987).Estimation techniques for tracking rapid parameter changes.Intern. Jal Control,vol.45,no4,pp.1387-1398.W.K.C HIU(1974).The economic design of cusum charts for controlling normal mean.Applied Statistics, vol.23,no3,pp.420-433.E.Y.C HOW(1980).A Failure Detection System Design Methodology.Ph.D.Thesis,M.I.T.,L.I.D.S.,Cam-bridge,MA.E.Y.C HOW and A.S.W ILLSKY(1984).Analytical redundancy and the design of robust failure detection systems.IEEE Trans.Automatic Control,vol.AC-29,no3,pp.689-691.Y.S.C HOW,H.R OBBINS and D.S IEGMUND(1971).Great Expectations:The Theory of Optimal Stop-ping.Houghton-Mifflin,Boston.R.N.C LARK,D.C.F OSTH and V.M.W ALTON(1975).Detection of instrument malfunctions in control systems.IEEE Trans.Aerospace Electronic Systems,vol.AES-11,pp.465-473.A.C OHEN(1987).Biomedical Signal Processing-vol.1:Time and Frequency Domain Analysis;vol.2: Compression and Automatic Recognition.CRC Press,Boca Raton,FL.J.C ORGE and F.P UECH(1986).Analyse du rythme cardiaque foetal par des m´e thodes de d´e tection de ruptures.Proc.7th INRIA Int.Conf.Analysis and optimization of Systems.Antibes,FR(in French).D.R.C OX and D.V.H INKLEY(1986).Theoretical Statistics.Chapman and Hall,New York.D.R.C OX and H.D.M ILLER(1965).The Theory of Stochastic Processes.Wiley,New York.S.V.C ROWDER(1987).A simple method for studying run-length distributions of exponentially weighted moving average charts.Technometrics,vol.29,no4,pp.401-407.H.C S¨ORG¨O and L.H ORV´ATH(1988).Nonparametric methods for change point problems.In Handbook of Statistics(P.R.Krishnaiah,C.R.Rao,eds.),vol.7,Elsevier,New York,pp.403-425.R.B.D AVIES(1973).Asymptotic inference in stationary gaussian time series.Advances Applied Probability, vol.5,no3,pp.469-497.J.C.D ECKERT,M.N.D ESAI,J.J.D EYST and A.S.W ILLSKY(1977).F-8DFBW sensor failure identification using analytical redundancy.IEEE Trans.Automatic Control,vol.AC-22,no5,pp.795-803.M.H.D E G ROOT(1970).Optimal Statistical Decisions.Series in Probability and Statistics,McGraw-Hill, New York.J.D ESHAYES and D.P ICARD(1979).Tests de ruptures dans un mod`e pte-Rendus de l’Acad´e mie des Sciences,vol.288,Ser.A,pp.563-566(in French).B IBLIOGRAPHY429 J.D ESHAYES and D.P ICARD(1983).Ruptures de Mod`e les en Statistique.Th`e ses d’Etat,Universit´e deParis-Sud,Orsay,France(in French).J.D ESHAYES and D.P ICARD(1986).Off-line statistical analysis of change-point models using non para-metric and likelihood methods.In Detection of Abrupt Changes in Signals and Dynamical Systems(M. Basseville,A.Benveniste,eds.).Lecture Notes in Control and Information Sciences,LNCIS77,Springer, New York,pp.103-168.B.D EVAUCHELLE-G ACH(1991).Diagnostic M´e canique des Fatigues sur les Structures Soumises`a des Vibrations en Ambiance de Travail.Th`e se de l’Universit´e Paris IX Dauphine(in French).B.D EVAUCHELLE-G ACH,M.B ASSEVILLE and A.B ENVENISTE(1991).Diagnosing mechanical changes in vibrating systems.Proc.SAFEPROCESS’91,Baden-Baden,FRG,pp.85-89.R.D I F RANCESCO(1990).Real-time speech segmentation using pitch and convexity jump models:applica-tion to variable rate speech coding.IEEE Trans.Acoustics,Speech,Signal Processing,vol.ASSP-38,no5, pp.741-748.X.D ING and P.M.F RANK(1990).Fault detection via factorization approach.Systems and Control Letters, vol.14,pp.431-436.J.L.D OOB(1953).Stochastic Processes.Wiley,New York.V.D RAGALIN(1988).Asymptotic solutions in detecting a change in distribution under an unknown param-eter.Statistical Problems of Control,Issue83,Vilnius,pp.45-52.B.D UBUISSON(1990).Diagnostic et Reconnaissance des Formes.Trait´e des Nouvelles Technologies,S´e rie Diagnostic et Maintenance,Herm`e s,Paris(in French).A.J.D UNCAN(1986).Quality Control and Industrial Statistics,5th edition.Richard D.Irwin,Inc.,Home-wood,IL.J.D URBIN(1971).Boundary-crossing probabilities for the Brownian motion and Poisson processes and techniques for computing the power of the Kolmogorov-Smirnov test.Jal Applied Probability,vol.8,pp.431-453.J.D URBIN(1985).Thefirst passage density of the crossing of a continuous Gaussian process to a general boundary.Jal Applied Probability,vol.22,no1,pp.99-122.A.E MAMI-N AEINI,M.M.A KHTER and S.M.R OCK(1988).Effect of model uncertainty on failure detec-tion:the threshold selector.IEEE Trans.Automatic Control,vol.AC-33,no12,pp.1106-1115.J.D.E SARY,F.P ROSCHAN and D.W.W ALKUP(1967).Association of random variables with applications. Annals Mathematical Statistics,vol.38,pp.1466-1474.W.D.E WAN and K.W.K EMP(1960).Sampling inspection of continuous processes with no autocorrelation between successive results.Biometrika,vol.47,pp.263-280.G.F AVIER and A.S MOLDERS(1984).Adaptive smoother-predictors for tracking maneuvering targets.Proc. 23rd Conf.Decision and Control,Las Vegas,NV,pp.831-836.W.F ELLER(1966).An Introduction to Probability Theory and Its Applications,vol.2.Series in Probability and Mathematical Statistics,Wiley,New York.R.A.F ISHER(1925).Theory of statistical estimation.Proc.Cambridge Philosophical Society,vol.22, pp.700-725.M.F ISHMAN(1988).Optimization of the algorithm for the detection of a disorder,based on the statistic of exponential smoothing.In Statistical Problems of Control,Issue83,Vilnius,pp.146-151.R.F LETCHER(1980).Practical Methods of Optimization,2volumes.Wiley,New York.P.M.F RANK(1990).Fault diagnosis in dynamic systems using analytical and knowledge based redundancy -A survey and new results.Automatica,vol.26,pp.459-474.430B IBLIOGRAPHY P.M.F RANK(1991).Enhancement of robustness in observer-based fault detection.Proc.SAFEPRO-CESS’91,Baden-Baden,FRG,pp.275-287.P.M.F RANK and J.W¨UNNENBERG(1989).Robust fault diagnosis using unknown input observer schemes. In Fault Diagnosis in Dynamic Systems-Theory and Application(R.Patton,P.Frank,R.Clark,eds.). International Series in Systems and Control Engineering,Prentice Hall International,London,UK,pp.47-98.K.F UKUNAGA(1990).Introduction to Statistical Pattern Recognition,2d ed.Academic Press,New York. S.I.G ASS(1958).Linear Programming:Methods and Applications.McGraw Hill,New York.W.G E and C.Z.F ANG(1989).Extended robust observation approach for failure isolation.Int.Jal Control, vol.49,no5,pp.1537-1553.W.G ERSCH(1986).Two applications of parametric time series modeling methods.In Mechanical Signature Analysis-Theory and Applications(S.Braun,ed.),chap.10.Academic Press,London.J.J.G ERTLER(1988).Survey of model-based failure detection and isolation in complex plants.IEEE Control Systems Magazine,vol.8,no6,pp.3-11.J.J.G ERTLER(1991).Analytical redundancy methods in fault detection and isolation.Proc.SAFEPRO-CESS’91,Baden-Baden,FRG,pp.9-22.B.K.G HOSH(1970).Sequential Tests of Statistical Hypotheses.Addison-Wesley,Cambridge,MA.I.N.G IBRA(1975).Recent developments in control charts techniques.Jal Quality Technology,vol.7, pp.183-192.J.P.G ILMORE and R.A.M C K ERN(1972).A redundant strapdown inertial reference unit(SIRU).Jal Space-craft,vol.9,pp.39-47.M.A.G IRSHICK and H.R UBIN(1952).A Bayes approach to a quality control model.Annals Mathematical Statistics,vol.23,pp.114-125.A.L.G OEL and S.M.W U(1971).Determination of the ARL and a contour nomogram for CUSUM charts to control normal mean.Technometrics,vol.13,no2,pp.221-230.P.L.G OLDSMITH and H.W HITFIELD(1961).Average run lengths in cumulative chart quality control schemes.Technometrics,vol.3,pp.11-20.G.C.G OODWIN and K.S.S IN(1984).Adaptive Filtering,Prediction and rmation and System Sciences Series,Prentice Hall,Englewood Cliffs,NJ.R.M.G RAY and L.D.D AVISSON(1986).Random Processes:a Mathematical Approach for Engineers. Information and System Sciences Series,Prentice Hall,Englewood Cliffs,NJ.C.G UEGUEN and L.L.S CHARF(1980).Exact maximum likelihood identification for ARMA models:a signal processing perspective.Proc.1st EUSIPCO,Lausanne.D.E.G USTAFSON, A.S.W ILLSKY,J.Y.W ANG,M.C.L ANCASTER and J.H.T RIEBWASSER(1978). ECG/VCG rhythm diagnosis using statistical signal analysis.Part I:Identification of persistent rhythms. Part II:Identification of transient rhythms.IEEE Trans.Biomedical Engineering,vol.BME-25,pp.344-353 and353-361.F.G USTAFSSON(1991).Optimal segmentation of linear regression parameters.Proc.IFAC/IFORS Symp. Identification and System Parameter Estimation,Budapest,pp.225-229.T.H¨AGGLUND(1983).New Estimation Techniques for Adaptive Control.Ph.D.Thesis,Lund Institute of Technology,Lund,Sweden.T.H¨AGGLUND(1984).Adaptive control of systems subject to large parameter changes.Proc.IFAC9th World Congress,Budapest.B IBLIOGRAPHY431 P.H ALL and C.C.H EYDE(1980).Martingale Limit Theory and its Application.Probability and Mathemat-ical Statistics,a Series of Monographs and Textbooks,Academic Press,New York.W.J.H ALL,R.A.W IJSMAN and J.K.G HOSH(1965).The relationship between sufficiency and invariance with applications in sequential analysis.Ann.Math.Statist.,vol.36,pp.576-614.E.J.H ANNAN and M.D EISTLER(1988).The Statistical Theory of Linear Systems.Series in Probability and Mathematical Statistics,Wiley,New York.J.D.H EALY(1987).A note on multivariate CuSum procedures.Technometrics,vol.29,pp.402-412.D.M.H IMMELBLAU(1970).Process Analysis by Statistical Methods.Wiley,New York.D.M.H IMMELBLAU(1978).Fault Detection and Diagnosis in Chemical and Petrochemical Processes. Chemical Engineering Monographs,vol.8,Elsevier,Amsterdam.W.G.S.H INES(1976a).A simple monitor of a system with sudden parameter changes.IEEE r-mation Theory,vol.IT-22,no2,pp.210-216.W.G.S.H INES(1976b).Improving a simple monitor of a system with sudden parameter changes.IEEE rmation Theory,vol.IT-22,no4,pp.496-499.D.V.H INKLEY(1969).Inference about the intersection in two-phase regression.Biometrika,vol.56,no3, pp.495-504.D.V.H INKLEY(1970).Inference about the change point in a sequence of random variables.Biometrika, vol.57,no1,pp.1-17.D.V.H INKLEY(1971).Inference about the change point from cumulative sum-tests.Biometrika,vol.58, no3,pp.509-523.D.V.H INKLEY(1971).Inference in two-phase regression.Jal American Statistical Association,vol.66, no336,pp.736-743.J.R.H UDDLE(1983).Inertial navigation system error-model considerations in Kalmanfiltering applica-tions.In Control and Dynamic Systems(C.T.Leondes,ed.),Academic Press,New York,pp.293-339.J.S.H UNTER(1986).The exponentially weighted moving average.Jal Quality Technology,vol.18,pp.203-210.I.A.I BRAGIMOV and R.Z.K HASMINSKII(1981).Statistical Estimation-Asymptotic Theory.Applications of Mathematics Series,vol.16.Springer,New York.R.I SERMANN(1984).Process fault detection based on modeling and estimation methods-A survey.Auto-matica,vol.20,pp.387-404.N.I SHII,A.I WATA and N.S UZUMURA(1979).Segmentation of nonstationary time series.Int.Jal Systems Sciences,vol.10,pp.883-894.J.E.J ACKSON and R.A.B RADLEY(1961).Sequential and tests.Annals Mathematical Statistics, vol.32,pp.1063-1077.B.J AMES,K.L.J AMES and D.S IEGMUND(1988).Conditional boundary crossing probabilities with appli-cations to change-point problems.Annals Probability,vol.16,pp.825-839.M.K.J EERAGE(1990).Reliability analysis of fault-tolerant IMU architectures with redundant inertial sen-sors.IEEE Trans.Aerospace and Electronic Systems,vol.AES-5,no.7,pp.23-27.N.L.J OHNSON(1961).A simple theoretical approach to cumulative sum control charts.Jal American Sta-tistical Association,vol.56,pp.835-840.N.L.J OHNSON and F.C.L EONE(1962).Cumulative sum control charts:mathematical principles applied to their construction and use.Parts I,II,III.Industrial Quality Control,vol.18,pp.15-21;vol.19,pp.29-36; vol.20,pp.22-28.432B IBLIOGRAPHY R.A.J OHNSON and M.B AGSHAW(1974).The effect of serial correlation on the performance of CUSUM tests-Part I.Technometrics,vol.16,no.1,pp.103-112.H.L.J ONES(1973).Failure Detection in Linear Systems.Ph.D.Thesis,Dept.Aeronautics and Astronautics, MIT,Cambridge,MA.R.H.J ONES,D.H.C ROWELL and L.E.K APUNIAI(1970).Change detection model for serially correlated multivariate data.Biometrics,vol.26,no2,pp.269-280.M.J URGUTIS(1984).Comparison of the statistical properties of the estimates of the change times in an autoregressive process.In Statistical Problems of Control,Issue65,Vilnius,pp.234-243(in Russian).T.K AILATH(1980).Linear rmation and System Sciences Series,Prentice Hall,Englewood Cliffs,NJ.L.V.K ANTOROVICH and V.I.K RILOV(1958).Approximate Methods of Higher Analysis.Interscience,New York.S.K ARLIN and H.M.T AYLOR(1975).A First Course in Stochastic Processes,2d ed.Academic Press,New York.S.K ARLIN and H.M.T AYLOR(1981).A Second Course in Stochastic Processes.Academic Press,New York.D.K AZAKOS and P.P APANTONI-K AZAKOS(1980).Spectral distance measures between gaussian pro-cesses.IEEE Trans.Automatic Control,vol.AC-25,no5,pp.950-959.K.W.K EMP(1958).Formula for calculating the operating characteristic and average sample number of some sequential tests.Jal Royal Statistical Society,vol.B-20,no2,pp.379-386.K.W.K EMP(1961).The average run length of the cumulative sum chart when a V-mask is used.Jal Royal Statistical Society,vol.B-23,pp.149-153.K.W.K EMP(1967a).Formal expressions which can be used for the determination of operating character-istics and average sample number of a simple sequential test.Jal Royal Statistical Society,vol.B-29,no2, pp.248-262.K.W.K EMP(1967b).A simple procedure for determining upper and lower limits for the average sample run length of a cumulative sum scheme.Jal Royal Statistical Society,vol.B-29,no2,pp.263-265.D.P.K ENNEDY(1976).Some martingales related to cumulative sum tests and single server queues.Stochas-tic Processes and Appl.,vol.4,pp.261-269.T.H.K ERR(1980).Statistical analysis of two-ellipsoid overlap test for real time failure detection.IEEE Trans.Automatic Control,vol.AC-25,no4,pp.762-772.T.H.K ERR(1982).False alarm and correct detection probabilities over a time interval for restricted classes of failure detection algorithms.IEEE rmation Theory,vol.IT-24,pp.619-631.T.H.K ERR(1987).Decentralizedfiltering and redundancy management for multisensor navigation.IEEE Trans.Aerospace and Electronic systems,vol.AES-23,pp.83-119.Minor corrections on p.412and p.599 (May and July issues,respectively).R.A.K HAN(1978).Wald’s approximations to the average run length in cusum procedures.Jal Statistical Planning and Inference,vol.2,no1,pp.63-77.R.A.K HAN(1979).Somefirst passage problems related to cusum procedures.Stochastic Processes and Applications,vol.9,no2,pp.207-215.R.A.K HAN(1981).A note on Page’s two-sided cumulative sum procedures.Biometrika,vol.68,no3, pp.717-719.B IBLIOGRAPHY433 V.K IREICHIKOV,V.M ANGUSHEV and I.N IKIFOROV(1990).Investigation and application of CUSUM algorithms to monitoring of sensors.In Statistical Problems of Control,Issue89,Vilnius,pp.124-130(in Russian).G.K ITAGAWA and W.G ERSCH(1985).A smoothness prior time-varying AR coefficient modeling of non-stationary covariance time series.IEEE Trans.Automatic Control,vol.AC-30,no1,pp.48-56.N.K LIGIENE(1980).Probabilities of deviations of the change point estimate in statistical models.In Sta-tistical Problems of Control,Issue83,Vilnius,pp.80-86(in Russian).N.K LIGIENE and L.T ELKSNYS(1983).Methods of detecting instants of change of random process prop-erties.Automation and Remote Control,vol.44,no10,Part II,pp.1241-1283.J.K ORN,S.W.G ULLY and A.S.W ILLSKY(1982).Application of the generalized likelihood ratio algorithm to maneuver detection and estimation.Proc.American Control Conf.,Arlington,V A,pp.792-798.P.R.K RISHNAIAH and B.Q.M IAO(1988).Review about estimation of change points.In Handbook of Statistics(P.R.Krishnaiah,C.R.Rao,eds.),vol.7,Elsevier,New York,pp.375-402.P.K UDVA,N.V ISWANADHAM and A.R AMAKRISHNAN(1980).Observers for linear systems with unknown inputs.IEEE Trans.Automatic Control,vol.AC-25,no1,pp.113-115.S.K ULLBACK(1959).Information Theory and Statistics.Wiley,New York(also Dover,New York,1968). K.K UMAMARU,S.S AGARA and T.S¨ODERSTR¨OM(1989).Some statistical methods for fault diagnosis for dynamical systems.In Fault Diagnosis in Dynamic Systems-Theory and Application(R.Patton,P.Frank,R. Clark,eds.).International Series in Systems and Control Engineering,Prentice Hall International,London, UK,pp.439-476.A.K USHNIR,I.N IKIFOROV and I.S AVIN(1983).Statistical adaptive algorithms for automatic detection of seismic signals-Part I:One-dimensional case.In Earthquake Prediction and the Study of the Earth Structure,Naouka,Moscow(Computational Seismology,vol.15),pp.154-159(in Russian).L.L ADELLI(1990).Diffusion approximation for a pseudo-likelihood test process with application to de-tection of change in stochastic system.Stochastics and Stochastics Reports,vol.32,pp.1-25.T.L.L A¨I(1974).Control charts based on weighted sums.Annals Statistics,vol.2,no1,pp.134-147.T.L.L A¨I(1981).Asymptotic optimality of invariant sequential probability ratio tests.Annals Statistics, vol.9,no2,pp.318-333.D.G.L AINIOTIS(1971).Joint detection,estimation,and system identifirmation and Control, vol.19,pp.75-92.M.R.L EADBETTER,G.L INDGREN and H.R OOTZEN(1983).Extremes and Related Properties of Random Sequences and Processes.Series in Statistics,Springer,New York.L.L E C AM(1960).Locally asymptotically normal families of distributions.Univ.California Publications in Statistics,vol.3,pp.37-98.L.L E C AM(1986).Asymptotic Methods in Statistical Decision Theory.Series in Statistics,Springer,New York.E.L.L EHMANN(1986).Testing Statistical Hypotheses,2d ed.Wiley,New York.J.P.L EHOCZKY(1977).Formulas for stopped diffusion processes with stopping times based on the maxi-mum.Annals Probability,vol.5,no4,pp.601-607.H.R.L ERCHE(1980).Boundary Crossing of Brownian Motion.Lecture Notes in Statistics,vol.40,Springer, New York.L.L JUNG(1987).System Identification-Theory for the rmation and System Sciences Series, Prentice Hall,Englewood Cliffs,NJ.。
Ornstein–Uhlenbeck process - Wikipedia, the f

Ornstein–Uhlenbeck process - Wikipedia,the f...Ornstein–Uhlenbeck process undefinedundefinedFrom Wikipedia, the free encyclopediaJump to: navigation, searchNot to be confused with Ornstein–Uhlenbeck operator.In mathematics, the Ornstein–Uhlenbeck process (named after LeonardOrnstein and George Eugene Uhlenbeck), is a stochastic process that, roughly speaking, describes the velocity of a massive Brownian particle under the influence of friction. The process is stationary, Gaussian, and Markov, and is the only nontrivial process that satisfies these three conditions, up to allowing linear transformations of the space and time variables.[1] Over time, the process tends to drift towards its long-term mean: such a process is called mean-reverting.The process x t satisfies the following stochastic differential equation:where θ> 0, μ and σ> 0 are parameters and W t denotes the Wiener process. Contents[hide]1 Application in physical sciences2 Application in financialmathematics3 Mathematical properties4 Solution5 Alternative representation6 Scaling limit interpretation7 Fokker–Planck equationrepresentation8 Generalizations9 See also10 References11 External links[edit] Application in physical sciencesThe Ornstein–Uhlenbeck process is a prototype of a noisy relaxation process. Consider for example a Hookean spring with spring constant k whose dynamics is highly overdamped with friction coefficient γ. In the presence of thermal fluctuations with temperature T, the length x(t) of the spring will fluctuate stochastically around the spring rest length x0; its stochastic dynamic is described by an Ornstein–Uhlenbeck process with:where σ is derived from the Stokes-Einstein equation D = σ2 / 2 = k B T / γ for theeffective diffusion constant.In physical sciences, the stochastic differential equation of an Ornstein–Uhlenbeck process is rewritten as a Langevin equationwhere ξ(t) is white Gaussian noise with .At equilibrium, the spring stores an averageenergy in accordance with the equipartition theorem.[edit] Application in financial mathematicsThe Ornstein–Uhlenbeck process is one of several approaches used to model (with modifications) interest rates, currency exchange rates, and commodity prices stochastically. The parameter μ represents the equilibrium or mean value supported by fundamentals; σ the degree of volatility around it caused by shocks, and θ the rate by which these shocks dissipate and the variable reverts towards the mean. One application of the process is a trading strategy pairs trade.[2][3][edit] Mathematical propertiesThe Ornstein–Uhlenbeck process is an example of a Gaussian process that has a bounded variance and admits a stationary probability distribution, in contrast tothe Wiener process; the difference between the two is in their "drift" term. For the Wiener process the drift term is constant, whereas for the Ornstein–Uhlenbeck process it is dependent on the current value of the process: if the current value of the process is less than the (long-term) mean, the drift will be positive; if the current valueof the process is greater than the (long-term) mean, the drift will be negative. In other words, the mean acts as an equilibrium level for the process. This gives the process its informative name, "mean-reverting." The stationary (long-term) variance is given byThe Ornstein–Uhlenbeck process is the continuous-time analogue ofthe discrete-time AR(1) process.three sample paths of different OU-processes with θ = 1, μ = 1.2, σ = 0.3:blue: initial value a = 0 (a.s.)green: initial value a = 2 (a.s.)red: initial value normally distributed so that the process has invariant measure [edit] SolutionThis equation is solved by variation of parameters. Apply Itō–Doeblin's formula to thefunctionto getIntegrating from 0 to t we getwhereupon we seeThus, the first moment is given by (assuming that x0 is a constant)We can use the Itōisometry to calculate the covariance function byThus if s < t (so that min(s, t) = s), then we have[edit] Alternative representationIt is also possible (and often convenient) to represent x t (unconditionally, i.e.as ) as a scaled time-transformed Wiener process:or conditionally (given x0) asThe time integral of this process can be used to generate noise with a 1/ƒpower spectrum.[edit] Scaling limit interpretationThe Ornstein–Uhlenbeck process can be interpreted as a scaling limit of a discrete process, in the same way that Brownian motion is a scaling limit of random walks. Consider an urn containing n blue and yellow balls. At each step a ball is chosen at random and replaced by a ball of the opposite colour. Let X n be the number of blueballs in the urn after n steps. Then converges to a Ornstein–Uhlenbeck process as n tends to infinity.[edit] Fokker–Planck equation representationThe probability density function ƒ(x, t) of the Ornstein–Uhlenbeck process satisfies the Fokker–Planck equationThe stationary solution of this equation is a Gaussian distribution with mean μ and variance σ2 / (2θ)[edit ] GeneralizationsIt is possible to extend the OU processes to processes where the background driving process is a L évy process . These processes are widely studied by OleBarndorff-Nielsen and Neil Shephard and others.In addition, processes are used in finance where the volatility increases for larger values of X . In particular, the CKLS (Chan-Karolyi-Longstaff-Sanders) process [4] with the volatility term replaced by can be solved in closed form for γ = 1 / 2 or 1, as well as for γ = 0, which corresponds to the conventional OU process.[edit ] See alsoThe Vasicek model of interest rates is an example of an Ornstein –Uhlenbeck process.Short rate model – contains more examples.This article includes a list of references , but its sources remain unclear because it has insufficient inline citations .Please help to improve this article by introducing more precise citations where appropriate . (January 2011)[edit ] References^ Doob 1942^ Advantages of Pair Trading: Market Neutrality^ An Ornstein-Uhlenbeck Framework for Pairs Trading ^ Chan et al. (1992)G.E.Uhlenbeck and L.S.Ornstein: "On the theory of Brownian Motion", Phys.Rev.36:823–41, 1930. doi:10.1103/PhysRev.36.823D.T.Gillespie: "Exact numerical simulation of the Ornstein–Uhlenbeck process and its integral", Phys.Rev.E 54:2084–91, 1996. PMID9965289doi:10.1103/PhysRevE.54.2084H. Risken: "The Fokker–Planck Equation: Method of Solution and Applications", Springer-Verlag, New York, 1989E. Bibbona, G. Panfilo and P. Tavella: "The Ornstein-Uhlenbeck process as a model of a low pass filtered white noise", Metrologia 45:S117-S126,2008 doi:10.1088/0026-1394/45/6/S17Chan. K. C., Karolyi, G. A., Longstaff, F. A. & Sanders, A. B.: "An empirical comparison of alternative models of the short-term interest rate", Journal of Finance 52:1209–27, 1992.Doob, J.L. (1942), "The Brownian movement and stochastic equations", Ann. of Math.43: 351–369.[edit] External linksA Stochastic Processes Toolkit for Risk Management, Damiano Brigo, Antonio Dalessandro, Matthias Neugebauer and Fares TrikiSimulating and Calibrating the Ornstein–Uhlenbeck process, M.A. van den Berg Calibrating the Ornstein-Uhlenbeck model, M.A. van den BergMaximum likelihood estimation of mean reverting processes, Jose Carlos Garcia FrancoRetrieved from ""。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Rapid prototyping of a Self-Timed ALU with FPGAs1Ortega-Cisneros S., 1Raygoza-Panduro J.J., 2Suardíaz Muro J., 1Boemo E. 1Escuela Politécnica Superior, Universidad Autónoma de Madrid, España 2Escuela Técnica Superior de Ingenieros Industriales, Universidad de Cartagenasusana.ortega@uam.es, jjraygoza@AbstractThis article presents the design and implementation of a Self-Timed Arithmetic Logic Unit (ALU) that has been developed as part o fan asynchronous microprocessor. This displays an inherent operational characteristic o flow consumption, owing to the synchronization signals that stop when the execution of an operation finishes (stoppable clock); that is to say, the dynamic consumption is zero, while it is not required again by an external request signal.It demonstrates the methodology of design of the Sel f-Timed controls which synchronize the data trans f er, as well as the characterization o f delay macros designed in FPGA editor for the adjustment of ALU processing times. It also summarizes the results of the implementation for a FPGA virtex II, as well as the parameters of area, distribution of tracks, delay, latency, consumption and fan-out.1. IntroductionThe design of non-synchronous digital systems constitutes an alternative for synchronizing large circuits. Therefore the methodology of self-timed (ST) design has advanced in the recent years. Among the advantages we can mention is its inherent operation in stoppable-clock mode, the absence of consumption peaks and its immunity to the skew of the clock. In a synchronous circuit the transmission or data processing is controlled globally by one or more phases of the clock. Whereas in a ST system, the data transfer is controlled by two signals: "request and acknowledge" as is normal in any asynchronous system [1]. The definition of the control signal format gives rise to two types of synchronization: protocol of 2 phases [2] and protocol of 4 phases [3,4]. This article presents the implementation of an ALU using the protocol of 4 phases. This has been selected in place of 2 phases, dueto the robustness of the technique, simplicity of implementation of the transmission blocks and the minimum use of the resources of the F PGA device. [5,6].At the present time the development of ST circuits has been centered on full-custom or cell-based prototypes, although the F PGAs are oriented towards the efficient implementation of synchronous circuits, at the present they constitute the only option available for fast prototypes and for the low cost of self-timed circuits.2. Description of a ST ALUThe ST Arithmetical Logical Unit has been developed as part of the asynchronous implementation of a microprocessor. The asynchronous circuit is composed of 4 main modules, as shown in the figure 1: 1. Arithmetical and Logical Unit 2. Instructions decoder 3. Asynchronous control 4.ST 4 phases pipelineThe Arithmetical Logical Unit is a combinatorial device composed of 3 main modules as can be seen in figure 1. The Module (a) or instruction block has a feeding signal of 16 bits, which enters directly from the outside to one of the two instruction entrances. The other entrance is feedback from the exit of the accumulator (module c).The ALU has 4 arithmetical instructions, 6 logics, 1 of comparison, 2 of register transference and 2 of input-output.The selection of the functions is made by means of the 15 signals “Io” up to “I14”, that activate the 15 channels of the multiplexor to illustrate the result of the operations (module b), which are related to the entrances and allow the passage of one of the logic, arithmetic or input-output functions.Figure 1. ST Arithmetical Logical UnitThe general module has 5 codifications for 15 instructions. Table 1 shows the selection code, the decoding of the operations (deco) and the occupation of these in the FPGA.3. Asynchronous ControlThe instructions are classified into 4 types ofdifferent operations, according to the number of activation pulses that are required for their execution. These are shown in the diagram of figure 2 and constitute the asynchronous control. The operations of type 1 require 4 pulses at the entrance that come from the ST 4 phase pipeline module to activate the ALU. The operations of type 2, require 2 pulses at the entrance, the operations of type 3 require 5 pulses and finally the operations type 4 require 9 pulses to codify 4 activation signals from the ALU. Some control lines are concentrated in an exit circuit allowing the accumulator to capture the data correctly. The line of "total test" of the circuit in figure 2, generates a pulse whenever an instruction is made, which is connected to an operations counter.InstructionMUX lineSelectionDeco OccupationSl LUT Reg. GatesLDA I2 000010001- - - -ADD I1 00010 0002 9 17 0 186 ROT_D I3 00011 0004 0 0 16131 ROT_I I4 00100 0008 0 0 16131COMPL I5 00101 0010 22 42 0 369 DES_D I6 00110 0020 0 0 16123 LDA, X I900111 0040 0 0 16131 INC, AI801000008013 21126 COMP I7 01001 0100 0 0 16131 LDA, Y I10 01010 0200 0 0 16131AND I11 01011 0400 16 16 0 96 OR I12 01100 0800 16 16 0 96 PTO_SAL- 01101 1000 0 0 16131RESTA I14 01110 2000 9 17 0 189 MUL I13 01111 4000 0 0 164,134Table 1. ALU InstructionsFigure 2. Asynchronous controlThe decoding of operation 1 is shown in figure 3, it requires several logic gates to make the transformation of the control signals “xi1” to “xi4” in order to activate the signals of the multiplexer and the accumulator; the elements comp_1 to comp_3 are controlled by the signal “deco1” that comes from the instructions decoder, permitting the transmission of the signals aslong as “deco” signal is actived.Figure 3. Logic operation 1The operation 2 requires 2 logical elements to transform the pulses from 2 signals from the ST control pipeline. One of these is required to activate the capture of the register and the other signal in order to count the instructions made. The decoding of operation 3 requires 5 signals from the ST control pipeline to activate the capture of data from the register, multiplexer and from the accumulator.F inally operation 4 is shown in figure 4, this operation requires 9 pulses for the decoding of theoperation. The control signal “xi1” and “deco 4” allow the capture of the operations in the register in order tomake the multiplication.Figure 4. Arithmetical operation 44. ST pipeline controlThe control units developed with ST circuits are frequently composed of micropipeline structures. These were proposals made by Ivan Sutherland at the end of the 1980s [1]. An ST pipeline structure consists of a successive series of control blocks that possess request and acknowledge signals, interconnected block by block, to facilitate the movement of information along all the circuit in a controlled and phased way. This type of structure is the fundamental base of the control circuits that are presented in this work.4.1. Four phase pipeline structuresThe majority of synchronous circuits have a data path by which the data is transferred during a process. A typical synchronous data path is formed by pipelines that have registers in their entrances and exits to store data that are processed by combinatorial circuits. These registers are controlled by clocks. On the other hand, asynchronous designs use two methods to control the transfer of data: bundled data [1] and dual rail [7].Pipeline architectures operating in bundled data consist of delegating the control over the validity of the data in the signal, in such a way that it operates together with the acknowledge signal of thecorresponding protocol.Figure 5. A bundled data pipelineIn figure 5 the illustration shows an architecture that follows the codification method in bundled data. One can see that it has a request signal “Req”, an acknowledge signal “Ack” and a data bus. A combinatorial logic block sends a request signal to the next block when the data is available, and this then sends a recognition signal back to the previous block, to indicate that the data has been received and is available for the next transfer. With this method we can completely separate the interface part from the combinatorial. In this way we can interact separately with both.F or the synchronization of the pipeline circuit to operate correctly the delay between the exit request signal of each block and the entrance request of the next stage should have an equal value at the time of the combinatorial circuit process [8].The advantage of this method is its simplicity. However, it has the inconvenience of operating over the maximum processing time for the combinatorial circuit. In this sense we fail to take advantage of quicker operating times.4.2. Delay MacrosThe implementation of delays in reconfigurable circuits is achieved through a macro in FPGA editor, as shown in figure 6.The slice of the F PGA virtex II is composed of 2 LUTs and 2 latches. F or the implementation of the delay the LUT <G> is used in the upper part of figure 6. It has a logic depth of 1, between the entrance “s_in_ibuf” and the output “s_sal_obuf’”.The delay total ΔTOT is composed of two classes of intrinsic delays of the F PGA that are the logic delay and that introduced by the interconnection path or route, these, in turn subdivide into different partial delays described in the equation 1.¨TOT = įPI + įLUT + įPO + įRUT(1)Where:įPI is the propagation delay between the entrance and exit pad of the tiopi module, with a value of 0.825 ns.įLUT is the combinational delay between the entrances of the LUTs F/G at the exits X/Y of the tilo module, with a value of 0.439 ns.įPO is the propagation delay between the entrance and the exit pad of the tioop module, with a value of 6.107 ns.įRUT is the propagation delay of the path or route of connection to the previous module.Figure 6 shows the architecture of a delay of 9.637 ns with three logia levels corresponding to tiopi, tilo and tioop modules. The values correspond to the FPGA Virtex II Xilinx XC2V1000-4FG256 [9].Figure 6. Implementation of delay macro in FPGATo increase the delay various macros are connectedin series, increasing the logic depth between theentrance and exit.The figure 7 describes the characterization of 75different delay modules, which shows that the totaldelay does not present a lineal behavior with respect tothe number of macros of which it is composed, owingto the variation of the delay values of the FPGA routes.The table 2 presents 6 examples of the circuitscharacterized. One observes that the number of macrosused in the implementation of the delay modulesmaintains a direct relationship with respect to the logiclevels; this provides an approximation of the resourcesthat will be used in the FPGA.Delay(ns)Figure 7. Total delays vs. macrosThis same table shows 6 results of themeasurements in the 75 delay modules onprogramming the FPGA. The value of T X1 indicates theentrance pulse (signal “s_in_ibuf”). T X2 is the exitpulse present in the circuit (signal “s_sal_obuf”). Thevalue T real represents the propagation delay present ineach module (T X2-T X1) and the T ps is the delay post-layout. The value of the delay in the FPGA tends to beless than the result measured during the simulation.Although one should consider that the increase inthe temperature in the FPGA alters the values of delayafter the device has operated for a long period.Table 2. Measurements of the delay circuit4.3 Implementation of the ST control pipelineA control element pipeline ST is used to regulatethe data flow through a segmented system. This canalso be used as an activation control for the differentstages of the system. The tasks carried out by each oneof the blocks are independent of one another and thetime of the stage can be different. [10]:Macros LogicallevelT X1(μs)T X2(μs)T real(ns)T ps(ns)1 343.6643.67109.635 722.8522.831217.5210 12 15.7215.711424.5130 32 25.3925.412236.9750 52 1.751.782650.5875 77 2.402.373465.49 Proceedings of the 2005 International Conference on Reconfigurable Computing and FPGAs (ReConFig 2005)In a pipeline structure (figure 5) of 25 asynchronous control blocks, the process of data transfer begins with the control pulse ‘Xi1’ and finalizes with ‘Xi25’,in such a way that the processing time X Lat is related to the difference between the last (Xi_u) and the first Xi (Xi_p) as is seen in the figure 5.or thecharacterization of these structures and to anticipate thenumber of macros (Nω) to use in a ST pipeline of aspecific size, we use the equation 2.NȦ = NIJ * (ret_2 + ret_1) (2)Where:Nt is the number of control blocks within thestructure minus 1.Ret_1 is equal to the delay in feedback, with a valueof 1.Ret_2 establishes the calculation time between theblocks, for this characterization, with a value of 3.Figure 8. Latency of different pipelinesFigure 8 shows a diagram with the characterizationof the latency for 25 pipeline control structures ofdifferent sizes. In that of the group of xi_p it is the timeform the start of the first control pulse generated by thefirst, and xi_u is the start of the final pulse produced bythe last control. D_n is the time that passes in order togenerate all the control pulses, or what it takes for thecomplete process to send data or latency.The value of the rising edge for the first pulse isfound to be around 409.71 ns and the rising edge of thefinal pulse is found to be in the range of 412.75 to509.57ns. The time cycle for each one of the structuresdemonstrates a gradual behavior on increasing thenumber of elements of which it is composed, for thismotive a pipeline control of 2 elements implemented inthe VIRTEX II is of 3.03ns and for 25 elements 99.30ns.5. Execution of ST ALUIn synchronous circuits the measurement ofoperations is traditionally based on operationfrequency of the clock. In the case of ST circuits thespeed depends on the delays incorporated into the STcontrol to modulate the transfer and activation of thecircuit operations.Each type of operation was characterized varyingthe delay and the number of millions of instructionsper second (MIPS) executed was observed. It displayeda diminution when increasing the delays. As shown infigure 9.MIPSDelay (ns)Figure 9. MIPS vs. delay (ns)The latency by type of operation which was displayedby the ALU when varying the number of delay macroswas more significant for the operations that require agreater number of pulses of control Xi during theprocess (type 3 and 4). The behavior of the latencyagainst the number of macros by type of operation isshown in figure 10.In synchronous circuits the fan-out of the globallines tends to be greater, especially the clock lines,enable, reset etc. In asynchronous circuits theinterconnection lines are local and therefore the level of fan-out is smaller. F or ST ALU 95% of the lines have a fan-out smaller than 20 and net delays of lessthan 4ns, as shown in figure 11.Figure 10. Latency of the ALU operations The line of reset that it is not drawn has a fan-out of 92 and a delay of 6 ns.D e l a y (n s )Fan OutFigure 11. Fan-out vs. net delayThe results of the implementation of the circuits in the F PGA virtexII are summarized in the figure 12. Where the ALU occupy more LUTs and registers.Figure 12. Occupation of the ST ALU6. Instantaneous CurrentIn order to measure the instantaneous current a current probe was used. This is an indirect method of measurement that detects the electromagnetic variation of the feed cable. The results of the measurement of the instantaneous current can be seen in figure 13.The measurements were made on an Avnet evaluation card. An ammeter was connected in series with the main feeder cable and the current probe monitored the same cable. The measurements of instantaneous current are registered on an oscilloscope. The results obtained of the measurement of current registered by the ammeter for ST ALU were 494 mA. With respect to its synchronous counterpart the current measured with the ammeter was 496 mA in execution. The measurements with the current probe, in the ST ALU detected a change of voltage peak to peak of 25 mV, as is observed in figure 13. In the case of its synchronous counterpart a voltage increase was observed, peak to peak, of 24 mV, throughout the time that the circuit stayed operating.As was observed in the synchronous ALU the changes of instantaneous current were more than those of the ST, from which we can deduce that the consumption of a synchronous circuit is greater.Y1 323.850 mV Y2 323.850 mV ΔY 25.2 mV CHI 10:115.0 mV/divDC FullFigure 13. Instantaneous current of the STALU7. ConclusionsThis article describes to the implementation of a Self-Timed ALU in reconfigurable circuits. In addition, it suggests some ideas for the design of these circuits in FPGAs, as well as the characterization of the measurements of the delays generated in real time and the occupation of the resources in Virtex II.The ALU has the characteristic to activate with an external pulse and eliminates the dependency on a global clock.It presented an analysis of the effect of the delay macros with different values on the behavior of the ST ALU with respect to the number of operations executed per second. A small reduction was observed in the consumption in the power supply line during the execution of an operation of the ST ALU compared to its synchronous counterpart. The feasibility was tested of making a fast prototype of ST circuits in a synchronous tool.8. AcknowledgmentThis work has been financed by the National Advice of Science and Technology of México (CONACYT).9. References[1] I. E. Sutherland, “Micropipelines”, Communications of the ACM , vol. 32, No. 6, June 1989, pp. 720-738.[2] P. Kudva and V. Akella, “Testing two-phase transition signalling based self-timed circuits in a synthesis environment,” in Proceedings o fthe 7th InternationalSymposium on High-Level Synthesis , IEEE Computer Society Press, May 1994, pp. 104–111.[3] S. B. Furber and P. Day, “Four-phase micropipeline latch control circuits,” IEEE Transactions on VLSI Systems , vol. 4 June 1996, pp. 247–253.[4] A. J. McAuley, “Four State Asynchronous Architectures”, IEEE transactions on computers , vol. 41, No. 2, Feb. 1992.[5] S. B. F urber and J. Liu, “Dynamic logic in four-phase micropipelines”, in Proc. Interna-tionalSymposium on Advanced Research in Asynchronous Circuits and Systems ,IEEE Computer Society Press, Mar. 1996.[6] Kees van Berkel and Arjan Bink. “Single-track handshaking signaling with application to micropipelines and handshake circuits”, In Proc. International Symposium on Advanced Research in Asynchronous Circuits and Systems,IEEE Computer Society Press, March 1996, pp. 122-133. [7] M. Dean, T. Williams, and D. Dill, “Efficient self-timing with level-encoded 2-phase dual-rail (LEDR),” in AdvancedResearch in VLSI (C. H. S´equin, ed.), MIT Press, 1991, pp. 55–70.[8] R. Kelly “Asynchronous Design Aspects of High-Performance Logic”, Thesis . University of Manchester. Department of Computer Science UK, 1995.[9] Co. Xilinx “Virtex-II Platform F PGA” User Guide , 1-800-255-7778 UG002 (v1.5). . Dec. 2002. [10] D. A. Gilbert and J. D. Garside, “A result forwarding mechanism for asynchronous pipelined systems,” in Proc. International Symposium on Advanced Research in Asynchronous Circuits and Systems, IEEE Computer Society Press, Apr. 1997, pp. 2–11.。
