信号与线性系统--实验三频域分析连续时间信号与系统
信号与系统实验
实验一信号与系统认知一、实验目的1、了解实验室的规章制度、强化安全教育、说明考核方法。
2、学习示波器、实验箱的使用、操作知识;3、学习常用连续周期信号的波形以及常用系统的作用。
二、实验仪器1、信号与系统实验箱(本次实验使用其自带的简易信号源,以及实验箱上的“信号通过系统”部分。
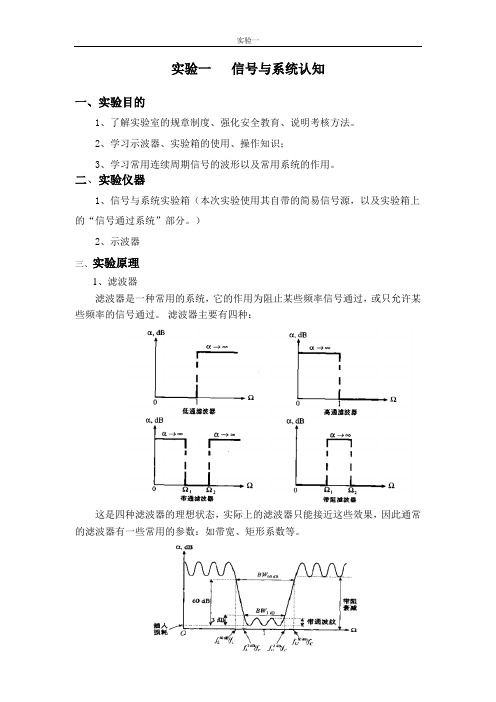
)2、示波器三、实验原理1、滤波器滤波器是一种常用的系统,它的作用为阻止某些频率信号通过,或只允许某些频率的信号通过。
滤波器主要有四种:这是四种滤波器的理想状态,实际上的滤波器只能接近这些效果,因此通常的滤波器有一些常用的参数:如带宽、矩形系数等。
通带范围:与滤波器最低衰减处比,衰减在3dB以下的频率范围。
2、线性系统线性系统是现实中广泛应用的一种系统,线性也是之后课程中默认为系统都具有的一种系统性质。
系统的线性表现在可加性与齐次性上。
齐次性:输入信号增加为原来的a倍时,输出信号也增加到原来的a倍。
四、预习要求1、复习安全操作的知识。
2、学习或复习示波器的使用方法。
3、复习典型周期信号的波形及其性质。
4、复习线性系统、滤波器的性质。
5、撰写预习报告。
五、实验内容及步骤1、讲授实验室的规章制度、强化安全教育、说明考核方法2、通过示波器,读出实验箱自带信号源各种信号的频率范围(1)测试信号源1的各种信号参数,并填入表1-1。
(2)测试信号源2的各种信号参数,并填入表1-2。
3、测量滤波器根据相应测量方法,用双踪示波器测出实验箱自带的滤波器在各频率点的输入输出幅度(先把双踪示波器两个接口都接到所测系统的输入端,调节到都可以读出输入幅度值,并把两侧幅度档位调为一致,记录下这个幅度值;之后,将示波器的一侧改接入所测系统的输出端,再调节用于输入的信号源,将信号频率其调至表1-3中标示的值,并使输入信号幅度保持原幅度值不变。
观察输出波形幅度的变化,并与原来的幅度作比较,记录变化后的幅度值。
),并将相应数据计入表1-3中。
4、测量线性系统(1)齐次性的验证自选一个输入信号,观察输出信号的波形并记录输入输出信号的参数,将输入信号的幅度增强为原信号的一定倍数后,再对输入输出输出参数进行记录,对比变化前后的输出。
信号与系统第4章 周期信号的频域分析(3学时)

T0 /2
0
x(t )sin(n 0t )dt
四、信号对称性与傅里叶系数的关系
3、半波重迭信号
~ x (t ) ~ x (t T0 / 2)
~ x (t )
A t
T0
T0 / 2 0
T0 / 2
T0
特点: 只含有正弦与余弦的偶次谐波分量,而无奇次谐波分量。
四、信号对称性与傅里叶系数的关系
~ x (t )
2 1 -4 -3 -2 -1 1 2 3 4
~ x (t ) ~ x1 (t ) ~ x2 (t )
nπ nπt t~ x (t ) 1.5 Sa ( ) cos( ) 2 2 n 1
~ x1 (t )
2
x 1(t ) 2
1 2 3 4
-4 -3 -2 -1
三、周期信号的功率谱
一、周期信号频谱的概念
连续时间周期信号可以表示为虚指数信号之和,其 中Cn 为傅里叶系数 。
~ x (t )
n =
Cn e
jn0t
1 Cn T0
T0 t 0
t0
~ x (t )e jn 0t dt
问题1:不同信号的傅里叶级数形式是否相同? 相同 问题2:不同信号的傅里叶级数不同表现在哪里? 系数
例3 课本P129
例4 已知连续周期信号的频谱如图,试写出信号的 Fourier级数表示式。 Cn
3 2 1 1 3 4 3 2
9
6
0
3
6
9
n
解: 由图可知 C0 4
C 1 3
C2 1
C 3 2
~ x (t )
连续时间信号的时域分析和频域分析

时域与频域分析的概述
时域分析
研究信号随时间变化的规律,主 要关注信号的幅度、相位、频率 等参数。
频域分析
将信号从时间域转换到频率域, 研究信号的频率成分和频率变化 规律。
02
连续时间信号的时
域分析
时域信号的定义与表示
定义
时域信号是在时间轴上取值的信号, 通常用 $x(t)$ 表示。
表示
时域信号可以用图形表示,即波形图 ,也可以用数学表达式表示。
05
实际应用案例
音频信号处理
音频信号的时域分析
波形分析:通过观察音频信号的时域波形,可 以初步了解信号的幅度、频率和相位信息。
特征提取:从音频信号中提取出各种特征,如 短时能量、短时过零率等,用于后续的分类或 识别。
音频信号的频域分析
傅里叶变换:将音频信号从时域转换 到频域,便于分析信号的频率成分。
通信系统
在通信系统中,傅里叶变 换用于信号调制和解调, 以及频谱分析和信号恢复。
时频分析方法
01
短时傅里叶变换
通过在时间上滑动窗口来分析信 号的局部特性,能够反映信号的 时频分布。
小波变换
02
03
希尔伯特-黄变换
通过小波基函数的伸缩和平移来 分析信号在不同尺度上的特性, 适用于非平稳信号的分析。
将信号分解成固有模态函数,能 够反映信号的局部特性和包络线 变化。
频域信号的运算
乘法运算
01
在频域中,两个信号的乘积对应于将它们的频域表示
相乘。
卷积运算
02 在频域中,两个信号的卷积对应于将它们的频域表示
相乘后再进行逆傅里叶变换。
滤波器设计
03
在频域中,通过对频域信号进行加权处理,可以设计
信号与线性系统分析--第三章

第三章 离散系统的时域分析
本章概述
离散时间域的方程求解
连续时间域 时间函数 微分方程 卷积积分 离散时间域 离散序列 差分方程 卷积求和
求解方法
迭代法 经典法 卷积法
连续时间信号、连续时间系统
连续时间信号
f(t)是连续变化的t的函数,除若干不连续点之外 对于任意时间值都可以给出确定的函数值。函数 的波形一般具有平滑曲线的形状,一般也称模拟 信号
f (n) .... f (1) (n 1) f (0) (n) f (1) (n 1) ...
i
f (i) (n i)
f(k ) f(2) f(-1) f(1) f(0) … 1 2 i f(i) … k
可推出:离散系统的零状态响应
y zs (n)
m
f (m) (n m)
单位阶跃序列
与阶跃函数的不同?
延时的单位阶跃序列
用单位样值序列来表示
u( n) ( n) ( n 1) ( n 2) ( n 3) (n k )
k 0
( n) u(n) u( n 1)
题目中 y0 y1 0 ,是激励加上以后的,不是初始状 态,需迭代求出 y 1, y 2 。
n 1 y1 3 y0 2 y 1 2u 1 2 u 0
0
0 0 2 y1 2 1 1
1 y 1 2
n0
y0 3 y 1 2 y 2 2 u 0 2 u 1
0 1
0 3 y 1 2 y 2 1
y 2 5 4
将初始状态代入方程求系数
总复习(信号与线性系统必过知识点)(课堂)-2022年学习资料

1.了连续时门素统的橇念-线性附不变系统-1齐次性et→rt-aet→art-2叠加性-e t+e2t-> t+rt-3线性-e,t→r,t-ae t+be2 t->ar t+br t-0-4时不变性et→rt-e -to→rt-to-drt-5微分性-de→-dt-6积分性-∫exlr→∫rxdx-●-7因果性tຫໍສະໝຸດ 0: t=0→t<0:rt=0
例1:一连续时间系统输入-输出关系为-r=Te以=eehr-0-试确定该系统是否为线性时不变系统。-解:⊙ 、积分系统是线性系统-.所以该系统是线性系统-o7e-=je-dr,令x=r--则贴:7-》cwa=edr ●-而u-=aodr=7-}-所以该系统是线性时不变系统。
例2:已知某线性时不变系统:-当激励et=,初始状态x10=1,X20-=2时,-响应rt=6e-2t-5 -3tt;-当激励et=3,初始状态保持不变时,响应-r2t=8e-2t-7e-3t。-求:(1激励e=0 初始状态x10=1,X20=2时的响应-r3t=?-2激励e①=2(①),初始状态为零时的响应r4=?-●
2.4本零状态响定的一般步骤-a求传输算子Hp;-b求单位冲激响应h;-c计算卷积;-0-●
3、连续时间系统的频域分析-完备正交函数集的概念-周期信号的傅立叶级数展开-非周期信号的傅立叶变换-傅立叶 换的性质-0-●
3.1常用完备正交岛数集-0-1三角正交函数集-cos nt,sinnt-n=0,1,2,Λ,00-to, o+T-2指数函数集-eine-n=0,±1,±2,Λ,±o0-●
内容回顾-2、系统分析-系统的描述:线性常系数微分方程-oooooOoooOO-连续系统-时域:-yt=e *ht-系统响应-的求解-频域:-Yjo=EjoHjo-复频域:-Y s=EsHs-系统的描述:线性常系数 分方程-离散系统-yk=ek*hk-不作要求-复频域:Y,(z=EzHz
第三、四章连续时间信号与系统的频域分析内容总结

第
连续时间信号与系统的频域分析总结
8 页
例15、试求信号f(t)=cos(4t+ )的频谱 。 3
解:
X
第
连续时间信号与系统的频域分析总结
9 页
例16、一因果LTI系统的输入和输出,由下列微分方程表示:(采用傅里叶变
换计算)。 (1)求系统的单位冲激响应 h( t ) ;
d 2 y( t ) dy( t )
X
第
连续时间信号与系统的频域分析内容总结
2 页
第四章是傅里叶变换在LTI系统分析中的应用。 在第三章信号频域分解、分析基础上,研究不同激励信号 通过系统的响应、信号通过系统无失真条件、理想低通滤波器 模型以及物理可实现条件、希尔伯特变换、抽样定理等主要内 容。
X
第
连续时间信号与系统的频域分析总结
3) (j
5)
1ห้องสมุดไป่ตู้
j
3
1
j 5
2
j
4
y z s(t ) e 3t (t ) e 5t (t ) 2e 4t (t )
X
第
连续时间信号与系统的频域分析总结
10 页
例17、如图所示系统,其乘法器的两个输入端分别为:f (t) sin(2t) , s(t) cos(6t)
系统的频率响应为
8
15y( t ) 2 f ( t )
dt 2
dt
(2)若 f ( t ) e4t( t ) ,求该系统的零状态响应 yzs (t) 。
解: (1)
H ( j)
2
11
j2 8 j 15 j 3 j 5
h(t) e 3t(t) e 5t(t)
(2)
苏州大学《信号系统与数字逻辑》科目考查的内容范围

苏州大学《信号系统与数字逻辑》科目考查的内容范围苏州大学硕士研究生入学考试《信号系统与数字逻辑》科目考查的内容范围《信号与线性系统》部分考试内容一、信号与系统的基本概念 1、信号的定义与分类 2、典型连续信号 3、信号的分解与运算 4、系统的定义与分类5、线性时不变系统的基本特征二、连续时间系统的时域分析 1、零输入响应与零状态响应 2、冲激响应与阶跃响应 3、系统的卷积积分分析三、傅里叶变换与傅里叶分析 1、傅里叶变换的定义、性质 2、取样信号的傅里叶变换 3、调幅信号的傅里叶变换 4、典型信号频谱5、周期与非周期信号的频谱分析6、系统的频域分析7、无失真传输8、理想滤波器四、拉普拉斯变换与拉普拉斯分析 1、拉普拉斯变换的定义、性质 2、常用信号的拉普拉斯变换 3、拉普拉斯逆变换 4、s域元件模型5、线性系统的s域分析5、周期信号的拉普拉斯变换6、取样信号的拉普拉斯变换7、拉普拉斯变换与傅里叶变换的关系五、系统函数与频率响应 1、系统函数2、系统函数的零、极点分布,零、极点分布与时域响应特性的关系、与频率响应的关系 3、全通系统、最小相位系统 4、系统稳定性、物理可实现性 5、系统框图、信号流图与系统模拟六、离散时间系统的时域分析 1、典型离散信号(序列)2、序列的运算与分解3、线性时不变离散系统的性质4、离散系统的基本单元5、离散系统的数学模型――差分方程6、离散线性卷积七、离散时间系统的Z域分析 1、Z变换的定义、性质 2、差分方程的Z变换求解 3、离散时间系统的系统函数 4、离散系统的稳定性 5、离散系统的频率响应 6、离散系统的模拟《数字电路》部分考试内容一、逻辑代数基础(一)逻辑代数的基本公式和常用公式(二)逻辑代数的基本定理(三)逻辑函数及其表示方法(四)逻辑函数的公式化简(五)逻辑函数的卡诺图化简(六)具有无关项的逻辑函数及其化简二、门电路(一)简单门电路1、半导体器件的开关特性……….2、简单与或非电路………. (二)CMOS门电路1、CMOS反相器特性………2、其他CMOS电路的特性……… (三)TTL门电路1、TTL反相器特性………2、其他TTL电路的特性……… 三、组合逻辑电路(一)组合逻辑电路的分析与设计方法1、完整的分析过程……….2、完整的设计过程………. (二)常用组合逻辑电路1、编码器………2、译码器3、数据选择器……….4、加法器……….5、数值比较器……….(三)组合逻辑电路中的竞争冒险四、触发器(一)触发器的电路结构和动作特点1、基本RS触发器……….2、同步RS触发器3、主从触发器……….4、边沿触发器……….(二)触发器的逻辑功能(D、 T、T’、 JK、 RS)及其描述方法1、特性表法………2、特性方程法3、状态转换图法……….4、逻辑符号……….(三)组合逻辑电路中的竞争冒险五、时序逻辑电路(一)同步时序逻辑电路分析方法(二)若干常用时序逻辑电路1、寄存器与移位寄存器………2、计数器3、顺序脉冲发生器………. (三)同步时序逻辑电路设计方法六、脉冲波形的产生与整形(一)施密特触发器(二)单稳态触发器(三)多谐振荡器(四)555定时器七、半导体存储器(一)只读存储器(二)随机存储器(三)存储器容量的扩展(四)用存储器实现组合逻辑函数(五)可编程逻辑器件基本概念20212021苏州大学2021年硕士研究生各专业录取人数苏州大学2021年硕士研究生各专业报名人数苏州大学硕士研究生各专业录取人数(2021、2021、2021年)2021--2021年各专业报名人数统计感谢您的阅读,祝您生活愉快。
第5章 连续时间信号与系统的频域分析

般的周期信号都满足狄里赫利条件,所以以后不再 提及。 ❖ 由以上的讨论可知,任意一个周期信号均可以展开 成以下的傅里叶级数
信号与系统
第5章 连续时间信号与系统的频域分析
n0tdt
T0 2
t0 T0 12 dt T0 t0
信号与系统
第5章 连续时间信号与系统的频域分析
❖ 式中,和均为正整数;0 2/T0 。上式说明三角函数 集是正交函数集。由于三角函数集中的元素有无穷 多个,所以三角函数集是完备正交集。也就是说, 任意一个周期信号 f (t) 均可展开成傅里叶级数,但 前提是必须满足以下的狄里赫利条件:
❖
❖ 所以
第5章 连续时间信号与系统的频域分析
(Cn e jn0t )*
Cn (e jn0t )*
C ejn0t n
(5-22)
❖
∞
f (t) C0 2 Re(Cn e jn0t )
(5-23)
n 1
❖ 2. 由指数函数集的正交性到指数形式的傅里叶级数
❖ 指数函数集 ejn0t n 0,1,2, 的元素为无数个不同角频率的虚
f
(t)
a0 2
N n 1
(ancos n0t
bnsin n0t)
信号与系统
第5章 连续时间信号与系统的频域分析
❖ 【例5-1】 求图5.2所示标准方波信号的傅里叶级数展开式。
❖ 解:由图5.2可以看出,该方波信号的周期为 T0 。在一个
周期内,f (t) 的表达式为
f
(t t T0 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
职教学院电子Z111班
覃春苗201102203001
实验三频域分析连续时间信号与系统
【实验目的】
通过借助MATLAB实现连续时间信号与系统的频域分析,熟悉和掌握MA TLAB有关频域和复频域分析信号与系统的基本命令函数。
【实验原理】
1.MATLAB信号处理工具箱提供的freqs函数可直接计算系统的频率响应的数值解。
其调用格式如下
H=freqs(b,a,w)
其中,a和b分别是H(jw)的分母和分子多项式的系数向量,w为形如w1:p:w2的向量,定义系统频率响应的频率范围,w1为频率起始值,w2为频率终止值,p为频率取样间隔。
H返回w所定义的频率点上,系统频率响应的样值。
2.MATLAB实现命令
1)[r,p,k]=residue(b,a)
功能:建立零极点留数形式的系统)函数
2)[z,p,k]=tf2zp(b,a) ,[b,a]=zp2tf(z,p,k)
功能:实现系统函数的传递函数与零极点增益形式之间的相互转换
注意:[b,a]=zp2tf(z,p,k) 中z,p,k为列向量
3)[r,p,k]=residue(b,a) ,[b,a]=residue(r,p,k)
功能:实现系统函数的传递函数与极点留数形式之间的相互转换
3.MATLAB提供的,用于分析连续时间系统)
(s
H的部分函数命令
1)计算系统函数)(s
H的零极点
命令1:roots
功能: z=roots(b) 求系统的零点; p=roots(a) 求系统的极点;
命令2:z=tzero(sys) , p=pole(sys)
功能:z=tzero(sys)得到系统的零点,p=pole(sys) 求系统的极点
2)作出系统函数)(s
H的零极点分布图
命令:pzmap(sys)
功能:绘制零极点图(poles-zeros map)
3)将系统函数的部分分式展开
命令:[r,p,k]=residue(b,a)
功能:)(s H 的部分分式展开
4)求系统的频率特性(w w H ~)()
命令:[H,w]=freqs(b,a)
功能:计算系统的频率响应
说明:命令中,w 自动取200个不同的频率值。
【实验内容】
练习题1 在频率]100,100[-∈ω范围内作出双边信号||4)(t e t x -=的幅度频谱图和相位频谱图。
w=[-100:0.02:100]; % 频率离散化
X=[1./(4-j*w)]+[1./(4+j*w)]; % 求频谱
subplot(2,1,1);plot(w,abs(X)); % 画出幅度频谱图
xlabel('w rad/s');ylabel('|X(w)|');
title('电子Z111 覃春苗 201102203001');
subplot(2,1,2);plot(w,angle(X)); % 画出相位频谱图
xlabel('w rad/s');ylabel('arg[X(w)]');
练习题2 使用roots 命令计算系统145
49925.104)(232++++-=s s s s s s H 的零极点,并用pzmap(sys)命令做出零极点分布图。
b=[1 -4 10.25]; % 系统函数的分子多项式的系数向量
a=[1 9 49 145]; % 系统函数的分母多项式的系数向量
sys=tf(b,a) %由分子分母多项式的系数向量生成系统函数的传递函数形式
z=roots(b) % 求系统的零点
p=roots(a) %求系统的极点
pzmap(sys) %绘制零极点分布图
title('电子Z111 覃春苗 201102203001');
练习题3 使用命令[r,p,k]=residue(b,a)把系统函数2
222)(234--+-+=s s s s s s H 转换成部分分式形式
b=[1 2 -2]; % 系统函数的分子多项式的系数向量
a=[1 2 -1 -2]; % 系统函数的分母多项式的系数向量
[r,p,k]=residue(b,a) %求出系统的按部分分式展开时的留数、极点和整式多项式的系数 % 注意:[r,p,k]的顺序不要乱
title('电子Z111 覃春苗 201102203001');
练习题4 零点在5.0=s ,极点在51.0j s ±-=,增益1=k 。
1) 请用zpk 和tf 命令建立系统的系统函数。
练习题4
2)系统是否稳定?若稳定,用freqs作出系统的幅频特性曲线图和相频特性曲线图。
稳定。
b=[1 -0.5]; %系统函数分子多项式的系数向量
a=conv(1,[1 0.2 25.01]);%求系统函数分母多项式的系数向量
[H,w]=freqs(b,a); %求系统的频率特性
subplot(2,1,1);plot(w,abs(H)); % 绘制系统幅频特性曲线图
xlabel('Frequency(rad/s)');
ylabel('Amplitude')
title('电子Z111 覃春苗 201102203001');
subplot(2,1,2);plot(w,angle(H));% 绘制系统相频特性曲线图
xlabel('Frequency(rad/s)');
ylabel('Angle')。
