判别分析作业
北航数理统计大作业2-聚类与判别分析

应用数理统计作业二学号:姓名:电话:二〇一四年十二月对NBA球队的聚类分析和判别分析摘要:NBA联盟作为篮球的最高殿堂深受广大球迷的喜爱,联盟的30支球队大家也耳熟能详,本文选取NBA联盟30支球队2013-2014常规赛赛季场均数据。
利用spss软件通过聚类分析对27个地区进行实力类型分类,并利用判断分析对其余3支球队对分类结果进行验证。
可以看出各球队实力类型与赛季实际结果相吻合。
关键词:聚类分析,判别分析,NBA目录1. 引言 (4)2、相关统计基础理论 (5)2.1、聚类分析 (5)2.2,判别分析 (6)3.聚类分析 (7)3.1数据文件 (7)3.2聚类分析过程 (9)3.3 聚类结果分析 (11)4、判别分析 (12)4.1 判别分析过程 (12)4.2判别检验 (17)5、结论 (20)参考文献 (21)致谢 (22)1. 引言1896年,美国第一个篮球组织"全国篮球联盟(简称NBL)"成立,但当时篮球规则还不完善,组织机构也不健全,经过几个赛季后,该组织就名存实亡了。
1946年4月6日,由美国波士顿花园老板沃尔特.阿.布朗发起成立了“美国篮球协会”(简称BAA)。
1949年在布朗的努力下,美国两大篮球组织BAA和NBL合并为“全国篮球协会”(简称NBA)。
NBA季前赛是 NBA各支队伍的热身赛,因为在每个赛季结束后,每支球队在阵容上都有相当大的变化,为了让各队磨合阵容,熟悉各自球队的打法,确定各队新赛季的比赛阵容、同时也能增进队员、教练员之间的沟通,所以在每个赛季开始之前,NBA就举办若干场季前赛,使他们能以比较好的状态投入到漫长的常规赛的比赛当中。
为了扩大NBA在全球的影响,季前赛有约三分之一的球队在美国以外的国家举办。
从总体上看,NBA的赛程安排分为常规赛、季后赛和总决赛。
常规赛采用主客场制,季后赛和总决赛采用七场四胜制的淘汰制。
[31]NBA常规赛从每年的11月的第一个星期二开罗,到次年的4月20日左右结束。
08聚类分析与判别分析的例题

聚类分析与判别分析的例题1、某超市经销十种品牌的饮料,其中有四种畅销,三种滞销,三种平销。
下表是这十种品牌饮料的销售价格(元)和顾客对各种饮料的口味评分、信任度评分的平均数。
(1)根据数据建立贝叶斯判别函数,并根据此判别函数对原样本进行回判。
(2)现有一新品牌的饮料再该超市试销,其销售价格为3.0,顾客对其口味的评分平均分为8,信任评分为5,试预测该饮料的销售情况。
2、银行的贷款部门需要判别每个客户的信用好坏(是否未履行还贷责任),以决定是否给予贷款。
可以根据贷款申请人的年龄、受教育程度、现从事工作的年龄、未变更住址的年数、收入,负债收入比例、信用卡债务、其他债务等来判断其信用情况。
下表是某银行的客户资料中抽取的部分数据,(1)根据样本资料分别用距离判别法、贝叶斯判别法和费系尔判别法建立判别函数和判别规则。
(2)某客户的如上情况资料为(53,1,9,18,50,11,20,2.02,3.58),对其进行信用好坏的判别。
目前信用好坏客户序号已履行还贷责任1 23 1 7 2 31 6.6 0.34 1.712 34 1 173 59 8.0 1.81 2.913 42 2 7 23 41 4.6 0.94 0.944 39 1 195 48 13.1 1.93 4.365 35 1 9 1 34 5.0 0.40 1.30未履行还贷责任6 37 1 1 3 24 15.1 1.80 1.827 29 1 13 1 42 7.4 1.46 1.658 32 2 11 6 75 23.3 7.76 9.729 28 2 2 3 23 6.4 0.19 1.2910 26 1 4 3 27 10.5 2.47 0.363、从胃癌患者、萎缩性胃炎患者和非胃炎患者中分别抽取五个病人进行思想生化指标的化验:血清铜蛋白、蓝色反应、尿吲哚乙酸和中性硫化物,数据见下表。
试用距离判别法建立判别函数,并根据此判别函数对原样本进行回判。
判别分析 实例共67页

35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
55、 为 中 华 之 崛起而 读书。 ——周 恩来
判别分析 实例
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
谢谢!
5—陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
判别分析1

2.实验内容(1)自选数据或者使用例题4-1、4-2数据完成判别分析。
(2)对判别分析结果进行分析。
(3)选定两个样本,对样本进行分类。
3.实验步骤例4-1:判别分析的一个重要应用是动植物的分类,最著名的一个例子是1936年费歇的鸢尾花数据。
鸢尾花为法国的国花,Setosa、erisolor、Virginica是三种有名的鸢尾花,其萼片是绚丽多彩的,和向上的花瓣不同,花萼是下垂的。
这三种鸢尾花很像,人们试图建立模型,根据萼片和花瓣的四个角度来对鸢尾花分类。
该数据给出150朵鸢尾花的萼片长(sepal length)、萼片宽(sepal length)、花瓣长(petal width)、花瓣宽(petal width)以及这些分别属于的种类共五个变量。
萼片和花瓣的长度为四个定量变量,而种类为分类变量。
这里三种鸢尾花各有50个观测值。
对数据进行判别分析的得到的分析结果如下:表1-1 分析觀察值處理摘要未加權的觀察值N 百分比有效150 100.0已排除遺漏或超出範圍群組代碼0 .0至少一個遺漏區別變數0 .0遺漏或超出範圍群組代碼及至0 .0少一個遺漏區別變數總計0 .0總計150 100.0输出结果表1-1分析的是各组变量的描述统计量和对各组均值是否相等的检验。
反应的是有效样本变量及变量缺失情况。
表1-2 群組統計資料被解释变量平均數標準偏差有效的 N (listwise)表1-5 測試結果Box's M 共變異等式檢定146.663F 近似值7.045df1 20df2 77566.751顯著性.000檢定相等母體共變異數矩陣的虛無假設。
输出结果1-4和表1-5是对各组协方差矩阵是否相等的Boxs’M检验。
表1-4反映协方差矩阵的秩和行列式的对数值。
由行列式值可以看出,协方差矩阵不是病态矩阵。
表1-5是对个总体协方差矩阵是否相等的统计检验。
由F值及其显著性水平,我们在0.05的显著性水平下拒绝原假设。
判别分析练习题

判别分析练习题判别分析练习题在统计学中,判别分析是一种用于分类和预测的方法。
它通过对不同类别的样本进行分析,构建一个分类模型,以便将未知样本分配到正确的类别中。
判别分析在各个领域都有广泛的应用,如医学诊断、金融风险评估等。
下面我将给大家提供一些判别分析的练习题,希望能够帮助大家更好地理解和应用这一方法。
1. 假设有两个类别的样本,每个样本都有两个变量。
已知两个类别的样本均值和协方差矩阵如下:类别1:均值为(1, 2),协方差矩阵为[[2, 1], [1, 2]]类别2:均值为(3, 4),协方差矩阵为[[3, 1], [1, 3]]现有一个未知样本(2, 3),请利用判别分析方法判断该样本属于哪个类别。
解答:首先,我们需要计算两个类别的判别函数值。
对于类别1,判别函数为:g1(x) = -0.5 * (x - μ1) * Σ1^-1 * (x - μ1)T - 0.5 * ln(|Σ1|) + ln(P1)其中,x为未知样本,μ1为类别1的均值,Σ1为类别1的协方差矩阵,P1为类别1的先验概率。
类似地,对于类别2,判别函数为:g2(x) = -0.5 * (x - μ2) * Σ2^-1 * (x - μ2)T - 0.5 * ln(|Σ2|) + ln(P2)其中,μ2为类别2的均值,Σ2为类别2的协方差矩阵,P2为类别2的先验概率。
根据给定的均值和协方差矩阵,我们可以计算出:μ1 = (1, 2), Σ1 = [[2, 1], [1, 2]]μ2 = (3, 4), Σ2 = [[3, 1], [1, 3]]假设两个类别的先验概率相等,即P1 = P2 = 0.5。
将未知样本(2, 3)代入判别函数中,可以计算出:g1(2, 3) = -4.5g2(2, 3) = -5.5由于g2(2, 3)的值较小,所以未知样本更有可能属于类别2。
2. 现有一个三类别的样本,每个样本有三个变量。
已知三个类别的样本均值和协方差矩阵如下:类别1:均值为(1, 2, 3),协方差矩阵为[[2, 1, 1], [1, 2, 1], [1, 1, 2]]类别2:均值为(4, 5, 6),协方差矩阵为[[3, 1, 2], [1, 3, 2], [2, 2, 3]]类别3:均值为(7, 8, 9),协方差矩阵为[[4, 1, 2], [1, 4, 2], [2, 2, 4]]现有一个未知样本(3, 4, 5),请利用判别分析方法判断该样本属于哪个类别。
聚类与判别分析作业

利用SPSS对全国各省进行经济类型聚类和判别分析摘要:本文利用SPSS统计软件对中国大陆(除港、澳、台之外)的31个省、市、自治区2000年到2009年的经济总量进行聚类分析,将这31个省、市、自治区分为了三大类,即经济发达地区、中等水平区、经济落后区。
并以这31个省级行政区10年的经济数据为样本,进行判别分析,建立了Fisher判别模型。
从判回代统计表可以看出该判别模型有着很高的正确率。
关键词:SPSS 聚类分析判别分析Fisher判别法一、引言利用各省以往经济数据对各省进行经济类型的划分,有助于了解各省的经济发展的状况,特别是能有助于了解全国各区域经济发展状况。
这对于相关部门制定相应的经济政策有一定的参考意义。
本文利用SPSS统计软件对全国31个省级行政区近10年的经济总量进行了聚类分析,把这31个地区划分为三个大类,即经济发达地区、中等水平区、经济落后区,然后对分好的类进行了判别分析,建立了判别函数。
从结果可以看出,其判别效果较好。
二、聚类分析和判别分析简介1、聚类分析法俗话说:“物以类聚,人以群分”。
对研究对象进行适当的分类,进而发现其规律性,是人们认识世界的一种基本方法。
研究怎样对事物进行合理分类(归类)的统计方法称为聚类分析。
依据分类对象的不同可以把聚类分析再分成Q型聚类和R型聚类,Q聚类是对样品进行聚类,R聚类是指对变量进行聚类。
聚类分析的基本原理是把某种性质相似的对象归于同一类,而不同的类之间则存在较大的差异。
为此,首先需要能刻画各个变量之间或者各个样本点之间的相似性,Q聚类一般使用“距离”度量样本点之间的相似性,R聚类则使用“相似系数”作为变量相似性的度量。
定义样本之间的距离可以采用欧氏距离、明考夫斯基距离、马氏距离、兰氏距离等测度;定义各变量之间的相似系数则多采用样本相关系数、夹角余弦等测度。
系统聚类法(Hierarchical Clustering Method )是最常用的一种聚类方法。
判别分析实验报告

判别分析实验报告一、引言判别分析是一种常用的统计分析方法,用于解决分类问题。
它通过分析已知类别的训练样本,构建一个分类模型,再用该模型对新样本进行分类预测。
本实验旨在通过判别分析方法,对一组实验数据进行分类分析,并评估分类模型的准确性和可靠性。
二、实验设计本次实验采用了以下步骤进行判别分析:1.数据收集:收集一组有标签的实验数据,包括特征变量和类别标签。
2.数据预处理:对收集到的数据进行清洗和预处理,包括缺失值处理、异常值处理等。
3.特征选择:根据实际需求和特征变量的相关性,选择合适的特征作为判别分析的输入变量。
4.训练模型:使用训练数据集训练判别分析模型,建立分类模型。
5.模型评估:使用测试数据集对分类模型进行评估,包括分类准确度、召回率、精确率等指标。
6.模型优化:根据评估结果,对分类模型进行优化,如调整模型参数、增加特征变量等。
三、实验结果经过以上步骤,我们得到了一个判别分析模型,并进行了评估。
以下是实验结果的总结:1.数据集描述:我们使用了一个包含1000个样本的数据集,每个样本有5个特征变量和一个类别标签。
2.数据预处理:我们对数据集进行了缺失值处理和异常值处理,确保数据的完整性和准确性。
3.特征选择:根据特征变量与类别标签的相关性,我们选择了3个最相关的特征作为判别分析的输入变量。
4.模型训练:根据训练数据集,我们使用了判别分析算法来训练模型。
模型的训练过程中,我们使用了交叉验证方法来评估模型的性能。
5.模型评估:使用测试数据集,我们对模型进行了评估。
评估结果显示,该模型的分类准确度达到了90%,召回率为85%,精确率为92%。
6.模型优化:根据评估结果,我们对模型进行了优化。
我们尝试了不同的特征组合和参数调整,最终将模型的准确度提高到了92%。
四、讨论与总结通过本次实验,我们得到了一个准确度较高的判别分析模型,并对其进行了评估和优化。
然而,在实际应用中,我们还需注意以下几点:1.数据质量:数据质量对判别分析模型的准确性有重要影响。
多元统计作业-判别分析
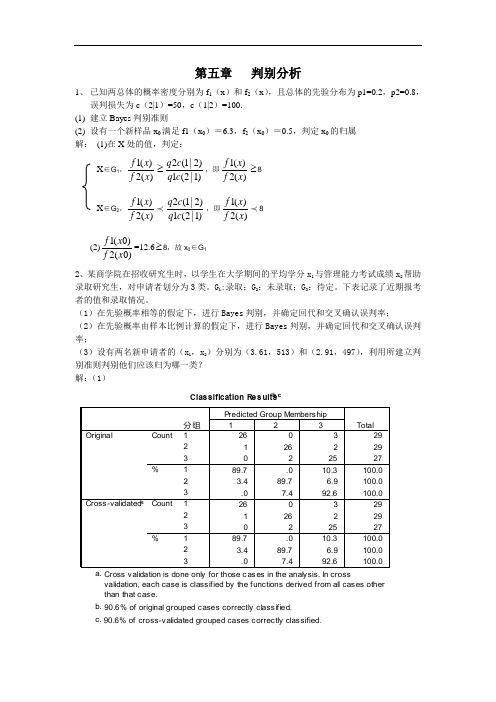
第五章 判别分析1、 已知两总体的概率密度分别为f 1(x )和f 2(x ),且总体的先验分布为p1=0.2,p2=0.8,误判损失为c (2|1)=50,c (1|2)=100. (1) 建立Bayes 判别准则(2) 设有一个新样品x 0满足f1(x 0)=6.3,f 2(x 0)=0.5,判定x 0的归属 解: (1)在X 处的值,判定:X ∈G 1,1()2()f x f x ≥2(1|2)1(2|1)q c q c ,即1()2()f x f x ≥8X ∈G 2,1()2()f x f x 2(1|2)1(2|1)q c q c ,即1()2()f x f x 8(2)1(0)2(0)f x f x =12.6≥8,故x 0∈G 12、某商学院在招收研究生时,以学生在大学期间的平均学分x 1与管理能力考试成绩x 2帮助录取研究生,对申请者划分为3类。
G 1:录取;G 2:未录取;G 3:待定。
下表记录了近期报考者的值和录取情况。
(1)在先验概率相等的假定下,进行Bayes 判别,并确定回代和交叉确认误判率;(2)在先验概率由样本比例计算的假定下,进行Bayes 判别,并确定回代和交叉确认误判率;(3)设有两名新申请者的(x 1,x 2)分别为(3.61,513)和(2.91,497),利用所建立判别准则判别他们应该归为哪一类? 解:(1)回代误判率:8/85=0.0941,交叉确认误判率同样为8/85=0.0941,第2号、3号、24号、30号、31号、58号、74号、75号被误判。
(2)号、30号、31号、58号、74号、75号被误判。
(3)建立Fisher线性判别准则W1=-151.902+60.431X1+0.172X2W2=-89.815+45.255X1+0.138X2W3=-110.818+53.024X1+0.137X2把(3.61,513)代入以上三式,W1=154.48991,W2=144.34955,W3=150.87964把(2.91,497)代入以上三式,W1=109.43621,W2=110.46305,W3=111.57084故第一个申请者判为W1(W1最大),第二个申请者判为W3(W3最大)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
判别分析作业
对教科书第P133页习题6做判别分析
答:上述两个表对总体数据进行了一个基本的分析,由表我们得知根据分组,不同
的数据在分组之后显著性差异有所不同.在分组后55岁组死亡概率、80岁组死亡概率,有明显的差异。
答:上表我们得知,由于0.299〉0.05,所以接受原假设,即个总体之间的协方差矩阵无显著差异,即相等。
答:上表说明:得出来的一个判别式,对原方差的解释为百分之百。
答:此表为Wilks' Lambda检验,目的是检验所得判别方程的显著性,从结果看判别方程是显著的。
上面两个表为标准化判别函数的系数(判别权重)与因子载荷,通过左面两个表,我们可以清楚地揭示出各个自变量对判别函数的贡献多少。
由此我们得出此判别函数主要是根据80岁组死亡概率,来判定其属于哪组的。
答:由上述两张表,我们可以清楚地看到未标准化判别系数及各组的重心,因此我们可以计算其临界点为-1.373,0.803,从而我们可以判断位置数据应属的组。
判别方程:Y1=0.076*X6-8.77
答:此为先验概率,我们假设其相等
Classification Function Coefficients
答:上表为三个fisher判别函数
Y1=0.582X6-30.209
Y2=0.878X6-67.417
Y3=0.546X6-26.761
答:上表为经过保存后,数据窗口所保存的简历它们的意思依次为原序号,原组数,预测组数,根据Bayes判别函数所得的得分,在第一组的可能性,在第二组的可能性,在第三组的可能性。
由此我们看到,在原组数中有4个值为缺失值,此为待被判别组,由此我们得出结论。
根据判别函数我们推测原未知组1号,推断为属于第二组,原未知组2号,推断为属于第三组,原未知组3号,推断为属于第二组,原未知组4号,推断为属于第一组,判别结束。
