高考数学导数中的零点问题解决方法
高考数学利用导数研究函数的零点

课堂考点探究
变式题 已知函数f(x)=ex-ax+sin x-1.(1)当a=2时,讨论函数f(x)的单调性;
课堂考点探究
解: 当a=2时,f(x)=ex-2x+sin x-1(x∈R),则f'(x)=ex-2+cos x,设h(x)=f'(x)=ex-2+cosx, 则h'(x)=ex-sin x,当x∈(-∞,0]时,ex≤1,所以f'(x)=ex-2+cos x≤-1+cos x≤0,所以f(x)在(-∞,0]上单调递减;当x∈(0,+∞)时,ex>1,所以h'(x)=ex-sin x>1-sin x≥0,所以f'(x)在(0,+∞)上单调递增,所以f'(x)>f'(0)=0,所以f(x)在(0,+∞)上单调递增.综上,f(x)在 (-∞,0]上单调递减;在(0,+∞)上单调递增.
[总结反思]根据函数零点个数确定参数取值范围的核心思想是“数形结合”,即通过函数的单调性确定函数图像与x轴的交点个数,或者通过两个相关函数图像的交点个数确定参数需满足的条件,进而求得参数的取值范围,解决问题的步骤是“先形后数”.
课堂考点探究
课堂考点探究
变式题 已知f(x)=x2-x+asin x.(1)当a=1时,求证:f(x)>0在(0,+∞)上恒成立;
课堂考点探究
例4 已知函数f(x)=x·cos x.(2)求证:当x∈时,方程2f(x)-1=0有且仅有2个不等的实数根.
高考数学总复习考点知识与题型专题讲解22 利用导数研究函数的零点

高考数学总复习考点知识与题型专题讲解§3.7 利用导数研究函数的零点考试要求 函数零点问题在高考中占有很重要的地位,主要涉及判断函数零点的个数或范围.高考常考查三次函数与复合函数的零点问题,以及函数零点与其他知识的交汇问题,一般作为解答题的压轴题出现. 题型一 利用函数性质研究函数的零点 例1已知函数f (x )=x sin x -1.(1)讨论函数f (x )在区间⎣⎢⎡⎦⎥⎤-π2,π2上的单调性;(2)证明:函数y =f (x )在[0,π]上有两个零点. (1)解 因为函数f (x )的定义域为R ,f (-x )=-x sin(-x )-1=f (x ),所以函数f (x )为偶函数,又f ′(x )=sin x +x cos x ,且当x ∈⎣⎢⎡⎦⎥⎤0,π2时,f ′(x )≥0,所以函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上单调递增,又函数f (x )为偶函数,所以f (x )在⎣⎢⎡⎭⎪⎫-π2,0上单调递减,综上,函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上单调递增,在⎣⎢⎡⎭⎪⎫-π2,0上单调递减.(2)证明 由(1)得,f (x )在⎣⎢⎡⎦⎥⎤0,π2上单调递增,又f (0)=-1<0,f ⎝ ⎛⎭⎪⎫π2=π2-1>0,所以f (x )在⎣⎢⎡⎦⎥⎤0,π2内有且只有一个零点, 当x ∈⎝ ⎛⎦⎥⎤π2,π时,令g (x )=f ′(x )=sin x +x cos x ,则g ′(x )=2cos x -x sin x ,当x ∈⎝ ⎛⎦⎥⎤π2,π时,g ′(x )<0恒成立,即g (x )在⎝ ⎛⎦⎥⎤π2,π上单调递减,又g ⎝ ⎛⎭⎪⎫π2=1>0,g (π)=-π<0,则存在m ∈⎝ ⎛⎦⎥⎤π2,π,使得g (m )=0,且当x ∈⎝ ⎛⎭⎪⎫π2,m 时,g (x )>g (m )=0,即f ′(x )>0,则f (x )在⎝ ⎛⎭⎪⎫π2,m 上单调递增,当x ∈(m ,π]时,有g (x )<g (m )=0,即f ′(x )<0,则f (x )在(m ,π]上单调递减, 又f ⎝ ⎛⎭⎪⎫π2=π2-1>0,f (π)=-1<0,所以f (x )在(m ,π]上有且只有一个零点,综上,函数y =f (x )在[0,π]上有2个零点.思维升华利用函数性质研究函数的零点,主要是根据函数单调性、奇偶性、最值或极值的符号确定函数零点的个数,此类问题在求解过程中可以通过数形结合的方法确定函数存在零点的条件.跟踪训练1(2023·芜湖模拟)已知函数f (x )=ax +(a -1)ln x +1x -2,a ∈R . (1)讨论f (x )的单调性;(2)若f (x )只有一个零点,求a 的取值范围.解 (1)函数f (x )的定义域为(0,+∞),f ′(x )=a +a -1x -1x 2=(ax -1)(x +1)x 2,①若a ≤0,则f ′(x )<0,f (x )在(0,+∞)上单调递减;②若a >0,则当x ∈⎝ ⎛⎭⎪⎫0,1a 时,f ′(x )<0,f (x )单调递减,当x ∈⎝ ⎛⎭⎪⎫1a ,+∞时,f ′(x )>0,f (x )单调递增.综上,当a ≤0时,f (x )在(0,+∞)上单调递减;当a >0时,f (x )在⎝ ⎛⎭⎪⎫0,1a 上单调递减,在⎝ ⎛⎭⎪⎫1a ,+∞上单调递增.(2)若a ≤0,f ⎝ ⎛⎭⎪⎫1e =a e +1-a +e -2=⎝ ⎛⎭⎪⎫1e -1a +e -1>0,f (1)=a -1<0.结合函数的单调性可知,f (x )有唯一零点.若a >0,因为函数在⎝ ⎛⎭⎪⎫0,1a 上单调递减,在⎝ ⎛⎭⎪⎫1a ,+∞上单调递增,所以要使得函数有唯一零点,只需f (x )min =f ⎝ ⎛⎭⎪⎫1a =1-(a -1)ln a +a -2=(a -1)(1-ln a )=0,解得a =1或a=e.综上,a ≤0或a =1或a =e. 题型二 数形结合法研究函数的零点例2(2023·郑州质检)已知函数f (x )=e x -ax +2a ,a ∈R . (1)讨论函数f (x )的单调性; (2)求函数f (x )的零点个数.解 (1)f (x )=e x -ax +2a ,定义域为R ,且f ′(x )=e x -a ,当a ≤0时,f ′(x )>0,则f (x )在R 上单调递增;当a >0时,令f ′(x )=0,则x =ln a , 当x <ln a 时,f ′(x )<0,f (x )单调递减;当x >ln a 时,f ′(x )>0,f (x )单调递增. 综上所述,当a ≤0时,f (x )在R 上单调递增;当a >0时,f (x )在(-∞,ln a )上单调递减,在(ln a ,+∞)上单调递增. (2)令f (x )=0,得e x =a (x -2),当a =0时,e x =a (x -2)无解,∴f (x )无零点, 当a ≠0时,1a =x -2e x ,令φ(x )=x -2e x ,x ∈R ,∴φ′(x )=3-xe x , 当x ∈(-∞,3)时,φ′(x )>0;当x ∈(3,+∞)时,φ′(x )<0,∴φ(x )在(-∞,3)上单调递增,在(3,+∞)上单调递减,且φ(x )max =φ(3)=1e 3, 又x →+∞时,φ(x )→0, x →-∞时,φ(x )→-∞, ∴φ(x )的图象如图所示.当1a >1e 3,即0<a <e 3时,f (x )无零点; 当1a =1e 3,即a =e 3时,f (x )有一个零点; 当0<1a <1e 3,即a >e 3时,f (x )有两个零点; 当1a <0,即a <0时,f (x )有一个零点.综上所述,当a ∈[0,e 3)时,f (x )无零点;当a ∈(-∞,0)∪{e 3}时,f (x )有一个零点;当a ∈(e 3,+∞)时,f (x )有两个零点.思维升华含参数的函数零点个数,可转化为方程解的个数,若能分离参数,可将参数分离出来后,用x 表示参数的函数,作出该函数的图象,根据图象特征求参数的范围或判断零点个数.跟踪训练2(2023·长沙模拟)已知函数f (x )=a ln x -2x . (1)若a =2,求曲线y =f (x )在x =1处的切线方程; (2)若函数f (x )在(0,16]上有两个零点,求a 的取值范围.解 (1)当a =2时,f (x )=2ln x -2x ,该函数的定义域为(0,+∞),f ′(x )=2x -1x ,又f (1)=-2,f ′(1)=1,因此,曲线y =f (x )在x =1处的切线方程为y +2=x -1,即x -y -3=0. (2)①当a ≤0时,f ′(x )=a x -1x<0,则f (x )在(0,+∞)上单调递减,不符合题意; ②当a >0时,由f (x )=a ln x -2x =0可得2a =ln xx ,令g (x )=ln x x,其中x >0,则直线y =2a 与曲线y =g (x )的图象在(0,16]内有两个交点, g ′(x )=x x -ln x2x x =2-ln x2x x,令g ′(x )=0,可得x =e 2<16,列表如下,所以函数g (x )在区间(0,16]上的极大值为g (e 2)=2e ,且g (16)=ln 2,作出g (x )的图象如图所示.由图可知,当ln 2≤2a <2e ,即e<a ≤2ln 2时,直线y =2a 与曲线y =g (x )的图象在(0,16]内有两个交点, 即f (x )在(0,16]上有两个零点, 因此,实数a 的取值范围是⎝ ⎛⎦⎥⎤e ,2ln 2.题型三 构造函数法研究函数的零点例3(12分)(2022·新高考全国Ⅰ)已知函数f (x )=e x -ax 和g (x )=ax -ln x 有相同的最小值. (1)求a ;[切入点:求f (x ),g (x )的最小值](2)证明:存在直线y =b ,其与两条曲线y =f (x )和y =g (x )共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.[关键点:利用函数的性质与图象判断e x -x =b ,x -ln x =b 的解的个数及解的关系]思维升华涉及函数的零点(方程的根)问题,主要利用导数确定函数的单调区间和极值点,根据函数零点的个数寻找函数在给定区间内的极值以及区间端点的函数值与0的关系,从而求得参数的取值范围.跟踪训练3(2021·全国甲卷)已知a>0且a≠1,函数f(x)=x aa x(x>0).(1)当a=2时,求f(x)的单调区间;(2)若曲线y=f(x)与直线y=1有且仅有两个交点,求a的取值范围.解(1)当a=2时,f(x)=x22x(x>0),f′(x)=x(2-x ln 2)2x(x>0),令f′(x)>0,则0<x<2ln 2,此时函数f(x)单调递增,令f ′(x )<0,则x >2ln 2,此时函数f (x )单调递减,所以函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0,2ln 2,单调递减区间为⎝ ⎛⎭⎪⎫2ln 2,+∞.(2)曲线y =f (x )与直线y =1有且仅有两个交点,可转化为方程x a a x =1(x >0)有两个不同的解,即方程ln x x =ln aa 有两个不同的解. 设g (x )=ln xx (x >0),则g ′(x )=1-ln x x 2(x >0), 令g ′(x )=1-ln xx 2=0,得x =e ,当0<x <e 时,g ′(x )>0,函数g (x )单调递增, 当x >e 时,g ′(x )<0,函数g (x )单调递减, 故g (x )max =g (e)=1e , 且当x >e 时,g (x )∈⎝ ⎛⎭⎪⎫0,1e ,又g (1)=0,所以0<ln a a <1e ,所以a >1且a ≠e , 即a 的取值范围为(1,e)∪(e ,+∞).课时精练1.(2023·济南质检)已知函数f (x )=ln x +axx ,a ∈R . (1)若a =0,求f (x )的最大值;(2)若0<a <1,求证:f (x )有且只有一个零点.(1)解 若a =0,则f (x )=ln x x ,其定义域为(0,+∞),∴f ′(x )=1-ln xx 2,由f ′(x )=0,得x =e ,∴当0<x <e 时,f ′(x )>0;当x >e 时,f ′(x )<0,∴f (x )在(0,e)上单调递增,在(e ,+∞)上单调递减,∴f (x )max =f (e)=1e .(2)证明 f ′(x )=⎝ ⎛⎭⎪⎫1x +a x -ln x -ax x 2=1-ln x x 2, 由(1)知,f (x )在(0,e)上单调递增,在(e ,+∞)上单调递减,∵0<a <1,∴当x >e 时,f (x )=ln x +ax x =a +ln x x>0, 故f (x )在(e ,+∞)上无零点;当0<x <e 时,f (x )=ln x +ax x ,∵f ⎝ ⎛⎭⎪⎫1e =a -e<0,f (e)=a +1e >0, 且f (x )在(0,e)上单调递增,∴f (x )在(0,e)上有且只有一个零点,综上,f (x )有且只有一个零点.2.函数f (x )=ax +x ln x 在x =1处取得极值.(1)求f (x )的单调区间;(2)若y =f (x )-m -1在定义域内有两个不同的零点,求实数m 的取值范围.解(1)f(x)的定义域为(0,+∞),f′(x)=a+ln x+1,由f′(1)=a+1=0,解得a=-1.则f(x)=-x+x ln x,∴f′(x)=ln x,令f′(x)>0,解得x>1;令f′(x)<0,解得0<x<1.∴f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1).(2)y=f(x)-m-1在(0,+∞)内有两个不同的零点,则函数y=f(x)与y=m+1的图象在(0,+∞)内有两个不同的交点.由(1)知,f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,f(x)min=f(1)=-1,f(e)=0,作出f(x)图象如图.由图可知,当-1<m+1<0,即-2<m<-1时,y=f(x)与y=m+1的图象有两个不同的交点.因此实数m的取值范围是(-2,-1).3.(2022·河南名校联盟模拟)已知f(x)=(x-1)e x-13ax3+13a(a∈R).(1)若函数f(x)在[0,+∞)上单调递增,求a的取值范围;(2)当a≤e时,讨论函数f(x)零点的个数.解(1)f(x)=(x-1)e x-13ax3+13a,则f′(x)=x(e x-ax).∵函数f(x)在[0,+∞)上单调递增,∴f′(x)=x(e x-ax)≥0在[0,+∞)上恒成立,则e x-ax≥0,x≥0.当x=0时,则1≥0,即a∈R;当x>0时,则a≤e x x,构建g(x)=e xx(x>0),则g′(x)=(x-1)e xx2(x>0),令g′(x)>0,则x>1,令g′(x)<0,则0<x<1,∴g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,则g(x)≥g(1)=e,∴a≤e,综上所述,a≤e.(2)f(x)=(x-1)e x-13ax3+13a=(x-1)⎣⎢⎡⎦⎥⎤e x-13a(x2+x+1),令f(x)=0,则x=1或e x-13a(x2+x+1)=0,对于e x-13a(x2+x+1)=0,即e xx2+x+1=13a,构建h(x)=e xx2+x+1,则h′(x)=x(x-1)e x (x2+x+1)2,令h′(x)>0,则x>1或x<0,令h′(x)<0,则0<x<1,∴h(x)在(-∞,0),(1,+∞)上单调递增,在(0,1)上单调递减,h(0)=1,h(1)=e3且h(x)>0,当x∈R时恒成立,则当a=e时,e xx2+x+1=13a有两个根x1=1,x2<0;当0<a<e时,e xx2+x+1=13a只有一个根x3<0;当a≤0时,e xx2+x+1=13a无根.综上所述,当a≤0时,f(x)只有一个零点;当0<a≤e时,f(x)有两个零点.4.(2022·全国乙卷)已知函数f(x)=ax-1x-(a+1)ln x.(1)当a=0时,求f(x)的最大值;(2)若f(x)恰有一个零点,求a的取值范围.解(1)当a=0时,f(x)=-1x-ln x(x>0),所以f′(x)=1x2-1x=1-xx2.当x∈(0,1)时,f′(x)>0,f(x)单调递增;当x∈(1,+∞)时,f′(x)<0,f(x)单调递减,所以f(x)max=f(1)=-1.(2)由f (x )=ax -1x -(a +1)ln x (x >0),得f ′(x )=a +1x 2-a +1x =(ax -1)(x -1)x 2(x >0). 当a =0时,由(1)可知,f (x )不存在零点;当a <0时,f ′(x )=a ⎝ ⎛⎭⎪⎫x -1a (x -1)x 2, 当x ∈(0,1)时,f ′(x )>0,f (x )单调递增,当x ∈(1,+∞)时,f ′(x )<0,f (x )单调递减,所以f (x )max =f (1)=a -1<0,所以f (x )不存在零点;当a >0时,f ′(x )=a ⎝ ⎛⎭⎪⎫x -1a (x -1)x 2, 当a =1时,f ′(x )≥0,f (x )在(0,+∞)上单调递增,因为f (1)=a -1=0, 所以函数f (x )恰有一个零点;当a >1时,0<1a <1,故f (x )在⎝ ⎛⎭⎪⎫0,1a ,(1,+∞)上单调递增,在⎝ ⎛⎭⎪⎫1a ,1上单调递减. 因为f (1)=a -1>0,所以f ⎝ ⎛⎭⎪⎫1a >f (1)>0, 当x →0+时,f (x )→-∞,由零点存在定理可知f (x )在⎝ ⎛⎭⎪⎫0,1a 上必有一个零点,所以a >1满足条件,当0<a <1时,1a >1,故f (x )在(0,1),⎝ ⎛⎭⎪⎫1a ,+∞上单调递增,在⎝ ⎛⎭⎪⎫1,1a 上单调递减. 因为f (1)=a -1<0,所以f ⎝ ⎛⎭⎪⎫1a <f (1)<0,当x →+∞时,f (x )→+∞,由零点存在定理可知f (x )在⎝ ⎛⎭⎪⎫1a ,+∞上必有一个零点,即0<a <1满足条件.综上,若f (x )恰有一个零点,则a 的取值范围为(0,+∞).。
专题07 利用导函数研究函数零点问题 (原卷版)-2024年高考数学复习解答题解题思路训练

专题07利用导函数研究函数零点问题(典型题型归类训练)目录一、必备秘籍..........................................................................................................1二、典型题型..........................................................................................................2题型一:判断(讨论)零点(根)个数问题...................................................2题型二:证明唯一零点问题..............................................................................3题型三:根据零点(根)的个数求参数...........................................................4三、专项训练. (6)一、必备秘籍2、函数零点的判定如果函数()y f x =在区间[,]a b 上的图象是连续不断的一条曲线,并且有()()0f a f b ⋅<,那么函数()y f x =在区间(,)a b 内有零点,即存在(,)c a b ∈,使得()0f c =,这个c 也就是()0f x =的根.我们把这一结论称为函数零点存在性定理.注意:单调性+存在零点=唯一零点3、利用导数确定函数零点的常用方法(1)图象法:根据题目要求画出函数的图象,标明函数极(最)值的位置,借助数形结合的思想分析问题(画草图时注意有时候需使用极限).(2)利用函数零点存在定理:先用该定理判定函数在某区间上有零点,然后利用导数研究函数的单调性、极值(最值)及区间端点值的符号,进而判断函数在该区间上零点的个数.4、利用函数的零点求参数范围的方法(1)分离参数(()a g x =)后,将原问题转化为()y g x =的值域(最值)问题或转化为直线y a =与()y g x =的图象的交点个数问题(优选分离、次选分类)求解;(2)利用函数零点存在定理构建不等式求解;(3)转化为两个熟悉的函数图象的位置关系问题,从而构建不等式求解.二、典型题型题型一:判断(讨论)零点(根)个数问题题型二:证明唯一零点问题2.(2023上·黑龙江·高三校联考阶段练习)已知函数()ln f x x x =+,()e ln xg x x a =+,且函数()f x 的零点是函数()g x 的零点.(1)求实数a 的值;(2)证明:()y g x =有唯一零点.3.(2023下·河南·高三校联考阶段练习)已知函数()ln f x ax x =-,a ∈R .(1)过坐标原点作()f x 的切线,求该切线的方程;(2)证明:当a<0时,2()0f x ax +=只有一个实数根.题型三:根据零点(根)的个数求参数三、专项训练8.(2023上·吉林长春·高一吉林省实验校考期中)已知函数()()22ln f x x a x a x =-++,()R a ∈(1)求函数的单调区间与极值点;(2)若4a =,方程()0f x m -=有三个不同的根,求m 的取值范围.9.(2023上·江苏·高三校联考阶段练习)已知函数()2sin cos f x x x x x =-⋅-.(1)若曲线()y f x =在点()()00,x f x 处的切线与x 轴平行,求该切线方程;(2)讨论曲线()y f x =与直线y a =的交点个数.10.(2023下·山东菏泽·高二校考阶段练习)给定函数()()3exf x x =+(1)判断()f x 的单调性并求极值;(2)讨论()()R f x m m =∈解的个数.四、证明题。
求解导数零点问题的四种策略

2020年第12期中学数学教学参考(下旬)'想方法求解导数零点问题的四种策略毛正燕(贵州省安顺市西秀区高级中学)余登高(贵州省安顺市西秀区岩腊乡三股水学校)摘要:导数零点是导数综合应用中非常重要的知识,其考查形式多样,问题设置一般较为复杂,尤其是导 数零点不可求问题。
本文给出四种策略下求解导数零点问题的示例,展现了一种策略独领风骚,多种策略 助力的解题过程。
关键词:导数;零点定理;函数文章编号:1002-2171 (2020) 12-0054-03导数作为高中数学中的重点内容,一直是高考函数压轴题涉及的主要知识。
导数零点问题考查形式多样,问题设置较为复杂,常常给学生的解题带来障碍。
下面笔者通过示例说明求解该类问题的四种策略。
1 一个定理——零点存在性定理在判断导函数/(:c)在给定区间U,6)内的单调 性后,可在区间(a,6)内取两个特殊值(往往取比较容易计算的具有明显特征的数值),计算对应的导函数值,并与〇进行比较,结合函数的零点存在性定理,就 可以得到导函数/'(x)在给定区间(a,6)内存在唯一 的零点。
例1(2019年高考数学全国卷I文科第20题第(I )问)已知函数 /(x) =2sin x—xcos x— x, /U)为/(X)的导函数。
证明:/(1)在区间(0,7T)内存在唯一零点。
分析:先对函数/(I)求导,然后对导函数再次求导,利用函数的单调性与最值,结合函数的零点存在性定理证明。
证明:由题意可得/^(工)=2cos x— [cos x+x(— sin x)] —l=cos x+xsin x一1,设函数g(x)=//(x)=c o s x+xsin x—1,贝!j(:r) =:ccos x。
当时,单调递增;当(|,7T)时,^/(:r)<0,g(jc)单调递减。
则函数g O)的最大值为 —1>〇。
又 g(0) =0,g(7t)=—2,可得 d f) .g(7t)<〇,即/'(f) ./(兀)<〇,所以根据函数的零点存在性定理,可知/(:c)在区间(0, 7t)内存在唯一零点。
导数问题中虚设零点的三个技巧

技巧1 整体代换,将超越式转化为普通式.
如果f′(x)是超越形式(对字母进行了有限次初等超越运算 包 括 无 理 数 乘 方、指 数、对 数、三 角、反三角等运算的解析式,称 为 初 等 超 越 式,简称超越式),并且f′(x)的零点是存在的但 无法求出,这时可采用虚设零点法,逐步分析出“零点”所在的范围 和满足 的 关 系 式,然后分析出相应的函数的单调性,最后通过恰当 运用函数的极值与零点所满足的“关系”推演出所要求的结果.通过 这种形式化的合理 代 换 或 推 理,谋求一种整体的转换和过渡,从 而将超越式转化为普通式,有效破解求解或推理证明中的难点.
Байду номын сангаас
如果f′(x)不是超越形式,而是可转化为二次函数,这时很容易想 当然,用求根公式把零点求出来,代入极 值 中 去.但 接 下 来 要 么 计 算 偏 烦,要 么无法化简,复杂的算式让人无处下手,导致后继工
作无法开展.正所谓“思 路 简 单,过 程 烦 人”.这 时有两个处理 技巧.
如果问 题 要 求 解(或 求 证)的结论与参数有关,利用关系式f′(x)=0 (大部 分 情 况 可 转 化 为二次方程),在保留 参 数 的 情 况 下,不 断 地 把 零 点的次数降到不可再降为止,再结合其他条件,建立含参数的方程(或 不 等 式),就可求出参数的值或参数的范围.
导数问题中虚设零点的三个 技巧
导数是解决函 数 单 调 性、极 值、最 值、不 等 式证 明等问题的“利 器”.与导数有关的数学问题往往成 为高考函数压轴题,求解这些压轴题时,经常会碰到 导函数具有零点但求解相对比较繁杂甚至无法求解的 情形.此时,可以将这个零点只设出来而不必求出来, 然后谋求一种整体的转换和过渡,再结合其他条件, 从而最终获得问题的解决.我们称这种解题方法为 “虚设零点”法.
高考数学专题一 微专题8 利用导数研究函数零点问题

④当x∈(π,+∞)时,ln(x+1)>1, 所以f(x)<0,从而f(x)在(π,+∞)上没有零点. 综上,f(x)有且仅有2个零点.
跟踪训练1 (2023·常德模拟)已知函数f(x)=x2+2-aln x(a∈R). x
(1)若f(x)在x=2处取得极值,求f(x)在点(1,f(1))处的切线方程;
因为 f(x)=x2+2x-aln x,x>0,
2x3-ax-2
所以 f′(x)= x2
(x>0),
令g(x)=2x3-ax-2,则g′(x)=6x2-a,
由 a>0,g′(x)=0,可得 x= a6,
所以 g(x)在0,
a6上单调递减,在
a6,+∞上单调递增,
由于 g(0)=-2<0,故当 x∈0,
a6时,g(x)<0,
又g(1)=-a<0,故g(x)在(1,+∞)上有唯一零点,设为x1,
从而可知f(x)在(0,x1)上单调递减,在(x1,+∞)上单调递增,
由于f(x)有唯一零点x0,故x1=x0,且x0>1,
所以有 2x30-ax0-2=0,x20+x20-aln x0=0,
联立得 2ln x0-x30-3 1-1=0,
(*)
令 h(x)=2ln x-x3-3 1-1,可知 h(x)在(1,+∞)上单调递增,
由于 h(2)=2ln 2-170<2×0.7-170<0,h(3)=2ln 3-2296>2×1-2296>0, 故方程(*)的唯一解,即f(x)的唯一零点x0∈(2,3),故[x0]=2.
考点二 由零点个数求参数范围
③若a<-1, (ⅰ)当x∈(0,+∞)时, 则g′(x)=ex-2ax>0, 所以g(x)在(0,+∞)上单调递增, 又g(0)=1+a<0,g(1)=e>0, 所以存在m∈(0,1), 使得g(m)=0,即f′(m)=0, 当x∈(0,m)时,f′(x)<0,f(x)单调递减, 当x∈(m,+∞)时,f′(x)>0,f(x)单调递增, 所以当x∈(0,m)时,f(x)<f(0)=0,
高考数学复习 《导数中的隐零点问题》

衢州三中微专题系列之《导数中的隐零点问题》衢州三中 李娜 知识要点求解导数题时,经常会碰到导函数存在零点但求解比较繁杂甚至无法求解的情形,我们将这类问题称为“隐零点”问题。
这类问题我们一般采用设而不求,通过整体代换和过渡,再结合其他条件,从而使问题得到解决。
解隐零点问题的一般策略:第一步:用零点存在性定理(或用二分法进一步缩小零点的范围)判断导函数零点的存在性。
列出零点方f ′(x 0)=0,并结合f(x)的单调性得到零点的范围。
第二步:将零点方程f ′(x 0)=0适当变形,整体代入最值式子中进行化简证明、求最值、解不等式等。
典例分析【类型一】不含参函数的隐零点问题(构造关于隐零点的单一函数进行求解)已知不含参函数,导函数方程的根存在,却无法求出,设方程的根为,则①有关系式成立,②注意确定的合适范围.例1 已知函数f (x )=(ae x﹣a ﹣x )e x(a ≥0,e=2.718…,e 为自然对数的底数),若f (x )≥0对于x ∈R 恒成立. (1)求实数a 的值;(2)证明:f (x )存在唯一极大值点x 0,且.【解答】(1)a=1,证明略;(2)证明:由(1)f (x )=e x(e x﹣x ﹣1),故f'(x )=e x(2e x﹣x ﹣2),令h (x )=2e x﹣x ﹣2,h'(x )=2e x﹣1, 所以h (x )在(﹣∞,ln)单调递减,在(ln,+∞)单调递增,h (0)=0,h (ln )=2eln ﹣ln ﹣2=ln2﹣1<0,h (﹣2)=2e ﹣2﹣(﹣2)﹣2=>0,∵h (﹣2)h (ln)<0由零点存在定理及h (x )的单调性知,方程h (x )=0在(﹣2,ln)有唯一根,)(x f 0)('=x f 0)('=x f 0x 0)('0=x f 0x设为x0且2e x0﹣x0﹣2=0,从而h(x)有两个零点x0和0,所以f(x)在(﹣∞,x0)单调递增,在(x0,0)单调递减,在(0,+∞)单调递增,从而f(x)存在唯一的极大值点x0即证,由2e x0﹣x0﹣2=0得e x0=,x0≠﹣1,∴f(x0)=e x0(e x0﹣x0﹣1)=(﹣x0﹣1)=(﹣x0)(2+x0)≤()2=,取等不成立,所以f(x0)<得证,又∵﹣2<x0<ln,f(x)在(﹣∞,x0)单调递增所以f(x0)>f(﹣2)=e﹣2[e﹣2﹣(﹣2)﹣1]=e﹣4+e﹣2>e﹣2>0得证,从而0<f(x0)<成立.例2 已知函数.(1)讨论的最值;(2)若,求证:..【解析】(1)依题意,得.①当时,,所以在上单调递减,故不存在最大值和最小值;②当时,由得,.当变化时,与的变化情况如下表(2)当,,设,则,设,由,可知在上单调递增.因为,,所以存在唯一的,使得.当变化时,与的变化情况如下表:由上表可知,在上单调递减,在上单调递增,故当时,取得极小值,也是最小值,即.由可得,所以.又,所以,所以,即,所以不等式成立.[来源:]【类型二】含参函数的隐零点问题对于含参数的隐零点问题,在整体代换时,需要利用零点方程得出参数与零点的关系,将参数用零点表示,再结合具体问题进行求解、已知含参函数,其中为参数,导函数方程的根存在,却无法求出,设方程的根为,则①有关系式成立,该关系式给出了的关系,②注意确定的合适范围,往往和的范围有关. 例3已知函数+3()ex mf x x =-,()()ln 12g x x =++.(Ⅰ)若曲线()y f x =在点()()00f ,处的切线斜率为1,求实数m 的值; (Ⅱ)当1m ≥时,证明:()3()f x g x x >-.),(a x f a 0),('=a x f 0)('=x f 0x 0)('0=x f a x ,00x a解:(Ⅰ)因为+3()ex mf x x =-,所以+2()e 3x m f x x '=-.………………………1分因为曲线()y f x =在点()()00f ,处的切线斜率为1,所以()0e 1mf '==,解得0m =.…………………………………………………2分(Ⅱ) 设()()+eln 12x mh x x =-+-,则()+1e 1x m h x x '=-+. 设()+1e 1x m p x x =-+,则()()+21e 01x m p x x '=+>+. 所以函数()p x =()+1e 1x m h x x '=-+在()+∞-1,上单调递增.………………6分 因为1m ≥,所以()()1e+1e 1e e e e e 10mmmmm m h ----+-+'-+=-=-<,()0e 10m h '=->.所以函数()+1e 1x m h x x '=-+在()+∞-1,上有唯一零点0x ,且()01e ,0m x -∈-+. …8分因为()00h x '=,所以0+01e1x mx =+,即()00ln 1x x m +=--.………………9分 当()00,x x ∈时,()0h x '<;当()0,x x ∈+∞时,()0h x '>.所以当0x x =时,()h x 取得最小值()0h x .……………………………………10分 所以()()()0+00e ln 12x mh x h x x ≥=-+-00121x m x =++-+ ()0011301x m x =+++->+. 综上可知,当1m ≥时,()3()f x g x x >-.……………………………………12分例4 已知函数f (x )=e x+a﹣lnx (其中e=2.71828…,是自然对数的底数). (Ⅰ)当a=0时,求函数a=0的图象在(1,f (1))处的切线方程; (Ⅱ)求证:当时,f (x )>e+1.【解答】(Ⅰ)解:∵a=0时,∴,∴f(1)=e,f′(1)=e﹣1,∴函数f(x)的图象在(1,f(1))处的切线方程:y﹣e=(e﹣1)(x﹣1),即(e﹣1)x﹣y+1=0;(Ⅱ)证明:∵,设g(x)=f′(x),则,∴g(x)是增函数,∵e x+a>e a,∴由,∴当x>e﹣a时,f′(x)>0;若0<x<1⇒e x+a<e a+1,由,∴当0<x<min{1,e﹣a﹣1}时,f′(x)<0,故f′(x)=0仅有一解,记为x0,则当0<x<x0时,f′(x)<0,f(x)递减;当x>x0时,f′(x)>0,f(x)递增;∴,而,记h(x)=lnx+x,则,⇔﹣a<⇔h(x0)<h(),而h(x)显然是增函数,∴,∴.综上,当时,f(x)>e+1.巩固练习1.已知函数.(1)求的极值点;(2)证明:.2.已知函数f(x)=x2﹣(a﹣2)x﹣alnx(a∈R).(Ⅰ)求函数y=f(x)的单调区间;(Ⅱ)当a=1时,证明:对任意的x>0,f(x)+e x>x2+x+2.3.已知函数的导函数为,且.(1)求函数的极值.(2)若,且对任意的都成立,求的最大值.4.已知函数.(Ⅰ)当a=2时,(i)求曲线y=f(x)在点(1,f(1))处的切线方程;(ii)求函数f(x)的单调区间;(Ⅱ)若1<a<2,求证:f(x)<﹣1.参考答案1.(2)设,则,设,则方程在区间内恰有一个实根.设方程在区间内的实根为,即.所以,当时,,此时单调递减;当时,,此时单调递增.所以由在上是减函数知,,故.综上.`2. 【解答】(Ⅰ)函数f(x)的定义域是(0,+∞),f′(x)=2x﹣(a﹣2)﹣=…(2分)当a≤0时,f′(x)>0对任意x∈(0,+∞)恒成立,所以,函数f(x)在区间(0,+∞)单调递增;…(4分)当a>0时,由f′(x)>0得x>,由f′(x)<0,得0<x<,所以,函数在区间(,+∞)上单调递增,在区间(0,)上单调递减;(Ⅱ)当a=1时,f(x)=x2+x﹣lnx,要证明f(x)+e x>x2+x+2,只需证明e x﹣lnx﹣2>0,设g(x)=e x﹣lnx﹣2,则问题转化为证明对任意的x>0,g(x)>0,令g′(x)=e x﹣=0,得e x=,容易知道该方程有唯一解,不妨设为x0,则x0满足e x0=,当x变化时,g′(x)和g(x)变化情况如下表x (0,x0)x0(x0,∞)g′(x)﹣0 +g(x)递减递增g(x)min=g(x0)=e x0﹣lnx0﹣2=+x0﹣2,因为x0>0,且x0≠1,所以g(x)min>2﹣2=0,因此不等式得证.3.(2)由(1)及题意知,对任意的都成立.令,则.令,则,所以函数在上为增函数,因为,,所以方程存在唯一实根,且,.故当时,,即;当时,,即.所以函数在上单调递减,在上单调递增,所以,所以,,又,故的最大值为.4.【解答】(Ⅰ)当a=2时,,定义域为(0,+∞),,f′(1)=﹣1﹣2=﹣3,f'(1)=2﹣2=0;所以切点坐标为(1,﹣3),切线斜率为0所以切线方程为y=﹣3;(ii)令g(x)=2﹣lnx﹣2x2,所以g(x)在(0,+∞)上单调递减,且g(1)=0所以当x∈(0,1)时,g(x)>0即f'(x)>0所以当x∈(1,+∞)时,g(x)<0即f'(x)<0综上所述,f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞).(Ⅱ)证明:f(x)<﹣1,即设,,设φ(x)=﹣ax2﹣lnx+2所以φ'(x)在(0,+∞)小于零恒成立即h'(x)在(0,+∞)上单调递减因为1<a<2,所以h'(1)=2﹣a>0,h'(e2)=﹣a<0,所以在(1,e2)上必存在一个x0使得,即,所以当x∈(0,x0)时,h'(x)>0,h(x)单调递增,当x∈(x0,+∞)时,h'(x)<0,h(x)单调递减,所以,因为,所以,令h(x0)=0得,因为1<a<2,所以,,因为,所以h(x0)<0恒成立,即h(x)<0恒成立,综上所述,当1<a<2时,f(x)<﹣1.。
高考数学:函数零点问题的处理方法
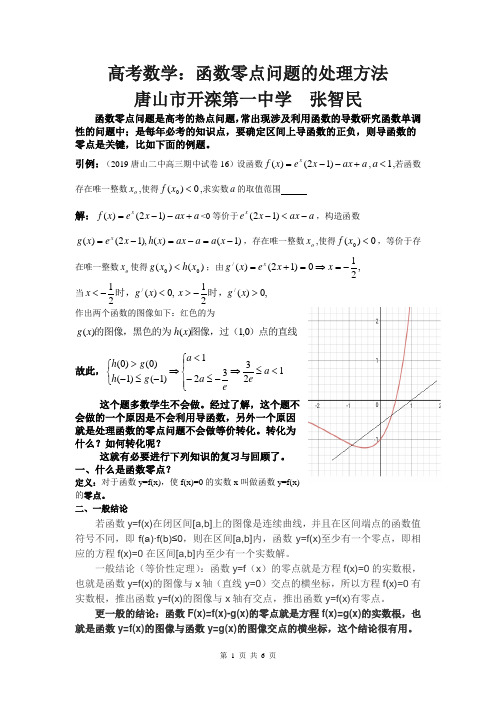
高考数学:函数零点问题的处理方法唐山市开滦第一中学 张智民函数零点问题是高考的热点问题,常出现涉及利用函数的导数研究函数单调性的问题中;是每年必考的知识点,要确定区间上导函数的正负,则导函数的零点是关键,比如下面的例题。
引例:(2019唐山二中高三期中试卷16)设函数a ax x e x f x+--=)12()(,1<a ,若函数存在唯一整数o x ,使得0)(0<x f ,求实数a 的取值范围解:a ax x e x f x +--=)12()(<0等价于a ax x e x -<-)12(,构造函数)1()(),12()(-=-=-=x a a ax x h x e x g x ,存在唯一整数o x ,使得0)(0<x f ,等价于存在唯一整数o x 使得)()(00x h x g <;由,210)12()(/-=⇒=+=x x e x g x当,0)(21/<-<x g x 时,,0)(21/>->x g x 时, 作出两个函数的图像如下:红色的为)点的直线图像,过(的图像,黑色的为0,1)()(x h x g故此,123321)1()1()0()0(<≤⇒⎪⎩⎪⎨⎧-≤-<⇒⎩⎨⎧-≤->a e e a a g h g h 这个题多数学生不会做。
经过了解,这个题不会做的一个原因是不会利用导函数,另外一个原因就是处理函数的零点问题不会做等价转化。
转化为什么?如何转化呢?这就有必要进行下列知识的复习与回顾了。
一、什么是函数零点?定义:对于函数y=f(x),使f(x)=0的实数x 叫做函数y=f(x)的零点。
二、一般结论若函数y=f(x)在闭区间[a,b]上的图像是连续曲线,并且在区间端点的函数值符号不同,即f(a)·f(b)≤0,则在区间[a,b]内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在区间[a,b]内至少有一个实数解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学导数中的零点问题解决方法-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN导数中的零点问题解决方法解决零点问题,需要采用数形结合思想,根据函数的图像或者趋势图像找出符合题意的条件即可,因此用导数判断出单调性作出函数图像或趋势图像至关重要。
一、能直接分离参数的零点题目此类问题较为简单,分离之后函数无参数,则可作出函数的准确图像,然后上下移动参数的值,看直线与函数交点个数即可。
例1.已知函数(),()ln a f x x g x x x =+=,若关于x 的方程2()()2g x f x e x=-只有一个实数根,求a 的值。
解析:22()ln ()22g x x f x e a x ex x x =-⇒=-+,令2ln ()2x h x x ex x=-+,'21ln ()22x h x x e x-=-+,令'()0h x =,则x e = 当0x e <<时,'()0h x >,()h x 单调递增;当x e >时,'()0h x <,()h x 单调递 减,2max 1()()h x h e e e==+ 注意这里()h x 的单调性不是硬解出来的,因为你会发现'()h x 的式子很复杂,但是如果把()h x 当成两个函数的和,即2ln (),()2x m x n x x ex x==-+,此时(),()m x n x 的单调性和极值点均相同,因此可以整体判断出()h x 的单调性和极值点。
所以21a e e=+(注意:有一个根转化为图像只有一个交点即可) 二、不能直接分离参数的零点问题(包括零点个数问题)这里需要注意几个转化,以三次函数为例,若三次函数有三个不同的零点,则函数必定有两个极值点,且极大值和极小值之积为负数,例如()f x 在区间(0,1)上有零点,此时并不能确定零点的个数,只能说明至少有一个零点,若函数在区间上单调,只需要用零点存在性定理即可,但是若函数在区间上不单调,则意味着()f x 在区间(0,1)上存在极值点。
在解决此类问题时常用的知识是零点存在定理和极限的相关知识,但必不可少的是求出函数的趋势图像,然后根据趋势图像找符合零点问题的条件即可,这里需要说明一下,参数影响零点的个数问题主要有两个方向,一是参数影响单调性和单调区间的个数,二是参数影响函数的极值或最值,而通过这两个方向就可以影响函数的趋势图像,进而影响零点的个数,因此分类讨论思想在此类问题中必不可少。
例2.已知函数32()31f x ax x =-+,若()f x 存在唯一的零点0x ,且00x >,则a 的取值范围是2()31f x x =-+有两个零点,不符合题意当0a >时,'2()363(2)f x ax x x ax =-=-,若'()0f x >,则20x x a><或若'()0f x <,则20x a<<,此时函数在(,0)-∞上单增,(1)20f a -=--< 此时在(,0)-∞上存在零点,不符合题意。
当0a <时,若'()0f x >,则20x a <<,若'()0f x <,则2x a<或0x > 此时要保证函数存在唯一的正零点,则2()0f a>,解得(,2)a ∈-∞- 注意:如果不是的大题没必要分类讨论,做出符合题意的图像反推即可例3.已知函数2()ln 2f x x x b x =++--在区间1[,]e e上有两个不同零点,求实数b 的取值范围。
解析:2'222(2)(1)()x x x x f x x x +-+-==,可知函数()f x 在(0,1)上递减,在(1,)+∞上递增,要保证函数()f x 在1[,]e e上有两个不同的零点,根据函数的趋势图像可 得必须满足1()02(1)011()0f e f b e e f e ⎧≥⎪⎪<⇒<≤+-⎨⎪≥⎪⎩例4.已知函数32()f x x ax b =++(1)讨论()f x 的单调性;(2)若b c a =-,当函数()f x 有三个不同的零点时,a 的取值范围恰好是33(,3)(1,)(,)22-∞-⋃⋃+∞,求c 的值。
解析:(1)当0a =时,()f x 在R 上单调递增当0a >时,()f x 在2(,),(0,)3a -∞-+∞上单调递增,在2(,0)3a -上单调递减;当0a <时,()f x 在2(,0),(,)3a -∞-+∞上单调递增,在2(0,)3a -上单调递减;(2)只有当0a ≠时才有可能满足()f x 有三个零点因为()f x 有两个极值点324(0),()327a fb f a b =-=+,要满足有三个零点必须满足2(0)()03a f f ⋅-<,结合bc a =-可得330044002727a a a a c a a c ><⎧⎧⎪⎪⎨⎨-+>-+<⎪⎪⎩⎩或,因为()f x 恰有三个零点时,a 的取值范围是33(,3)(1,)(,)22-∞-⋃⋃+∞ 所以题目可以转化为34027a a c -+>在33(1,)(,)22a ∈⋃+∞上恒成立,且34027a a c -+<在(,3)a ∈-∞-上恒成立 设34()27h a a a c =-+,对其求导可得()h a 在33(,),(,)22-∞-+∞递增,在33(,)22-递减,因此()h a 图像必须满足以下趋势: 所以(3)0101311()02f c c c f -≤⎧-≤⎧⎪⇒⇒=⎨⎨-≥≥⎩⎪⎩ 验证:当1c =时,322()1(1)[(1)1]f x x ax a x x a x a =++-=++-+- 函数有三个不等的实数根,所以2()(1)10h x x a x a =+-+-=有两个不相等且不等于-1的实数根,所以必须满足033(,3)(1,)(,)(1)022a h ∆>⎧⇒∈-∞-⋃⋃+∞⎨-≠⎩ 综上,1c =第一问很简单,但是是解决第二问必要的前提,第二问题目中函数有三个不同的零点,但是题目中有两个参数,类似于双参数问题解决方法,最后将两个参数中已知的那个作为自变量,然后转化为恒成立问题即可,三个零点意味着两个极值的积为负值,然后再根据不同的a 的取值转化为函数恒成立问题,通过函数的趋势图像即可解出符合题意的条件。
但是很多同学缺省最后检验的步骤,同时也不理解为什么需要验证,如果不验证,则即便满足有三个零点,此时的a 的取值范围也可以不是题目中给出的范围,注意这个恰字就说明了必须要进行最后的验证。
例6.已知函数2()1x f x e ax bx =---(1)设()g x 是函数()f x 的导函数,求函数()g x 在区间[0,1]上的最小值;(2)若(1)0f =,函数()f x 在区间(0,1)内有零点,求a 的取值范围。
解析:(1)'()2,()2x x g x e ax b g x e a =--=-当0a ≤时,'()0g x >,()g x 在[0,1]递增,min ()(0)1g x g b ==-当0a >时,令'()0g x =,ln 2x a =,此时0,1,ln 2a 位置不确定因此需要讨论Case1:当ln21a ≥时,2e a ≥,此时()g x 在[0,1]递减, min ()(1)2g x g e a b ==-- Case1:当ln 20a ≤时,12a ≤,此时()g x 在[0,1]上递增, min ()(0)1g x g b ==- Case3:当0ln 21a <<时,即122e a <<,此时 min ()(ln 2)22ln 2g x g a a a a b ==-- 综上所述min 11()21()22ln 2()222()2b a e g x a a a b a e e a b a ⎧-≤⎪⎪⎪=--<<⎨⎪⎪--≥⎪⎩(2)本题目隐藏一个条件即(0)0f =,又知(1)0f =,所以如果()f x 在区间(0,1)内有零点,则()f x 在(0,1)内至少有两个极值点或者至少有三个单调区间或者说()g x 在(0,1)内不可以恒正也不可以恒负。
(要好好理解这句话)题目中有两个参数,根据(1)0f =可得1b e a =--,若当12a ≤或2e a ≥时,函数()g x 为单调函数,不符合题意,故a 只能在1(,)22e 内取值,此时min ()32ln 21g x a a a e =--+,且要满足32ln 210a a a e --+<才可令'()32ln 21,()12ln 2h x x x x e h x x =--+=-,根据单调性可知min ()10h x e =+<,此时min g()0x <成立,因此要保证()f x 在(0,1)上至少有三个单调区间,则需要满足条件122(0)021(1)0e a g e a g ⎧<<⎪⎪>⇒-<<⎨⎪>⎪⎩题目第二问的关键是理解原函数单调区间的个数和导函数零点个数之间的关系,建议同学们在做第二问的时候把相应的图作出来就明白了。
总结:处理零点问题不管是处在函数的题目里面还是导数的题目里面,方法都是一样的,都是需要用到数形结合思想,通过判断单调性,既可以大致的将函数的趋势图像都作出来,然后根据题目的要求作出合适的函数图像以及列出不等式即可。
