网络图知识点
(完整版)高中物理知识点总结和知识网络图(大全)
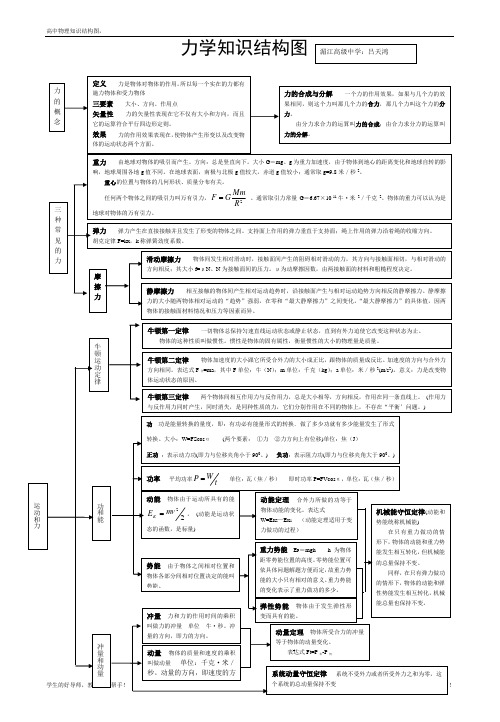
力学知识结构图匀变速直线运动基本公式:V t =V 0+atS=V 0t+21at 2as V V t2202+=20tV V V +=运动的合成与分解 已知分运动求合运动叫运动的合成,已知合运动求分运动叫运动的分解。
运动的合成与分解遵守平行四边形定则平抛物体的运动特点:初速度水平,只受重力。
分析:水平匀速直线运动与竖直方向自由落体的合运动。
规律:水平方向 Vx = V 0,X=V 0t竖直方向 Vy = gt ,y =221gt 合 速 度 V t =,22y x V V +与x 正向夹角tg θ=xy V v匀速率圆周运动特点:合外力总指向圆心(又称向心力)。
描述量:线速度V ,角速度ω,向心加速度α,圆轨道半径r ,圆运动周期T 。
规律:F= mr V2=m ω2r = mr T 224π物体 的 运 动A 0 t/sX/cm T λx/cm y/cmA 0V天体运动问题分析1、行星与卫星的运动近似看作匀速圆周运动遵循万有引力提供向心力,即 =m =m ω2R=m( )R 2、在不考虑天体自转的情况下,在天体表面附近的物体所受万有引力近似等于物体的重力,F 引=mg,即 =mg,整理得GM=gR 2。
3、考虑天体自传时:(1)两极 (2)赤道平均位移:02tv v s vt t +==模型题2.非弹性碰撞:碰撞过程中所产生的形变不能够完全恢复的碰撞;碰撞过程中有机械能损失.非弹性碰撞遵守动量守恒,能量关系为:12m 1v 21+12m 2v 22>12m 1v 1′2+12m 2v 2′2 3.完全非弹性碰撞:碰撞过程中所产生的形变完全不能够恢复的碰撞;碰撞过程中机械能损失最多.此种情况m 1与m 2碰后速度相同,设为v ,则:m 1v 1+m 2v 2=(m 1+m 2)v 系统损失的动能最多,损失动能为 ΔE km =12m 1v 21+12m 2v 22-12(m 1+m 2)v 21.弹性碰撞:碰撞过程中所产生的形变能够完全恢复的碰撞;碰撞过程中没有机械能损失.弹性碰撞除了遵从动量守恒定律外,还具备:碰前、碰后系统的总动能相等,即 12m 1v 21+12m 2v 22=12m 1v 1′2+12m 2v 2′2特殊情况:质量m 1的小球以速度v 1与质量m 2的静止小球发生弹性正碰,根据动量守恒和动能守恒有m 1v 1=m 1v 1′+m 2v 2′,12m 1v 21=12m 1v 1′2+12m 2v 2′2.碰后两个小球的速度分别为: v 1′=m 1-m 2m 1+m 2v 1,v 2′=2m 1m 1+m 2v 1动量碰撞如图所示,在水平光滑直导轨上,静止着三个质量为m =1 kg 的相同的小球A 、B 、C 。
六年级数学网络图知识点

六年级数学网络图知识点引言:在六年级数学学习中,网络图是一个重要的知识点。
网络图主要是用来表示事物之间的关系,并且能够帮助我们解决实际生活中的问题。
本文将介绍六年级学生需要了解和掌握的网络图知识点,帮助他们建立起良好的数学基础。
一、网络图概述网络图是数学中的一个重要工具,它能够清晰地表示事物之间的联系和相互作用关系。
网络图主要由节点和边组成,节点表示事物,边表示它们之间的关系。
在网络图中,可以找出事物之间的最短路径、关键节点等信息。
二、网络图的表示方法1. 邻接矩阵表示法:邻接矩阵是一种二维数组来表示网络图。
如果两个节点之间存在边,则在对应的矩阵位置上标记为1,否则标记为0。
通过邻接矩阵,可以清晰地看出节点之间的连接情况。
2. 邻接表表示法:邻接表是一种链表的形式来表示网络图。
对于每一个节点,用链表的方式存储与之相邻的节点。
通过邻接表,可以快速地找到某个节点的相邻节点。
三、网络图的常见应用网络图在实际生活中有着广泛的应用,下面列举了一些常见的应用场景。
1. 城市道路规划:可以使用网络图来表示城市中道路的连接情况,进而规划出最短路径或者交通拥堵情况。
2. 电路布线:网络图可以用来表示电路中元器件之间的连接情况,可以帮助我们设计出电路布线方案。
3. 社交网络分析:通过网络图可以清晰地表示出社交网络中人与人之间的关系,可以用于社交网络分析、信息传播等研究。
四、网络图的相关概念1. 连通图和非连通图:如果网络图中的任意两个节点之间都存在路径,则该网络图是连通图;如果存在孤立节点,即某个节点无法到达其他节点,则该网络图是非连通图。
2. 最短路径:网络图中两个节点之间的最短路径是指节点之间路径长度最短的路径。
3. 关键节点:在网络图中,某个节点的删除会导致整个网络图变为非连通图,则该节点被称为关键节点。
五、总结网络图是六年级数学中的重要知识点,通过学习和掌握网络图,能够培养学生的逻辑思维能力和问题解决能力。
第一章 行列式主要知识点网络图

11
例3 计算4阶行列式(加边法)
1+x 1 1 1− x 1 1 1 1 1 1 1 1
D=
1+y 1 1 1− y
,
解 显然当x=0或y=0时,D=0,当x≠0和y ≠ 0时,利 x=0 y=0 D 0 x≠0 y 0 用展开定理,
1 1 0 1+x D= 0 0 0 1 1 1 1 1 1 1 1 1 1 1 -1 x 1 0 1 0 1 0
n
i = j, i ≠ j. i = j, i ≠ j.
第1章
●定义法 ●递推法 ●加边法
计 算
●数学归纳法 ●公式法 ●拆项法 ●乘积法 ●析因子法
应 用
●克拉默法则 ●齐次线性方程组有非零解的充要条件
3
二、主要定理
1、行列式的展开定理.
第1章
a11
a12 ⋯ a1n
a21 a22 ⋯ a2n D= ⋯ ⋯ ⋯ ⋯ an1 an2 ⋯ ann
a11
0
⋯
0 0 ⋮
a22 ⋯ a2n a21 a22 ⋯ = ⋮ ⋱ ⋮ ⋮ ⋮ ⋱ 0 ⋯ ann
an1 an2 ⋯ ann
= a11a22 ⋯ann .
0 0 D= ⋮ ⋯ 0 a1n a11 a12 ⋯ a1n ⋯ a2n−1 a2n a21 a22 ⋯ 0 = ⋰ ⋮ ⋮ ⋮ ⋮ ⋰ ⋮ an1 0 ⋯ 0
1-x 1 1 = -1 0 −x 0 0 1 1+y 1 -1 0 0 y 0 1 1 1-y -1 0 0 0 −y
12
1 1
1
1
1 0 = x2 y2. 0
0 x 0 0 = 0 0 -x 0 0 0 0 0 0 0
项目管理-单-双代号网络图

例1 将下图所示双代号网络图改画成单代号网络图。
双代号网络图单代号网络图例2 比较例1的两张网络图,说明其主要差别在哪里?两种网络图的主要差别有以下两点:1. 双代号网络图中的每一项工作都由两个对应的代号来表示;而单代号网络图中的每一项工作则由一个独立的代号来表示,每一个节点都表示一项工作。
2. 双代号网络图中,工作间的逻辑关系可借助于虚工作(虚箭号)来表示,而在单代号网络图中,工作间的逻辑关系则用箭号来表示,因此单代号网络图中不会出现虚箭号。
一幅单代号网络图中,只会出现两个虚设的工作节点,那就是表示计划开始的虚工作节点和表示计划结束的虚工作节点。
例3 下图为一单号网络图,网络图各圆圈中横线上边的数字是工作代号,横线下边的数字是工作持续时间。
试用图上计算法计算各工作的最早可能开始时间ES i、最迟必须开始时间LS i、总时差TF i和局部时差FF i,标记出关键线路并确定总工期。
解:根据题意用图算法推算出的各工作时间参数,见上图,关键线路用粗箭号表示。
该网络图的计划总工期为11天。
例4 某工程的单代号网络如下图所示。
试用表上计算法求出网络图中各工作的ES i、EF、LS i、LF i、TF i、和FF i;确定关键工作并在图上说明关键线路;确定计划总工期(注:i下图中圆圈内横线上边为工作代号,横线下边为工作持续时间)。
解:用表算法推算了各工作的时间参数见下表。
该网络图的关键线路共有3条,它们分别为:计划总工期为19天。
一、网络计划技术基本概念二、网络图的绘制:知识点总结与归纳三、网络计划时间参数的计算(一)、网络计划时间参数的概念(二)、双代号网络计划时间参数的计算双代号网络计划的时间参数既可以按工作计算,也可以按节点计算。
A.按工作计算法所谓按工作计算法,就是以网络计划中的工作为对象,直接计算各项工作的时间参数。
这些时间参数包括:工作的最早开始时间和最早完成时间、工作的最迟开始时间和最迟完成时间、工作的总时差和自由时差。
项目管理网络图练习

【项目管理】一级建造师网络图知识点一、双代号网络图6个时间参数的计算方法(图上计算法)从左向右累加,多个紧前取大,计算最早开始结束;从右到左累减,多个紧后取小,计算最迟结束开始。
自由时差=紧后工作最早开始时间最小值-本工作最早完成时间上方之差或下方之差是总时差。
总结:1、以终点节点为完成节点的工作,总时差等于自由时差2、计划工期等于计算工期,关机线路上的关键工作总时差为0,自由时差也为0;3、本工作的总时差等于紧后工作总时差最小值与本工作自由时差之和。
二、双代号时标网络图双代号时标网络计划是以时间坐标为尺度编制的网络计划,以实箭线表示工作,以虚箭线表示虚工作,以波形线表示工作的自由时差。
双代号时标网络图1、关键线路在时标双代号网络图上逆方向看,没有出现波形线的线路为关键线路(包括虚工作)。
如图中①→②→⑥→⑧2、时差计算1)自由时差双代号时标网络图自由时差的计算很简单,就是该工作箭线上波形线的长度。
如A工作的FF=0,B工作的FF=1但是有一种特殊情况,很容易忽略。
如上图,E工作的箭线上没有波形线,但是E工作与其紧后工作之间都有时间间隔,此时E工作的自由时差=E与其紧后工作时间间隔的最小值,即E的自由时差为1。
2)总时差。
总时差的简单计算方法:计算哪个工作的总时差,就以哪个工作为起点工作(一定要注意,即不是从头算,也不是从该工作的紧后算,而是从该工作开始算),寻找通过该工作的所有线路,然后计算各条线路的波形线的长度和,该工作的总时差=波形线长度和的最小值。
还是以上面的网络图为例,计算E工作的总时差:以E工作为起点工作,通过E工作的线路有EH和EJ,两条线路的波形线的和都是2,所以此时E的总时差就是2。
再比如,计算C工作的总时差:通过C工作的线路有三条,CEH,波形线的和为4;CEJ,波形线的和为4;CGJ,波形线的和为1,那么C的总时差就是1。
大家只要掌握如下知识点一般可以对付网络方面的考题。
1 总时差=最迟完成时间—尚需完成时间。
双代号网络图六个参数计算方法(各实务专业通用)

双代号⽹络图六个参数计算⽅法(各实务专业通⽤)寄语:不管⼀建、⼆建,双代号是必考点,再复杂的⽹络图也能简单化,本⼯作室整理了三页纸供⼤家快速掌握,希望⼤家多学多练,掌握该知识点,⾄少⼗分收⼊囊中。
双代号⽹络图六个参数计算的简易⽅法⼀、⾮常有⽤的要点:任何⼀个⼯作总时差≥⾃由时差⾃由时差等于各时间间隔的最⼩值(这点对六时参数的计算⾮常⽤⽤)关键线路上相邻⼯作的时间间隔为零,且⾃由时差=总时差最迟开始时间—最早开始时间(最⼩)关键⼯作:总时差最⼩的⼯作最迟完成时间—最早完成时间(最⼩)在⽹络计划中,计算⼯期是根据终点节点的最早完成时间的最⼤值⼆、双代号⽹络图六时参数我总结的计算步骤(⽐书上简单得多)①②t 过程做题次序:1 4 5 ES LS TF236FSLFFF步骤⼀:1、A 上再做 A 下2、做的⽅向从起始⼯作往结束⼯作⽅向;3、起点的 A 上=0,下⼀个的 A 上=前⼀个的 A 下当遇到多指向时,要取数值⼤的 A 下A 上4、 A 下=A 上+t 过程(时间)步骤⼆:1、 B 下再做 B 上2、做的⽅向从结束点往开始点3、结束点 B 下=T (需要的总时间结束点 B 上=T-t 过程(时间)4、 B 下=前⼀个的 B 上(这⾥的前⼀个是从终点起算的)遇到多指出去的时,取数值⼩的 B 上B 上=B 下—t 过程(时间)步骤三:总时差=B 上—A 上=B 下—A 下如果不相等,你就是算错了步骤四:⾃由时差=紧后⼯作 A 上(取最⼩的)—本⼯作 A 下=紧后⼯作的最早开始时间—本⼯作的最迟开始时间(有多个紧后⼯作的取最⼩值)例:紧后⼯作A 上有9 和11 取⼩值9,=9-9(本⼯作的A 下)=0从左到右计算,遇到有⼤⼩时取⼤;沿线累加,逢圈取⼤。
从右到左计算,遇到有⼤⼩时取⼩;逆线累减,逢圈取⼩。
高中数学知识点分类网络结构图
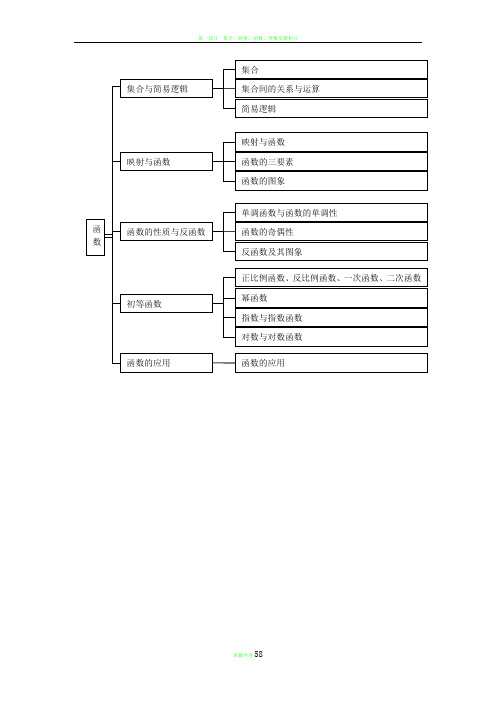
;;=⇔⊆=⇔⊆=⇔⊆A B B A B A B A A B A B I A Bn-个A中元素有n个,则A的子集共有2n个,真子集有21集合间的运算2n R a +∈则2n n a n a ++≥平均值不等式2nnn a a n++≥当且仅当2,,)n 时取等号1111221n j n j n n n a b a b a b a b a b a b ++≤++≤+++,n Z 是∀,,nx 是区间1122)()()()n n n n q x q f x q f x q f x ++≤+++,,,1n i q R q +∈=∑)。
上凸函数不等号转向.1}n ma+仍是等比数列,其公比为)lim n n a ++=sin sin αtan tan 1tan tan α±2(AB x =,则a ⊥b2PP 所成比112222221cos ||||a b a b a ba b a b a ++⋅⋅==⋅+212()(x x y y =-+-空间向量的直角坐标运算律若123(,,a a a a =,12(,,b b b b =则①113(a b a b +=+,11(a b a b -=-123(,)()a a a R λλλλλ=∈,11a b a b ⋅=+②13//a ba b λλ⇔=,110a b a b ⊥⇔+若111(,,)A x y z 则2(AB x =-模长公式若12(,,a a a a =21||a a a a a =⋅=+空间向量的运算,,(OB OA AB a b BA OA OB a b OP a λλ=+=+=-=-=空间向量的加减与数乘OB OA AB =+=a +b ,AB OB OA =-,,(OP λ=a a b + c ⑶数乘分配律:λ(a + ) =λa +λb .平行六面体向量的数乘积||||cos ,a b a b a b ⋅=⋅⋅<>空间向量数乘积的性质①||cos ,a e a a e ⋅=<>.②0a b a b ⊥⇔⋅=.③2||a a a =⋅.空间向量数量积运算律①()()()a b a b a b λλλ⋅=⋅=⋅②a b b a ⋅=⋅(交换律) ③()a b c a b a c ⋅+=⋅+⋅(分配律)④e a = a e =|a |cos ,a e⑤ab a b = 0⑥当a 与b 同向时,a b = |a ||b |;当a 与b 反向时,a b = |a ||b |.特别的a a = |a |2或||a a a =⋅⑦cos ,||||a ba b a b ⋅=Bα∈,则l αβ=且l,则A、B、C 。
网络图绘制及双代号网络计划时间参数的计算

网络图绘制及双代号网络计划时间参数的计算(1)一、网络计划技术基本概念二、网络图的绘制:知识点总结与归纳三、网络计划时间参数的计算(一)、网络计划时间参数的概念(二)、双代号网络计划时间参数的计算双代号网络计划的时间参数既可以按工作计算,也可以按节点计算。
A.按工作计算法所谓按工作计算法,就是以网络计划中的工作为对象,直接计算各项工作的时间参数。
这些时间参数包括:工作的最早开始时间和最早完成时间、工作的最迟开始时间和最迟完成时间、工作的总时差和自由时差。
此外,还应计算网络计划的计算工期。
为了简化计算,网络计划时间参数中的开始时间和完成时间都应以时间单位的终了时刻为标准。
如第3天开始即是指第3天终了(下班)时刻开始,实际上是第4天上班时刻才开始;第5天完成即是指第5天终了(下班)时刻完成。
下面是按工作计算法计算时间参数的过程。
1.计算工作的最早开始时间和最早完成时间工作最早开始时间和最早完成时间的计算应从网络计划的起点节点开始,顺着箭线方向依次进行。
其计算步骤如下:(1)以网络计划起点节点为开始节点的工作,当未规定其最早开始时间时,其最早开始时间为零。
(2)工作的最早完成时间可利用公式(3—3)进行计算:EFi-J=ESi-j+Di—j (3—3)(3)其他工作的最早开始时间应等于其紧前工作最早完成时间的最大值。
(4)网络计划的计算工期应等于以网络计划终点节点为完成节点的工作的最早完成时间的最大值。
2.确定网络计划的计划工期网络计划的计划工期应按公式(3—1)或公式(3—2)确定。
①当已规定了要求工期时,计划工期不应超过要求工期,即:Tp≤Tr(3—1)②当未规定要求工期时,可令计划工期等于计算工期,即:Tp=Tc(3—2)3.计算工作的最迟完成时间和最迟开始时间工作最迟完成时间和最迟开始时间的计算应从网络计划的终点节点开始,逆着箭线方向依次进行。
其计算步骤如下:(1)以网络计划终点节点为完成节点的工作,其最迟完成时间等于网络计划的计划工期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、双代号网络图6个时间参数的计算方法(图上计算法)
从左向右累加,多个紧前取大,计算最早开始结束;
从右到左累减,多个紧后取小,计算最迟结束开始。
紧后左上-自己右下=自由时差。
上方之差或下方之差是总时差。
计算某工作总时差的简单方法:①找出关键线路,计算总工期;
②找出经过该工作的所有线路,求出最长的时间
③该工作总时差=总工期-②
二、双代号时标网络图
双代号时标网络计划是以时间坐标为尺度编制的网络计划,以实箭线表示工作,以虚箭线
表示虚工作,以波形线表示工作的自由时差。
双代号时标网络图:
file:///C:/DOCUME~1/ADMINI~1/LOCALS~1/Temp/WML`ZUS$8NCVU(%7M%5VUJI.gif
此图无法上传,可去QQ:288216291 群共享里重新下载。
QQ:288216291
1、关键线路
在时标双代号网络图上逆方向看,没有出现波形线的线路为关键线路(包括虚工作)。
如图中①→②→⑥→⑧
2、时差计算
1)自由时差
双代号时标网络图自由时差的计算很简单,就是该工作箭线上波形线的长度。
如A工作的FF=0,B工作的FF=1
但是有一种特殊情况,很容易忽略。
如上图,E工作的箭线上没有波形线,但是E工作与其紧后工作之间都有时间间隔,此时E工作的自由时差=E与其紧后工作时间间隔的最小值,即E的自由时差为1。
2)总时差。
总时差的简单计算方法:
计算哪个工作的总时差,就以哪个工作为起点工作(一定要注意,即不是从头算,也不是从该工作的紧后算,而是从该工作开始算),寻找通过该工作的所有线路,然后计算各条线路的波形线的长度和,该工作的总时差=波形线长度和的最小值。
还是以上面的网络图为例,计算E工作的总时差:
以E工作为起点工作,通过E工作的线路有EH和EJ,两条线路的波形线的和都是2,所以此时E的总时差就是2。
再比如,计算C工作的总时差:通过C工作的线路有三条,CEH,波形线的和为4;CEJ,波形线的和为4;CGJ,波形线的和为1,那么C的总时差就是1。
