北师大版2020八年级数学下册期末综合复习培优测试题C(附答案)

合集下载

2020年北师大版八年级下册数学《期末考试题》(附答案解析)

北师大版八年级下册数学期末测试卷学校________ 班级________ 姓名________ 成绩________一、选择题（共10个小题，每小题3分，共30分）1.下列图形不是中心对称图形的是( )A. B. C. D.2.若代数式14a -在实数范围内有意义，则实数a 的取值范围为( ) A. 4a =B. 4a >C. 4a <D. 4a ≠3.不等式x ≤-1的解集在数轴上表示正确的是（） A. B. C.D.4.下列多项式中，不是完全平方式的是( ) A. 214x x -+B. 22961a b ab -+C.221394m mn n ++ D. 431025x x --5.已知实数a ，b ，若a ＞b ，则下列结论错误的是 A. a-7＞b-7 B. 6+a ＞b+6C.55a b ＞ D. -3a ＞-3b6.关于x 的分式方程522x mx x -=++有增根，则m 的值为( ) A. 0B. 5-C. 2-D. 7-7.如图，在平面直角坐标系中，一次函数y ax b =+经过(0,2)A ，(3,0)B 两点，则不等式0ax b +>解是( )A. 0x >B. 3x >C. 0x <D. 3x <8.一个菱形的两条对角线的长分别为5和8，那么这个菱形的面积是( )A. 40B. 20C. 10D. 259. 下列命题中，真命题是（） A. 对角线相等的四边形是矩形 B. 对角线互相垂直的四边形是菱形C. 对角线互相平分的四边形是平行四边形D. 对角线互相垂直平分的四边形是正方形 10.关于x 的分式方程2322x m mx x++=--的解为正实数，则实数m 的取值范围是( )A. 6m <-且2m ≠B. 6m >且2m ≠C. 6m <且2m ≠-D. 6m <且2m ≠二、填空题：（共4个小题，每小题4分，共16分）11.计算：2111x x x -=++__．12.因式分解：224a a -=___．13.一个n 边形的内角和为1080°，则n=________.14.如图，将△AOB 绕点O 按逆时针方向旋转45°后得到△A′OB′，若∠AOB=15°，则∠AOB′的度数是______．三、解答题（共6小题，满分54分）15.(1)解不等式组：23112(2)2x x x +>⎧⎪⎨-≤+⎪⎩(2)解方程：11222x x x -=---. 16.先化简，再求值：22211m m m -+-÷（m ﹣1﹣11m m -+），其中m 3 17.如图，在△ABC 中，∠B ＝30°，边AB 的垂直平分线分别交AB 和BC 于点D ，E ，且AE 平分∠BAC ．（1）求∠C 的度数；（2）若CE ＝1，求AB 的长．18.如图，在平面直角坐标系中，Rt △ABC 的三个顶点分别是A （﹣3，2），B （0，4），C （0，2）．（1）将△ABC 以点C 为旋转中心旋转180°，画出旋转后对应的△A 1B 1C 1，平移△ABC ，若点A 的对应点A 2的坐标为（0，﹣4），画出平移后对应的△A 2B 2C 2；（2）若将△A 1B 1C 1绕某一点旋转可以得到△A 2B 2C 2，请直接写出旋转中心的坐标．19.一个批发兼零售的文具店规定：凡一次购买铅笔300枝以上，（不包括300枝），可以按批发价付款，购买300枝以下，（包括300枝）只能按零售价付款．小明来该店购买铅笔，如果给八年级学生每人购买1枝，那么只能按零售价付款，需用120元，如果购买60枝，那么可以按批发价付款，同样需要120元，（1）这个八年级的学生总数在什么范围内？（2）若按批发价购买6枝与按零售价购买5枝的款相同，那么这个学校八年级学生有多少人？ 20.如图，正方形ABCD 中，AB ＝4，点E 是对角线AC 上的一点，连接DE ．过点E 作EF ⊥ED ，交AB 于点F ，以DE 、EF 为邻边作矩形DEFG ，连接AG ．（1）求证：矩形DEFG 是正方形；（2）求AG +AE 的值；（3）若F 恰为AB 中点，连接DF 交AC 于点M ，请直接写出ME 的长．四、填空题（共5小题，每小题4分，满分20分）21.当k ＝_____时，100x 2﹣kxy +49y 2是一个完全平方式．22.已知不等式组2123x a x b -<⎧⎨->⎩的解集是11x -<<，则(1)(1)a b ++的值是的___．23.某商品的标价比成本高%p ，当该商品降价出售时，为了不亏本，降价幅度不得超过%d ，若用p 表示d ，则d =___．24.已知：如图，AD 、BE 分别是ABC ∆的中线和角平分线，AD BE ⊥，2AD BE ==，则AC 的长等于__．25.如图，矩形纸片ABCD 中，AD ＝5，AB ＝3．若M 为射线AD 上的一个动点，将△ABM 沿BM 折叠得到△NBM ．若△NBC 是直角三角形．则所有符合条件的M 点所对应的AM 长度的和为_____．二、解答题：（共3个小题，共30分）26.某学校计划组织全校1500名师生外出参加集体活动．经过研究，决定租用当地租车公司一共60辆A 、B 两种型号客车作为交通工具．下表是租车公司提供给学校有关两种型号客车的载客量和租金信息：型号载客量租金单价 A30人/辆 400元/辆 B20人/辆300元/辆注：载客量指的是每辆客车最多可载该校师生的人数．学校租用A 型号客车x 辆，租车总费用为y 元． (1)求y 与x 的函数解析式，请直接写出x 的取值范围；(2)若要使租车总费用不超过22000元，一共有几种租车方案？并结合函数性质说明哪种租车方案最省钱？ 27.菱形ABCD 中，∠BAD ＝60°，BD 是对角线，点E 、F 分别是边AB 、AD 上两个点，且满足AE ＝DF ，连接BF与DE相交于点G．（1）如图1，求∠BGD的度数；（2）如图2，作CH⊥BG于H点，求证：2GH＝GB+DG；（3）在满足（2）的条件下，且点H在菱形内部，若GB＝6，CH＝43，求菱形ABCD的面积．28.在平面直角坐标系中，过点C（1，3）、D（3，1）分别作x轴的垂线，垂足分别为A、B．（1）求直线CD和直线OD的解析式；（2）点M为直线OD上的一个动点，过M作x轴的垂线交直线CD于点N，是否存在这样的点M，使得以A、C、M、N为顶点的四边形为平行四边形？若存在，求此时点M的横坐标；若不存在，请说明理由；（3）若△AOC沿CD方向平移（点C在线段CD上，且不与点D重合），在平移的过程中，设平移距离为2t，△AOC与△OBD重叠部分的面积记为s，试求s与t的函数关系式．答案与解析一、选择题（共10个小题，每小题3分，共30分）1.下列图形不是中心对称图形的是( )A. B. C. D.【答案】D 【解析】【分析】根据中心对称图形的概念求解．【详解】A 、是中心对称图形．故不能选； B 、是中心对称图形．故不能选； C 、是中心对称图形．故不能选； D 、不是中心对称图形．故可以选．故选D【点睛】本题考查了中心对称图形的概念：中心对称图形是要寻找对称中心，旋转180度后与原图重合． 2.若代数式14a -在实数范围内有意义，则实数a 的取值范围为( ) A. 4a = B. 4a > C. 4a <D. 4a ≠【答案】D 【解析】根据“分式有意义，分母不为0”得： a-4≠0 解得：a≠4. 故选D.3.不等式x ≤-1的解集在数轴上表示正确的是（） A. B. C.D.【答案】B【解析】【分析】根据数轴的表示方法表示即可.（注意等于的时候是实心的原点.）【详解】根据题意不等式x ≤-1的解集是在-1的左边部分，包括-1. 故选B.【点睛】本题主要考查实数的数轴表示，注意有等号时应用实心原点表示. 4.下列多项式中，不是完全平方式的是( ) A. 214x x -+B. 22961a b ab -+C.221394m mn n ++ D. 431025x x --【答案】D 【解析】【分析】根据完全平方公式即可求出答案．【详解】A.原式21()2x =-，故A 错误；B.原式2(31)ab =-，故B 错误；C.原式21(3)2m n =+，故C 错误；故选D ．【点睛】本题考查完全平方公式，解题的关键是熟练运用完全平方公式. 5.已知实数a ，b ，若a ＞b ，则下列结论错误的是 A. a-7＞b-7 B. 6+a ＞b+6 C.55a b ＞ D. -3a ＞-3b【答案】D 【解析】A.∵a ＞b ，∴a-7＞b-7，∴选项A 正确；B.∵a ＞b ，∴6+a ＞b+6，∴选项B 正确；C.∵a ＞b ，∴55a b ＞，∴选项C 正确； D.∵a ＞b ，∴-3a ＜-3b ，∴选项D 错误. 故选D.6.关于x 的分式方程522x mx x -=++有增根，则m 的值为( )A. 0B. 5-C. 2-D. 7-【答案】D 【解析】分析：增根是化为整式方程后产生的不适合分式方程的根．所以应先确定增根的可能值，让最简公分母x+2=0，得到x=-2，然后代入化为整式方程的方程算出m 的值即可．详解：方程两边都乘（x+2），得：x-5=m ， ∵原方程有增根， ∴最简公分母：x+2=0，解得x=-2，当x=-2时，m=-7．故选D ．点睛：此题考查了分式方程增根的知识．注意增根问题可按如下步骤进行： ①让最简公分母为0确定增根； ②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．7.如图，在平面直角坐标系中，一次函数y ax b =+经过(0,2)A ，(3,0)B 两点，则不等式0ax b +>的解是( )A. 0x >B. 3x >C. 0x <D. 3x <【答案】D 【解析】【分析】将A （0，2），B （3，0）代入y=ax+b 得出a ，b 值，再代入ax+b ＞0即可求出答案. 【详解】将A （0，2），B （3，0）代入y=ax+b{b=23a+b=0得b=22a=-3⎧⎨⎩，即2-x+2>03，x<3.正确选D.【点睛】根据函数的图象和交点坐标即可求得结果.此题考查了反比例函数与一次函数的交点问题，关键是注意掌握数形结合思想的应用.8.一个菱形的两条对角线的长分别为5和8，那么这个菱形的面积是( ) A. 40 B. 20 C. 10 D. 25【答案】B 【解析】根据菱形的面积=对角线之积的一半，可知菱形的面积为5×8÷2=20. 故选B.9. 下列命题中，真命题是（） A. 对角线相等的四边形是矩形 B. 对角线互相垂直的四边形是菱形 C. 对角线互相平分的四边形是平行四边形 D. 对角线互相垂直平分的四边形是正方形【答案】C 【解析】试题分析：A 、两条对角线相等且相互平分的四边形为矩形；故本选项错误； B 、对角线互相垂直的平行四边形是菱形；故本选项错误； C 、对角线互相平分的四边形是平行四边形；故本选项正确； D 、对角线互相垂直平分且相等的四边形是正方形；故本选项错误．故选C ．10.关于x 的分式方程2322x m mx x++=--的解为正实数，则实数m 的取值范围是( )A. 6m <-且2m ≠B. 6m >且2m ≠C. 6m <且2m ≠-D. 6m <且2m ≠【答案】D 【解析】【分析】先根据分式方程的解法，求出用m 表示x 的解，然后根据分式有解，且解为正实数构成不等式组求解即可.【详解】2322x m mx x++=-- 去分母，得 x+m+2m=3（x-2）解得x=62m -+ ∵关于x 的分式方程2322x m mx x++=--的解为正实数 ∴x-2≠0，x ＞0 即62m -+≠2，62m -+＞0，解得m≠2且m ＜6 故选D.点睛：此题主要考查了分式方程的解和分式方程有解的条件，用含m 的式子表示x 解分式方程，构造不等式组是解题关键.二、填空题：（共4个小题，每小题4分，共16分）11.计算：2111x x x -=++__．【答案】1x - 【解析】【分析】原式利用同分母分式的减法法则计算即可求出值．【详解】原式=()()2x 1x 1x 1x 1x 1x 1+--==-++. 故答案为:x-1.【点睛】本题考查了分式的加减法，熟练掌握运算法则是解题的关键． 12.因式分解：224a a -=___．【答案】2a （a-2）【解析】【详解】2242(2)-=-a a a a13.一个n 边形的内角和为1080°，则n=________. 【答案】8【解析】【分析】直接根据内角和公式()2180n-⋅︒计算即可求解.【详解】（n﹣2）•180°=1080°，解得n=8．故答案为8．【点睛】主要考查了多边形的内角和公式.多边形内角和公式：()2180n-⋅︒.14.如图，将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，若∠AOB=15°，则∠AOB′的度数是______．【答案】30°【解析】【分析】根据旋转的性质旋转前后图形全等以及对应边的夹角等于旋转角，进而得出答案即可．【详解】解：∵将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，∴∠A′OA=45°，∠AOB=∠A′OB′=15°，∴∠AOB′=∠A′OA﹣∠A′OB=45°﹣15°=30°故答案为30°．【点睛】考查旋转的性质，找出旋转角是解题的关键.三、解答题（共6小题，满分54分）15.(1)解不等式组：23112(2)2xx x+>⎧⎪⎨-≤+⎪⎩(2)解方程：11222xx x-=---.【答案】(1)16x-<…；(2)无解．【解析】【分析】（1）分别求出不等式组中两不等式的解集，找出两解集的公共部分即可；（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【详解】(1)由①得：1x >-，由②得：6x „，则不等式组的解集为16x -<„；(2)去分母得：1124x x -=--+，解得：2x =，经检验2x =是增根，分式方程无解．【点睛】此题考查了解分式方程，以及解一元一次不等式组，熟练掌握运算法则是解本题的关键．16.先化简，再求值：22211m m m -+-÷（m ﹣1﹣11m m -+），其中m ＝3．【答案】原式＝1m ，3．【解析】【详解】试题分析：先将所给分式按照运算顺序化简为1m，然后把3m =代入计算即可．试题解析：原式＝22(1)1(1)(1)11m m m m m m -+⋅-+--+＝1(1)m m m --＝1m； ∴当3m =时，原式＝333= 考点：分式的化简求值．17.如图，在△ABC 中，∠B ＝30°，边AB 的垂直平分线分别交AB 和BC 于点D ，E ，且AE 平分∠BAC ．（1）求∠C 的度数；（2）若CE ＝1，求AB 的长．【答案】（1）90C =o ∠；（2）23AB =【解析】【分析】（1）先由线段垂直平分线的性质及∠B=30°求出∠BAE=30°，再由AE 平分∠BAC 可得出∠EAC=∠BAE=30°，由三角形内角和定理即可求出∠C 的度数．（2）先求出∠EAC ＝30°，在Rt △AEC 中，利用特殊角的三角函数求解直角三角形，可解得AC 的长为3，再在Rt △ABC 中，利用特殊角的三角函数求解直角三角形，可解得AB 的长．【详解】（1）∵DE 是线段AB 的垂直平分线，∠B ＝30°，∴∠BAE ＝∠B ＝30°，∵AE 平分∠BAC ，∴∠EAC ＝∠BAE ＝30°，即∠BAC ＝60°，∴∠C ＝180°﹣∠BAC ﹣∠B ＝180°﹣60°﹣30°＝90°．（2）∵∠C ＝90°，∠B ＝30°，∴∠BAC ＝60°∵AE 平分∠BAC∴∠EAC ＝30°∵CE ＝1，∠C ＝90°∴AC ＝tan 30EC o=3， ∴AB ＝sin 30AC o =23．【点睛】本题考查的是线段垂直平分线的性质及会利用特殊的三角函数值解直角三角形是解答此题的关键． 18.如图，在平面直角坐标系中，Rt △ABC 的三个顶点分别是A （﹣3，2），B （0，4），C （0，2）．（1）将△ABC 以点C 为旋转中心旋转180°，画出旋转后对应的△A 1B 1C 1，平移△ABC ，若点A 的对应点A 2的坐标为（0，﹣4），画出平移后对应的△A 2B 2C 2；（2）若将△A 1B 1C 1绕某一点旋转可以得到△A 2B 2C 2，请直接写出旋转中心的坐标．【答案】（1）图形见解析；（2）P 点坐标为（32，﹣1）．【解析】【分析】（1）分别作出点A、B关于点C的对称点，再顺次连接可得；由点A的对应点A2的位置得出平移方向和距离，据此作出另外两个点的对应点，顺次连接可得；（2）连接A1A2、B1B2，交点即为所求．【详解】（1）如图所示：A1（3，2）、C1（0，2）、B1（0，0）；A2（0，-4）、B2（3，﹣2）、C2（3，﹣4）．（2）将△A1B1C1绕某一点旋转可以得到△A2B2C2，旋转中心的P点坐标为（32，﹣1）．【点睛】本题主要考查作图-旋转变换、平移变换，解题关键是根据旋转变换和平移变换的定义作出变换后的对应点．19.一个批发兼零售的文具店规定：凡一次购买铅笔300枝以上，（不包括300枝），可以按批发价付款，购买300枝以下，（包括300枝）只能按零售价付款．小明来该店购买铅笔，如果给八年级学生每人购买1枝，那么只能按零售价付款，需用120元，如果购买60枝，那么可以按批发价付款，同样需要120元，（1）这个八年级的学生总数在什么范围内？（2）若按批发价购买6枝与按零售价购买5枝的款相同，那么这个学校八年级学生有多少人？【答案】（1）240人＜八年级学生数≤300人（2）这个学校八年级学生有300人．【解析】【分析】答：八年级学生总数为人(1)关系式为：学生数≤300，学生数+60>300列式求值即可；(2)批发价为每支x元，则零售价为每支元,列方程求解【详解】解：(1)有已知，240人<总数≤300人；(2)批发价为每支x元，则零售价为每支元可列方程求得x=经检验x=符合题意学生总数为人20.如图，正方形ABCD中，AB＝4，点E是对角线AC上的一点，连接DE．过点E作EF⊥ED，交AB于点F，以DE、EF为邻边作矩形DEFG，连接AG．（1）求证：矩形DEFG是正方形；（2）求AG+AE的值；（3）若F恰为AB中点，连接DF交AC于点M，请直接写出ME的长．【答案】（1）见解析；（2）AE+AG＝＝42；（3）EM＝52．【解析】【分析】（1）如图，作EM⊥AD于M，EN⊥AB于N．只要证明△EMD≌△ENF即可解决问题；（2）只要证明△ADG≌△CDE，可得AG=EC即可解决问题；（3）如图，作EH⊥DF于H．想办法求出EH，HM即可解决问题；【详解】（1）如图，作EM⊥AD于M，EN⊥AB于N．∵四边形ABCD是正方形，∴∠EAD＝∠EAB，∵EM⊥AD于M，EN⊥AB于N，∴EM＝EN，∵∠EMA＝∠ENA＝∠DAB＝90°，∴四边形ANEM是矩形，∴∠MEN＝∠DEF＝90°，∴∠DEM＝∠FEN，∵∠EMD＝∠ENF＝90°，∴△EMD≌△ENF，∴ED＝EF，∵四边形DEFG是矩形，∴四边形DEFG是正方形．（2）∵四边形DEFG是正方形，四边形ABCD是正方形，∴DG＝DE，DC＝DA＝AB＝4，∠GDE＝∠ADC＝90°，∴∠ADG＝∠CDE，∴△ADG≌△CDE，∴AG＝CE，∴AE+AG＝AE+EC＝AC＝2AD＝42．（3）如图，作EH⊥DF于H．∵四边形ABCD是正方形，∴AB＝AD＝4，AB∥CD，∵F是AB中点，∴AF＝FB∴DF∵△DEF 是等腰直角三角形，EH ⊥AD ，∴DH ＝HF ，∴EH ＝12DF ∵AF ∥CD ，∴AF ：CD ＝FM ：MD ＝1：2，∴FM ＝3，∴HM ＝HF ﹣FM在Rt △EHM 中，EM 3．【点睛】本题考查正方形的性质、全等三角形的判定和性质、矩形的性质和判定、解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．四、填空题（共5小题，每小题4分，满分20分）21.当k ＝_____时，100x 2﹣kxy +49y 2是一个完全平方式．【答案】±140．【解析】【分析】利用完全平方公式的结构特征判断即可得到结果．完全平方公式（a ±b ）2= a 2±2ab+b 2.【详解】∵100x 2﹣kxy+49y 2是一个完全平方式，∴k ＝±140．故答案为±140．【点睛】此题考查了完全平方式，熟练掌握完全平方公式是解本题关键．22.已知不等式组2123x a x b -<⎧⎨->⎩的解集是11x -<<，则(1)(1)a b ++的值是的___．【答案】-2【解析】【分析】先求出两个不等式的解集，再求其公共解，然后根据不等式组的解集列出求出a 、b 的值，再代入代数式进行计算即可得解．【详解】2123x a x b -<⎧⎨->⎩①②，由①得，12a x +<，由②得，23x b >+，所以，不等式组的解集是1232a b x ++<<， Q 不等式组的解集是11x -<<，231b ∴+=-，112a +=，解得1a =，2b =-，所以，(1)(1)(11)(21)2a b ++=+-+=-．故答案2-．【点睛】本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．23.某商品的标价比成本高%p ，当该商品降价出售时，为了不亏本，降价幅度不得超过%d ，若用p 表示d ，则d =___．【答案】1%p d p =+ 【解析】本题主要考查列代数式. 此题中最大的降价率即是保证售价和成本价相等，可以把成本价看作单位1，根据题意即可列式．解：设成本价是1，则（1+p%）（1-d%）=1． 1-d%=11%p +， 1%p d p =+24.已知：如图，AD 、BE 分别是ABC ∆的中线和角平分线，AD BE ⊥，2AD BE ==，则AC 的长等于__．【答案】35 【解析】【分析】过D 点作DF ∥BE ，则DF=12BE=1，F 为EC 中点，在Rt △ADF 中求出AF 的长度，根据已知条件易知G 为AD 中点，因此E 为AF 中点，则AC=32AF ．【详解】过D 点作//DF BE ，AD Q 是ABC ∆的中线，AD BE ⊥，F ∴为EC 中点，AD DF ⊥，2AD BE ==Q ，则1DF =，22215AF =+BE Q 是ABC ∆的角平分线，AD BE ⊥，ABG DBG ∴∆≅∆，G ∴为AD 中点，E ∴为AF 中点，AE EF CF ∴==，3352AC AF ∴== 35．【点睛】本题考查了三角形中线、三角形中位线定理和角平分线的性质以及勾股定理的应用，作出辅助线构建直角三角形是解题的关键．25.如图，矩形纸片ABCD 中，AD ＝5，AB ＝3．若M 为射线AD 上的一个动点，将△ABM 沿BM 折叠得到△NBM ．若△NBC 是直角三角形．则所有符合条件的M 点所对应的AM 长度的和为_____．【答案】10．【解析】【分析】根据四边形ABCD 为矩形以及折叠的性质得到∠A=∠MNB=90°，由M 为射线AD 上的一个动点可知若△NBC 是直角三角形，∠NBC=90°与∠NCB=90°都不符合题意，只有∠BNC=90°．然后分 N 在矩形ABCD 内部与 N 在矩形ABCD 外部两种情况进行讨论，利用勾股定理求得结论即可．【详解】∵四边形ABCD 为矩形，∴∠BAD ＝90°，∵将△ABM 沿BM 折叠得到△NBM ，∴∠MAB ＝∠MNB ＝90°．∵M 为射线AD 上的一个动点，△NBC 是直角三角形，∴∠NBC ＝90°与∠NCB ＝90°都不符合题意，∴只有∠BNC ＝90°．①当∠BNC ＝90°，N 在矩形ABCD 内部，如图1．∵∠BNC ＝∠MNB ＝90°，∴M 、N 、C 三点共线，∵AB ＝BN ＝3，BC ＝5，∠BNC ＝90°，∴NC＝4．设AM＝MN＝x，∵MD＝5﹣x，MC＝4+x，∴在Rt△MDC中，CD2+MD2＝MC2，32+（5﹣x）2＝（4+x）2，解得x＝1；当∠BNC＝90°，N在矩形ABCD外部时，如图2．∵∠BNC＝∠MNB＝90°，∴M、C、N三点共线，∵AB＝BN＝3，BC＝5，∠BNC＝90°，∴NC＝4，设AM＝MN＝y，∵MD＝y﹣5，MC＝y﹣4，∴在Rt△MDC中，CD2+MD2＝MC2，32+（y﹣5）2＝（y﹣4）2，解得y＝9，则所有符合条件的M点所对应的AM和为1+9＝10．故答案为10．【点睛】本题考查了翻折变换（折叠问题），矩形的性质以及勾股定理，难度适中．利用数形结合与分类讨论的数学思想是解题的关键．二、解答题：（共3个小题，共30分）26.某学校计划组织全校1500名师生外出参加集体活动．经过研究，决定租用当地租车公司一共60辆A、B 两种型号客车作为交通工具．下表是租车公司提供给学校有关两种型号客车的载客量和租金信息：注：载客量指的是每辆客车最多可载该校师生的人数．学校租用A 型号客车x 辆，租车总费用为y 元．(1)求y 与x 的函数解析式，请直接写出x 的取值范围；(2)若要使租车总费用不超过22000元，一共有几种租车方案？并结合函数性质说明哪种租车方案最省钱？【答案】(1)y 与x 的函数解析式为10018000(3060)y x x =+剟；(2)一共有11种租车方案，当租用A 型车辆30辆，B 型车辆30辆时，租车费用最省钱．【解析】【分析】（1）根据题意可以得到y 与x 的函数关系式，然后根据总人数可以求出x 的取值范围，本题得以解决；（2）根据题意可以得到关于x 的不等式，然后根据一次函数的性质即可解答本题．【详解】(1)由题意可得，400300(60)10018000y x x x =+-=+，3020(60)1500x x +-Q …，解得，30x …，即y 与x 的函数解析式为10018000(3060)y x x =+剟； (2)由题意可得，1001800022000x +„，解得，40x „，3040x ∴剟，x Q 为整数，30x ∴=、31、32、33、⋯、40，∴共有11种租车方案，10018000y x =+Q ，y ∴随x 的增大而增大，∴当30x =时，y 取得最小值，此时21000y =，6030x -=，答：一共有11种租车方案，当租用A 型车辆30辆，B 型车辆30辆时，租车费用最省钱．【点睛】本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和不等式的性质解答．27.菱形ABCD 中，∠BAD ＝60°，BD 是对角线，点E 、F 分别是边AB 、AD 上两个点，且满足AE ＝DF ，连接BF 与DE 相交于点G ．（1）如图1，求∠BGD 的度数；（2）如图2，作CH ⊥BG 于H 点，求证：2GH ＝GB +DG ；（3）在满足（2）的条件下，且点H 在菱形内部，若GB ＝6，CH ＝43，求菱形ABCD 的面积．【答案】（1）∠BGD ＝120°；（2）见解析；（3）S 四边形ABCD ＝3．【解析】【分析】（1）只要证明△DAE ≌△BDF ，推出∠ADE=∠DBF ，由∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°，推出∠BGD=180°-∠BGE=120°；（2）如图3中，延长GE 到M ，使得GM=GB ，连接BD 、CG ．由△MBD ≌△GBC ，推出DM=GC ，∠M=∠CGB=60°，由CH ⊥BG ，推出∠GCH=30°，推出CG=2GH ，由CG=DM=DG+GM=DG+GB ，即可证明2GH=DG+GB ；（3）解直角三角形求出BC 即可解决问题；详解】（1）解：如图1﹣1中，∵四边形ABCD 是菱形，∴AD ＝AB ，∵∠A ＝60°，∴△ABD 是等边三角形，∴AB ＝DB ，∠A ＝∠FDB ＝60°，在△DAE 和△BDF 中，AD BD A BDF AE DF =⎧⎪∠=∠⎨⎪=⎩，∴△DAE ≌△BDF ，∴∠ADE ＝∠DBF ，∵∠EGB ＝∠GDB+∠GBD ＝∠GDB+∠ADE ＝60°，∴∠BGD ＝180°﹣∠BGE ＝120°．（2）证明：如图1﹣2中，延长GE 到M ，使得GM ＝GB ，连接CG ．∵∠MGB ＝60°，GM ＝GB ，∴△GMB 是等边三角形，∴∠MBG ＝∠DBC ＝60°，∴∠MBD ＝∠GBC ，在△MBD 和△GBC 中，MB GB MBD GBC BD BC =⎧⎪∠=∠⎨⎪=⎩，∴△MBD ≌△GBC ，∴DM ＝GC ，∠M ＝∠CGB ＝60°，∵CH ⊥BG ，∴∠GCH ＝30°，∴CG ＝2GH ，∵CG ＝DM ＝DG+GM ＝DG+GB ，∴2GH ＝DG+GB ．（3）如图1﹣2中，由（2）可知，在Rt △CGH 中，CH ＝GCH ＝30°，∴tan30°＝GH CH， ∴GH ＝4，∵BG ＝6，∴BH ＝2，在Rt △BCH 中，BC=∵△ABD ，△BDC 都是等边三角形，∴S 四边形ABCD ＝2•S △BCD ＝（2＝【点睛】本题考查菱形的性质、等边三角形的判定和性质、全等三角形的判定和性质，直角三角形30度角性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型． 28.在平面直角坐标系中，过点C （1，3）、D （3，1）分别作x 轴的垂线，垂足分别为A 、B ．（1）求直线CD 和直线OD 的解析式；（2）点M 为直线OD 上的一个动点，过M 作x 轴的垂线交直线CD 于点N ，是否存在这样的点M ，使得以A 、C 、M 、N 为顶点的四边形为平行四边形？若存在，求此时点M 的横坐标；若不存在，请说明理由；（3）若△AOC 沿CD 方向平移（点C 在线段CD 上，且不与点D 重合），在平移的过程中，t ，△AOC 与△OBD 重叠部分的面积记为s ，试求s 与t 的函数关系式．【答案】（1）直线OD的解析式为y＝13x；（2）存在．满足条件的点M的横坐标34或214，理由见解析；（3）S＝﹣16（t﹣1）2+13．【解析】【分析】（1）理由待定系数法即可解决问题；（2）如图，设M（m，13m），则N（m，-m+4）．当AC=MN时，A、C、M、N为顶点的四边形为平行四边形，可得|-m+4-13m|=3，解方程即可；（3）如图，设平移中的三角形为△A′O′C′，点C′在线段CD上．设O′C′与x轴交于点E，与直线OD交于点P；设A′C′与x轴交于点F，与直线OD交于点Q．根据S=S△OFQ-S△OEP=12OF•FQ-12OE•PG计算即可；【详解】（1）设直线CD的解析式为y＝kx+b，则有331k bk b+=⎧⎨+=⎩，解得-14kb=⎧⎨=⎩，∴直线CD的解析式为y＝﹣x+4．设直线OD的解析式为y＝mx，则有3m＝1，m＝13，∴直线OD的解析式为y＝13 x．（2）存在．理由：如图，设M（m，13m），则N（m，﹣m+4）．当AC＝MN时，A、C、M、N为顶点的四边形为平行四边形，∴|﹣m+4﹣13m|＝3，解得m＝34或214，∴满足条件的点M的横坐标34或214．（3）如图，设平移中的三角形为△A′O′C′，点C′在线段CD上．设O′C′与x轴交于点E，与直线OD交于点P；设A′C′与x轴交于点F，与直线OD交于点Q．2t，所以水平方向的平移距离为t（0≤t＜2），则图中AF＝t，F（1+t，0），Q（1+t，13+13t），C′（1+t，3﹣t）．设直线O′C′的解析式为y＝3x+b，将C′（1+t，3﹣t）代入得：b＝﹣4t，∴直线O′C′的解析式为y＝3x﹣4t．∴E（43t，0）．联立y＝3x﹣4t与y＝13x，解得x＝32t，∴P（32t，12t）．过点P作PG⊥x轴于点G，则PG＝12t．∴S＝S△OFQ﹣S△OEP＝12OF•FQ﹣12OE•PG＝12（1+t）（13+13t）﹣12•43t•12t＝﹣16（t﹣1）2+13．【点睛】本题考查一次函数综合题、待定系数法、函数图象上点的坐标特征、平行四边形、平移变换、图形面积计算等知识点，有一定的难度．第（2）问中，解题关键是根据平行四边形定义，得到MN=AC=3，由此列出方程求解；第（3）问中，解题关键是求出S的表达式，注意图形面积的计算方法．。

2020年北师大版初二下册数学期末培优检测试题及答案

八年级数学下册期末培优检测试题一．选择题（满分30分，每小题3分）1．式子﹣a，，，，中，分式有（）A．1个B．2个C．3个D．4个2．已知分式的值等于零，则x的值为（）A．1 B．±1 C．﹣1 D．3．一元一次不等式x+1＜2的解集在数轴上表示为（）A．B．C．D．4．下列等式从左到右的变形属于因式分解的是（）A．a2﹣2a+1＝（a﹣1）2B．a（a+1）（a﹣1）＝a3﹣aC．6x2y3＝2x2•3y3D．x2+1＝x（x+）5．计算：1252﹣50×125+252＝（）A．100 B．150 C．10000 D．225006．点M（2，﹣1）先向左平移3个单位长度，再向上平移2个单位长度得到的点的坐标是（）A．（5，1）B．（﹣1，1）C．（﹣1，2）D．（5，﹣3）7．如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1＝2∠2，则∠AEF的度数为（）A．60°B．65°C．72°D．75°8．如图，将一张平行四边形纸片撕开并向两边水平拉伸，若拉开的距离为1cm，AB＝2cm，∠B＝60°，则拉开部分的面积（即阴影面积）是（）A．1cm2 B．cm2 C．cm2 D．2cm29．如图，将矩形ABCD绕点A旋转至矩形AB′C′D′位置，此时AC的中点恰好与D点重合，AB′交CD于点E．若AB＝6，则△AEC的面积为（）A．12 B．4C．8D．610．如图，在△ABC中，AB＝AC，AD为BC边上的高，点E为AC的中点，连接DE．若△ABC 的周长为20，则△CDE的周长为（）A．10 B．12 C．14 D．16二．填空题（满分24分，每小题4分）11．对于有理数m，我们规定[m]表示不大于m的最大整数，例如[1.2]＝1，[3]＝3，[﹣2.5]＝﹣3，若[]＝﹣5，则整数x的取值是．12．因式分解：a3﹣9ab2＝．13．如果代数式m2+2m＝1，那么÷的值为．14．如图，DE是△ABC的边AB的垂直平分线，D为垂足，DE交AC于点E，且AC＝8，BC＝5．则△BEC的周长是．15．如图，四边形ABCD中，AD∥BC，AD＝3，BC＝8，E是BC的中点，点P以每秒1个单位长度的速度从A点出发，沿AD向点D运动；点Q同时以每秒2个单位长度的速度从点C 出发，沿CB向点B运动，点P停止运动时，点Q也随之停止运动．当运动时间t＝秒时，以点P，Q，E，D为顶点的四边形是平行四边形．16．如图，在△ABC中，点M为BC的中点，AD为△ABC的外角平分线，且AD⊥BD，若AB＝6，AC＝9，则MD的长为．三．解答题17．（6分）因式分解：（1）m3﹣16m（2）9a2（x﹣y）+4b2（y﹣x）18．（6分）解下列分式方程（1）＝（2）＝﹣219．如图，在Rt△ABC中，∠A＝30°，BC＝1，点D，E分别是直角边BC，AC的中点，求DE的长．四．解答题20．（7分）先化简：，再从不等式2m﹣1＜6的正整数解中选一个适当的数代入求值．21．（7分）如图，四边形ABCD为平行四边形，∠DAB的平分线AE交CD于点F，交BC的延长线于点E，连接BF．（1）求证：BE＝CD；（2）若BF⊥AE，∠BEA＝45°，AB＝4，则平行四边形ABCD的面积是．22．（7分）某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降，今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为90万元，今年销售额只有80万元．（1）求今年5月份A款汽车每辆售价多少万元；（2）为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知B款汽车每辆进价为7.5万元，每辆售价为10.5万元，A款汽车每辆进价为6万元，若卖出这两款汽车共15辆后，获利不低于39万元，求B款汽车至少卖出多少辆？五．解答题23．（9分）如图，已知△ABC的三个顶点的坐标分别为A（﹣2，3），B（﹣6，0），C（﹣1，0）．（1）画出△ABC关于原点中心对称的△A′B′C′，其中A，B，C的对应点分别为A′，B′，C′；（2）在（1）的基础上，将△A′B′C′向上平移4个单位长度，画出平移后的△A″B″C″，并写出C′的对应点C″的坐标；（3）请直接写出：以A，B．C为顶点的平行四边形ABCD的第四个顶点D的坐标．24．（9分）已知，在△ABC中，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别为D，E．（1）如图1，求证：DE＝AD+BE；（2）如图2，点O为AB的中点，连接OD，OE．请判断△ODE的形状？并说明理由．25．（9分）在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（6，0），点B（0，8）．以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F，记旋转角为α（0°＜α＜90°）．（I）如图①，当α＝30°时，求点D的坐标；（Ⅱ）如图②，当点E落在AC的延长线上时，求点D的坐标；（Ⅲ）当点D落在线段OC上时，求点E的坐标（直接写出结果即可）．参考答案一．选择题1．解：根据分式的概念可得：，，是分式，共有3个故选：C．2．解：根据题意得，所以x＝1．故选：A．3．解：不等式x+1＜2，解得：x＜1，如图所示：故选：B．4．解：A、是因式分解，故本选项符合题意；B、不是因式分解，故本选项不符合题意；C、不是因式分解，故本选项不符合题意；D、不是因式分解，故本选项不符合题意；故选：A．5．解：1252﹣50×125+252＝（125﹣25）2＝10000．故选：C．6．解：点M（2，﹣1）先向左平移3个单位长度，再向上平移2个单位长度得到的点的坐标是（2﹣3，﹣1+2），即（﹣1，1），故选：B．7．解：由翻折的性质可知：∠AEF＝∠FEA′，∵AB∥CD，∴∠AEF＝∠1，∵∠1＝2∠2，设∠2＝x，则∠AEF＝∠1＝∠FEA′＝2x，∴5x＝180°，∴x＝36°，∴∠AEF＝2x＝72°，故选：C．8．解：由平行四边形的一边AB＝2cm，∠B＝60°，可知平行四边形的高为：h＝2sin B＝cm．设拉开后平行四边形的长为acm，拉开前平行四边形的长为bcm，则a﹣b＝1cm，则拉开部分的面积为：S＝ah﹣bh＝（a﹣b）h＝1×＝cm2．故选：C．9．解：∵旋转后AC的中点恰好与D点重合，即AD＝AC′＝AC，∴在Rt△ACD中，∠ACD＝30°，即∠DAC＝60°，∴∠DAD′＝60°，∴∠DAE＝30°，∴∠EAC＝∠ACD＝30°，∴AE＝CE，在Rt△ADE中，设AE＝EC＝x，则有DE＝DC﹣EC＝AB﹣EC＝6﹣x，AD＝×6＝2，根据勾股定理得：x2＝（6﹣x）2+（2）2，解得：x＝4，∴EC＝4，＝EC•AD＝4．则S△AEC故选：B．10．解：∵AB＝AC，AD为BC边上的高，∴BD＝DC，∵△ABC的周长为20，∴AC+CD＝10，在Rt△ADC中，点E为AC的中点，∴DE＝AC＝AE，∴△CDE的周长＝DE+EC+DC＝AE+EC+CD＝AC+CD＝10，故选：A．二．填空题11．解：∵[m]表示不大于m的最大整数，∴﹣5≤＜﹣4，解得：﹣17≤x＜﹣14，∴整数x为﹣17，﹣16，﹣15，故答案为﹣17，﹣16，﹣15．12．解：a3﹣9ab2＝a（a2﹣9b2）＝a（a﹣3b）（a+3b）．故答案为：a（a﹣3b）（a+3b）．13．解：÷＝＝m2+2m，因为m2+2m＝1，所以÷的值为1，故答案为：114．解：∵DE是线段AB的垂直平分线，∴EA＝EB，∴△BEC的周长＝BC+CE+EB＝BC+CE+EA＝BC+AC＝13，故答案为：13．15．解：由已知梯形，当Q运动到E和B之间，设运动时间为t，则得：2t﹣＝3﹣t，解得：t＝，当Q运动到E和C之间，设运动时间为t，则得：﹣2t＝3﹣t，解得：t＝1，故当运动时间t为1或秒时，以点P，Q，E，D为顶点的四边形是平行四边形．故答案为：1或．16．解：延长BD交CA的延长线于E，∵AD为∠BAC的平分线，BD⊥AD，∴∠EAD＝∠BAD，∠ADE＝∠ADB＝90°，∵AD＝AD，∴△ADE≌△ADB（AAS），∴BD＝DE，AB＝AE＝6，∴CE＝AC+AE＝9+6＝15，又∵M为△ABC的边BC的中点，∴DM是△BCE的中位线，∴MD＝CE＝×15＝7.5．故答案为：7.5．三．解答题17．解：（1）m3﹣16m＝m（m2﹣16）＝m（m+4）（m﹣4）；（2）9a2（x﹣y）+4b2（y﹣x）＝（x﹣y）（9a2﹣4b2）＝（3a+2b）（3a﹣2b）（x﹣y）．18．解：（1）去分母得，2（x+1）﹣3（x﹣1）＝x+3，移项合并同类项得，x＝1，经检验：x＝1是原方程的增根，原方程无解；（2）去分母得，2x＝3﹣4x+4，移项合并同类项得，x＝，经检验：x＝是原方程的解．19．解：∵在Rt△ABC中，∠C＝90°，∠A＝30°，∴AB＝2BC＝2．又∵点D、E分别是BC，AC的中点，∴DE是△ACB的中位线，∴DE＝AB＝1．四．解答题20．解：原式＝÷（﹣）＝•＝，解不等式2m﹣1＜6得m＜，所以m的正整数解为1、2、3，∵m≠2且m≠±3，∴m＝1，当m＝1时，原式＝．21．证明：（1）∵四边形ABCD是平行四边形∴AB＝CD，AD∥BC∴∠E＝∠DAE∵AE平分∠DAB∴∠BAE＝∠DAE∴∠BAE＝∠E∴AB＝BE∴BE＝CD（2）如图，∵AB＝BE，∠BEA＝45°，∴∠BAE＝∠BEA＝45°∴AB＝BE＝4，∠ABE＝90°∴S△ABE＝AB×BE＝8∵AB＝BE，BF⊥AE∴BF＝EF∴S△ABF ＝S△ABE＝4，∴S▱ABCD＝2S△ABF＝8故答案为：822．（1）解：设今年5月份A款汽车每辆售价为x万元，根据题意，得．解得x＝8．经检验，x＝8是原方程的解．答：今年5月份A款汽车每辆售价为8万元；（2）解：设B款汽车卖出a辆，根据题意，得a（10.5﹣7.5）+（15﹣a）×（8﹣6）≥39，解得a≥9．答：B款汽车至少卖出9辆．五．解答题23．解：（1）如图，△A′B′C′即为所求；（2）如图所示，△A″B″C″即为所求，点C″的坐标为（1，4）；（3）如图，点D即为所求，其坐标为（﹣7，3）或（3，3）或（﹣5，﹣3）．24．（1）证明：如图1，∵BE⊥CE，AD⊥CE，∴∠E＝∠ADC＝90°，∴∠EBC+∠BCE＝90°．∵∠BCE+∠ACD＝90°，∴∠EBC＝∠DCA．在△CEB和△ADC中，，∴△CEB≌△ADC（AAS），∴BE＝DC，AD＝CE．∴DE＝DC+CE＝AD+BE，即DE＝AD+BE；（2）△DOE等腰直角三角形，理由如下：如图2，连接OC，∵AC＝BC，∠ACB＝90°，点O是AB中点，∴AO＝BO＝CO，∠CAB＝∠CBA＝45°，CO⊥AB，∴∠AOC＝∠BOC＝∠ADC＝∠BEC＝90°，∵∠BOC+∠BEC+∠ECO+∠EBO＝360°，∴∠EBO+∠ECO＝180°，且∠DCO+∠ECO＝180°，∴∠DCO＝∠EBO，且DC＝BE，CO＝BO，∴△DCO≌△EBO（SAS），∴EO＝DO，∠EOB＝∠DOC，同理可证：△ADO≌△CEO，∴∠AOD＝∠COE，∵∠AOD+∠DOC＝90°，∴∠DOC+∠COE＝90°，∴∠DOE＝90°，且DO＝OE，∴△DOE是等腰直角三角形．25．解：（I）过点D作DG⊥x轴于G，如图①所示：∵点A（6，0），点B（0，8）．∴OA＝6，OB＝8，∵以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，∴AD＝AO＝6，α＝∠OAD＝30°，DE＝OB＝8，在Rt△ADG中，DG＝AD＝3，AG＝DG＝3，∴OG＝OA﹣AG＝6﹣3，∴点D的坐标为（6﹣3，3）；（Ⅱ）过点D作DG⊥x轴于G，DH⊥AE于H，如图②所示：则GA＝DH，HA＝DG，∵DE＝OB＝8，∠ADE＝∠AOB＝90°，∴AE＝＝＝10，∵AE×DH＝AD×DE，∴DH＝＝＝，∴OG＝OA﹣GA＝OA﹣DH＝6﹣＝，DG＝＝＝，∴点D的坐标为（，）；（Ⅲ）连接AE，作EG⊥x轴于G，如图③所示：由旋转的性质得：∠DAE＝∠AOC，AD＝AO，∴∠AOC＝∠ADO，∴∠DAE＝∠ADO，∴AE∥OC，∴∠GAE＝∠AOD，∴∠DAE＝∠GAE，在△AEG和△AED中，，∴△AEG≌△AED（AAS），∴AG＝AD＝6，EG＝ED＝8，∴OG＝OA+AG＝12，∴点E的坐标为（12，8）．1、学而不思则罔，思而不学则殆。

北师大版八年级数学下册期末总复习培优练习题(含答案)

A. / 1B. / 2C. / 3D. / 4・选择题1.如图，△ ABCg 着由点B 到点E 的方向，平移到△ DEF 若BG= 5, EG= 3,则平移的距离6.下列因式分解正确的是（8.如图，ABCD1平行四边形，则下列各角中最大的是期末测试卷A. 7B. 5 2 .不等式3xv2 (x+2)的解是()A. x>2B. x<2C 3 D. 2C x>4D. x<43 .下列图形中，既是轴对称图形，又是中心对称图形的是（）A B 人④4 .已知av b,下列式子不成立的是（）A.a +Kb +1 「 1 kc. -ya>--bB. 4av 4b D.如果CV0,那么包〈二 c c 5. 一个多边形的内角和等于12600 ,则从此多边形一个顶点引出的对角线有（） A. 4条 B. 5条D. 7条 A. — a +a 3= - a (1+a2) B. 2a-4b+2=2 (a — 2b) C. a 2+4b 2= ( a +2b) 2D. a 2 - 2a+1 = ( a T) 2 7.化简 A. ,5置 2 Oxy 的结果是（B. D. 4y为（）9.如图，四边形 ABC3平行四边形,OA= 1, AB= 3,点C 在x 轴的负半轴上，将平行四边A. 3B. 2.5C. 1.5D. 1ADEF AD 经过点Q 点F 恰好落在x 轴的正半 A. （ 1,6）B. （- 1,-心）C.（北，1）10.如果kb<0,且不等式 kx+b>0解集是x< -—,那么函数 k y=kx +b 的图象只可能是下CF± AE 于 F, AB= 5, AC= 2,则 DF 的长形ABC 啖点A 逆时针旋转得到平行四边形列的（12.如图，△ ABC^, AD 是中线，AE 是角平分线, 为（）.填空题13 .因式分解：5x2-2x=.14 .若分式用；，的值为零,则x 的值为 1-2 ------15 .如图，/AOB / BOP PC// OA PDL OA 若/ AOB= 45 , PC= 6,则 PD 的长为16 .如图，四边形 ABCW, ABL BD CDL BD AB= 3, BD= 4, DC= 6, M为 AC 的中点，则三.解答题17 . ( 1)分解因式：7x 2-63(2)解分式方程:),其中 a 2+a- 1 = 0.(3)解不等式并将解集在数轴上表示出来.18.先化简，再求值:19.如图，在平面直角坐标系中，Rt^ABC勺三个顶点分别是A (-3, 2) , B (0, 4) , C(0, 2).(1)将△ABCA点C为旋转中心旋转180° ,画出旋转后对应的△ ABG平移4 ABC若点A的对应点A的坐标为(1, - 4),画出平移后对应的△ ABG;(2)若将△ ABC绕某一点旋转可以得到^ A2&C2；请直接写出旋转中心的坐标；(3)在x轴上有一点P,使得PA+PB的值最小，请直接写出点P的坐标.20.如图，在^ ABC中，/ ACB= 90° , D为AB边上一点，连接CD E为CD中点，连接BE并延长至点F,使得EF= EB,连接DF交AC于点G,连接CF.(1)求证：四边形DBC用平行四边形；(2)若/ A= 30° , BC= 4, CF= 6,求CD的长.21.如图，在^ ABC^, / J 90° ,边AC的垂直平分线分别交AG AB于点D, E.(1)求证：E为AB的中点;(2)若/A=60* , Si”,求BE的长.22. 一台收割机的工作效率相当于一个农民工作效率的120倍，用这台机器收割10公顷小麦比80个农民人工收割这些小麦要少用1小时.(1)这台收割机每小时收割多少公顷小麦？(2)通过技术革新，这台收割机的工作效率得到了提升，收割10公顷小麦比100个农民人工收割这些小麦要少用了0.8小时.求这台收割机的工作效率相当于一个农民工作效率的多少倍？23.如图1,在平面直角坐标系中，直线BC y=- 3x+9,直线BD与x轴交于点A,点B为(2, 3),点D为(0,三)(1)求直线BD的函数解析式；(2)找出y轴上一点P,使彳ABCWAACP勺面积相等，求出点P的坐标；(3)如图2, E为线段AC上一点，连接BE 一动点F从点B出发，沿线段BE以每秒2 个单位运动到点E再沿线段EA以每秒正个单位运动到A后停止，设点F在整个运动过程中所用时间为t ,求t的最小值.参考答案一.选择题1. D.2. D.3. C.4. D.5. C.6. D.7. C.8. C.9. B.10. A.11. C.12. C.二.填空题13.x (5x-2)14.- 2.15. 3 _ \三.解答题17.解：(1) 7x2- 63=7 (x2 - 9)=7(x+3) ( x— 3);(2)原方程化为:检验：当x=- 4时，x-2W0, 所以x=- 4是原方程的解，即原方程的解为x=- 4;f 2-X 30⑶12Kl②•.•解不等式①得：x>- 1,解不等式②得：x<2.5,・,.不等式组的解集为-1wxv2.5 ,2a a_l 我18.解：原式=[五方―ET+:京=—―--£2L夏QT) a(a-t-l)电二工=F，a当a2+a — 1 = 0 时，a2= 1 — a,则原式=件=-1.19.解：(1)如图所示；(2)如图，旋转中心为(2, - 1);(3)作点A关于x轴的对称点A ,连接A B交x轴于点P,则点P即为所求点,•A (-3, 2),••A (-3, - 2).设直线A B的解析式为y=kx+b (kw0),. A (-3, - 2) , B (0, 4),,, f b=4 ，解得彳[b=4，直线A B的解析式为y=2x+4,:当y=0 时，x= — 2,•••P (-2, 0)20.证明：(1)二.点E为CD43点，. CE= DE. EF= BE,••・四边形DBC屋平行四边形.(2)•••四边形DBCF1平行四边形，. CF AR DF// BC・•./FCG= /A= 30° , C CGF= / CG& Z ACB= 90° .在Rt^FCG中，CF= 6, 前十口，戊々血.•.DF= BC= 4,. DG= 1.在RtADCG^, CD= JcG*+DG2=2行21.( 1)证明：ACB= 90° , / A= 60° 连接CE A•••线段DE是边AC的垂直平分线,.•.AE= CE・. / A= 60° ,・•.△AC既等边三角形,. AC= CE= AE, /ACE= 60 ,，/ ECB= 30 =/ B,. CE= BE,.•.AE= BE,即E 为AB 的中点;（2）解：•••边 AC 的垂直平分线分别交 AC AB 于点D, E, CD =J5，. AC= 2CD= 2/3,•.在 RtA ACE^, Z ACB= 90 , AC=班，/ B= 30 ,.•.AB= 2AC= 4^,即 BE= AE= -j-AB= 2M.22 .解：（1）设一个农民每小时收割小麦 x 公顷，则一台收割机每小时收割 120x 公顷,由题意得： —1 =7n7~~,80s120k解得：* =击，经检验，x =击是原方程的根.，收割机每小时收割小麦： :120= 5公顷，答：这台收割机每小时收割 5公顷小麦.（2）设这台收割机的工作效率相当于一个农民工作效率的解得：n= 150 经检验，n = 150是原方程的根答：这台收割机的工作效率相当于一个农民工作效率的 150倍.23 .解：（1）设直线BD 的函数解析式为y=k^^D ,把点D 的坐标代入得22k 吟,解得k=-^-,n 倍，则由（1）知一个农民每小时收割小麦/公顷, 台收割机每小时收割立公顷，10 24+0.8 由题意10100 乂击・•・直线BD的函数解析式为(2)过点B作B"//x轴交y轴于点R,作直线BP关于x轴对称轴直线l交y轴于点P2,••Pi (0, 3),,• ・关于x轴对称轴，•• l的解析式为y= - 3,••P2 (0, - 3).(3)以AE为斜边在AE下方构造等腰Rt^AEG如图2,图2AE W^EG,BE AE rb BE H EG，当得B、E、G共线时，BE+EG最小, 过点B作BG LAG于点G',易得A ( - 2, 0),二.AG的解析式为y=—x —2,BG的解析式为y = x+1,y=x-nl・•.t的最小值三包2 w 2。

2020年北师大版数学八年级下册《期末考试题》(附答案)

2020年北师大版数学八年级下册期末测试学校________ 班级________ 姓名________ 成绩________一、选择题（每小题3分，共30分）1.已知等腰三角形的两条边长分别是2和4，则它的周长是（） A. 8 B. 10C. 810或D. 无法确定2.要使分式3xx +有意义，x 的取值范围为（） A. 3x ≠-B. 0x >C. 0x ≥D. 3x ≠-且0x >3.下列不等式的变形中，不正确的是（） A. 若a b >，则11a b +>+ B. 若a b ->-，则a b < C. 若13x y -<，则3x y >- D. 若3x a ->，则13x a >-4.关于x 的不等式组()2240x a x ⎧->⎨-<⎩的解集为4x >，那么a 的取值范围为（）A. 4a ≤B. 4a <C. 4a ≥D. 4a >5.已知，多项式212x mx --可因式分解为()()34x x +-，则m 的值为（） A. -1B. 1C. -7D. 76.多项式322363a b a b -因式分解时，应提取的公因式为（） A. 223a bB. 323a bC. 233a bD. 333a b7.下列图形中，既是轴对称图图形又是中心对称图形的是（）A.B.C.D.8.一艘轮船在静水中的最大航速为40/km h ，它以最大航速沿河顺流航行100km 所用时间，和它以最大航速沿河逆流航行80km 所用时间相等，设河水的流速为/v km h ，则可列方程为（） A.100804040v v =+-B.100804040v v =-+ C.100804040v v=+- D.100804040v v=-+ 9.下列各组条件中，不能判定四边形ABCD 是平行四边形的是（） A. AB CD ∥，AD BC ∥B. AB CD ∥，AD BC =C. AB CD ∥，AB CD =D. AB CD =，AD BC =10.如图，把ABC ∆绕着点A 逆时针旋转20︒得到ADE ∆，30BAC ∠=︒，则BAE ∠的度数为（）A. 10︒B. 20︒C. 30°D. 50︒二、填空题（每小题3分，共24分）11.已知，23x y =，则x y x y+=-______. 12.因式分解：2212a abb -+-=______.13.已知，14y x =-+，234y x =-，若12y y ≥，则x 可以取的值为______. 14.已知正多边形的一个外角等于40°，那么这个正多边形的边数为__________.15.已知直角三角形的两直角边a 、b 满足()2860a b -+-=，则斜边c 上中线的长为______. 16.如图，1l 与2l 穿过正六边形ABCDEF ，且12l l P ，则12∠-∠的度数为______.17.如图，平行四边形ABCD 对角线相交于点O ，且OM AC ⊥，平行四边形ABCD 的周长为8，则CDM ∆的周长为______.18.如图，在Rt ABC ∆中，90ACB ∠=︒，30A ∠=︒，D ，E ，F 分别为AB ，AC ，AD 的中点，3EF =，则BC 的长度为__.三、解答题（第19、20、21题各6分，共18分）19.解不等式组：（1）()0.20.313232x x x x ≤+⎧⎪⎨->+⎪⎩；（2）123255x -<-≤.20.解分式方程：（1）22124x x =--；（2）211323x x x-=+--. 21.先化简，再求值：24433x x x x x --⎛⎫-÷⎪--⎝⎭，其中1x =. 四、解答题（第22、23、24题各8分共24分）22.如图，在四边形ABCD 中，E 、F 、G 、H 分别是AD 、BC 、BD 、EF 的中点，GH EF ⊥.求证：AB CD =.23.如图，点B 、F 、C 、E 在一条直线上，FB CE =，//AB ED ，//AC FD ，AD 交BE 于O ．求证：AD 与BE 互相平分，24.如图，在ABC ∆中，90C ∠=︒，AD 是BAC ∠的平分线，DE AB ⊥于点E ，点F 在边AC 上，BD DF =.求证：（1）CF EB =；（2）2AB AF EB =+.五、解答题（第25、26题各12分，共24分）25.如图所示，将ABC ∆置于平面直角坐标系中，()1,4A -，()3,2B -，()2,1C -.（1）画出ABC ∆向下平移5个单位得到的111A B C ∆，并写出点1A 的坐标；（2）画出ABC ∆绕点O 顺时针旋转90︒得到的222A B C ∆，并写出点2A 的坐标；（3）画出以点O 为对称中心，与ABC ∆成中心对称的333A B C ∆，并写出点3A 的坐标.26.某图书馆计划选购甲、乙两种图书.甲图书每本价格是乙图书每本价格的2.5倍，如果用900元购买图书，则单独购买甲图书比单独购买乙图书要少18本. （1）甲、乙两种图书每本价格分别为多少元？（2）如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本，且用于购买甲、乙两种图书的总费用不超过1725元，那么该图书馆最多可以购买多少本乙图书？答案与解析一、选择题（每小题3分，共30分）1.已知等腰三角形的两条边长分别是2和4，则它的周长是（） A. 8 B. 10C. 810或D. 无法确定【答案】B 【解析】试题分析：题目中没有明确底和腰，故要分情况讨论，再结合三角形的三边关系分析即可. 当2为腰时，三边长为2、2、4，而，此时无法构成三角形；当2为底时，三边长为2、4、4，此时可以构成三角形，则它的周长是故选B.考点：等腰三角形的性质，三角形的三边关系点评：解答本题的关键是熟练掌握三角形的三边关系：三角形的任两边之和大于第三边，任两边之差小于第三边.2.x有意义，x 的取值范围为（） A. 3x ≠- B. 0x >C. 0x ≥D. 3x ≠-且0x >【答案】C 【解析】【分析】根据分式有意义的条件可得30x +≠,再根据二次根式有意义的条件可得0x ≥,再解即可. 【详解】由题意得: 30x +≠,且0x ≥, 解得: 0x ≥,所以，C 选项是正确的.【点睛】此题主要考查了分式和二次根式有意义的条件,关键是掌握分式有意义的条件是分母不等于零,二次根式中的被开方数是非负数3.下列不等式的变形中，不正确的是（） A. 若a b >，则11a b +>+B. 若a b ->-，则a b <C. 若13x y -<，则3x y >- D. 若3x a ->，则13x a >-【答案】D 【解析】【分析】根据不等式的基本性质进行判断。

2020年北师大版初二数学下册期末检测试题(含答案)

八年级数学下册期末检测试卷一．选择题（本大题共有10小题，每小题3分，共30分．）1．对于函数xy k=，若2=x 时，3-=y ，则这个函数的解析式是（） A. xy 6=B. x y 61=C. x y 6　-=D. x y 61　-=2. xy 2-=图象上有两点A(x 1,y 1)和 B(x 2,y 2)，若y 1<y 2<0, 则x 1与x 2的关系是（） A ．0 < x 1 < x 2 B ．0 > x 1 > x 2 C ．x 1 < x 2 < 0 D ．x 1 > x 2> 03.下列命题是真命题的是（） (A)相等的角是对顶角 (B)两直线被第三条直线所截，内错角相等 (C)若n m n m ==则,22(D)有一角对应相等的两个菱形相似.4.若16)3(22+-+x m x 是完全平方式，则m 的值是（） (A)-1 (B)7 (C)7或-1 (D)5或1.5.下列命题是真命题的是（） A.9是不等式()2131x x -+<+的一个解 B.当1x =-时，分式2122x x +-的值为0 C.某运动员在亚运会某项比赛中，连续四次成绩为80，80，80，80，则该组数据的方差为0D.三内角之比为3︰4︰5的三角形为直角三角形 6.解关于x 的方程113-=--x mx x 产生增根，则常数m 的值等于（） (A)-1 (B)-2 (C)1 (D)27.有旅客m 人，如果每n 个人住一间客房，还有一个人无房间住，则客房的间数为（） (A)nm 1- (B)nm 1+ (C)nm-1 (D)nm +1 8．如图，矩形AOBC 中，点A 的坐标为（0，8)，点D 的纵坐标为3，若将矩形沿直线AD 折叠，则顶点C 恰好落在边OB 上E 处，那么图中阴影部分的面积为（）A.30 B ．32 C ．34 D ．169.若分式方程244x ax x =+--有增根，则a 的值为（） A. 4 B. 2 C. 1 D. 010.如图所示，△ABC 中，点D 在边BC 上，点E 在边AC 上，且AB ∥ED ，连接BE ，若AE ︰EC ＝3︰5，则下列结论错误的是（） A.AB ︰ED ＝5︰3 B.△EDC 与△ABC 的周长比为5︰8 C.△EDC 与△ABC 的面积比为25︰64 D.△BED 与△EDC 的面积比为3︰5A DCEAB D C二．填空题（本大题共有8小题，每小题2分，共16分．）11．如果不等式组⎩⎨⎧>-≥+m x x x 148无解，则m 的取值范围是 12．若1x =-是关于x 的方程2220x ax a +-=的一个根，则a =_______.13.如图所示：∠A=50°，∠B=30°，∠BDC=110°，则∠C=______°；ABCD14．如果一次函数y =（2－m ）x ＋m-3的图象经过第二、三、四象限，那么m 的取值范围是_________ 15.如图所示，是某建筑工地上的人字架. 已知这个人字架的夹角∠1＝120°，那么∠2－∠3的度数为________.23116.一组按规律排列的式子：3x y ，52x y -，73x y，94x y -，…，（0xy ≠），则第2011个式子是________（n 为正整数）. 17．如图，△ABC 中，∠ACB=90°，AC=BC=1，取斜边的中点，向斜边做垂线，画出一个新的等腰直角三角形，如此继续下去，直到所画直角三角形的斜边与△ABC 的BC 边重叠为止，此时这个三角形的斜边长为__________．18.小康利用下面的方法测出月球与地球的距离：如图所示，在月圆时，把一枚五分的硬币（直径约为2.4cm ）放在离眼睛点O 约2.6米的AB 处，正好把月亮遮住. 已知月球的直径约为3500km ，那么月球与地球的距离约为 ____________________（结果保留两个有效数字）. 3.8×510kmD E CBAO三.解答题（本大题共54分）17、（1）（5分）已知x = -2，求x x x x 12112+-÷⎪⎭⎫ ⎝⎛-的值。

北师大版2020八年级数学下册期末复习综合训练题(培优含答案)

2．D
【解析】
【分析】
根据解一元一次不等式基本步骤：去括号、移项、合并同类项、系数化为1可得．
【详解】
，
，
，
，
故选D．
【点睛】
本题考查了解一元一次不等式，解题的关键是严格遵循解不等式的基本步骤，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．
3．C
【解析】
【分析】
根据分式有意义的条件可得a-1≠0，再解不等式即可．
A．外部B．内部C．斜边的中点D．不能确定
8．如图，在直角梯形ABCD中，AD∥BC，∠B=90度，AC将梯形分成两个三角形，其中△ACD是周长为18cm的等边三角形，则该梯形的中位线的长是（）
A．9cmB．12cmC． cmD．18cm
9．下列各式从左到右的变形中，是分解因式的是( )
A．x2-9+6x＝(x+3)(x-3)+6xB．(x+5)(x-2)＝x2+3x-10
（2）解不等式组： .
27．如图，在△ABC中，D是BC边上一点，AB=13，AD=12，BD=5，CD=9，求AC的长.
28．在平面直角坐标系中，已知点A（2，0），点B（0，2 ），点O（0，0）．△AOB绕着O顺时针旋转，得△A′OB′，点A、B旋转后的对应点为A′、B′，记旋转角为α．
（I）如图1，若α=30°，求点B′的坐标；
25．如图1，在△ABC中，∠ACB=90°，AC=BC，CD为AB边上的中线，点E、F分别在AC、BC边上，且ED⊥DF.
(1)求证：△CDE≌△BDF；
(2)如图2，作EG⊥AB于G，FH⊥AB于H，求证：EG+FH=CD．
26．（1）计算：|2﹣ |+（）﹣1﹣（3﹣π）0﹣（﹣1）2019．

北师大版2020八年级数学下册期末复习综合训练题(基础含答案)

北师大版2020八年级数学下册期末复习综合训练题（基础含答案）1．如图，线段AB ，DE 的垂直平分线交于点C ，且72ABC EDC ∠=∠=，92AEB ∠=，则EBD ∠的度数为( )A ．168B ．158C ．128D ．1182．Rt △ABC 中，∠C=90°，∠B=54°，则∠A 的度数是（）A ．66°B ．36°C ．56D ．46°3．在下列图形中，是中心对称图形的是( )A ．B ．C ．D ． 4．下列给出四个式子，①x ＞2；②a≠0；③5＜3；④a≥b ，其中是不等式的是（） A ．①④B ．①②④C ．①③④D ．①②③④ 5．马小虎在计算一个多边形的内角和时，由于粗心少算了2个内角，其和等于830，则该多边形的边数是( )A ．7B ．8C ．7或8D ．无法确定 6．等腰三角形中有一个角为50°，它的一条腰上的高与底边的夹角为( ) A ．25° B ．25°或40° C ．40° D ．90°7．如图，在一次实践活动课上，小刚为了测量池塘B 、C 两点间的距离，他先在池塘的一侧选定一点A ，然后测量出AB 、AC 的中点D 、E ，且10DE =，于是可以计算出池塘B 、C 两点间的距离是（）．A ．5mB ．10mC ．15mD ．20m8．若关于x 的不等式组221x m x m ->⎧⎨-<-⎩无解，则m 的取值范围（） A ．m ＞3 B ．m ＜3 C ．m ≤3 D ．m ≥39．将点M （﹣1，﹣5）向右平移3个单位长度得到点N ，则点N 所处的象限是（） A ．第一象限B ．第二象限10．若分式31x x +有意义，则（） A ．x≠－1 B ．x≠±1 C ．x 可为任何实数 D ．x≠011．如图，线段AB=CD ，AB 与CD 相交于点O ，且∠AOC=60°，CE 是由AB 平移所得，AC 与BD 不平行，则AC+BD 与AB 的大小关系是：AC+BD_____AB ．（填“＞”“＜”或“=”）12．把多项式2a 3﹣4a 2+2a 分解因式的结果是_____．13．方程2635210x x x -++=0的解是________. 14．用“<”或“>”填空： (1)若x ＞y ，则－2x _____2y －；（2）若x ＋2＞y ＋2，则－x______－y ；（3）若a ＞b ，则1－a ________ 1－b ；（4）已知13x －5＜13y －5，则x ___ y. 15．已知△ABC 的周长为16，面积为20，其内角平分线交于点O ，则点O 到边BC 的距离为________．16．计算：20122-⎛⎫+-= ⎪⎝⎭ ___________________ 172222(3)(3)10x y x y +++-=无解，那么m 的值应为___________．18．若x 的倒数与本身相等，则226336x x x x x x --+÷-+-=________ 19．如图，在平行四边形ABCD 中，2AB AD ==，60A ∠=︒，M 是AD 边的中点，若线段MA 绕点M 旋转得到线段MA '，如图，连接A C '，则A C '长度的最小值是__________．20．如图是某机器零件的设计图纸，用不等式表示零件长度的合格尺寸，则长度l 的取值范围是______________．21．如图，矩形OABC 和ABEF ，()3,4B ．()1画出矩形OABC 绕点O 逆时针旋转90后的矩形111OA B C ，并写出1B 的坐标为________，点B 运动到点 1B 所经过的路径的长为________；()2若点E 的坐标为()5,2，则点F 的坐标为________，请画一条直线l 平分矩形OABC 与ABEF 组成图形的面积（保留必要的画图痕迹）．22．如图，已知点A 、C 分别在∠GBE 的边BG 、BE 上，且AB=AC ，AD ∥BE ，∠GBE 的平分线与AD 交于点D ，连接CD ．求证：①AB=AD ；②CD 平分∠ACE ．23．()1计算：421121)63--+-⨯；()2计算：222x 1x x x x x 1-+⎛⎫-⋅ ⎪-⎝⎭． 24．先化简241(1)93x x x -÷---再从13、3、4中选一个你喜欢的数代人求值. 25．解方程：22216224x x x x x -+-=+--26．解方程:()()13-1x-1x-1x 2=+27．化简22+31923a a a a a a⋅----，并求值，其中 a 与 2、3 构成∆ABC 的三边，且a 为整数. 28．因式分解(1)(4)(1)3p p P -++ (2)22344xy x y y --29．2412x x --30．一组学生乘汽车去旅游，预计共需车费120元．后来人数增加了14，车费用仍不变，这样每人可少摊3元，原来这组学生有多少人？参考答案1．C【解析】【分析】连接CE ，依据线段AB ，DE 的垂直平分线交于点C ，可得CA CB =，CE CD =，判定ACE ≌BCD ，可得AEC BDC ∠∠=，设AEC BDC α∠∠==，则BDE 72α∠=-，CEB 92α∠=-，()BED DEC CEB 7292αα20∠∠∠=-=--=-，即可得到BDE 中，()()EBD 18072αα20128∠=----=．【详解】如图，连接CE ，线段AB ，DE 的垂直平分线交于点C ，CA CB ∴=，CE CD =，ABC EDC 72DEC ∠∠∠===，ACB ECD 36∠∠∴==，ACE BCD ∠∠∴=，在ACE 和BCD 中，CA CB ACE BCD CE CD ∠∠=⎧⎪=⎨⎪=⎩，ACE ∴≌()BCD SAS ，AEC BDC ∠∠∴=，设AEC BDC α∠∠==，则BDE 72α∠=-，CEB 92α∠=-，()BED DEC CEB 7292αα20∠∠∠∴=-=--=-， BDE ∴中，()()EBD 18072αα20128∠=----=，故选C ．【点睛】本题主要考查了线段垂直平分线的性质以及全等三角形的判定与性质的运用，解决问题的关键是依据全等三角形的对应角相等，以及三角形内角和定理得出结论．2．B【解析】【分析】根据三角形内角和定理：三角形的三个内角的和等于180°即可求解.【详解】解：∵在△ABC 中，∠C=90°，∠B=54°，∴∠A=180°-∠C -∠B=180°-90°-54°=36°，故答案为B.【点睛】本题考查了三角形的内角和定理，掌握三角形内角和为180°是解决本题的关键.3．C【解析】【分析】【详解】A 、旋转180°后不能与自身重合，不是中心对称图形；B 、旋转180°后不能与自身重合，不是中心对称图形；C 、旋转180°后能与自身重合，是中心对称图形；D 、旋转180°后不能与自身重合，不是中心对称图形．故选C ．【点睛】本题考查了中心对称图形的概念，若一个图形绕某一点旋转180°后能与自身重合，则此图形是中心对称图形．4．D【分析】根据不等式的概念：用不等号(),,,,><≠≥≤表示不等关系的式子，叫做不等式．【详解】解：①x >2；②a ≠0；③5<3；④a ≥b ，是不等式，故选D.【点睛】考查不等式的定义，掌握不等式的概念：用不等号(),,,,><≠≥≤表示不等关系的式子，叫做不等式是解题的关键.5．C【解析】【分析】n 边形的内角和是（n-2）•180°，即为180°的（n-2）倍，多边形的内角一定大于0度，小于180度，因而多边形中，除去2个内角外，其余内角和与180度的商加上2，以后所得的数值，比这个数值大1或2的整数就是多边形的边数．【详解】设少加的2个内角和为x 度，边数为n ．则（n-2）×180=830+x ，即（n-2）×180=4×180+110+x ，因此x=70，n=7或x=250，n=8．故该多边形的边数是7或8．故选C ．【点睛】本题考查了多边形的内角和定理，正确理解多边形内角的大小的特点，以及多边形的内角和定理是解决本题的关键．6．B【解析】【分析】根据题意先画出图形，再分两种情况：50°为底角和50°为顶角求出答案．当50°为底角时，∵∠B＝∠ACB＝50°，∴∠BCD＝40°；当50°为顶角时，∵∠A＝50°，∠B＝∠ACB＝65°，∴∠BCD＝25°．故选：C．【点睛】本题考查了等腰三角形的性质以及三角形的内角和定理，是基础知识要熟练掌握．注意分类讨论思想的应用．7．D【解析】试题解析：∵点D、E是ABC△中AB、AC边上中点，∴12DE BC=，∵10mDE=，∴20mBC=．故选D.8．C【解析】根据“大大小小找不着”可得不等式2+m≥2m -1，即可得出m 的取值范围．【详解】221x m x m ->⎧⎨-<-⎩①② ，由①得：x ＞2+m ，由②得：x ＜2m ﹣1，∵不等式组无解，∴2+m≥2m ﹣1，∴m≤3，故选C ．【点睛】考查了解不等式组，根据求不等式的无解，遵循“大大小小解不了”原则得出是解题关键． 9．D【解析】试题解析：点M (−1,−5)向右平移3个单位长度,即横坐标变为132,-+=纵坐标不变. 得到点N 的坐标为(2,−5)，故点N 在第四象限.故选D.10．C【解析】根据分式有意义的条件是分母不等于零，列不等式即可得出答案．解：∵0x ≥， ∴10x +>，∴当x 取任何实数时，分式31x x +有意义. 故选C.11．=【解析】分析：根据三角形的三边关系，及平移的基本性质可得．详解：由平移的性质知，AB与CE平行且相等，所以四边形ACEB是平行四边形，BE=AC，当B、D、E不共线时，∵AB∥CE，∠DCE=∠AOC=60°，∵AB=CE，AB=CD，∴CE=CD，∴△CED是等边三角形，∴DE=AB，根据三角形的三边关系知BE+BD=AC+BD＞DE=AB，即AC+BD＞AB．当D、B、E共线时，AC+BD=AB．故答案为=．点睛：本题考查了平移的性质，利用了：1、三角形的三边关系；2、平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．12．2a（a﹣1）2．【解析】【分析】先提取公因式2a，然后利用完全平方公式继续分解即可求得答案．【详解】2a3-4a2+2a=2a（a2-2a+1）=2a（a-1）2．故答案为2a（a-1）2．【点睛】本题考查了用提公因式法和公式法进行因式分解．注意先提公因式，再利用公式法分解，同时因式分解要彻底，直到不能分解为止．13．x=4【解析】【分析】因为()()25521025x x x x x x +=++=+，，所以可确定方程最简公分母为()25x x +，去分母后化为整式方程求解．【详解】方程两边同乘以2x (x +5)，去分母得：6×2−3x =0，解得x =4.经检验x =4是原方程的解。

北师大版2020八年级数学下册期末综合复习培优测试卷C(附答案详解)

17．先化简，再求值：（1+ ）÷ ，其中x＝﹣3．
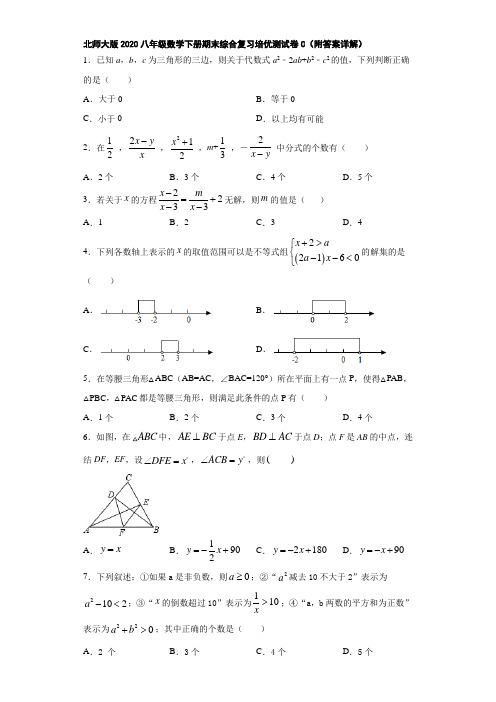
18．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE.已知∠ABC＝60°，EF⊥AB，垂足为F，连接DF.
(1)证明：△ACB≌△EFB；
(2)求证：四边形ADFE是平行四边形．
19．陈老师所在的学校为加强学生的体育锻炼，需要购买若干个足球和篮球，他曾两次在某商场购买过足球和篮球，两次购买足球和篮球的数量和费用如下表：
北师大版2020八年级数学下册期末综合复习培优测试卷C（附答案详解）
1．已知a，b，c为三角形的三边，则关于代数式a2﹣2ab+b2﹣c2的值，下列判断正确的是（）
A．大于0B．等于0
C．小于0D．以上均有可能
2．在，，，m+ ，－中分式的个数有（）
A．2个B．3个C．4个D．5个
3．若关于的方程无解，则的值是（）
10．如图，中，，，点为中点，且，的平分线与的垂直平分线交于点，将沿（在上，在上）折叠，点与点恰好重合，则为________度．
11．将点Q(10，2)绕着原点O旋转1800后落到Q`处，那么点Q`的坐标是（________）.
12．（______________）．
（2）若∠1=40°，求∠2的度数．
23．画图并填空：
(1)如图，画出三角形ABC先向右平移6格，再向下平移2格得到的三角形A1B1C1；
(2)连接AA1，BB1，直接写出线段AA1与BB1的关系；
(3)直接写出三角形ABC的面积是多少平方单位．
24．如下图，和是等腰直接角三角形，，点为边上一点，连接，交于点，点恰好是中点，连接 .

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

26．如图，△ABC≌△ADC，AM是△ABC中∠BAC的角平分线，仅用无刻度直尺（不必写作法，但得保留作图痕迹）作出△ADC中∠DAC的角平分线AN.
27．如图1,在四边形中， , .
(1)求证： ;
(2)如图2,点在线段上，点在线段的延长线上，连接 , ,求证：是的平分线;
(3)如图3,在(2)的条件下，点在线段的延长线上，的平分线交于点 ,若．,求的度数.
【详解】
解：A、∵42+52≠62，
∴以4、5、6为边不能组成直角三角形，故本选项不符合题意；
B、∵22+32≠42，
∴以2、3、4为边不能组成直角三角2≠132，
∴以11、12、13为边不能组成直角三角形，故本选项不符合题意；
D、∵82+152=172，
∴8、15、17为边能组成直角三角形，故本选项符合题意；
A．4，5，6B．2，3，4C．11，12，13D．8，15，17
3．若，则下列各式正确的是
A． B． C． D．
4．下列欧洲足球俱乐部标志中，是中心对称图形的是（）
A． B． C． D．
5．如图，在△ABC中，BC＝4，BC边上的中线AD＝2，AB+AC＝3+ ，则S△ABC等于（）
A． B． C． D．
21．如图，在中，，是的平分线，于点，点在上，，求证： .
22．如图，已知，请解答下列问题：
（1）利用尺规作图方法，作的角平分线；（保留做图痕迹，不写作法）
（2）在（1）的条件下，若的长为，的长为，请直接写出与的面积比值.
23．如图，在中，，，是的角平分线，，垂足为 .
6．如图，在Rt△ABC中，∠C=90°, BE平分∠ABC，ED垂直平分AB于D，若AC=9，则AE的值是（）
A． B． C．6D．4
7．等腰三角形腰长为13，底边长为10，则它底边上的高为( )
A．12B．7C．5D．6
8．如图所示，△ABC中，AB＝AC，∠B＝36°，D、E是BC上两点，且∠ADE＝∠AED＝2∠BAD，则图中等腰三角形共有（）
28．△ABC的三边长分别为a，b，c，且2a+ab＝2c+bc，请判断△ABC是等边三角形、等腰三角形，还是直角三角形？并说明理由．
29．解下列方程：
（1）（2）
30．定义运算，：当时，，；当时，，；如：，；，；，．根据该定义运算完成下列问题：
（1），，当时，，；
（2）若，，求的取值范围；
（3）如图，已知直线与相交于点，若，，结合图象，直接写出的取值范围是．
参考答案
1．B
【解析】
【分析】
先根据多边形的内角和公式分别求得正六边形和正五边形的每一个内角的度数，再根据多边形的内角和公式求得∠APG的度数．
【详解】
(6﹣2)×180°÷6＝120°，
（1）已知，求的长.
（2）求证： .
24．因式分解：
25．列方程解应用题：
某商店在2016年至2018年期间销售一种礼盒．2016年，该商店用2200元购进了这种礼盒并且全部售完：2018年，这种礼盒每盒的进价是2016年的一半，且该商店用2100元购进的礼盒数比2016年的礼盒数多100盒．那么，2016年这种礼盒每盒的进价是多少元？
18．如图，在中，BC的垂直平分线ED交AB于点E，交BC于点D，连接CE，若，，则的周长为______．
19．如图，A、B的坐标分别为（2，0）、（0，1），若将线段AB平移至A1B1，A1、B1的坐标分别为（3，1）、（a，b），则a-b的值为_____．
20．若△ABC中，(b－a)(b＋a)=c2，则∠B=____________；
(5﹣2)×180°÷5＝108°，
∠APG＝(6﹣2)×180°﹣120°×3﹣108°×2
＝720°﹣360°﹣216°
＝144°，
故选B．
【点睛】
本题考查了多边形内角与外角，关键是熟悉多边形内角和定理：(n﹣2)•180 (n≥3)且n为整数)．
2．D
【解析】
【分析】
根据勾股定理的逆定理，只要两边的平方和等于第三边的平方即可构成直角三角形．分别求出各选项中两个较小的数的平方和和最大数的平方即可判断．
北师大版2020八年级数学下册期末综合复习培优测试题C（附答案）
1．把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合，按照如图所示的方式叠放在一起，延长LG交AF于点P，则∠APG＝（）
A．141°B．144°C．147°D．150°
2．下列各组数据中的三个数，可作为三边长构成直角三角形的是（）
15．若与互为相反数，则的值为________________．
16．如图，两车从南北方向的路段AB的A端出发，分别向东、向西行进相同的距离，到达C，D两地，此时可以判断C，D到B的距离相等，用到的数学道理是___．
17．如图，三角形ABC的面积为1，将三角形ABC沿着过AB的中点D的直线折叠，使点A落在BC边上的处，折痕为DE，若此时点E是AC的中点，则图中阴影部分的面积为______________．
故选：D．
【点睛】
本题考查勾股定理的逆定理，已知三条线段的长，判断是否能构成直角三角形的三边，判断的方法是：根据两个较小的数的平方和是否等于最大数的平方即可判断．
A．3个B．4个C．5个D．6个
9．能够铺满地面的正多边形组合是()．
A．正三角形和正五边形
B．正方形和正六边形
C．正方形和正八边形
D．正六边形和正八边形
10．如图，一个长为2、宽为1的长方形以下面的“姿态”从直线的左侧水平平移至右侧（下图中的虚线是水平线），其中，平移的距离是（）
A．1B．2C．3D．
11．分解因式： __________．
12．在平面直角坐标系中，点，的坐标分别为，，若将线段平移至，且点的坐标为，则点的坐标为______.
13．已知关于x的分式方程的解是负数，则m的取值范围是______.
14．如图，在中，，以顶点为圆心，适当长度为半径画弧，分别交于点，再分别以点为圆心，大于的长为半径画弧，两弧交于点，作射线交于点．若，则 _____．