小升初数学总复习
小升初数学总复习知识梳理数的整除(附答案)

小升初总复习数与代数第一单元数的认识第2节数的整除知识梳理典例精讲【例1】把自然数A和B分解质因数后分别是A=2×3×11×m,B=2×3×7×m。
A、B两数的最大公因数是78,这两个数的最小公倍数是多少?【分析】这里要明白最大公因数和最小公倍数的意义,A、B两数的最大公因数就是这两个数的全部公有的质因数的积,也就是2×3×m;A、B两数的最小公倍数就是这两个数的全部公有质因数及各自独有质因数的积,也就是2×3×m×11×7.根据两个数的最大公因数是78,求出m的值,本题便迎刃而解。
【解】因为2×3×m=78,所以m=78÷2×3=13,因此2×3×m×11×7=78×11×7=155。
答:这两个数的最小公倍数是155.即时演练1.25和30的最大公因数是(),最小公倍数是()。
2. 把自然数A和B分解质因数后分别是A=2×3×m,B=2×7×m。
A、B两数的最大公因数是22,这两个数的最小公倍数是多少?3.两个数的最小公倍数是150,最大公因数是15.这两个数分别是()和()。
【例2】有一些糖果,如果把6个装一包少1个;如果8个装一包也少一个;如果把5个装一包还是少一个。
这些糖果至少有多少个?【分析】这些糖果,把6个装一包少1个说明糖果的总个数比6的倍数少1个;8个装一包也少一个说明糖果总个数比8的倍数少1个;把5个装一包还是少一个说明糖果的总个数比5的倍数少1个。
所以这些糖果的总个数比5、6、8的公倍数少1,这里求至少有糖果多少个,就是求比5、6、8的最小公倍数少1的数。
【解】5、6、8的最小公倍数是120.120-1=119(个)答:这些糖果至少有119个。
小升初数学总复习练习题

小升初数学总复习练习题一、填空题1、篮球个数是足球的125%,篮球比足球多()%,足球个数是篮球的()%,足球个数比篮球少()%。
2、排球个数比篮球多18%,排球个数相当于篮球的()%。
3、足球个数比篮球少20%。
排球个数比篮球多18%,()球个数最多,()球个数最少。
4、果园里种了60棵果树,其中36棵是苹果树。
苹果树占总棵数的()%,其余的果树占总棵数的()%。
5、女生人数占全班的百分之几 = ()÷()杨树的棵数比柏树多百分之几 =()÷()实际节约了百分之几 = ()÷()比计划超产了百分之几 = ()÷()6、20的40%是(),36的10%是(),50千克的60%是()千克,800米的25%是()米。
7、进口价a元的一批货物,税率和运费都是货物价值的10%,这批货物的成本是()元。
二、解决实际问题1、白兔有25只,灰兔有30只。
灰兔比白兔多百分之几?2、四美食盐厂上月计划生产食盐450吨,实际生产了480吨。
实际比计划多生产了百分之几?3、小明家八月份用电80千瓦时,小亮家比小明家节约10千瓦时,小亮家比小明家八月份节约用电百分之几?4、某化肥厂9月份实际生产化肥5000吨,比计划超产500吨。
比计划超产百分之几?5、蓝天帽业厂去年收入总额达900万元,按国家的税率规定,应缴纳17%的增值税。
一共要缴纳多少万元的增值税?6、爸爸买了一辆价值12万元的家用轿车。
按规定需缴纳10%的车辆购置税。
爸爸买这辆车共需花多少钱?7、7、李叔叔于2000年1月1日在银行存了活期储蓄1000元,如果每月的利率是0.165%,存款三个月时,可得到利息多少元?本金和利息一共多少元?8、叔叔今年存入银行10万元,定期二年,年利率4.50% ,二年后到期,扣除利息税5% ,得到的利息能买一台6000元的电脑吗?9、小华妈妈是一名光荣的中国共产党员,按党章规定,工资收入在400-600元的,每月党费应缴纳工资总额的0.5%,在600-800元的应缴纳1%,在800-1000元的,应缴纳1.5%,在1000以上的应缴纳2%,小华妈妈的工资为2400元,她这一年应缴纳党费多少元?10、常熟新开了一家永乐生活电器,“十•一”节日期间,那里的商品降价幅度很大。
小学六年级(小升初)数学总复习知识梳理+练习+答案-整数和小数的认识(部分有答案)
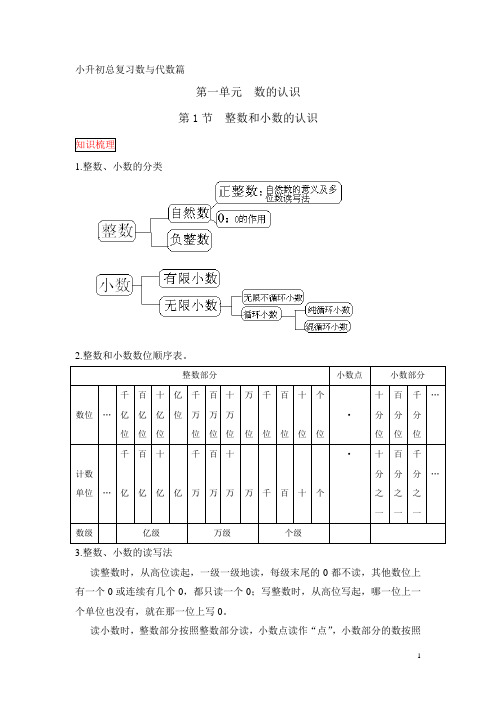
小升初总复习数与代数篇第一单元数的认识第1节整数和小数的认识知识梳理1.整数、小数的分类2.整数和小数数位顺序表。
整数部分小数点小数部分数位…千亿位百亿位十亿位亿位千万位百万位十万位万位千位百位十位个位·十分位百分位千分位…计数单位…千亿百亿十亿亿千万百万十万万千百十个·十分之一百分之一千分之一…数级亿级万级个级3.整数、小数的读写法读整数时,从高位读起,一级一级地读,每级末尾的0都不读,其他数位上有一个0或连续有几个0,都只读一个0;写整数时,从高位写起,哪一位上一个单位也没有,就在那一位上写0。
读小数时,整数部分按照整数部分读,小数点读作“点”,小数部分的数按照顺序依次读出每一位上的数;写小数时,整数部分按整数部分写,小数点写在个位右下角,然后依次写出小数部分每一个数位上的数字。
4.小数的基本性质: 在小数的末尾添上“0”或者去掉“0”,小数的大小不变。
5.大小比较:整数比大小,先看位数,位数多的数大;位数相同,从最高位看起,相同数位上的数大的那个数大;小数比大小,先比整数部分,整数部分大的这个数就大,整数部分相同的,比小数部分第一位,第一位大的这个数大,以此类推。
6.改写和省略把一个较大的数改写成以“万”或“亿”作单位,改写后的数是准确的数;把一个数根据需要省略某一位后面的尾数,省略后的数是一个近似数。
7. 小数点位置移动引起小数大小变化:小数点向右移动一位、两位、三位……原来的数就扩大到它的10倍、100倍、1000倍……反之,小数点向左移动一位、两位、三位……原来的数就缩小到它的101、1001、10001……【例1】阅读下面内容,回答问题。
2011年11月,在我国经济快速增长的拉动下,我国汽油生产总量为6899000吨,我国柴油生产总量为14132000吨,发电量达37130000万千瓦时。
(1)2011年11月我国汽油生产总量,读作:( )吨,改写成以“万吨”作单位的数是( )万吨。
小升初数学知识专项训练总复习六含解析

【解析】
思路分析:把一个长方形按3 : 1放大,长方形的长和宽各扩大了3倍,面积就扩大了原来的9倍。
名师详解:假设原来的长是a,原来的宽是b,原来的面积是a2,扩大后的长为3a,宽为3b,面积为9ab,放大后的长方形与原长方形面积的比是9ab:ab =9:1;因而选:D.
易错提示:学生们会认为放大后的新长方形与原长方形的面积比也是3:1,这样就错了。放大后的新长方形与原长方形的面积比是9:1,新的长方形的长与宽都扩大了3倍,所以面积比是9:1。
三、计算题
42.直接写出得数。
43.计算下列各题,怎样算简便就怎样算。
44.计算下面各题,能简便计算的要简便计算。
45.解方程或解比例
46.解方程。
47.解方程。
48.解方程。
49.求未知数x.
x﹣ =
x+ x=
x:2.1=0.4:0.9.
50.脱式计算。
四、判断题
51.假分数的倒数一定都是真分数。()
小升初总复习(6)
一、选择题
1.“合唱团里有男生43人,比女生人数的2倍多3人。合唱团的女生有多少人?”设该合唱团的女生有r人,下面的方程中,正确的是()。
A. (43-x)×2=3 B. 2x—43=3C. 2x-3=43D. 2x+3=43
2.小红和小刘合作完成一项工程,小红单独完成需要4小时,小刘单独完成需要5小时,两人合作需要( )小时完成这项工程。
5.【答案】B
【解析】
思路分析:本题考查图形面积的计算及分数平均分的知识。
名师详解:把长方形平均分成7份,阴影部分占前三份的一半,用七分之三乘二分之一,即可得解。因而选B。
易错提示:学生没有审清题会导致出错。注意的是,利用分数的意义和分数的乘法来解决问题,把问题分两步思考是解决此题的关键。
小升初小学数学总复习题

第一章 数的有关问题第一节 数位及数的表示1.在110~130这21个数中,将所有奇数的十位与个位之间加一个小数点;再将所有偶数的百 位与十位之间加一个小数点,经变换后的21个数之和是 .2.把一个两位数的个位数字与十位数字交换后得到一个新数,它与原数相减的差恰好等于两 个相同数的积(不为零),则满足以上条件的原两位数中最小的一个是 .3.一个三位数,各位数字分别为a 、b 、c ,它们互不相等,且都不为零.用a 、b 、c 共可排得 六个不同的三位数,其和为2442.则六个数中最大的一个是 .4.有一个四位数,在它的某位数字前加上一个小数点,再与这个四位数相加,得数是1997.7 8,这个四位数是___________.5.有一类小于200的自然数,每一个数的各位数字之和是奇数,而且都是两个两位数的乘积 (例如144=12×12).那么,这一类自然数中第三大的数是___________.6.三个连续奇数的积的个位数最小是___________.7.设A 和B 都是自然数,并且满足3317311=+B A ,那么A+B =___________.8.一个六位数,十万位上的数是一个质数,万位上的数是一个合数,千位上的数是万位上 数的2倍,百位上的数是十万位与千位上的数的平均数,十位上的数是个位上数的3倍,已知 这个六位数的各位数字之和是9的倍数,那么这个数是___________.9.甲乙两数的和是30,甲数的小数点向左移动一位后等于乙数的一半,那么甲数是 .10.从1978到2010的自然数中,恰在拐弯处的数是 .11.如图1,圆周上顺序排列着1,2,3,…,12这12个数,我们规定:相邻的四个数a 1,a 2,a 3,a 4,顺序颠倒为a 4,a 3,a 2,a 1称为一次“变换”(如1,2,3,4变 为4,3,2,1又如11,12,1,2变为2,1,12,11).能否经过有限次“变换”,将12个数 的顺序变为9,1,2,3,…8,10,11,12(如图2)?请说明理由.第二节 数的整除1.已知六位数□1995□能被45整除,则所有满足条件的六位数共有 个.2.如果六位数□□1994能被85整除,那么它的最后两位数是 .3.一个四位数能被两个连续的两位整数整除,这个四位数除以其中的一个,商是141;它除以另一个,商比141大.这个四位数是 .4.有四个数,每次选取其中三个数算出它们的平均数,再加上另外一个数,用这种方法计算了四次,分别得到以下四个数:86,92,100,106那么,原来四个数的平均数是 .5.某个七位数1993□□□能够同时被2,3,4,5,6,7,8,9整除,那么它的最后三位数字依次是 .6.修改五位数21847某一数位上的数字,可以得到737的倍数,那么修改后的数是 .7.如果两数的和是64,两数的积可以整除4875,那么这两数的差等于 .8.四个数的和是408,这四个数分别能被2、3、5、7整除,而且商相同.这四个数分别是 .9.下面一个1983位数43421个991333⋯⋯□43421个991444⋯⋯中间漏写了一个数字(方框),已知这个多位数能被7整除,那么中间方框内的数字是 .10.在29前面连续写上若干个1994,得到一个多位数19941994…199429.如果这个多位数可以被11整除,那么这个多位数的位数最少是 .11.从1~9这九个数字中选出八个数字,分别组成能被12整除的、无重复数字的最小八位数和最大八位数,则最小八位数是,最大八位数是 .12.在2002后面补上三个数字,组成一个七位数,使它分别能被2、3、5、11整除,这个七位数最小是___________.13.从一个三位数中,减去7,则能被7整除;减去8,则能被8整除;减去9,则能被9整除. 这个三位数是 .第三节余数问题1.1111+2×1111+3×1111+…+1111×1111被7除所得的余数是 .2.在所有的两位数中,用较大的自然数除以较小的自然数,得到的余数最大可以达到 .3.一个自然数被9除余1,所得的商被8除也余1.再把第2次所得的商除以8得商为a余7.又知这个自然数被17除余4,所得的商被17除余15,商是a的2倍,这个自然数是 .4.除以3余1,除以4,5,7不足2的三位数是 .5.用某自然数a去除2002,得到的商是46,余数是r.则a= ,r= .6.除以3余1,除以5余2,除以7余4的最小三位数是 .7.两数相除商5余5,如果被除数扩大5倍,除数不变,则商是27,余数是3,原被除数是,除数是 .8.7599除以一个质数,所得余数是9,这个质数最小是 .9.678除以一个数,不完全商是13,并且除数与余数的差是8,除数是,余数是 .10.一个三位数除以9余6,除以4余2,除以5余1,这样的数中最大的一个是 .11.某三位数的各位数字都不为零,并且这个三位数被它的各位数字之和除,所得的商最小可能是 .12.8.77÷5.3除到一位小数时,商是1.6,余数是___________.13.在下面算式的方框内填数,使带余数的除法的余数最大.□÷78=245…□14.一个数能被3、5、7整除,若用11去除则余1.这个数最小是 .15.某校五年级有学生若干人.(1)若3人一行最后余2人,7人一行最后余2人,11人一行最后也余2人,五年级最少有学生多少人?(2)若3人一行最后余1人,7人一行最后余5人,11人一行最后余9人,五年级最少有学生多少人?第四节约数与倍数1.A=2×5×7,B=2×3×7,A和B的最大公约数是,最小公倍数是 .2.三个连续整数的和是18,它们的最大公约数是,最小公倍数是 ___________.3.三个质数的最大公约数是1,最小公倍数是105,这三个质数是 .4.已知N为自然数,它是83的倍数,并且N2有63个因数,则N的最小值是 .5.三个互不相等的自然数,已知每个数均为2的倍数,每两个数的和均为3的倍数,而三个数的和为5的倍数,则这三个数的和最小是 .6.9的约数有1,3,9三个,16的约数有1,2,4,8,16五个,那么144(即9×16)的约数共有个.7.三个互不相同的自然数之和为370,它们的最小公倍数最小能够是 .8.有两个两位数的自然数,它们的最大公约数是8,最小公倍数是96,这两个自然数的和是 .9.a,b,c是100以内的三个整数,a与b,a与c的最大公约数分别是12和15,a,b,c的最小公倍数是120,那么,a,b,c分别是 .10.把一张正方形的纸剪成边长是5厘米的小正方形,比剪成边长为6厘米的小正方形多99个,两种剪法都没有余下一点纸片,原来这张正方形纸的面积是 .11.设n是一个四位数,它的9倍恰好是其反序数(例如:123的反序数是321).则n= .12.恰有6个约数的两位数有个.13.把26、33、34、35、63、85、91、143分成若干组,要求每一组中任意两个数最大公约数是1,那么至少要分多少组?14.庆祝“六一”节,学校扎了红花180朵,黄花234朵,白花360朵,把这些花扎成三色的花束.所有的花束里的红花朵数相同,黄花朵数相同,白花朵数也相同,至多扎几束花正好把花用完,每束中的红花、黄花、白花各几朵?15.从运动场一端到另一端全长96米,从一端起到另一端每隔4米插一面小红旗.现在要改成每隔6米插一面小红旗,问可以不必拔出来的小红旗有多少面?16.一盒围棋子,4只4只数多3只,6只6只数多5只,15只15只数多14只,这盒围棋子在150- 200只之间.问这盒围棋子有多少只?第五节 乘方与周期1.1×1+2×1×2+3×1×2×3+4×1×2×3×4+5×1×2×3×4×5+6×1×2×3×4×5×6+7× 1×2×3×4×5×6×7+8×1×2×3×4×5×6×7×8=___________.2.20012001×20022002的末位数的数字是___________.3.4434421个1887777⋯⋯⨯⨯⨯×444344421个199313131313⨯⋯⋯⨯⨯⨯积的尾数是___________.4.1219-811的个位数是___________.5.19491949的末位数是___________.6.把8,88,888,……,43421819928888个⋯⋯这1992个数相加,所得的个位数是 ,十位数是 ,百位数是 . 7.112=121,1112=1232111112=1234321 111112=123454321问:(1)11111112= . (2)12345678987654321=2 8.求44443444421个5585858585⨯⋯⋯⨯⨯⨯积的尾数. 9.1991个9与1990个8与1989个7的连乘积的个位数字是 .10.先观察下面每一行的数有什么规律,然后在括号内填上一个适当的数,使它符合这个 规律.(1)0,3,7,12, ,25,33,(2)1,4,7,10, ,16,19(3)2,6,18,54, ,486,1458(4)1,4,9,16,25, ,49,64(5)1,1,2,3,5,8, ,21,34, (6)2,3,5,8,12,17, ,30,38(7)1,4,13,40,121, ,11.因为:13=1×1×1=123=2×2×2=813+23=1+8=9(1+2)2=3×3=913+23+33=1+8+27=36 (1+2+3)2=6×6=3613+23+33+44=1+8+27+64=100(1+2+3+4)2=10×10=100……那么:13+23+33+…+993+1003=?12.把自然数按下图规则从1开始排列:第一行: 1第二行: 2,3,4第三行: 5,6,7,8,9第四行: 10,11,12,13,14,15……在第100行中有个数.13.把你的猜想填入括号里.(1)9×6=5499×96=9504999×996=9950049999×9996=99950004……43 421个n 999⋯⋯×43421个)1(999-⋯⋯n6=(2)9×7=6399×97=9603999×997=9960039999×9997=99960003……43 421个n 999⋯⋯×43421个)1(999-⋯⋯n7=(3)若设9×k=AB (其中k=1,2,3,…,9,AB=10A+B),则猜想有:43 421个n 999⋯⋯×43421个)1(999-⋯⋯nk=14.有数组:(1,1,1),(2,4,8),(3,9,27),…,求第100组的三个数之和是多少?15.四个小动物换位,开始小猪、小羊、小狗、小鹿分别坐在第1、2、3、4号位置上(如下图 ).第一次它们上、下两排换位,第二次左、右换位,第三次又上、下交换,第四次左、右交换.这样交替进行下去,问十次换座位后,小狗坐在第几号座位上?16.分析一下规律,再按照这个规律找出“?”所代表的数.17.根据每小题前两组图形中三个数的关系,填出后一组图形空圈中的数.18.左下图是由九个小人排列的方阵,但有一个小人没有到位,请你从下面的6个小人中,选 一位小人放到问号位置,你认为最合适的人选是 号.第六节 循环与近似1.把71化成小数后将小数点后面的第1001位四舍五入,那么第1000位是 .2.划去小数0.57383后面的若干个连续的数字后,再在最后一个数字上添上表示循环的小圆 点,得到的最大、最小的数分别是 .3.假定n 是一个自然数,d 是1~9中的一个数码,若296n =0.d05,则n = . 4.两个整数部分都是8的一位小数相乘,乘积用四舍五入法保留一位小数的近似值是68.1, 这两个数乘积的准确值是 .5.在一个循环小数0.123456*7中,如果要使这个循环小数第100位的数字是 5,那么表示循环节的另一个小圆点,应加在数字___________上.6.在循环小数0.*A B *C 中,已知小数点右边前1000位上各数 字之和为4664,且A ,B ,C 中有两个数是相等的,则A ,B ,C 分别是 .7.在混合循环小数2.71828*1的某一位上再添一个表示循环的圆点,使新产 生的循环小数尽可能大.请写出新的循环小数.8.循环小数1.100102**30,移动前一个循环的圆点,使新的循环小数 尽可能小,这个新的循环小数是___________.9.循环小数0.*1 99251*7与0.*3 4563*7.这两个循环小数在小数点后第 位,首次同时出现该 位上的数字都是7.10.分数139化成小数后,小数点后面第2001位上的数字是 . 11.0.012345670012345670001234567……(相邻的两个1234567之间0的个数按自然数列顺序 递增),这个无穷小数的小数点后的第1624位是多少?12.两个带小数相乘,乘积四舍五入以后是60.0,这两个数都只是一位小数,两个数的整数 部分都是7.这两个带小数的乘积四舍五入以前是___________.13.假定n 是一个自然数,d 是1~9中的一个数码,若444n =0.*5 d *7,则n=___________. 14.有一个小数为0.12345678912111213……998999,其中小数部分的数字由依次写下的整 数1~699得到的.问小数点右边第1995位数字是多少?15.冬冬在计算乘法2.4*3乘以一个数a 时,把2.4*3看成2.4 3,使乘积比正确结果减少0.5,则正确结果是( ).16.已知AB1=0.*C D *B ,其中A ,B ,C ,D 是0~9中的不同数字,则A ,B ,C ,D 分别为_________. 17.把74化成小数后,小数点后第一百零一位的数字是( ),若 把小数点的一百个数字相加,所得的和是( ).18.将72化为循环小数后,在小数点后面可找到一段数,使这段数的各 数字之和为2001.那么首次出现这一现象是从小数点后第 个数到第 个数.19.0.**54是纯循环小数,如果保留两位小数,取它的近似值是 .第七节 分数问题1.有甲、乙两个数,甲数的43等于乙数的125,甲数的52比乙数的121大45.甲数是 ,乙数是 .2.两个分数之和等于1147125,它们分子之比是5∶11,而分母之比是 3 ∶7,这两个分数分别是 .3.已知:A ×120%=43×B =C ÷203=D ÷121,把A ,B ,C ,D 四个数按从大到小的顺序排列起来. 4.有一个最简分数,把它的分子与分母都加上分母,所得到的新分数是原分数的3倍,这个 最简分数是 . 5.一个分数,如果分子加8,分母减10,它化简后的值等于43;如果分子减3,分母减10,它化简后的值就等于21,这个分数是 . 6.用285,5615,1201分别去除某分数,所得的商都是整数,这个分数最小是 . 7.用8063除或用14765乘后的结果都是自然数的最小分数是 . 8.有一种最简分数,它们的分子与分母的乘积都是140,如果把所有这样的分数从小到大排 列,那么第三个分数是 .9.一个分数,如果它的分子加上一个数,则等于21,如果它的分母减 去同一个数,则等于61,原来这个分数是 .10.131,1,1110,1513,1916,…是一串有规律的数,这串数中第9个数是 ,如果其中某个数的分母是1999,那么这个数的分子是___________.11.一个最简分数,分子与分母的和是62,若分子减去1,分母减去7,所得新分数约简后为 73,原分数是 . 12.有一个分数,分子比分母小13,若分子加上18,分母加上21,分数值不变,原分数是 .第二章 计算问题第一节 四则运算1.353×2345+5555÷25625+654.3×362. ⎝⎛⎪⎪⎭⎫⨯+⨯1992199185336.3199211÷953÷3433⎪⎭⎫ ⎝⎛÷+⨯+⨯⨯3125.2433325.0240034.0÷132+84.221+0.039÷[201×(2.31÷0.077)]-0.5265.[0.314÷15.7+(5-3.47)×632]÷104.2×416.18÷231+0.65×138-72×18+135×0.657.23.3×(2-75%)+56×141+(1+25%)×28.8.⎥⎦⎤⎢⎣⎡+÷-)522553(513×⎥⎦⎤⎢⎣⎡⨯-÷35)4110031(7.29.⎥⎦⎤⎢⎣⎡÷-⨯-100921420)2125(×3.2+0.24÷5110.157+⎥⎦⎤⎢⎣⎡-÷-)5324.6(76.01575×(3.625-385)11.1999×(5.22×1045+510023)÷(5.23×1045-5.22)12.41×(4.85÷85-3.6+6.15×353)+[5.5-1.75×(132+2119)]13.[10041×(85+0.375)-2.25×41]÷0.2514.6.25×6.6+3.3×641+1.1×625%15.24×(481-261)-0÷1÷0.314第二节简便算法 1.9998+998+99+9+62.627124894894123267-⨯⨯+3.4)7225.0()127321(32⨯+-+4.3100000111113100001111310001113100113101++++5.77151771417713177121⨯+⨯+⨯+⨯6.1-(8141-)-(16181-)-(321161-)-(641321-)7.98989898×99999999÷1010101÷111111118.125000125×444711+125000125×1364819.15131131111191971751⨯+⨯+⨯+⨯+⨯10.901721561421301201+++++11.1998×(20091111-)+11×(2009119981-)-2009×(19981111+)+312.(209594×1.65-202079594+×209594)×47.5×0.8×2.5+10÷513.421÷132+0.31×0.6+0.19×100114.2253×3207×585÷(3.35 ×5.625×2.12)15.2222001200120022002120022002+⨯-+-16.56789×9999917.119571956195719551956-⨯⨯+18.987654321×1235-987654322×123419.3194+461915×0.25+0.625×461915+461915×0.12520.(3.14×7.42+2.58×3.14)÷(3.25+3.14-341)21.73737310101×51122.(9.79×475+375×498)×( 385-1÷298)23.1-20000120001*********----24.(3.91+373+6.09+674)×(281-1.125)+(1÷32-1.5)×61514 25.943+9943+99943+999943+126.9999×2222+3333×333427.%)41()4811216131(%)361()321161814121(-⨯----⨯++++28.1993×199.2-1992×199.1第三节 分数的拆分1.在下列等式的括号里填适当的数.(分母不能重复)(1)185=)(1)(1 + (2)3625=)(1 +)(1 +)(1 +)(1 (3)152=)(1 +)(1 +)(1 (4)201= )(1 +)(1 +)(1 +)(1 +)(1 2.计算题: (1)94×56.87+94×43.48+6×100.35(2)8-32-255219521432992632352152------(3)4171411414111121181108516521⨯+⨯+⨯+⨯+⨯(4)(12-2110×2)+(10-2110×8)+(8-2110×4)+(6-2110×12)+(2-2110×6)+(4-2110×10)(5)54321⨯⨯⨯+65431⨯⨯⨯+76541⨯⨯⨯ +…+15141321⨯⨯⨯+161514131⨯⨯⨯(6)5311⨯⨯+7531⨯⨯+9751⨯⨯+11971⨯⨯+131191⨯⨯+1513111⨯⨯(7)(1-31)×(1-51)×(1-71) ×(1-91)×(1-111)×(1-131)×(1-15)(8)1514131211413121111312111015432243211⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⋯+⨯⨯⨯+⨯⨯⨯(9)100991535215251151501⨯+⋯+⨯+⨯+⨯(10)1332213318133171331611715117511741173-⋯----+⋯+++(11)1992+21-131+221-331+421-531+…+199021-199131(12)( 21-41)+(41-61)+(61-81)+…+(481-501)(13)(1+9219)+(1+9219×2)+(1+9219×3)+…+(1+9219×10)+(1+9219×11)(14)1263842421729348622431⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯(15)121×131×141×151×…×11001(16)215⨯+545435325⨯+⨯+⨯+…+5049549485⨯+⨯(17)121+261+3121+4201+…+204201(18)(1+337)+(1+337×2)+(1+337×3)+…+(1+337×10)+(1+337×11)(19)(1-221⨯)×(1-331⨯)×…×(1-10101⨯)(20)12017111171419141117118158513521⨯+⨯+⨯+⨯+⨯+⨯(21)(41998499×4.8+454×519981499)÷565÷274第四节 其他简算方法 计算题1.1+2+3+…+1989+19902.(1+3+5+...+1989)-(2+4+6+ (1988)3.1992-1988+1984-1980+1976-1972+……+8-44.1-3+5-7+9-11+…-1999+20015.1.725+2.725+3.725+…+60.7256.(23114332541+++)×(4-109)7.40556+8074+9444+926+110008.(413121++ +…+301)+(32+42+…+302)+(43+53+63+…+303)+…+(2928+3028)+30299.2523119724221086++⋯+++++⋯+++10.302-292+28+-272+…+42-32+22+1211.1+211++3211+++43211++++ …+1003211+⋯+++ 12.(766554433221+++++)2+(766554433221+++++)×21-(1+21+32+43+54+65+76)×(7665544332++++)13.1+272185617421630152014121361++++++14.32191998999个⋯×32191998999个⋯+32191998999个⋯15.1081861641421⨯+⨯+⨯+⨯+…+100981⨯16.1+2-3-4+5+6-7-8+9+10-11-12+…+1982-1983-1984+1985+1986-1987-1988+1989+199017.1992+1991-1990-1989+1988+1987-1986-1985+…+4+3-2-118.1992-1989+1986-1983+…+12-9+6-319.10×3210100010个⋯=3210101010个⋯1.0961.01.01.0011.0个÷⋯÷÷÷÷=?第五节 繁分数化简化简 1.737373737325252525252.49÷777777723.2542169334.9332236351233591725102531168⨯÷⨯÷⨯5.2141312114++++6.201)3135.0(625.4)43375.0611(5.286331)738.0()4332(311÷--÷+-+÷+÷+-7.25.0)76.324.12()03.283.2(75.0)6.24.3()6.24.13(÷+⨯-÷-⨯+ 8.15050110331102211011110019914131211++⋯++++++-+⋯+-+-9.78.967.856.745.634.523.4?2.3789678567456345234123++++++++++++10.451553612427938623912010516481263842421⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯+⨯+⨯⨯+⨯⨯+⨯⨯11.66666666666612345654321⨯++++++++++12.361383948330⨯-⨯13.)3143(215.1)3143(2131-⨯⨯⎥⎦⎤⎢⎣⎡-⨯+。
【数学】小升初总复习数学归类讲解及训练(含答案)

小学数学总复习专题讲解及训练模拟试题一、圆柱体积1、求下面各圆柱的体积。
(1)底面积0.6平方米,高0.5米(2)底面半径是3厘米,高是5厘米。
(3)底面直径是8米,高是10米。
(4)底面周长是25.12分米,高是2分米。
2、有两个底面积相等的圆柱,第一个圆柱的高是第二个圆柱的4/7。
第一个圆柱的体积是24立方厘米,第二个圆柱的的体积比第一个圆柱多多少立方厘米?3、在直径0.8米的水管中,水流速度是每秒2米,那么1分钟流过的水有多少立方米?4、牙膏出口处直径为5毫米,小红每次刷牙都挤出1厘米长的牙膏。
这支牙膏可用36次。
该品牌牙膏推出的新包装只是将出口处直径改为6毫米,小红还是按习惯每次挤出1厘米长的牙膏。
这样,这一支牙膏只能用多少次?5、一根圆柱形钢材,截下1.5米,量得它的横截面的直径是4厘米。
如果每立方厘米钢重7.8克,截下的这段钢材重多少千克?(得数保留整千克数。
)6、把一个棱长6分米的正方体木块,削成一个最大的一圆柱体,这个圆柱的体积是多少立方分米?7、右图是一个圆柱体,如果把它的高截短3厘米,它的表面积减少94.2平方厘米。
这个圆柱体积减少多少立方厘米?二、圆锥体积1、选择题。
(1)一个圆锥体的体积是a 立方米,和它等底等高的圆柱体体积是()①31a 立方米②3a 立方米③9立方米(2)把一段圆钢切削成一个最大的圆锥体,圆柱体体积是6立方米,圆锥体体积是()立方米①6立方米②3立方米③2立方米2、判断对错。
(1)圆柱的体积相当于圆锥体积的3倍………()(2)一个圆柱体木料,把它加工成最大的圆锥体,削去的部分的体积和圆锥的体积比是2:1………()(3)一个圆柱和圆锥等底等高,体积相差21立方厘米,圆锥的体积是7立方厘米………()3、填空(1)一个圆柱体积是18立方厘米,与它等底等高的圆锥的体积是()立方厘米。
(2)一个圆锥的体积是18立方厘米,与它等底等高的圆柱的体积是()立方厘米。
(3)一个圆柱与和它等底等高的圆锥的体积和是144立方厘米。
小升初数学总复习题库

小升初数学总复习题库数学是小升初考试中的重要科目之一,为了帮助学生更好地复习数学知识,提高解题能力,以下是一些精选的数学复习题,涵盖了小学数学的主要知识点。
一、基础运算1. 计算下列各题:- 56 × 78- 1234 - 2345- 0.75 + 1.25- 3.14 × 2.52. 完成以下分数的加减法:- 1/4 + 3/8- 5/6 - 2/3二、分数和小数1. 将下列分数化为最简形式:- 8/12- 15/302. 将下列小数转换为分数,并化简:- 0.75- 0.333...三、比例和比例尺1. 如果一个比例尺是1:500,那么在地图上1厘米代表实际地面上的多少米?2. 已知比例为3:4,如果一个数是比例中的3部分,求4部分对应的数值。
四、几何图形1. 一个长方形的长是15厘米,宽是10厘米,求其周长和面积。
2. 一个圆的半径是7厘米,求其周长和面积。
五、应用题1. 小明买了3个苹果和2个橙子,苹果每斤10元,橙子每斤8元,小明一共花了多少钱?2. 一个班级有48名学生,其中女生占3/5,求女生和男生各有多少人?六、百分数1. 一个商品原价100元,打8折后的价格是多少?2. 一个班级有50名学生,其中80%的学生通过了考试,求通过考试的学生人数。
七、方程和不等式1. 解方程:3x + 5 = 232. 解不等式:2x - 7 < 9八、数据的收集与处理1. 一个班级有30名学生,他们的数学成绩分别为:85, 90, 78, 82, 88, 92, 76, 84, 95, 80, 81, 83, 79, 91, 87, 93, 86, 75, 77, 94, 89, 74, 96。
求这组数据的平均分和中位数。
2. 根据上述数据,绘制频数分布直方图。
九、逻辑推理1. 一个班级有5个学生,他们的数学成绩分别是:A, B, C, D, E。
已知B的成绩高于A,C的成绩高于D,E的成绩最高。
小升初数学总复习分类专题复习及训练(含答案)

小升初数学总复习分类专题复习及训练(一)主要内容求一个数比另一个数多(少)百分之几、纳税问题学习目标1、使学生在现实情境中,理解并掌握“求一个数比另一个数多(少)百分之几”的基本思考方法,并能正确解决相关的实际问题。
2、使学生在探索“求一个数比另一个数多(少)百分之几”方法的过程中,进一步加深对百分数的理解,体会百分数与日常生活的密切联系,增强自主探索和合作交流的意识,提高分析问题和解决问题的能力。
3、使学生初步认识纳税和税率,理解和掌握应纳税额的计算方法。
4、初步培养学生的纳税意识,继续感知数学就在身边,提高知识的应用能力。
5、培养和解决简单的实际问题的能力,体会生活中处处有数学。
考点分析1、一个数比另一个数多(少)百分之几 = 一个数比另一个数多(少)的量÷另一个数。
2、应该缴纳的税款叫做应纳税额,应纳税额与各种收入的比率叫做税率,应纳税额 = 收入×税率典型例题例1、(解决“求一个数比另一个数多百分之几”的实际问题)向阳客车厂原计划生产客车5000辆,实际生产5500辆。
实际比计划多生产百分之几?分析与解:要求“实际比计划多生产百分之几”,就是求实际比计划多生产的辆数占计划产量的百分之几,把原计划产量看作单位“1”。
两者之间的关系可用线段图表示。
计划产量5000辆实际比计划多的实际产量5500辆解答:方法1:5500 – 5000 = 500(辆)……实际比计划多生产500辆500 ÷ 5000 = 0.1 = 10%……实际比计划多生产百分之几方法2:5500 ÷ 5000 = 110%……实际产量相当于原计划的110%110% - 100% = 10%……实际比计划多生产百分之几答:实际比计划多生产10%。
例2、(解决“求一个数比另一个数少百分之几”的实际问题)向阳客车厂原计划生产客车5000辆,实际生产5500辆。
计划比实际少生产百分之几?分析与解:要求“计划比实际少生产百分之几”,就是求计划比实际少生产的辆数占实际产量的百分之几,把实际产量看作单位“1”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章数与代数第一节数的认识一、基础知识(一)整数:1.整数的读法和写法例:“3121700”读作:三百一十二万一千七百2.整数的近似数“四舍五入”3.整数的运算加法:减法:乘法:除法:四则混合运算:4.自然数:5.数的整除:①整数a除以整数b(b≠0),除得的商是整数而没有余数,我们就说a能被b整除,或者说b能整除a。
②如果数a能被数b(b≠0)整除,a就叫做b的倍数,b就叫做a的约数(或a的因数)。
倍数和约数是相互依存的。
③个位上是0、2、4、6、8的数,都能被2整除。
个位上是0或5的数,都能被5整除。
一个数的各位上的数的和能被3整除,这个数就能被3整除。
一个数各位数上的和能被9整除,这个数就能被9整除。
能被3整除的数不一定能被9整除,但是能被9整除的数一定能被3整除。
一个数的末两位数能被4(或25)整除,这个数就能被4(或25)整除一个数的末三位数能被8(或125)整除,这个数就能被8(或125)整除。
④偶数、奇数⑤一个数,如果只有1和它本身两个约数,这样的数叫做质数(或素数)⑥一个数,如果除了1和它本身还有别的约数,这样的数叫做合数。
注意:1不是质数也不是合数,自然数除了1外,不是质数就是合数。
⑦每个合数都可以写成几个质数相乘的形式。
其中每个质数都是这个合数的因数,叫做这个合数的质因数。
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
⑧几个数公有的约数,叫做这几个数的公约数。
其中最大的一个,叫做这几个数的最大公约数。
⑨公约数只有1的两个数,叫做互质数,成互质关系的两个数,有下列几种情况:1和任何自然数互质;相邻的两个自然数互质;两个不同的质数互质。
当合数不是质数的倍数时,这个合数和这个质数互质。
⑩几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数。
(二)小数:1.小数的读法和写法:2.小数的分类:①纯小数、带小数②有限小数:小数部分的数位是有限的小数,叫做有限小数;无限小数:小数部分的数位是无限的小数,叫做无限小数。
③无限不循环小数:一个数的小数部分,数字排列无规律且位数无限.循环小数:一个数的小数部分,有一个数字或者几个数字依次不断重复出现,这个数叫做循环小数。
(三)分数:1.分数的意义①把单位“1”平均分成若干份,表示这样的一份或者几份的数叫做分数。
②在分数里,中间的横线叫做分数线;分数线下面的数,叫做分母,表示把单位“1”平均分成多少份;分数线下面的数叫做分子,表示有这样的多少份。
③把单位“1”平均分成若干份,表示其中的一份的数,叫做分数单位。
2.分数的分类①真分数:②假分数:③带分数:3.约分和通分①把一个分数化成同它相等但是分子、分母都比较小的分数,叫做约分。
②分子分母是互质数的分数,叫做最简分数。
③把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
4.百分数①表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。
②百分数通常用"%"来表示。
百分号是表示百分数的符号。
(四)常见的量1.时间2.长度3.面积4.体积5.容积6.质量二、能力训练1.一个九位数,最高位是是奇数中最小的合数,百万位上是最小的质数,万位上是最大的一位数,千位上是同时能被2和3整除的一位数,百位上是最小的合数,其余各位上都是最小的自然数,这个数写作________________,读作________________。
2.三个连续奇数的和是645。
这三个奇数中,最小的奇数是________________。
3.在一条长50米的大路两旁,每隔5米栽一棵树(两端都要栽),一共可栽___________棵树。
4.被减数减去减数,差是0.4,被减数、减数与差的和是2,减数是____________。
5.两个数的积是45.6,一个因数扩大100倍,另一个因数缩小到原来的101,积是____________。
6.74的分数单位是____________,它含有____________个这样的单位,它的倒数是____________。
7.73的分子加上12,要使分数的大小不变,分母应加上____________。
8.一个三位小数,保留两位小数取近似值后是 5.60,这个三位小数最小是____________,最大是____________。
9.5是8的____________%,8是5的____________%,5比8少____________%,8比5多____________%。
10.自然数按因数的个数分,可以分为( ).A.奇数和偶数B.素数和合数C.奇数、偶数和1D.素数、合数、0和111.已知a+b=5,(a 、b 均为自然数),则a 和b 两个数的最大公因数是( )。
A.5B.bC.aD.112.分数单位是1/11的最大真分数和最小假分数的和是( )。
A .21/11 B.2 C.20/11 D.113.下面各组数,一定不能成为互质数的一组是( )。
A.质数与合数B.奇数与偶数C.质数与质数D.偶数与偶数14.把210分解质因数是( )。
A.210=2×7×3×5×1B.210=2×5×21C.210=3×5×2×7D.210=2×5×21×115.两个奇数的和( )。
A.是奇数B.是偶数C.可能是奇数,也可能是偶数D.一定不是奇数16.一个合数至少有( )个约数。
A.1B.2C.3D.417.有4、5、7、8这四个数,能组成( )组互质数。
A.3B.4C.5D.618.四位数“3AA1”是9的倍数,则A=________。
19.能同时被2,3,5整除的最大三位数是_______。
20.所有能被3整除的两位数的和是________。
三、拓展提高1.在10以内任意选两个不同的素数,就可以写一个分数,其中最小的是____________。
2.如果A和B是自然数,并且A÷B=5.那么A和B的最小公倍数是____________,5是____________的因数。
3.两个素数的和是31,这两个素数的积是____________。
4.将循环小数3.102和0.215转换成分数。
5.有三十个数:1.64,1.64+130,1.64+230,……,1.64+2830,1.64+2930,如果取每个数的整数部分(例如:1.64的整数部分是1,1.64+1130的整数部分是2)。
并且将这些的整数相加,那么它们的和是多少?6.设一个五位数abcad,其中d-b=3,若这个数能被11整除,则a的范围是_________,c=_____。
7.能同时被2,5,7整除的最大五位数是_________。
8.六位数X2010Y能被88整除,则X、Y的取值分别为多少?A.X=9,Y=4B.X=7,Y=4C.X=9,Y=8D.X=8,Y=49.有一大筐苹果和梨分成若干堆,如果你一定可以找到这样的两堆,其苹果数之和与梨数之和都是偶数,最少要把这些苹果和梨分成_______堆。
10.有两个容器,一个容量为27升,一个容量为15升,如何利用他们从一桶油中倒出6升油来?第二节比与比例一、基础知识1.比的意义和性质(1)比的意义:两个数相除又叫做两个数的比。
①“:”是比号,读作“比”。
比号前面的数叫做比的前项,比号后面的数叫做比的后项(比的后项不能是零)。
比的前项除以后项所得的商,叫做比值。
②同除法比较,比的前项相当于被除数,后项相当于除数,比值相当于商。
③比值通常用分数表示,也可以用小数表示,有时也可能是整数。
④根据分数与除法的关系,可知比的前项相当于分子,后项相当于分母,比值相当于分数值。
(2)比的性质:比的前项和后项同时乘上或者除以相同的数(0除外),比值不变,这叫做比的基本性质。
(3)求比值和化简比①求比值的方法:用比的前项除以后项,它的结果是一个数值可以是整数,也可以是小数或分数。
②根据比的基本性质可以把比化成最简单的整数比。
它的结果必须是一个最简比,即前、后项是互质的数。
(4)比例尺①数值比例尺:图上距离:实际距离=比例尺②线段比例尺:在图上附有一条注有数目的线段,用来表示和地面上相对应的实际距离。
2.比例的意义和性质(1)比例的意义表示两个比相等的式子叫做比例。
组成比例的四个数,叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
(2)比例的性质在比例里,两个外项的积等于两个两个内向的积。
这叫做比例的基本性质。
(3)解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个数比例中的另外一个未知项。
求比例中的未知项,叫做解比例。
3.正比例和反比例(1)成正比例的量两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。
用字母表示y/x=k(一定)(2)成反比例的量两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,他们的关系叫做反比例关系。
用字母表示x×y=k(一定)二、能力训练1.在比例中,两个内项的积是6,其中一个外项是23,另一个外项__________。
2.如果y=5x,那么x和y成__________比例。
3.一幅地图上用5厘米表示实际距离20千米,这幅地图的比例尺是__________。
4.1.2千克∶250克化成最简整数比是__________,比值是__________。
5.一个三个角形三个内角度数的比是1∶4∶1,这是一个__________三角形。
6.如果7x=8y,那么x∶y=__________。
7.男生人数比女生多20%,则女生人数与男生人数的比是__________,女生比男生少__________。
8.已知甲数的1/6相当于乙数的1/5,那么甲数的一半相当于乙数的__________。
9.把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量.()A.成正比例B.成反比例C.不成比例10.和一定,加数和另一个加数.()A.成正比例B.成反比例C.不成比例11.在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成正比例关系是(),成反比例关系是().A.汽车每次运货吨数一定,运货次数和运货总吨数.B.汽车运货次数一定,每次运货的吨数和运货总吨数.C.汽车运货总吨数一定,每次运货的吨数和运货的次数.三、拓展提高1.把280棵树苗栽在两块长方形地上,一块长15米,宽8米;另一块长12米,宽4米,如按面积大小分配栽种,这两块地分别要栽多少棵?2.配制一种农药,其中药与水的比为1∶150。
